Abstract
An accurate and spatially continuous estimation of terrestrial latent heat flux (LE) is crucial to the management and planning of water resources for arid and semi-arid areas, for which LE estimations from different satellite sensors unfortunately often contain data gaps and are inconsistent. Many integration approaches have been implemented to overcome these limitations; however, most suffer from either the persistent bias of relying on datasets at only one resolution or the spatiotemporal inconsistency of LE products. In this study, we exhibit an integration case in the midstream of the Heihe River Basin of northwest China by using a multi-resolution Kalman filter (MKF) method to develop continuous and consistent LE maps from satellite LE datasets across different resolutions. The Moderate Resolution Imaging Spectroradiometer (MODIS) LE product (MOD16), the Landsat-based LE product derived from the Landsat 7 Enhanced Thematic Mapper Plus (ETM+) sensor, and ground observations of eddy covariance flux tower from June to September 2012 are used. The integrated results illustrate that data gaps of MOD16 dropped to less than 0.4% from the original 27–52%, and the root-mean-square error (RMSE) between the LE products decreased by 50.7% on average. Our findings indicate that the MKF method has excellent capacity to fill data gaps, reduce uncertainty, and improve the consistency of multiple LE datasets at different resolutions.
1. Introduction
Terrestrial latent heat flux (LE) describes the heat flux of transpiration and evaporation from the land surface to the atmosphere and plays an indispensable role in understanding the global energy balance and water cycle [1,2]. In arid and semi-arid areas, such as large portions of China, LE represents more than 70% of the annual water balance [3]. The reliable acquisition of LE is conducive to advancing a wide variety of scientific explorations and societal fields, including, but not limited to, climate forecasting [4], sustainable agriculture development [5,6], and the management of basin water resources [7,8], especially for those arid and semi-arid areas.
LE is difficult to measure and predict, however, particularly over regional-to-global scales [9,10]. With the rapid development of new technologies during the past several decades, estimating LE via satellite remote sensing provides an unprecedented opportunity to acquire temporally and spatially continuous LE data at regional-to-global scales [11]. Although there are a large amount of remotely sensed LE products available with different resolutions, uncertainties still remain among the individual LE products due to the error of algorithm inputs, the differences of model mechanisms, physical parameterization, and scaling effects [12,13]. For instance, the Moderate Resolution Imaging Spectroradiometer (MODIS) LE product (MOD16) has been substantially applied because it can cover the global land surface with moderate spatial resolution (1 km/500 m) and high temporal resolution (8 days) [14]. In relatively dry environments, however, MOD16 exhibits large uncertainty due to inadequate description of the soil moisture and the inconsistency between the meteorological inputs (e.g., average and minimum air temperature, incident photosynthetically active radiation, specific humidity) and the MODIS images [15]. In addition, some remotely sensed LE products fail to deal appropriately with complicated surface heterogeneity characteristics and the diversity of landscape types, and hence, there are data gaps in current LE products. For instance, arid and semi-arid regions with large barren or sparsely vegetated areas are often excluded from MOD16. Xiong et al. (2015) reported 70% missing data in the MOD16 of the Heihe River Basin (HRB) [16], which is situated in one of the most hydrologically vulnerable areas in the arid and semi-arid regions of northwest China [17,18]. Currently, the water scarcity conflicts with user needs, and the issue has become increasingly intense due to the increasing use of irrigation water for the midstream in the HRB [19]. To resolve the intense conflict, the first step is to better quantify water budgets at the field scale through accurate and high spatiotemporal resolution estimates of land surface LE [20]. Unfortunately, the data gaps stated above limit the comprehensive understanding of regional water budgets over these areas.
To overcome these limitations, many data fusion methods have been proposed to improve accuracy and spatiotemporal consistencies of LE data by integrating multiple products. Two major types of data integration are being used. The first integrates the input parameters and then estimates LE. Ma et al. [18] merged the input parameters (e.g., normalized difference vegetation index, leaf rea index, fractional vegetation cover, emissivity, land surface temperature) for estimating LE using the enhanced spatial and temporal adaptive reflectance fusion model (ESTARFM) and then estimated daily LE for the middle reaches of the HRB. Yet, great complexity and potential uncertainties of the inputs hinder such an integration type and its universal applicability. The other type directly integrates LE products building on various methods. For instance, Yao et al. [21] merged five LE products using the Bayesian model averaging (BMA) method and improved the accuracy of global LE estimates comparing with ground observations from over 300 flux sites. Feng et al. [22] integrated the MOD16 and the Priestley–Taylor Jet Propulsion Laboratory (PT-JPL) model [23] using an empirical orthogonal function (EOF) method. The integrated LE product showed a lowest bias of 3.67 W/m2 and highest R2 of 0.84 through the validation of 22 eddy covariance (EC) sites, compared with original datasets. However, these methods are generally used at the same spatial resolutions, and the scaling issues across different resolutions are rarely considered.
Recently, a multi-resolution Kalman filter (MKF) method has been explored to take advantage of multi-resolution data and to fill data gaps, by assuming a linear tree structure that is autoregressive in levels of resolution [24]. One of the MKF method’s strengths lies in the integration of multiple variables across different resolutions. For instance, He et al. [25] integrated three Albedo products with multi-resolution, and the results showed that the data gaps were significantly filled based on the supporting data from other scales. Wang et al. [26] compared the MKF method with the optimal interpolation (OI) method when integrating leaf area index (LAI) products and found that the computation efficiency of the MKF method is also high, and significantly meets the requirements of large satellite-based datasets. Although the MKF method has been substantially carried out over high-level satellite products, the advantages of this method have not been applied to resolving LE data gaps, which requires further exploration, especially in arid and semi-arid areas.
Herein, given the immense data gaps of the MOD16 in arid and semi-arid areas, we integrated two satellite-based LE products (the MOD16 and Landsat-based LE products) using the MKF method, and generated spatially and temporally consistent LE products across different resolutions. The objectives of this study are: (1) to integrate the MOD16 and Landsat-based LE products using the MKF method; and (2) to assess the performance of the MKF method, including the magnitude of remaining data gaps and the accuracy of the two LE products after the integration.
2. Study Area and Data
2.1. Study Area and Ground Observations
The Heihe River Basin (HRB), located at 97°24′–102°10′E and 37°41′–42°42′N, covers approximately 143,600 km2 in the arid region of northwestern China [19,27].
The study area is situated in the midstream of the HRB (Figure 1), which is characterized by annual air temperature of 7.3 °C (1971–2000) and annual precipitation of 130.4 mm [28]. The land cover types follow the classification from Internation Geosphere–Biosphere Program (IGBP) and consist of barren and sparsely vegetated, cropland, grassland, urban and built-up, deciduous broadleaf forest, evergreen needleleaf forest, and water body. The main crops, including maize, wheat, and vegetables, are distributed along the irrigated region in the midstream.
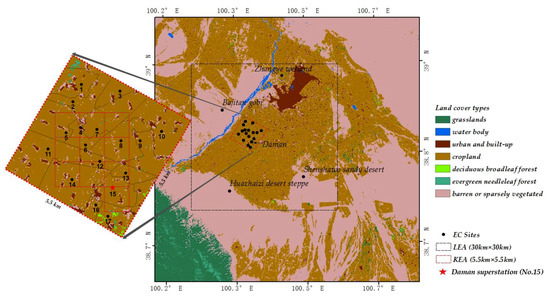
Figure 1.
Land cover types (IGBP classification) of the study area and the location of EC sites. LEA: large experimental area, KEA: kernel experimental area.
To better understand how LE interacts under the heterogeneity of land surfaces across multiple spatial resolutions [29], the “Multi-Scale Observation Experiment on Evapotranspiration over heterogeneous land surfaces 2012” (HiWATER-MUSOEXE) thematic experiment was conducted in the middle reaches of the HRB from May to September 2012, involving a flux observation matrix that was composed of two nested matrices [30,31]. One was a 30 km × 30 km large experimental area (LEA) in an oasis-desert area, and the other was a 5 km × 5 km kernel experimental area (KEA) inside the oasis (Figure 3, left). As shown in Table 1, the LEA included one superstation (Daman) and four regular stations (Zhangye wetland, Shenshawo sandy desert, Huazhaizi desert steppe and Bajitan Gobi). The KEA, which was within the LEA, contained 17 stations.

Table 1.
Summary of EC Sites in the midstream of the Heihe River Basin [11].
To obtain the daily LE, half-hourly LE measured by the EC instruments was calculated, and the energy non-closure problem was fixed using the Bowen ratio closure method developed by Twine et al. (2000) [32]. Technical details of the data processing procedure can be found in Liu et al. (2013, 2018) [33,34].
2.2. Remotely Sensed Data
2.2.1. MODIS LE Product
The MODIS LE product (MOD16) was modified and updated by Mu et al. [35,36] from the Penman–Monteith equation [37] adapted by Cleugh et al. [38]. The MOD16 algorithm logic separates daytime and nighttime LE, divides canopy and soil into wet and dry components, and modifies the vegetation cover with the fraction of absorbed photosynthetically active radiation. The latest version 6 of MOD16 was released in 2017 and is an eight-day composite product at 500 m pixel resolution [39]. Since MOD16 uses a sinusoidal tiling system, a reprojection was carried out onto the Universal Transverse Mercator (UTM) projection to match with the Landsat scenes using the MODIS Reprojection Tool. MODIS tile h25v05 for 2012 covering the study area was selected as the input.
2.2.2. Landsat-Based LE Product
The Landsat L1T data from the Landsat7 Enhanced Thematic Mapper Plus (ETM+) sensor are geometrically and radiometrically calibrated and projected under the UTM coordinate system, with a pixel size of 30 m × 30 m taken over a period of 16 days. We acquired these data from the United States Geological Survey for the period of June to September 2012 with p133r33 scenes. The Landsat ecosystem disturbance adaptive processing system (LEDAPS) tool [40] was employed to remove the radiation error. LEDAPS outputs may include some possible residual cloud and shadow pixels; hence, to match with the ground observations and reduce the risk of undetected pixel contamination, only Landsat scenes with less than 30% cloud coverage were exploited in this study.
We produced the Landsat-based LE product using the modified satellite-based Priestley–Taylor (MS–PT) algorithm [41]. This was developed on the basis of the Priestley–Taylor model and exhibits great agreement with the field-measured LE from 16 EC flux towers in China. Constrained by the normalized difference vegetation index (NDVI) and apparent thermal inertia (ATI), it avoids the computational complexities of aerodynamic resistance parameters. The inputs of the MS–PT algorithm only require NDVI, the air temperature (Ta), the diurnal air temperature range (DT) for ATI, and the net radiation (Rn). We calculated NDVI from the Landsat data and obtained Ta, DT, and Rn from the China Meteorological Forcing Dataset [42,43], which integrates multiple surface meteorological and environmental data sources with a spatiotemporal resolution of 0.1° and 3 h. To take full use of this meteorological reanalysis dataset, we applied the daily gridded data in 2012 based on the previous work of Zhang et al. [44]. Appendix B provides detailed descriptions of the MS–PT algorithm.
3. Methodology
3.1. The MKF Method
The data at different spatial resolutions were organized in an autoregressive tree structure (Figure 2). All the grids covered the same area but each level of the tree served the a different resolution [45]. Each node s had a “parent” pa(s) and “children” ch(s). The scale that only consisted of one pixel was the “root” node. There are two models required in the MKF method: (1) state conversion model and (2) measurement model.
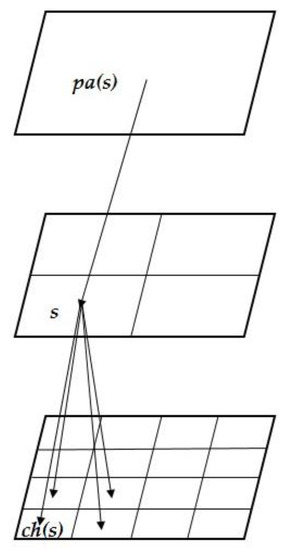
Figure 2.
Multi-resolution Kalman filter (MKF) data structure [25].
Firstly, the state conversion model represents how the multiscale stochastic process converts from coarse scale to fine scale and can be expressed using Ref. [46]
where ys is the estimated value at the scale s, and ypa(s) is the variable at the parent node. As estimates the state transition from the parent to children. Ws controls the scale variability and follows a normal distribution N (0, Q(s)). Accordingly, there is an equation describing the variable at node s from its children node ch(s) [47].
Secondly, the measurement model links the satellite measurement to the “true” data:
where zs is the measurement variable at node s with white noise which has a normal distribution N (0, R(s)). Cs is a measurement matrix and is set to the identity matrix because both satellite measurement and the variable are LE and cover the same area in this study.
The state conversion model of Equation (1) and the measurement model of Equation (2) form the general framework of the MKF method. Chou et al. [48] extended a tree-like data structure to describe this algorithm. The multiresolution variables are computed from a fine-to-coarse sweep first, in which estimates are recursively propagated from the fine scale to the next coarser scale, and then a coarse-to-fine sweep, which implements from the root scale to the finest scale. The fine-to-coarse sweep is ascending to fill in the data gaps at each scale from the finer variables. The descending coarse-to-fine sweep integrates both fine and coarse variables and updates information at each scale. A technical description of the MKF method is given in Appendix A.
Our study requires several steps to implement the integration using the MKF method (Figure 3). First, the LE products are compared against the LE measured by the eddy covariance (EC) method to evaluate the uncertainties. Second, a basic assumption of the MKF method is zero-mean in the spatial process of each variable, and thereby it is required to extract the trend surface of the LE products. Building on the detrended LE data, we obtain the observation error at the finest scale using the standard deviation of the relative difference between the finest data and the ground observations derived from the HiWATER-MUSOEXE thematic experiment. For the observation error at other scales, we estimate the relative difference between the current nodes and the aggregated data from their children nodes. The errors were postulated to be invariant to time and location in the study area to simplify the problem. Third, starting from the finest scale, the fine-to-coarse sweep is implemented to fill all data gaps at each scale. When proceeding to the root node, the descending coarse-to-fine sweep is applied to update the variables into the optimal estimation at each scale. Landsat-based LE product serves at the finest scale, and MOD16 is in the middle of the tree structure in this study. Finally, we add the trend surface back to the optimal estimation, and then two LE products can be smoothed and consistent at different resolutions.
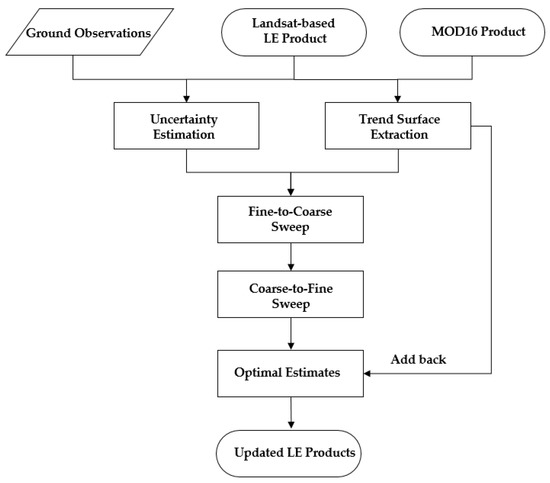
Figure 3.
The framework of LE data integration using the MKF method.
3.2. Assessment Metrics
The performance of the MKF method is assessed with three criteria for quantification in this study: Bias, the root-mean-square error (RMSE), and the relative RMSE in percentage terms (RMSE %). The bias describes the mean difference between the observed values and the estimated values. The RMSE reflects how reliable the model is; the larger the RMSE, the lower the model performance. The RMSE % provides the relative error of the model and is sensitive to outliers. These criteria are given by
where Xobs and Xest describe the observed values and estimated values, respectively.
4. Results and Discussion
4.1. Integration of Satellite-Derived LE Products
The MKF method is designed to address variables having an expectation of zero mean in the spatial process at each scale. However, the LE products generally cannot satisfy the requirement of the MKF method, and hence, it is necessary to select a proper detrending method to extract the spatial trend surface from the original data. Previous research has presented several ways to do so, such as spline fitting and lognormal space [49,50]. These methods are quite time-consuming [51], and thus, Shi et al. [52] found a simple average way that is suitable for the MKF method after comparing two detrending methods. We applied this method to extract the trend surface and added the updated spatial residual back to the trend surface to generate the integrated LE data.
The fine-to-coarse sweep and the coarse-to-fine sweep of the MKF method were implemented on the Landsat-based LE product and the MOD16 product. Building on the availability of the clear scenes with less than 30% contaminated pixels, the original LE products and the corresponding integrated results were compared for time series from DOY (day of year) 177 to DOY193 and DOY 217 to DOY 249 for 2012 in the midstream of the HRB (Figure 4). Eight integration cases in total were exhibited in this time range. Cloud/shadow pixels and data gaps were masked with dark blue color (0 value) in two LE products. One may note that the same Landsat scenes might be shared by the adjacent DOY cases.
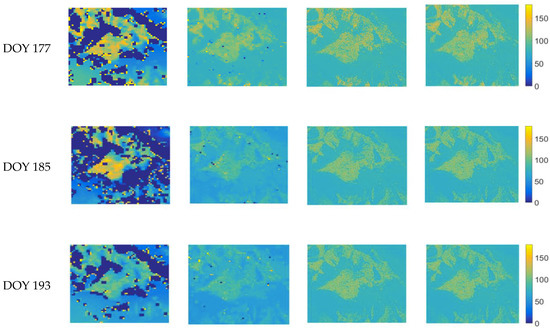
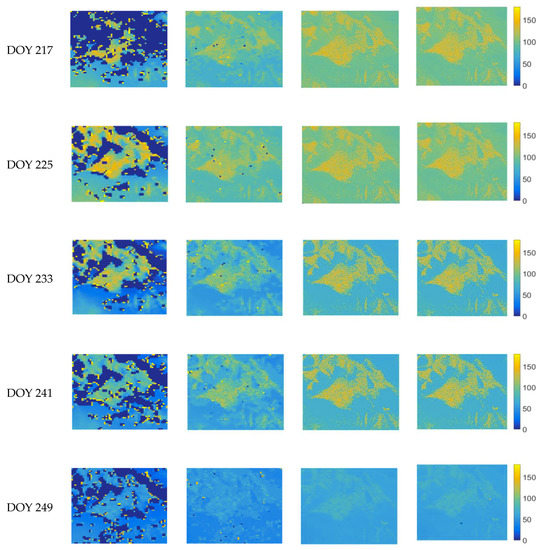
Figure 4.
The integration comparison before and after MKF for DOY (day of year) 225, DOY 233, DOY 241, and DOY 249 in 2012. The order, from left to right, is the LE from original MODIS, MKF-integrated MODIS, original Landsat, and MKF-integrated Landsat. Dark blue color means no data.
For MOD16, there were approximately 27–52% obvious data gaps before the integration, mostly in barren or sparsely vegetated areas. After employing the MKF method, this decreased to less than 0.4% on average and MOD16 became consistent and smooth compared to the original. Moreover, the spatial distribution of MOD16 is more in line with that of the Landsat, which means two LE products remain consistent across different resolutions. Generally, data at finer resolution provide more detailed information of the spatial random processes, whereas coarser data represent average information. Landsat is capable of capturing details of the LE spatial distribution and fills the gaps for MOD16. However, there are still few missing values in MOD16 and we noticed that those abrupt changes mainly came from the margin of the original data gaps, because all of the children nodes were calculated and transferred to their sharing parent nodes, rather than just a single child node. Owing to the scale effect and the spatial heterogeneity, the original data gaps could have a negative impact on the integration performance.
For the Landsat-based LE product, MKF integration lowers Landsat data in the DOY 233, DOY 241, and DOY 249 cases due to the large difference between Landsat and MOD16. This hints that data at coarser resolutions could also bring information to finer data. The MKF method could adjust data at all scales to maintain consistency and smoothness. However, there are smaller changes than for MOD16, indicating that the fine-to-coarse sweep, which aims to fill the gaps, plays a major role, and the coarse-to-fine sweep did not show significant effects within the implementation of the MKF-based integration. This is due to the fact that the original data gaps of MOD16 were filled from the Landsat in the ascending process, MOD16 did not adjust the variables much for the finer scale, and Landsat retained the values of the ascending process when descending.
4.2. Comparison before and after MKF
4.2.1. Spatial Assessment of the MKF Integration Performance
Integration performance was compared by aggregating Landsat into a MODIS-like scale to unify the matrix size. We drew the histogram of the difference between the aggregated Landsat and MOD16 before and after the MKF method to present the integration performance. The difference was calculated as MOD16 minus aggregated Landsat. Owing to a number of the data gaps, the missing pixels from MOD16 were all removed to avoid potential errors and only valid pixels were concerned when calculating the difference between the aggregated Landsat and MOD16. The filled pixels of MOD16 after MKF integration were verified individually.
The distribution of the difference between the two LE products is indicated by gray bars (Figure 5), which were relatively scattered showing large inconsistency before the integration. After the MKF method, the red bars were significantly concentrated, and the difference was restricted to ±10 W/m2 in most cases. The outliers with absolute difference larger than 20 W/m2 were more than approximately 14% of the total, whereas the numbers of those outliers dropped to less than 1% after the integration. This hints that the two LE products were made more consistent across different resolutions through the MKF method.
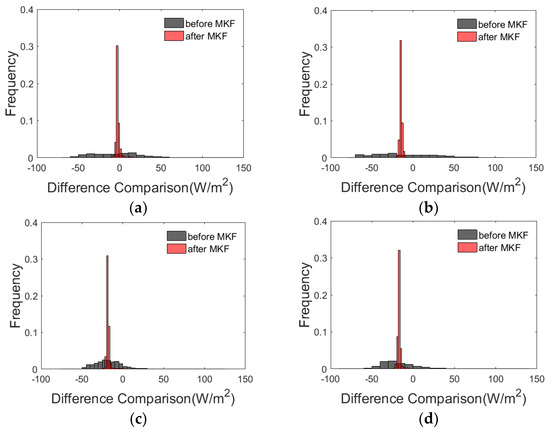
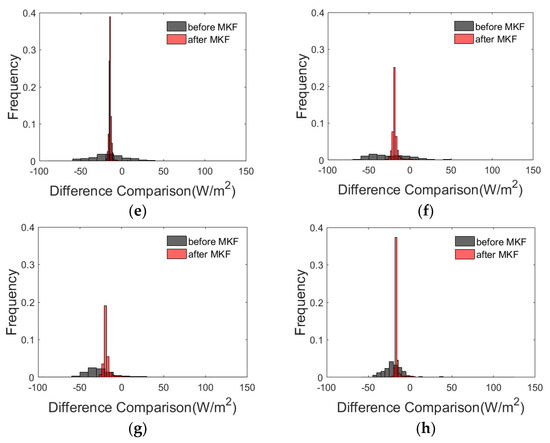
Figure 5.
Comparison of the integration difference between the aggregated Landsat and MOD16 before and after MKF on time series. (a) DOY 177; (b) DOY 185; (c) DOY 193; (d) DOY 217; (e) DOY 225; (f) DOY 233; (g) DOY 241; (h) DOY 249.
To further quantify how well the MKF method performs, several assessment criteria were used (Table 2). Compared to the original difference between the aggregated Landsat and MOD16, the difference after MKF integration was decreased and the RMSE greatly reduced, by 50.7% on average. The lower RMSE % also implied fewer outliers. Thus, it is safe to conclude that the MKF method is able to smooth data and reduce the inconsistency of different LE products across different resolutions. However, the absolute bias increased after MKF integration, which is due to the fact that the differences of the two original LE products were substantially scattered and positive values offset negative values. After integration, the bias was more concentrated and persistent relying on the physical structure of the algorithm. Hence, we contend that the integration performance would be limited if the inputs largely deviate from each other.

Table 2.
Statistical comparison of the assessment criteria before and after MKF.
4.2.2. Evaluation of the MKF Performance Using Ground Observations
Two groups of data validations were plotted in scatterplots showing the accuracy of the LE products before and after MKF (Figure 6). The original missing pixels from MOD16 were still excluded to avoid potential error.
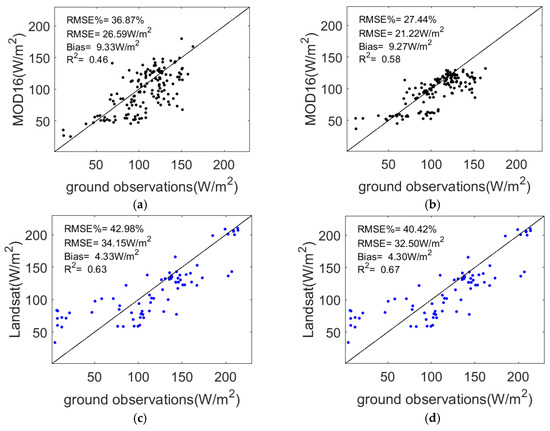
Figure 6.
Validations of LE products versus ground observations before and after MKF. (a) MOD16 before MKF; (b) MOD16 after MKF; (c) Landsat-based LE before MKF; (d) Landsat-based LE after MKF.
After the MKF-based integration, MOD16 was highly improved with a decrease in RMSE% from 36.87% to 27.44%, a decrease in RMSE from 26.59 W/m2 to 21.22 W/m2, a fall in bias from 9.33 W/m2 to 9.27 W/m2, and an increase in R2 from 0.46 to 0.58. Likewise, the RMSE% of the integrated Landsat data decreased from 42.98% to 40.42%, the RMSE fell from 34.15 W/m2 to 32.5 W/m2, the bias decreased from 4.33 W/m2 to 4.3 W/m2, and the R2 improved from 0.63 to 0.67. The slight improvement illustrates that the coarse-to-fine sweep of the MKF method offered few updates for Landsat, and the uncertainty of the original LE products might be further propagated to the integrated LE data.
The original missing pixels, after being filled, were compared against ground observations (Figure 7). These missing pixels were mainly distributed in three sites: Shenshawo sandy desert, site 5, and site 11, covering barren land and cropland. After MKF-based integration, the filled pixels of MOD16 exhibited that the RMSE% was 38.14%, the RMSE was 30.04 W/m2, the bias was 7.82 W/m2, and the R2 was 0.57. Note that there is obvious underestimation of MOD16, which mainly comes from cropland, and was actually introduced by Landsat data that underestimated cropland during the fine-to-coarse sweep of the MKF method.
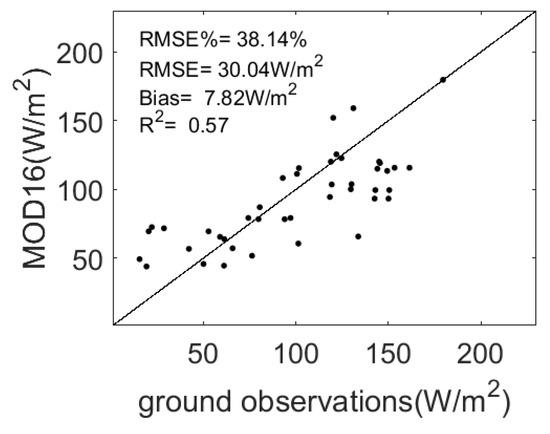
Figure 7.
Validation of filled pixels from MOD16 versus ground observations after MKF.
Other than filling gaps and yielding consistent LE data across different resolutions, the MKF method therefore exhibited a capacity for improving the accuracy for LE products through the validations above. Given that the overestimation showed better agreement with EC ground observations than the underestimation in MKF-integrated MOD16, and there was similar and less-changed underestimation in Landsat, it implied that the data uncertainty also propagated during the MKF implementation. For maximum accuracy of the integrated results, we propose that the inputs for MKF integration cannot have great differences among each other.
4.3. Discussion
4.3.1. Uncertainty Analysis
Three problems are associated with the integrated result validations: The mechanism of MKF integration, scaling effects, and the errors from inputs, including of the original LE products and the EC ground observations. First, integrating and adjusting pixel values in the MKF method suggests a high dependence on the weighted values derived from the uncertainty at each scale, which implies that the smaller the uncertainty of an estimate, the larger the influence of that estimate in the integrating process. In this study, the uncertainties that came from satellite characteristics and the estimated algorithms were invariant in temporal and spatial variations to simplify the problem and hence, the matrix of the weighted values might be imperfect.
Second, the mismatch in scale among different datasets might lead to uncertainty of the MKF-integrated result evaluation. The ground measurements represent a point-based value, and the footprint of the flux tower site is approximately several hundred meters, while the spatial resolution of the Landsat-based LE product is only 30 m [53]. The direct evaluation with the satellite-based images may be unreasonable. It is possible that the spatial uncertainty is further reinforced in heterogeneous areas such as the midstream of the HRB. The abrupt changes in integrated MOD16 indicated the original data gaps were also considered as the children nodes when transferring to the next scale under scaling effects.
Finally, the input errors are an important issue. Landsat-based LE products exhibited the discrepancies of different land cover types and underestimated in the growing season, especially for cropland and wetland (e.g., 1–17 sites and Zhangye wetland) situated in the irrigated artificial oasis. Yao et al. (2014) [54] evaluated the ability of the MS–PT algorithm using the ground observations from 40 global flux towers; results showed that the R2 varied from 0.4 to 0.7 and the RMSE varied from approximately 37.5 W/m2 to 44.4 W/m2 for cropland and wetland. This is consistent with our validation results (i.e., R2 is 0.67 and RMSE is 32.5 W/m2). Neglecting the differences in parameters from different biome types and complex terrain may cause the errors [55], and such findings are in accordance with previous studies over northeast China [44]. The errors could be reduced by 5–25% if calibrating the Priestley–Taylor coefficients controlled by the ground observations towards different biome types and climatic zones [56]. For MOD16, underestimation also exists because the soil moisture constraint in MOD16 applied relatively humidity (RH) and vapor pressure deficit (VPD) as indicators of water stress [44]. During the irrigation period, the soil water content in the surface and root layers is generally high and the overestimation of water stress, parameterized by RH and atmospheric VPD, brought about the underestimation of the soil evaporation in the arid and semi-arid midstream of the HRB [57]. Researchers drew similar conclusions in China [58], the United States [59], eastern Asia [60], and Brazil [61] when evaluating MOD16. Large errors and uncertainty may be introduced by these approximations and assumptions. Moreover, the integration evaluation greatly relies on the accuracy of EC ground observations, which were considered as true LE values in this study. However, Wang et al. (2015) [62] reported 16% uncertainty in LE observations derived from the HiWATER–MUSOEXE flux matrix. Even though we corrected the energy imbalance, errors that were caused by complexity in wind variation, footprint representation, and sampling variability are still unclear [23,63]. These corrections still cause large errors of EC ground observations in results [64].
4.3.2. Superiority and Recommendation for the MKF integration
We propose that the MKF method is scalable to other areas and applicable to serve other integrations of satellite LE products suffering from the issues mentioned in this study for two reasons, namely, high efficiency and comprehensive consideration of multiple datasets’ advantages across different resolutions. The MKF method executes mere seconds to complete an integration case and is very time efficient, whereas optimal interpolation usually requires several hours [26]. Additionally, the great superiority of the MKF method is integrating multiple satellite datasets at different resolutions. Since data at different resolutions capture various information, we filled the data gaps and retained those data consistent with their own resolution in this study. Previous research showed that the MKF method has the capacity to fill Albedo data gaps derived from a multi-angle imaging spectroradiometer (MISR) and to maintain their consistency in spatial processes [25].
For integrating multiple satellite datasets at different resolutions and taking full use of the MKF method, we recommend that one original input should be relatively precise, at least due to mutual propagation because the performance of the MKF method highly depends on how accurate the uncertainty estimation of the datasets is and how largely those datasets deviate from each other. Moreover, we evaluated two LE products with ground observations and estimated the weighted values for each scale based on the uncertainty of each product. To mitigate the scaling effects and extend this approach to other areas, especially for heterogeneous land surfaces, the observation uncertainty matrix might be more accurate for the integration process when referring to a “true” LE map instead of point-based values. This forms the foundation of our ongoing research.
5. Conclusions
Accurate and spatiotemporally consistent satellite-driven LE products are essential to quantify and improve regional water budgets, especially for arid and semi-arid areas. Current individual LE products, however, exhibit spatiotemporal discontinuity and uncertainties due to sensor characteristics or the physical structure of the LE estimating algorithm. This study showcased our efforts to overcome the current limitations by integrating satellite-driven LE products at different resolutions.
We presented an integration study of the midstream of the HRB of northwest China using the MKF method, which aims to improve current LE products from multiple datasets at different resolutions and produce spatiotemporal continuous LE products. We integrated the MOD16 product and Landsat-based LE product and demonstrated the merits of this approach in integrating datasets across different resolutions.
Our comparison and validation results indicated that the data gaps of MOD16 were filled, the integrated LE products were more continuous in their spatial distribution, and the accuracies of LE products were improved. The MKF method thereby shows great potential to take full use of data at various resolutions and to generate consistent LE products in other areas that suffer from the same issues.
This study used ground observations to estimate the uncertainties of LE products and to further acquire weighted values as background values for scale conversion. However, scaling effects might lead to negative influences for MKF integration. Future work will focus on accurately evaluating the uncertainties of the LE products as well as estimating and generating more precise LE products for heterogeneous land surfaces.
Author Contributions
J.X. and Y.Y. designed the work and prepared the manuscript. K.T. revised the manuscript. Y.L. and S.L. corrected and improved the manuscript. K.S., K.J., and X.Z. provided the data and conducted the remotely sensed image processing. X.C. and X.B. contributed by providing additional analysis to the discussion.
Funding
This work was partially supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA20100101) and the Natural Science Fund of China (No. 41671331).
Acknowledgments
We thank Tongren Xu, Zhongli Zhu, and Ziwei Xu from Faculty of Geographical Science, Beijing Normal University, China, for their suggestions to improve this manuscript. MOD16 products were obtained online (https://lpdaac.usgs.gov/products/mod16a2v006/). Landsat data were provided at https://landsat.usgs.gov/. The ground observations of heat fluxes are downloaded freely via Heihe Data Center (http://www.heihedata.org/).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Details of the MKF Method
The MKF method is performed in two steps through the autoregressive tree structure: The fine-to-coarse sweep ascends from the leaves to the root for the state estimates (define s+ is a descendant of s) and its variance P(s|s+); and the coarse-to-fine sweep descends from the root to the leaves for the finally updated estimates and P(s).
Appendix A.1. Initialization
Each node s of variables at the first scale is initialized before the two sweeps, namely [45]:
where P*(s) presents the variance of the unconditioned state before applying the MKF algorithm. One can note that variables are required to be zero mean in the spatial process, and hence, the surface extraction is also implemented in this step.
Appendix A.2. Fine-to Coarse Sweep
The fine-to-coarse sweep is to incorporate the state conversion predicted values to the scale s and the observed values z(s) at scale s by the following equation [65]:
where Cs is the measurement matrix and K(s) is Kalman gain given by Ref. [66]:
Here, V(s) is the innovation covariance:
Every child node provides an estimate to their parent nodes, where the children of a node s are denoted by , i = 1, …, q. According to the state conversion model, can be estimated from each child to predict y(s):
All the predicted nodes from the lower scale are integrated into the parent nodes and the integrated takes the form:
The optimal estimator consists of a weighted sum of the estimates from its children. It is implied from (A7) that the larger the uncertainty P(s) of an estimate, the smaller the adjustment influence of that estimate in the ascending sweep. Through (A1) to (A7), predicted values from the state conversion model and the observations from the measurement model are recursively integrated.
Appendix A.3. Coarse-to-Fine Sweep
After arriving to the root node with the fine-to-coarse sweep, the coarse-to-fine descending sweep starts at the next finer scale from the root node, continuing to the finest scale. This process aims to obtain the final updated estimate and have the similar form given by:
where J(s) is a weighting coefficient, namely:
Appendix B. Details of the MS-PT Algorithm Logic
The MS-PT algorithm developed by Yao et al. [41] separates LE into the sum of four parts: The unsaturated soil evaporation (LEds), the saturated wet soil surface evaporation (LEws), the canopy transpiration (LEc), and the canopy interception evaporation (LEic). Each part can be calculated by:
where is the Priestley–Taylor coefficient; is the slope of the saturation water vapor pressure curve; is the psychrometric constant; fwet is the wet surface fraction; fsm is the soil moisture constraint; fT is the plant temperature constraint; Rns and Rnc are the net radiation into soil and vegetation, respectively; G is the soil heat flux; DT represents the diurnal air temperature range and DTmax describes the maximum DT (40 °C); fc is the vegetation cover fraction; and NDVImax and NDVImin are the maximum and the minimum NDVI, with the values of 0.95 and 0.05, respectively in this algorithm [67].
References
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on Estimation of Land Surface Radiation and Energy Budgets From Ground Measurement, Remote Sensing and Model Simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Yu, J.; Chen, J.; Liu, S.; Lin, Y.; Fisher, J.B.; McVicar, T.R.; Cheng, J.; Jia, K.; et al. A simple temperature domain two-source model for estimating agricultural field surface energy fluxes from Landsat images. J. Geophys. Res. Atmos. 2017, 122, 5211–5236. [Google Scholar] [CrossRef]
- Gao, G.; Chen, D.; Xu, C.Y.; Simelton, E. Trend of estimated actual evapotranspiration over China during 1960–2002. J. Geophys. Res. Atmos. 2007, 112, 8. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Farahani, H.J.; Howell, T.A.; Shuttleworth, W.J.; Bausch, W.C. Evapotranspiration: Progress in Measurement and Modeling in Agriculture. Trans. ASABE 2007, 50, 1627–1638. [Google Scholar] [CrossRef]
- Cheng, J.; Kustas, W.P. Using Very High Resolution Thermal Infrared Imagery for More Accurate Determination of the Impact of Land Cover Differences on Evapotranspiration in an Irrigated Agricultural Area. Remote Sens. 2019, 11, 18. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Allen, R.G. SEBAL Model with Remotely Sensed Data to Improve Water-Resources Management under Actual Field Conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Yu, G.R.; Bonnefond, J.M.; Chen, J.Q.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Rao, V.U.M.; Reddy, D.R.; Banerjee, S.; Venkatesh, H.; Pandey, V.; Kar, G.; Mukherjee, J.; Vyas, S.P. Latent heat flux estimation in clear sky days over Indian agroecosystems using noontime satellite remote sensing data. Agric. For. Meteorol. 2015, 149, 1646–1665. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Yong, G.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. Atmos. 2012, 117, 13113. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Liu, S.; Jia, K.; Zhang, X.; Xiao, Z.; Fisher, J.B.; Mu, Q.; et al. Improving global terrestrial evapotranspiration estimation using support vector machine by integrating three process-based algorithms. Agric. For. Meteorol. 2017, 242, 55–74. [Google Scholar] [CrossRef]
- Di, S.C.; Li, Z.L.; Tang, R.; Wu, H.; Tang, B.H.; Lu, J. Integrating two layers of soil moisture parameters into the MOD16 algorithm to improve evapotranspiration estimations. Int. J. Remote Sens. 2015, 36, 4953–4971. [Google Scholar] [CrossRef]
- Yang, Y.; Long, D.; Shang, S. Remote estimation of terrestrial evapotranspiration without using meteorological data. Geophys. Res. Lett. 2013, 40, 3026–3030. [Google Scholar] [CrossRef]
- Xiong, Y.J.; Zhao, S.H.; Tian, F.; Qiu, G.Y. An evapotranspiration product for arid regions based on the three-temperature model and thermal remote sensing. J. Hydrol. 2015, 530, 392–404. [Google Scholar] [CrossRef]
- Tongren, X.; Zhixia, G.; Shaomin, L.; Xinlei, H.; Yangfanyu, M.; Ziwei, X.; Youlong, X.; Jingfeng, X.; Yuan, Z.; Yanfei, M. Evaluating Different Machine Learning Methods for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Ma, Y.; Shaomin, L.; Song, L.; Xu, Z.; Zhu, Z. Estimation of daily evapotranspiration and irrigation water efficiency at a Landsat-like scale for an arid irrigation area using multi-source remote sensing data. Remote Sens. Environ. 2018, 216, 715–734. [Google Scholar] [CrossRef]
- Cheng, G.; Li, X.; Zhao, W.; Xu, Z.; Feng, Q.; Xiao, S.; Xiao, H. Integrated study of the water–ecosystem–economy in the Heihe River Basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Ge, Y.; Li, H.; Han, F.; Hu, X.; Tian, W.; Tian, Y.; Pan, X.; Nian, Y. Hydrological Cycle in the Heihe River Basin and Its Implication for Water Resource Management in Endorheic Basins. J. Geophys. Res. Atmos. 2018, 123, 890–914. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Feng, F.; Li, X.; Yao, Y.; Liang, S.; Chen, J.; Zhao, X.; Jia, K.; Pintér, K.; Mccaughey, J.H. An Empirical Orthogonal Function-Based Algorithm for Estimating Terrestrial Latent Heat Flux from Eddy Covariance, Meteorological and Satellite Observations. PLoS ONE 2016, 11, e0160150. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Chou, K.C.; Willsky, A.S.; Nikoukhah, R. Multiscale systems, Kalman filters, and Riccati equations. Autom. Control. IEEE Trans. 1992, 39, 479–492. [Google Scholar] [CrossRef]
- He, T.; Liang, S.; Wang, D.; Shuai, Y.; Yu, Y. Fusion of Satellite Land Surface Albedo Products Across Scales Using a Multiresolution Tree Method in the North Central United States. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3428–3439. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S. Using multiresolution tree to integrate MODIS and MISR-L3 LAI products. IEEE Int. Geosci. Remote Sens. Symp. 2010, 38, 1027–1030. [Google Scholar] [CrossRef]
- Cheng, G.D.; Xiao, H.L.; Zhong-Min, X.U.; Jin-Xiu, L.I.; Ming-Feng, L.U. Water Issue and Its Countermeasure in the Inland River Basins of Northwest China—A Case Study in Heihe River Basin. J. Glaciol. Geocryol. 2006, 28, 406–413. [Google Scholar] [CrossRef]
- Mcvicar, T.; Roderick, M.L.; Donohue, R.J.; Li, J.; Thomas, G.V.N.; Paul, G.T.; Jürgen, G.; Deepak, J.; Youcef, H.; Natalie, M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416, 182–205. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Wang, W.; Hu, X.; Xu, Z.; Wen, J. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 170083. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Xin, L.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (HiWater) scientific objectives and experimental design (EI). Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Ma, M.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 180072. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006. NASA EOSDIS Land Process. DAAC 2017. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Cheng, J.; Liu, S.; Fisher, J.B.; Zhang, X.; Jia, K.; Zhao, X.; Qin, Q.; Zhao, B. MODIS-driven estimation of terrestrial latent heat flux in China based on a modified Priestley–Taylor algorithm. Agric. For. Meteorol. 2013, 171–172, 187–202. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C.K. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Jie, H.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116, D20104. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, Y.; Wang, Z.; Jia, K.; Chen, X. Satellite-Derived Spatiotemporal Variations in Evapotranspiration over Northeast China during 1982–2010. Remote Sens. 2017, 9, 1140. [Google Scholar] [CrossRef]
- Vyver, H.V.D.; Roulin, E. Scale-recursive estimation for merging precipitation data from radar and microwave cross-track scanners. J. Geophys. Res. Atmos. 2009, 114, D08104. [Google Scholar] [CrossRef]
- Gupta, R.; Venugopal, V.; Foufoula-Georgiou, E. A methodology for merging multisensor precipitation estimates based on expectation-maximization and scale-recursive estimation. J. Geophys. Res. Atmos. 2015, 111, D02102. [Google Scholar] [CrossRef]
- Luettgen, M.R.; Willsky, A.S. Likelihood calculation for a class of multiscale stochastic models, with application to texture discrimination. IEEE Trans. Image Process. 1995, 4, 194–207. [Google Scholar] [CrossRef]
- Chou, C.K. A Stochastic Modeling Approach to Multiscale Signal Processing. Mass. Inst. Technol. 1991. Available online: https://pdfs.semanticscholar.org/6350/caa3c42a2c12b0342706fe53197820d58ade.pdf (accessed on 30 July 2019).
- Tustison, B.; Foufoula-Georgiou, E.; Harris, D. Scale-recursive estimation for multisensor Quantitative Precipitation Forecast verification: A preliminary assessment. J. Geophys. Res. Atmos. 2002, 107. CIP-1-CIP 2–14. [Google Scholar] [CrossRef]
- Gorenburg, I.P.; Mclaughlin, D.; Entekhabi, D. Scale-recursive assimilation of precipitation data. Adv. Water Resour. 2001, 24, 941–953. [Google Scholar] [CrossRef]
- Yue, W.; Zhu, J. On estimation and prediction for multivariate multiresolution tree-structured spatial linear models. Stat. Sin. 2006, 16, 981–1020. [Google Scholar] [CrossRef]
- Shi, L.; Liang, S.; Cheng, J.; Zhang, Q. Integrating ASTER and GLASS broadband emissivity products using a multi-resolution Kalman filter. Int. J. Digit. Earth 2016, 9, 1098–1116. [Google Scholar] [CrossRef]
- Baldocchi, D. Breathing of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Zhao, S.; Zhang, Y.; Qin, Q.; Cheng, J.; Jia, K.; Xie, X.; Zhang, N.; Liu, M. Validation and Application of the Modified Satellite-Based Priestley-Taylor Algorithm for Mapping Terrestrial Evapotranspiration. Remote Sens. 2014, 6, 880–904. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Wang, K.; Jia, K.; Cheng, J.; Jiang, B.; Fisher, J.B.; Mu, Q.; et al. A satellite-based hybrid algorithm to determine the Priestley-Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216–233. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Houborg, R.; Starks, P.J.; Agam, N. A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Hu, G.; Li, J. Monitoring of Evapotranspiration in a Semi-Arid Inland River Basin by Combining Microwave and Optical Remote Sensing Observations. Remote Sens. 2015, 7, 3056–3087. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, Q.; Liu, J. The Performances of MODIS-GPP and -ET Products in China and Their Sensitivity to Input Data (FPAR/LAI). Remote Sens. 2014, 7, 135–152. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 global terrestrial evapotranspiration products in various climates and land cover types in Asia. Ksce J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Ruhoff, A.L.; Paz, A.R.; Aragao, L.E.O.C.; Mu, Q.; Malhi, Y.; Collischonn, W.; Rocha, H.R.; Running, S.W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Int. Assoc. Sci. Hydrol. Bull. 2013, 58, 1658–1676. [Google Scholar] [CrossRef]
- Wang, J.; Zhuang, J.; Wang, W.; Liu, S.; Xu, Z. Assessment of uncertainties in eddy covariance flux measurement based on intensive flux matrix of HiWATER-MUSOEXE. IEEE Geosci. Remote Sens. Lett. 2015, 12, 259–263. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Han, D.; Field, C. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H.A. A Re-Evaluation of Long-Term Flux Measurement Techniques Part I: Averaging and Coordinate Rotation. Bound. Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Fieguth, P.W.; Karl, W.C.; Willsky, A.S.; Wunsch, C. Multiresolution optimal interpolation and statistical analysis of TOPEX/POSEIDON satellite altimetry. Geosci. Remote Sens. IEEE Trans. 1995, 33, 280–292. [Google Scholar] [CrossRef]
- Kannan, A.; Ostendorf, M.; Karl, W.C.; Castanon, D.A.; Fish, R.K. ML parameter estimation of a multiscale stochastic process using the EM algorithm. IEEE Trans. Signal. Process. 2002, 48, 1836–1840. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.J.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol. 2009, 379, 92–110. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).