1. Introduction
With the development of remote sensing technology, there is a growing demand for the accurate detection of single trees based on high-resolution remote sensing images. Single tree detection is useful for forest management, afforestation and utilisation of forest resources. Single tree detection technology is a cross-research field of relevance for computer vision, photogrammetry and remote sensing fields and has become a hot topic in recent years [
1,
2]. Tree detection methods based on remote sensing images can be divided into two categories: pixel-based tree detection methods and object-based tree detection methods.
Early tree detection methods with remote sensing images are usually based on pixels. The most commonly used pixel-based method is the local-maximum method [
3,
4]. This kind of method usually extracts the maximum value of the local area as the centre of a tree, combined with the region-growing method, watershed segmentation method and other methods to detect single trees. For example, Novotny et al. [
5] proposed a local-maximum method with a variable window size and used the region-growing method to detect trees. Culvenor [
6] proposed a method based on image texture information to detect a single tree. They believed that the tree canopy vertex is a maximum value in the image, while the surrounding points are smaller. Therefore, they continued expanding from the maximum point to the surrounding points and stopped expanding once the value started to rise. This method does not require defining window size parameters as opposed to finding local maximum values. Hirschmugl et al. [
7] proposed an algorithm to find the crown centre by eliminating non-crown regions before using the Levenberg–Marquardt algorithm (LMA), based on the comparison of existing crown centre acquisition methods. Pouliot et al. [
8] designed an adaptive multi-scale single tree detection method. First, they selected the best Gaussian smoothing parameters according to the relationship between the number of local maximum values and the value of the Gaussian smoothing parameters, and then used the extracted local maximum points as a single tree through the adaptive window size. Because these local-maximum methods cannot be classified according to the overall features of trees, the accuracy of selecting seed points in a complex background will also be reduced, thus affecting the accuracy of single tree detection. In addition, the template-matching method [
9,
10,
11] is also a pixel-based method, which uses the template of a tree to calculate the area with the same size as the area in the image successively and calculates the sum of squared errors of all the pixel points. However, this method cannot match the area with which the trees are located in a crowded manner, and the canopies often overlap.
The object-based tree detection method can better reflect the overall features of trees and improve the accuracy of tree detection by incorporating a machine learning algorithm. Hellesen et al. [
12] proposed combining an object-based image analysis method with a classification tree algorithm to find the best classification features to distinguish shrubs, trees and background grasslands. When LiDAR-derived data were used as auxiliary information, the classification accuracy of object-based CIR orthographic image analysis was significantly improved. Laliberte et al. [
13] proposed a method combining image segmentation and object-based classification to monitor the changes of vegetation over time, combining spectral and spatial image information, which is very close to the way that humans intuitively interpret information from aerial photographs. In addition, the multi-scale analysis combined with the hierarchical segmentation method is effective in the ecological sense, and the shrub density can be determined in the coarse-level classification. Salim et al. [
14] used a method of scale-invariant feature transform (SIFT) to extract the key points of palm trees and put them into the extreme learning machine (ELM) for learning classification, thereby realising the detection of a single tree. However, SIFT selects the features of several key points in the sample, which is slightly less accurate than the global feature method based on RGB. Lin et al. [
15] proposed a method of automatic training and data selection. They used the overall colour, texture, entropy and other visual features of trees in aerial images to train a pixel-level classifier, and the training process and data selection were based on two-level clustering. However, this method requires manually specifying extracted features and setting limits for the corresponding parameters for different scenarios, and it is difficult to detect a single tree accurately without prior knowledge.
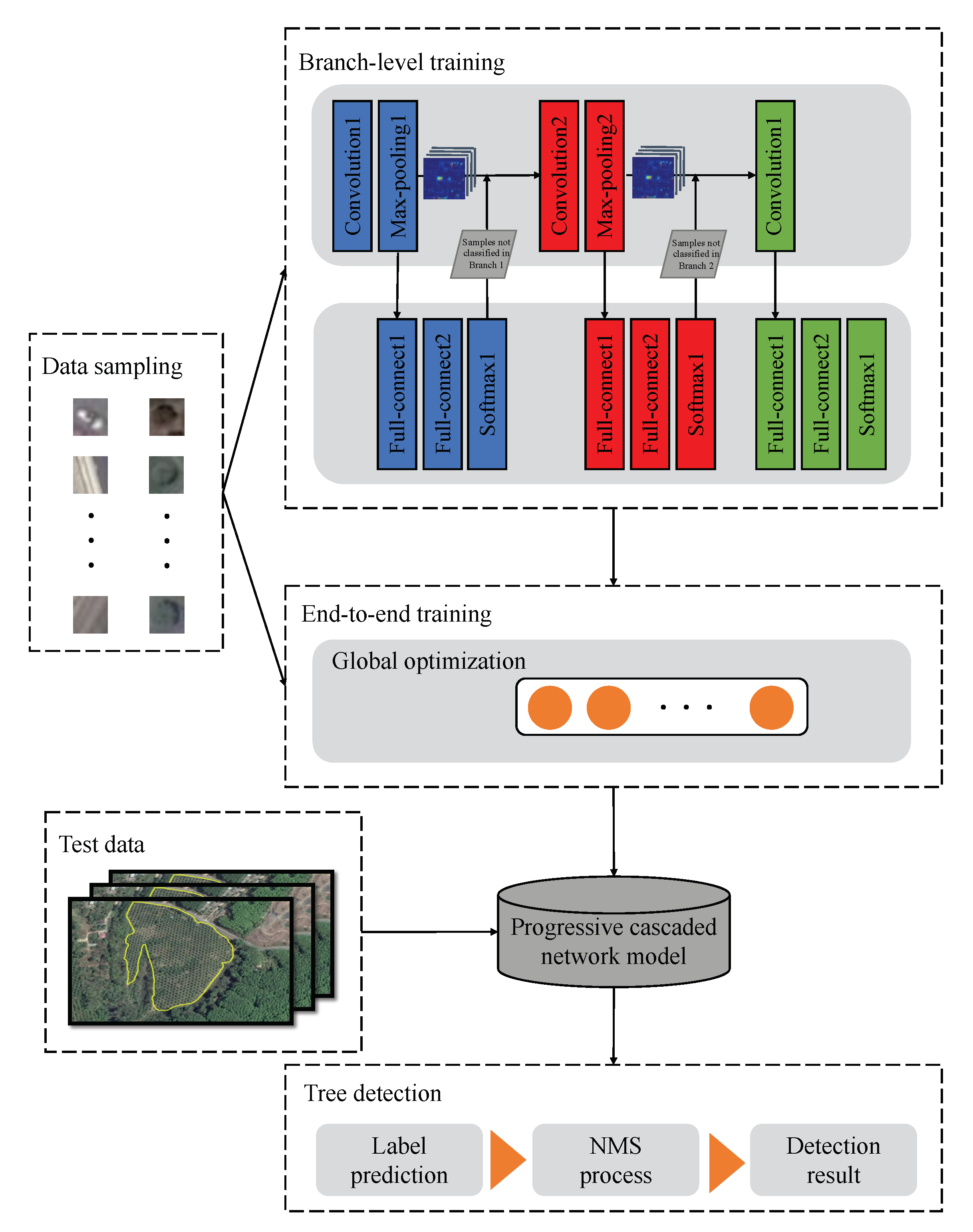
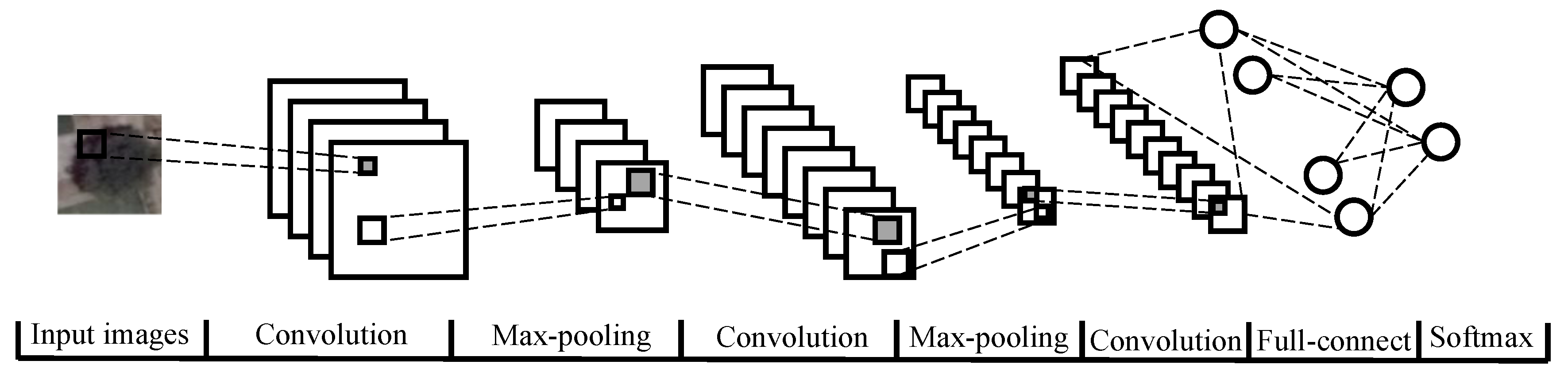
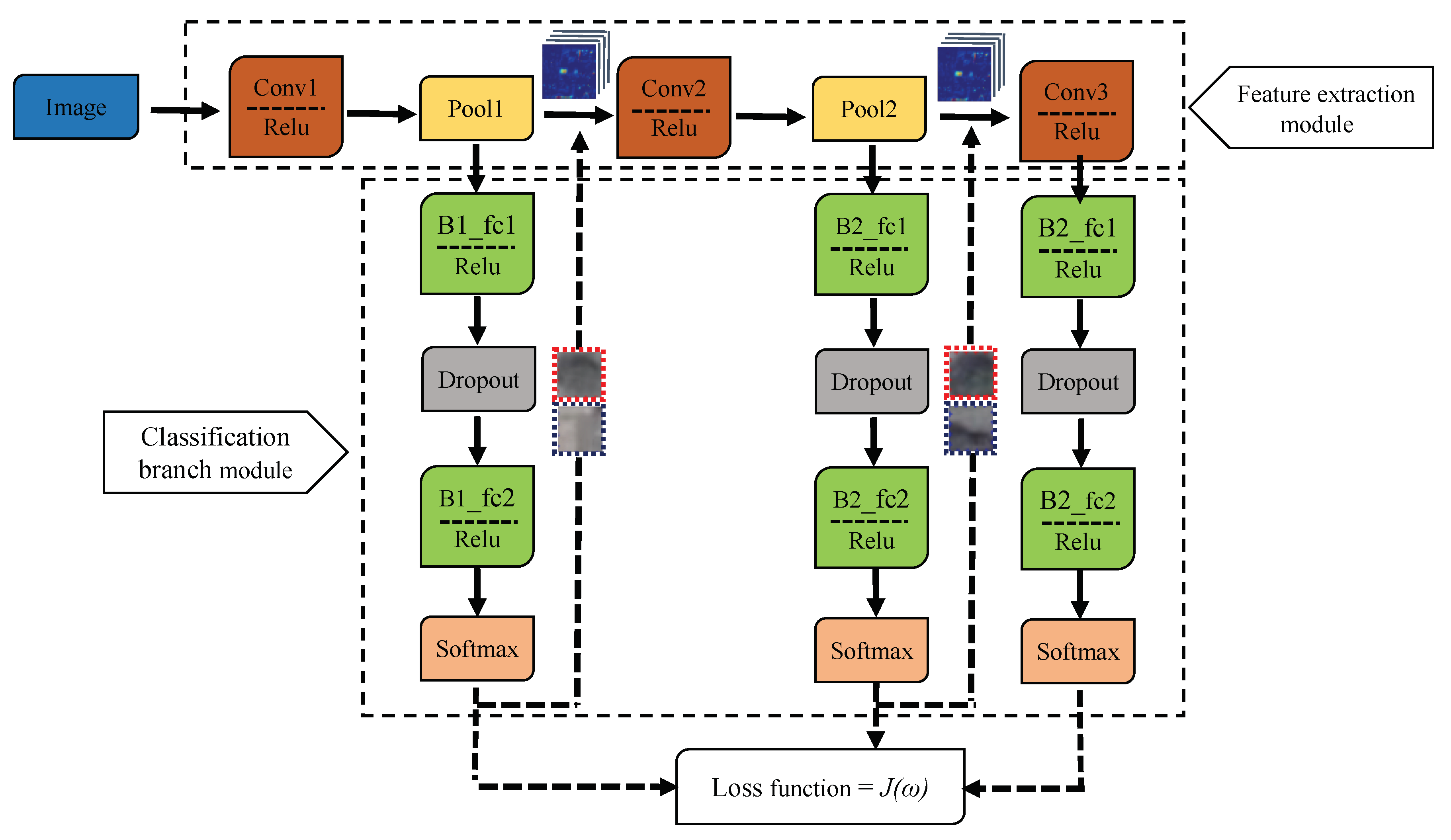
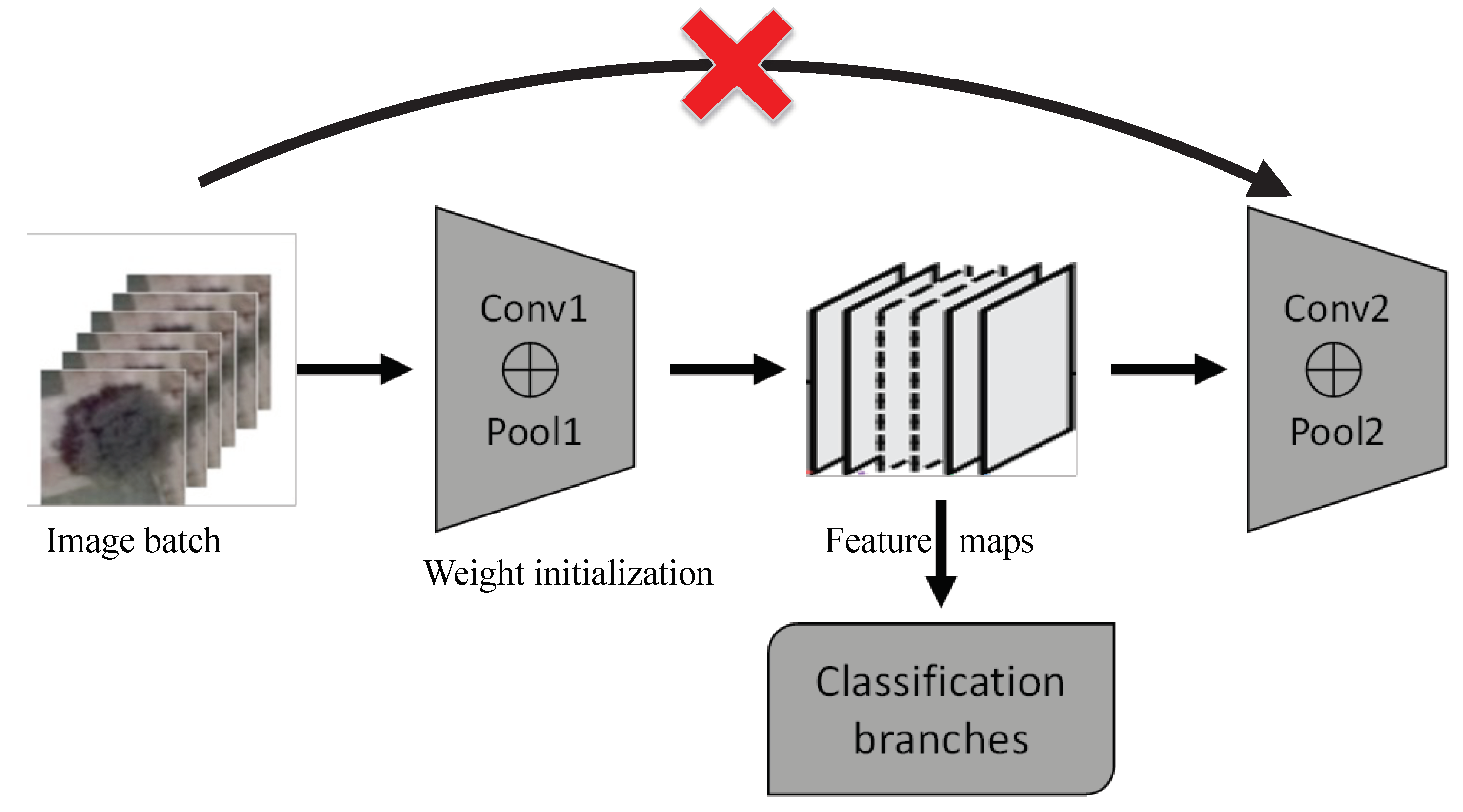
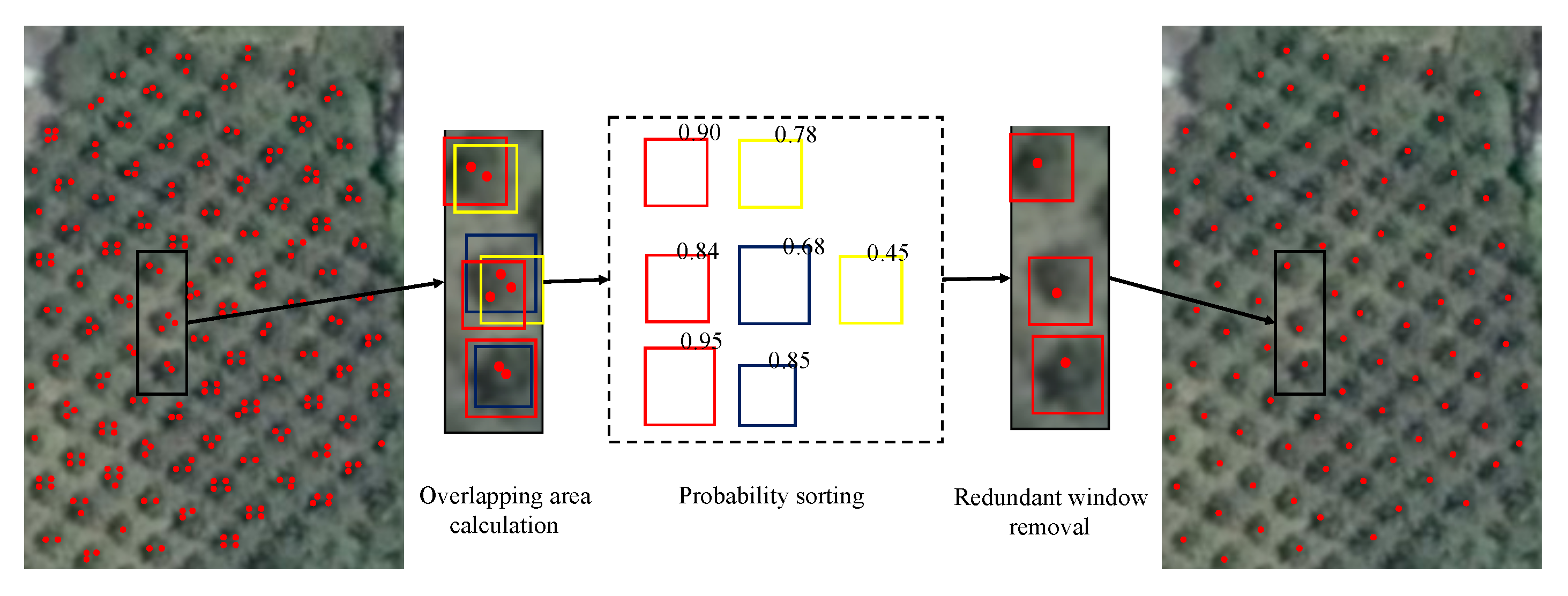
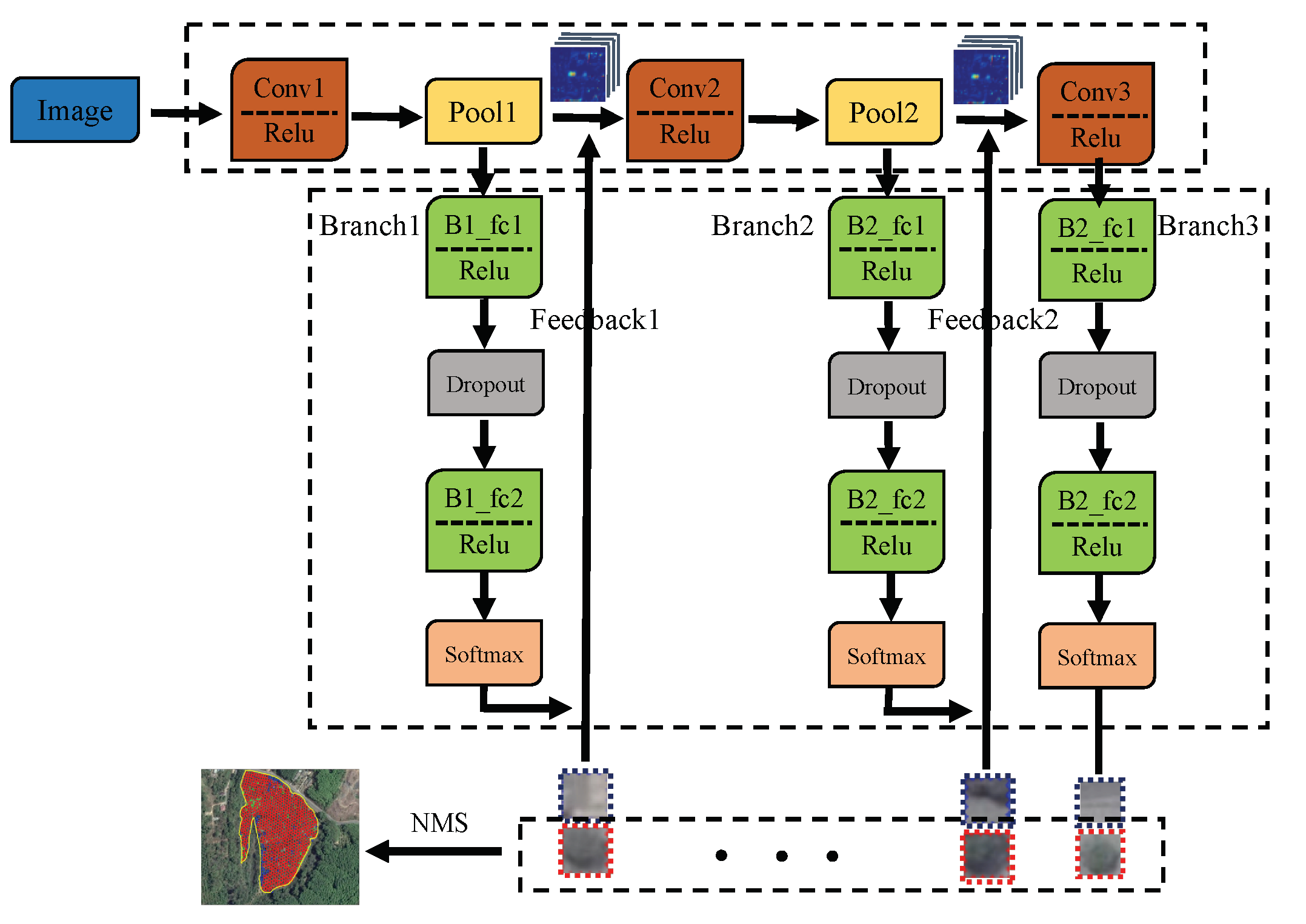
In recent years, with the increasing application of the convolutional neural network (CNN) algorithm in target recognition and image classification of computer vision, researchers have also begun to apply CNN to tree detection of remote sensing images [
16,
17,
18,
19,
20] to solve the problems in traditional single tree detection methods. For example, the robustness of the seed point selection or template-matching method in the pixel-based detection approaches in complex scenarios is low, and the feature parameters of different scenarios need to be specified by prior knowledge in the object-based detection methods. The CNN does not require prior knowledge of artificially specified features and can continuously learn in-depth features based on numerous images. The conventional single tree detection algorithm first extracts the features and then conducts the classifier training, while the CNN network combines these two separate processes; thus, the bottom, colour, contour and other local low-level features are gradually abstracted to the high-level features. Li et al. [
21] applied the method based on a deep learning convolutional neural network to the detection of densely planted oil palm trees in Malaysia. Overall, 96% of the manually marked trees in the test area were correctly detected. Emilio et al. [
22] proposed a CNN-based
Ziziphus lotus shrub detection method with Google Earth imagery as the data source and achieved a better detection result than the other single tree detection methods. In addition, other CNN-based algorithms such as Faster-RCNN [
23] and YOLO (You Only Look Once) [
24] can also be used to detect target objects, but if the resolution of the image is not high enough, such methods will miss some small trees. In general, tree detection methods based on convolutional neural networks are effective when the trees are similar in size and the scene is simple, but its robustness is not ideal for scenarios with complex backgrounds and diverse trees, such as trees and shrubs growing together, different tree species, etc. Since the convolutional neural network can only be trained for all candidate tree samples, most errors of commission and omission occur in the hard-to-classify samples with similar colour to background, unclear canopy contour and abnormal shape caused by illumination shadows. To improve the precision of the recognition of hard-to-classify samples, a progressive cascaded convolutional neural network for the single-tree detection method is proposed in this paper. Tree samples of different classification difficulties are trained and tested by different classification branches. The method cascades through three convolution layers and pooling layers based on the LeNet variant network and then forms the feature extraction modules. The remaining network layers are used as classification branch modules. By allowing the data sample to pass through each classification branch, it is fed back to the feature extraction module to determine whether it needs to be progressed into the next classification branch to extract the deeper features. As a result, the method can quickly identify parts of the low-level branches that are either clearly trees or not trees, and the high-level branches can extract more features of the sample to handle hard-to-classify samples. In addition, we propose a two-phase training and a method of feature maps that are partly shared to improve the efficiency of model training. This paper is not the first object detection method using cascaded convolutional neural networks for images [
25,
26], but the model designed for single tree detection in this study has many advantages, for example, the later classification branches can directly use the feature graph from the previous classification branch, avoiding the recalculation of the feature maps from the original diagram layer by layer; moreover, the network can be combined to train parameters in a global optimisation way, whereas previous cascading networks are basically independent networks.
2. Study Areas
This paper uses the highly accessible Google Earth imagery data [
27] compared to expensive, private, and difficult to obtain satellite remote sensing images. In this study, three test areas were selected, located in Thailand, USA and China.
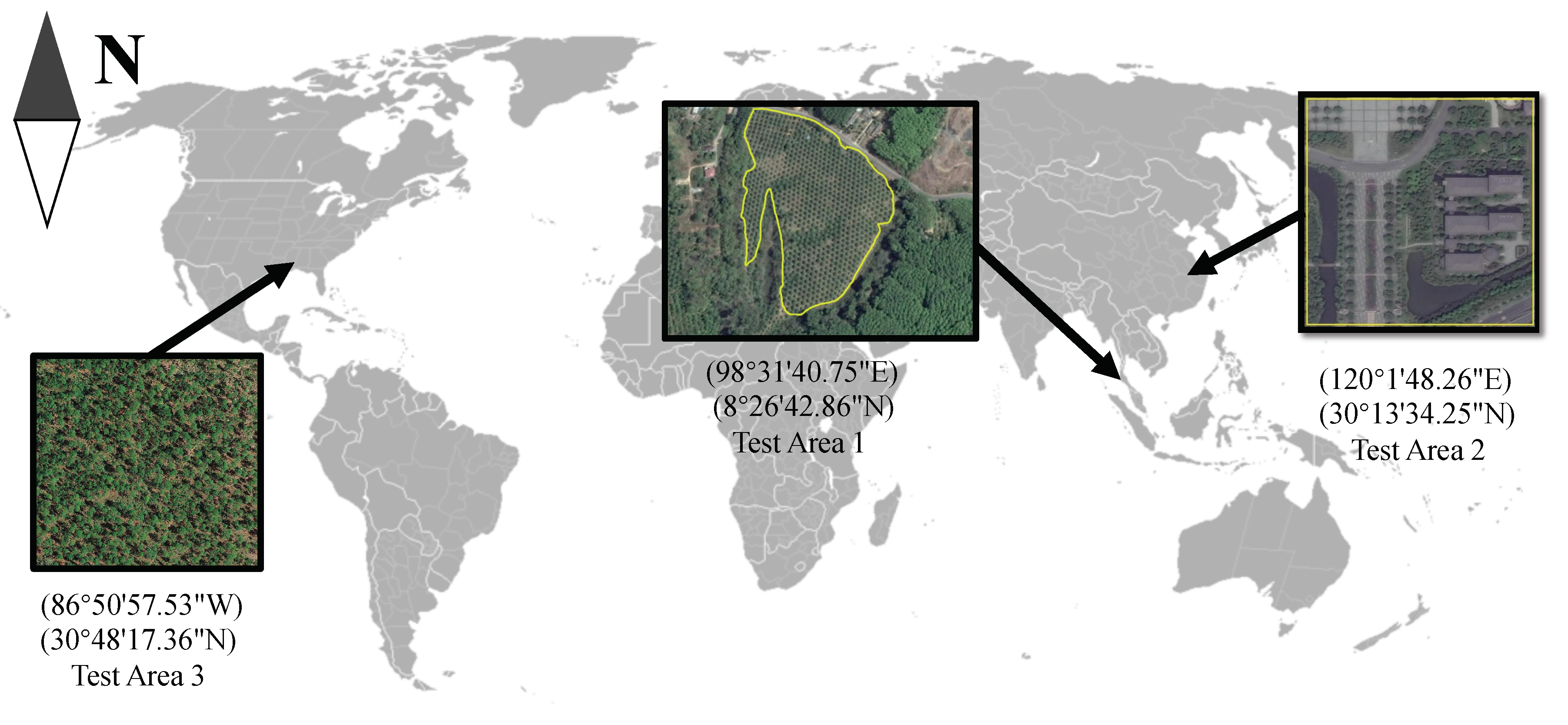
Figure 1 shows a schematic of the location of the test areas. The reference tree is defined in the yellow line because trees outside the yellow line cannot be judged by human eyes. Test Area 1 is the palm tree plantation scenario in Phang Nga, Thailand, located at
east longitude and
north latitude. Palm trees are an important economic crop in Thailand, and more than 800 reference trees in Test Area 1 were selected. Test Area 2 is a complex greening area in Hangzhou, China, located at
east longitude and
north latitude. This area not only has different tree species but also rivers, buildings, roads, etc., and 254 reference trees were selected in Test Area 2. Test Area 3 is a real forest area in Florida, USA, located at
west longitude and
north latitude. In total, 261 reference trees were selected in Test Area 3. For a real forest area, the single tree detection is the basis for more effective forest management, thus we also tested our algorithm in Test Area 3.
5. Conclusions
High-resolution remote sensing images have been widely used in urban greening planning, forest management, large area forest yield estimation and other applications. Currently, researchers have developed a variety of methods to extract single trees and their features from various types of digital aerial photographs. However, the generalisation performance of the existing single-tree detection methods is weak; it is difficult to detect the scene of a complex forest because of the similar colour between the tree and background, unclear canopy contour and abnormal shape caused by illumination shadows. Therefore, these existing methods cannot be used in a wide range of tree detection scenarios.
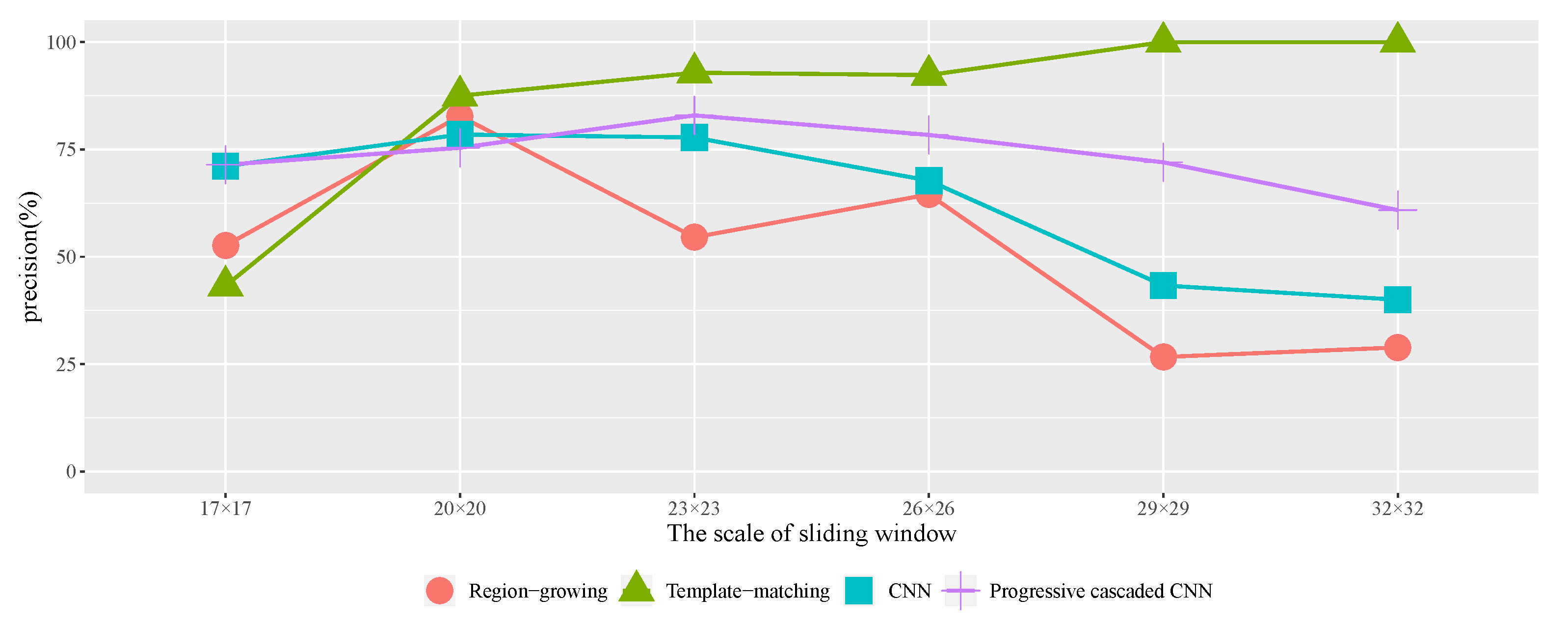
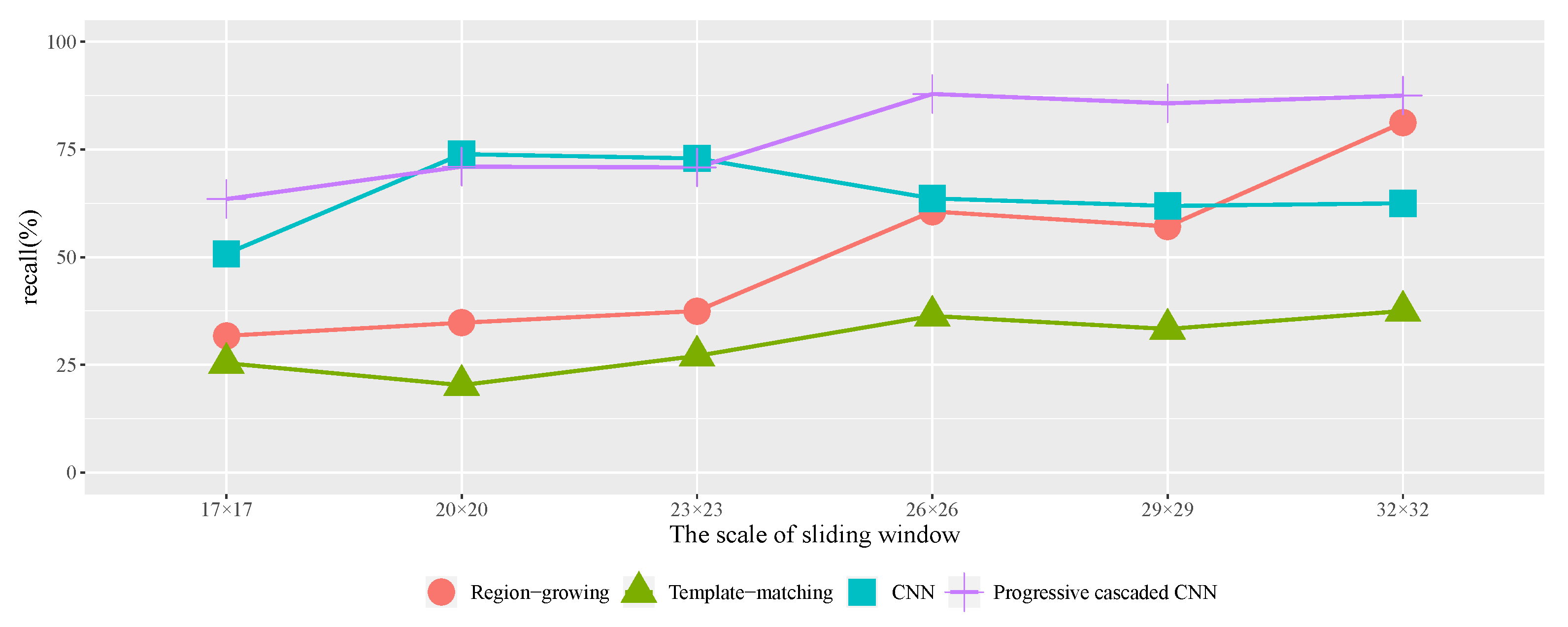
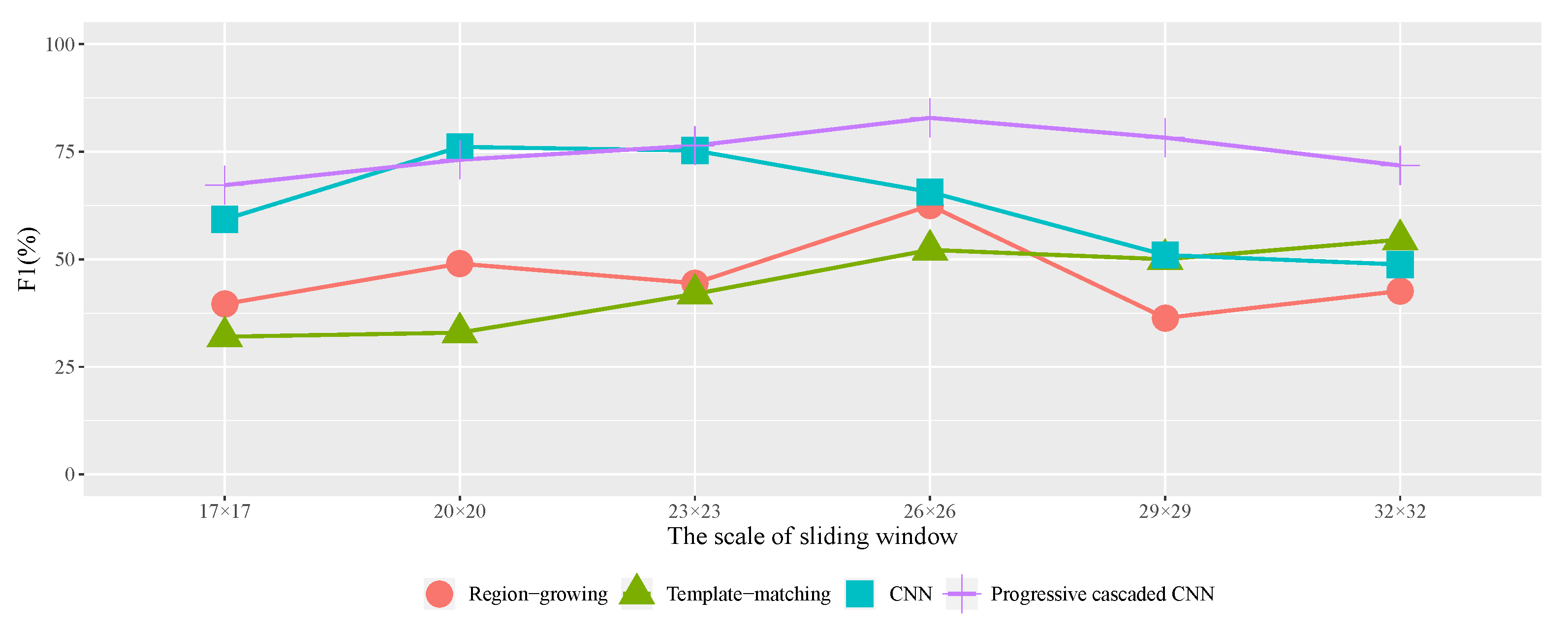
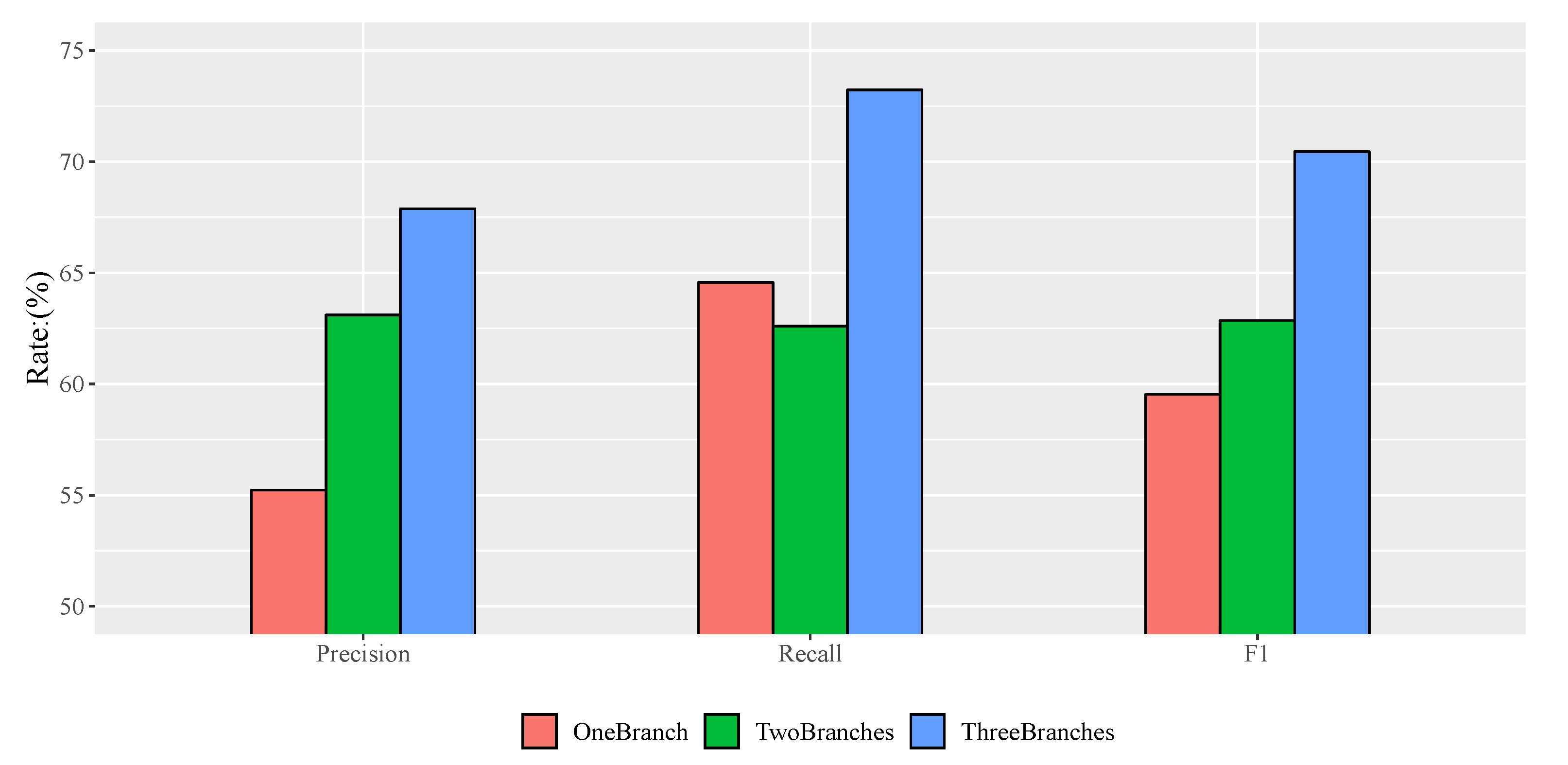
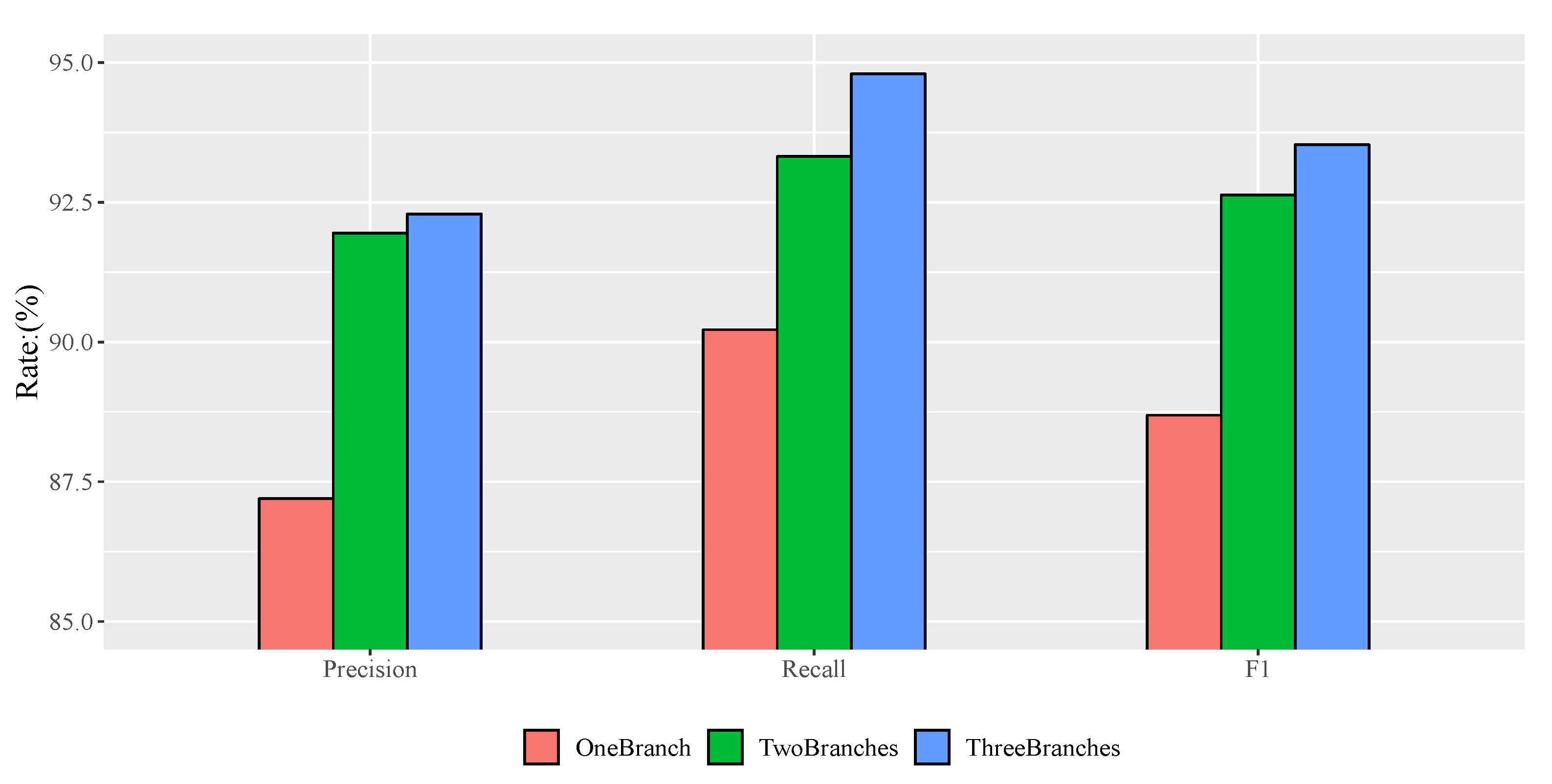
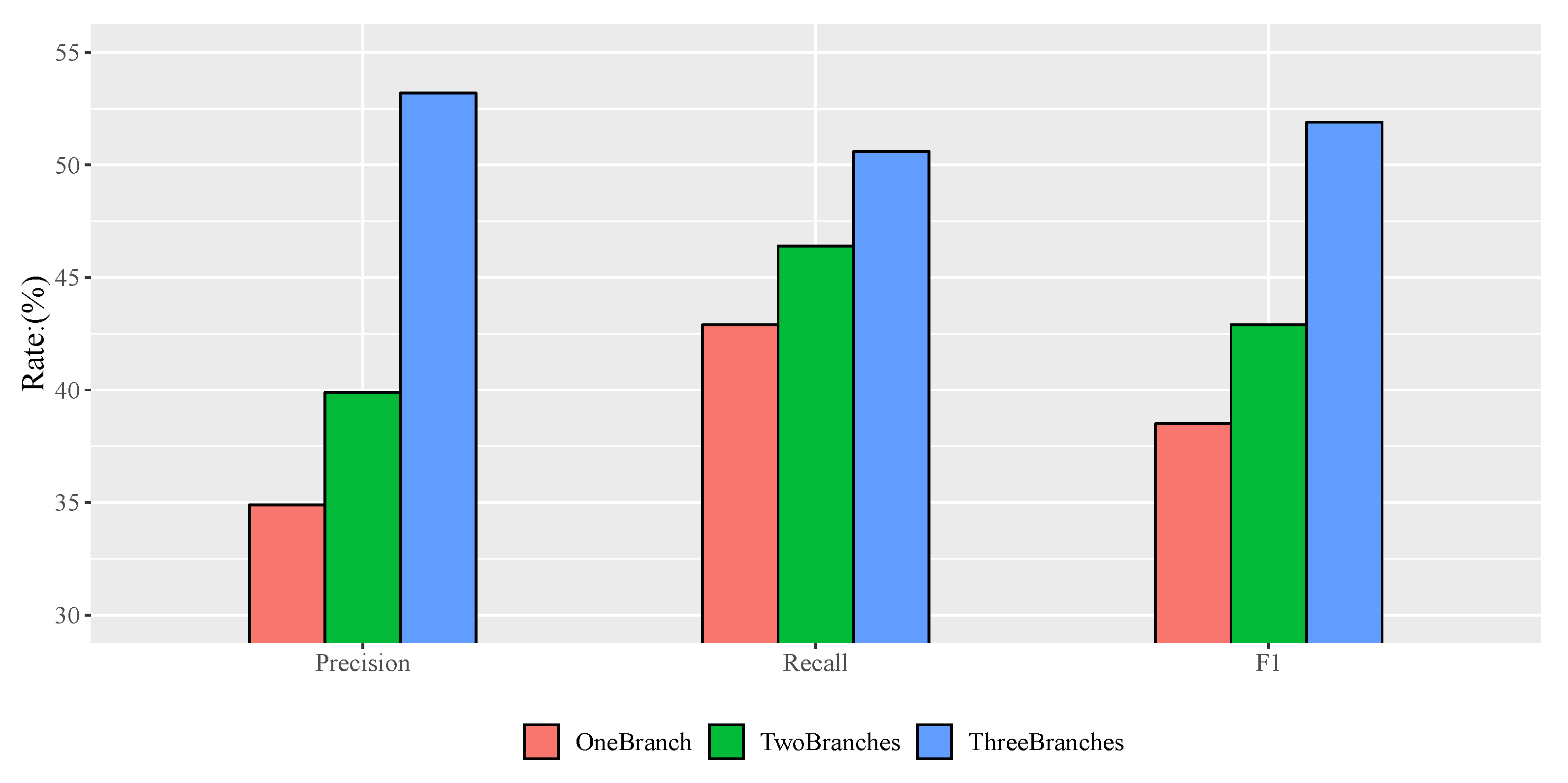
To detect single trees automatically and effectively, a single tree detection method with a high-resolution remote sensing image based on a progressive cascaded convolutional neural network is proposed in this paper. Most existing studies are based on expensive and hard-to-obtain satellite remote sensing images, and, in this study, different types of single tree samples from high-resolution images in Google Maps were calibrated and used to train cascaded convolutional neural networks. The progressive cascading of three convolutional neural networks was carried out, allowing different classification branches of the network to train samples of different difficulties. Simultaneously, a two-phase training method was adopted to speed up the training process. After model training, this model was used to detect single trees in three test areas. The test results show that the single tree detection method with a high-resolution image based on the cascaded convolutional neural network proposed in this paper is more effective than the existing methods. It is believed that the algorithm will have a wider application scenario in the future of diverse tree detection scenarios.
However, the problems encountered in the actual detection process are much more than these. For example, there are cases where adjacent trees are stuck in many scenarios. Creating effective distinguishing statistics on these trees has become an urgent problem to be solved in future work. At the same time, the single tree detection method based on sliding windows needs to scale the target window of different sizes, which will cause the problem of loss of target information and is a major cause of errors of commission and omission. For targets of different scales, even a small number of targets requires a sliding calculation of the entire image, resulting in extremely low efficiency, which will also be the focus of future work.