Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and LAI Measurements
2.2. UAV-Based Image Acquisition
2.3. Image Processing
2.3.1. Color Index (CI) Calculation
2.3.2. Texture Measurements
2.4. Regression Modeling Methods
2.4.1. Simple Linear Regression (LR)
2.4.2. Multiple Linear Regression (MLR)
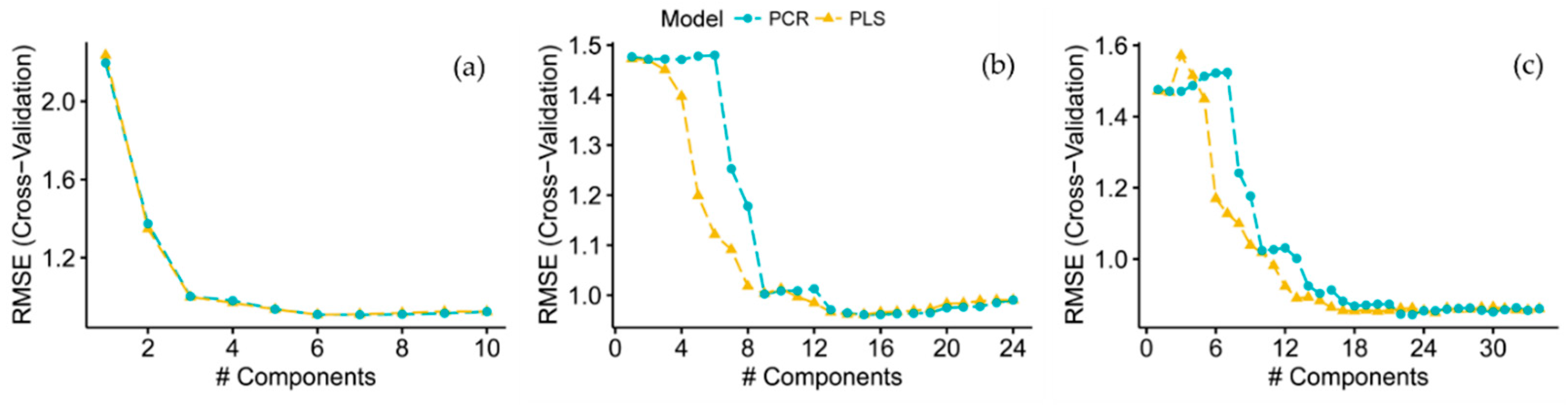
2.4.3. Principal Component Regression (PCR) and Partial Least Squares Regression (PLS)
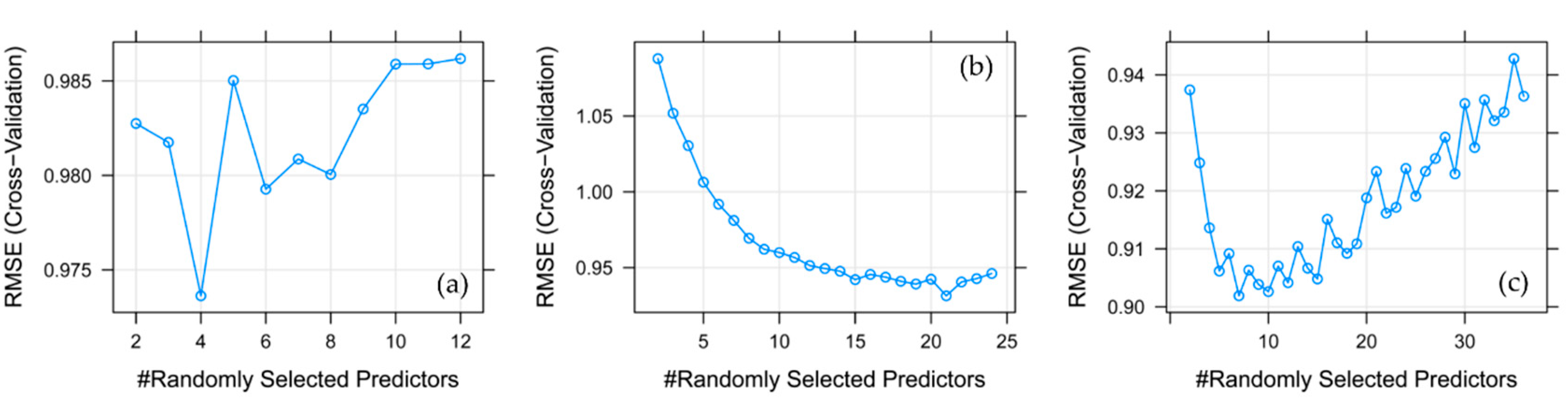
2.4.4. Random Forest (RF)
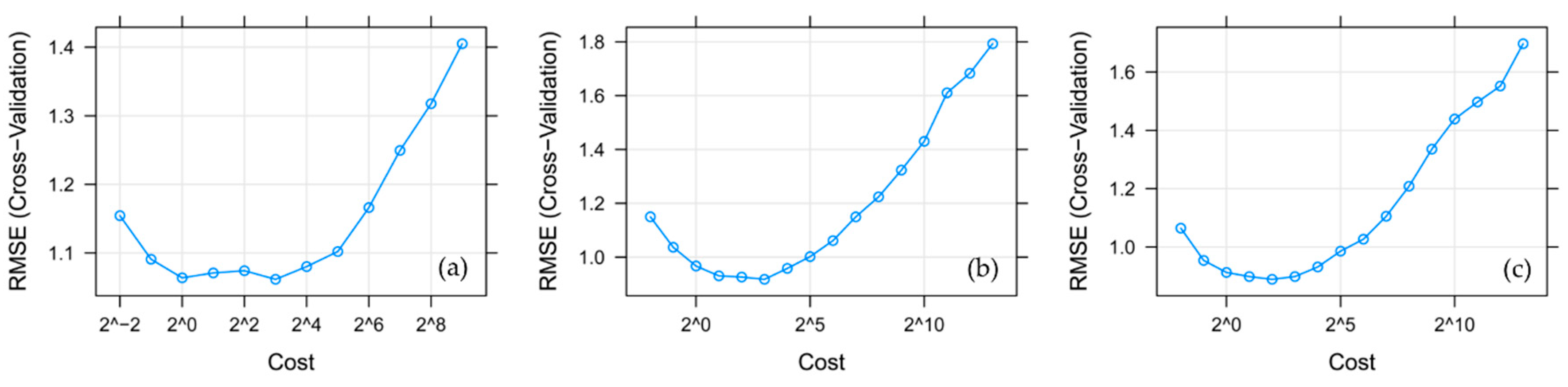
2.4.5. Support Vector Machine (SVM)
2.5. Statistical Analysis
3. Results
3.1. Variability of Rice Leaf Area Index
3.2. Simple Linear Regression Modeling for LAI Estimation
3.3. Multivariate Regression Modeling
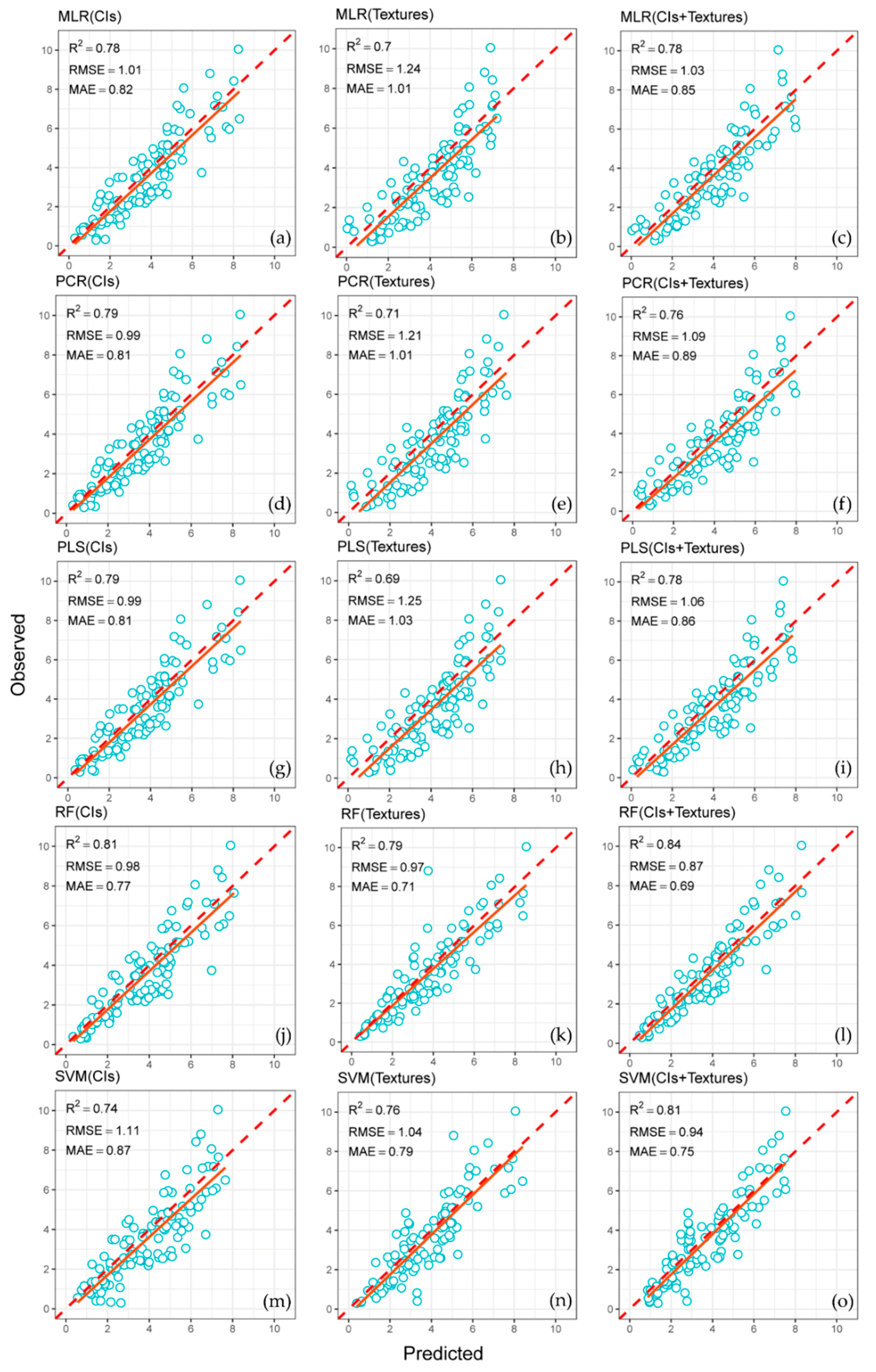
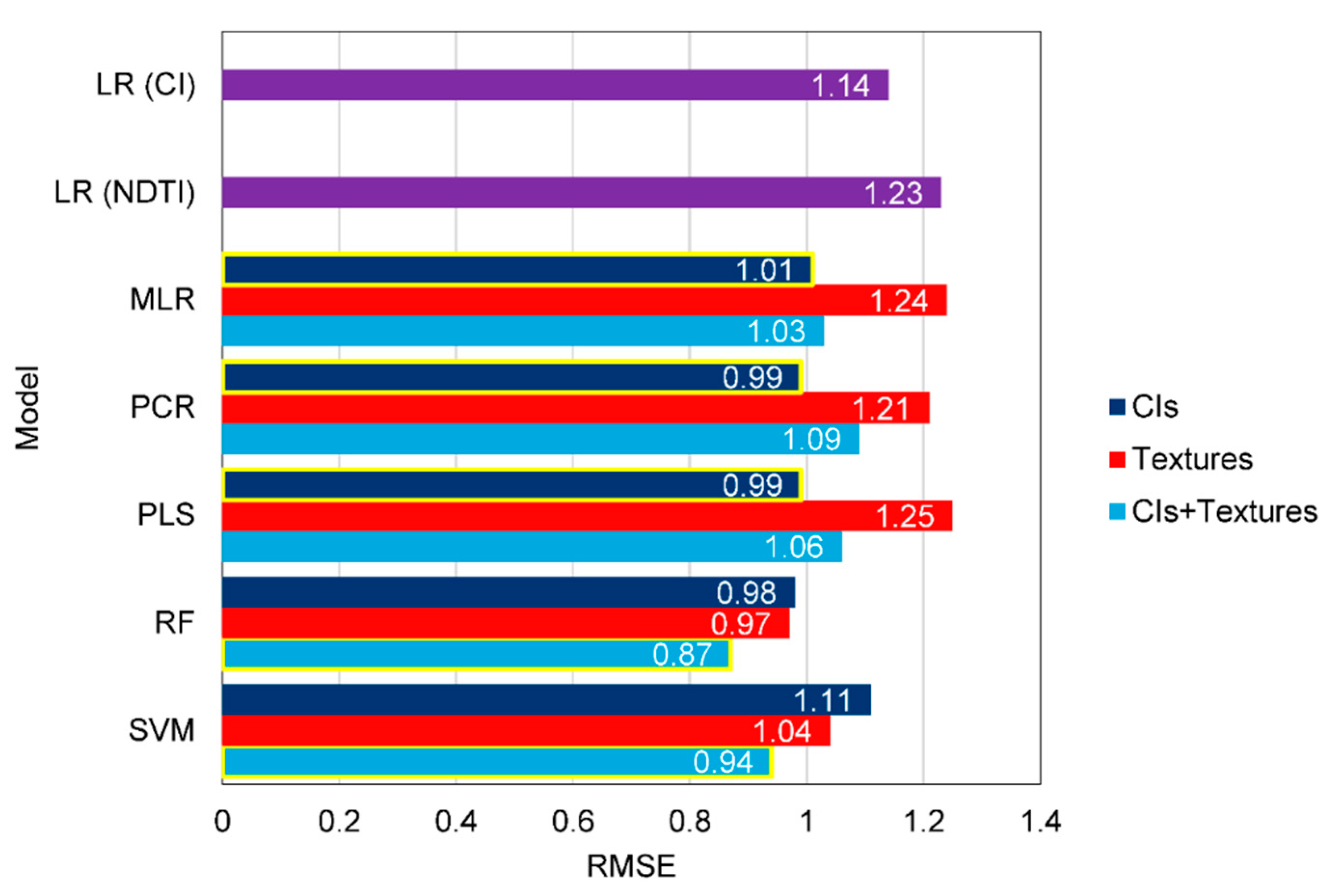
3.4. Accuracy Assessment of the Predicted LAIs
4. Discussion
4.1. Combination of Color and Texture Information for Crop LAI Estimation
4.2. Comparison of Different Multivariate Regression Methods
4.3. Potential of Consumer-Grade UAV-Based Digital Imagery for Crop Monitoring
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: II. The Effect of Varying Nutrient Supply on Net Assimilation Rate and Leaf Area. Ann. Bot. 1947, 11, 375–407. [Google Scholar] [CrossRef]
- Wells, R. Soybean Growth Response to Plant Density: Relationships among Canopy Photosynthesis, Leaf Area, and Light Interception. Crop Sci. 1991, 31, 755–761. [Google Scholar] [CrossRef]
- Loomis, R.S.; Williams, W.A. Maximum Crop Productivity: An Extimate 1. Crop Sci. 1963, 3, 67–72. [Google Scholar] [CrossRef]
- Richards, R.A.; Townley-Smith, T.F. Variation in leaf area development and its effect on water use, yield and harvest index of droughted wheat. Aust. J. Agric. Res. 1987, 38, 983–992. [Google Scholar] [CrossRef]
- Duchemin, B.; Maisongrande, P.; Boulet, G.; Benhadj, I. A simple algorithm for yield estimates: Evaluation for semi-arid irrigated winter wheat monitored with green leaf area index. Environ. Model. Softw. 2008, 23, 876–892. [Google Scholar] [CrossRef]
- Jefferies, R.A.; Mackerron, D.K.L. Responses of potato genotypes to drought. II. Leaf area index, growth and yield. Ann. Appl. Biol. 2010, 122, 105–112. [Google Scholar] [CrossRef]
- Li, S.; Ding, X.; Kuang, Q.; Ata-Ul-Karim, S.T.; Cheng, T.; Liu, X.; Tan, Y.; Zhu, Y.; Cao, W.; Cao, Q. Potential of UAV-Based Active Sensing for Monitoring Rice Leaf Nitrogen Status. Front. Plant Sci. 2018, 9, 1834. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Liu, Q.; Liu, Q.; Li, X. LAI retrieval and uncertainty evaluations for typical row-planted crops at different growth stages. Remote Sens. Environ. 2008, 112, 94–106. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Luo, J.; Jin, X.; Xu, Y.; Yang, W. Quantification winter wheat LAI with HJ-1CCD image features over multiple growing seasons. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 104–112. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Liang, Y.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Using a Portable Active Sensor to Monitor Growth Parameters and Predict Grain Yield of Winter Wheat. Sensors 2019, 19, 1108. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Ge, X.; Shen, P.; Li, W.; Liu, X.; Cao, Q.; Zhu, Y.; Cao, W.; Tian, Y. Predicting Rice Grain Yield Based on Dynamic Changes in Vegetation Indexes during Early to Mid-Growth Stages. Remote Sens. 2019, 11, 387. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Yao, X.; Wang, N.; Liu, Y.; Cheng, T.; Tian, Y.; Chen, Q.; Zhu, Y. Estimation of Wheat LAI at Middle to High Levels Using Unmanned Aerial Vehicle Narrowband Multispectral Imagery. Remote Sens. 2017, 9, 1304. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Jin, X.; Yuan, H.; Li, Z.; Zhou, C.; Yang, G.; Tian, Q.; Yue, J.; Feng, H.; et al. A Comparison of Crop Parameters Estimation Using Images from UAV-Mounted Snapshot Hyperspectral Sensor and High-Definition Digital Camera. Remote Sens. 2018, 10, 1138. [Google Scholar] [CrossRef]
- Xu, X.Q.; Lu, J.S.; Zhang, N.; Yang, T.C.; He, J.Y.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Inversion of rice canopy chlorophyll content and leaf area index based on coupling of radiative transfer and Bayesian network models. ISPRS J. Photogramm. Remote Sens. 2019, 150, 185–196. [Google Scholar] [CrossRef]
- Kanning, M.; Kühling, I.; Trautz, D.; Jarmer, T. High-Resolution UAV-Based Hyperspectral Imagery for LAI and Chlorophyll Estimations from Wheat for Yield Prediction. Remote Sens. 2018, 10, 2000. [Google Scholar] [CrossRef]
- Lu, N.; Zhou, J.; Han, Z.; Li, D.; Cao, Q.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Improved estimation of aboveground biomass in wheat from RGB imagery and point cloud data acquired with a low-cost unmanned aerial vehicle system. Plant Methods 2019, 15, 17. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, Q. Comparison RGB Digital Camera with Active Canopy Sensor Based on UAV for Rice Nitrogen Status Monitoring. In Proceedings of the 2018 7th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Hangzhou, China, 6–9 August 2018. [Google Scholar]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2019, 20, 611–629. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Hong, G.; Luo, M.R.; Rhodes, P.A. A study of digital camera colorimetric characterization based on polynomial modeling. Color Res. Appl. 2001, 26, 76–84. [Google Scholar] [CrossRef]
- Richardson, M.D.; Karcher, D.E.; Purcell, L.C. Quantifying turfgrass cover using digital image analysis. Crop Sci. 2001, 41, 1884–1888. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color Indices for Weed Identification Under Various Soil, Residue, and Lighting Conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Meyer, G.E.; Neto, J.C. Verification of color vegetation indices for automated crop imaging applications. Comput. Electron. Agric. 2008, 63, 282–293. [Google Scholar] [CrossRef]
- Mao, W.; Wang, Y.; Wang, Y. Real-time detection of between-row weeds using machine vision. In Proceedings of the 2003 ASAE Annual Meeting; American Society of Agricultural and Biological Engineers, Las Vegas, NV, USA, 27–30 July 2003. [Google Scholar]
- Neto, J.C. A combined statistical-soft computing approach for classification and mapping weed species in minimum -tillage systems. Ph.D. Thesis, University of Nebraska – Lincoln, Lincoln, NE, USA, August 2004. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Kawashima, S.; Nakatani, M. An algorithm for estimating chlorophyll content in leaves using a video camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially located platform and aerial photography for documentation of grazing impacts on wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Hague, T.; Tillett, N.D.; Wheeler, H. Automated crop and weed monitoring in widely spaced cereals. Precis. Agric. 2006, 7, 21–32. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Volume 26. [Google Scholar]
- Massy, W.F. Principal components regression in exploratory statistical research. J. Am. Stat. Assoc. 1965, 60, 234–256. [Google Scholar] [CrossRef]
- Williams, P.; Norris, K. Near-Infrared Technology in the Agricultural and Food Industries; American Association of Cereal Chemists, Inc.: St. Paul, MN, USA, 1987. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Caputo, B.; Sim, K.; Furesjo, F.; Smola, A. Appearance-based object recognition using SVMs: Which kernel should I use? In Proceedings of the NIPS Workshop on Statistical Methods for Computational Experiments in Visual Processing and Computer Vision, Whistler, BC, Canada, 13 December 2002. [Google Scholar]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab-an S4 package for kernel methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef]
- Kaivosoja, J.; Näsi, R.; Hakala, T.; Viljanen, N.; Honkavaara, E. Applying Different Remote Sensing Data to Determine Relative Biomass Estimations of Cereals for Precision Fertilization Task Generation. In Proceedings of the 8th International Conference on Information and Communication Technologies in Agriculture, Food and Environment (HAICTA 2017), Chania, Greece, 21–24 September 2017. [Google Scholar]
- Zhou, X.; Zheng, H.B.; Xu, X.Q.; He, J.Y.; Ge, X.K.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on UAV ultrahigh-ground-resolution image textures and vegetation indices. ISPRS J. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Yang, G.; Li, Z. A Comparison of Regression Techniques for Estimation of Above-Ground Winter Wheat Biomass Using Near-Surface Spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Myers, R.H. Classical and Modern Regression with Applications; Duxbury Press: Belmont, CA, USA, 1990. [Google Scholar]
- Li, W.; Niu, Z.; Wang, C.; Huang, W.; Chen, H.; Gao, S.; Li, D.; Muhammad, S. Combined use of airborne LiDAR and satellite GF-1 data to estimate leaf area index, height, and aboveground biomass of maize during peak growing season. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4489–4501. [Google Scholar] [CrossRef]
- Ni, J.; Yao, L.; Zhang, J.; Cao, W.; Zhu, Y.; Tai, X. Development of an Unmanned Aerial Vehicle-Borne Crop-Growth Monitoring System. Sensors 2017, 17, 502. [Google Scholar] [CrossRef] [PubMed]
- Snow, C. Seven Trends That Will Shape the Commercial Drone Industry in 2019. Available online: https://www.forbes.com/sites/colinsnow/2019/01/07/seven-trends-that-will-shape-the-commercial-drone-industry-in-2019/ (accessed on 31 May 2019).
- DroneAG Developing Skippy Scout App to Automate Drone Crop Scouting | Farm and Plant Blog. Available online: https://www.farmandplant.ie/blog/ag-equipment-news/2019/04/droneag-developing-skippy-scout-app-to-automate-drone-crop-scouting (accessed on 19 July 2019).
- Sanches, G.M.; Duft, D.G.; Kölln, O.T.; Luciano, A.C.D.S.; De Castro, S.G.Q.; Okuno, F.M.; Franco, H.C.J. The potential for RGB images obtained using unmanned aerial vehicle to assess and predict yield in sugarcane fields. Int. J. Remote Sens. 2018, 39, 5402–5414. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.; Li, Y.; Cen, H.; Zhu, J.; Yin, W.; Wu, W.; Zhu, H.; Sun, D.; Zhou, W.; He, Y. Combining UAV-Based Vegetation Indices and Image Classification to Estimate Flower Number in Oilseed Rape. Remote Sens. 2018, 10, 1484. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Peña, J.M. An automatic object-based method for optimal thresholding in UAV images: Application for vegetation detection in herbaceous crops. Comput. Electron. Agric. 2015, 114, 43–52. [Google Scholar] [CrossRef]
- Rasmussen, J.; Ntakos, G.; Nielsen, J.; Svensgaard, J.; Poulsen, R.N.; Christensen, S. Are vegetation indices derived from consumer-grade cameras mounted on UAVs sufficiently reliable for assessing experimental plots? Eur. J. Agron. 2016, 74, 75–92. [Google Scholar] [CrossRef]
- Duan, T.; Zheng, B.; Guo, W.; Ninomiya, S.; Guo, Y.; Chapman, S.C. Comparison of ground cover estimates from experiment plots in cotton, sorghum and sugarcane based on images and ortho-mosaics captured by UAV. Funct. Plant Biol. 2017, 44, 169–183. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating Biomass of Barley Using Crop Surface Models (CSMs) Derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Wu, J.; Lee, D.; Jiao, L.; Shi, G. Laplacian pyramid-based downsampling combined with directionlet interpolation for low-bit rate compression. In Proceedings of the MIPPR 2009: Remote Sensing and GIS Data Processing and Other Applications; International Society for Optics and Photonics, Yichang, China, 30 October–1 November 2009. [Google Scholar]
- Wang, Y.; Zhang, K.; Tang, C.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Estimation of Rice Growth Parameters Based on Linear Mixed-Effect Model Using Multispectral Images from Fixed-Wing Unmanned Aerial Vehicles. Remote Sens. 2019, 11, 1371. [Google Scholar] [CrossRef]
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer: New York, NY, USA, 2009. [Google Scholar]
- Kuwata, K.; Shibasaki, R. Estimating crop yields with deep learning and remotely sensed data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
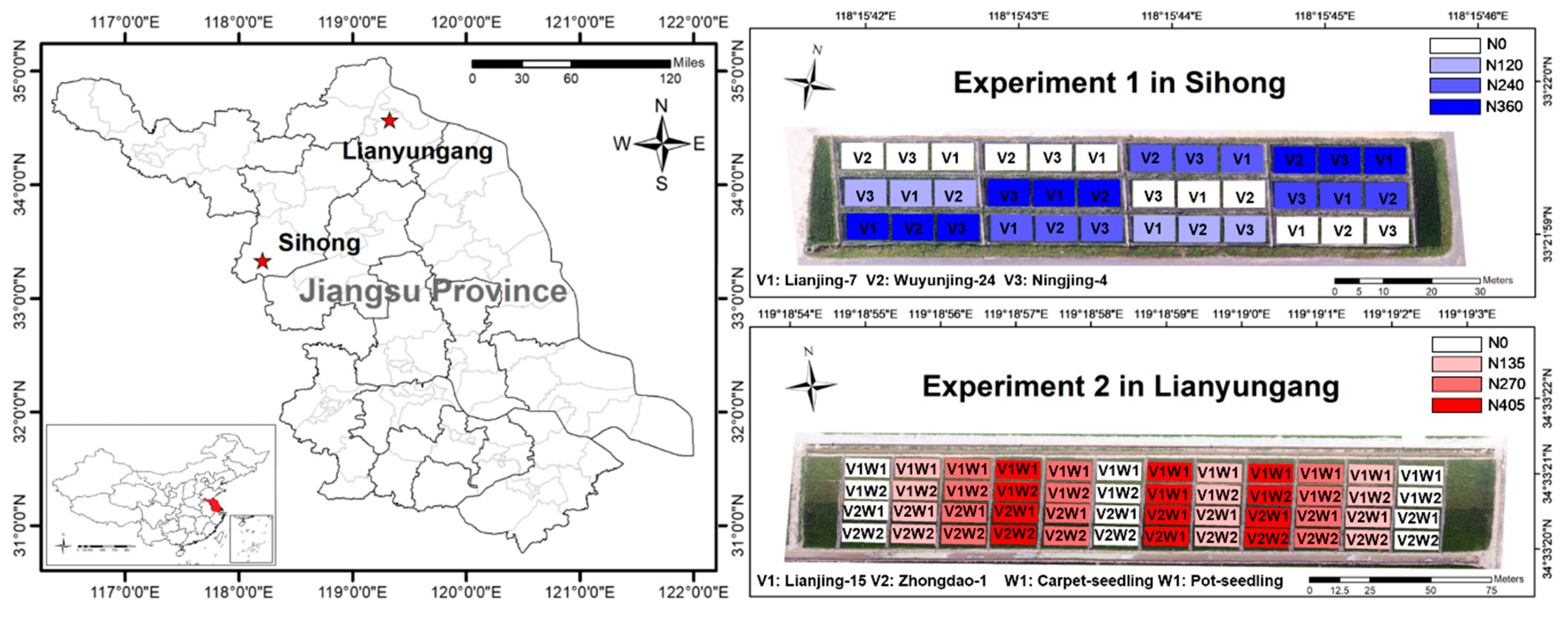

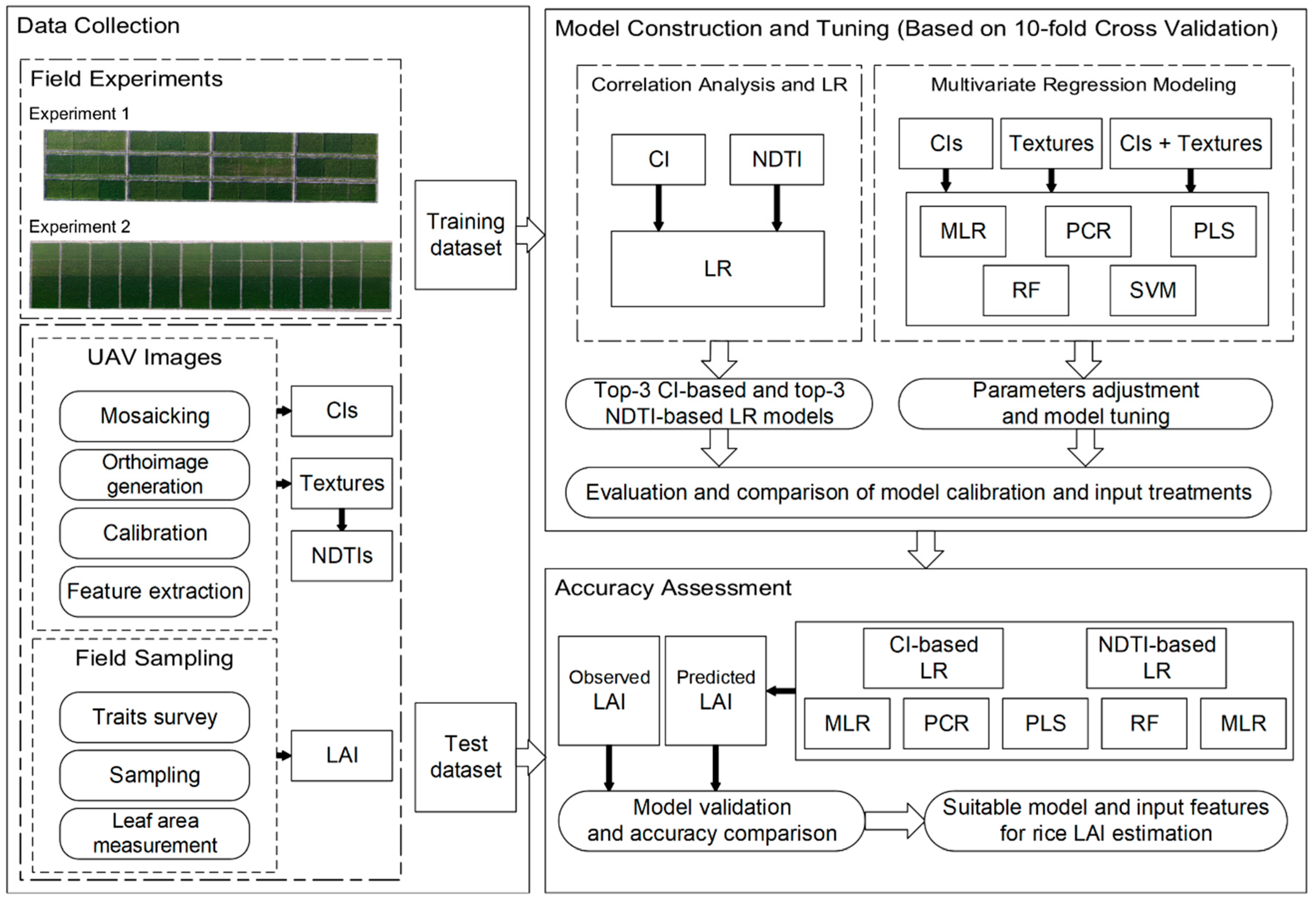
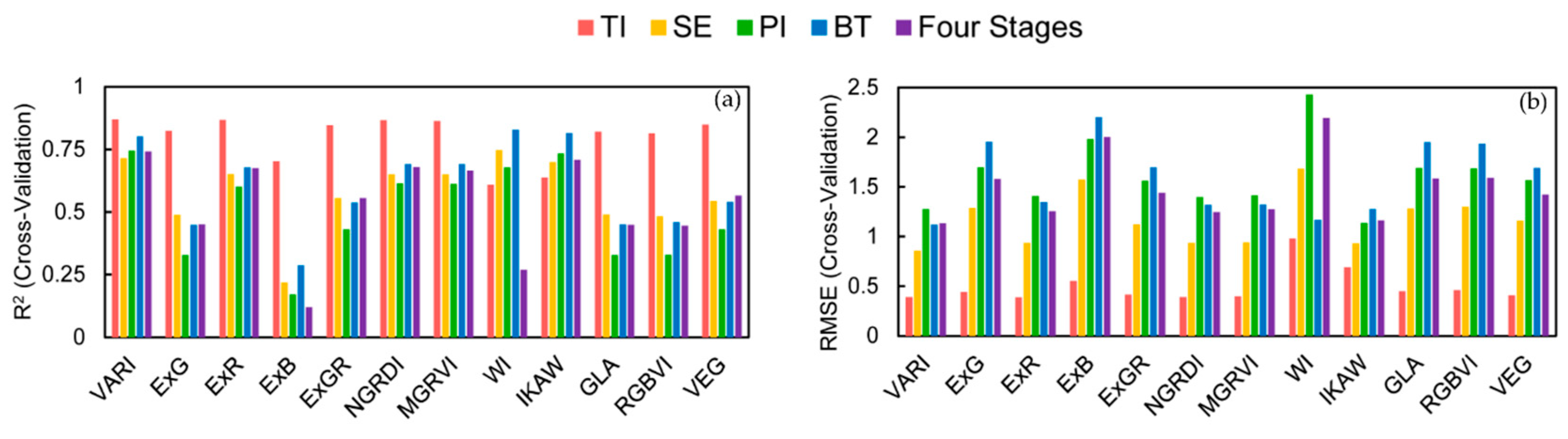
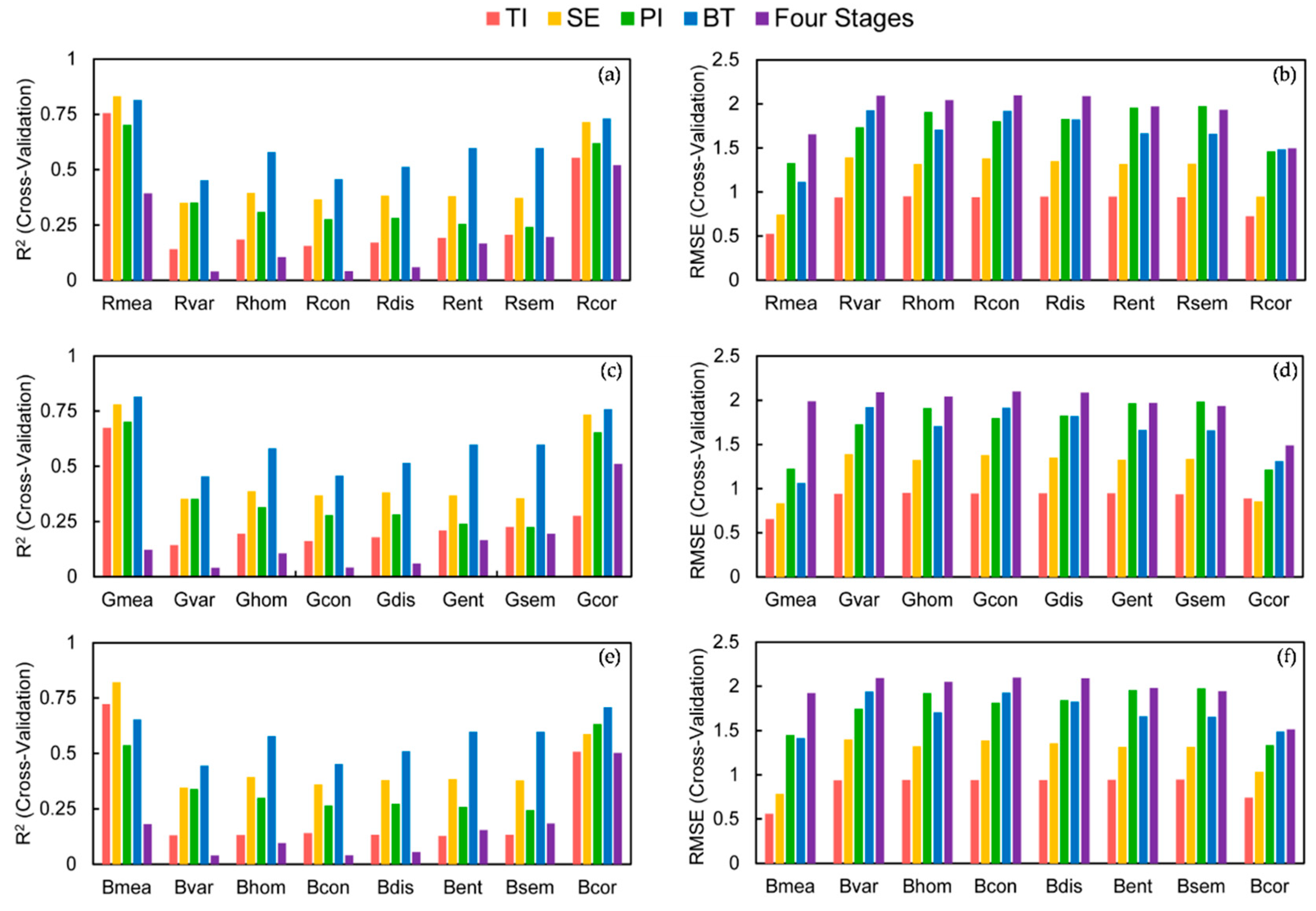


| Experiment | Year | Location | Samples | Transplanting Date | Sensing and Sampling Date |
|---|---|---|---|---|---|
| Experiment 1 | 2016 | Sihong | 144 | 25 June | 27 July (TI), |
| 3 August (SE), | |||||
| 11 August (PI), | |||||
| 18 August (BT) | |||||
| Experiment 2 | 2017 | Lianyungang | 192 | 19 June | 27 July (TI), |
| 3 August (SE), | |||||
| 10 August (PI), | |||||
| 20 August (BT) |
| CI | Name | Formula | Reference |
|---|---|---|---|
| VARI | Visible Atmospherically Resistant Index | (g − r)/(g + r − b) | Gitelson et al. [28] |
| ExG | Excess Green Vegetation Index | 2g − r − b | Woebbecke et al. [29] |
| ExR | Excess Red Vegetation Index | 1.4r − g | Meyer et al. [30] |
| ExB | Excess Blue Vegetation Index | 1.4b − g | Mao et al. [31] |
| ExGR | Excess Green minus Excess Red Vegetation Index | E × G − E × R | Neto et al. [32] |
| NGRDI | Normalized Green-Red Difference Index | (g − r)/(g + r) | Tucker [33] |
| MGRVI | Modified Green Red Vegetation Index | (g2 − r2)/(g2 + r2) | Tucker [33] |
| WI | Woebbecke Index | (g − b)/(r − g) | Woebbecke et al. [29] |
| IKAW | Kawashima Index | (r − b)/(r + b) | Kawashima et al. [34] |
| GLA | Green Leaf Algorithm | (2g − r − b)/(2g + r + b) | Louhaichi et al. [35] |
| RGBVI | Red Green Blue Vegetation Index | (g2 − b * r)/(g2 + b * r) | Bendig et al. [36] |
| VEG | Vegetativen | g/(rab(1−a)), a = 0.667 | Hague et al. [37] |
| Stages | Samples | LAI | ||||
|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | CV | ||
| Training dataset | ||||||
| TI | 56 | 0.25 | 4.36 | 1.93 | 0.99 | 51.26% |
| SE | 56 | 0.41 | 6.85 | 3.36 | 1.57 | 46.76% |
| PI | 56 | 0.82 | 8.67 | 4.05 | 2.00 | 49.27% |
| BT | 56 | 0.93 | 10.34 | 5.08 | 2.29 | 45.08% |
| All stages | 224 | 0.25 | 10.34 | 3.60 | 2.11 | 58.48% |
| Test dataset | ||||||
| TI | 28 | 0.29 | 3.98 | 1.94 | 0.97 | 50.28% |
| SE | 28 | 0.40 | 5.17 | 3.06 | 1.50 | 48.90% |
| PI | 28 | 0.81 | 8.07 | 3.92 | 2.03 | 51.82% |
| BT | 28 | 1.15 | 10.05 | 4.99 | 2.28 | 45.58% |
| All stages | 112 | 0.29 | 10.05 | 3.48 | 2.07 | 59.69% |
| Index | Variable | Model Equation | R2 | RMSE |
|---|---|---|---|---|
| CI | VARI | LAI = 14.836 * VARI − 0.6889 | 0.74 | 1.13 |
| IKAW | LAI = −32.687 * IKAW + 4.2477 | 0.71 | 1.16 | |
| NGRDI | LAI = 23.922 * NGRDI − 0.5704 | 0.68 | 1.24 | |
| NDTI | NDTI (Rmea, Gmea) | LAI = −23.123 * NDTI(Rmea, Gmea) − 0.5719 | 0.72 | 1.15 |
| NDTI (Rmea, Bmea) | LAI = −29.595 * NDTI(Rmea, Bmea) + 4.3718 | 0.71 | 1.17 | |
| NDTI (Rcor, Bcor) | LAI = −22.009 * NDTI(Rcor, Bcor) + 4.548 | 0.58 | 1.38 |
| Method | CI | Textures | Cis + Textures | |||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| MLR | 0.82 | 0.92 | 0.81 | 0.99 | 0.85 | 0.86 |
| PLS | 0.83 | 0.91 | 0.82 | 0.96 | 0.86 | 0.84 |
| PCR | 0.83 | 0.91 | 0.82 | 0.96 | 0.86 | 0.84 |
| RF | 0.80 | 0.97 | 0.79 | 0.93 | 0.84 | 0.90 |
| SVM | 0.76 | 1.06 | 0.83 | 0.92 | 0.85 | 0.89 |
| Index | Variable | R2 | RMSE | MAE |
|---|---|---|---|---|
| CI | VARI | 0.70 | 1.14 | 0.94 |
| IKAW | 0.65 | 1.31 | 1.06 | |
| NGRDI | 0.66 | 1.22 | 0.98 | |
| NDTI | NDTI (Rmea, Gmea) | 0.65 | 1.23 | 0.98 |
| NDTI (Rmea, Bmea) | 0.65 | 1.30 | 1.02 | |
| NDTI (Rcor, Bcor) | 0.41 | 1.72 | 1.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sens. 2019, 11, 1763. https://doi.org/10.3390/rs11151763
Li S, Yuan F, Ata-UI-Karim ST, Zheng H, Cheng T, Liu X, Tian Y, Zhu Y, Cao W, Cao Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sensing. 2019; 11(15):1763. https://doi.org/10.3390/rs11151763
Chicago/Turabian StyleLi, Songyang, Fei Yuan, Syed Tahir Ata-UI-Karim, Hengbiao Zheng, Tao Cheng, Xiaojun Liu, Yongchao Tian, Yan Zhu, Weixing Cao, and Qiang Cao. 2019. "Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation" Remote Sensing 11, no. 15: 1763. https://doi.org/10.3390/rs11151763
APA StyleLi, S., Yuan, F., Ata-UI-Karim, S. T., Zheng, H., Cheng, T., Liu, X., Tian, Y., Zhu, Y., Cao, W., & Cao, Q. (2019). Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sensing, 11(15), 1763. https://doi.org/10.3390/rs11151763










