Improving the Positioning Accuracy of Satellite-Borne GNSS-R Specular Reflection Point on Sea Surface Based on the Ocean Tidal Correction Positioning Method
Abstract
1. Introduction
2. Data, Methodology and Results
2.1. Data and Model
2.1.1. TDS-1 Satellite Data
2.1.2. EGM2008 Model
2.1.3. TPXO8 Model
2.2. Methodology
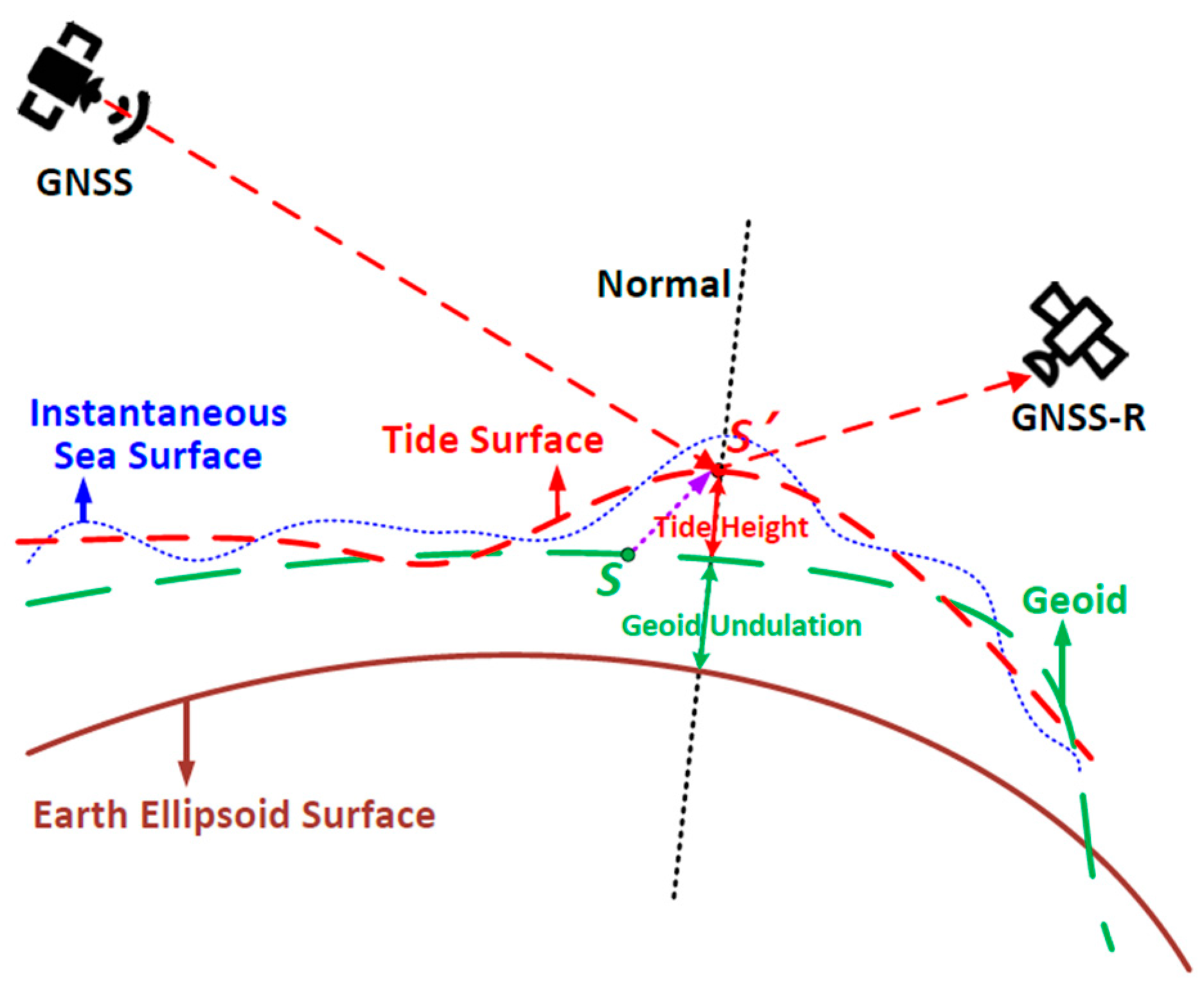
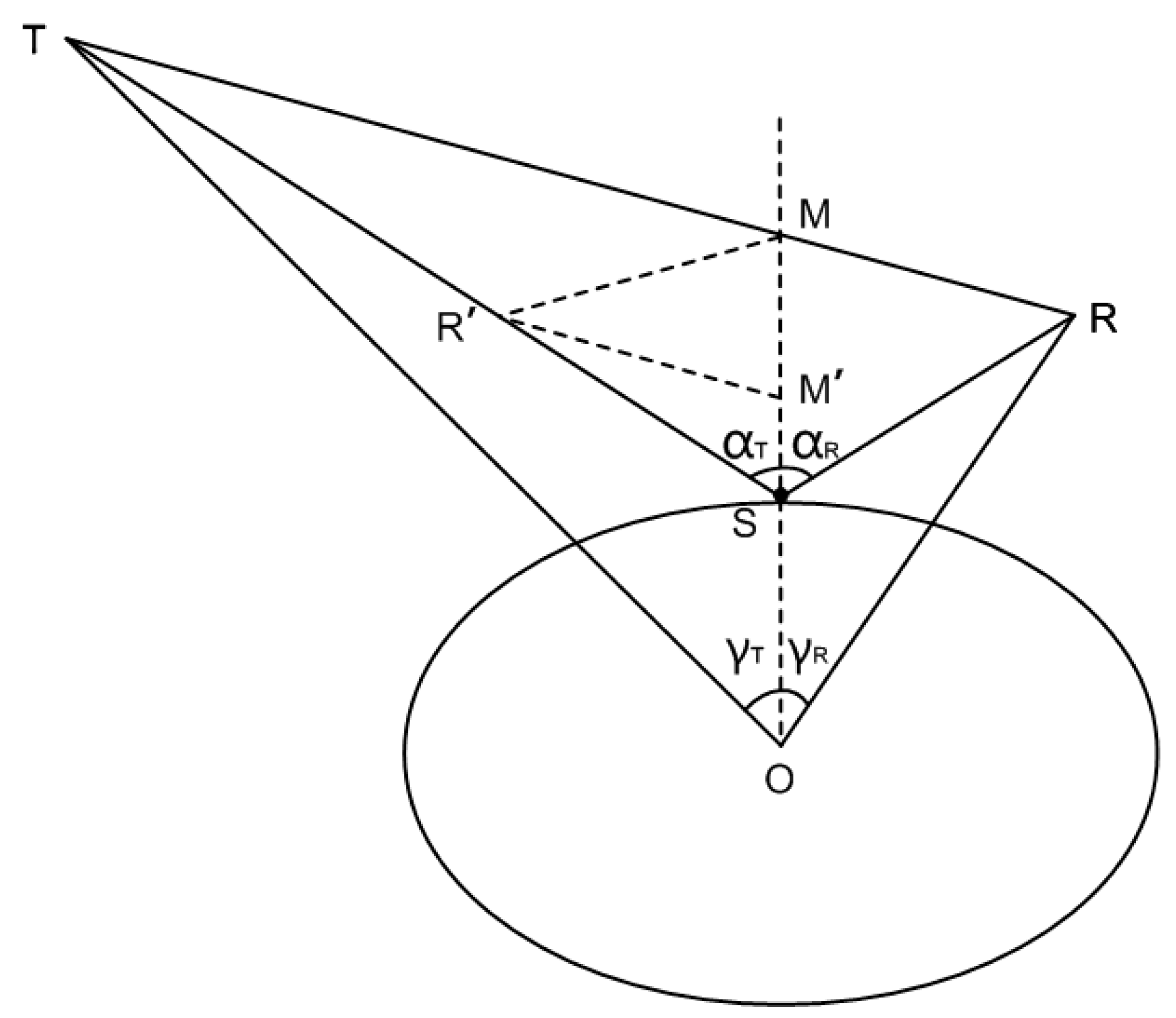
2.2.1. Correction Positioning
2.2.2. Ocean Tidal Correction
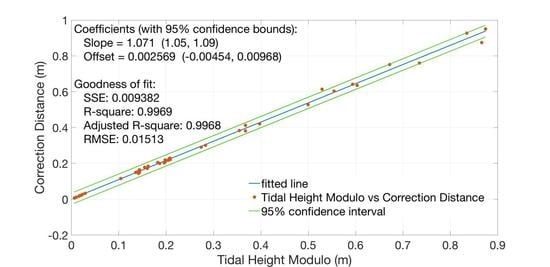
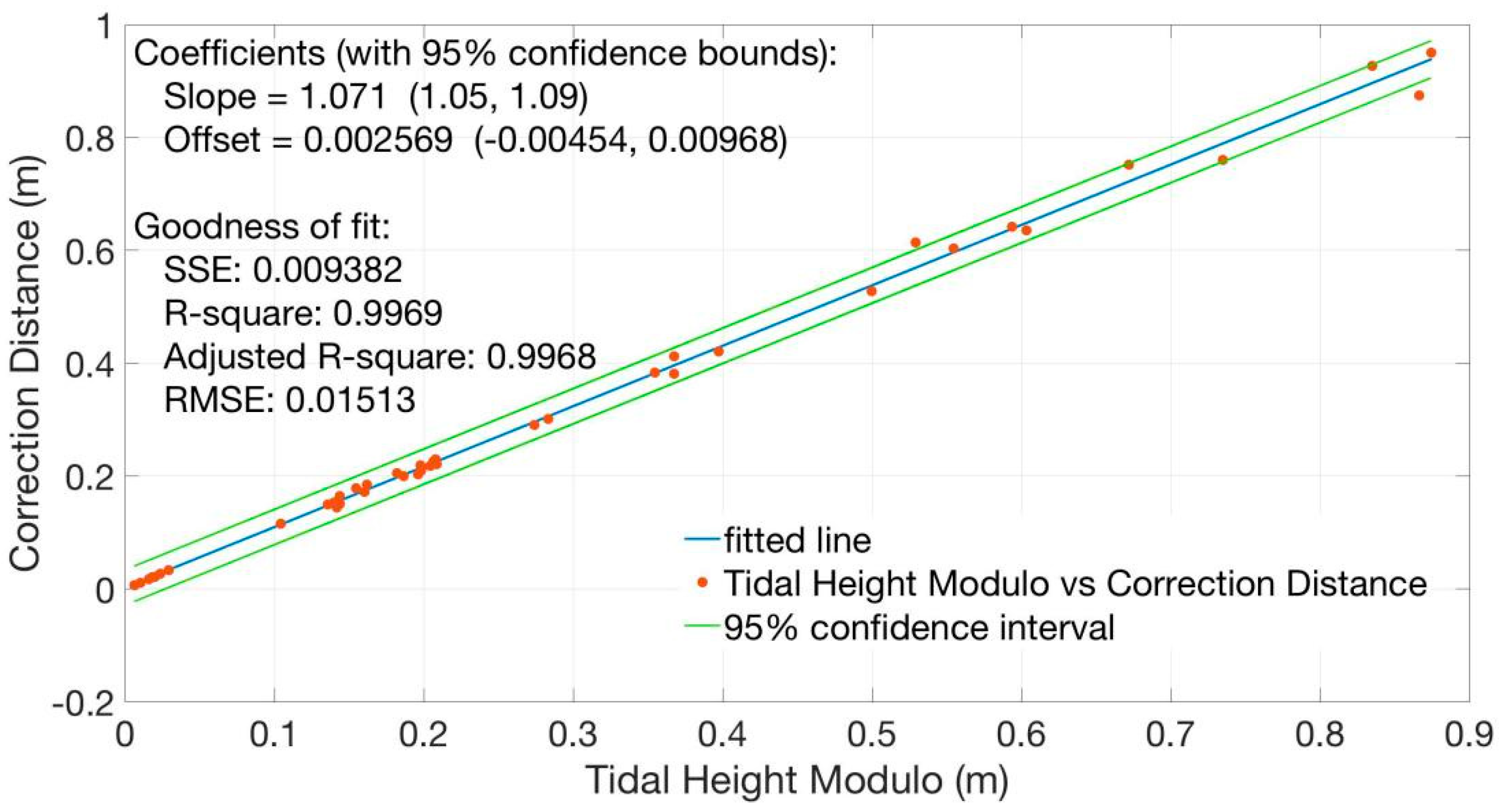
2.3. Results
3. Discussion
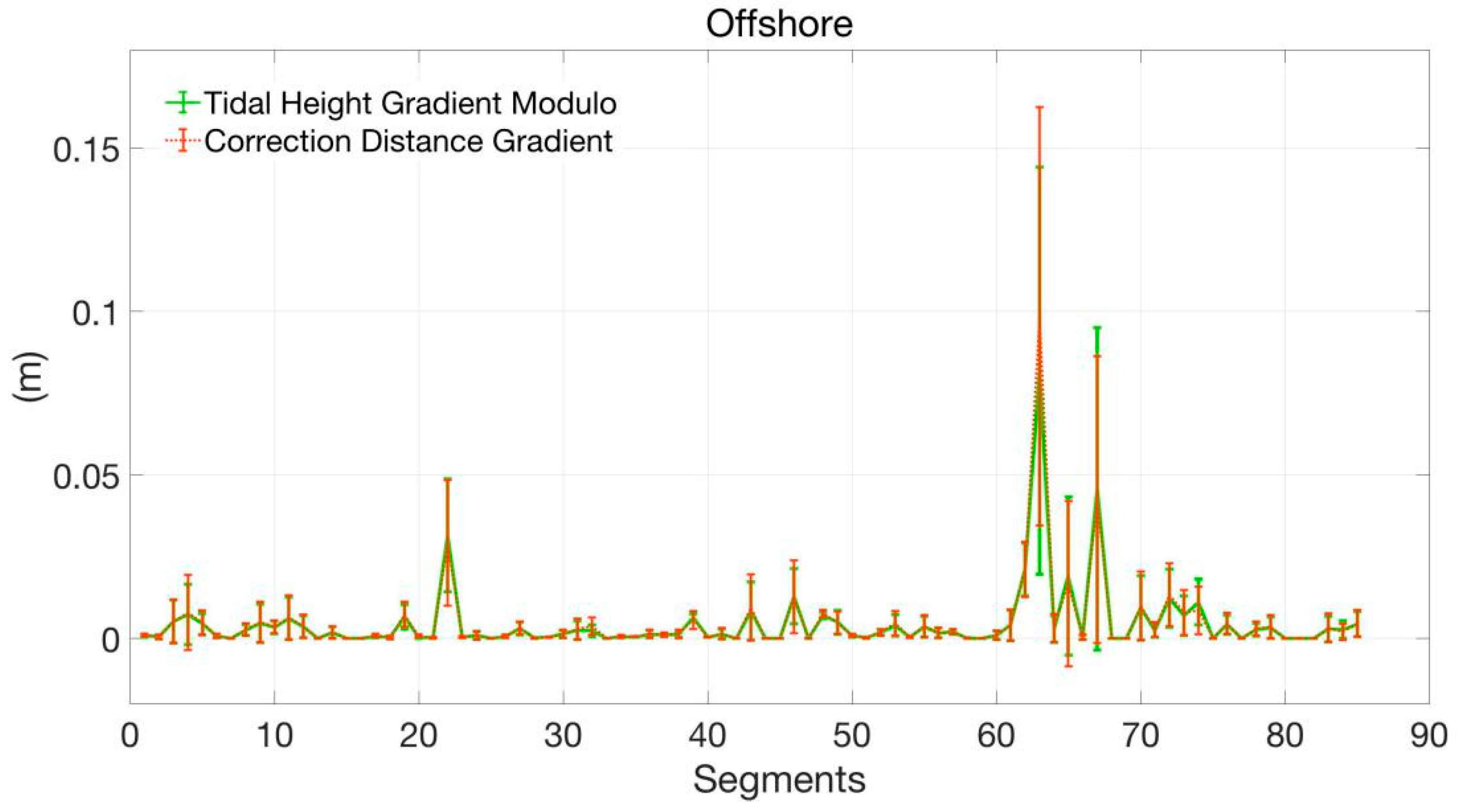
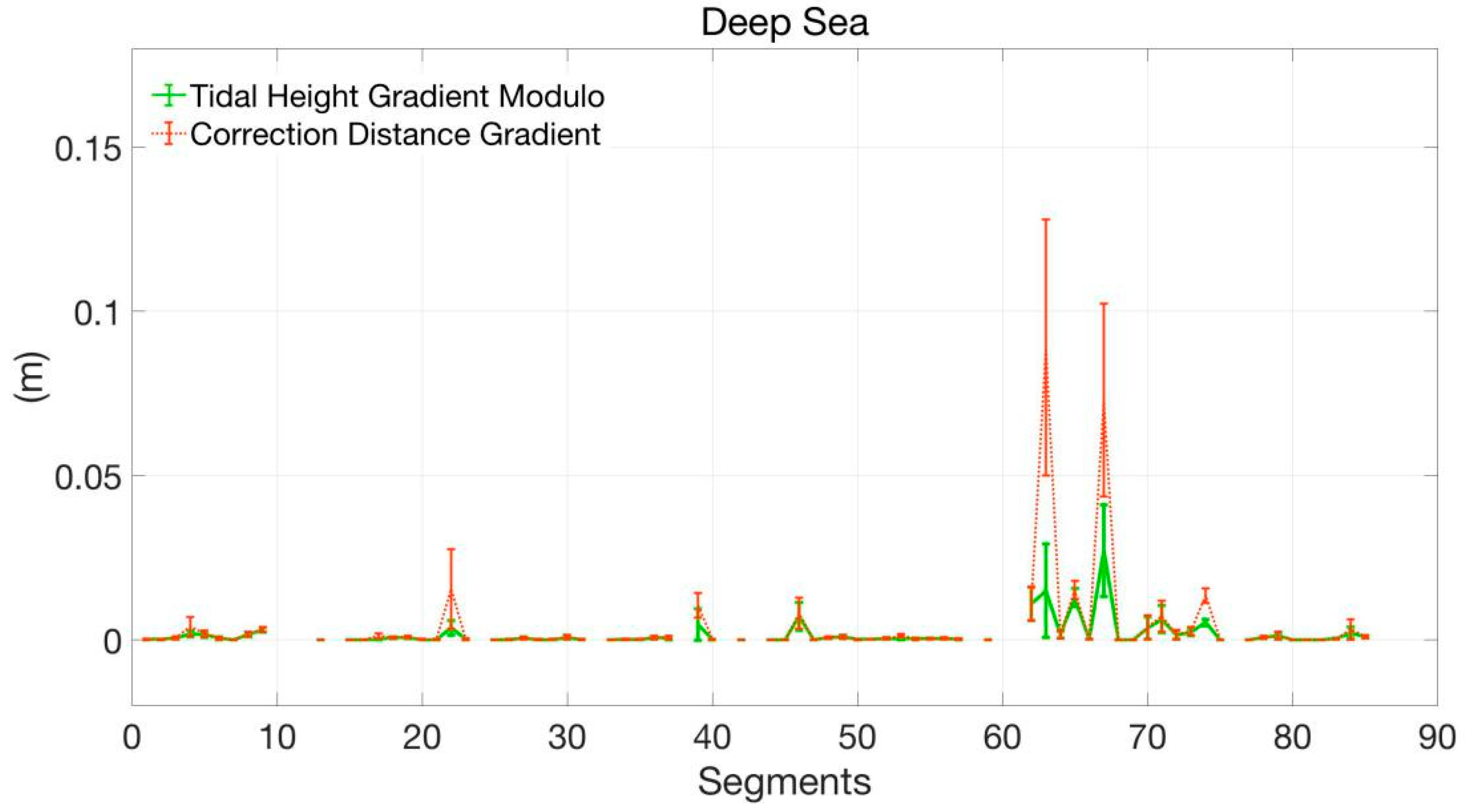
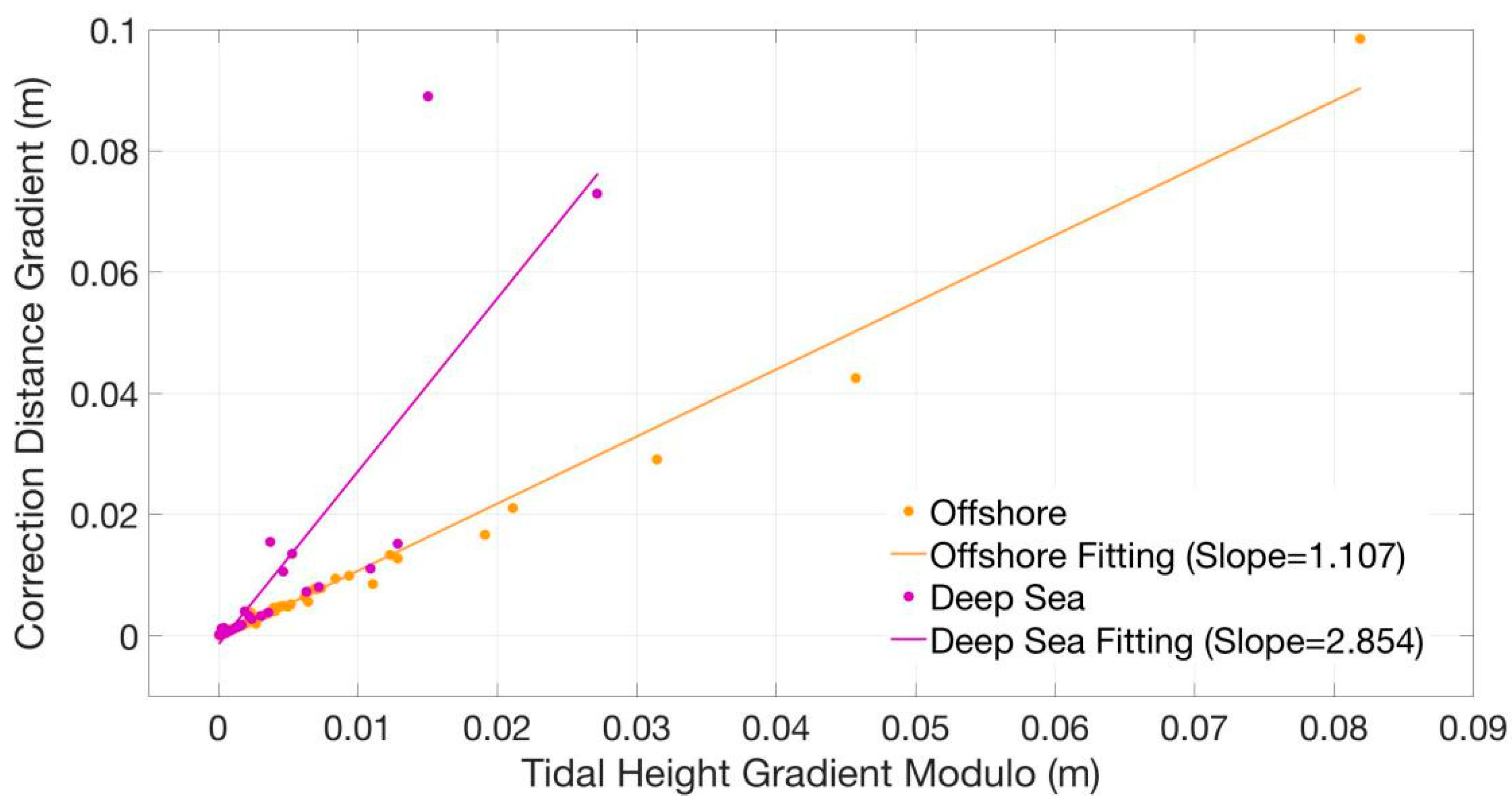
3.2. Division of Offshore and Deep Sea
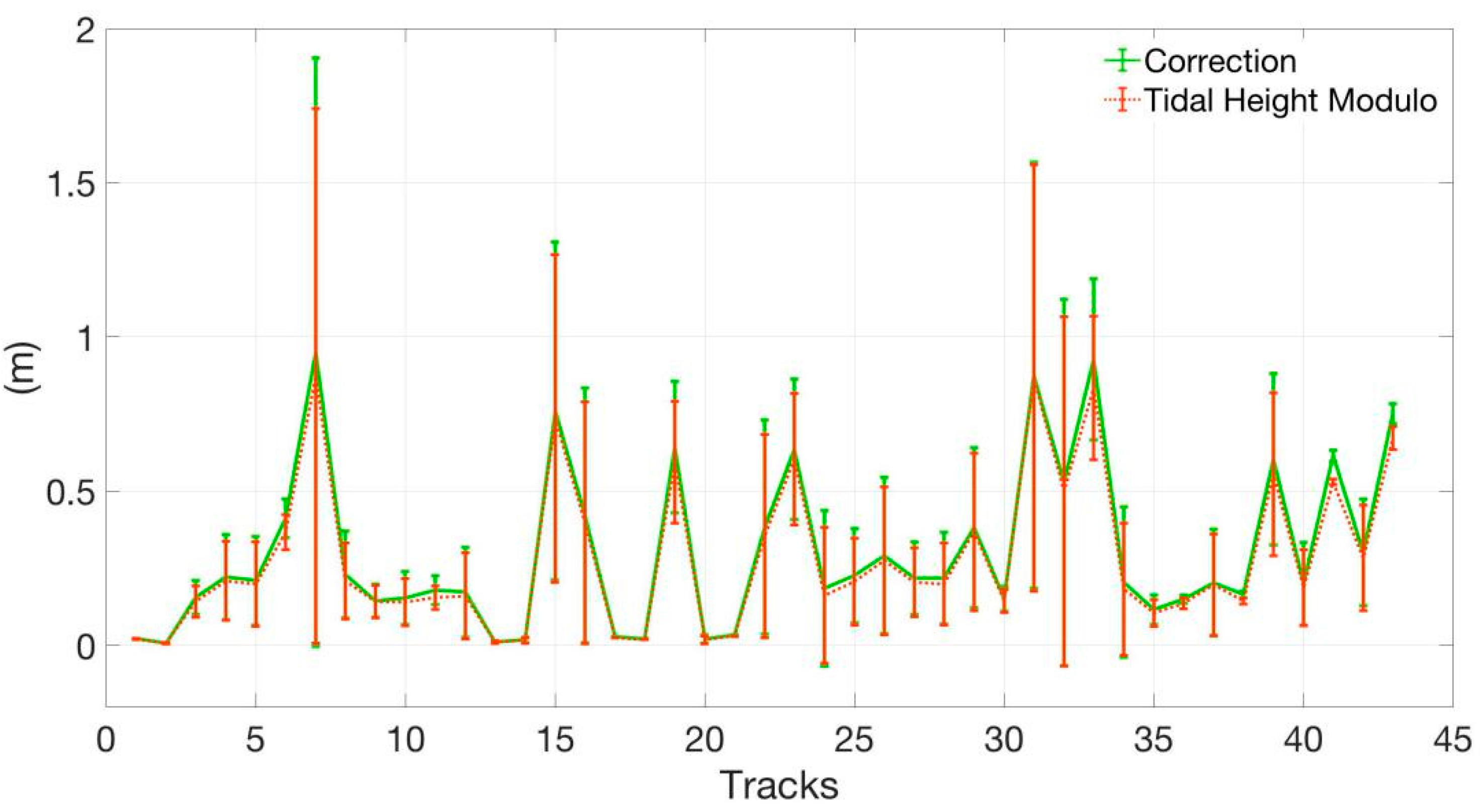
- Filtering the tracks across both sea and land.There are 28 tracks cross both sea and land among all the 43 tracks, the sea parts of these tracks are extracted.
- The tidal height gradient and the corresponding tidal elevation position correction gradient of each track is calculated and detrended, the average is then subtracted, and the modulo is taken at last.
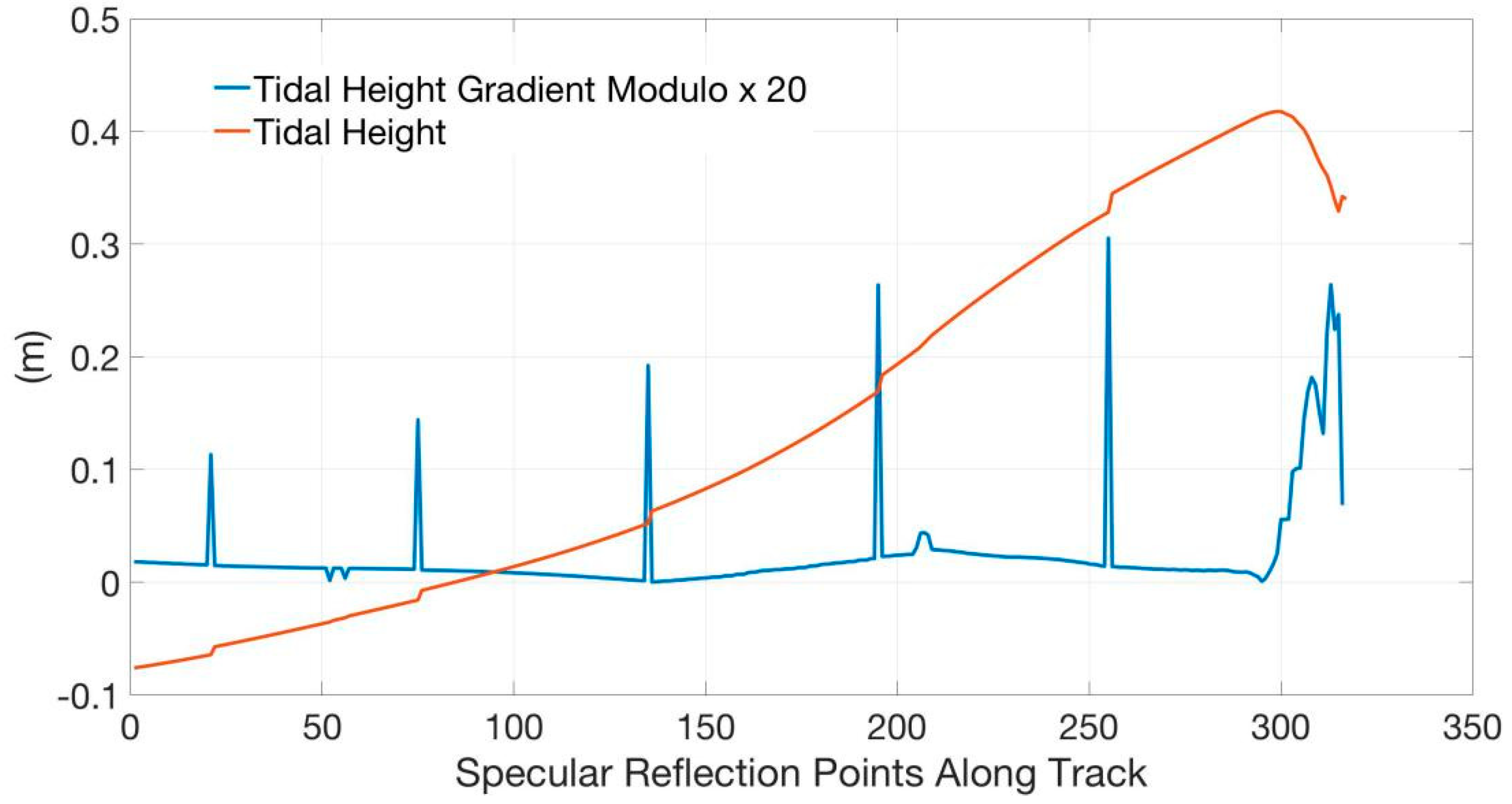
- Division of the offshore and the deep sea segments.Since some of the offshore tracks repeatedly cross land and sea, or cross islands, peninsulas, etc., one track is often divided into multiple sea sub-tracks by land, and the sub-tracks mostly contain offshore segments. Moreover, due to the complexity of the global coastline and tracks characteristics (length, direction, curvature, distribution, etc. [13]), the position of the offshore segment in the track is complicated. It could be divided into four cases: the offshore part is at one end of the track, at both ends of the track, in the middle of the track (the middle of the track is close to the land) or the entire segment is in the offshore (generally short tracks). The points where the tidal height gradient modulo in each track (or sub-track) are greater than 3 times the standard deviation η of the tidal height gradient modulo of the track are extracted. Then, the offshore and deep-sea segments are divided by these points according to the above four specific cases. Choosing too large a multiple of η would ignore some of the tidal height gradient points with sudden changes in the offshore, so that the offshore segment cannot be completely extracted. If the multiple is set too small, some high frequency peaks would be misjudged as offshore tidal height gradient mutation points. In addition, judging the continuous variation characteristics of the tidal height gradient requires the segment to be long enough, segments with more than 10 continuous points are selected.
- Eliminating tidal height gradient jumping points.The points where the tidal height gradient modulo is greater than 3η in the deep sea segments are eliminated, and the tidal height gradient jumping peaks caused by the TDS-1 data jumping are well removed. According to the above filtering and division, 67 offshore segments are obtained, which contain 2476 specular reflection points, each segment has an average of about 37 points. And 54 deep sea segments are obtained, which contain 5716 specular reflection points, each with an average of approximately 106 points.
3.3. Tidal Height Gradient and the Tidal Positioning Correction Gradient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Ruf, C.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The NASA EV-2 cyclone global navigation satellite system (CYGNSS) mission. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–7. [Google Scholar]
- Ruf, C.; Lyons, A.; Unwin, M.; Dickinson, J.; Rose, R.; Rose, D.; Vincent, M. CYGNSS: Enabling the future of hurricane prediction [remote sensing satellites]. IEEE Geosci. Remote Sens. Mag. 2013, 1, 52–67. [Google Scholar] [CrossRef]
- Available online: http://www.cast.cn/Item/Show.asp?m=1&d=6544 (accessed on 5 June 2019).
- Gleason, S.; Lowe, S.; Zavorotny, V. GNSS Applications Methods; Artech House: Boston, MA, USA, 2009; Volume 16, pp. 399–434. [Google Scholar]
- Semmling, M. Altimetric Monitoring of Disko Bay using Interferometric GNSS Observations on L1 and L2. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2012. [Google Scholar]
- Semmling, M.; Beckheinrich, J.; Wickert, J.; Beyerle, G.; Schön, S.; Fabra, F.; Pflug, H.; He, K.; Schwabe, J.; Scheinert, M. Sea surface topography retrieved from GNSS reflectometry phase data of the GEOHALO flight mission. Geophys. Res. Lett. 2014, 41, 954–960. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Martín-Neira, M.; Cardellach, E.; Ribó, S.; Yang, D. The impact of inter-modulation components on interferometric GNSS-Reflectometry. Remote Sens. 2016, 8, 1013. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Southwell, B.; Dempster, A. A new approach to determine the specular point of forward reflected gnss signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 639–646. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Ribo, S.; Martín-Neira, M. Revisiting the GNSS-R waveform statistics and its impact on altimetric retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Lake level and surface topography measured with spaceborne GNSS-Reflectometry from CYGNSS mission: Example for the lake qinghai. Geophys. Res. Lett. 2018, 45, 13–332. [Google Scholar] [CrossRef]
- Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the GNSS-R Specular Reflection Point Positioning Accuracy Using the Gravity Field Normal Projection Reflection Reference Surface Combination Correction Method. Remote Sens. 2019, 11, 33. [Google Scholar] [CrossRef]
- Helm, A. Ground-Based GPS Altimetry with the L1 OpenGPS Receiver Using Carrier Phase-Delay Observations of Reflected GPS Signals. Ph.D. Thesis, Postdam Deutsches GFZ, Potsdam, Germany, 2008. [Google Scholar]
- Wu, S.-C.; Meechan, T.; Young, L. The potential use of GPS signals as ocean altimetry observation. In Proceedings of the National Technical Meeting, Santa Monica, CA, USA, 14–16 January 1997. [Google Scholar]
- Yang, D.; Zhang, Q. GNSS Reflected Signal Processing: Fundamentals and Applications; Publishing House of Electronics Industry: Beijing, China, 2012. [Google Scholar]
- Kostelecky, J.; Klokocnik, J.; Wagner, C.A. Geometry and acuracy of reflecting points in bistatic satelite altimetry. J. Geod. 2005, 79, 421–430. [Google Scholar] [CrossRef]
- Beyerle, G.; Hocke, K. Observation and Simulation of Direct and Reflected GPS Signals in Radio Occultation Experiment. Geophys. Res. Lett. 2001, 28, 1895–1898. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Martín-Neira, M. Altimetric Analysis of the Sea-Surface GPS-Reflected Signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Skolnik, M. Radar Handbook; McGraw-Hill, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Gao, F.; Xu, T.; Wang, N.; Jiang, C.; Du, Y.; Nie, W.; Xu, G. Spatiotemporal Evaluation of GNSS-R Based on Future Fully Operational Global Multi-GNSS and Eight-LEO Constellations. Remote Sens. 2018, 10, 67. [Google Scholar] [CrossRef]
- Jales, P.; Unwin, M. MERRByS Product Manual—GNSS Reflectometry on TDS-1 with the SGR-ReSI.; Surrey Satellite Technology LTD: Guildford, UK, 2017. [Google Scholar]
- Liu, Y. Calibration Technology for HY-2 Radar Atimeter Sea Surface Height. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2014. [Google Scholar]
- Rosmorduc, V.; Benveniste, J.; Lauret, O.; Maheu, C.; Milagro, M.; Picot, N. Radar Altimetry Tutorial and Toolbox. 2011. Available online: http://www.altimetry.info (accessed on 20 May 2019).
- Schwiderski, W. On charting global ocean tides. Rev. Geophys. 1980, 18, 243–268. [Google Scholar] [CrossRef]
- LeProvost, C.; Genco, L.; Lyard, F. Spectroscopy of the world ocean tides from a finite element hydrodynamic model. J. Geophys. Res. Ocean. 1994, 99, 24777–24797. [Google Scholar] [CrossRef]
- Cheng, Y.; Andersen, B. Multimission empirical ocean tide modeling for shallow waters and polar seas. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Egbert, D.; Bennett, F.; Foreman, G. TOPEX/Poseidon tides estimated using a global inverse model. J. Geophys. Res. 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Egbert, D.; Ray, D. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 2000, 405, 775–778. [Google Scholar] [CrossRef]
- Egbert, D.; Erofeeva, Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Savcenko, R.; Bosch, W. E0TO8a–A New Global Tide Model from Multi—Mission Altimetry; Report No. 81; Deutsche Geodatisches Forschungsinstitut (DGFI): Mfinchen, Germany, 2008. [Google Scholar]
- Ray, R.D. A Global Ocean Tide Model from TOPEX/Poseidon Altimetry: GOT99.2; NASA/TM-1999-209478; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MD, USA, 1999.
- Murphy, C.; Moore, P.; Woodworth, P. Short-arc calibration of the TOPEX/Poseidon and ERS1 altimeters utilizing in situ data. J. Geophys. Res. 1996, 101, 14191–14200. [Google Scholar] [CrossRef]
- Mitchum, G. Monitoring the Stability of Satellite Altimeters with Tide Gauge. J. Atmos. Ocean. Technol. 1998, 15, 721–730. [Google Scholar] [CrossRef]
- Hwang, C.; Chen, S. Fourier and Wavelet Analyses of TOPEX/Poseidon-derived Sea Level Anomaly over the South China Sea: A Contribution to the South China Sea Monsoon Experiment. J. Geophys. Res. 2000, 105, 28785–28804. [Google Scholar] [CrossRef]
- Rignot, E.; Padman, L.; MacAyeal, R.; Schmeltz, M. Observation of ocean tides below the Filchner and Ronne Ice Shelves, Antarctica, using synthetic aperture radar interferometry: Comparison with tide model predictions. J. Geophys. Res. Ocean. 2000, 105, 19615–19630. [Google Scholar] [CrossRef]
- Dong, X.; Woodworth, P.; Moore, P.; Bingley, R. Absolute calibration of the TOPEX/Poseidon altimeters using UK tide gauges, GPS, and precise, local geoid-differences. Mar. Geod. 2002, 25, 189–204. [Google Scholar] [CrossRef]
- Woodworth, P.; Moore, P.; Dong, X.; Bingley, R. Absolute calibration of the Jason-1 altimeter using UK tide gauges. Mar. Geod. 2004, 27, 95–106. [Google Scholar] [CrossRef]
- Baltazar, A.O. Range and Geophysical Corrections in Coastal Regions: And Implications for Mean Sea Surface Determination, Volume Coastal Altimetry; Technical University of Denmark; Springer: Berlin/Heidelberg, Germany, 2011; pp. 103–146. ISBN 978-3-642-12795-3. [Google Scholar]
- Liu, Y.; Tang, J.; Zhu, J.; Lin, M.; Zhai, W.; Chen, C. An improved method of absolute calibration to satellite altimeter: A case study in the Yellow Sea, China. Acta Oceanol. Sin. 2014, 33, 103–112. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Saleh, J. Error propagation with geographic specificity for very high degree geopotential models. In Gravity, Geoid and Space Missions; Jekeli, C., Bastos, L., Fernandes, J., Eds.; Springer: Berlin, Germany, 2005; p. 129. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Bao, J.; Xu, J. Tide Analysis from Altimeter Data and the Establishment and Application of Tide Model; Surveying and Mapping Press: Beijing, China, 2013. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Feng, S.; Li, F.; Li, S. Introduction to Ocean Science; Higher Education Press: Beijing, China, 2016. [Google Scholar]
| Tidal Height (m) | Correction Distance (m) | X (m) | Y (m) | Z (m) | B (°) | L (°) | |
|---|---|---|---|---|---|---|---|
| mean | 2.829 × 10−1 | 3.054 × 10−1 | 1.371 × 10−1 | 7.802 × 10−2 | 2.197 × 10−1 | 5.939 × 10−7 | 1.036 × 10−6 |
| std | 1.639 × 10−1 | 1.747 × 10−1 | 8.317 × 10−2 | 5.127 × 10−2 | 1.467 × 10−1 | 5.423 × 10−7 | 1.119 × 10−6 |
| Offshore | Deep Sea | |||
|---|---|---|---|---|
| mean | std | mean | std | |
| Tidal Height Gradient Modulo (m) | 5.835 × 10−3 | 4.768 × 10−3 | 2.342 × 10−3 | 1.356 × 10−3 |
| Correction Gradient Modulo (m) | 6.122 × 10−3 | 5.023 × 10−3 | 5.267 × 10−3 | 2.417 × 10−3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the Positioning Accuracy of Satellite-Borne GNSS-R Specular Reflection Point on Sea Surface Based on the Ocean Tidal Correction Positioning Method. Remote Sens. 2019, 11, 1626. https://doi.org/10.3390/rs11131626
Wu F, Zheng W, Li Z, Liu Z. Improving the Positioning Accuracy of Satellite-Borne GNSS-R Specular Reflection Point on Sea Surface Based on the Ocean Tidal Correction Positioning Method. Remote Sensing. 2019; 11(13):1626. https://doi.org/10.3390/rs11131626
Chicago/Turabian StyleWu, Fan, Wei Zheng, Zhaowei Li, and Zongqiang Liu. 2019. "Improving the Positioning Accuracy of Satellite-Borne GNSS-R Specular Reflection Point on Sea Surface Based on the Ocean Tidal Correction Positioning Method" Remote Sensing 11, no. 13: 1626. https://doi.org/10.3390/rs11131626
APA StyleWu, F., Zheng, W., Li, Z., & Liu, Z. (2019). Improving the Positioning Accuracy of Satellite-Borne GNSS-R Specular Reflection Point on Sea Surface Based on the Ocean Tidal Correction Positioning Method. Remote Sensing, 11(13), 1626. https://doi.org/10.3390/rs11131626