Clustering of Wall Geometry from Unstructured Point Clouds Using Conditional Random Fields
Abstract
1. Introduction
2. Background and Related Work
3. Methodology
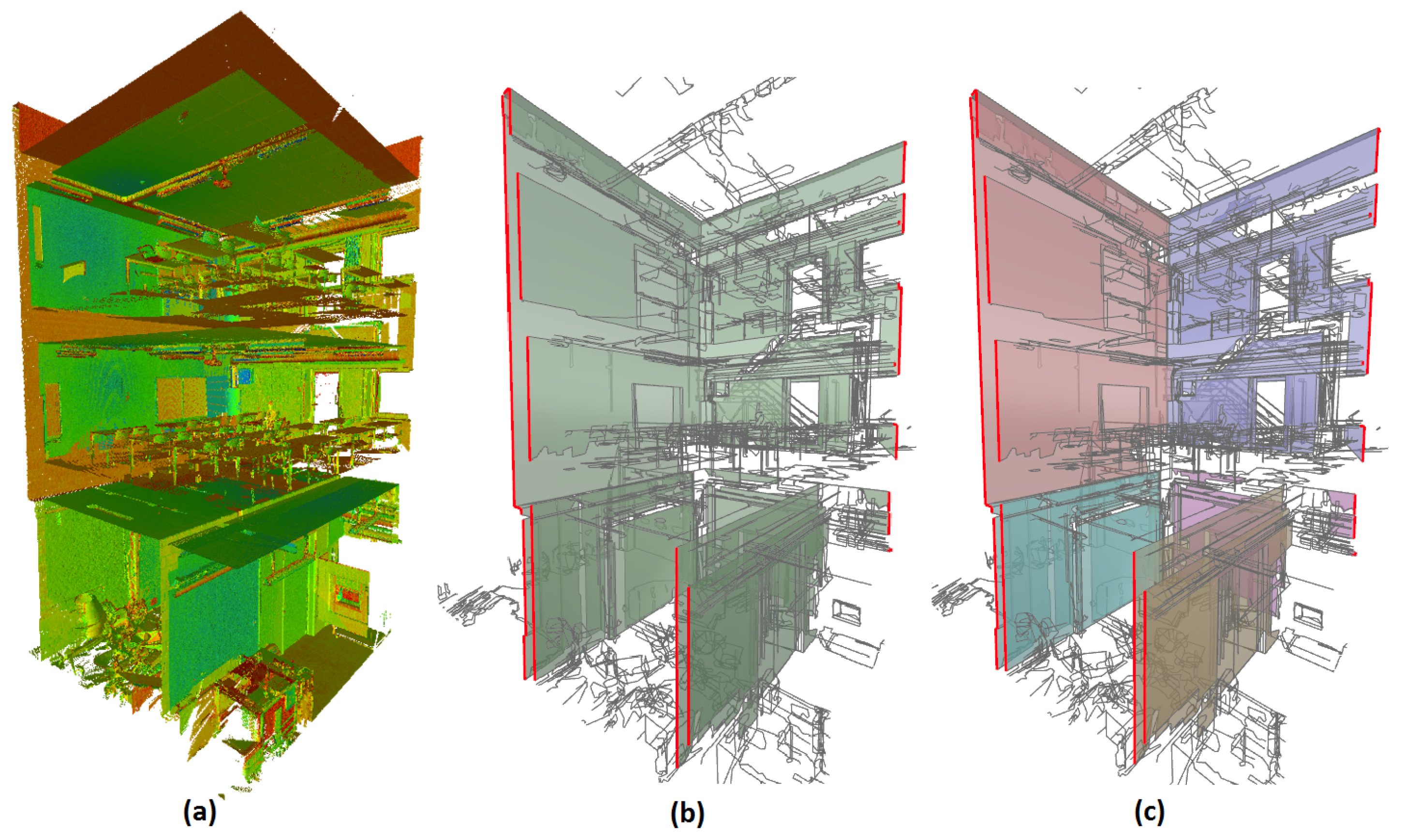
3.1. Data Preprocessing
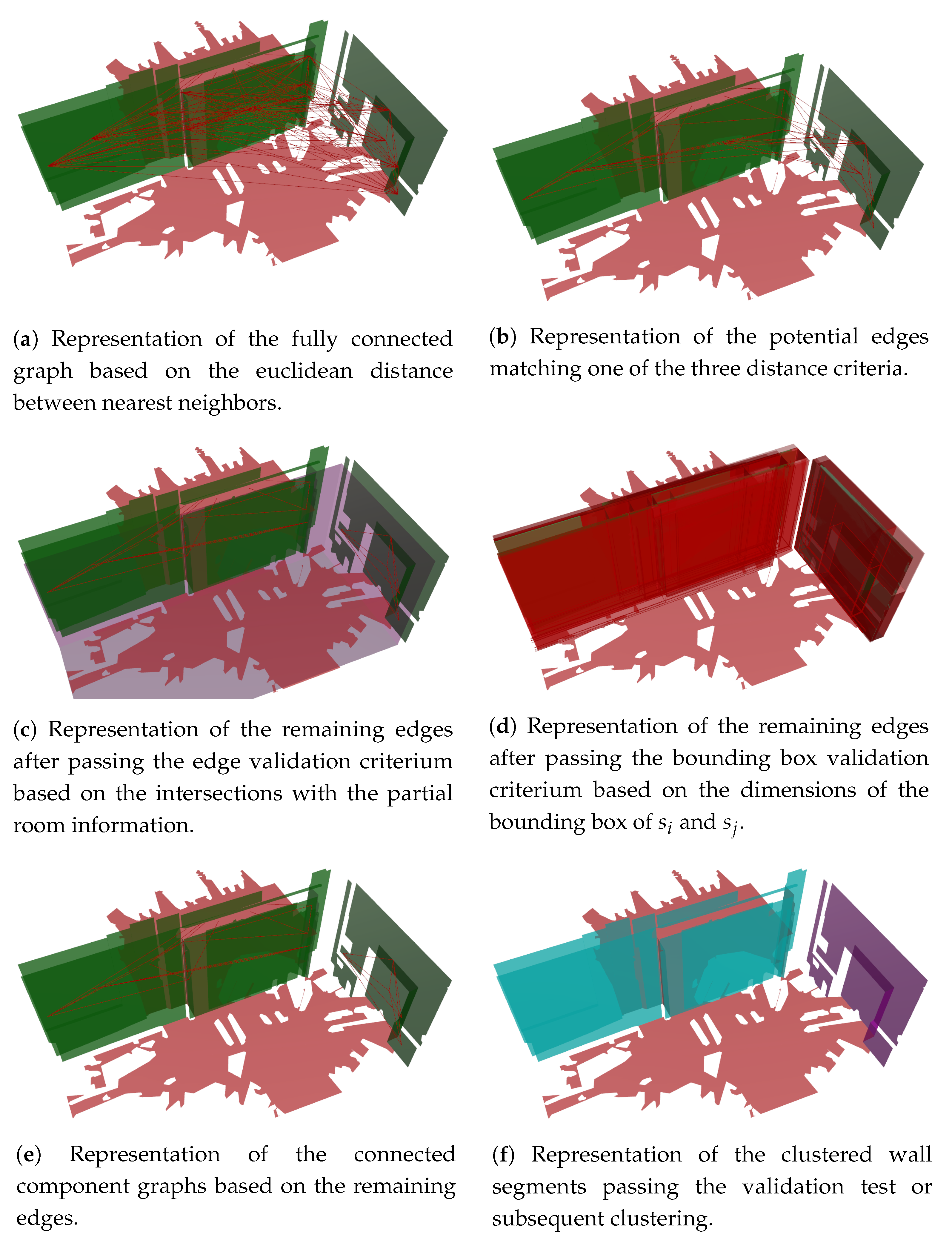
3.2. Connected Component Graph Creation
3.3. Clustering
3.3.1. Seeding
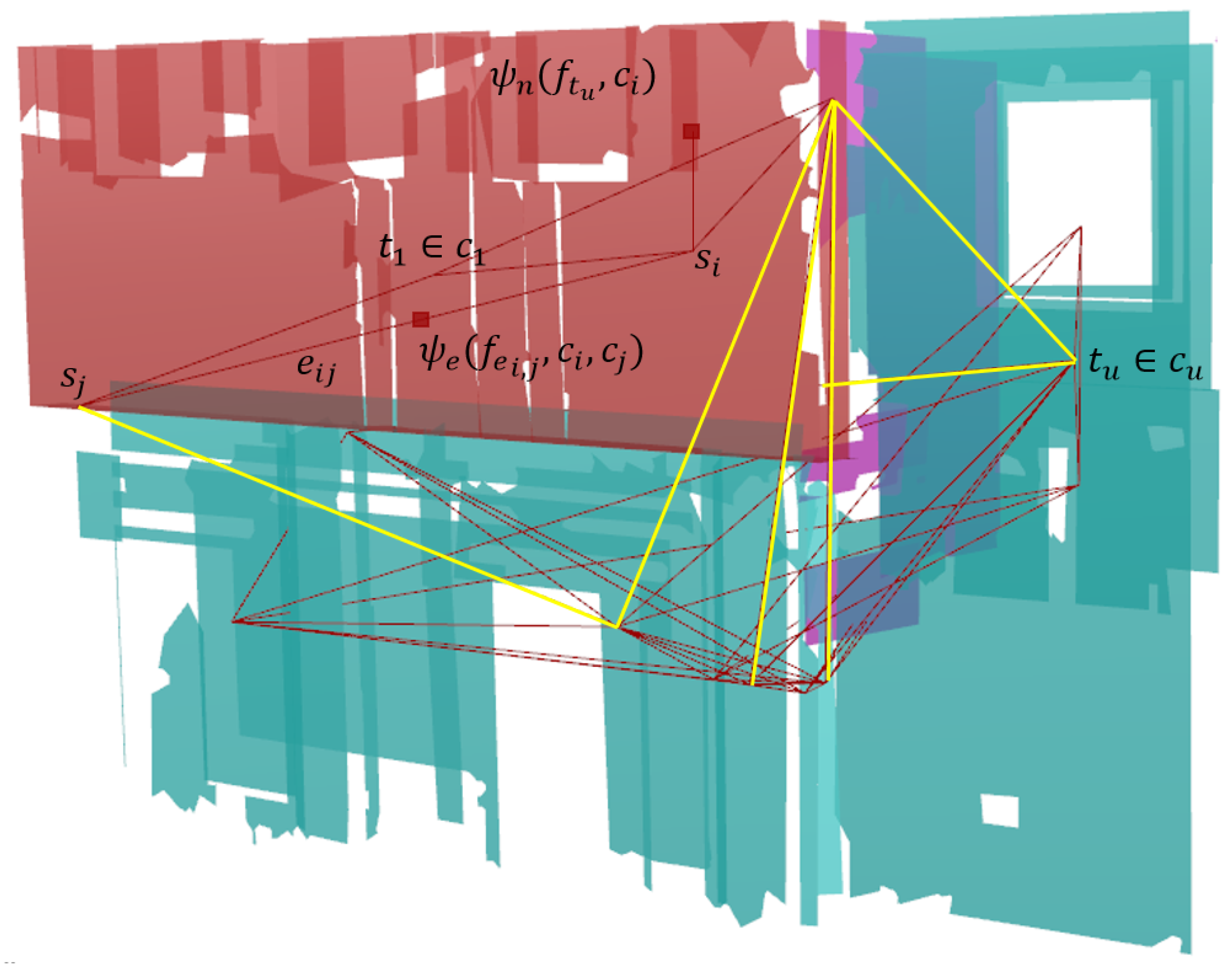
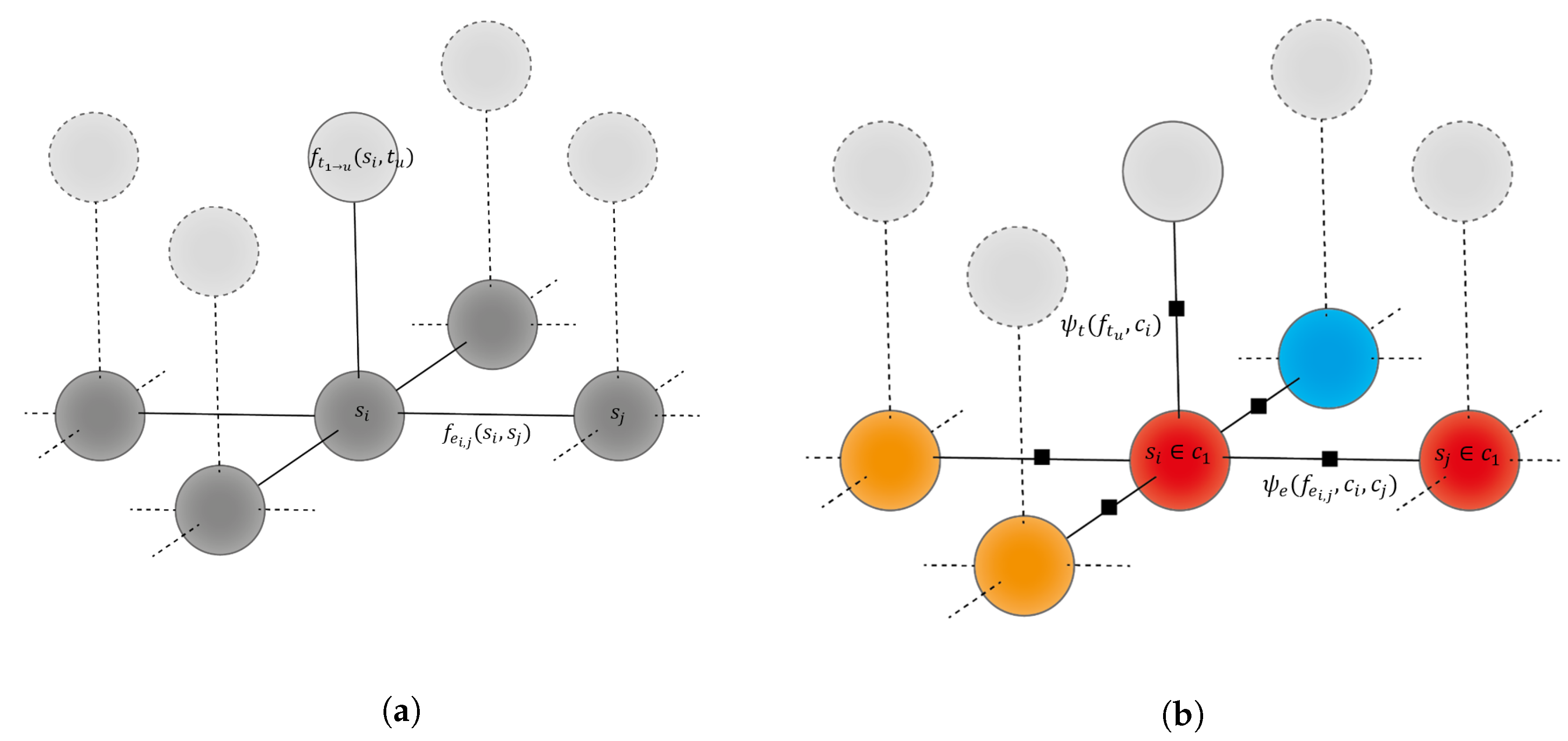
3.3.2. Potential Computation
3.3.3. Probability Estimation
4. Experiments
4.1. Experiment 1: Technology Campus
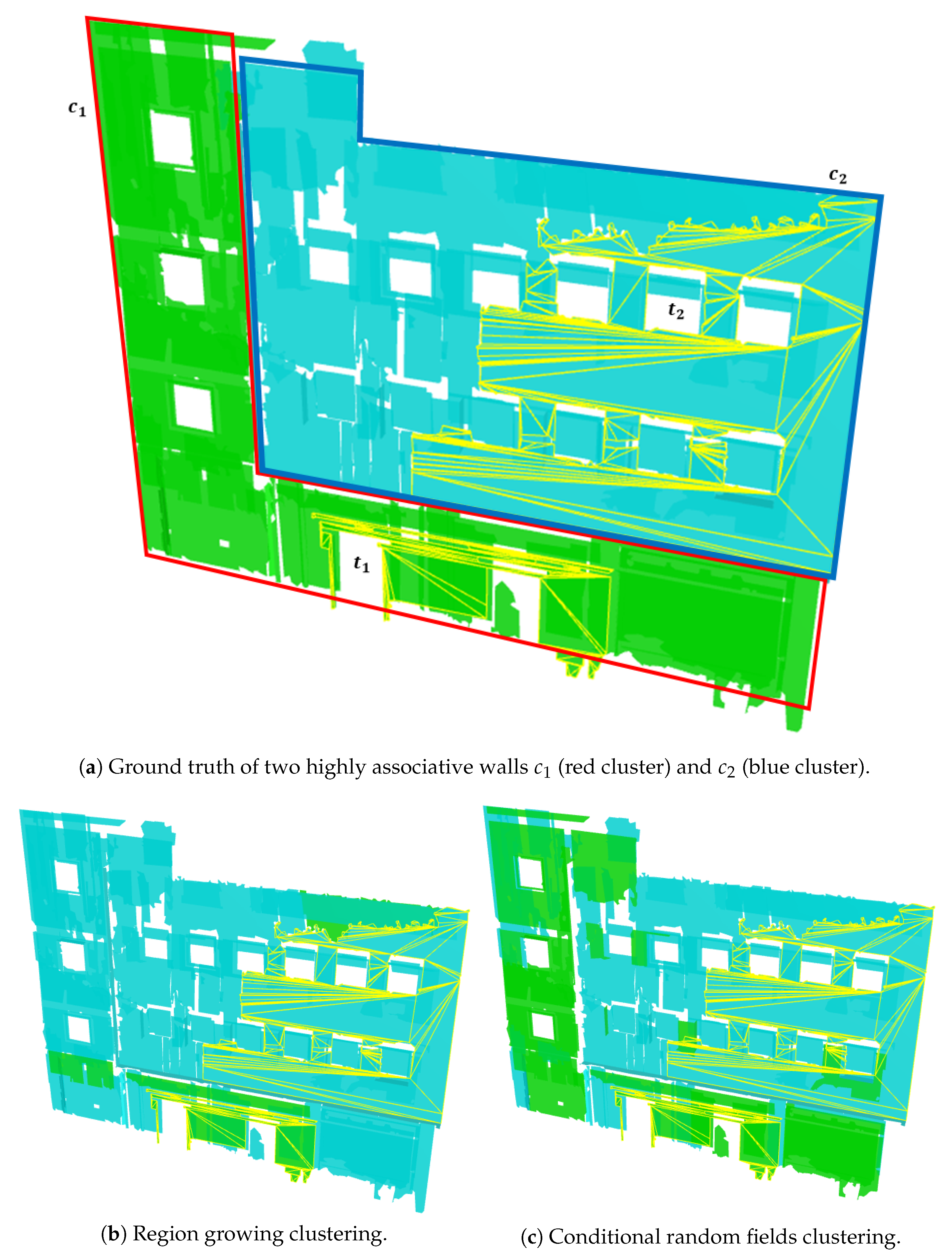
4.2. Experiment 2: 2D-3D-Semantics Stanford
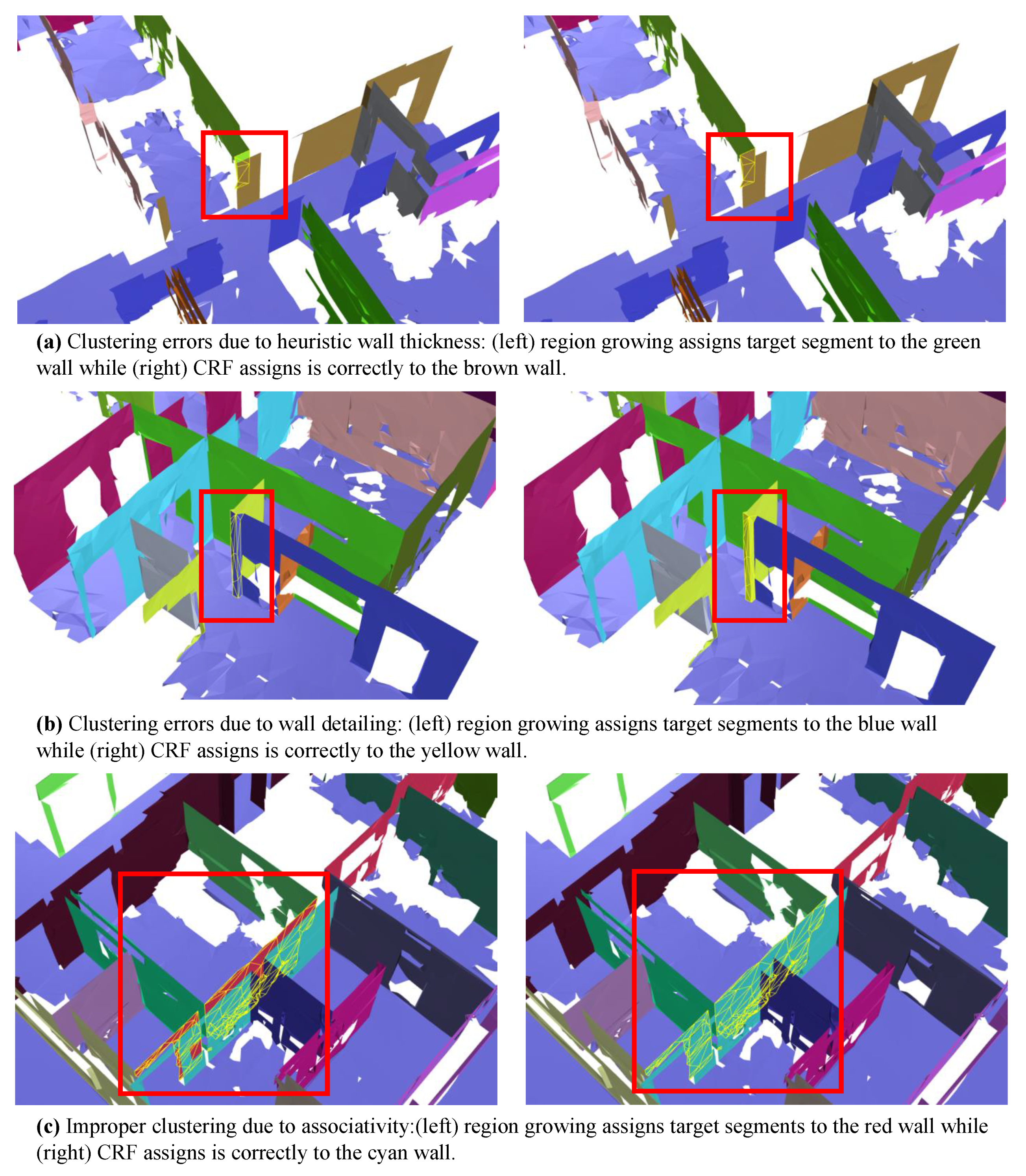
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings—Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef]
- Patraucean, V.; Armeni, I.; Nahangi, M.; Yeung, J.; Brilakis, I.; Haas, C. State of research in automatic as-built modelling. Adv. Eng. Inform. 2015, 29, 162–171. [Google Scholar] [CrossRef]
- Bassier, M.; Vergauwen, M. Clustering of wall geometry from unstructured point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W9, 101–108. [Google Scholar] [CrossRef]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Nguyen, A.; Le, B. 3D point cloud segmentation: A survey 3D. In Proceedings of the 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Philippines, 12–15 November 2013; pp. 225–230. [Google Scholar] [CrossRef]
- Landrieu, L.; Mallet, C.; Weinmann, M. Comparison of belief propagation and graph-cut approaches for contextual classification of 3D lidar point cloud data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Anagnostopoulos, I.; Patraucean, V.; Brilakis, I.; Vela, P. Detection of walls, floors and ceilings in point cloud data. In Proceedings of the Construction Research Congress 2016, San Juan, Puerto Rico, 31 May–2 June 2016. [Google Scholar]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Dimitrov, A.; Golparvar-Fard, M. Segmentation of building point cloud models including detailed architectural/structural features and MEP systems. Autom. Constr. 2015, 51, 32–45. [Google Scholar] [CrossRef]
- Barnea, S.; Filin, S. Segmentation of terrestrial laser scanning data using geometry and image information. ISPRS J. Photogramm. Remote Sens. 2013, 76, 33–48. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Cheng, J.; Chen, B.; Jia, F.; Chen, Z.; Li, J. Line segment extraction for large scale unorganized point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 102, 172–183. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, M.; Geng, N.; He, D.; Chang, J.; Zhang, J.J. A self-adaptive segmentation method for a point cloud. Vis. Comput. 2018, 34, 659–673. [Google Scholar] [CrossRef]
- Vosselman, G.; Rottensteiner, F. Contextual segment-based classification of airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 354–371. [Google Scholar] [CrossRef]
- Bassier, M.; Vergauwen, M.; Van Genechten, B. Automated semantic labelling of 3D vector models for Scan-to-BIM. In Proceedings of the 4th Annual International Conference on Architecture and Civil Engineering (ACE 2016), Singapore, 25–26 April 2016; pp. 93–100. [Google Scholar] [CrossRef]
- Xiong, X.; Adan, A.; Akinci, B.; Huber, D. Automatic creation of semantically rich 3D building models from laser scanner data. Autom. Constr. 2013, 31, 325–337. [Google Scholar] [CrossRef]
- Nikoohemat, S.; Peter, M.; Oude Elberink, S.; Vosselman, G. Exploiting Indoor Mobile Laser Scanner Trajectories for Semantic Interpretation of Point Clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-2/W4, 355–362. [Google Scholar] [CrossRef]
- Oesau, S.; Lafarge, F.; Alliez, P. Indoor scene reconstruction using feature sensitive primitive extraction and graph-cut. ISPRS J. Photogramm. Remote Sens. 2014, 90, 68–82. [Google Scholar] [CrossRef]
- Jung, J.; Hong, S.S.; Jeong, S.; Kim, S.; Cho, H.; Hong, S.S.; Heo, J. Productive modeling for development of as-built BIM of existing indoor structures. Autom. Constr. 2014, 42, 68–77. [Google Scholar] [CrossRef]
- Xiong, X.; Huber, D. Using Context to Create Semantic 3D Models of Indoor Environments. In Proceedings of the British Machine Vision Conference 2010, Aberystwyth, UK, 30 August–2 September 2010; pp. 45.1–45.11. [Google Scholar] [CrossRef]
- Anand, A.; Koppula, H.S.; Joachims, T.; Saxena, A. Contextually Guided Semantic Labeling and Search for 3D Point Clouds. Int. J. Robot. Res. 2012, 32, 19–34. [Google Scholar] [CrossRef]
- Wolf, D.; Prankl, J.; Vincze, M. Fast semantic segmentation of 3D point clouds using a dense CRF with learned parameters. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Lotte, R.; Haala, N.; Karpina, M.; Aragao, L.; Shimabukuro, Y. 3D Façade Labeling over Complex Scenarios: A Case Study Using Convolutional Neural Network and Structure-From-Motion. Remote Sens. 2018, 10, 1435. [Google Scholar] [CrossRef]
- Tylecek, R.; Sara, R. Spatial pattern templates for recognition of objects with regular structure. In Proceedings of the German Conference on Pattern Recognition, Saarbrucken, Germany, 3–6 September 2013. [Google Scholar]
- Korc, F.; Forstner, W. eTRIMS Image Database for Interpreting Images of Man-Made Scenes; Technical Report 1; University of Bonn, Department of Photogrammetry: Bonn, Germany, 2009. [Google Scholar]
- Teboul, O.; Simon, L.; Koutsourakis, P.; Paragios, N. Segmentation of building facades using procedural shape priors. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Gröger, G.; Plümer, L. CityGML—Interoperable semantic 3D city models. ISPRS J. Photogramm. Remote Sens. 2012, 71, 12–33. [Google Scholar] [CrossRef]
- Turner, E.; Zakhor, A. Floor plan generation and room labeling of indoor environments from laser range data. In Proceedings of the International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (GRAPP), Lisbon, Portugal, 5–8 January 2014; pp. 1–12. [Google Scholar] [CrossRef]
- Mura, C.; Mattausch, O.; Jaspe Villanueva, A.; Gobbetti, E.; Pajarola, R. Automatic room detection and reconstruction in cluttered indoor environments with complex room layouts. Comput. Graph. 2014, 44, 20–32. [Google Scholar] [CrossRef]
- Adan, A.; Huber, D. 3D Reconstruction of interior wall surfaces under occlusion and clutter. In Proceedings of the 2011 International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission, Hangzhou, China, 16–19 May 2011; pp. 275–281. [Google Scholar] [CrossRef]
- Previtali, M.; Barazzetti, L.; Brumana, R.; Scaioni, M. Towards automatic indoor reconstruction of cluttered building rooms from point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-5, 281–288. [Google Scholar] [CrossRef]
- Budroni, A.; Böhm, J. Automatic 3D modelling of indoor Manhattan-world scenes from laser data. In Proceedings of the ISPRS Commission V Mid-Term Symposium: Close Range Image Measurement Techniques, Newcastle upon Tyne, UK, 21–24 June 2010; Volume XXXVIII, pp. 115–120. [Google Scholar]
- Valero, E.; Adán, A.; Cerrada, C. Automatic method for building indoor boundary models from dense point clouds collected by laser scanners. Sensors 2012, 12, 16099–16115. [Google Scholar] [CrossRef] [PubMed]
- Thomson, C.; Boehm, J. Automatic geometry generation from point clouds for BIM. Remote Sens. 2015, 7, 11753–11775. [Google Scholar] [CrossRef]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Reconstructing building interiors from images. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 80–87. [Google Scholar] [CrossRef]
- Ochmann, S.; Vock, R.; Wessel, R.; Klein, R. Automatic reconstruction of parametric building models from indoor point clouds. Comput. Graph. 2016, 54, 94–103. [Google Scholar] [CrossRef]
- Derpanis, K.G. Overview of the RANSAC algorithm. Image Rochester NY 2010, 4, 2–3. [Google Scholar] [CrossRef]
- Ikehata, S.; Yang, H.; Furukawa, Y. Structured Indoor Modeling. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; p. 1540012. [Google Scholar] [CrossRef]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D semantic parsing of large-scale indoor spaces. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Armeni, I.; Sax, S.; Zamir, A.R.; Savarese, S.; Sax, A.; Zamir, A.R.; Savarese, S. Joint 2D-3D-Semantic Data for Indoor Scene Understanding. arXiv 2017, arXiv:1702.01105. [Google Scholar]
- He, X.; Zhang, X.; Xin, Q. Recognition of building group patterns in topographic maps based on graph partitioning and random forest. ISPRS J. Photogramm. Remote Sens. 2018, 136, 26–40. [Google Scholar] [CrossRef]
- Gilani, S.A.N.; Awrangjeb, M.; Lu, G. An automatic building extraction and regularisation technique using LiDAR point cloud data and orthoimage. Remote Sens. 2016, 8, 258. [Google Scholar] [CrossRef]
- Mura, C.; Mattausch, O.; Pajarola, R. Piecewise-planar Reconstruction of Multi-room Interiors with Arbitrary Wall Arrangements. Comput. Graph. Forum 2016, 35, 179–188. [Google Scholar] [CrossRef]
- Sutton, C.; Mccallum, A. An Introduction to conditional random fields. Found. Trends Mach. Learn. 2011, 4, 267–373. [Google Scholar] [CrossRef]
- Strom, J.; Richardson, A.; Olson, E. Graph-based segmentation for colored 3D laser point clouds. In Proceedings of the IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems, (IROS 2010), Taipei, Taiwan, 18–22 October 2010; pp. 2131–2136. [Google Scholar] [CrossRef]
- Pordel, M.; Hellström, T. Semi-automatic image labelling using depth information. Computers 2015, 4, 142–154. [Google Scholar] [CrossRef]
- Landrieu, L.; Raguet, H.; Vallet, B.; Mallet, C.; Weinmann, M. A structured regularization framework for spatially smoothing semantic labelings of 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 132, 102–118. [Google Scholar] [CrossRef]
- Bassier, M.; Van Genechten, B.; Vergauwen, M. Classification of sensor independent point cloud data of building objects using random forests. J. Build. Eng. 2019, 21, 468–477. [Google Scholar] [CrossRef]
- Schmidt, M. Graphical Model Structure Learning with 1-Regularization. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2010. [Google Scholar]
- Bassier, M.; Van Genechten, B.; Vergauwen, M. Octree-Based Region Growing and conditional random fields. In Proceedings of the 2017 5th International Workshop LowCost 3D—Sensors, Algorithms, Applications, Hamburg, Germany, 28–29 October 2017; pp. 28–29. [Google Scholar] [CrossRef]
- Michailidis, G.T.; Pajarola, R. Bayesian graph-cut optimization for wall surfaces reconstruction in indoor environments. Vis. Comput. 2017, 33, 1347–1355. [Google Scholar] [CrossRef]

| Dataset | 3D Points | 3D Meshes | Wall Segments | Wall Objects | Time [s] | Recall [%] | Precision [%] |
|---|---|---|---|---|---|---|---|
| Area 1 | 43,956,907 | 158,500 | 235 | 84 | 4.3 | 94.8 | 86.0 |
| Area 2 | 470,023,210 | 361,830 | 284 | 82 | 12.9 | 80.4 | 89.0 |
| Area 3 | 18,662,173 | 147,420 | 160 | 61 | 2.6 | 96.1 | 76.8 |
| Area 4 | 43,278,148 | 201,735 | 281 | 96 | 6.3 | 89.6 | 90.6 |
| Area 5 | 78,649,818 | 198,220 | 344 | 54 | 2.0 | 89.5 | 89.2 |
| Area 6 | 41,308,364 | 198,590 | 248 | 71 | 4.9 | 93.7 | 85.1 |
| Average | 115,979,770 | 211,500 | 259 | 75 | 5.5 | 90.6 | 86.1 |
| Dataset | Connected Components | Potential Seeds | Wall objects | Time [s] | Recall [%] | Precision [%] |
|---|---|---|---|---|---|---|
| Area 1 | 8 | 87 | 84 | 3.6 | 84.8 | 81.0 |
| Area 2 | 6 | 95 | 82 | 10.2 | 76.4 | 83.0 |
| Area 3 | 4 | 65 | 61 | 1.9 | 88.1 | 76.3 |
| Area 4 | 6 | 96 | 96 | 4.3 | 88.6 | 89.5 |
| Area 5 | 6 | 57 | 54 | 2.0 | 86.7 | 86.1 |
| Area 6 | 4 | 73 | 71 | 4.1 | 85.6 | 83.7 |
| Average | 6 | 79 | 75 | 4.4 | 85.0 | 83.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassier, M.; Vergauwen, M. Clustering of Wall Geometry from Unstructured Point Clouds Using Conditional Random Fields. Remote Sens. 2019, 11, 1586. https://doi.org/10.3390/rs11131586
Bassier M, Vergauwen M. Clustering of Wall Geometry from Unstructured Point Clouds Using Conditional Random Fields. Remote Sensing. 2019; 11(13):1586. https://doi.org/10.3390/rs11131586
Chicago/Turabian StyleBassier, Maarten, and Maarten Vergauwen. 2019. "Clustering of Wall Geometry from Unstructured Point Clouds Using Conditional Random Fields" Remote Sensing 11, no. 13: 1586. https://doi.org/10.3390/rs11131586
APA StyleBassier, M., & Vergauwen, M. (2019). Clustering of Wall Geometry from Unstructured Point Clouds Using Conditional Random Fields. Remote Sensing, 11(13), 1586. https://doi.org/10.3390/rs11131586






