Double-Rice System Simulation in a Topographically Diverse Region—A Remote-Sensing-Driven Case Study in Hunan Province of China
Abstract
1. Introduction
2. Materials and Methods
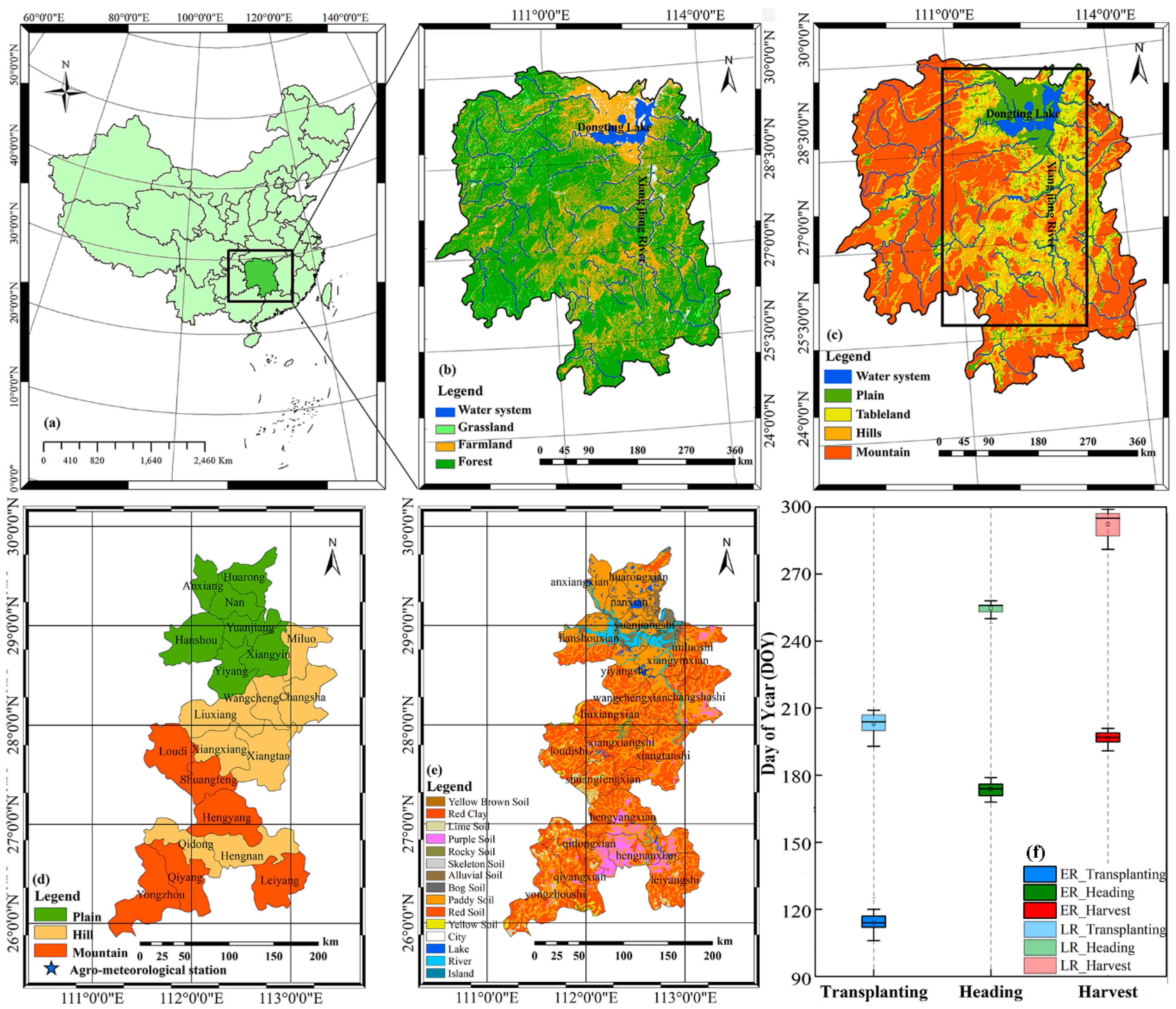
2.1. Study Area
2.2. MCWLA-Rice Model
2.3. Data
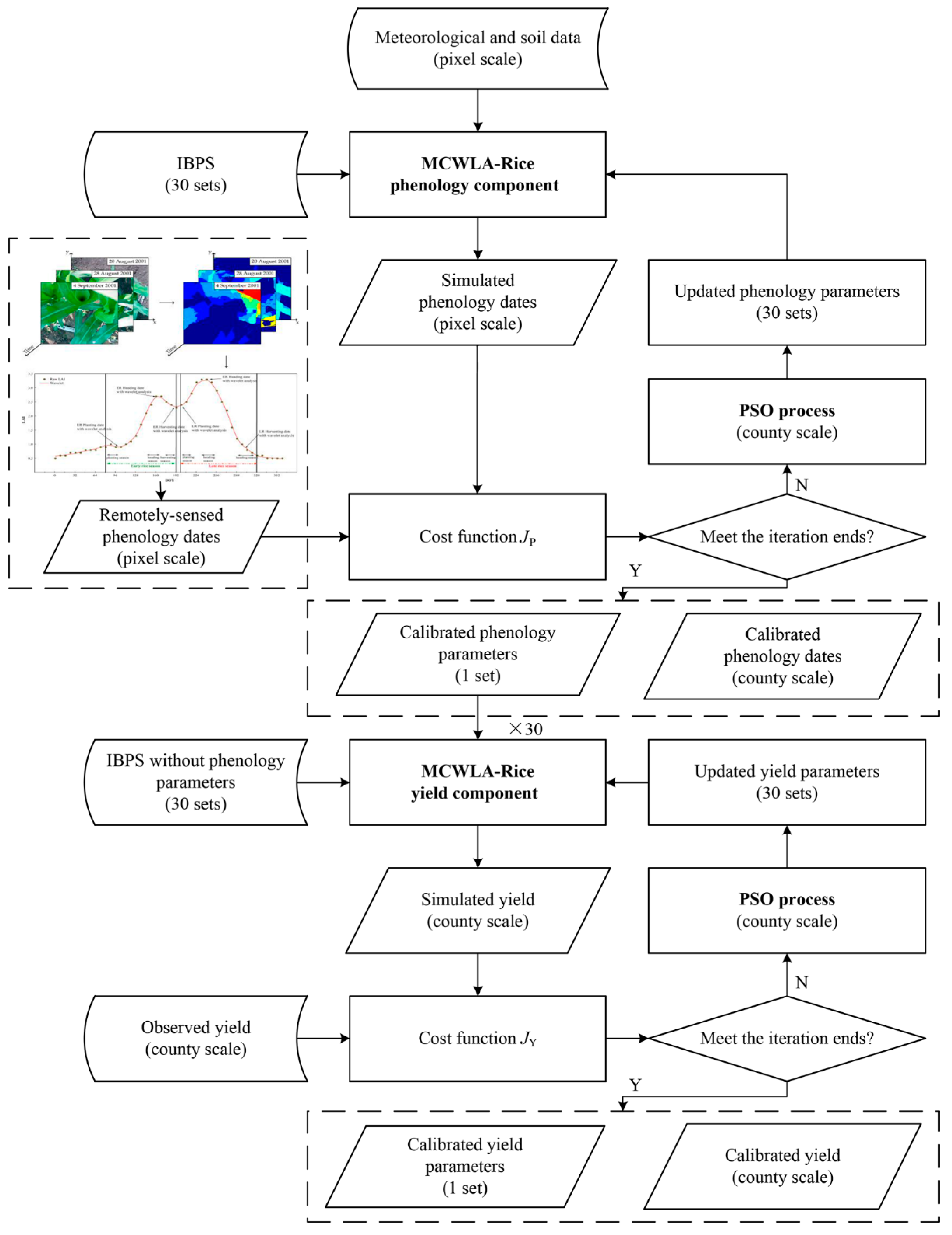
2.4. Calibration and Validation Framework
2.4.1. Calibration Process
2.4.2. Validation Process
2.5. Evaluation Methods
- ,
- ,
- ,
3. Results and Discussion
3.1. Evaluation of Model Simulation
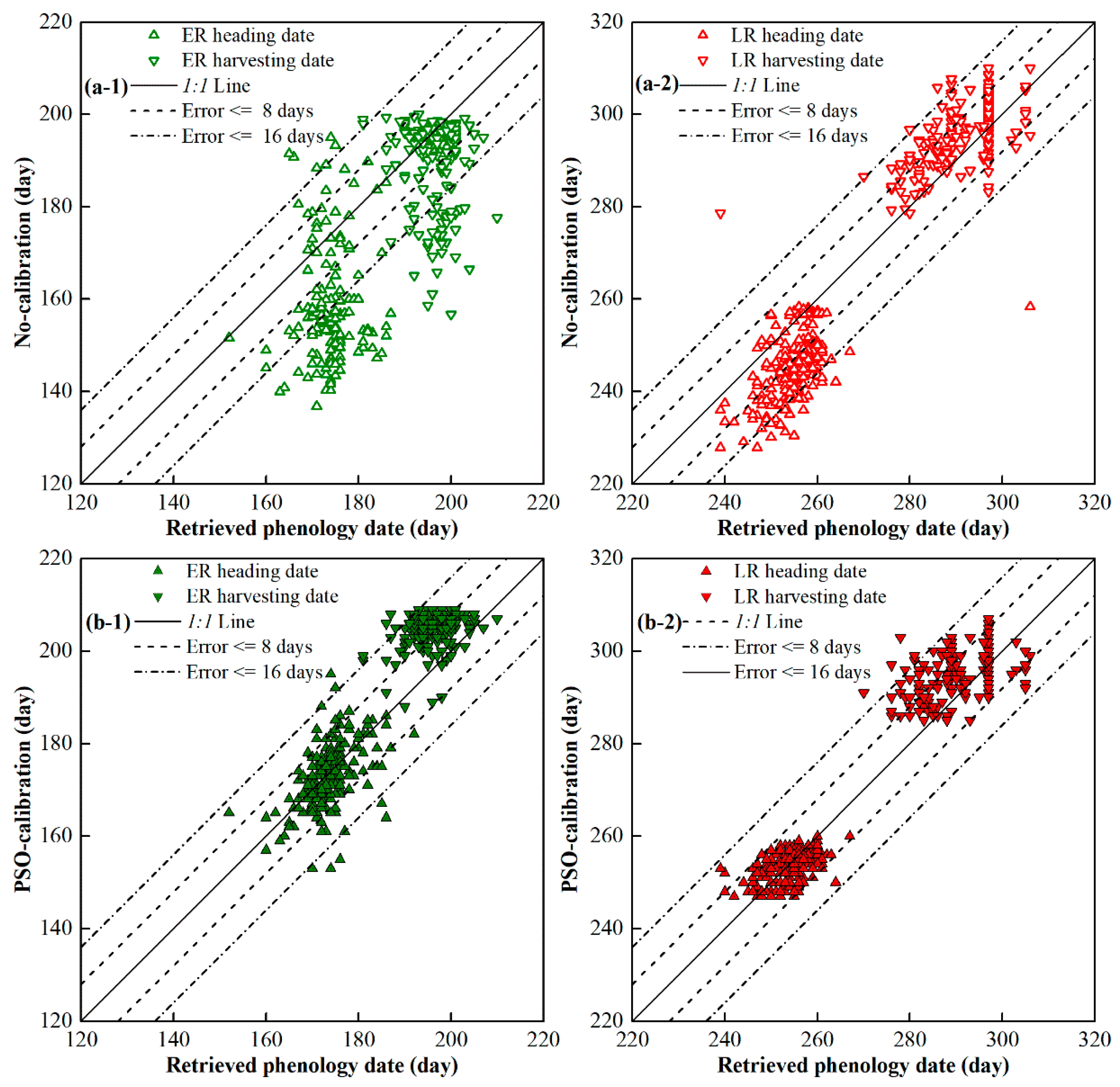
3.1.1. Calibration for Phenology Dates
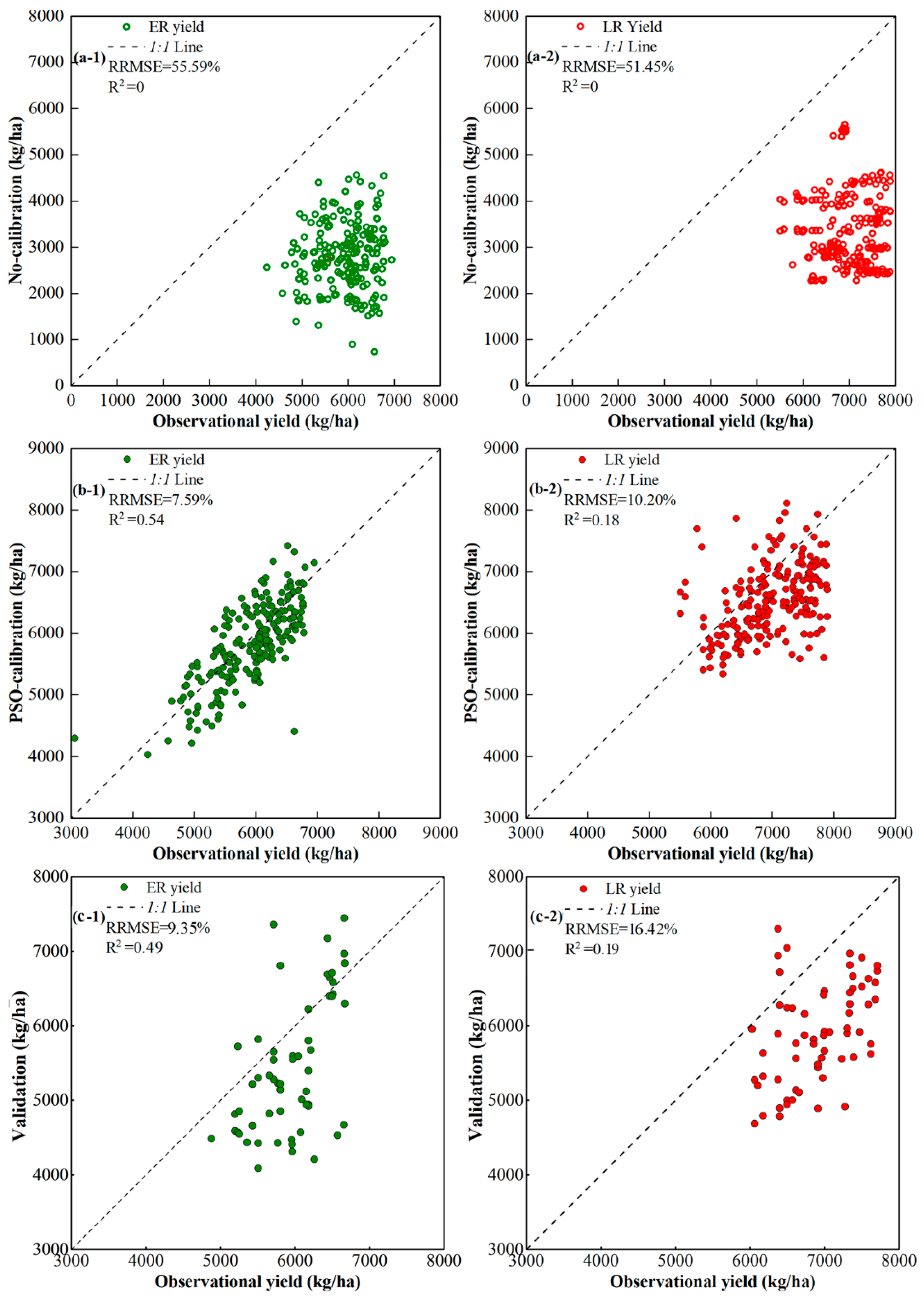
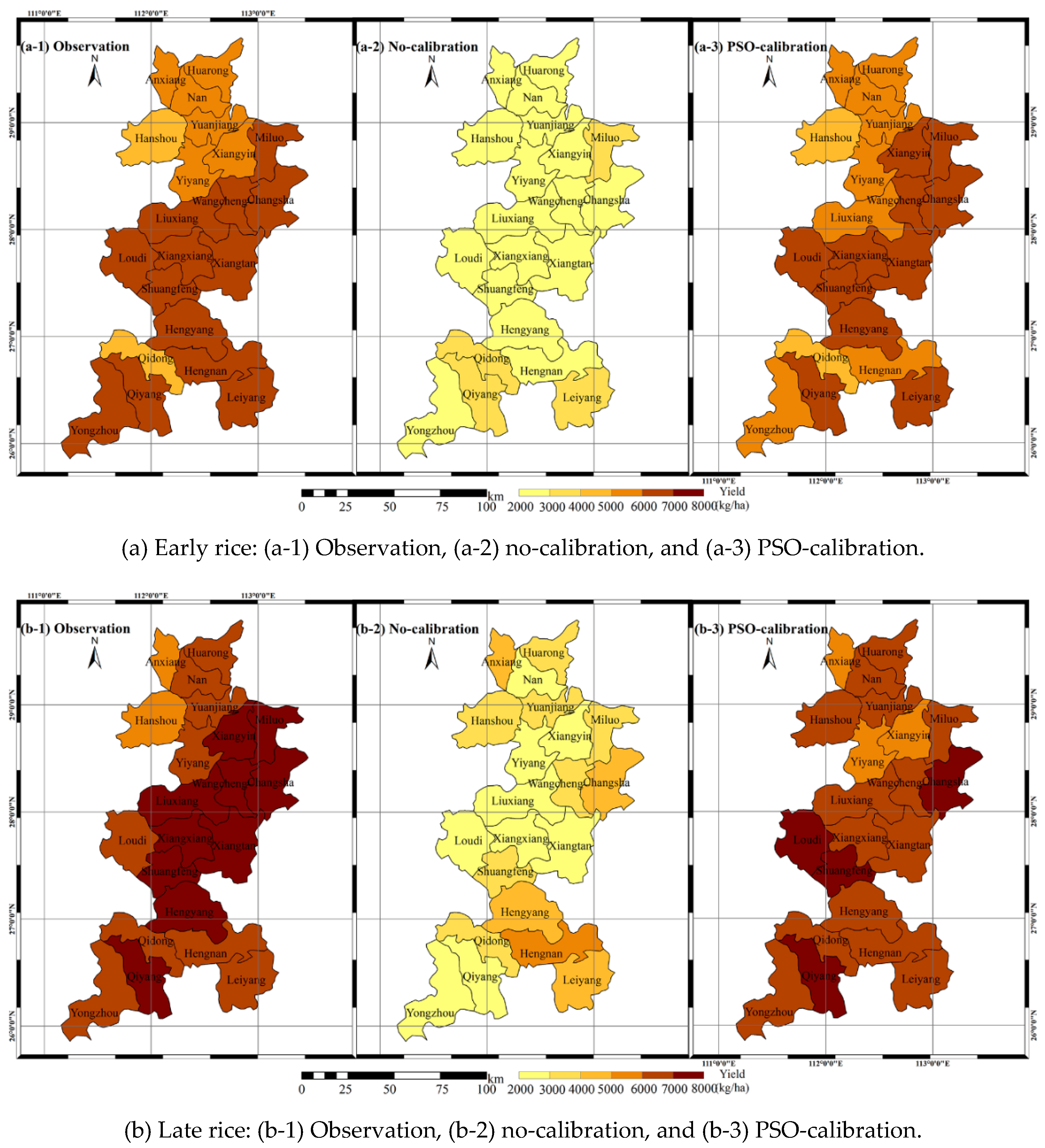
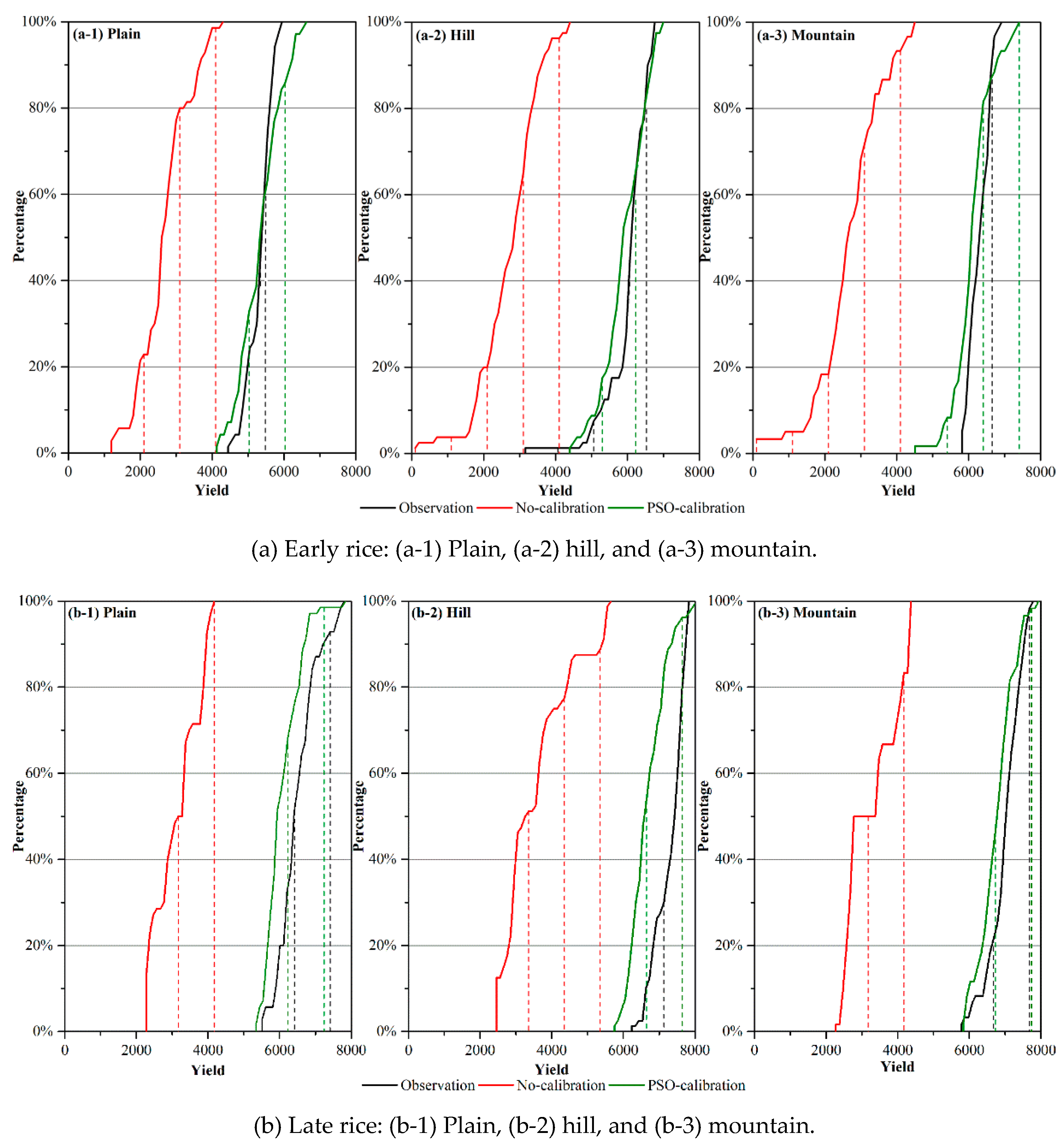
3.1.2. Calibration and Validation for Final Yield
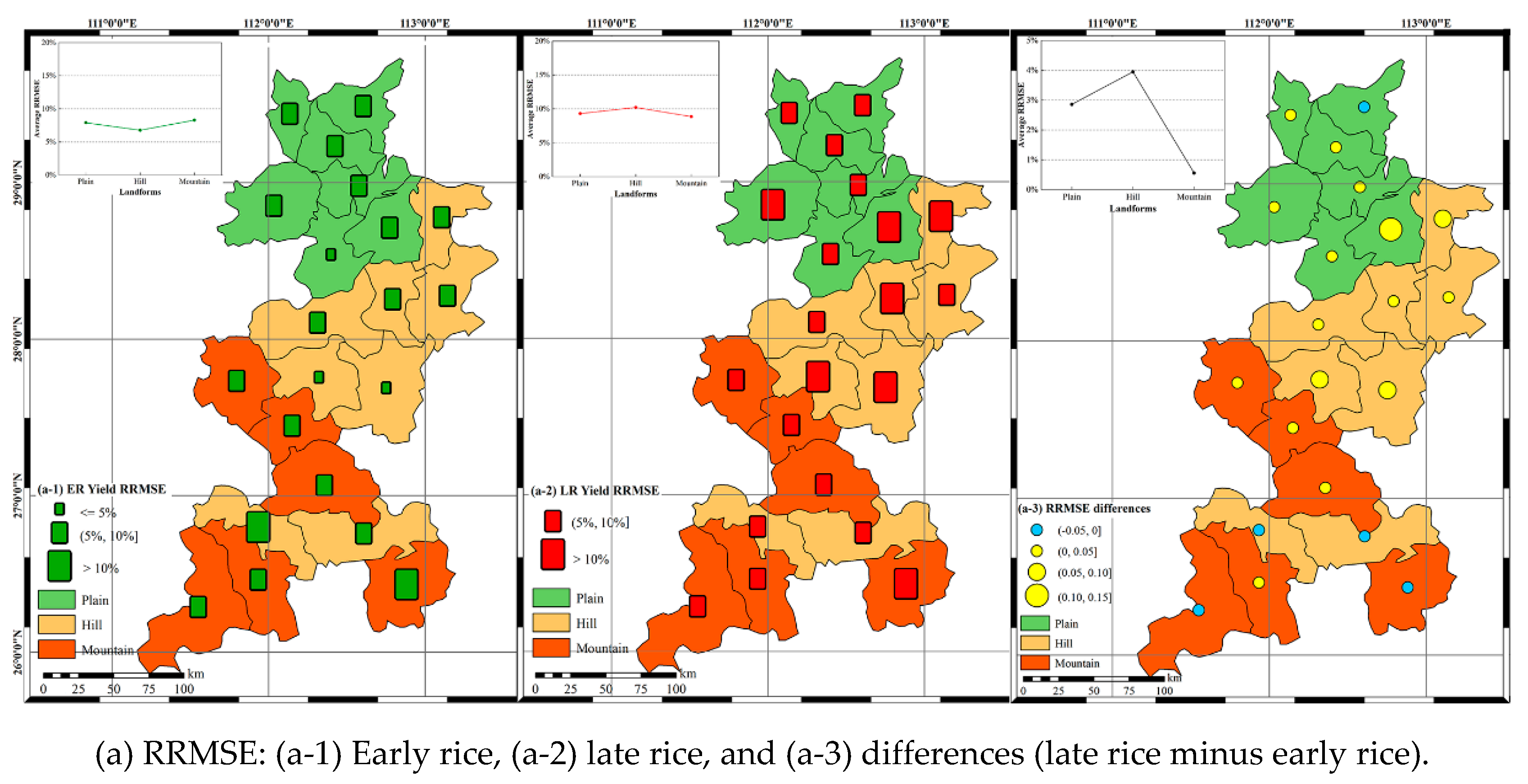
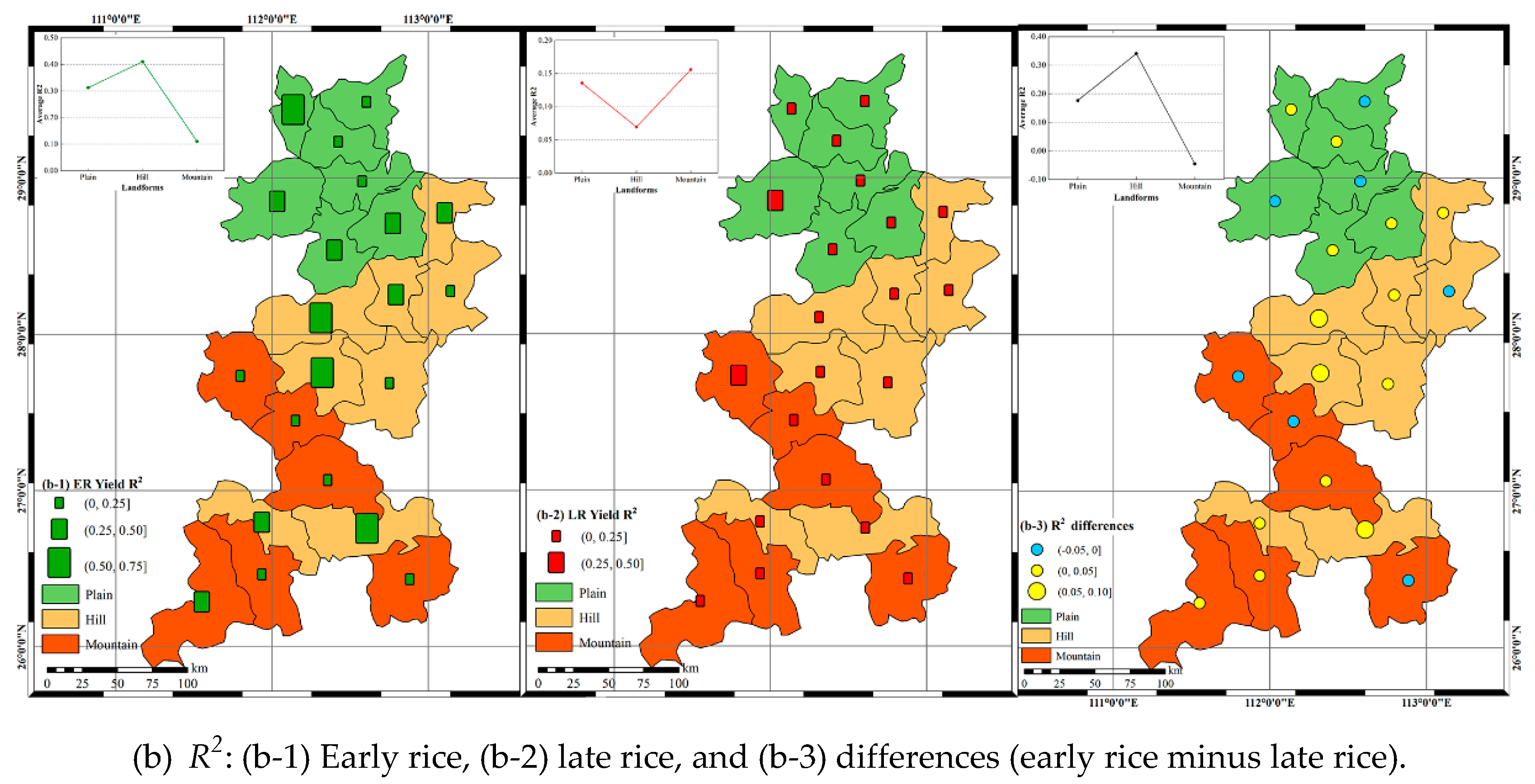
3.2. Simulation Improvements on Different Landforms
3.3. Simulation Differences Between Early Rice and Late Rice on Different Landforms
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations (FAO). FAOSTAT Database 2010. 2010. Available online: http://www.fao.org/fishery/org/GlobalRecord/en (accessed on 14 July 2010).
- Seck, P.A.; Diagne, A.; Mohanty, S.; Wopereis, M.C. Crops that feed the world 7: Rice. Food Secur. 2012, 4, 7–24. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Z.; Song, X.; Chen, Y.; Wei, X.; Shi, P.; Tao, F. Temperature variations and rice yields in China: Historical contributions and future trends. Clim. Change 2014, 124, 777–789. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, S.; Zhang, Z. Spatiotemporal changes of wheat phenology in China under the effects of temperature, day length and cultivar thermal characteristics. Eur. J. Agron. 2012, 43, 201–212. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Z.; Chen, Y.; Wei, X.; Feng, B.; Tao, F. How much yield loss has been caused by extreme temperature stress to the irrigated rice production in China? Clim. Chang. 2016, 134, 635–650. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Robertson, G.P.; Thelen, K.D.; Harwood, R.R. Management, topographical, and weather effects on spatial variability of crop grain yields. Agron. J. 2005, 97, 514–523. [Google Scholar] [CrossRef]
- Huang, X.; Wang, L.; Yang, L.; Kravchenko, A.N. Management effects on relationships of crop yields with topography represented by wetness index and precipitation. Agron. J. 2008, 100, 1463. [Google Scholar] [CrossRef]
- Kumhálová, J.; Kumhála, F.; Kroulík, M.; Matějková, Š. The impact of topography on soil properties and yield and the effects of weather conditions. Precis. Agric. 2011, 12, 813–830. [Google Scholar] [CrossRef]
- Zhang, X.C.; Liu, W.Z. Simulating potential response of hydrology, soil erosion, and crop productivity to climate change in Changwu tableland region on the Loess Plateau of China. Agric. For. Meteorol. 2005, 131, 127–142. [Google Scholar] [CrossRef]
- Greene, J.S.; Maxwell, E. Climatic impacts on winter wheat in Oklahoma and potential applications to climatic and crop yield prediction. Int. J. Biometeorol. 2007, 52, 117–126. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, Z. Climate change, wheat productivity and water use in the North China Plain: A new super-ensemble-based probabilistic projection. Agric. For. Meteorol. 2013, 170, 146–165. [Google Scholar] [CrossRef]
- Dhungana, P.; Eskridge, K.M.; Weiss, A.; Baenziger, P.S. Designing crop technology for a future climate: An example using response surface methodology and the CERES-Wheat model. AGR Syst. 2006, 87, 63–79. [Google Scholar] [CrossRef]
- Cho, K.; Falloon, P.; Gornall, J.; Betts, R.; Clark, R. Winter wheat yields in the UK: Uncertainties in climate and management impacts. Clim. Res. 2012, 54, 49–68. [Google Scholar] [CrossRef]
- Easterling, W.E.; Chhetri, N.; Niu, X. Improving the realism of modeling agronomic adaptation to climate change: Simulating technological substitution. In Issues in the Impacts of Climate Variability and Change on Agriculture; Mearns, L.O., Ed.; Springer: Dordrecht, The Netherlands, 2003; pp. 149–173. [Google Scholar] [CrossRef]
- Lobell, D.B.; Cassman, K.G.; Field, C.B. Crop yield gaps: Their importance, magnitudes, and causes. Annu. Rev. Environ. Resour. 2009, 34, 179–204. [Google Scholar] [CrossRef]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed]
- Tao, F.; Zhang, Z. Climate change, high-temperature stress, rice productivity, and water use in Eastern China: A new superensemble-based probabilistic projection. J. Appl. Meteorol. Clim. 2013, 52, 531–551. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Tubiello, F.N.; Goldberg, R.; Mills, E.; Bloomfield, J. Increased crop damage in the US from excess precipitation under climate change. Glob. Environ. Chang. 2002, 12, 197–202. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, T.; Wang, J.; Cheng, Z.; Shi, P. Contribution of climatic and technological factors to crop yield: Empirical evidence from late paddy rice in Hunan Province, China. Stoch. Environ. Res. Risk A 2016, 30, 2019–2030. [Google Scholar] [CrossRef]
- Tubiello, F.N.; Donatelli, M.; Rosenzweig, C.; Stockle, C.O. Effects of climate change and elevated CO2 on cropping systems: Model predictions at two Italian locations. Eur. J. Agron. 2000, 13, 179–189. [Google Scholar] [CrossRef]
- Tubiello, F.N.; Ewert, F. Simulating the effects of elevated CO2 on crops: Approaches and applications for climate change. Eur. J. Agron. 2002, 18, 57–74. [Google Scholar] [CrossRef]
- Trnka, M.; Dubrovský, M.; Semerádová, D.; Žalud, Z. Projections of uncertainties in climate change scenarios into expected winter wheat yields. Theor. Appl. Climatol. 2004, 77, 229–249. [Google Scholar] [CrossRef]
- Landau, S.; Mitschell, R.A.C.; Barnett, V.; Colls, J.J.; Craigon, J.; Moore, K.L.; Payne, R.W. Testing winter wheat simulation models’ predictions against observe UK grain yields. Agric. For. Meteorol. 1998, 89, 85–99. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Hatfield, J.L.; Jackson, T.J.; Akhmedov, B.; Prueger, J.; Stern, A. Crop condition and yield simulations using Landsat and MODIS. Remote Sens. Environ. 2004, 92, 548–559. [Google Scholar] [CrossRef]
- Noory, H.; Van Der Zee, S.E.A.T.M.; Liaghat, A.M.; Parsinejad, M.; Van Dam, J.C. Distributed agro-hydrological modeling with SWAP to improve water and salt management of the Voshmgir Irrigation and Drainage Network in Northern Iran. Agric. Water Manag. 2011, 98, 1062–1070. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Liu, G.; Jiang, Z.; Huang, C. Improving Winter Wheat Yield Estimation from the CERES-Wheat Model to Assimilate Leaf Area Index with Different Assimilation Methods and Spatio-Temporal Scales. Remote Sens. 2017, 9, 190. [Google Scholar] [CrossRef]
- Setiyono, T.D.; Quicho, E.D.; Gatti, L.; Campos-Taberner, M.; Busetto, L.; Collivignarelli, F.; García-Haro, F.J.; Boschetti, M.; Khan, N.I.; Holecz, F. Spatial Rice Yield Estimation Based on MODIS and Sentinel-1 SAR Data and ORYZA Crop Growth Model. Remote Sens. 2018, 10, 293. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, X.; Liu, M. Assimilating Remote Sensing Phenological Information into the WOFOST Model for Rice Growth Simulation. Remote Sens. 2019, 11, 268. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Leff, B.; Ramankutty, N.; Foley, J.A. Geographic distribution of major crops across the world. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Xu, X.; Kuang, W.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; Yu, D.; Wu, S.; et al. Spatial patterns and driving forces of land use change in China during the early 21st century. J. Geogr. Sci. 2010, 20, 483–494. [Google Scholar] [CrossRef]
- Liu, J.; Kuang, W.; Zhang, Z.; Xu, X.; Qin, Y.; Ning, J.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; et al. Spatiotemporal characteristics, patterns, and causes of land-use changes in China since the late 1980s. J. Geogr. Sci. 2014, 24, 195–210. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, Z.; Liu, J.; Yokozawa, M. Modelling the impacts of weather and climate variability on crop productivity over a large area: A new super-ensemble-based probabilistic projection. Agric. For. Meteorol. 2009, 149, 1266–1278. [Google Scholar] [CrossRef]
- Streck, N.A.; Weiss, A.; Xue, Q.; Baenziger, P.S. Improving predictions of developmental stages in winter wheat: A modified Wang and Engel model. Agric. Meteorol. 2003, 115, 139–150. [Google Scholar] [CrossRef]
- Tao, F.; Yokozawa, M.; Zhang, Z. Modelling the impacts of weather and climate variability on crop productivity over a large area: A new process-based model development, optimization, and uncertainties analysis. Agric. For. Meteorol. 2009, 149, 831–850. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, X.; Chen, Y.; Wang, P.; Wei, X.; Tao, F. Dynamic variability of the heading–flowering stages of single rice in China based on field observations and NDVI estimations. Int. J. Biometeorol. 2015, 59, 643–655. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, Y.; Wang, C.; Wang, P.; Tao, F. Future extreme temperature and its impact on rice yield in China. Int. J. Climatol. 2017, 37, 4814–4827. [Google Scholar] [CrossRef]
- Shuai, J.; Zhang, Z.; Tao, F.; Shi, P. How ENSO affects maize yields in China: Understanding the impact mechanisms using a process-based crop model. Int. J. Climatol. 2016, 36, 424–438. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, P.; Zhang, Z.; Tao, F.; Wei, X. Rice yield development and the shrinking yield gaps in China, 1981–2008. Reg. Environ. Chang. 2017, 17, 2397–2408. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F.; Wang, P.; Wei, X. Spatio-temporal patterns of winter wheat yield potential and yield gap during the past three decades in North China. Field Crop. Res. 2017, 206, 11–20. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Impacts of climate change and climate extremes on major crops productivity in China at a global warming of 1.5 and 2.0 °C. Earth Syst. Dyn. 2018, 9, 543. [Google Scholar] [CrossRef]
- Yuan, W.; Xu, B.; Chen, Z.; Xia, J.; Xu, W.; Chen, Y.; Wu, X.; Fu, Y. Validation of China-wide interpolated daily climate variables from 1960 to 2011. Theor. Appl. Climatol. 2015, 119, 689–700. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). The Digitized Soil Map of the World (Release 1.0) World Soil Resources Report 67; FAO: Rome, Italy, 1991. [Google Scholar]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Moulin, S.; Kergoat, L.; Cayrol, P.; Dedieu, G.; Prévot, L. Calibration of a coupled canopy functioning and SVAT model in the ReSeDA experiment. Towards the assimilation of SPOT/HRV observations into the model. Agronomie 2002, 22, 681–686. [Google Scholar] [CrossRef]
- Ines, A.V.; Mohanty, B.P.; Shin, Y. An unmixing algorithm for remotely sensed soil moisture. Water Resour. Res. 2013, 49, 408–425. [Google Scholar] [CrossRef]
- Xu, L.; Yang, M.; Steward, B.L. System of field operations for double-cropped paddy rice production mechanization in South China. In Proceedings of the Agricultural Biosystems Engineering Conference, Louisville, KY, USA, 7–10 August 2011; Paper 32. Available online: http://lib.dr.iastate.edu/abe_eng_conf/32 (accessed on 10 August 2011).
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Chen, Y.; Tao, F.; Zhang, J.; Zhang, W. Comparing different smoothing methods to detect double-cropping rice phenology based on LAI products—A case study in the Hunan province of China. Int. J. Remote Sens. 2018, 39, 6405–6428. [Google Scholar] [CrossRef]
- Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Phototgramm. 1992, 47, 145–161. [Google Scholar] [CrossRef]
- Plummer, L.N.; Busenberg, E.; Riggs, A.C. In-situ growth of calcite at Devils Hole, Nevada: Comparison of field and laboratory rates to a 500,000 year record of near-equilibrium calcite growth. Aquat. Geochem. 2000, 6, 257–274. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, S.; Zhang, Z. Changes in rice disasters across China in recent decades and the meteorological and agronomic causes. Reg. Environ. Chang. 2013, 13, 743–759. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Rivington, M.; Bellocchi, G.; Matthews, K.B.; Buchan, K. Evaluation of three model estimations of solar radiation at 24 UK stations. Agric. For. Meteorol. 2005, 132, 228–243. [Google Scholar] [CrossRef]
- Bellocchi, G.; Rivington, M.; Donatelli, M.; Matthews, K. Validation of biophysical models: Issues and methodologies. In Sustainable Agriculture; Lichtfouse, E., Hamelin, M., Navarrete, M., Debaeke, P., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 2, pp. 577–603. [Google Scholar] [CrossRef]
- Coucheney, E.; Buis, S.; Launay, M.; Constantin, J.; Mary, B.; de Cortázar-Atauri, I.G.; Ripoche, D.; Beaudoin, N.; Ruget, F.; Andrianarisoa, K.S.; et al. Accuracy, robustness and behavior of the STICS soil–crop model for plant, water and nitrogen outputs: Evaluation over a wide range of agro-environmental conditions in France. Environ. Modell. Softw. 2015, 64, 177–190. [Google Scholar] [CrossRef]
- Wallach, D.; Goffinet, B.; Bergez, J.E.; Debaeke, P.; Leenhardt, D.; Aubertot, J.N. Parameter estimation for crop models. Agron. J. 2001, 93, 757–766. [Google Scholar] [CrossRef]
- Angulo, C.; Rötter, R.; Lock, R.; Enders, A.; Fronzek, S.; Ewert, F. Implication of crop model calibration strategies for assessing regional impacts of climate change in Europe. Agric. For. Meteorol. 2013, 170, 32–46. [Google Scholar] [CrossRef]
- Guillaume, S.; Bergez, J.E.; Wallach, D.; Justes, E. Methodological comparison of calibration procedures for durum wheat parameters in the STICS model. Eur. J. Agron. 2011, 35, 115–126. [Google Scholar] [CrossRef]
- Belder, P.; Bouman, B.A.M.; Spiertz, J.H.J. Exploring options for water savings in lowland rice using a modelling approach. Agric. Syst. 2007, 92, 91–114. [Google Scholar] [CrossRef]
- Boling, A.A.; Bouman, B.A.M.; Tuong, T.P.; Murty, M.V.R.; Jatmiko, S.Y. Modelling the effect of groundwater depth on yield-increasing interventions in rainfed lowland rice in Central Java, Indonesia. Agric. Syst. 2007, 92, 115–139. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, J.; Yang, X. Non-stationary thermal time accumulation reduces the predictability of climate change effects on agriculture. Agric. For. Meteorol. 2008, 148, 1412–1418. [Google Scholar] [CrossRef]
- Shen, S.; Yang, S.; Li, B.; Tan, B.; Li, Z.; Le Toan, T. A scheme for regional rice yield estimation using ENVISAT ASAR data. Sci. China Ser. D 2009, 52, 1183–1194. [Google Scholar] [CrossRef]
- Chen, J.S.; Huang, J.X.; Lin, H.; Fei, Z.Y. Rice yield estimation by assimilation remote sensing into crop growth model. Sci. China Inf. Sci. 2010, 2010, 173–183. (In Chinese) [Google Scholar]
- Wang, J. Rice Information Extraction Studies Based on Multi-Source Remote Sensing Data Integrating and Data Assimilating. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2016. (In Chinese). [Google Scholar]
- Qing, X.G.; Ai, Z.Y. On regional distribution of rice cultivation in Hunan Province. Res. Agric. Mod. 2007, 28, 704–708. (In Chinese) [Google Scholar]
- Deryng, D.; Sacks, W.J.; Barford, C.C.; Ramankutty, N. Simulating the effects of climate and agricultural management practices on global crop yield. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change factors? Glob. Change Biol. 2014, 20, 2301–2320. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Q.; Zhou, J.; Zhang, G.; Chen, C.; Wang, J. Assimilating remote sensing information into a coupled hydrology-crop growth model to estimate regional maize yield in arid regions. Ecol. Model. 2014, 291, 15–27. [Google Scholar] [CrossRef]
| Researches | Shen et al. [66] | Chen et al. [67] | Wang et al. [68] | Present Research |
|---|---|---|---|---|
| Study area | 1000 ha | 7000 ha | 11,500 ha | 1,686,600 ha |
| Crop | Single rice | Early rice | Single rice | Double rice |
| Referenced data | Advanced Synthetic Aperture Radar | HJ-1 A/B | HJ-1 A/B, Landsat 8 | MODIS and ground observations |
| Crop model | WOFOST | WOFOST | ORYZA2000 | MCWLA-Rice |
| Intermediate variable | Backscattering coefficients | LAI | LAI | Retrieved phenology dates |
| RRMSE | 12.70% | 7.20% | 7.04% | 7.59% (best average for early rice) and 10.20% (best average for late rice) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, Z.; Wang, C.; Tao, F. Double-Rice System Simulation in a Topographically Diverse Region—A Remote-Sensing-Driven Case Study in Hunan Province of China. Remote Sens. 2019, 11, 1577. https://doi.org/10.3390/rs11131577
Zhang J, Zhang Z, Wang C, Tao F. Double-Rice System Simulation in a Topographically Diverse Region—A Remote-Sensing-Driven Case Study in Hunan Province of China. Remote Sensing. 2019; 11(13):1577. https://doi.org/10.3390/rs11131577
Chicago/Turabian StyleZhang, Jing, Zhao Zhang, Chenzhi Wang, and Fulu Tao. 2019. "Double-Rice System Simulation in a Topographically Diverse Region—A Remote-Sensing-Driven Case Study in Hunan Province of China" Remote Sensing 11, no. 13: 1577. https://doi.org/10.3390/rs11131577
APA StyleZhang, J., Zhang, Z., Wang, C., & Tao, F. (2019). Double-Rice System Simulation in a Topographically Diverse Region—A Remote-Sensing-Driven Case Study in Hunan Province of China. Remote Sensing, 11(13), 1577. https://doi.org/10.3390/rs11131577





