Estimating Live Fuel Moisture Using SMAP L-Band Radiometer Soil Moisture for Southern California, USA
Abstract
1. Introduction
2. Materials and Methods
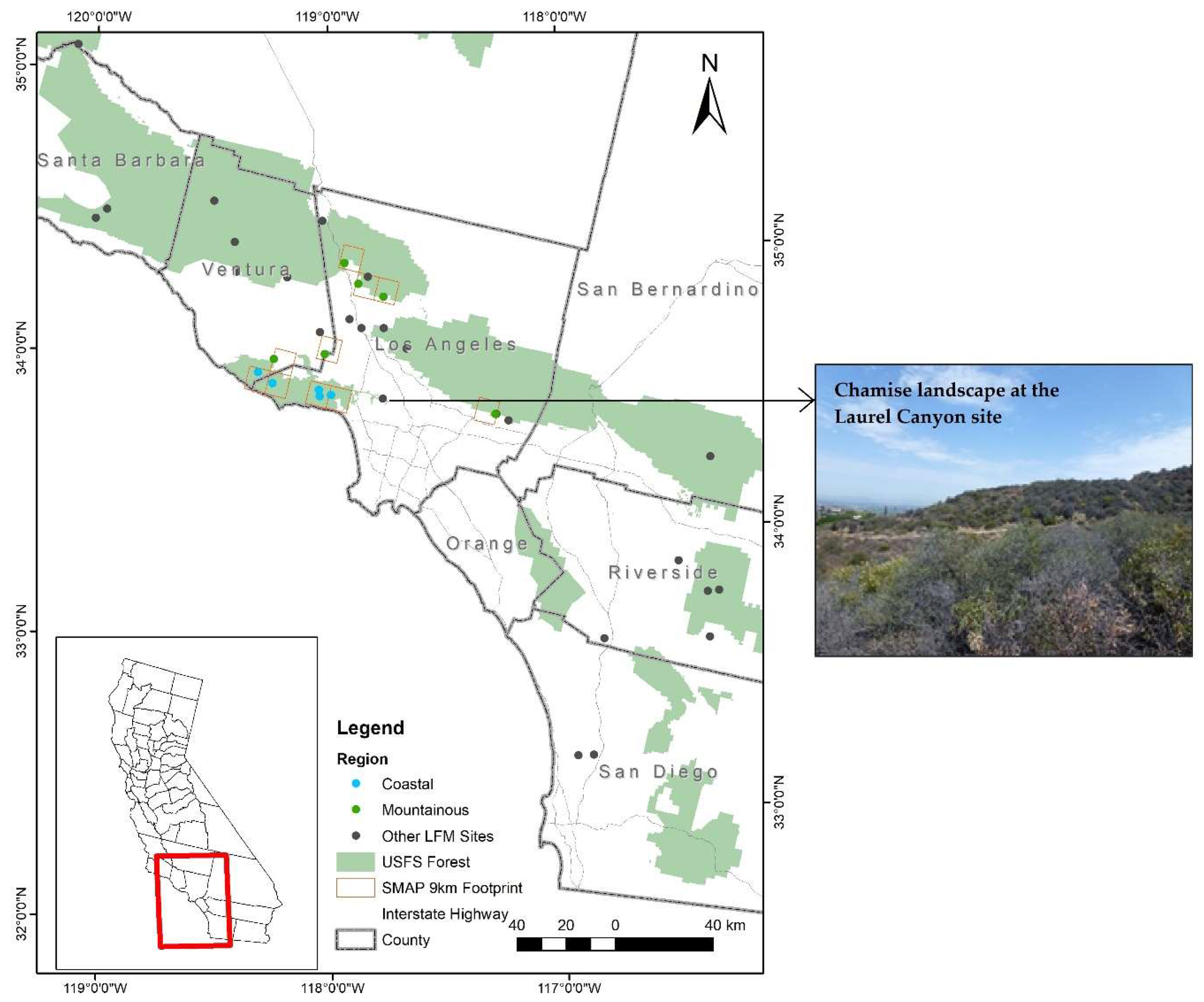
2.1. LFM Observations in Southern California
2.2. Remote Sensing Data
2.3. Meteorological Variable Preparation
2.4. Regression Model Development
2.4.1. Lag Extraction
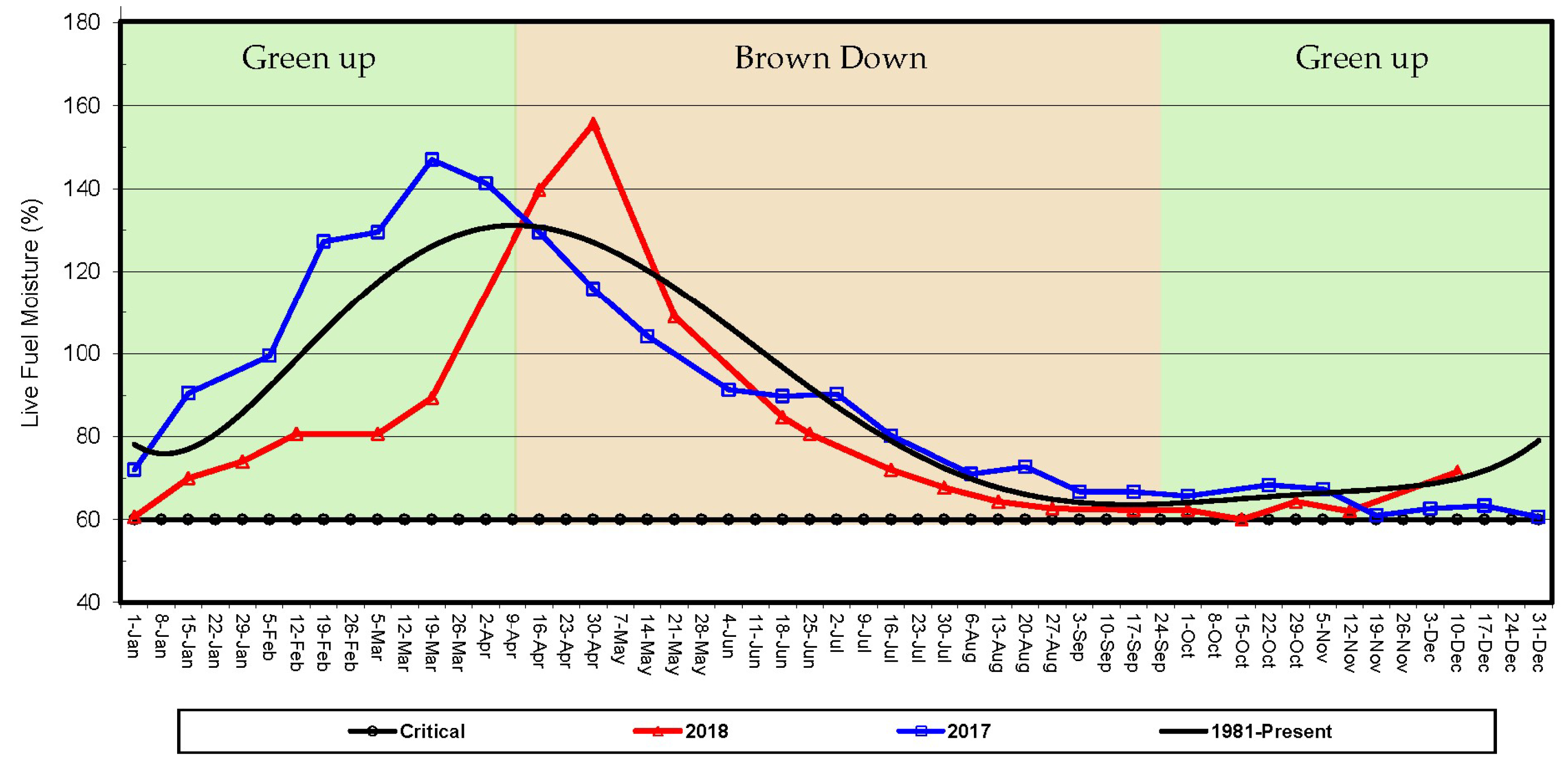
2.4.2. Phenological Phase Definition
2.4.3. Regression Models Using the Synchronized SMAP SM
2.4.4. Regression Models Using the Accumulative SMAP SM
3. Results
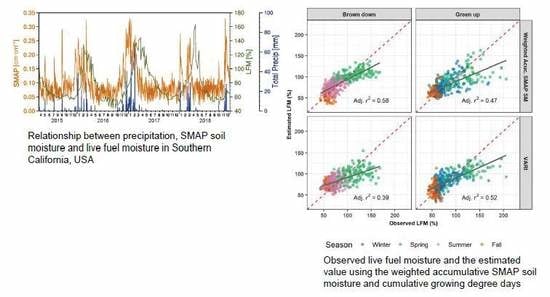
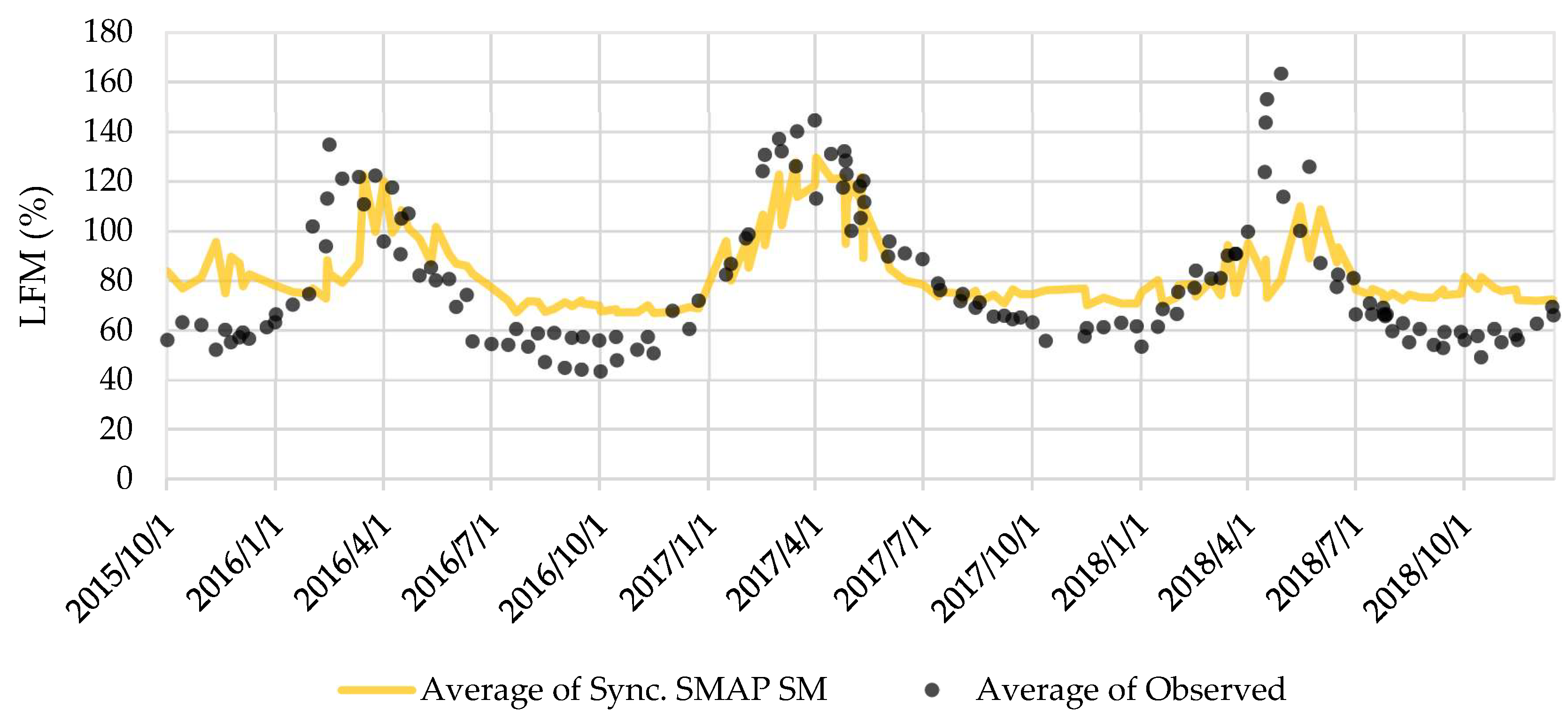
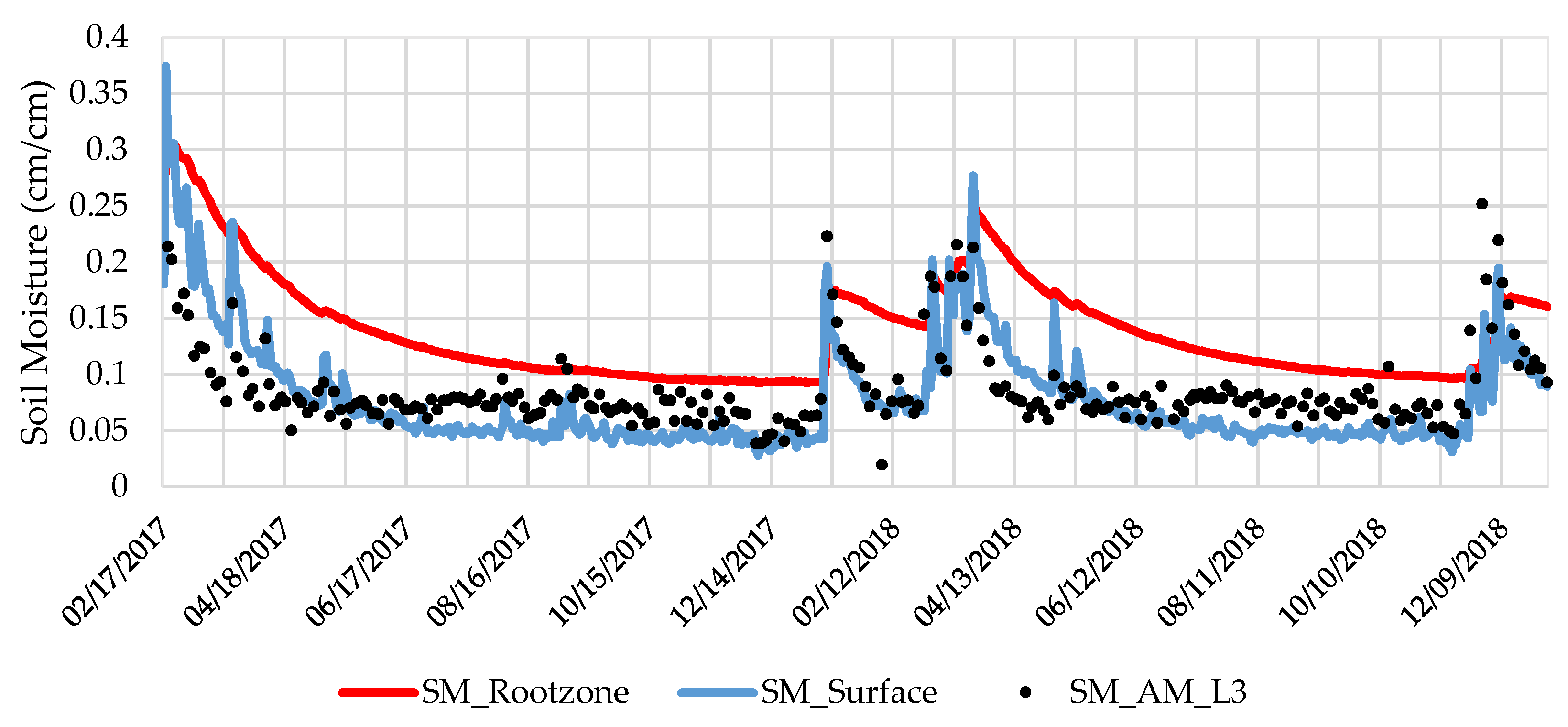
3.1. Relationship between Precipitation, SMAP SM, and LFM
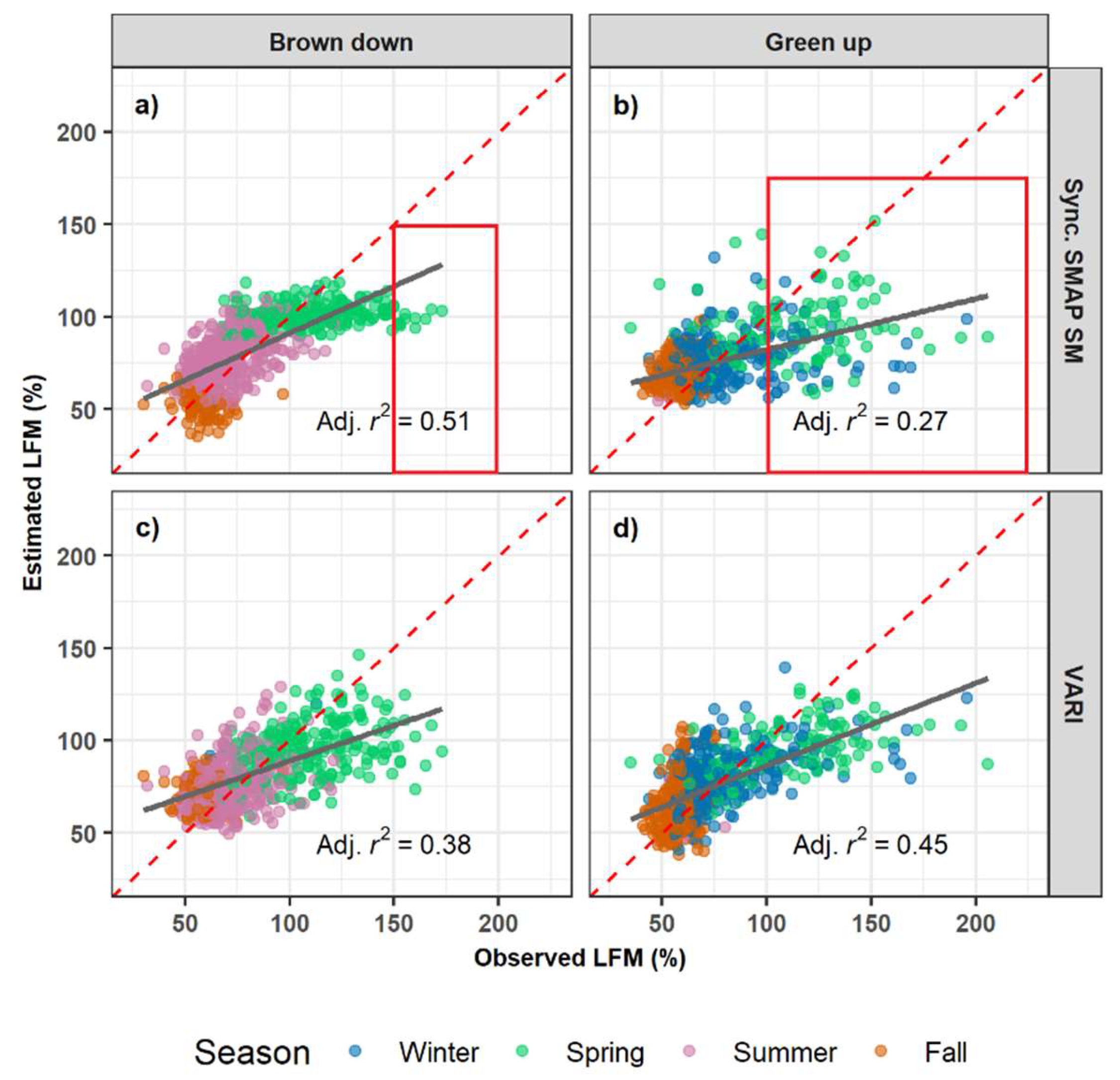
3.2. LFM Estimation Using the Synchronized SMAP SM
3.3. LFM Estimation with the Consideration of GDD
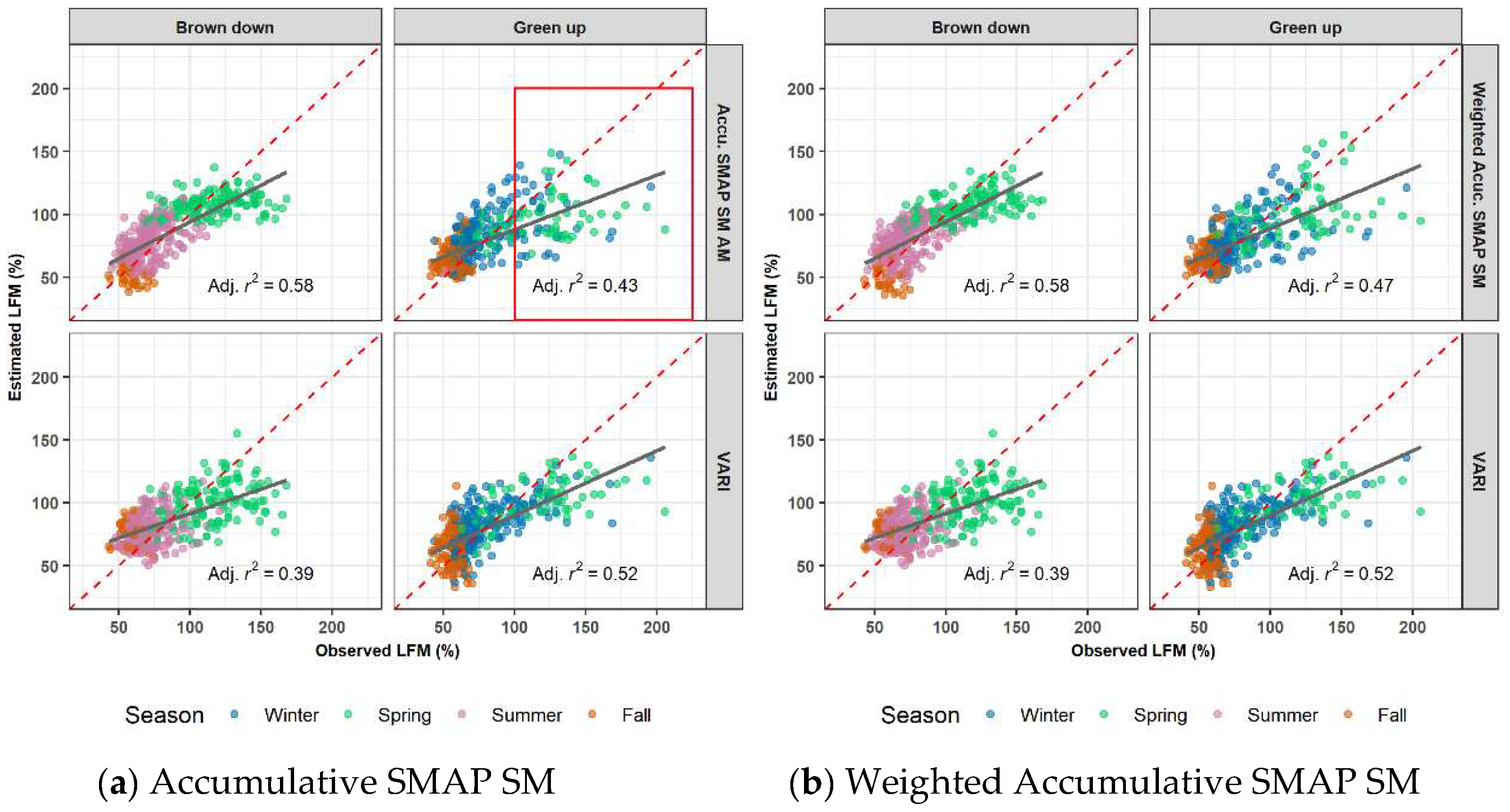
3.4. LFM Estimation Using the Accumulated SMAP SM
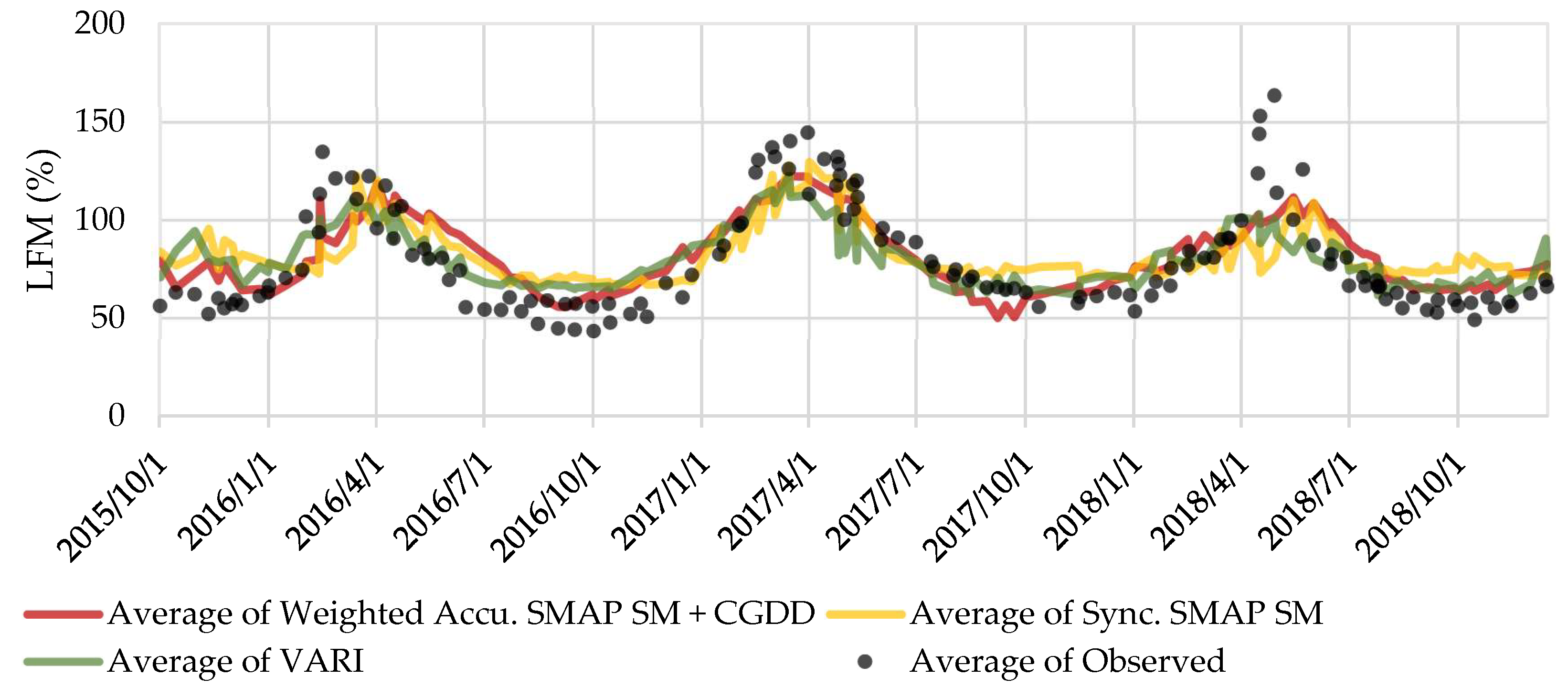
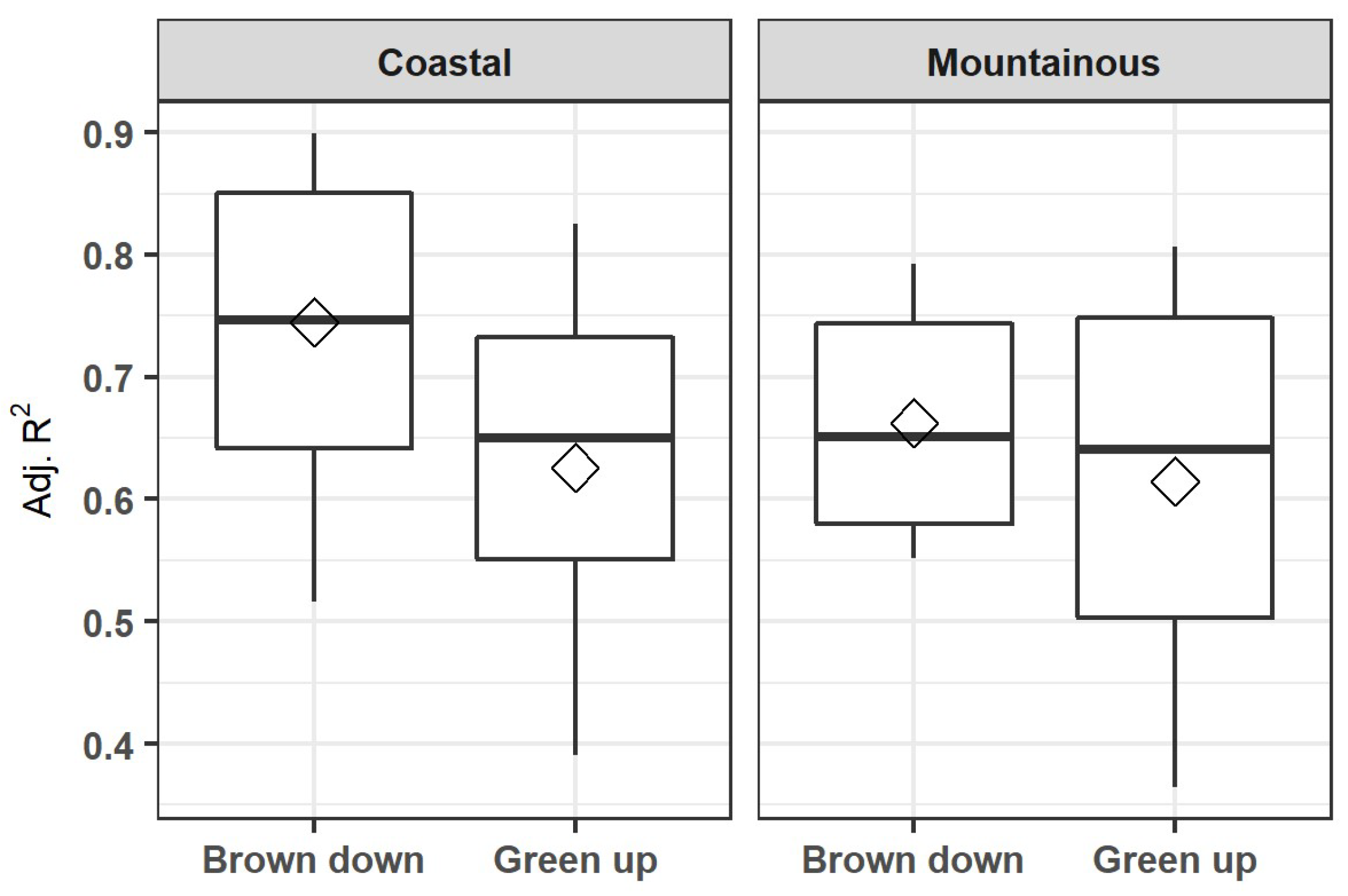
3.5. Model Comparison and Validation
4. Discussion
4.1. SMAP SM for LFM Estimation and Outlook
4.2. Separating Green-up and Brown-down Period for LFM Modeling
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Syphard, A.D.; Radeloff, V.C.; Keuler, N.S.; Taylor, R.S.; Hawbaker, T.J.; Stewart, S.I.; Clayton, M.K. Predicting spatial patterns of fire on a southern California landscape. Int. J. Wildland Fire 2008, 17, 602–613. [Google Scholar] [CrossRef]
- Keeley, J.E.; Syphard, A.D. Climate change and future fire regimes: Examples from California. Geosci. Can. 2016, 6, 37. [Google Scholar] [CrossRef]
- Simard, A.J. The Moisture Content of Forest Fuels; University of California: Oakland, CA, USA, 1968. [Google Scholar]
- Services, E.G.B.P. National Fuel Moisture Database 2009 User Guide; U.S. Forest Service: Salt Lake City, UT, USA, 2009.
- Bradshaw, L.S.; Deeming, J.E.; Burgan, R.E.; Cohen, J.D. The 1978 National Fire-Danger Rating System: Technical Documentation. General Technical Report INT-169; Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1984; Volume 169, p. 44.
- Chuvieco, E.; Cocero, D.; Riano, D.; Martin, P.; Martınez-Vega, J.; de la Riva, J.; Perez, F. Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sens. Environ. 2004, 92, 322–331. [Google Scholar] [CrossRef]
- Fan, L.; Wigneron, J.-P.; Xiao, Q.; Al-Yaari, A.; Wen, J.; Martin-StPaul, N.; Dupuy, J.-L.; Pimont, F.; Al Bitar, A.; Fernandez-Moran, R. Evaluation of microwave remote sensing for monitoring live fuel moisture content in the Mediterranean region. Remote Sens. Environ. 2018, 205, 210–223. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E.; Riano, D. Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agric. For. Meteorol. 2008, 148, 523–536. [Google Scholar] [CrossRef]
- Yebra, M.; Quan, X.W.; Riano, D.; Larraondo, P.R.; van Dijk, A.I.J.M.; Cary, G.J. A fuel moisture content and flammability monitoring methodology for continental Australia based on optical remote sensing. Remote Sens. Environ. 2018, 212, 260–272. [Google Scholar] [CrossRef]
- Jurdao, S.; Yebra, M.; Guerschman, J.P.; Chuvieco, E. Regional estimation of woodland moisture content by inverting Radiative Transfer Models. Remote Sens. Environ. 2013, 132, 59–70. [Google Scholar] [CrossRef]
- Peterson, S.H.; Roberts, D.A.; Dennison, P.E. Mapping live fuel moisture with MODIS data: A multiple regression approach. Remote Sens. Environ. 2008, 112, 4272–4284. [Google Scholar] [CrossRef]
- Myoung, B.; Kim, S.H.; Nghiem, S.V.; Jia, S.; Whitney, K.; Kafatos, M.C. Estimating Live Fuel Moisture from MODIS Satellite Data for Wildfire Danger Assessment in Southern California USA. Remote Sens. 2018, 10, 87. [Google Scholar] [CrossRef]
- Roberts, D.A.; Dennison, P.E.; Peterson, S.; Sweeney, S.; Rechel, J. Evaluation of airborne visible/infrared imaging spectrometer (AVIRIS) and moderate resolution imaging spectrometer (MODIS) measures of live fuel moisture and fuel condition in a shrubland ecosystem in southern California. J. Geophys. Res. Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riano, D.; Zylstra, P.; Hunt, E.R.; Danson, F.M.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Danson, F.; Bowyer, P. Estimating live fuel moisture content from remotely sensed reflectance. Remote Sens. Environ. 2004, 92, 309–321. [Google Scholar] [CrossRef]
- Palmer, K.F.; Williams, D. Optical properties of water in the near infrared. JOSA 1974, 64, 1107–1110. [Google Scholar] [CrossRef]
- Qi, Y.; Dennison, P.E.; Spencer, J.; Riaño, D. Monitoring Live Fuel Moisture Using Soil Moisture and Remote Sensing Proxies. Fire Ecol. 2012, 8, 71–87. [Google Scholar] [CrossRef]
- Peterson, S.H.; Moritz, M.A.; Morais, M.E.; Dennison, P.E.; Carlson, J.M. Modelling long-term fire regimes of southern California shrublands. Int. J. Wildland Fire 2011, 20, 1–16. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T. SMAP Handbook–Soil Moisture Active Passive: Mapping Soil Moisture and Freeze/Thaw from Space; JPL Publication: Pasadena, CA, USA, 2014. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Fournier, S.; Reager, J.; Lee, T.; Vazquez-Cuervo, J.; David, C.; Gierach, M. SMAP observes flooding from land to sea: The Texas event of 2015. Geophys. Res. Lett. 2016, 43, 10338–310346. [Google Scholar] [CrossRef]
- Mishra, A.; Vu, T.; Veettil, A.V.; Entekhabi, D. Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrol. 2017, 552, 620–632. [Google Scholar] [CrossRef]
- Felfelani, F.; Pokhrel, Y.; Guan, K.; Lawrence, D.M. Utilizing SMAP Soil Moisture Data to Constrain Irrigation in the Community Land Model. Geophys. Res. Lett. 2018, 45, 12892–12902. [Google Scholar] [CrossRef]
- Jones, L.A.; Kimball, J.S.; Reichle, R.H.; Madani, N.; Glassy, J.; Ardizzone, J.V.; Colliander, A.; Cleverly, J.; Desai, A.R.; Eamus, D. The SMAP Level 4 Carbon Product for Monitoring Ecosystem Land–Atmosphere CO2 Exchange. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6517–6532. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Liu, J.; Bélair, S.; Luo, X. Assessment of SMAP soil moisture for global simulation of gross primary production. J. Geophys. Res. Biogeosci. 2017, 122, 1549–1563. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Konings, A.G.; Piles, M.; Rötzer, K.; McColl, K.A.; Chan, S.K.; Entekhabi, D. Vegetation optical depth and scattering albedo retrieval using time series of dual-polarized L-band radiometer observations. Remote Sens. Environ. 2016, 172, 178–189. [Google Scholar] [CrossRef]
- Chaparro, D.; Piles, M.; Vall-llossera, M.; Camps, A.; Konings, A.G.; Entekhabi, D. L-band vegetation optical depth seasonal metrics for crop yield assessment. Remote Sens. Environ. 2018, 212, 249–259. [Google Scholar] [CrossRef]
- Chaparro, D.; Vall-llossera, M.; Piles, M.; Camps, A.; Rüdiger, C.; Riera-Tatché, R. Predicting the Extent of Wildfires Using Remotely Sensed Soil Moisture and Temperature Trends. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2818–2829. [Google Scholar] [CrossRef]
- Holgate, C.M.; van Dijk, A.I.J.M.; Cary, G.J.; Yebra, M. Using alternative soil moisture estimates in the McArthur Forest Fire Danger Index. Int. J. Wildland Fire 2017, 26, 806–819. [Google Scholar] [CrossRef]
- Barbour, M.G.; Keeler-Wolf, T.; Schoenherr, A.A. Terrestrial Vegetation of California; University of California Press: Berkeley, CA, USA, 2007. [Google Scholar]
- Weise, D.R.; Hartford, R.A.; Mahaffey, L. Assessing Live Fuel Moisture for Fire Management Applications; United States Department of Agriculture: Washington, DC, USA, 1998; pp. 49–55.
- National Plant Data Team, The PLANTS Database. Available online: https://plants.sc.egov.usda.gov/ (accessed on 18 May 2019).
- Jow, W.M.; Bullock, S.H.; Kummerow, J. Leaf turnover rates of Adenostoma fasciculatum (Rosaceae). Am. J. Bot. 1980, 67, 256–261. [Google Scholar] [CrossRef]
- Wohlgemuth, P.M.; Lilley, K.A. Sediment Delivery, Flood Control, and Physical Ecosystem Services in Southern California Chaparral Landscapes. In Valuing Chaparral: Ecological, Socio-Economic, and Management Perspectives; Underwood, E.C., Safford, H.D., Molinari, N.A., Keeley, J.E., Eds.; Springer International Publishing: Berlin, Germany, 2018; pp. 181–205. [Google Scholar]
- Sean, A.P.; Carol, M.; John, T.A.; Lisa, M.H.; Marc-Andr, P.; Solomon, Z.D. How will climate change affect wildland fire severity in the western US? Environ. Res. Lett. 2016, 11, 035002. [Google Scholar]
- U.S. Forest Service, National Fuel Moisture Database. Available online: https://www.wfas.net/index.php/national-fuel-moisture-database-moisture-drought-103 (accessed on 1 February 2019).
- FAO/IIASA/ISRIC/ISSCAS/JRC. Harmonized World Soil Database (Version 1.2), 2012th ed.; FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2012. [Google Scholar]
- Kim, S.-b.; van Zyl, J.; Dunbar, S.; Njoku, E.; Johnson, J.; Moghaddam, M.; Shi, J.; Tsang, L. SMAP L2 & L3 Radar Soil Moisture (Active) Data Products; Jet Propulsion Laboratory: Pasadena, CA, USA, 2012.
- O’Neill, P.E.; Chan, S.; Njoku, G.E.; Jackson, T.; Bindlish, R. SMAP Enhanced L3 Radiometer Global Daily 9 Km EASE-Grid Soil Moisture, Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018.
- Chan, S.K.; Bindlish, R.; O’Neill, P.; Jackson, T.; Njoku, E.; Dunbar, S.; Chaubell, J.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Ford, T.W.; Quiring, S.M. Comparison of Contemporary In Situ, Model, and Satellite Remote Sensing Soil Moisture With a Focus on Drought Monitoring. Water Resour. Res. 2019, 55, 1565–1582. [Google Scholar] [CrossRef]
- Steven Chan, R.B.; Hunt, R.; Jackson, T.; Kimball, J. Soil Moisture Active Passive (SMAP) Ancillary Data Report: Vegetation Water Content; Jet Propulsion Laboratory: Pasadena, CA, USA; California Instite of Technology: Pasadena, CA, USA, 2013.
- Prentice, I.C.; Cramer, W.; Harrison, S.P.; Leemans, R.; Monserud, R.A.; Solomon, A.M. Special Paper: A Global Biome Model Based on Plant Physiology and Dominance, Soil Properties and Climate. J. Biogeogr. 1992, 19, 117–134. [Google Scholar] [CrossRef]
- Bollero, G.A.; Bullock, D.G.; Hollinger, S.E. Soil Temperature and Planting Date Effects on Corn Yield, Leaf Area, and Plant Development. Agron. J. 1996, 88, 385–390. [Google Scholar] [CrossRef]
- Crimmins, T.M.; Marsh, R.L.; Switzer, J.R.; Crimmins, M.A.; Gerst, K.L.; Rosemartin, A.H.; Weltzin, J.F. USA National Phenology Network Gridded Products Documentation; US Geological Survey: Reston, VA, USA, 2017.
- PRISM Climate Group. PRISM Gridded Climate Data. Available online: http://prism.oregonstate.edu/ (accessed on 4 February 2019).
- Di Luzio, M.; Johnson, G.L.; Daly, C.; Eischeid, J.K.; Arnold, J.G. Constructing retrospective gridded daily precipitation and temperature datasets for the conterminous United States. J. Appl. Meteorol. Clim. 2008, 47, 475–497. [Google Scholar] [CrossRef]
- Eklundh, L.; Jönsson, P. TIMESAT: A Software Package for Time-Series Processing and Assessment of Vegetation Dynamics. In Remote Sensing Time Series; Kuenzer, C., Dech, S., Wagner, W., Eds.; Springer: Berlin, Germany, 2015; pp. 141–158. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Noether, G.E. Why Kendall Tau? Teach. Stat. 1981, 3, 41–43. [Google Scholar] [CrossRef]
- Ruffault, J.; Martin-St Paul, N.; Pimont, F.; Dupuy, J.L. How well do meteorological drought indices predict live fuel moisture content (LFMC)? An assessment for wildfire research and operations in Mediterranean ecosystems. Agric. For. Meteorol. 2018, 262, 391–401. [Google Scholar] [CrossRef]



| Model | Equation | Explanation of Model |
|---|---|---|
| Synchronized SMAP SM | LFM at time t was determinated by SMAP SM at time t-lag | |
| Synchronized SMAP SM + Cumulative GDD | LFM at t was determinated by SMAP SM at time t-lag and the cumulative GDD from the start of water year to t | |
| Accumulative SMAP SM + Cumulative GDD | LFM at t was determinated by accumulated SMAP SM from t0-lag to t and the cumulative GDD from the start of water year to t | |
| Weighted Accumulative SMAP SM + Cumulative GDD | LFM at t was determinated by the weighted accumulated SMAP SM from t-lag to t and the cumulative GDD from the start of water year to t; weight (W) decreased from past to present in a logarithm form. | |
| VARI only (Reference) | LFM at t was determined by VARI at t | |
| Cumulative GDD only | LFM at t was determined by the cumulative GDD at t | |
| VARI + Cumulative GDD | LFM at t was determined by VARI and cumulative GDD at t |
| Model | Adjusted R2 | Overall RMSE (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Overall | Brown down | Green up | Winter | Spring | Summer | Fall | ||
| Synchronized SMAP SM | 0.358 | N/A | N/A | 0.187 | 0.055 | 0.211 | 0.018 | 23.202 |
| Synchronized SMAP SM + Cumulative GDD | 0.484 | 0.51 | 0.25 | 0.173 | 0.096 | 0.257 | 0.003 | 20.805 |
| Accu. SMAP SM + Cumulative GDD | 0.510 | 0.56 | 0.43 | 0.244 | 0.11 | 0.258 | 0.005 | 20.284 |
| Weighted Accu. SMAP SM + Cumulative GDD | 0.529 | 0.58 | 0.47 | 0.290 | 0.179 | 0.226 | 0.005 | 19.876 |
| VARI only (reference model) | 0.442 | 0.39 | 0.52 | 0.371 | 0.181 | 0.094 | 0.004 | 21.628 |
| Cumulative GDD only | 0.339 | 0.53 | 0.15 | 0.017 | 0.012 | 0.138 | 0.010 | 23.546 |
| VARI + Cumulative GDD (reference model) | 0.56 | 0.57 | 0.526 | 0.368 | 0.196 | 0.152 | 0.006 | 21.467 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Kim, S.H.; Nghiem, S.V.; Kafatos, M. Estimating Live Fuel Moisture Using SMAP L-Band Radiometer Soil Moisture for Southern California, USA. Remote Sens. 2019, 11, 1575. https://doi.org/10.3390/rs11131575
Jia S, Kim SH, Nghiem SV, Kafatos M. Estimating Live Fuel Moisture Using SMAP L-Band Radiometer Soil Moisture for Southern California, USA. Remote Sensing. 2019; 11(13):1575. https://doi.org/10.3390/rs11131575
Chicago/Turabian StyleJia, Shenyue, Seung Hee Kim, Son V. Nghiem, and Menas Kafatos. 2019. "Estimating Live Fuel Moisture Using SMAP L-Band Radiometer Soil Moisture for Southern California, USA" Remote Sensing 11, no. 13: 1575. https://doi.org/10.3390/rs11131575
APA StyleJia, S., Kim, S. H., Nghiem, S. V., & Kafatos, M. (2019). Estimating Live Fuel Moisture Using SMAP L-Band Radiometer Soil Moisture for Southern California, USA. Remote Sensing, 11(13), 1575. https://doi.org/10.3390/rs11131575