An Approach to Moho Topography Recovery Using the On-Orbit GOCE Gravity Gradients and Its Applications in Tibet
Abstract
1. Introduction
2. Methodology
3. Numerical Experiment
3.1. Study Area and Data Processing
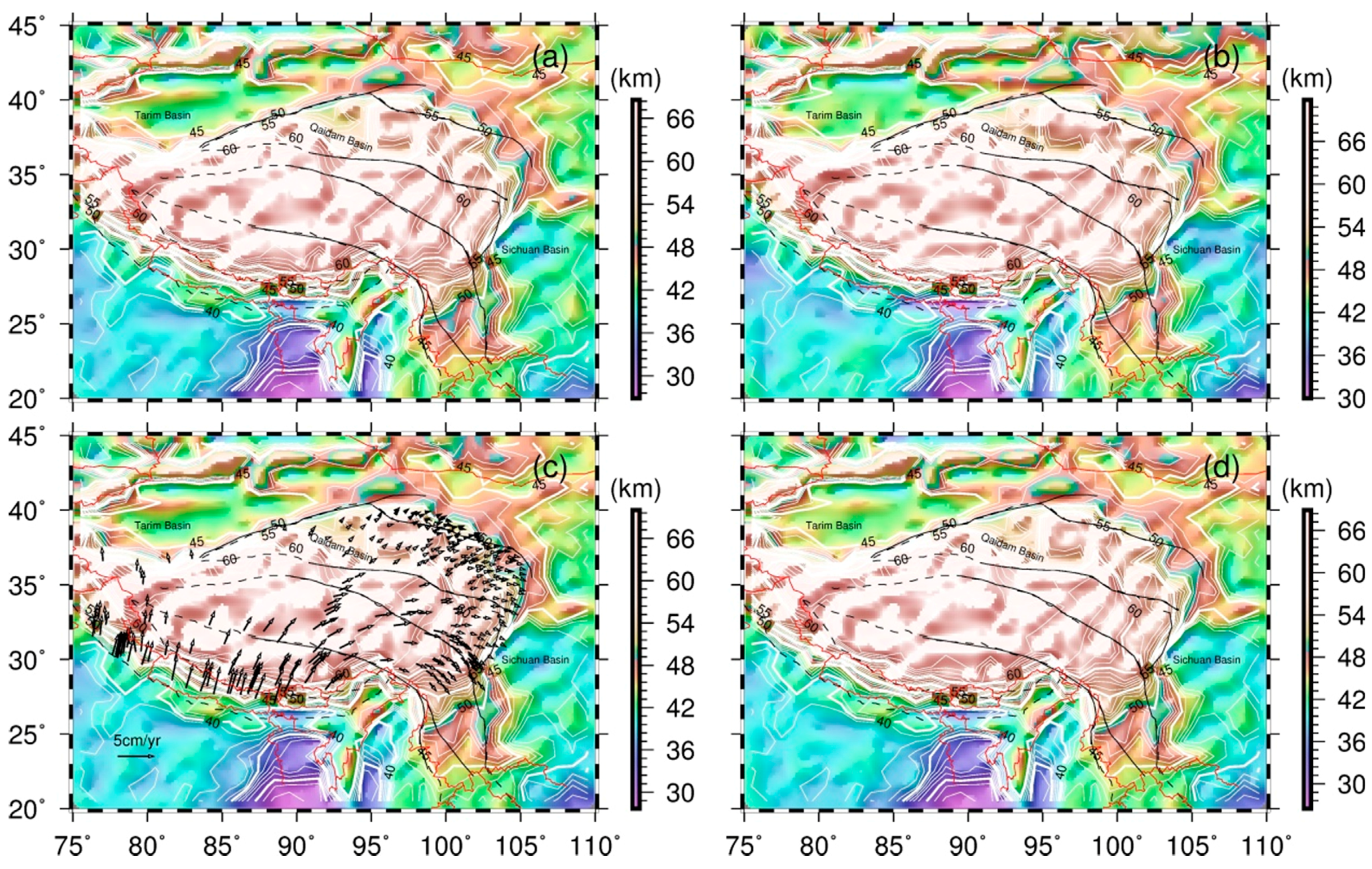
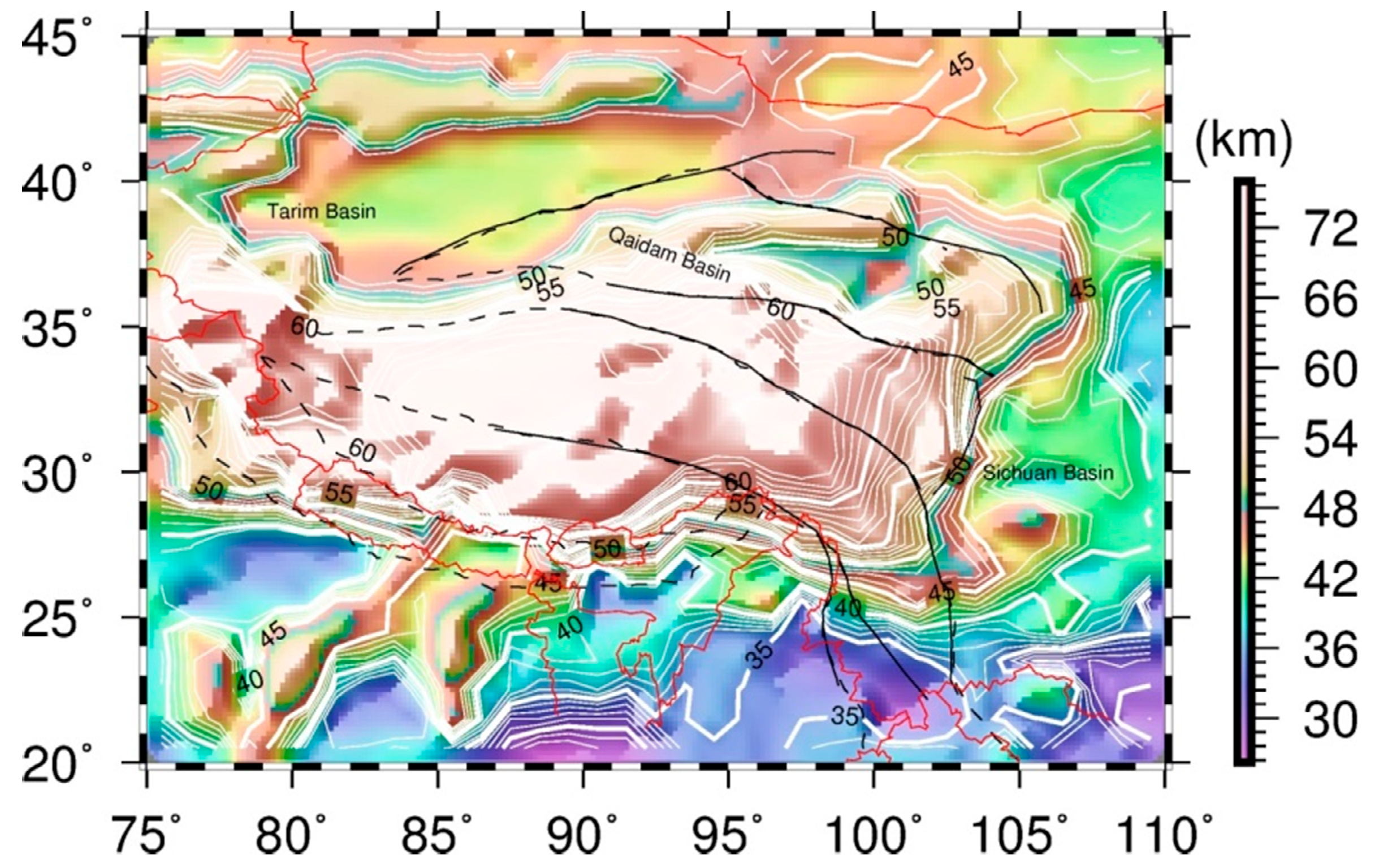
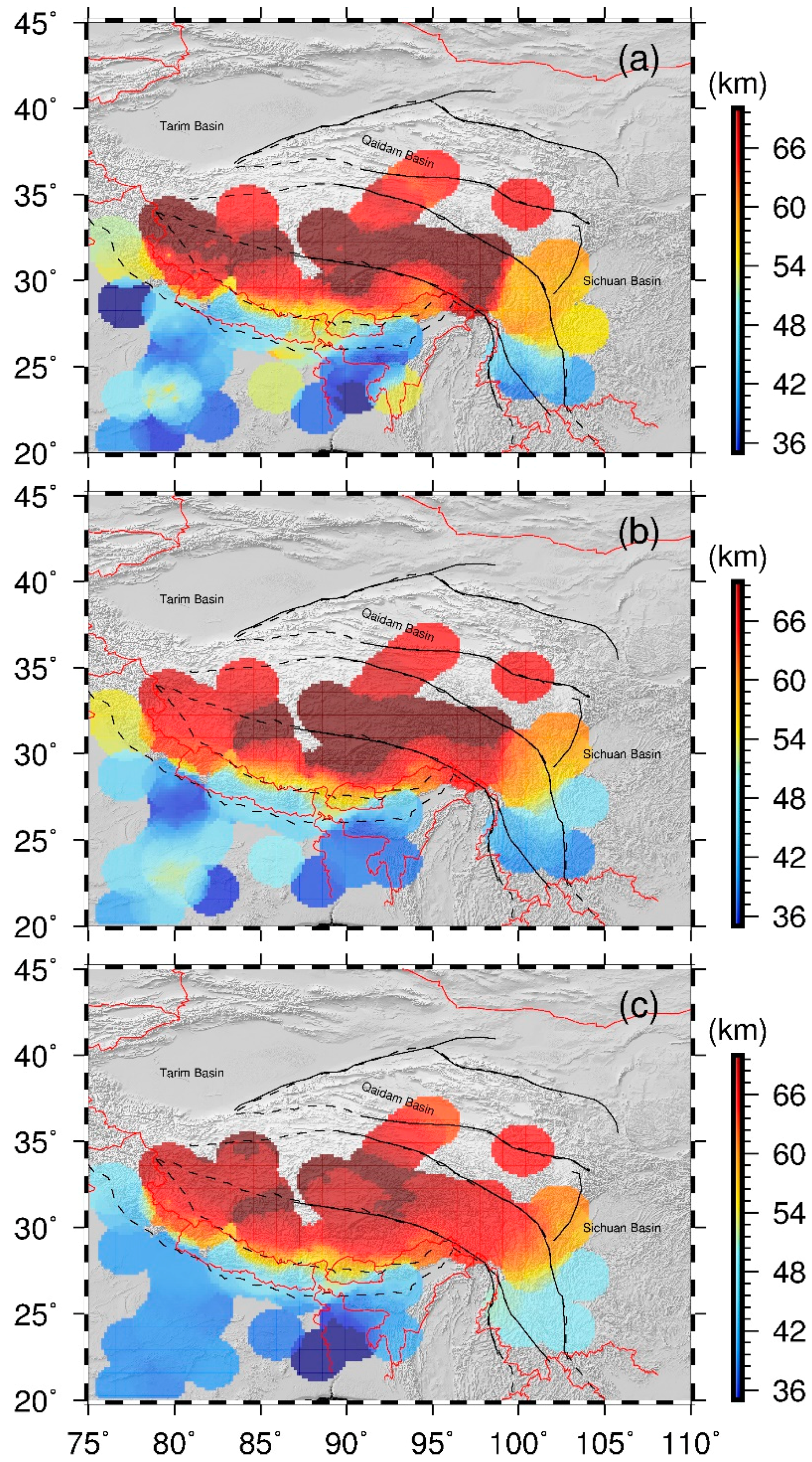
3.2. Moho Topography
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Gao, R.; Xiong, X.; Li, Q.; Lu, Z. The Moho depth of Qinghai-Tibet Plateau revealed by seismic detection. Acta Geosci. Sin. 2009, 30, 761–773. [Google Scholar]
- Shin, Y.H.; Shum, C.K.; Braitenberg, C.; Lee, S.M.; Na, S.; Choi, K.S.; Hsu, H.; Park, Y.; Lim, M. Moho topography, ranges and folds of Tibet by analysis of global gravity models and Goce data. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Liu, Z.W.; Luo, Z.C.; Wu, Y.H.; Wang, H.H. Moho topography of the Tibetan Plateau using multi-scale gravity analysis and its tectonic implications. J. Asian Earth Sci. 2017, 138, 378–386. [Google Scholar] [CrossRef]
- Tapponnier, P.; Peltzer, G.; Le Dain, A.Y.; Armijo, R. Propagating extrusion tectonics in Asia: New insights from simple experiments with plasticine. Geology 1982, 10, 611–616. [Google Scholar] [CrossRef]
- Gao, R.; Chen, C.; Lu, Z.; Brown, L.D.; Xiong, X.; Li, W.; Deng, G. New constraints on crustal structure and Moho topography in Central Tibet revealed by SinoProbe deep seismic reflection profiling. Tectonophysics 2013, 606, 160–170. [Google Scholar] [CrossRef]
- Tseng, J.; Kan, Y. Deep sub-basement reflections in the western part of Chai-da-mu Basin. Chin. J. Sin. 1961, 10, 120–125. [Google Scholar]
- Zhao, W.; Nelson, K.D.; Che, J.; Quo, J.; Lu, D.; Wu, C.; Liu, X. Deep seismic reflection evidence for continental underthrusting beneath southern Tibet. Nature 1993, 366, 557–559. [Google Scholar] [CrossRef]
- Kao, H.; Gao, R.; Rau, R.; Shi, D.; Chen, R.; Guan, Y.; Wu, F.T. Seismic image of the Tarim basin and its collision with Tibet. Geology 2001, 29, 575–578. [Google Scholar] [CrossRef]
- Kind, R.; Yuan, X.; Saul, J.; Nelson, D.; Sobolev, S.V.; Mechie, J.; Zhao, W.; Kosarev, G.; Ni, J.; Achauer, U.; et al. Seismic images of crust and upper mantle beneath Tibet: Evidence for Eurasion plate subduction. Science 2002, 298, 1219–1221. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, F.; Liu, J.; Chen, H. Crust and upper mantle structure beneath western China from P wave travel time tomography. J. Geophys. Res. 2002, 107, 2220. [Google Scholar] [CrossRef]
- Zhang, Z.; Klemperer, S.L. West-east variation in crustal thickness in northern Lhasa block, central Tibet, from deep seismic sounding data. J. Geophys. Res. 2005, 110, B09403. [Google Scholar] [CrossRef]
- Zhao, J.; Mooney, W.D.; Zhang, X.; Li, Z.; Jin, Z.; Okaya, N. Crustal structure across the Altyn Tagh Range at the northern margin of the Tibetan Plateau and tectonic implications. Earth Planet. Sci. Lett. 2006, 241, 804–814. [Google Scholar] [CrossRef]
- Xu, L.; Rondenay, S.; van der Hist, R.D. Structure of the crust beneath the southeastern Tibetan Plateau from teleseismic receiver functions. Phys. Earth Planet. Int. 2007, 165, 176–193. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, R.; Teng, J. Study on crustal, lithospheric and asthenospheric thickness beneath the Qinghai-Tibet Plateau and its adjacent areas. Chin. Sci. Bull. 2007, 52, 797–804. [Google Scholar] [CrossRef]
- Lou, H.; Wang, C.; Lü, Z.; Yao, Z.; Dai, S.; You, H. Deep tectonic setting of the 2008 Wenchuan Ms8.0 earthquake in southwestern China. Sci. China Ser. D Earth Sci. 2009, 52, 166–179. [Google Scholar] [CrossRef]
- Lu, Z.; Gao, R.; Li, Q.; He, R.; Kuang, C.; Hou, H.; Xiong, X.; Guan, Y.; Wang, H. Test of deep seismic reflection profiling across central uplift of Qiangtang terrane in Tibetan Plateau. J. Earth Sci. 2009, 20, 438–447. [Google Scholar] [CrossRef]
- Yang, H.; Hu, J.; Li, G.; Zhao, H.; Wen, L. Analysis of the crustal thickness and Poisson’s ratio in eastern Tibet from teleseismic receiver functions. Geophys. J. Int. 2011, 186, 1380–1388. [Google Scholar] [CrossRef]
- Obrebski, M.; Allen, R.M.; Zhang, F.; Pan, J.; Wu, Q.; Hung, S. Shear wave tomography of China using joint inversion of body and surface wave constraints. J. Geophys. Res. 2012, 117, B01311. [Google Scholar] [CrossRef]
- Xu, X.; Ding, Z.; Shi, D.; Li, X. Receiver function analysis of crustal structure beneath the eastern Tibetan plateau. J. Asian Earth Sci. 2013, 73, 121–127. [Google Scholar] [CrossRef]
- Tian, X.; Liu, Z.; Si, S.; Zhang, Z. The crustal thickness of NE Tibet and its implication for crustal shortening. Tectonophysics 2014, 634, 198–207. [Google Scholar] [CrossRef]
- Koulakov, I.; Maksotova, G.; Mukhopadhyay, S.; Raoof, J.; Kayal, J.R.; Jakovlev, A.; Vasilevsky, A. Variations of the crustal thickness in Nepal Himalayas based on tomographic inversion of regional earthquake data. Solid Earth 2015, 6, 207–216. [Google Scholar] [CrossRef]
- Zheng, H.; Li, T.; Gao, R. The progress of seismic tomography research in the Tibetan Plateau. Geophys. Geochem. Explor. 2011, 35, 160–164. [Google Scholar]
- Tapley, B.D.; Bettadpur, M.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, Z.; Zhou, Z.; Li, Q.; Zhong, B.; Lu, B.; Hsu, H. Impact of different kinematic empirical parameters processing strategies on temporal gravity field model determination. J. Geophys. Res. Solid Earth 2018, 123, 10252–10276. [Google Scholar] [CrossRef]
- Rummel, R.; Balmino, G.; Johannessen, J.; Visser, P.; Woodworth, P. Dedicated gravity field missions—Principle and aims. J. Geodyn. 2002, 33, 3–20. [Google Scholar] [CrossRef]
- Vening Meinesz, F.A. Une nouvelle méthode pour la réduction isostatique régionale de Í intensité de la pesanteur. Bull. Geod. 1931, 29, 33–51. [Google Scholar] [CrossRef]
- Parker, R.L. The rapid calculation of potential anomalies. Geophys. J. R. Astron. Soc. 1972, 31, 447–455. [Google Scholar] [CrossRef]
- Shin, Y.H.; Xu, H.Z.; Braitenberg, C.; Fang, J.; Wang, Y. Moho undulations beneath Tibet from GRACE-integrated gravity data. Geophys. J. Int. 2007, 170, 971–985. [Google Scholar] [CrossRef]
- Shin, Y.H.; Shum, C.K.; Braiternberg, C.; Lee, S.M.; Xu, H.; Choi, K.S.; Baek, J.H.; Park, J.U. Three-dimensional fold structure of the Tibetan Moho from Grace gravity data. Geophys. Res. Lett. 2009, 36, L01302. [Google Scholar] [CrossRef]
- Moritz, H. (Ed.) The Figure of the Earth; Wichmann: Karlsruhe, Germany, 1990. [Google Scholar]
- Sjöberg, L.E. Solving Vening Meinesz-Moritz inverse problem in isostasy. Geophys. J. Int. 2009, 179, 1527–1536. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. A method of estimating the Moho density contrast with a tentative application by EGM08 and CRUST2.0. Acta Geophys. 2011, 59, 502–525. [Google Scholar] [CrossRef]
- Oldenburg, D.W. The inversion and interpretation of gravity anomalies. Geophysics 1974, 39, 526–536. [Google Scholar] [CrossRef]
- Bagherbandi, M. A comparison of three gravity inversion methods for crustal thickness modelling in Tibet plateau. J. Asian Earth Sci. 2012, 43, 89–97. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W. Expressions for the global gravimetric Moho modeling in spectral domain. Pure Appl. Geophys. 2014, 171, 1877–1896. [Google Scholar] [CrossRef]
- Chen, W.; Tenzer, R. Moho modeling in spatial domain: A case study under Tibet. Adv. Space Res. 2017, 59, 2855–2869. [Google Scholar] [CrossRef]
- Eshagh, M.; Hussain, M.; Tenzer, R.; Romeshkani, M. Moho density constrast in central Eurasia from GOCE gravity gradients. Remote Sens. 2016, 8, 418. [Google Scholar] [CrossRef]
- Eshagh, M.; Hussain, M. An approach to Moho discontinuity recovery from on-orbit GOCE data with application over Indo-Pak region. Tectonophysics 2016, 690, 253–262. [Google Scholar] [CrossRef]
- Eshagh, M.; Ebadi, S.; Tenzer, R. Isostatic GOCE Moho model for Iran. J. Asian Earth Sci. 2017, 138, 12–24. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, H.; Zhong, B.; Luo, Z. Regional gravity field recovery using the GOCE gravity gradient tensor and heterogeneous gravimetry and altimetry data. J. Geophys. Res. Solid Earth 2017, 122, 6928–6952. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of incorrectly formulated problems and regularization method. Sov. Math. Doki. 1963, 4, 1035–1038. [Google Scholar]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. Siam J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Leech, M.L.; Singh, S.; Jain, A.; Klemperer, S.L.; Manickavasagam, R. The onset of India-Asia continental collision: Early, steep subduction required by the timing of UHP metamorphism in the western Himalaya. Earth Planet. Sci. Lett. 2005, 234, 83–97. [Google Scholar] [CrossRef]
- Li, Q.; Gao, R.; Lu, Z.; Guan, Y.; Zhang, J.; Li, P.; Karplus, M. The thickness and structural characteristics of the crust across Tibetan plateau from active-sources seismic profiles. Earthq. Sci. 2009, 22, 21–31. [Google Scholar] [CrossRef]
- Gao, R.; Lu, Z.; Klemperer, S.L.; Wang, H.; Dong, S.; Li, W.; Li, H. Crustal-scale duplexing beneath the Yarlung Zangbo suture in the western Himalaya. Nat. Geosci. 2016, 9, 555. [Google Scholar] [CrossRef]
- Argand, E. La Tectonique de l’Asie. In Proceedings of the 13th International Geological Congress, Brussels, Belgium, August 1922; pp. 171–372. [Google Scholar]
- Nelson, K.D. Partially molten middle crust beneath southern Tibet; synthesis of Project INDEPTH result. Science 1996, 274, 1684–1688. [Google Scholar] [CrossRef]
- Yang, Y.; Ritzwoller, M.H.; Zheng, Y.; Shen, W.; Levshin, A.L.; Xie, Z. A synoptic view of the distribution and connectivity of the mid-crustal low velocity zone beneath Tibet. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Xu, C.; Luo, Z.; Sun, R.; Zhou, H.; Wu, Y. Multilayer densities using a wavelet-based gravity method and their tectonic implications beneath the Tibetan Plateau. Geophys. J. Int. 2018, 213, 2085–2095. [Google Scholar] [CrossRef]
- Gruber, T.; Rummel, R.; Abrikosov, O.; van Hees, R. GOCE level 2 Product Data Handbook. GO-MA-HPF-GS-0110, Issue 4.3 2010. Available online: https://earth.esa.int/c/document_library/get_file?folderId=14168&name=DLFE-591.pdf (accessed on 28 June 2019).
- Hirt, C.; Rexer, M. Earth2014: 1 arc-min shape, topography, bedrock and ice-sheet models – Available as gridded data and degree—10,800 spherical harmonics. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 103–112. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0—A 1-degree global model of Earth’s crust. EGU Gen. Assem. Conf. Abstr. 2013, 15, 2658. [Google Scholar]
- Yin, Z.; Teng, J.; Liu, H. The 2-D crustal structure study in the Yadong-Damxung region of the Xizang Plateau. Bull. Chin. Acad. Geol. Sci. 1990, 21, 239–245. [Google Scholar]
- Li, H.; Xu, X.; Jiang, M. Deep dynamical processes in the central-southern Qinghai-Tibet Plateau—Receiver functions and travel-time residuals analysis of north Hi-Climb. Sci. China Ser. D Earth Sci. 2008, 51, 1297–1305. [Google Scholar] [CrossRef]
- Hirn, A.; Nercessian, A.; Sapin, M.; Jobert, G.; Xu, Z.; Gao, E.; Lu, D.; Teng, J. Lhasa block and bordering sutures-a continuation of a 500-km Moho traverse through Tibet. Nature 1984, 307, 25–27. [Google Scholar] [CrossRef]
- Royden, L.H.; Burchfiel, B.C.; King, R.W.; Wang, E.; Chen, Z.; Shen, F.; Liu, Y. Surface deformation and lower crustal flow in eastern Tibet. Science 1997, 276, 788–790. [Google Scholar] [CrossRef] [PubMed]
- Royden, L.H.; Burchfiel, B.C.; van der Hilst, R.D. The geological evolution of the Tibetan Plateau. Science 2008, 321, 1054–1058. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.K.; Royden, L.H. Topographic ooze: Building the eastern margin of Tibet by lower crustal flow. Geology 2000, 28, 703–706. [Google Scholar] [CrossRef]
- Singh, A.; Ravi Kumar, M.; Mohanty, D.D.; Singh, C.; Biswas, R.; Srinagesh, D. Crustal structure beneath India and Tibet: New constraints from inversion of receiver functions. J. Geophys. Res. Solid Earth 2017, 122, 7839–7859. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Z.; Basal, J.; Fan, W. 3-D density structure under South China constrained by seismic velocity and gravity data. Tectonophysics 2014, 627, 159–170. [Google Scholar] [CrossRef]
- Shen, W.; Ritzwoller, M.H.; Kang, D.; Kim, Y.; Ning, J.; Lin, F.C.; Wang, W.; Zheng, Y.; Zhou, L. A seismic reference model for the crust and uppermost mantle beneath China from surface wave dispersion. Geophys. J. Int. 2016, 206, 954–979. [Google Scholar] [CrossRef]
- Kern, H.; Popp, T.; Gorbatsevich, F.; Zharikov, A.; Lobanov, K.V.; Smirnov, Y.P. Pressure and temperature dependence of VP and VS in rocks from the superdeep well and from surface analogues at Kola and the nature of velocity anisotropy. Tectonophysics 2001, 338, 113–134. [Google Scholar] [CrossRef]
- Currie, C.A. The deep roots of the Rocky Mountains: Geophysical studies of western Canada. J. Stud. Sci. Technol. 2016, 9, 35–41. [Google Scholar] [CrossRef][Green Version]


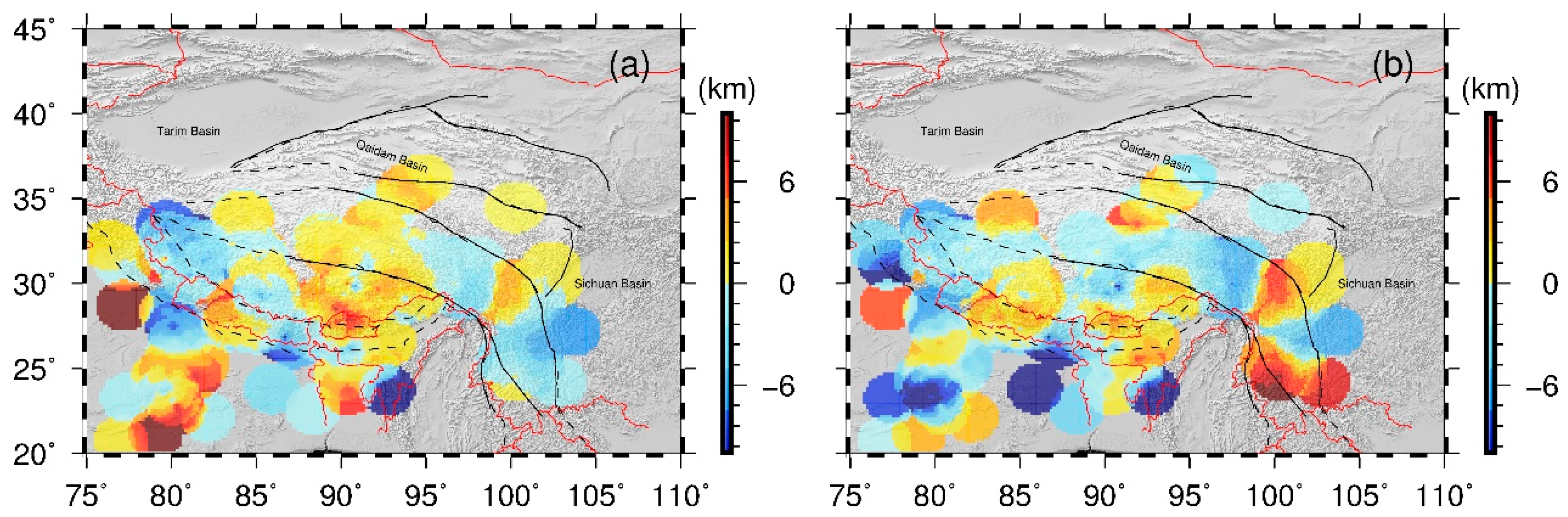
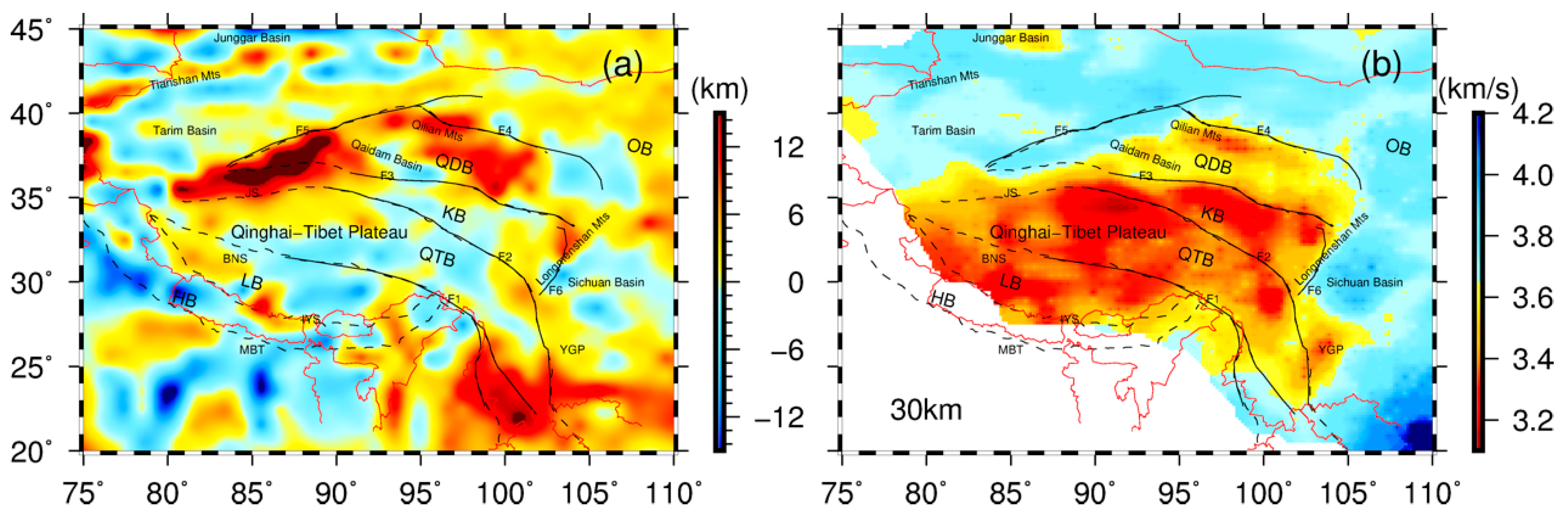
| Name | MAX | MIN | MEAN | STD | RMS | COFF |
|---|---|---|---|---|---|---|
| CRUST 1.0 | 74.81 | 27.00 | 47.74 | 9.91 | / | / |
| MX | 68.16 | 27.07 | 48.31 | 9.62 | / | / |
| MY | 71.14 | 30.19 | 49.48 | 9.54 | / | / |
| MZ | 69.45 | 27.81 | 48.89 | 9.60 | / | / |
| MJ | 68.51 | 26.76 | 48.83 | 9.71 | / | / |
| MX-CRUST 1.0 | 17.63 | −17.12 | 0.57 | 5.59 | 5.61 | 0.84 |
| MY-CRUST 1.0 | 20.40 | −15.39 | 1.74 | 5.72 | 5.98 | 0.83 |
| MZ-CRUST 1.0 | 18.46 | −15.50 | 1.15 | 5.44 | 5.56 | 0.85 |
| MJ-CRUST 1.0 | 19.16 | −15.39 | 1.09 | 5.54 | 5.64 | 0.84 |
| Name | MAX | MIN | MEAN | STD | RMS | COFF (Unitless) |
|---|---|---|---|---|---|---|
| Singh et al. (2017) | 86.82 | 31.60 | 60.32 | 11.92 | / | / |
| MJ | 71.52 | 33.05 | 59.89 | 11.16 | / | / |
| CRUST 1.0 | 75.04 | 35.59 | 60.01 | 11.03 | / | / |
| MJ-Singh et al. (2017) | 20.44 | −21.15 | −0.44 | 5.88 | 5.90 | 0.87 |
| CRUST 1.0- Singh et al. (2017) | 14.98 | −15.43 | −0.32 | 5.33 | 5.34 | 0.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, J.; Xu, C.; Luo, Z.; Wu, Y.; Zhou, B.; Yan, J. An Approach to Moho Topography Recovery Using the On-Orbit GOCE Gravity Gradients and Its Applications in Tibet. Remote Sens. 2019, 11, 1567. https://doi.org/10.3390/rs11131567
Wan J, Xu C, Luo Z, Wu Y, Zhou B, Yan J. An Approach to Moho Topography Recovery Using the On-Orbit GOCE Gravity Gradients and Its Applications in Tibet. Remote Sensing. 2019; 11(13):1567. https://doi.org/10.3390/rs11131567
Chicago/Turabian StyleWan, Jiakuan, Chuang Xu, Zhicai Luo, Yihao Wu, Boyang Zhou, and Jianguo Yan. 2019. "An Approach to Moho Topography Recovery Using the On-Orbit GOCE Gravity Gradients and Its Applications in Tibet" Remote Sensing 11, no. 13: 1567. https://doi.org/10.3390/rs11131567
APA StyleWan, J., Xu, C., Luo, Z., Wu, Y., Zhou, B., & Yan, J. (2019). An Approach to Moho Topography Recovery Using the On-Orbit GOCE Gravity Gradients and Its Applications in Tibet. Remote Sensing, 11(13), 1567. https://doi.org/10.3390/rs11131567





