Geographic and Climatic Attributions of Autumn Land Surface Phenology Spatial Patterns in the Temperate Deciduous Broadleaf Forest of China
Abstract
1. Introduction
2. Materials and Methods
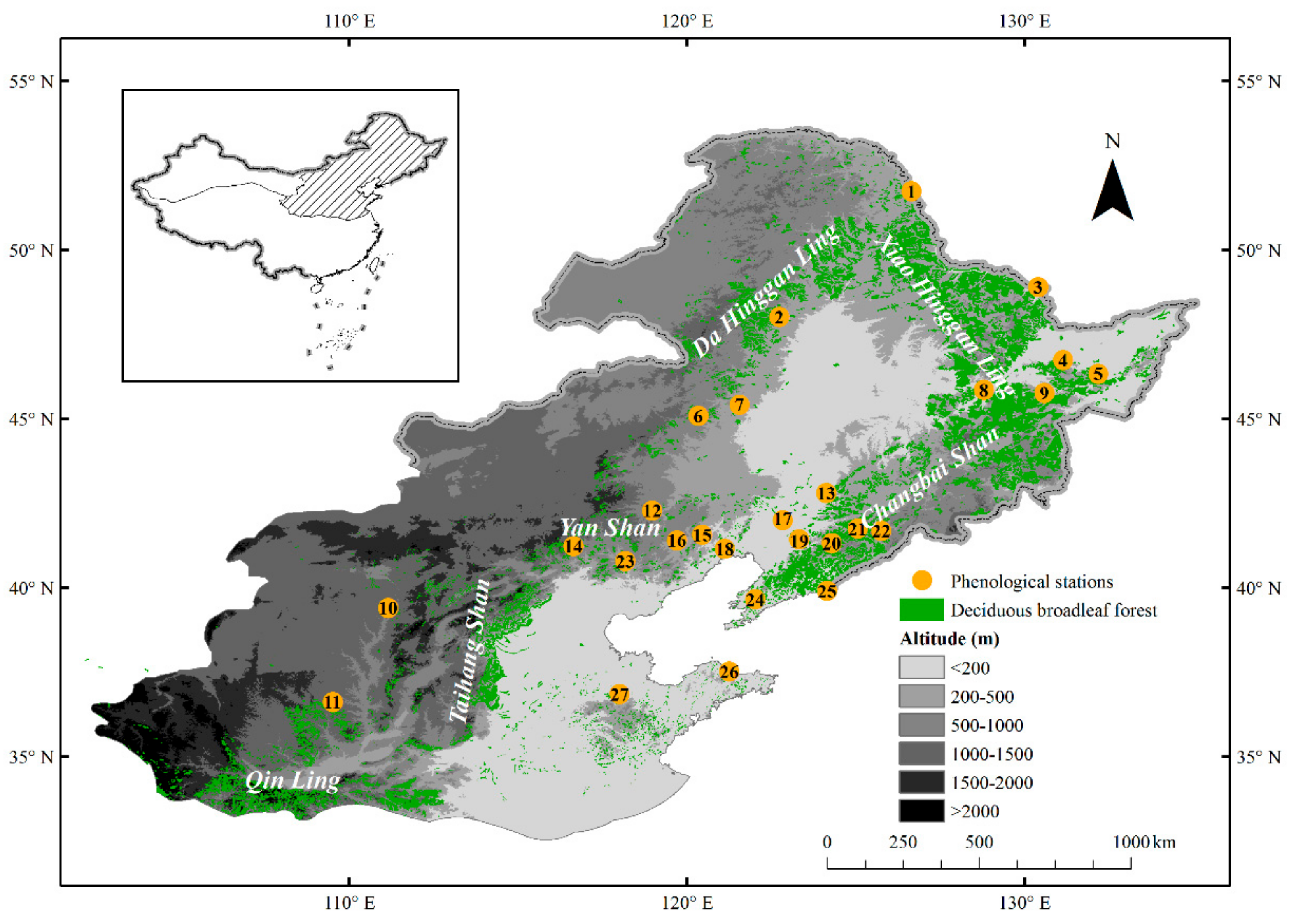
2.1. Study Area
2.2. Phenological and Meteorological Data
2.3. MODIS Data and Processing
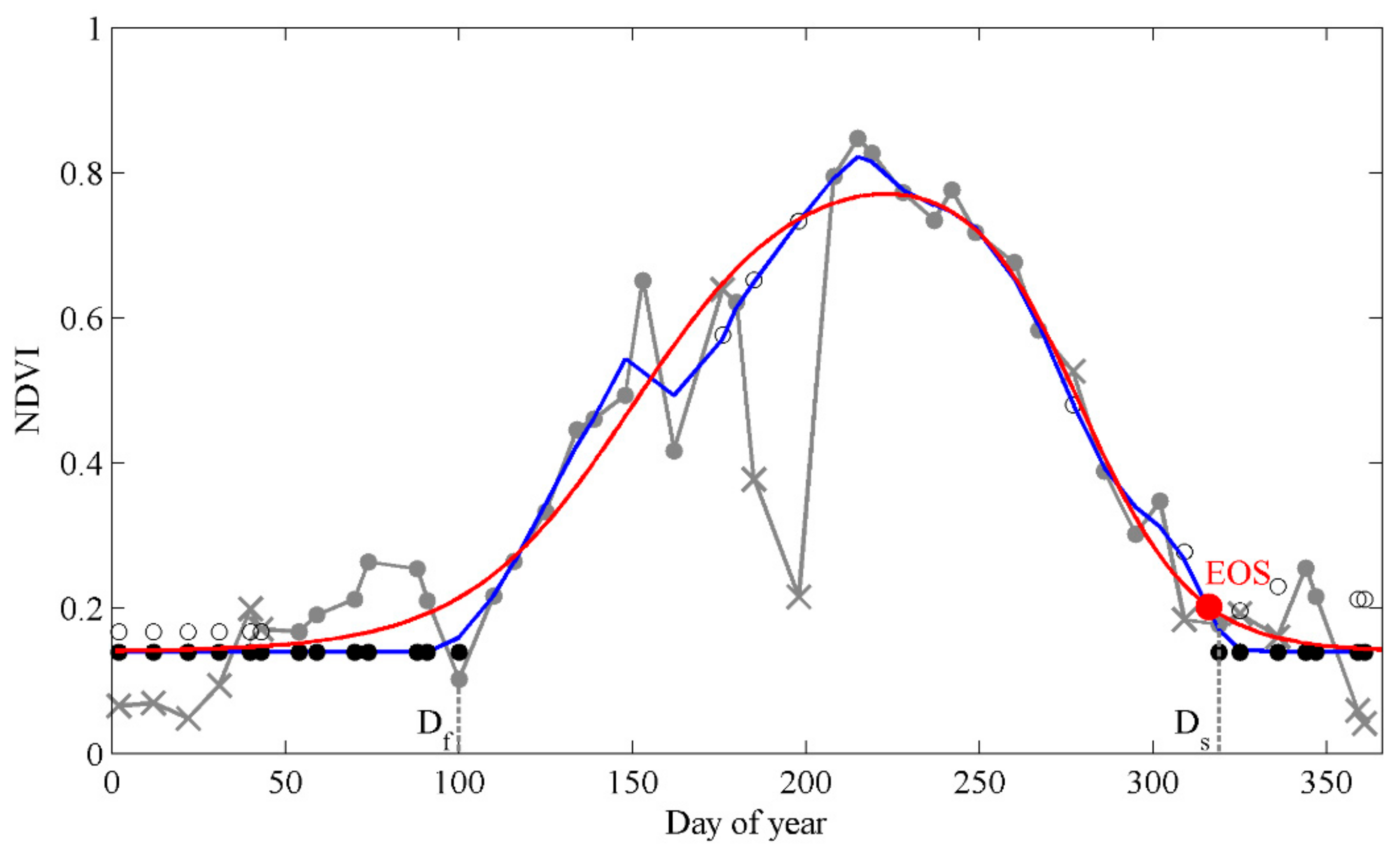
2.4. Spatial Phenology Models Based on Geo-Location Indicators and Climatic Factors
3. Results
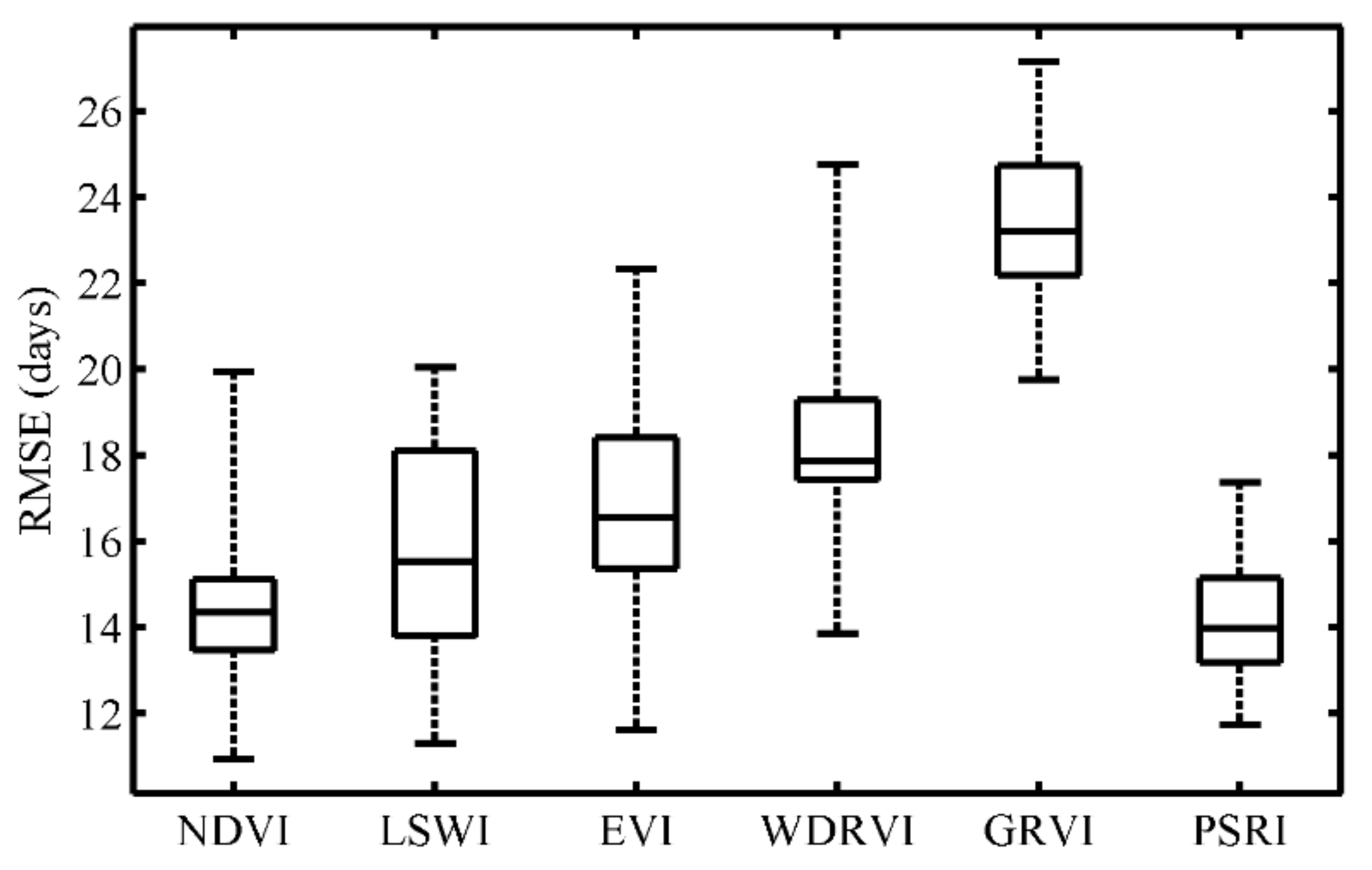
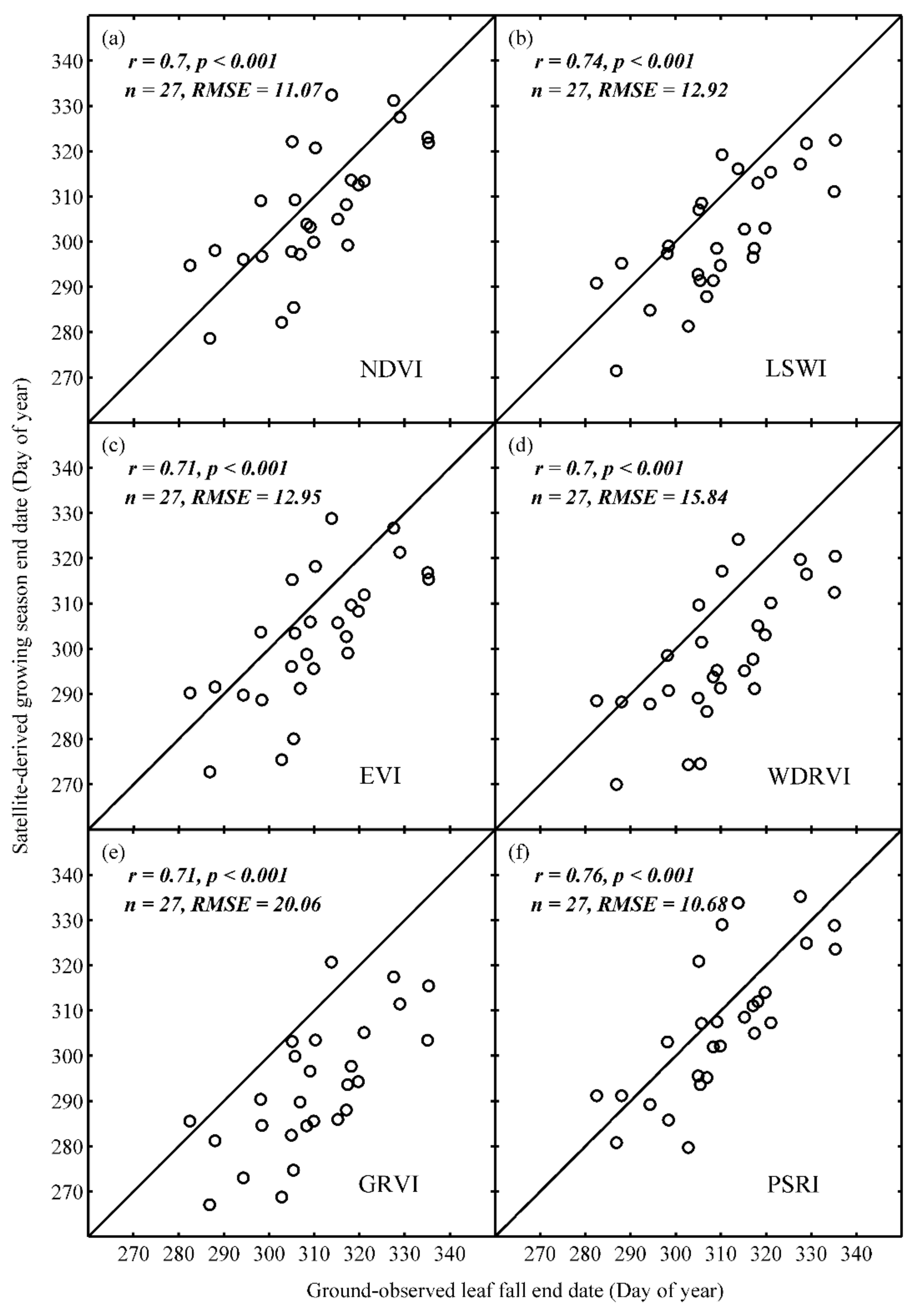
3.1. Ground Validation of EOS Retrieved from Different Vegetation Indices
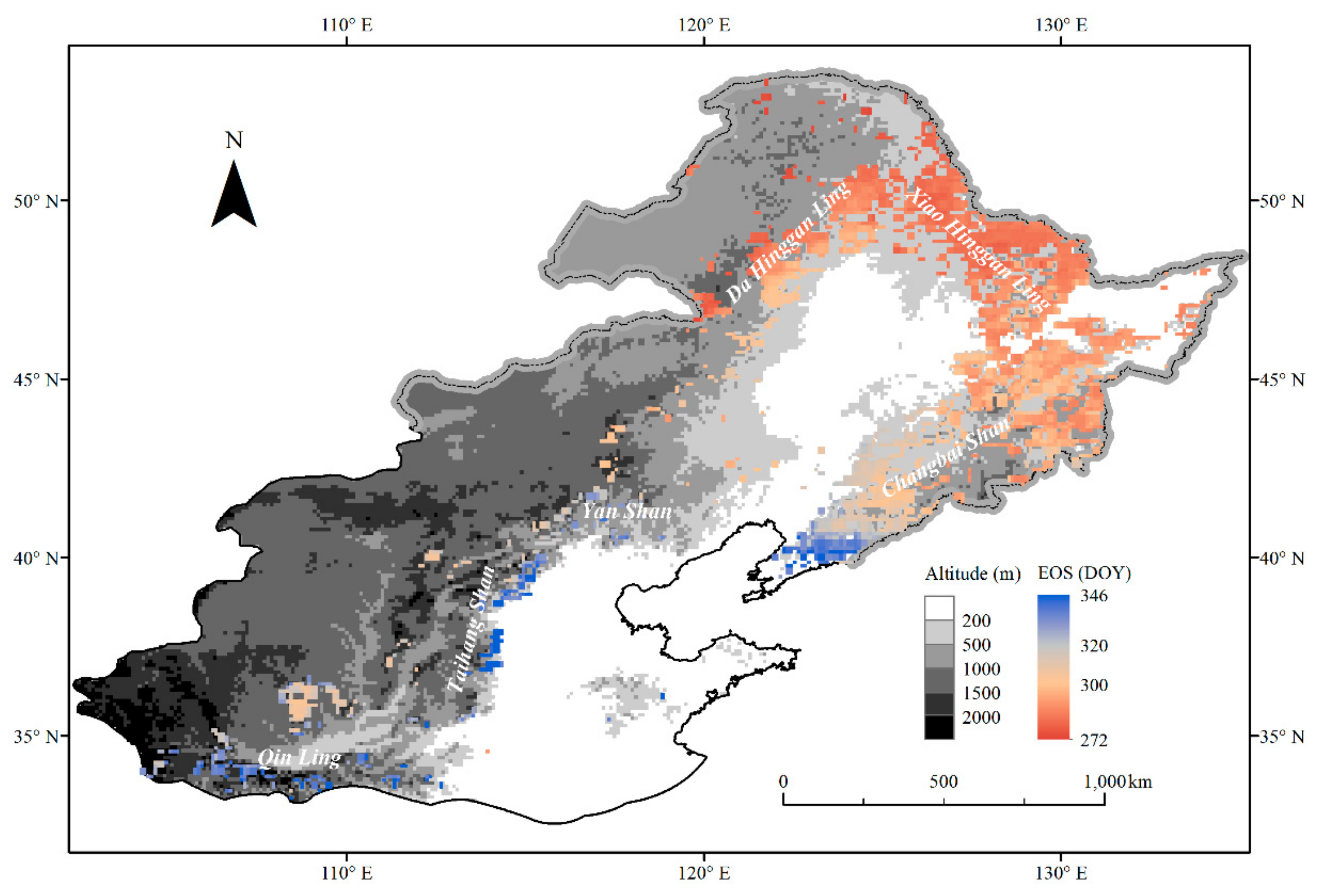
3.2. Spatial Patterns of EOS and Their Relation to Geo-Location Factors
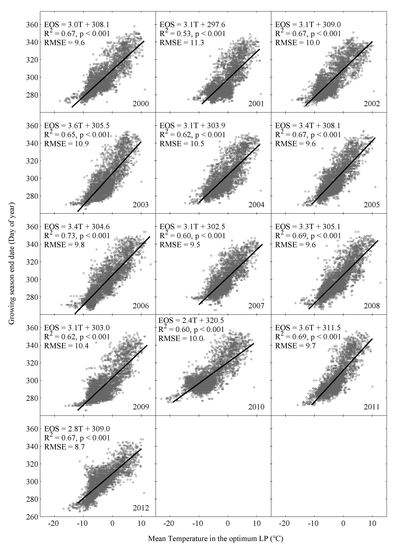
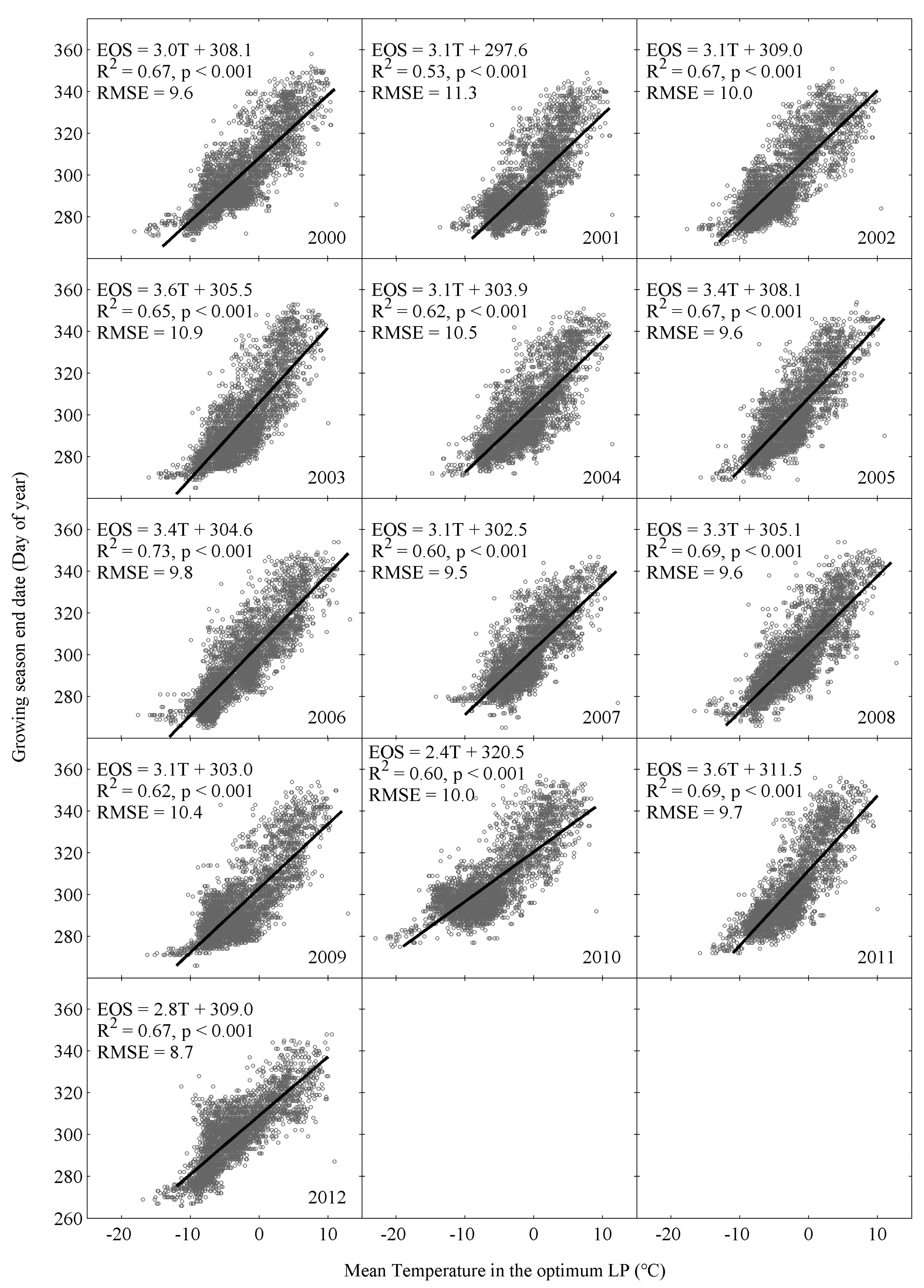
3.3. Spatial Relationship between EOS and Climatic Factors
4. Discussion
5. Conclusions
- 1.
- PSRI-derived EOS can more accurately capture spatial variations of ground-observed leaf fall dates of dominant trees on the multi-year average and in each year than the other five vegetation indices. The spatial variation of PSRI-derived EOS dates correlate significantly and positively with the spatial variation of ground based leaf fall dates in each year.
- 2.
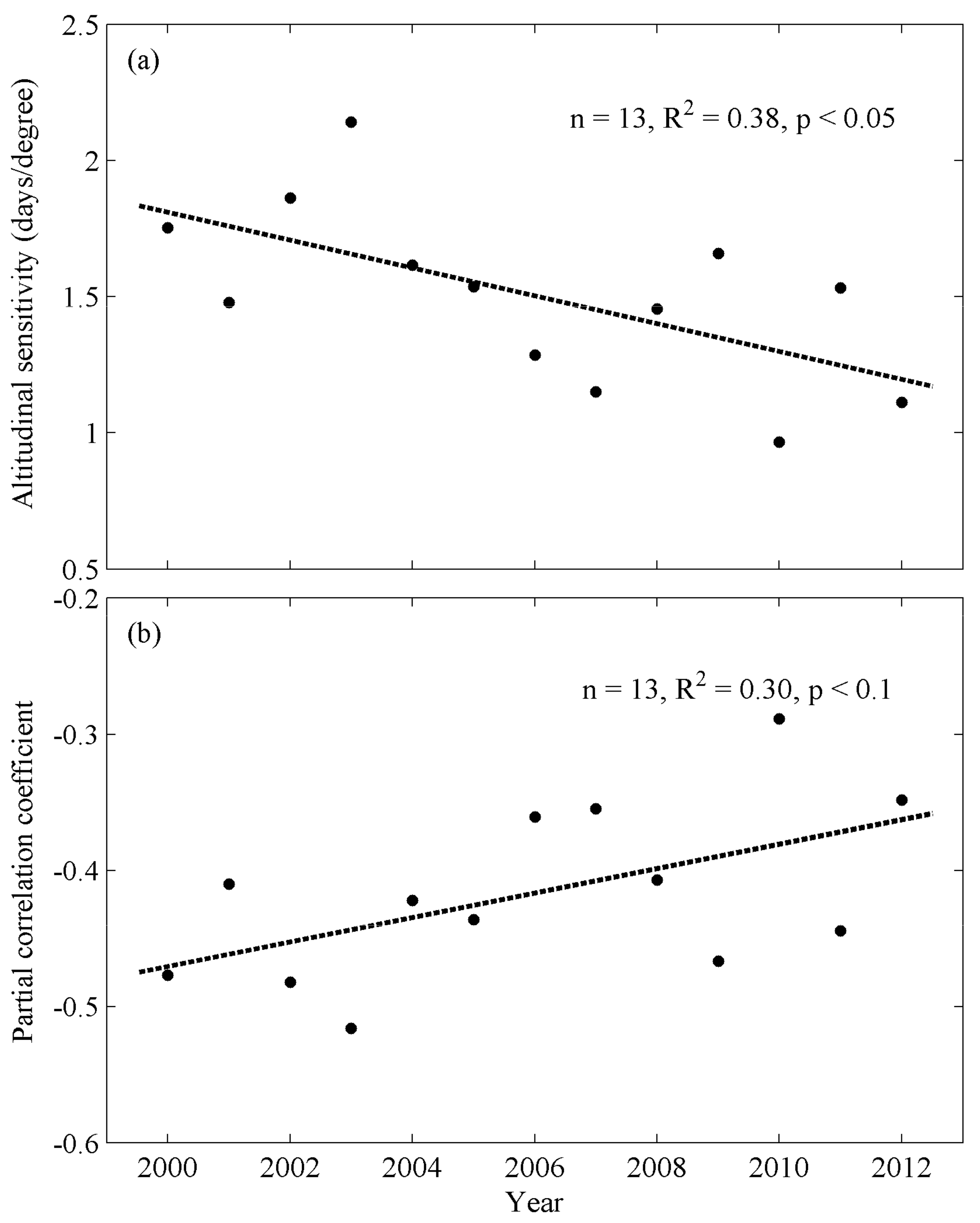
- Multi-year mean PSRI-derived EOS represent a latitudinal sensitivity of −2.98 days per degree northward, a longitudinal sensitivity of −1.03 days per degree eastward and an altitudinal sensitivity of −1.5 days per 100 m upward. The altitudinal sensitivity of EOS became weaker and weaker from 2000 to 2012, which might be attributable to larger delaying rates of EOS dates at high elevations than at low elevations under recent climate warming.
- 3.
- Temperature-based phenological models can explain more spatial variations of EOS with less simulation errors than the precipitation-based models in the study area. Thus, the spatial variation of remotely sensed EOS are controlled mainly by spatial variations of temperature, rather than precipitation.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Kross, A.S.E.; Roulet, N.T.; Moore, T.R.; Lafleur, P.M.; Humphreys, E.R.; Seaquist, J.W.; Flanagan, L.B.; Aurela, M. Phenology and its role in carbon dioxide exchange processes in northern peatlands. J. Geophys. Res. Biogeosci. 2014, 119, 1370–1384. [Google Scholar] [CrossRef]
- Churkina, G.; Schimel, D.; Braswell, B.H.; Xiao, X.M. Spatial analysis of growing season length control over net ecosystem exchange. Glob. Chang. Biol. 2005, 11, 1777–1787. [Google Scholar] [CrossRef]
- Kljun, N.; Black, T.A.; Griffis, T.J.; Barr, A.G.; Gaumont-Guay, D.; Morgenstern, K.; McCaughey, J.H.; Nesic, Z. Response of net ecosystem productivity of three boreal forest stands to drought. Ecosystems 2006, 9, 1128–1144. [Google Scholar] [CrossRef]
- Chen, X.; Xu, L. Temperature controls on the spatial pattern of tree phenology in China’s temperate zone. Agric. For. Meteorol. 2012, 154–155, 195–202. [Google Scholar] [CrossRef]
- Garonna, I.; de Jong, R.; de Wit, A.J.; Mucher, C.A.; Schmid, B.; Schaepman, M.E. Strong contribution of autumn phenology to changes in satellite-derived growing season length estimates across Europe (1982–2011). Glob. Chang. Biol. 2014, 20, 3457–3470. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.Y.; Gough, C.M.; Chen, J.M.; Gonsamo, A. Evidence of autumn phenology control on annual net ecosystem productivity in two temperate deciduous forests. Ecol. Eng. 2013, 60, 88–95. [Google Scholar] [CrossRef]
- Liu, G.; Chen, X.; Zhang, Q.; Lang, W.; Delpierre, N. Antagonistic effects of growing season and autumn temperatures on the timing of leaf coloration in winter deciduous trees. Glob. Chang. Biol. 2018, 24, 3537–3545. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, X.; Silander, J.A., Jr. Deciduous forest responses to temperature, precipitation, and drought imply complex climate change impacts. Proc. Natl. Acad. Sci. USA 2015, 112, 13585–13590. [Google Scholar] [CrossRef]
- Fu, Y.S.H.; Campioli, M.; Vitasse, Y.; De Boeck, H.J.; Van den Berge, J.; AbdElgawad, H.; Asard, H.; Piao, S.L.; Deckmyn, G.; Janssens, I.A. Variation in leaf flushing date influences autumnal senescence and next year’s flushing date in two temperate tree species. Proc. Natl. Acad. Sci. USA 2014, 111, 7355–7360. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, Y.H.; Zeng, Z.; Huang, M.; Li, X.; Piao, S. Temperature, precipitation, and insolation effects on autumn vegetation phenology in temperate China. Glob. Chang. Biol. 2016, 22, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, A.D. Periodical Events and Natural Law as Guides to Agricultural Research and Practice; No. 9; US Government Printing Office: Washington, DC, USA, 1918; pp. 1–42.
- Nakahara, M. Phenology; Kawadesyobo Press: Tokyo, Japan, 1948. (In Japanese) [Google Scholar]
- Gong, G.F.; Jin, W.M. On the geographical distribution of phenodate in China. Acta Geogr. Sin. 1983, 38, 33–40. (In Chinese) [Google Scholar]
- Park-Ono, H.S.; Kawamura, T.; Yoshino, M. Relationships between flowering date of cherry blossom (Prumus yedoensis) and air temperature in East Asia. In Proceeding of the 13th International Congress of Biometerology, Calgary, AB, Canada, 12–18 September 1993; pp. 207–220. [Google Scholar]
- Rötzer, T.; Chmielewski, F.M. Phenological maps of Europe. Clim. Res. 2001, 18, 249–257. [Google Scholar] [CrossRef]
- Liang, L. Beyond the Bioclimatic Law: Geographic adaptation patterns of temperate plant phenology. Prog. Phys. Geogr. 2016, 40, 811–834. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Zhou, L.M.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology in China’s temperate vegetation. Glob. Chang. Biol. 2006, 12, 672–685. [Google Scholar] [CrossRef]
- Nagai, S.; Nasahara, K.N.; Muraoka, H.; Akiyama, T.; Tsuchida, S. Field experiments to test the use of the normalized-difference vegetation index for phenology detection. Agric. For. Meteorol. 2010, 150, 152–160. [Google Scholar] [CrossRef]
- Townsend, P.A.; Singh, A.; Foster, J.R.; Rehberg, N.J.; Kingdon, C.C.; Eshleman, K.N.; Seagle, S.W. A general Landsat model to predict canopy defoliation in broadleaf deciduous forests. Remote Sens. Environ. 2012, 119, 255–265. [Google Scholar] [CrossRef]
- Wu, C.; Gonsamo, A.; Gough, C.M.; Chen, J.M.; Xu, S. Modeling growing season phenology in North American forests using seasonal mean vegetation indices from MODIS. Remote Sens. Environ. 2014, 147, 79–88. [Google Scholar] [CrossRef]
- Vanbeveren, S.P.P.; Bloemen, J.; Balzarolo, M.; Broeckx, L.S.; Sarzi-Falchi, I.; Verlinden, M.S.; Ceulemans, R. A comparative study of four approaches to assess phenology of Populus in a short-rotation coppice culture. iForest 2016, 9, 682–689. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Rautiainen, M.; Mõttus, M.; Heiskanen, J.; Akujärvi, A.; Majasalmi, T.; Stenberg, P. Seasonal reflectance dynamics of common understory types in a northern European boreal forest. Remote Sens. Environ. 2011, 115, 3020–3028. [Google Scholar] [CrossRef]
- Cole, B.; McMorrow, J.; Evans, M. Spectral monitoring of moorland plant phenology to identify a temporal window for hyperspectral remote sensing of peatland. ISPRS J. Photogramm. Remote Sens. 2014, 90, 49–58. [Google Scholar] [CrossRef]
- Ren, S.; Chen, X.; An, S. Assessing plant senescence reflectance index-retrieved vegetation phenology and its spatiotemporal response to climate change in the Inner Mongolian Grassland. Int. J. Biometeorol. 2016, 61, 601–612. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.Q.; Tan, Z.J.; Schwartz, M.D.; Xu, C.X. Determining the growing season of land vegetation on the basis of plant phenology and satellite data in Northern China. Int. J. Biometeorol. 2000, 44, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.Q.; Xu, C.X.; Tan, Z.J. An analysis of relationships among plant community phenology and seasonal metrics of Normalized Difference Vegetation Index in the northern part of the monsoon region of China. Int. J. Biometeorol. 2001, 45, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green leaf phenology at Landsat resolution: Scaling from the field to the satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
- Busetto, L.; Colombo, R.; Migliavacca, M.; Cremonese, E.; Meroni, M.; Galvagno, M.; Rossini, M.; Siniscalco, C.; Morra Di Cella, U.; Pari, E. Remote sensing of larch phenological cycle and analysis of relationships with climate in the Alpine region. Glob. Chang. Biol. 2010, 16, 2504–2517. [Google Scholar] [CrossRef]
- Editorial Board of Vegetation Map of China CAS. 1:1,000,000 Vegetation Atlas of China; Hou, X., Ed.; Science Press: Beijing, China, 2001. (In Chinese) [Google Scholar]
- China Meterological Administration (Ed.) Observation Criterion of Agricultural Meteorology; China Meterological Press: Beijing, China, 1993. (In Chinese)
- Chen, Y.Y.; Yang, K.; He, J.; Qin, J.; Shi, J.C.; Du, J.Y.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116, 15. [Google Scholar] [CrossRef]
- Vermote, E.F.; ElSaleous, N.; Justice, C.O.; Kaufman, Y.J.; Privette, J.L.; Remer, L.; Roger, J.C.; Tanre, D. Atmospheric correction of visible to middle-infrared EOS-MODIS data over land surfaces: Background, operational algorithm and validation. J. Geophys. Res. Atmos. 1997, 102, 17131–17141. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancements and Retrogradation of Natural Vegetation; Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974; pp. 1–137. [Google Scholar]
- Xiao, X.M.; Boles, S.; Liu, J.Y.; Zhuang, D.F.; Liu, M.L. Characterization of forest types in Northeastern China, using multi-temporal SPOT-4 VEGETATION sensor data. Remote Sens. Environ. 2002, 82, 335–348. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gaoa, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H. Climate controls on vegetation phenological patterns in northern mid- and high latitudes inferred from MODIS data. Glob. Chang. Biol. 2004, 10, 1133–1145. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Hogda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Xiao, X.M.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.Y.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Castro, K.L.; Sanchez-Azofeifa, G.A. Changes in spectral properties, chlorophyll content and internal mesophyll structure of senescing Populus balsamifera and Populus tremuloides leaves. Sensors 2008, 8, 51–69. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, H.; Dai, J.; Alatalo, J.; Ge, Q. Modeling spatiotemporal variations in leaf coloring date of three tree species across China. Agric. For. Meteorol. 2017, 249, 310–318. [Google Scholar] [CrossRef]
- Cufar, K.; De Luis, M.; Saz, M.A.; Crepinsek, Z.; Kajfez-Bogataj, L. Temporal shifts in leaf phenology of beech (Fagus sylvatica) depend on elevation. Trees Struct. Funct. 2012, 26, 1091–1100. [Google Scholar] [CrossRef]
- Chen, X.Q.; Hu, B.; Yu, R. Spatial and temporal variation of phenological growing season and climate change impacts in temperate eastern China. Glob. Chang. Biol. 2005, 11, 1118–1130. [Google Scholar] [CrossRef]
| Abbreviations 1 | Moderate Resolution Imaging Spectroradiometer (MODIS) Bands | Equations 2 | References |
|---|---|---|---|
| NDVI | 1,2 | NDVI = (RNIR − RRED)/(RNIR + RRED) | [37] |
| LSWI | 2,5 | LSWI = (RNIR − RSWIR)/(RNIR + RSWIR) | [38] |
| EVI | 1,2,3 | EVI = 2.5 × (RNIR − RRED )/(1 + RNIR + 6 × RRED − 7.5 × RBLUE) | [39] |
| WDRVI | 1,2 | WDRVI = (0.2 × RNIR − RRED)/(0.2 × RNIR + RRED) | [40] |
| GRVI | 1,4 | GRVI = (RGREEN − RRED)/(RGREEN + RRED) | [41] |
| PSRI | 1,2,4 | PSRI = ( RRED − RGREEN)/ RNIR | [25] |
| Year | NDVI | LSWI | EVI | WDRVI | GRVI | PSRI |
|---|---|---|---|---|---|---|
| 2000 | 0.76 ***1 | 0.82 *** | 0.71 *** | 0.76 *** | 0.68 *** | 0.75 *** |
| 2001 | 0.59 ** | 0.57 ** | 0.57 ** | 0.62 *** | 0.55 ** | 0.62 *** |
| 2002 | 0.59 ** | 0.73 *** | 0.53 ** | 0.63 *** | 0.49 * | 0.53 ** |
| 2003 | 0.64 *** | 0.69 *** | 0.66 *** | 0.66 *** | 0.36 | 0.70 *** |
| 2004 | 0.55 ** | 0.63 *** | 0.56 ** | 0.59 ** | 0.65 *** | 0.64 *** |
| 2005 | 0.47 * | 0.61 *** | 0.49 ** | 0.49 ** | 0.56 ** | 0.64 *** |
| 2006 | 0.56 ** | 0.70 *** | 0.68 *** | 0.66 *** | 0.63 *** | 0.67 *** |
| 2007 | 0.31 | 0.44 * | 0.42 * | 0.37 | 0.43 * | 0.55 ** |
| 2008 | 0.35 | 0.40 * | 0.35 | 0.32 | 0.37 | 0.47 * |
| 2009 | 0.51 ** | 0.55 ** | 0.56 ** | 0.44 * | 0.47 * | 0.67 *** |
| 2010 | 0.55 ** | 0.65 *** | 0.57 ** | 0.52 ** | 0.66 *** | 0.75 *** |
| 2011 | 0.79 *** | 0.59 ** | 0.79 *** | 0.78 *** | 0.52 ** | 0.71 *** |
| 2012 | 0.57 ** | 0.54 ** | 0.18 | 0.47 ** | 0.45 * | 0.69 *** |
| Year | (Day of the Year (DOY)) | a0 | ax (d/°N) | ay (d/°E) | az (d/100m) | RMSE (days) | R2 | rx | ry | rz |
|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 298.9 | 596.05 | −2.78 | −1.30 | −1.75 | 8.8 | 0.73 *1 | −0.72 * | −0.46 * | −0.48 * |
| 2001 | 293.7 | 590.65 | −2.41 | −1.45 | −1.48 | 8.9 | 0.71 * | −0.66* | −0.50* | −0.41* |
| 2002 | 295.9 | 605.44 | −2.90 | −1.35 | −1.86 | 9.2 | 0.72 * | −0.72 * | −0.46 * | −0.48 * |
| 2003 | 295.9 | 629.01 | −3.13 | −1.45 | −2.14 | 9.6 | 0.73 * | −0.73 * | −0.47 * | −0.52 * |
| 2004 | 299.3 | 567.87 | −3.02 | −0.99 | −1.61 | 9.4 | 0.70* | −0.72 * | −0.35 * | −0.42 * |
| 2005 | 298.5 | 569.05 | −2.97 | −1.03 | −1.54 | 8.6 | 0.73 * | −0.75* | −0.39* | −0.44* |
| 2006 | 297.1 | 559.99 | −3.83 | −0.67 | −1.29 | 9.0 | 0.78 * | −0.81 * | −0.25 * | −0.36 * |
| 2007 | 298.7 | 533.39 | −2.57 | −0.90 | −1.15 | 8.2 | 0.70* | −0.72 * | −0.36 * | −0.35 * |
| 2008 | 298.6 | 544.7 | −3.41 | −0.68 | −1.45 | 8.8 | 0.74 * | −0.78 * | −0.26 * | −0.41 * |
| 2009 | 294.6 | 623.29 | −2.36 | −1.71 | −1.66 | 8.5 | 0.75 * | −0.67 * | −0.58 * | −0.47 * |
| 2010 | 305.2 | 544.27 | −2.58 | −0.94 | −0.97 | 8.7 | 0.70 * | −0.70 * | −0.36 * | −0.29 * |
| 2011 | 300.0 | 555.19 | −3.49 | −0.72 | −1.53 | 8.4 | 0.77 * | −0.81 * | −0.29 * | −0.44 * |
| 2012 | 298.6 | 474.61 | −3.27 | −0.18 | −1.11 | 8.1 | 0.72 * | −0.80 * | −0.08 * | −0.35 * |
| Mean | 298.1 | 568.73 | −2.98 | −1.03 | −1.50 | 7.1 | 0.80 * | −0.81 * | −0.46 * | −0.50 * |
| Year | rt | rp |
|---|---|---|
| 2000 | 0.78 *1 | −0.02 |
| 2001 | 0.62 * | 0.18 * |
| 2002 | 0.80 * | −0.12 * |
| 2003 | 0.76 * | 0.11 * |
| 2004 | 0.73 * | 0.10 * |
| 2005 | 0.74 * | 0.03 |
| 2006 | 0.80 * | 0.05 * |
| 2007 | 0.68 * | −0.02 |
| 2008 | 0.78 * | 0.25 * |
| 2009 | 0.76 * | −0.09 * |
| 2010 | 0.64 * | 0.17 * |
| 2011 | 0.75 * | 0.48 * |
| 2012 | 0.80 * | 0.11 * |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, W.; Chen, X.; Liang, L.; Ren, S.; Qian, S. Geographic and Climatic Attributions of Autumn Land Surface Phenology Spatial Patterns in the Temperate Deciduous Broadleaf Forest of China. Remote Sens. 2019, 11, 1546. https://doi.org/10.3390/rs11131546
Lang W, Chen X, Liang L, Ren S, Qian S. Geographic and Climatic Attributions of Autumn Land Surface Phenology Spatial Patterns in the Temperate Deciduous Broadleaf Forest of China. Remote Sensing. 2019; 11(13):1546. https://doi.org/10.3390/rs11131546
Chicago/Turabian StyleLang, Weiguang, Xiaoqiu Chen, Liang Liang, Shilong Ren, and Siwei Qian. 2019. "Geographic and Climatic Attributions of Autumn Land Surface Phenology Spatial Patterns in the Temperate Deciduous Broadleaf Forest of China" Remote Sensing 11, no. 13: 1546. https://doi.org/10.3390/rs11131546
APA StyleLang, W., Chen, X., Liang, L., Ren, S., & Qian, S. (2019). Geographic and Climatic Attributions of Autumn Land Surface Phenology Spatial Patterns in the Temperate Deciduous Broadleaf Forest of China. Remote Sensing, 11(13), 1546. https://doi.org/10.3390/rs11131546