Fusion of Change Vector Analysis in Posterior Probability Space and Postclassification Comparison for Change Detection from Multispectral Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
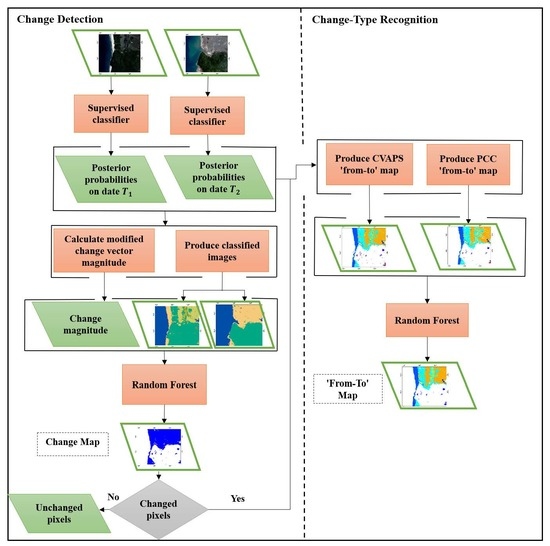
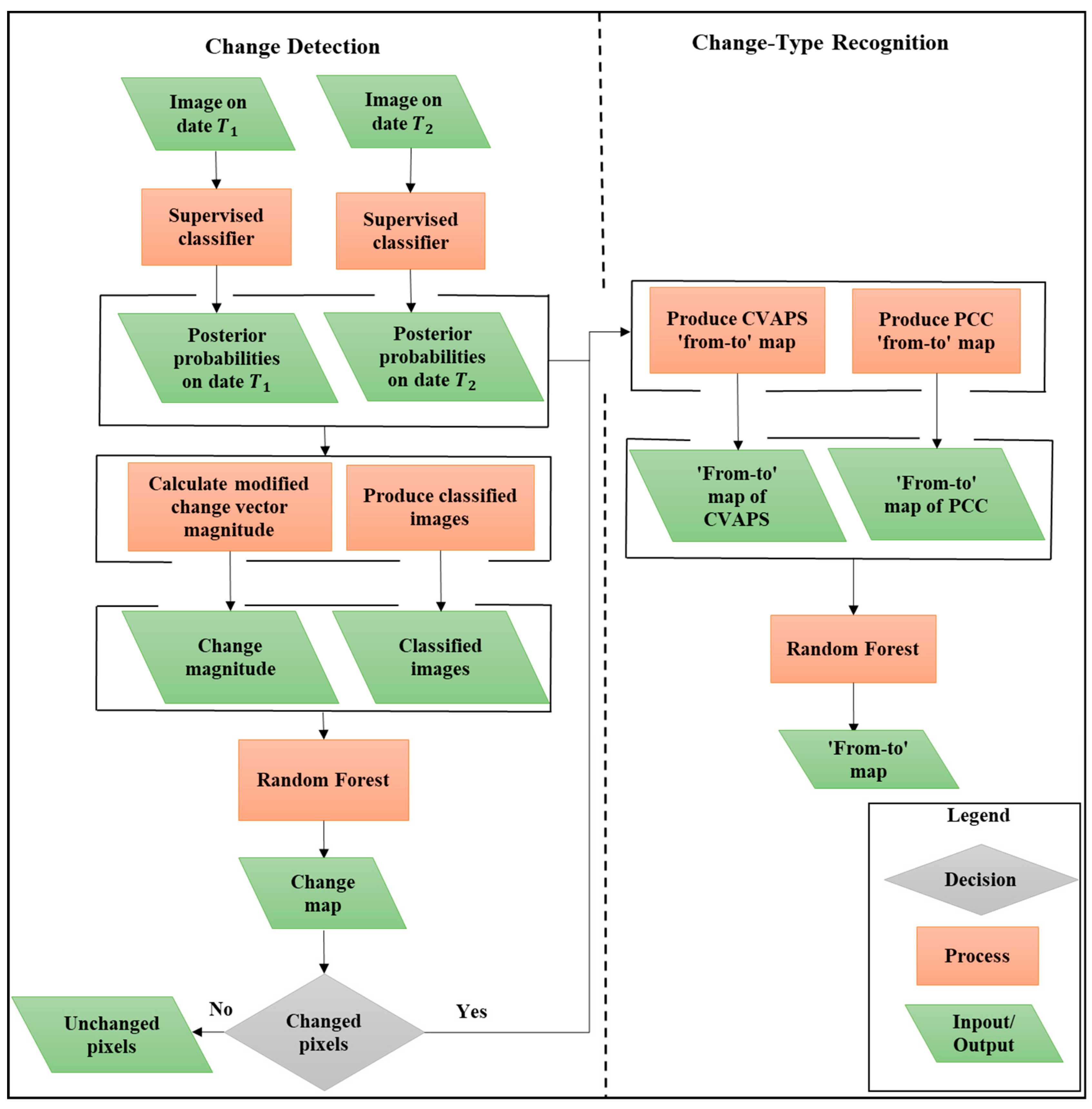
2.1. Proposed Method
2.1.1. Change Detection
2.1.2. Change-Type Recognition
3. Description of Data Sets and Experiments
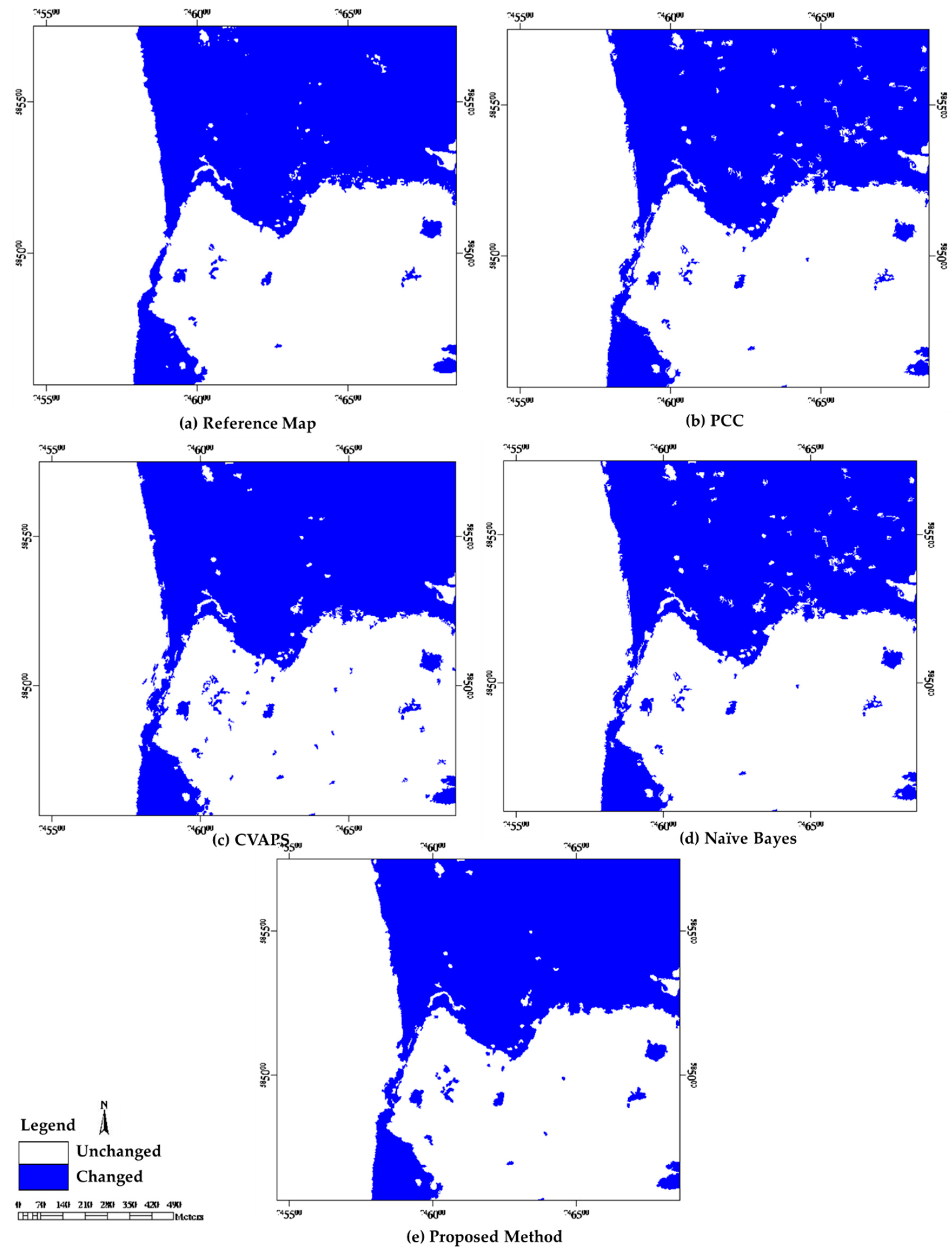
3.1. Experiment I
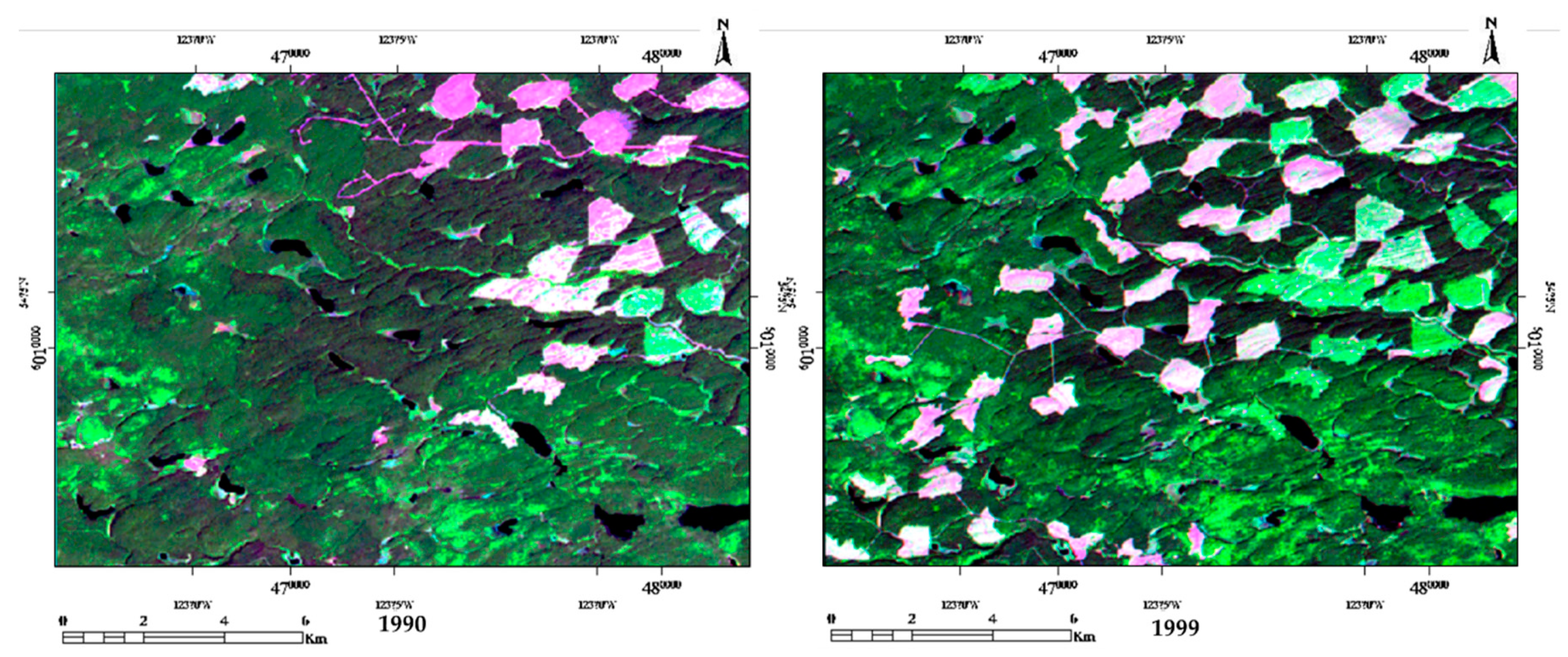
3.1.1. Study Area and Data
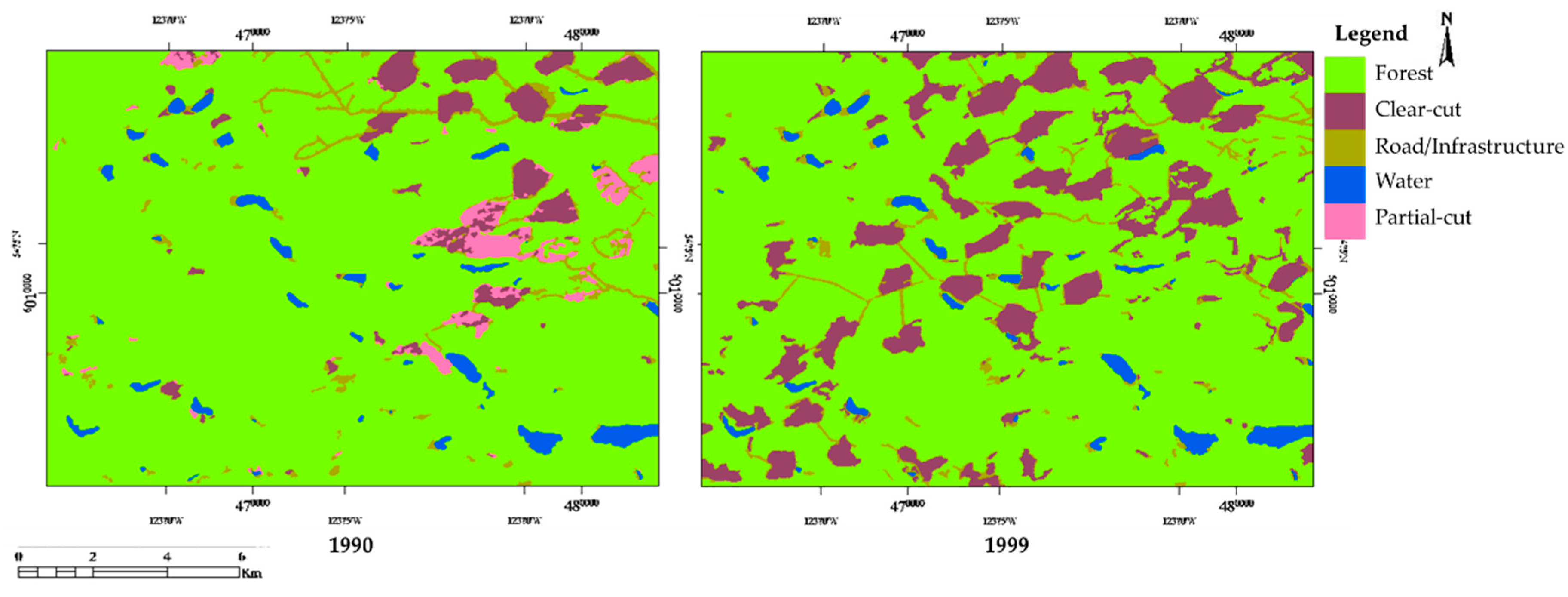
3.1.2. Data Processing
3.1.3. Accuracy Assessment
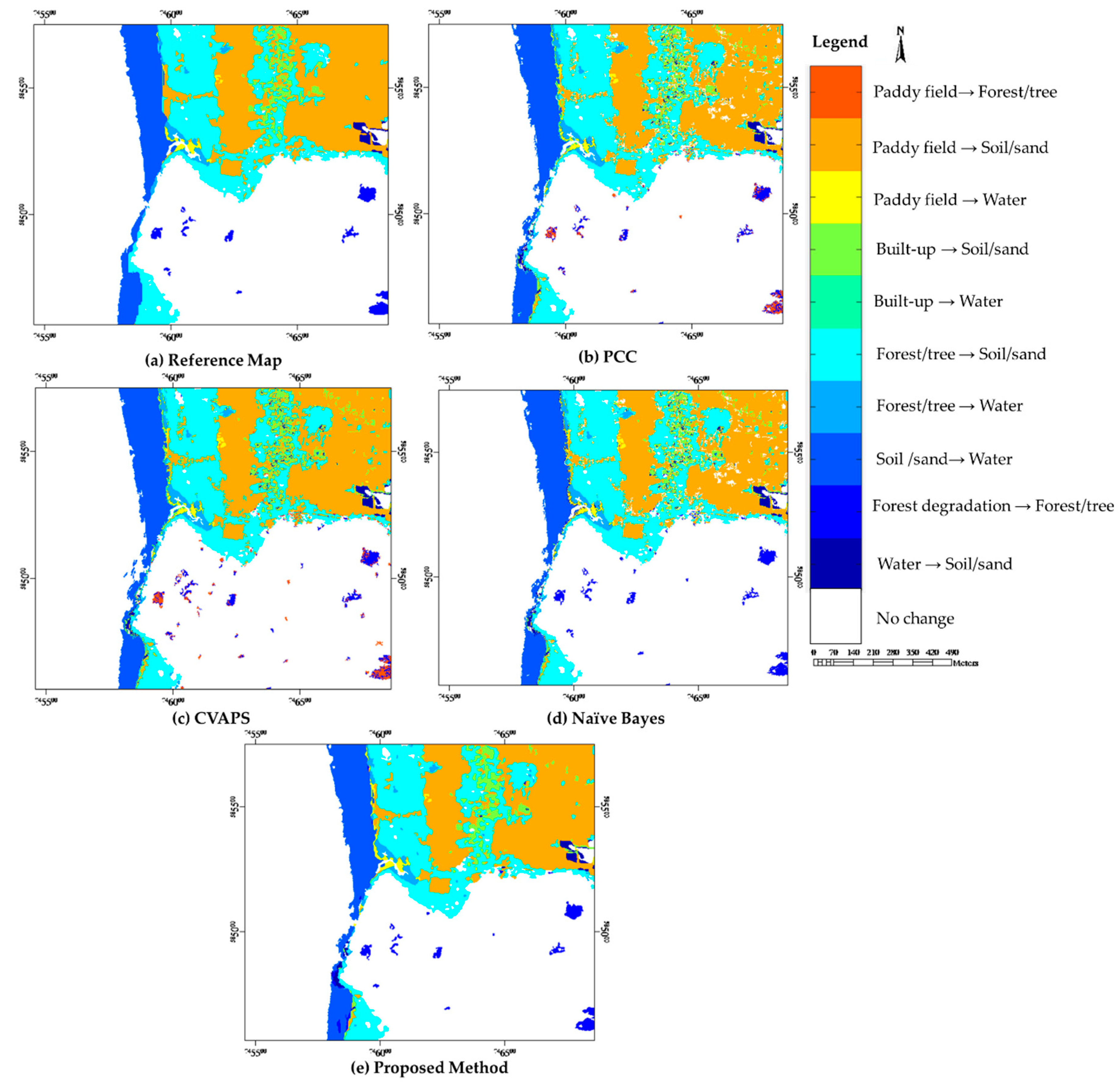
3.2. Experiment II
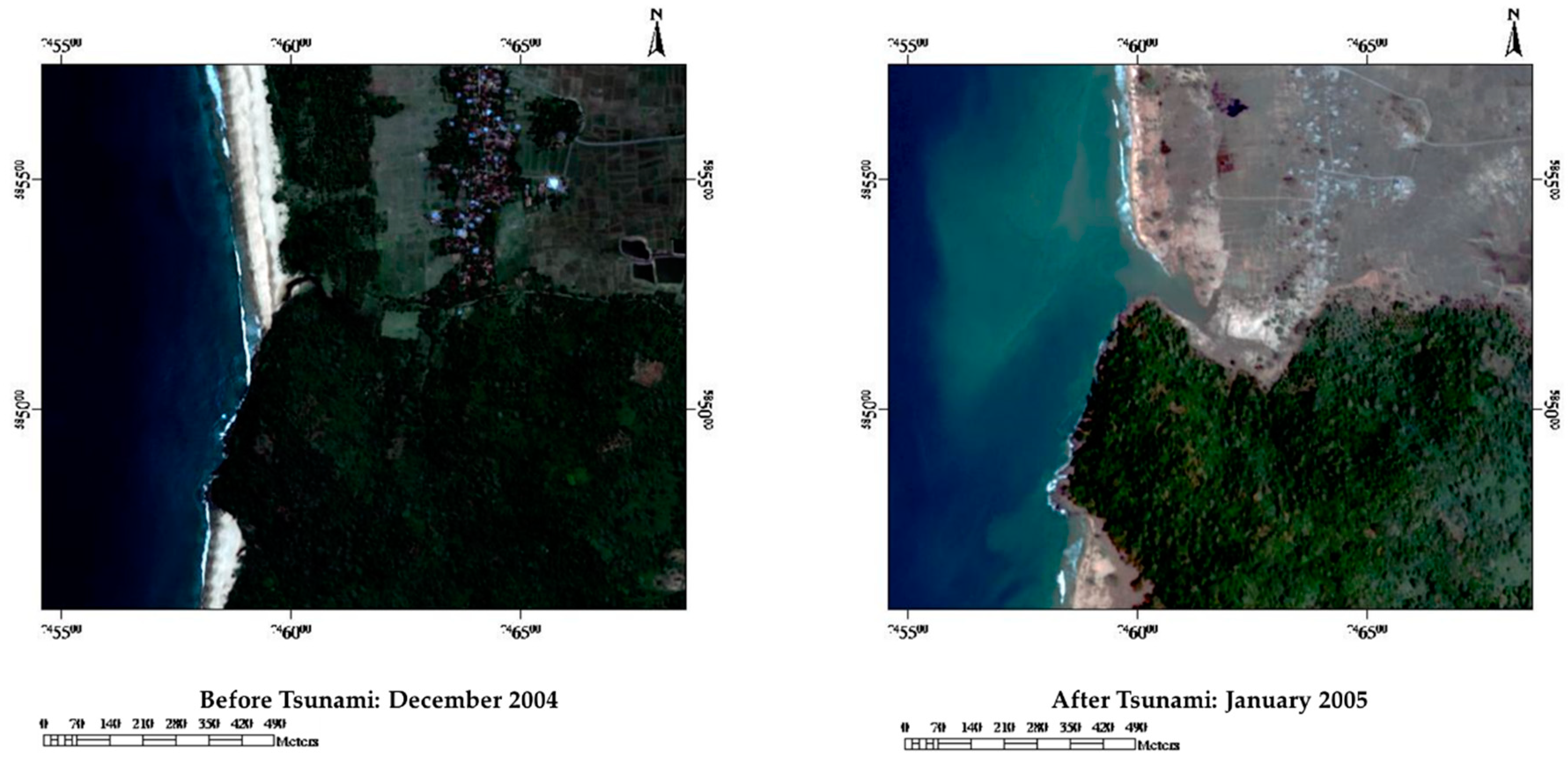
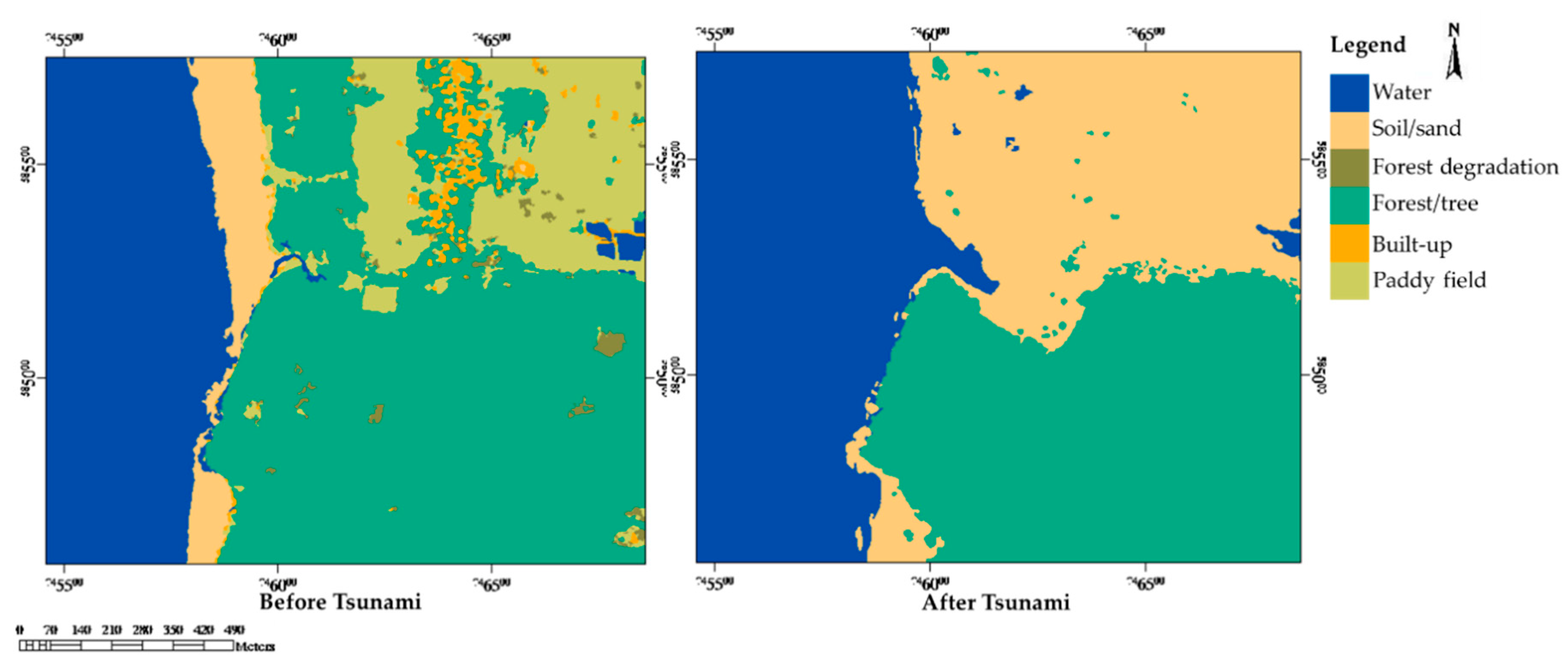
3.2.1. Study Area and Data
3.2.2. Data Processing
3.2.3. Accuracy Assessment
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fung, T. Land use and land cover change detection with Landsat MSS and SPOT HRV data in Hong Kong. Geocarto Int. 1992, 7, 33–40. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Shi, Y.; Yamaguchi, Y. An automated approach for updating land cover maps based on integrated change detection and classification methods. ISPRS J. Photogramm. Remote Sens. 2012, 71, 86–95. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, J.; Yu, X.; Tang, P. A land-cover change detection method using data-oriented composite-kernel-based one-class support vector machine. Geocarto Int. 2017, 32, 1049–1068. [Google Scholar] [CrossRef]
- Chou, T.; Lei, T.; Wan, S.; Yang, L. Spatial knowledge databases as applied to the detection of changes in urban land use. Int. J. Remote Sens. 2005, 26, 3047–3068. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Cui, X.; Chen, J. Change vector analysis in posterior probability space: A new method for land cover change detection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 317–321. [Google Scholar] [CrossRef]
- Carvalho Júnior, O.A.; Guimarães, R.F.; Gillespie, A.R.; Silva, N.C.; Gomes, R.A. A new approach to change vector analysis using distance and similarity measures. Remote Sens. 2011, 3, 2473–2493. [Google Scholar] [CrossRef]
- Singh, S.; Talwar, R. A comparative study on change vector analysis based change detection techniques. Sadhana 2014, 39, 1311–1331. [Google Scholar] [CrossRef]
- Tewkesbury, A.P.; Comber, A.J.; Tate, N.J.; Lamb, A.; Fisher, P.F. A critical synthesis of remotely sensed optical image change detection techniques. Remote Sens. Environ. 2015, 160, 1–14. [Google Scholar] [CrossRef]
- Waske, B.; van der Linden, S. Classifying multilevel imagery from SAR and optical sensors by decision fusion. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1457–1466. [Google Scholar] [CrossRef]
- Du, P.; Liu, S.; Xia, J.; Zhao, Y. Information fusion techniques for change detection from multi-temporal remote sensing images. Inf. Fusion 2013, 14, 19–27. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Hou, B.; Liu, G. Using combined difference image and k-means clustering for SAR image change detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 691–695. [Google Scholar] [CrossRef]
- Jia, L.; Li, M.; Zhang, P.; Wu, Y.; An, L.; Song, W. Remote-sensing image change detection with fusion of multiple wavelet kernels. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3405–3418. [Google Scholar] [CrossRef]
- Singh, A.; Singh, K.K. Unsupervised change detection in remote sensing images using fusion of spectral and statistical indices. Egypt. J. Remote Sens. Space Sci. 2018, 21, 345–351. [Google Scholar] [CrossRef]
- Luo, H.; Liu, C.; Wu, C.; Guo, X. Urban change detection based on Dempster–Shafer theory for multitemporal very high-resolution imagery. Remote Sens. 2018, 10, 980. [Google Scholar] [CrossRef]
- Waske, B.; Braun, M. Classifier ensembles for land cover mapping using multitemporal SAR imagery. ISPRS J. Photogramm. Remote Sens. 2009, 64, 450–457. [Google Scholar] [CrossRef]
- Foody, G.; Boyd, D. Detection of partial land cover change associated with the migration of inter-class transitional zones. Int. J. Remote Sens. 1999, 20, 2723–2740. [Google Scholar] [CrossRef]
- Veh, G.; Korup, O.; Roessner, S.; Walz, A. Detecting Himalayan glacial lake outburst floods from Landsat time series. Remote Sens. Environ. 2018, 207, 84–97. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. Ser. B (Methodol.) 1986, 48, 259–302. [Google Scholar] [CrossRef]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]

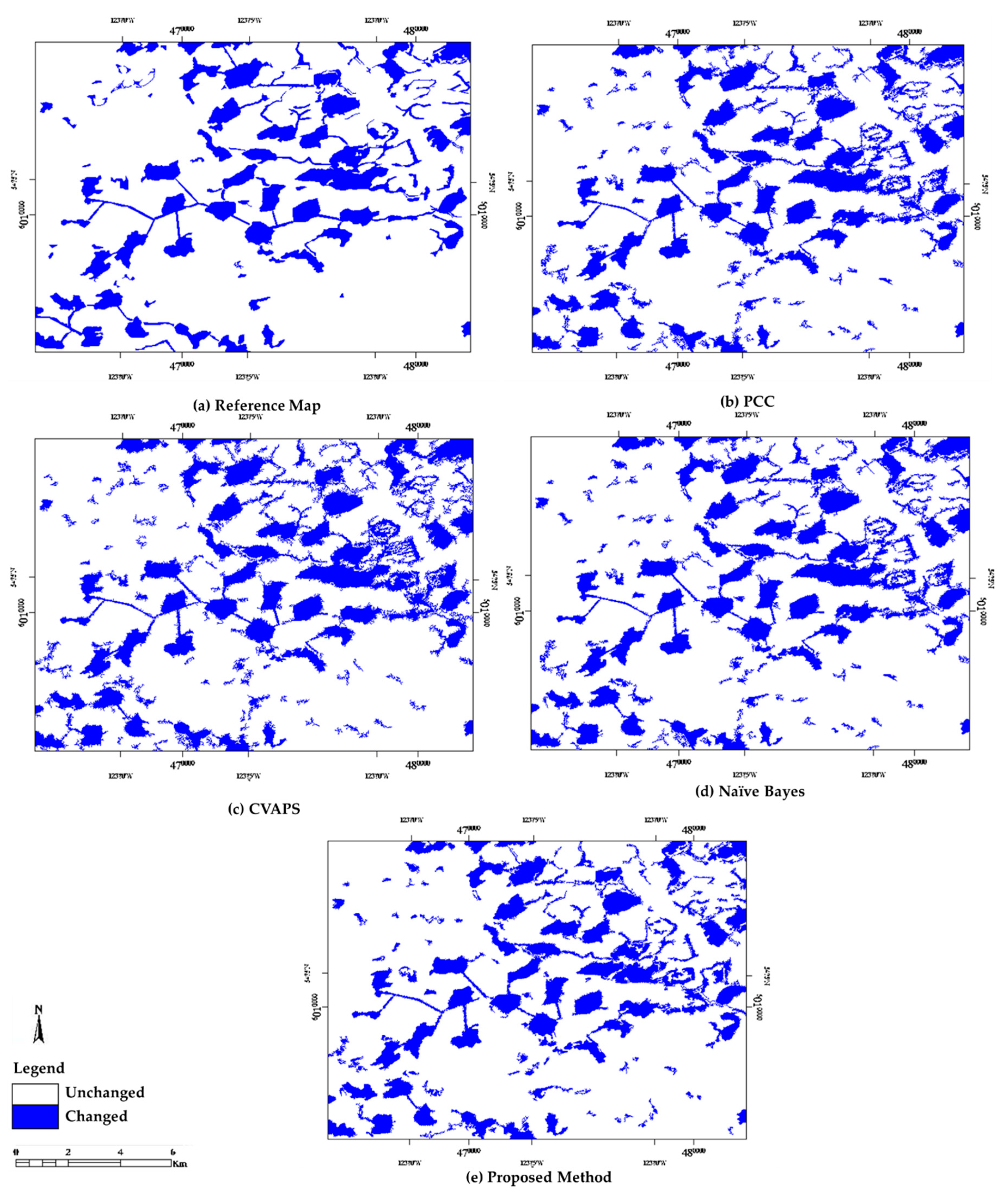
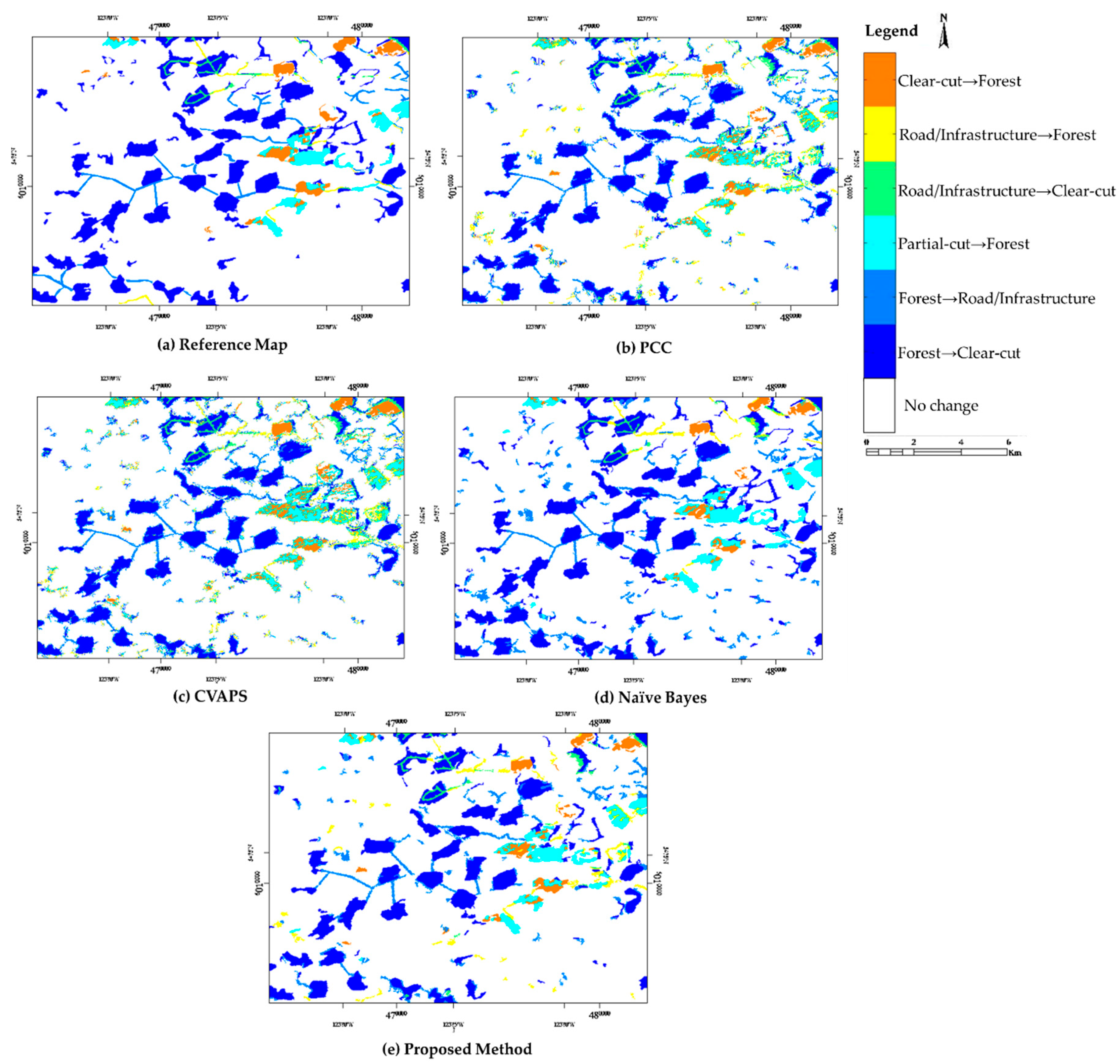
| Method | User’s Accuracy | Producer’s Accuracy | Overall Accuracy | Kappa | ||
|---|---|---|---|---|---|---|
| Changed | Unchanged | Changed | Unchanged | |||
| CVAPS | 80.7% | 83.3% | 84% | 79.9% | 81.9% | 0.63 |
| PCC | 85.2% | 81.4% | 80.4% | 86.1% | 83.2% | 0.66 |
| Naïve Bayes | 85.2% | 81.4% | 80.4% | 86.1% | 83.2% | 0.66 |
| Proposed | 80.6% | 89.4% | 88.4% | 82.2% | 85% | 0.70 |
| Method | Overall Accuracy | Kappa |
|---|---|---|
| CVAPS | 69.8% | 0.64 |
| PCC | 65.4% | 0.60 |
| Naïve Bayes | 64% | 0.58 |
| Proposed Method | 71.2% | 0.67 |
| Method | User’s Accuracy | Producer’s Accuracy | Overall Accuracy | Kappa | ||
|---|---|---|---|---|---|---|
| Changed | Unchanged | Changed | Unchanged | |||
| CVAPS | 96.9% | 98.4% | 98.4% | 96.8% | 97.6% | 0.95 |
| PCC | 96.2% | 98.4% | 98.3% | 96.3% | 97.3% | 0.94 |
| Naïve Bayes | 96.2% | 98.4% | 98.3% | 96.3% | 97.3% | 0.94 |
| Proposed | 99.2% | 97.7% | 97.7% | 99.1% | 98.4% | 0.96 |
| Method | Overall Accuracy | Kappa |
|---|---|---|
| CVAPS | 82.6% | 0.80 |
| PCC | 80% | 0.77 |
| Naïve Bayes | 83.8% | 0.81 |
| Proposed Method | 89.1% | 0.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakeri, F.; Huang, B.; Saradjian, M.R. Fusion of Change Vector Analysis in Posterior Probability Space and Postclassification Comparison for Change Detection from Multispectral Remote Sensing Data. Remote Sens. 2019, 11, 1511. https://doi.org/10.3390/rs11131511
Zakeri F, Huang B, Saradjian MR. Fusion of Change Vector Analysis in Posterior Probability Space and Postclassification Comparison for Change Detection from Multispectral Remote Sensing Data. Remote Sensing. 2019; 11(13):1511. https://doi.org/10.3390/rs11131511
Chicago/Turabian StyleZakeri, Fatemeh, Bo Huang, and Mohammad Reza Saradjian. 2019. "Fusion of Change Vector Analysis in Posterior Probability Space and Postclassification Comparison for Change Detection from Multispectral Remote Sensing Data" Remote Sensing 11, no. 13: 1511. https://doi.org/10.3390/rs11131511
APA StyleZakeri, F., Huang, B., & Saradjian, M. R. (2019). Fusion of Change Vector Analysis in Posterior Probability Space and Postclassification Comparison for Change Detection from Multispectral Remote Sensing Data. Remote Sensing, 11(13), 1511. https://doi.org/10.3390/rs11131511