Abstract
In the last few years, the world has been turning to the exploitation of renewable energy sources due to increased awareness of environmental protection and increased consumption of fossil fuels. In this research, by applying geographic information systems and integrating them with multi-criteria decision making methods, an area suitable for the construction and exploitation of renewable energy sources is determined. The research uses not only climate, spatial, environmental, and geomorphological parameters but also socioeconomic parameters, population, unemployment, and number of tourist nights as well as electricity consumption. By applying spatial analysis, rasters of all parameters were created using GRASS GIS software. Using the analytic hierarchy process, the calculated rasters are assigned with weight coefficients, and the sum of all those rasters gives the final raster of optimal locations for the construction of solar power plants in Croatia. To test the accuracy of the obtained results, sensitivity analysis was performed using different weight coefficients of the parameters. From the sensitivity analysis results, as well as a histogram and statistical indicators of the three rasters, it is apparent that raster F1 gives the best results. The most decisive parameters in determining the optimal solar plant locations that result from this research are GHI, land cover, and distance to the electricity network.
1. Introduction
In recent years, due to increased consumption of fossil fuels, high CO2 emissions in the atmosphere, and environmentally irreversible damage to the environment, the world is increasingly turning to renewable, environmentally-friendly sources of energy. Renewable energy sources come from nature and can be renewed, such as energy from wind, hydropower, geothermal energy, tidal energy, solar energy, and biomass energy. Renewable energy sources have been used for many years, and their growth is expected in the coming years.
Given the initiative and the strategy signed by the 200 states, including Croatia, under the Paris Agreement [1], there is a need to increase the use of renewable energy sources. The aim of exploiting renewable energy sources is to protect the environment, but it also leads to an increase in local and regional development as well as an increase in the employment of the population. In addition to reducing environmental pollution, reducing greenhouse gas emissions caused by the use of fossil fuels improves the quality of life and increases the safety of the population.
The use of renewable energy sources depends on local and regional characteristics and numerous parameters that need to be explored before the start of power plant construction. Using remote sensing and geographic information systems, as well as multi-criteria spatial data analysis, an area suitable for building or exploiting some of the forms of renewable energy sources is defined. Given the need for the construction of “green power plants”, there is also a need for creating spatial studies based on geographic information systems (GIS).
The creation of spatial studies and the application of geographic information systems in defining the potential for exploitation of renewable energy sources began in the early 1990s. Geographic information systems and algorithms used for data analysis have been significantly modified over the last 20 years and have been improved, so they have become an inescapable tool for spatial planning and the definition of the potential for exploiting renewable energy sources.
Solar radiation data should be collected to determine the potential for solar energy exploitation [2,3]. The work of Šúri and Hofierka [4], Martins et al. [5], Amillo et al. [6], and Huld [7] as one of the types of solar radiation refer to global horizontal irradiation (GHI), which was used in this research as a solar potential parameter. To determine the GHI, the GRASS GIS software was used, i.e., its module r.sun developed by Hofierka and Šúri [8], and later used by numerous other authors [2,3,7,9,10].
When determining the optimal locations and calculating the potential of renewable energy sources, numerous parameters with different influence on the result are used, so both geographic information systems and multi-criteria decision making (MCDM) are applied. The authors of [11,12,13,14,15] used GIS and MCDM to determine the optimal locations for solar energy exploitation. Geographic information systems serve as a means of visualization of optimal locations for the construction of solar power plants, as well as a tool for performing spatial analysis. As Sanchez-Lozano et al. [11] and Tahri et al. [14] pointed out, multi-criteria decision making methods are applied due to a large number of criteria and sub-criteria influencing the decision making. Asakereh et al. [13] used fuzzy analytic hierarchy process (AHP) and GIS to select potential locations for solar energy plants in Shodirwan Region in Iran. Uyan [12] and Georgiou and Skarlatos [15] used constraint parameters as well as additional buffer areas around them to emphasize protection of those areas (e.g., protection areas, built-up area, water bodies, road infrastructure).
Analyses of selected geomorphological, environmental, climatic, spatial, and socioeconomic parameters and the application of the analytic hierarchy process (AHP) have determined areas suitable for the exploitation of solar energy and the construction of solar power plants.
The research conducted in this paper was based on open data and open source software to enable the applicability of developed methods in other locations in the world.
2. Materials and Methods
2.1. Study Area
The study area of this research is the land territory of the Republic of Croatia (Figure 1), situated in South-East Europe. The land territory covers 56,594 km2. Due to Croatia’s warm climate and an annual average of more than 2000 sunny hours on the Adriatic coast, it is a good candidate for solar energy exploitation [10].
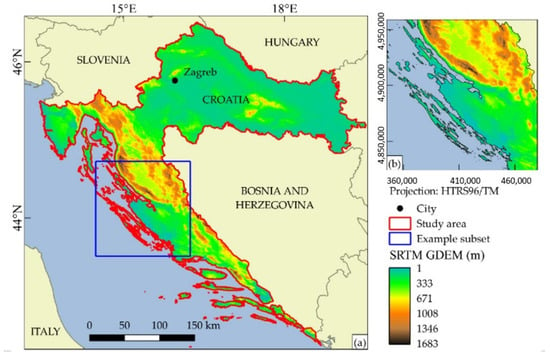
Figure 1.
(a) Study area and example subset location; (b) example subset.
2.2. Integration of GIS and MCDM
The development of new technologies and methods for spatial data gathering has led to large amounts of data that are difficult to process, store, and manage. Therefore, as a result of the need for cost-effective, efficient, and accurate spatial data management methods, GIS was developed [16]. Geographic information systems enable faster and easier manipulation of spatial data, but their most significant advantage is the ability to perform spatial, attribute, and multi-criteria analyses.
The exploitation of solar energy and power plant construction depends on numerous spatial and other parameters that, before choosing the optimal location for construction, should be researched in detail. Therefore, there is a need for the creation of spatial planning based on geographic information systems that will take into account all the crucial parameters for the solar power plant construction.
Numerous authors use GIS tools to define solar energy potential but at the same time use different parameters and their values. Broesamle et al. [17], Fluri [18], Clifton and Boruff [19], and Lehman [20] determined the solar energy potential in their research, and they defined the best locations for solar power plant construction.
In the context of multi-criteria decision making, the decision-making problem is most often seen as a problem in which the decision maker must decide on one of the alternatives that are known or need to be generated, taking into account all relevant factors or criteria (Figure 2).
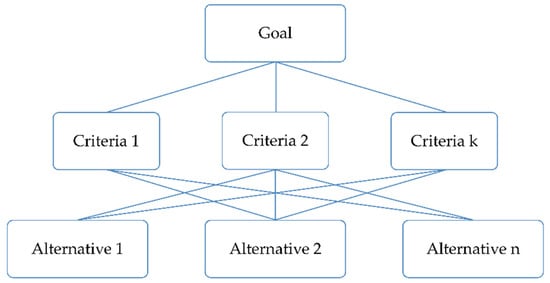
Figure 2.
The basic diagram in multi-critical decision making [21].
Multi-criteria decision making methods are divided into [22,23]:
- Multi-attribute decision making (MADM); and
- Multi-objective decision making (MODM).
Kumar et al. [24] presented an analysis of the most frequently used multi-criteria decision making methods and their application, and concluded that the weighted sum model and the analytical hierarchy process are most commonly used for energy planning, while TOPSIS (technique for order of preference by similarity to ideal solution) and ELECTRE (eimination et choix traduisant la realité; ELimination and Choice Expressing REality) methods are applied to energy management. The authors also pointed out that because of the specificity of decision making in energy planning, hybrid methods of multi-criteria decision making are increasingly used. Ramanathan and Ganesh [25] and Ishizaka and Labib [26] stated the benefits of AHP for energy planning, such as simple application, flexibility, intuition, and ability to qualitatively and quantitatively address the criteria. Since this research encompasses a large number of parameters and different resolutions all used for determination of optimal solar power plant locations, the AHP method has been applied.
AHP is based on determining the hierarchy of problems and evaluating elements at hierarchical levels until the weight factors of all elements are determined in the final synthesis [27]. Through this, the problem is structured in the hierarchy, and the selected elements are defined as the goal, criteria, sub-criteria, and alternatives. Defining the hierarchy is the first step in applying AHP, followed by a pairwise comparison from the same hierarchy level based on common criteria using the Saaty scale (Table 1).

Table 1.
Saaty scale [27,28].
By comparing individual pairs of alternatives of the corresponding hierarchical level, the local weights of criteria and sub-criteria are calculated, expressed in integer numbers and entered in a matrix whose element values are reciprocal [29]:
The alternatives are Ai (i = 1, …, n), while the weight ratio of pairs is given in each element of the matrix , which can be expressed by the following expression [29]:
where and are local weights of elements i and j in relation to a superior element.
2.3. Determination of Research Parameters
In order to determine the optimal locations for solar power plant construction on the mainland and the islands of the Republic of Croatia, it was first necessary to define the exact parameters. Some of the parameters are necessary to determine an optimal location, while others contribute to a higher quality result. Sanchez-Lozano et al. [11] divided the parameters needed for energy planning into the following categories:
- Climate;
- Geomorphological;
- Spatial; and
- Environmental.
During the solar energy exploitation research, a need to introduce additional parameters to determine the potential locations for the solar power plant construction occurred. Very often, decisive influence in making the final decision on the location of solar power plants has economic and/or political importance of the construction on a particular area as well as construction costs, not just climatic, geomorphological, spatial, and environmental parameters. Introducing additional parameters aims to bring closer the needs of the population with energy planning. Therefore, socioeconomic parameters such as the population, the unemployed percentage, the number of tourist night, and electricity consumption are introduced as additional parameters. Including georeferenced socioeconomic parameters enables the definition of locations for solar energy exploitation that consider the substantial differences in electricity consumption in the Republic of Croatia, especially in the summer months and in tourist destinations with a large number of tourist nights. Data on unemployment can also be important since Croatia has a high percentage of unemployment, and the construction and maintenance of solar power plants would create new jobs, thus reducing unemployment.
The research covered parameters listed in Table 2 and Table 3. Different spatial data sources were used in the research to determine spatial parameters. Most of them are globally and freely available. OpenStreetMap (OSM) was used to define road and railway infrastructure, administrative units, as well as water bodies. The OSM data timeframe is 2018. Shuttle Radar Topography Mission’s (SRTM) global digital elevation model (GDEM) with ~30 m (1 arc-second) spatial resolution from 2014 was used to define geomorphological parameters. CORINE land cover (CLC) 2012 was used to define land cover. CLC was produced on remote sensing classification methods based on the optical satellite imagery and has minimum mapping area of 25 ha. Protected areas were defined in 2018 using the ENVI portal from the Croatian Agency for Environment and Nature, while the electricity network was defined using the Basic Topographic Database (TTB) in 2016 by the State Geodetic Administration. Furthermore, averaged GHI data (30 m x 30 m) were calculated in GRASS GIS software for the entire territory of Croatia using the method developed and described in the research by Gašparović et al. [10]. The accuracy of GHI was tested based on the solar irradiation ground measurements obtained from baseline surface radiation network (BSRN) stations and stations from the Meteorological and Hydrological Institute of Croatia (DHMZ) and compared with commercial Solar Radiation Data (SoDa) downloaded from the SoDa web portal. Accuracy analysis published in previous research [10] shows that GHI has 3% higher accuracy than SoDa obtained by calculating deviations from BSRN stations and 0.5% higher accuracy in comparison with DHMZ stations, 0.5%. The final GHI, used in this research, is expressed through the daily mean value of GHI in the period from 2011 to 2013. The three-year period was used to exclude the influence of extreme atmospheric conditions caused by global warming and achieve better quality and reliability. All spatial data used in this research are transformed into the Croatia terrestrial reference system (HTRS96/TM). All used raster data were resampled to the 30 m × 30 m spatial resolution because SRTM GDEM and GHI data were in 30 m spatial resolution. Figure 3 shows all spatial data used in the research.

Table 2.
Constraint parameters.

Table 3.
Parameters and criteria of research.
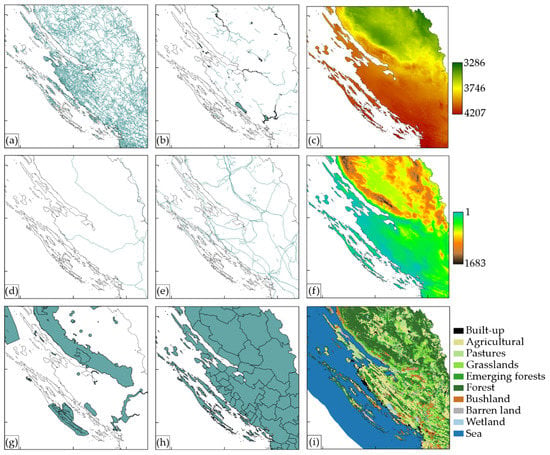
Figure 3.
Data used in the research: (a) road infrastructure—OpenStreetMap (OSM); (b) water bodies—OSM; (c) average daily global horizontal irradiation (GHI) (Wh/m2) [10]; (d) railway infrastructure—OSM; (e) electricity network—TTB; (f) Shuttle Radar Topography Mission’s (SRTM) global digital elevation model (GDEM) (m); (g) protected areas—ENVI; (h) administrative units—OSM (i) CORINE Land Cover 2012.
The research also used the socioeconomic parameters, the population, and the number of tourist nights published by the Croatian Bureau of Statistics and the unemployed data obtained from the Croatian Employment Office. The population was acquired from the 2011 consensus, while the number of tourist nights was obtained for 2016 as then eVisitor, a unique and central place of tourist registration in Croatia, was released. The unemployed data were obtained for 2012 for all administrative units in Croatia. The average annual electricity consumption was calculated based on the annual electricity consumption for the period from 2011 to 2013, which was downloaded from the European Statistics portal. Since some areas of Croatia are highly touristic in summer months, a lot of pressure on the electricity network is made by the increase of population caused by tourists. Therefore, the number of tourist nights was also used to calculate average electricity consumption for each administrative unit. From annual statistics on the number of tourist nights, the daily average of tourist nights was determined for each administrative unit, which was then added to the population. Then, the newly calculated population was multiplied, with average electricity consumption per person. Estimation of average electricity consumption for each administrative unit (Ei) was calculated according to the expression:
where:
- —population number;
- —number of tourist nights;
- —average annual electricity consumption in Croatia;
- —population number in Croatia; and
- —administrative unit.
The research excluded some areas where construction is not possible regardless of their other characteristics because of environmental protection, protection of cultural heritage or legislative barriers. As constraint parameters in determining optimal locations for solar power plants construction, Uyan [12] used a 500 m buffer of built-up area, a 100 m buffer of roads, and a 500 m buffer of protected areas (e.g., archaeological sites, military zones, forest areas, areas of animal protection, biological areas) as constraint parameters. Furthermore, for selecting optimal solar power plant locations, Georgiou and Skarlatos [15] used a 200 m buffer of built-up area, a 200 m buffer of shoreline and 100 m of water bodies, a 200 m buffer of protected sites, and a 50 m buffer of roads as constraint parameters.
Based on previously mentioned research [12,15], as constraint parameters in our research, three types of areas and buffers around them (Table 2) were used. In built-up areas, the construction of solar power plants is not possible and because of that, those areas were defined as one of the constraint parameters as well as the area distanced 100 m from it. The 100 m buffer around the built-up area was used to distance potential solar power plant locations from it. Water bodies are also constraint parameter as well as the area distanced 100 m from it, since a high risk of flooding exists in those areas. The research excluded all protected areas and sites, and area distanced 100 m around them, while construction is forbidden in those areas. The additional buffer was used to further protect the areas in order not to undermine their protection. The research included numerous parameters, from which GHI has the most influence on the decision making, while solar radiation is not equal in all parts of Croatia. Spatial parameters are also very important, and one of the most decisive factors in this research. The biggest weight was given to distance to the electricity network since the planned power plant should be connected to the power grid, and it is important that it be near the existing grid. The distance to settlements was used, since the assumption is that solar power plants will be built near large electricity consumers. When determining the influence of the distance to the electricity network, it was established that distances up to 10 km from the power lines are acceptable for the construction of solar power plants. The distance to the electricity network was calculated for each pixel of the raster, which was then normalized. The pixel value distance 0 m from the electricity network is equal to 1 and then linearly decreases to a maximum acceptable distance of 10 km when it reaches 0. For distances over 10 km, the pixel value is 0. Similar to the previous one, an important sub-criterion is the distance to road infrastructure, because when increasing the distance from the roads, the construction and maintenance cost increases. The distance to road infrastructure was also calculated for each pixel of the raster, which was then normalized, and the pixel value 1 denotes the area best for construction, and areas not suitable for construction have value 0. The maximum acceptable distance to roads is 3 km. Distance to railway infrastructure was also used in the research but with minimum weight, since Croatia has outdated railway infrastructure. In this research, it was determined that the acceptable distance to the railway is 20 km.
Land cover is divided into eight classes: barren land, grasslands, bushland, pastures, emerging forests, agricultural land, forest, and wetland. The most suitable classes for construction are barren land, grasslands, and bushland, while they are economically least valuable land and easy to exploit. Pastures and emerging forests can also be used but have smaller weights in decision making. Economically more valuable land, which is in the function of other activities, such as agricultural land and forests, is less suitable for the construction of solar power plants. Although some authors suggest forests as a constraint parameter, they have been used in this research since 50% of the territory of Croatia is forests, and their exclusion would drastically reduce the study area. However, forests are assigned with very low weight and, in combination with other parameters such as elevation and slope, are almost excluded from the research. The least weight is given to the wetland since the construction on such terrain is extremely demanding and economically unprofitable.
Geomorphological sub-criteria influence the process of determining optimal locations for solar power plant construction. The highest weight, and therefore the importance, is given to the slope determined based on SRTM GDEM. The slope of the terrain is an important criterion, since the increase in the terrain incline increases the construction cost, and the construction and installation of solar power plants is more difficult. From the research of Tahri et al. [14], it was determined that the maximum acceptable slope is 25%. A normalized raster is defined where the pixel value 1 indicates the best area for construction with a 0% slope, and pixel value 0 indicates the area that is not suitable for construction with a slope higher than 25%. The orientation is given a smaller weight but is still considered to be an important sub-criterion, because the south-facing areas are more exposed to solar radiation and thus more suitable for exploiting the solar potential. Normalizing the orientation raster gave the following values: 0.3 north, 0.6 east, and west, and south 1. The lowest weight of the geomorphological sub-criteria has altitude, since the construction at higher altitudes means higher construction and transport costs. In this study, it was determined that a maximum acceptable altitude is 500 m. By normalizing the raster, pixels from 0 m to 150 m above sea level gained value 1, while pixels with height over 150 m were linearly decreasing to 0 (maximum acceptable elevation of 500 m).
From the socioeconomic parameters, the highest weight is given to electricity consumption, while it is more cost-effective to build a solar power plant in the area where demand and electricity consumption are higher. The population and the number of tourist nights are given a medium weight, because the construction is planned in the area where the demand for electricity is higher, and it is to be expected that these are also areas with higher population. The lowest weight of socioeconomic sub-criteria is the percentage of unemployment, since these data do not significantly affect the choice of locations, but they can be socially important as construction and maintenance of solar power plants will create new jobs.
2.4. Determination of Weight Coefficients of Parameters with AHP
Based on the previously described parameters, the hierarchy model of criteria and sub-criteria was developed (Figure 4).
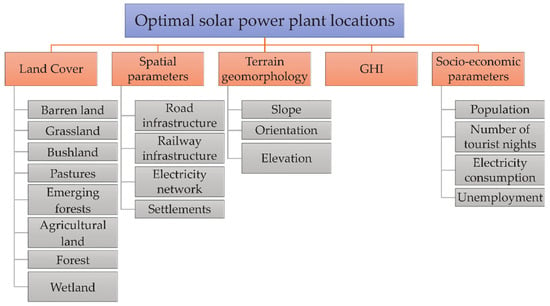
Figure 4.
Analytic hierarchy process (AHP) criteria and sub-criteria model for determining optimal locations for solar power plant construction.
The main criteria comparison (Table 4) was made by applying the Saaty scale on individual pairs of criteria. Local weights for the main criteria were calculated based on the AHP method. The sub-criteria comparison with calculated local weight for each type of parameters is shown in Appendix A (Table A1, Table A2, Table A3 and Table A4).

Table 4.
Main criteria comparison with local weights.
3. Results
This section describes the results of the research. Since the study area is the entire territory of the Republic of Croatia, and it is not possible to discern the details on the map, an example subset in the Zadar County area was introduced. All analyses (Figure 5 and Figure 6) were performed in the GRASS GIS software (version 7.2.1; Open Source Geospatial Foundation; Chicago; USA) in a spatial resolution of 30 m × 30 m in the official reference coordinate system of the Republic of Croatia HTRS96/TM (EPSG: 3765).
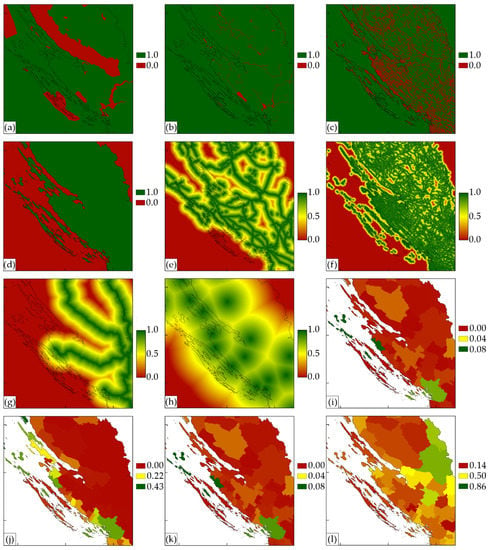
Figure 5.
Spatial and socioeconomic criteria layers: (a) protected areas; (b) water bodies; (c) built-up area; (d) mainland; (e) distance to electricity network; (f) distance to road infrastructure; (g) distance to railway infrastructure; (h) distance to settlements; (i) population; (j) number of tourist nights; (k) electricity consumption; and (l) unemployment.
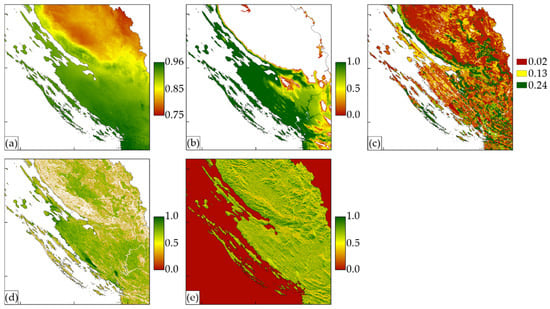
Figure 6.
Climate, land cover and geomorphological layers: (a) GHI; (b) elevation; (c) land cover; (d) slope; (e) orientation.
Using the analytic hierarchy process, the calculated rasters were assigned with weight coefficients, and the sum of all those rasters gives the final raster of optimal locations for the construction of solar power plants in Croatia. To calculate the final raster, the following expression was used:
where:
- —GHI;
- —land cover;
- —slope;
- —orientation;
- —elevation;
- —distance to settlements;
- —distance to electricity network;
- —distance to road infrastructure;
- —distance to railway infrastructure;
- —electricity consumption;
- —population;
- —number of tourist nights; and
- —unemployment.
In order to show the level of suitability for each parameter used in the research, sensitivity analysis was performed, and the results were classified into five categories for each parameter (Figure 7).
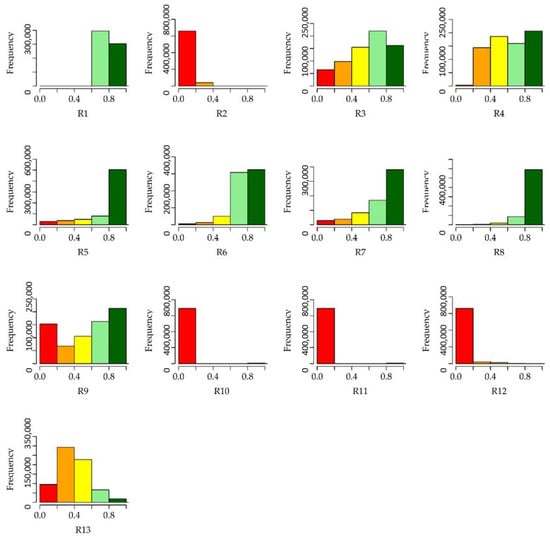
Figure 7.
The sensitivity analysis results of the parameters used in AHP classified into five categories.
In order to test the accuracy of the results obtained with multi-criteria analysis and the subjectivity of the expert judgment, a sensitivity analysis is recommended [30]. The sensitivity analysis made in this research considered the effect of criteria weight changes in three cases [31]:
- Criteria and weights described in this paper (F1, Figure 8a);
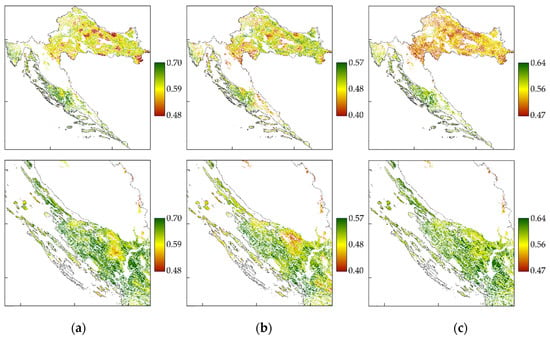 Figure 8. Locations suitable for solar power plant construction in the Republic of Croatia: (a) F1; (b) F2; (c) F3.
Figure 8. Locations suitable for solar power plant construction in the Republic of Croatia: (a) F1; (b) F2; (c) F3. - Criteria described in the paper with equal weights (F2, Figure 8b); and
- Criteria described in the paper and changed weights–lower weight is given to spatial parameters (F3, Figure 8b).
In order to analyze the results of the three cases with locations suitable for solar power plants construction, histograms (Figure 9) of three final rasters (F1, F2 and F3) were created, and statistical indicators were calculated (Table 5).
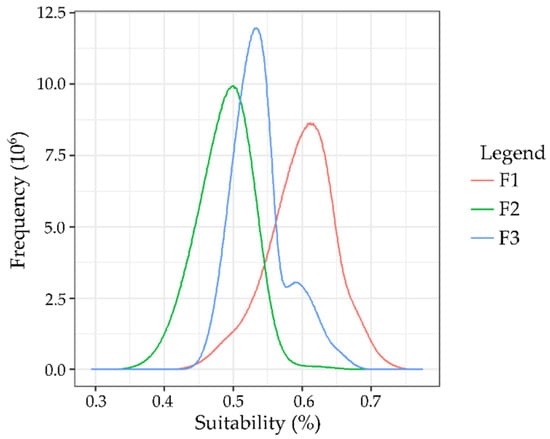
Figure 9.
Final raster histograms for selecting the optimal location for solar power plants construction.

Table 5.
Statistical indicators of the sensitivity analysis results.
In order to show the level of suitability for each of the three cases and final raster, the sensitivity analysis results were classified into five categories (Figure 10).
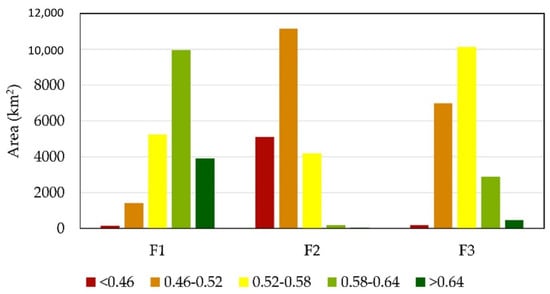
Figure 10.
The sensitivity analysis results of the final three rasters classified into five categories.
To emphasize the importance of each parameter used in the research, the weight ratio of all parameters for F1 raster is shown in Figure 11. The most decisive parameter in determining the optimal solar plant locations that result from this research are GHI (R1), land cover (R2), and distance to electricity network (R7).
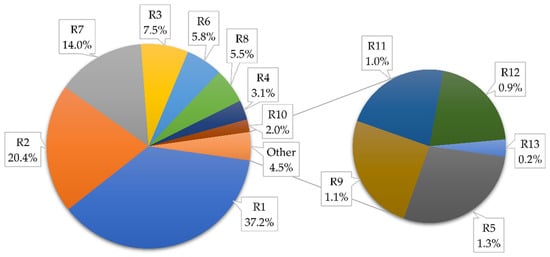
Figure 11.
Influence of all parameter weights on final raster F1.
4. Discussion
The visual analysis of rasters F1, F2, and F3 shows that F2 has the least suitable locations for the solar power plants construction (Figure 8). On the F2 raster, the influence of administrative units, that is, socioeconomic parameters is seen, suggesting that not all parameters have equal influence on determining the optimal location for exploiting the solar potential. Comparison of the F1 and F3 rasters shows that F1 gives better results with no visible impact of the administrative unit boundaries, but areas with a higher number of inhabitants and tourist nights are more suitable for the construction of solar power plants.
It is seen from the histogram (Figure 9) that F2 has the finest spread and the lowest values, and it can be concluded that the multi-criteria decision making applied to F2 and F3 yields better results than the raster with equal weights. Raster F1 has a wider and optimum pixel spread compared to F3 and also has a larger percentage of the most suitable locations for solar power plants construction.
Sensitivity analysis statistical indicators (Table 5) show that raster F3 has the smallest range, which means it gives the worst results compared to the other two rasters. Raster F2 has the lowest minimum and maximum values, so it can be concluded that it is not suitable either. Raster F1 has the highest maximum and mean value as well as a range, which is important for better classification of suitable locations, so compared to the other two rasters, it gives the best results.
From Figure 10, it can be concluded that raster F1 has the most area, 7%, in the highest suitability category, while raster F2 has the least, only 0.05% of the area. The previous results confirm the preceding conclusion that raster F1 gives the best results. It can also be concluded that due to numerous parameters, as well as their rigorous values, 63.5% of the land surface of Croatia is unsuitable for exploiting the solar potential.
Based on the sensitivity analysis statistical indicators, histogram, as well as a visual analysis of the final rasters, it can be concluded that the F1 raster gives the best results for determining optimal locations for exploiting the solar potential and building solar power plants in the Republic of Croatia.
5. Conclusions
The main purpose of this research was to define the parameters needed to determine the potential of solar energy exploitation on the territory of the Republic of Croatia and to apply multi-criteria decision making and geographic information systems to determine the optimal locations for the construction of solar power plants. Open-source software and data were used in this research to ensure repeatability of the research.
The basic parameter for determining the optimal location for solar power plant construction is the value of the solar potential. For research, the previously developed GHI modeling algorithm was used [10]. In addition to climatic (GHI), other important parameters include spatial, environmental, geomorphological, and socioeconomic data, which are being also used by other authors in relevant research [10,31].
The multi-criteria decision-making method AHP defines the weights for each criterion and sub-criterion, and using geographic information systems, the optimal location for solar energy exploitation in the Republic of Croatia is determined. In order to independently confirm the results obtained, sensitivity analysis with two additional cases was made. The second analysis defined equal weights for all parameters, while in the third analysis, the weights of the parameters used in the study were changed, and lower weight was given to spatial parameters.
Based on the statistical analysis of the histogram and the statistical values of the sensitivity analysis, it can be concluded that raster F1 provides optimal results for the solar energy exploitation and the construction of solar power plants in the Republic of Croatia. The parameters with the most influences in determining the optimal solar plant locations that result from this research are GHI, land cover, and distance to the electricity network. It is important to emphasize, based on this research, 63.49% of the area covering the mainland and the islands of the Republic of Croatia is unsuitable for solar energy exploitation. Raster F1 has the highest percentage of area, 7%, in the most suitable category for the exploitation of solar potential and solar power plant construction in the Republic of Croatia according to statistical analysis and area classification into five suitability categories.
Future research should be based on the official national spatial data with higher accuracy, which should produce better results. Since Croatia is obliged to meet the goals set by the Europe 2020 Strategy for smart, sustainable, and inclusive growth, a large number of spatial research intended for determining the potential of renewable energy sources is expected in the forthcoming years.
Author Contributions
Conceptualization, I.G. and M.G.; methodology, I.G.; software, I.G.; validation, I.G. and M.G.; formal analysis, I.G.; investigation, I.G.; writing—original draft preparation, I.G.; writing—review and editing, I.G. and M.G.; visualization, I.G. and M.G.; supervision, I.G. and M.G.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive feedback that has helped to improve the work and its presentation.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Comparison of spatial sub-criteria with local weights.
Table A1.
Comparison of spatial sub-criteria with local weights.
| Sub-Criteria | Settlements | Electricity Network | Road Infrastructure | Railway Infrastructure | Weight Coefficient |
|---|---|---|---|---|---|
| Settlements | 1 | 0.333 | 1 | 7 | 0.220 |
| Electricity network | 3 | 1 | 3 | 9 | 0.529 |
| Road infrastructure | 1 | 0.333 | 1 | 6 | 0.209 |
| Railway infrastructure | 0.143 | 0.111 | 0.167 | 1 | 0.042 |
| λ = 4.107 | Cl = 0.036 | CR = 0.040 | |||

Table A2.
Comparison of land cover sub-criteria with local weights.
Table A2.
Comparison of land cover sub-criteria with local weights.
| Sub-Criteria | Barren Land | Grassland | Bushland | Pastures | Emerging Forests | Agricultural Land | Forest | Wetland | Weight Coefficient |
|---|---|---|---|---|---|---|---|---|---|
| Barren land | 1 | 2 | 2 | 3 | 5 | 7 | 9 | 9 | 0.300 |
| Grassland | 0.5 | 1 | 2 | 3 | 5 | 6 | 7 | 9 | 0.239 |
| Bushland | 0.5 | 0.5 | 1 | 2 | 3 | 5 | 7 | 9 | 0.173 |
| Pastures | 0.333 | 0.333 | 0.5 | 1 | 2 | 3 | 5 | 7 | 0.110 |
| Emerging forests | 0.2 | 0.2 | 0.333 | 0.5 | 1 | 3 | 5 | 7 | 0.083 |
| Agricultural land | 0.143 | 0.167 | 0.2 | 0.333 | 0.333 | 1 | 3 | 5 | 0.049 |
| Forest | 0.111 | 0.143 | 0.143 | 0.2 | 0.2 | 0.333 | 1 | 3 | 0.028 |
| Wetland | 0.111 | 0.111 | 0.111 | 0.143 | 0.143 | 0.2 | 0.333 | 1 | 0.018 |
| λ = 8.704 | Cl = 0.101 | CR = 0.071 | |||||||

Table A3.
Comparison of geomorphology sub-criteria with local weights.
Table A3.
Comparison of geomorphology sub-criteria with local weights.
| Sub-criteria | Slope | Orientation | Elevation | Weight Coefficient |
|---|---|---|---|---|
| Slope | 1 | 3 | 5 | 0.633 |
| Orientation | 0.333 | 1 | 3 | 0.260 |
| Elevation | 0.2 | 0.333 | 1 | 0.106 |
| λ = 3.055 | Cl = 0.028 | CR = 0.048 | ||

Table A4.
Comparison of socioeconomic sub-criteria with local weights.
Table A4.
Comparison of socioeconomic sub-criteria with local weights.
| Sub-Criteria | Electricity Consumption | Population | Number of Tourist Nights | Unemployment | Weight Coefficient |
|---|---|---|---|---|---|
| Electricity consumption | 1 | 2 | 3 | 9 | 0.489 |
| Population | 0.5 | 1 | 1 | 7 | 0.246 |
| Number of tourist nights | 0.333 | 1 | 1 | 7 | 0.225 |
| Unemployment | 0.111 | 0.143 | 0.143 | 1 | 0.040 |
| λ = 4.093 | Cl = 0.031 | CR = 0.034 | |||
References
- UNFCCC. Adoption of the Paris Agreement, FCCC/CP/2015/Add.1; United Nations Framework Convention on Climate Change: Paris, France, 2015. [Google Scholar]
- Camargo, L.R.; Zink, R.; Dorner, W.; Stoeglehner, G. Spatio-temporal modeling of roof-top photovoltaic panels for improved technical potential assessment and electricity peak load offsetting at the municipal scale. Comput. Environ. Urban Syst. 2015, 52, 58–69. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Zhou, J.; Ibrahim, A.N.; Li, M. An open-source 3D solar radiation model integrated with a 3D Geographic Information System. Environ. Model. Softw. 2015, 64, 94–101. [Google Scholar] [CrossRef]
- Šúri, M.; Hofierka, J. A new GIS-based solar radiation model and its application to photovoltaic assessments. Trans. GIS 2004, 8, 175–190. [Google Scholar] [CrossRef]
- Martins, F.R.; Pereira, E.B.; Abreu, S.L. Satellite-derived solar resource maps for Brazil under SWERA project. Sol. Energy 2007, 81, 517–528. [Google Scholar] [CrossRef]
- Amillo, A.G.; Huld, T.; Müller, R. A new database of global and direct solar radiation using the eastern meteosat satellite, models and validation. Remote Sens. 2014, 6, 8165–8189. [Google Scholar] [CrossRef]
- Huld, T. PVMAPS: Software tools and data for the estimation of solar radiation and photovoltaic module performance over large geographical areas. Sol. Energy 2017, 142, 171–181. [Google Scholar] [CrossRef]
- Hofierka, J.; Šúri, M. The solar radiation model for Open source GIS: Implementation and applications. In Proceedings of the Open Source GIS-GRASS Users Conference, Trento, Italy, 11–13 September 2002; pp. 51–70. [Google Scholar]
- Hofierka, J.; Kaňuk, J.; Gallay, M. The spatial distribution of photovoltaic power plants in relation to solar resource potential: The case of the Czech Republic and Slovakia. Morav. Geogr. Rep. 2014, 22, 26–33. [Google Scholar] [CrossRef]
- Gašparović, I.; Gašparović, M.; Medak, D. Determining and analysing solar irradiation based on freely available data: A case study from Croatia. Environ. Dev. 2018, 26, 55–67. [Google Scholar] [CrossRef]
- Sanchez-Lozano, J.M.; Teruel-Solan, J.; Soto-Elvira, P.L.; Socorro García-Cascales, M. Geographical Information Systems (GIS) and Multi-Criteria Decision Making (MCDM) methods for the evaluation of solar farms locations: Case study in southeastern Spain. Renew. Sustain. Energy Rev. 2013, 24, 544–556. [Google Scholar] [CrossRef]
- Uyan, M. GIS-based solar farms site selection using analytic hierarchy process (AHP) in Karapinar region, Konya/Turkey. Renew. Sustain. Energy Rev. 2013, 28, 11–17. [Google Scholar] [CrossRef]
- Asakereh, A.; Omid, M.; Alimardani, R.; Sarmadian, F. Developing a GIS-based Fuzzy AHP Model for Selecting Solar Energy Sites in Shodirwan Region in Iran. Int. J. Adv. Sci. Technol. 2014, 68, 37–48. [Google Scholar] [CrossRef]
- Tahri, M.; Hakdaoui, M.; Maanan, M. The evaluation of solar farm locations applying Geographic Information System and Multi-Criteria Decision-Making methods: Case study in southern Morocco. Renew. Sustain. Energy Rev. 2015, 51, 1354–1362. [Google Scholar] [CrossRef]
- Georgiou, A.G.; Skarlatos, D. Optimal site selection for sitting a solar park using multi-criteria decision analysis and geographical information systems. Geosci. Instrum. Methods 2016, 5, 321–332. [Google Scholar] [CrossRef]
- Weng, Q. Remote Sensing and GIS Integration: Theories, Methods, and Applications: Theory, Methods, and Applications; McGraw-Hill Education: New York, NY, USA, 2009. [Google Scholar]
- Broesamle, H.; Mannstein, H.; Schillings, C.; Trieb, F. Assessment of solar electricity potentials in North Africa based on satellite data and a geographic information system. Sol. Energy 2001, 70, 1–12. [Google Scholar] [CrossRef]
- Fluri, T. The potential of concentrating solar power in South Africa. Energy Policy 2009, 37, 5075–5080. [Google Scholar] [CrossRef]
- Clifton, J.; Boruff, B.J. Assessing the potential for concentrated solar power development in rural Australia. Energy Policy 2010, 38, 5272–5280. [Google Scholar] [CrossRef]
- Lehman, R.G. Concentrated Solar Thermal Facilities: A GIS Approach for Land Planning. Master’s Thesis, University of Southern California, Los Angeles, CA, USA, May 2011. [Google Scholar]
- Gade, P.K.; Osuri, M. Evaluation of Multi Criteria Decision Making Methods for Potential Use in Application Security. Master’s Thesis, School of Computing Blekinge Institute of Technology, Karlskrona, Sweden, May 2014. [Google Scholar]
- Triantaphyllou, E. Multi-Criteria Decision Making Methods: A Comparative Study; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Jankowski, P. Integrating geographical information systems and multiple criteria decision-making methods. Int. J. Geogr. Inf. Sci. 1995, 9, 251–273. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Ramanathan, R.; Ganesh, L. Energy resource allocation incorporating qualitative and quantitative criteria: An integrated model using goal programming and AHP. Socioecon. Plan. Sci. 1995, 29, 197–218. [Google Scholar] [CrossRef]
- Ishizaka, A.; Labib, A. Analytic hierarchy process and expert choice: Benefits and limitations. OR Insight 2009, 22, 201–220. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Srđević, B.; Suvočarev, K.; Srđević, Z. Analitički hijerarhijski proces: Individualna i grupna konzistentnost donosilaca odluka. Vodoprivreda 2009, 41, 13–21. [Google Scholar]
- Cameron, D.R.; Cohen, B.S.; Morrison, S.A. An approach to enhance the conservation-compatibility of solar energy development. PLoS ONE 2012, 7, e38437. [Google Scholar] [CrossRef] [PubMed]
- Gašparović, I. Geospatial Analysis of Solar Energy Potential in the Republic of Croatia Using Multi-Criteria Decision Making. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, November 2018. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).