Spaceborne GNSS-R Observation of Global Lake Level: First Results from the TechDemoSat-1 Mission
Abstract
1. Introduction
2. Data and Methods
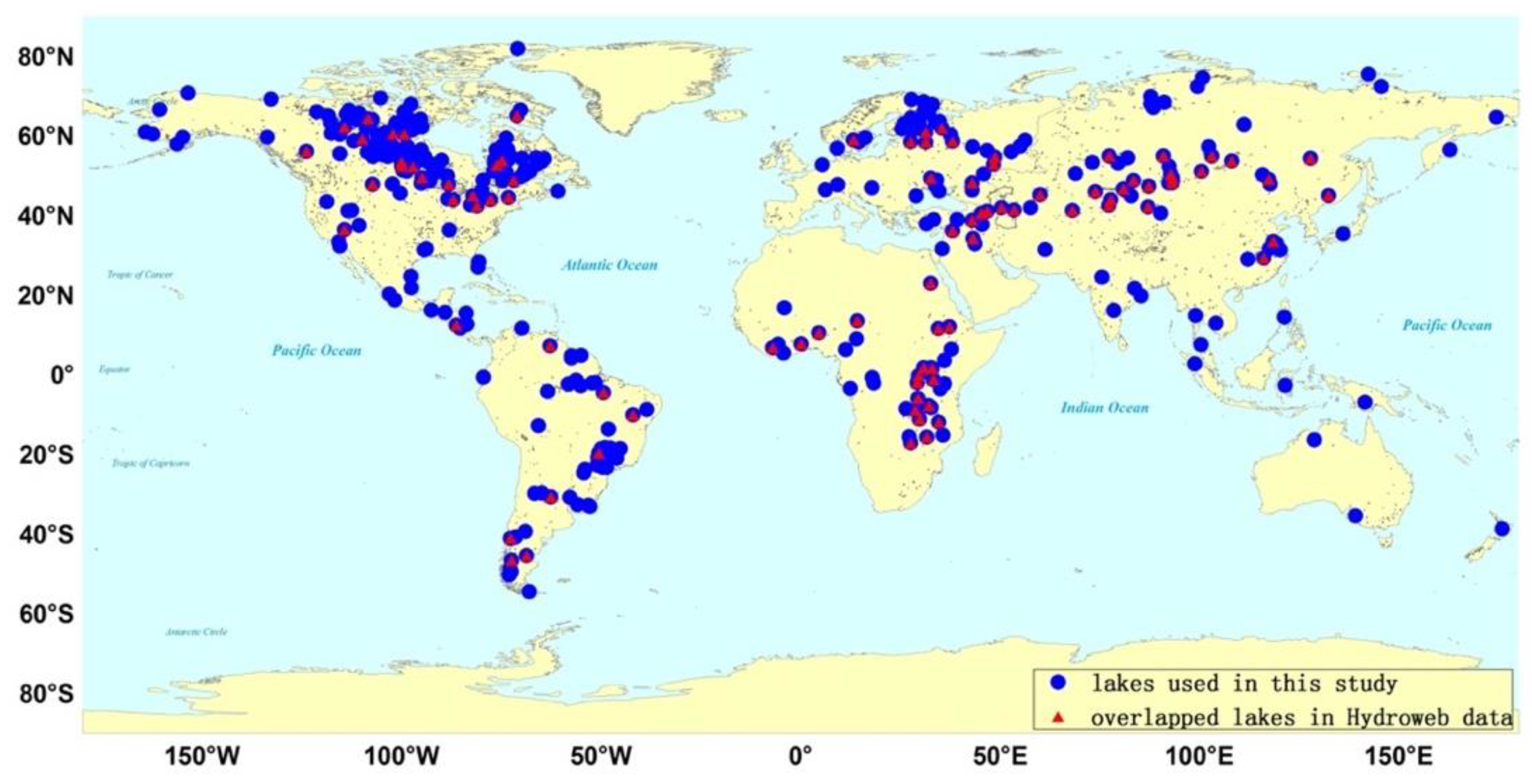
2.1. Data Description
2.2. Data Preprocessing
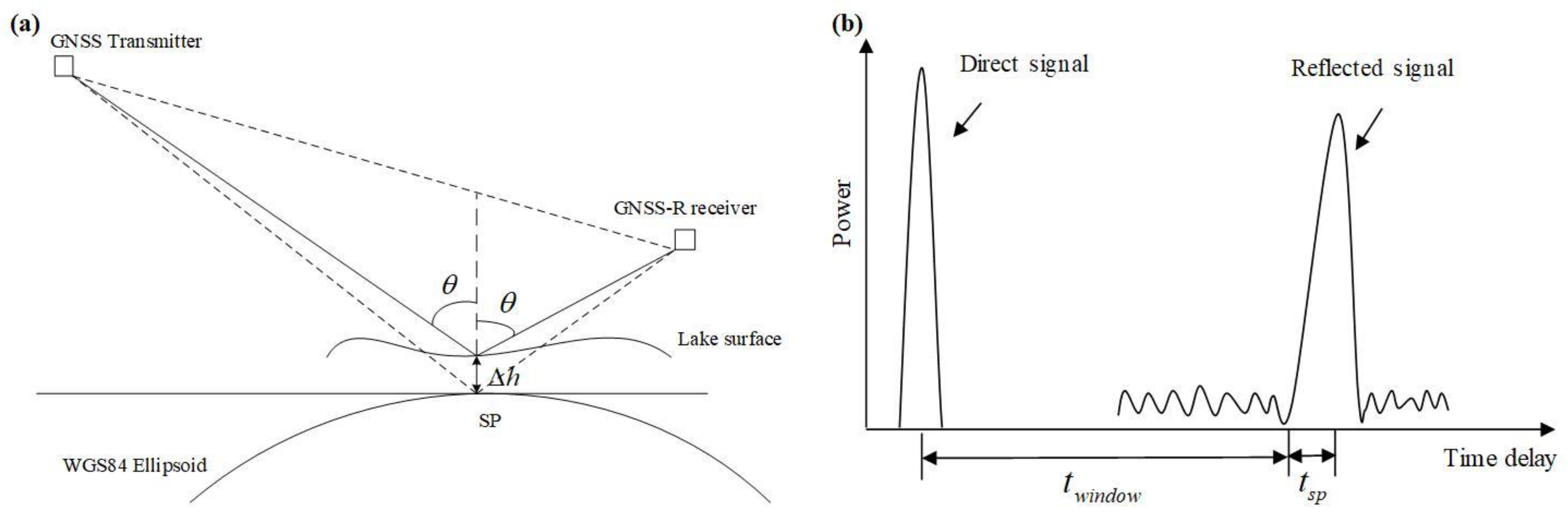
2.3. Lake Level Retrieval
3. Results and Discussions
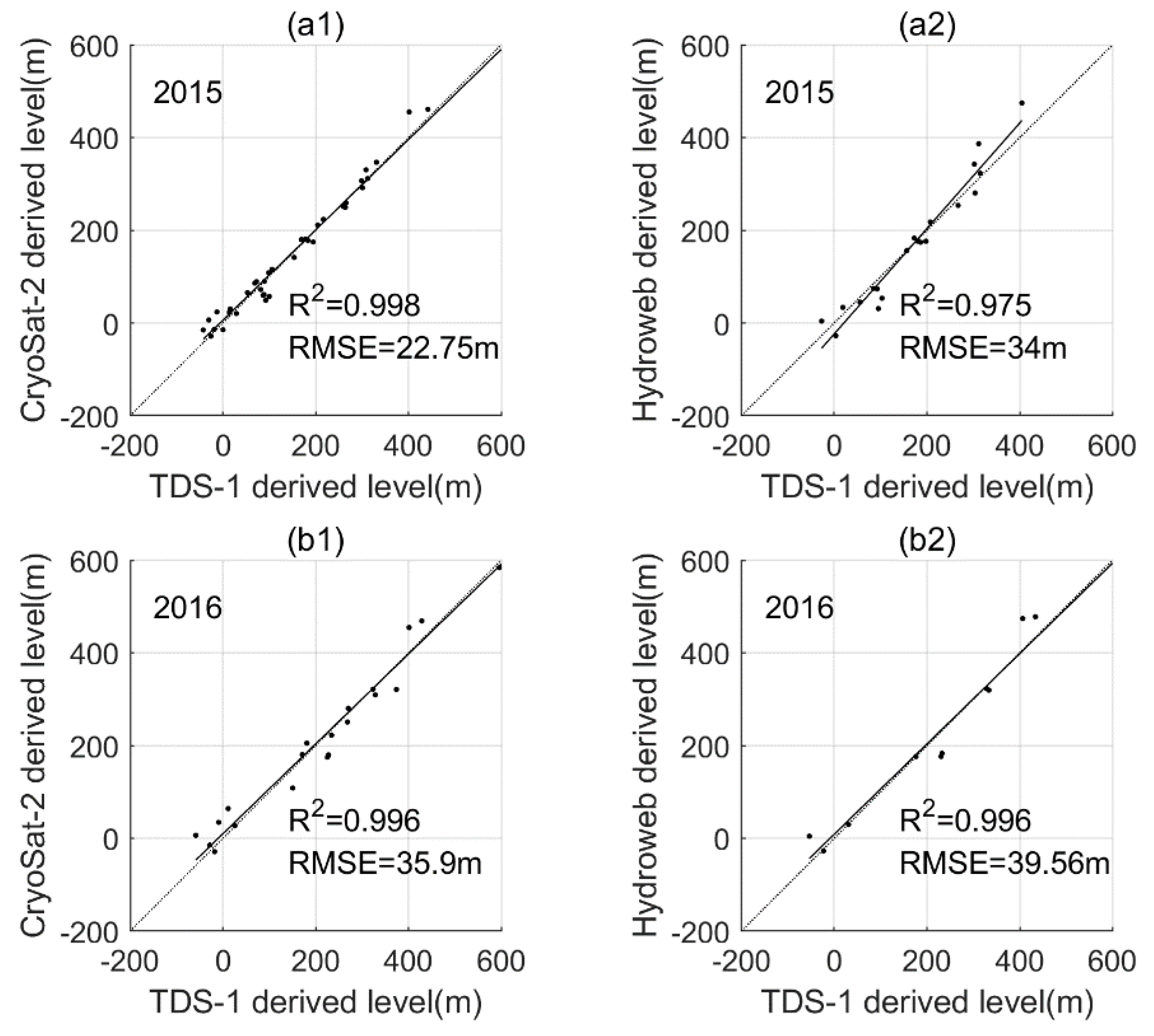
3.1. Overall Evaluations and Comparisons
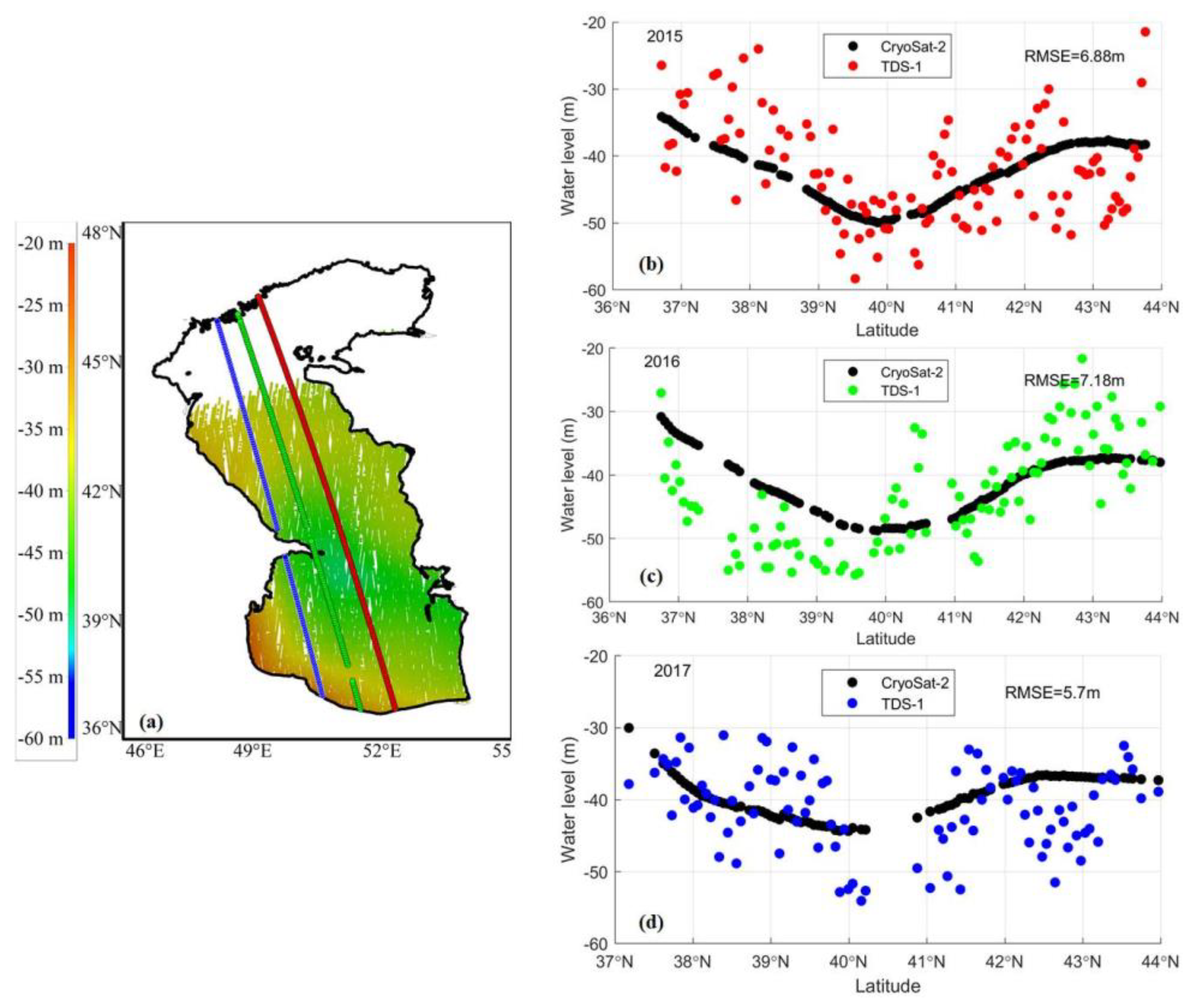
3.2. Spatial and Temporal Analyses
3.3. Limitations of the Data and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wan, W.; Liu, B.; Zeng, Z.; Chen, X.; Wu, G.; Xu, L.; Chen, X.; Hong, Y. Using CYGNSS Data to Monitor China’s Flood Inundation during Typhoon and Extreme Precipitation Events in 2017. Remote Sens. 2019, 11, 854. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Fabra, F.; Li, W.; Ribó, S.; Hernández-Pajares, M. Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1. Remote Sens. 2017, 9, 742. [Google Scholar] [CrossRef]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Chew, C.; Reager, J.T.; Small, E. CYGNSS data map flood inundation during the 2017 Atlantic hurricane season. Sci. Rep. 2018, 8, 9336. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Zhao, L.; Xie, H.; Liu, B.; Li, H.; Cui, Y.; Ma, Y.; Hong, Y. Lake surface water temperature change over the Tibetan Plateau from 2001–2015: A sensitive indicator of the warming climate. Geophys. Res. Lett. 2018, 45, 11–77. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Seasonal and abrupt changes in the water level of closed lakes on the Tibetan Plateau and implications for climate impacts. J. Hydrol. 2014, 514, 131–144. [Google Scholar] [CrossRef]
- Song, C.; Ye, Q.; Sheng, Y.; Gong, T. Combined ICESat and CryoSat-2 Altimetry for Accessing Water Level Dynamics of Tibetan Lakes over 2003–2014. Water 2015, 7, 4685–4700. [Google Scholar] [CrossRef]
- Biancamaria, S.; Andreadis, K.M.; Durand, M.; Clark, E.A.; Rodriguez, E.; Mognard, N.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Oudin, Y. Preliminary Characterization of SWOT Hydrology Error Budget and Global Capabilities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 6–19. [Google Scholar] [CrossRef]
- Yu, K.; Rizos, C.; Dempster, A. GNSS-Based Model-Free Sea Surface Height Estimation in Unknown Sea State Scenarios. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1424–1435. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Lowe, S.; Zuffada, C.; Chao, Y. 2-cm GPS altimetry over Crater Lake. Geophys. Res. Lett. 2001, 22, 4343–4346. [Google Scholar] [CrossRef]
- Bai, W.; Sun, Y.; Fu, Y.; Zhu, G.; Du, Q.; Zhang, Y.; Han, Y.; Cheng, C. GNSS-R open-loop difference phase altimetry: Results from a bridge experiment. Adv. Space Res. 2012, 50, 1150–1157. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Lake Level and Surface Topography Measured with Spaceborne GNSS-Reflectometry From CYGNSS Mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 13332–13341. [Google Scholar] [CrossRef]
- Jales, P.; Unwin, M. MERRByS Product Manual: GNSS-Reflectometry on TDS-1 with the SGR-ReSI; Surrey Satellite Technology Limited: Guildford, UK, 2016; p. 23. [Google Scholar]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Mayer, V. CryoSat-2 for Hydrological Purposes: Data Processing, Visualization and Analysis. Bachelor’s Thesis, University of Stuttgart, Stuttgart, Germany, 2013. [Google Scholar]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Unwin, M.; Jales, P.; Tye, J.; Roselló, J. An Assessment of Non-geophysical Effects in Spaceborne GNSS Reflectometry Data from the UK TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3418–3429. [Google Scholar] [CrossRef]
- Garrison, J.L.; Katzberg, S.J. The Application of Reflected GPS Signals to Ocean Remote Sensing. Remote Sens. Environ. 2000, 73, 175–187. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martín-Neira, M.; Fabra, F.; Nogués-Correig, O.; Ribó, S.; Kainulainen, J.; Camps, A.; Addio, S.D. Consolidating the Precision of Interferometric GNSS-R Ocean Altimetry Using Airborne Experimental Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global Ocean Altimetry With GNSS Reflections From TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- Wan, W.; Xiao, P.; Feng, X.; Li, H.; Ma, R.; Duan, H.; Zhao, L. Monitoring lake changes of Qinghai-Tibetan Plateau over the past 30 years using satellite remote sensing data. Chin. Sci. Bull. 2014, 59, 1021–1035. [Google Scholar] [CrossRef]
- Hoque, M.; Jakowski, N. Ionospheric Propagation Effects on GNSS Signals and New Correction Approaches. In Global Navigation Satellite Systems—Signal, Theory and Applications; InTech: Rijeka, Croatia, 2012; pp. 381–426. ISBN 978-953-307-843-4. [Google Scholar]
- Martin-Neira, M.; Addio, S.D.; Buck, C.; Floury, N.; Prieto-Cerdeira, R. The PARIS Ocean Altimeter In-Orbit Demonstrator. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2209–2237. [Google Scholar] [CrossRef]
- Li, Z.; Zuffada, C.; Lowe, S.; Lee, T.; Zlotnicki, V. Analysis of GNSS-R Altimetry for Mapping Ocean Mesoscale Sea Surface Heights Using High-Resolution Model Simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4631–4632. [Google Scholar] [CrossRef]
- Zuffada, C.; Li, Z.; Nghiem, S.V.; Lowe, S.; Shah, R.; Clarizia, M.P.; Cardellach, E. The rise of GNSS reflectometry for Earth remote sensing. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5111–5114. [Google Scholar]
- Camps, A.; Park, H.; Domènech, E.V.i.; Pascual, D.; Martin, F.; Rius, A.; Ribo, S.; Benito, J.; Andrés-Beivide, A.; Saameno, P.; et al. Optimization and Performance Analysis of Interferometric GNSS-R Altimeters: Application to the PARIS IoD Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1436–1451. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Ribó, S.; Martín-Neira, M. Revisiting the GNSS-R Waveform Statistics and Its Impact on Altimetric Retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Cardellach, E.; Wickert, J.; Baggen, R.; Benito, J.; Camps, A.; Catarino, N.; Chapron, B.; Dielacher, A.; Fabra, F.; Flato, G.; et al. GNSS Transpolar Earth Reflectometry exploriNg System (G-TERN): Mission Concept. IEEE Access 2018, 6, 13980–14018. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Li, W.; Andrés-Beivide, A.; Ballesteros-Sels, X. “Cookie”: A Satellite Concept for GNSS Remote Sensing Constellations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4593–4610. [Google Scholar] [CrossRef]
- Høeg, P.; Fragner, H.; Dielacher, A.; Zangerl, F.; Koudelka, O.; Høeg, P.; Wickert, J. PRETTY: Grazing altimetry measurements based on the interferometric method. In Proceedings of the 5th Workshop on Advanced RF Sensors and Remote Sensing Instruments, ARSI’17, Noordwijk, The Netherlands, 12–14 September 2017. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Wan, W.; Chen, X.; Zhu, S.; Liu, B.; Hong, Y. Spaceborne GNSS-R Observation of Global Lake Level: First Results from the TechDemoSat-1 Mission. Remote Sens. 2019, 11, 1438. https://doi.org/10.3390/rs11121438
Xu L, Wan W, Chen X, Zhu S, Liu B, Hong Y. Spaceborne GNSS-R Observation of Global Lake Level: First Results from the TechDemoSat-1 Mission. Remote Sensing. 2019; 11(12):1438. https://doi.org/10.3390/rs11121438
Chicago/Turabian StyleXu, Liwen, Wei Wan, Xiuwan Chen, Siyu Zhu, Baojian Liu, and Yang Hong. 2019. "Spaceborne GNSS-R Observation of Global Lake Level: First Results from the TechDemoSat-1 Mission" Remote Sensing 11, no. 12: 1438. https://doi.org/10.3390/rs11121438
APA StyleXu, L., Wan, W., Chen, X., Zhu, S., Liu, B., & Hong, Y. (2019). Spaceborne GNSS-R Observation of Global Lake Level: First Results from the TechDemoSat-1 Mission. Remote Sensing, 11(12), 1438. https://doi.org/10.3390/rs11121438





