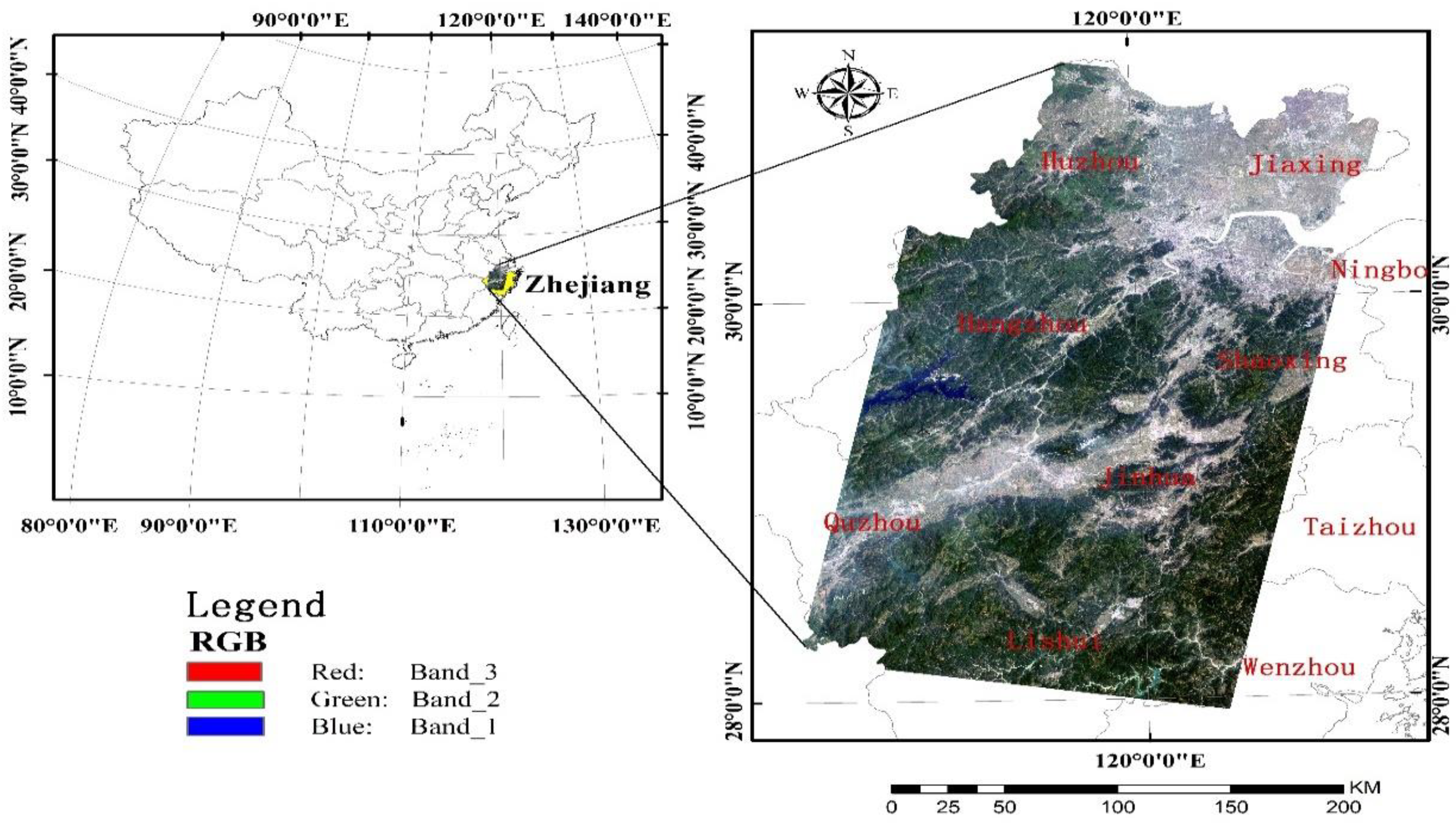
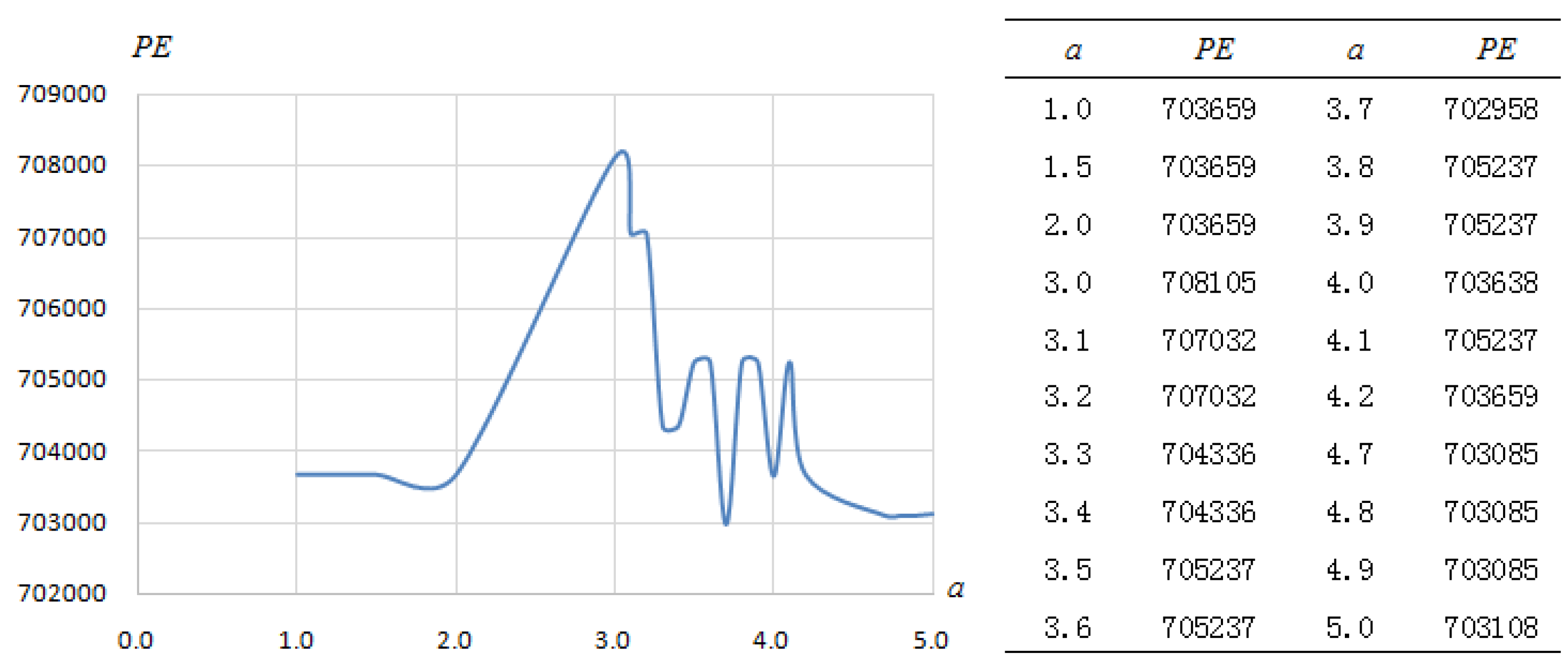
1. Introduction
The importance of forest ecosystem services function has been universally acknowledged, especially in that it plays an important role in maintaining global carbon balance. Deforestation and conversion of forestland use types can cause carbon emissions to the atmosphere, thereby influencing the global climate as well as environmental changes [
1,
2,
3,
4,
5]. Forest biomass accounts for about 90% of the global terrestrial vegetation biomass, which is not only an important indicator of forest carbon sequestration capacity, but also an important parameter for assessing forest carbon budget [
6,
7,
8]. Under the current situation that global climate change has attracted common attention, ecosystem function requires accurate forest biomass estimation and its dynamic changes [
9].
Total forest biomass includes aboveground biomass (AGB) and underground biomass. As a result of the difficulty in collecting field survey data for underground biomass, most of the biomass research is concentrated in the above-ground biomass segment [
10]. There are many ways to estimate forest biomass. The most accurate method is on the basis of on-site measurements, but the labor costs and economic costs of on-site measurement are too high, and are not suitable for large-area census [
11,
12,
13]. In order to meet large-area forest biomass surveys, currently an effective rapid estimation method is the forest AGB survey which combines remote sensing images and plot data. Roy et al. [
14] used multiple regression equations of brightness and humidity to predict biomass. Næsset et al. [
15] used a log-transformed linear regression model to match the linear relationship between lidar variables and ground biomass. Zheng et al. [
16] used multiple regression analysis to couple the AGB values which are obtained from the field measurements of the DBH to the various vegetation indices derived from the landsat 7 ETM+ data, thereby generating an initial biomass map. Sun et al. [
17] used the airborne lidar and SAR data and used Stepwise regression (SR) to select and predict variables in the study of Howland, Maine, USA, which gradually selected the high index of laser vegetation imaging sensor (LVIS) data of rh50 and rh75. Kumar et al. [
18] combined multi-level statistical techniques for IRS P-6 LISS III satellite data to estimate biomass. Based on Landsat TM, ALOS PALSAR data, Gao et al. [
19] used parameters, non-parametric and machine learning methods to conduct forest biomass research and found that the linear regression method was still an important tool for AGB modeling, especially the AGB range of 40–120 Mg/Ha; he also found that machine learning and nonparametric algorithms have limited effectiveness in improving AGB estimates within this range. Zhao et al. [
20] used TM, PALSAR, image band and texture information as alternative variables in their research, and used the multivariate SR method to establish the biomass estimation model.
Among the methods of estimating biomass using remote sensing technology, the linear regression model is one of the important methods. Remote sensing data contains many potential variables that can be used for the estimation modeling of biomass, which includes multi-spectral and even hyperspectral data, vegetation indices derived from spectral data, texture data. In addition, terrain data, meteorological data, etc. can also be used for the construction of models. A large number of variables bring difficulties to the construction of linear regression models. Some variables can be recognized as not important variables and then be removed through some preliminary analyses. Some variables perform well when tested singly. However, it is not necessary to bring them all into the model because they are highly correlated to each other. Since the correlation between variables is high, it is easy to result in the problems such as serious collinearity, the difficulty in the selection of important variables, the model is not concise, and the prediction results are unstable. How to choose variables and to build a simple, stable and accurate model is an important issue in the construction of remote sensing biomass models. At present, many methods have been put forward to deal with the problem of collinearity and variable selection encountered in the construction of linear models. Some of these methods are commonly used in the construction of biomass models, such as SR, and others have not appeared in the report about the construction of biomass models. This paper uses some important methods, which are put forward by the predecessors to overcome the collinearity and solve the variable selection problem, to conduct biomass modeling and compare their ability in the construction of biomass models.
The current linear model variable selection methods can be generally divided into two categories. One category is the subset selection, such as SR, a method of this category selects a so-called optimal subset (according to a certain criterion, see
Section 4.3) from the original variable set. Parameters in the final model established by a subset selection method are the same as estimated by ordinary least square (OLS) according to the variable subset. The other category is the coefficient shrink, which has almost no application in biomass modeling, such as the Lasso (Least Absolute Shrinkage and Selection Operator) method. The principle of it is generally to add a penalty function to the objective function and reduce the number of variables of the model by shrinking the coefficients corresponding to the variables. Parameters in the final model established by a coefficient shrink method are different from the parameters estimated by OLS according to the final variable subset.
At present, the methods of coefficient shrink are widely used in other disciplines and fields. For example, Fujino et al. [
21] used a variety of regression models to predict the future improvement of visual acuity in glaucoma patients. It is found that the prediction error (PE) of the Lasso method is smaller than that of OLS when the sample size is small. In order to accurately predict the cost of highway project construction and prevent the cost from rising, a parameterized cost estimation model is developed. Zhang et al. [
22] found that the model obtained by the LASSO method is easier to understand, and that the average absolute error, average absolute percent error and root mean square error of the Lasso model are better than that of the OLS method. Roy et al. [
23] predicted the change of Goldman Sachs Group Inc stock price based on the Lasso method. The prediction effect of the Lasso model is better than that of the ridge regression (RR) model. Maharlouei et al. [
24] used AdaLasso (Adaptive Least Absolute Shrinkage and Selection Operator) to perform multivariate regression analysis on the effect of exclusive breast-feeding time on Iranian infants. The results show that AdaLasso has more advantages than RR in the complexity and prediction accuracy of the model compared with RR in the presence of a large number of variables. Shahraki et al. [
25] used two regression models, AdaLasso and RR, to study the main factors affecting death after liver transplantation. The results showed that AdaLasso was superior to the traditional regression model as a punishment model. Zhang et al. [
26] used the Lasso, AdaLasso, SCAD (Smoothly Clipped Absolute Deviation) model to select the parameters of the key indexes in the process of cigarette drying and to determine the best drying method. The coefficient shrink method is superior to the traditional SR method, and the SCAD method is the best. In these studies, the coefficient shrink model performs better than the traditional linear regression model, which shows that the coefficient shrink method is more powerful in the selection of variables and parameter estimation.
In this paper, four subset selection methods (SR, BIC (Bayesian Information Criterion), AIC (Akaike Information Criterion) and CP criterion) and four coefficient shrink methods (LASSO, ADALASSO, SCAD and NNG (Non-Negative garrote) are compared. In addition, OLS and Ridge Regression (RR) are also added to the comparison. As the most basic parameter estimation method of the linear regression model, OLS can be used to estimate the variances of parameters. Therefore, the significance of single parameter can be tested by the t-test, and the importance of corresponding variables can be known. Sometimes it can also be used to explain the choice of variables. However, because of the existence of correlation between variables, the importance of such variables is not very helpful in selecting variables. In practical applications, it is seldom directly based on the significance of a single variable to select variables, especially when the number of variables is large. In addition, SR is based on an objective function that is similar to that of OLS, and to automatically search for an optical subset through some tests under some criteria. However, it is already called another method. So this paper classifies OLS into a class of methods without variable selection capability. RR is specifically for collinearity and has no variable selection capability.
These methods have different purposes in common applications. The purpose of four subset selection methods and four coefficient shrink methods is to select variable subsets. The purpose of OLS is to directly estimate parameters after the variable set has been determined and it is assumed to be free of collinearity, while the purpose of RR is to directly estimate parameters after the variable set has been determined and the variables have serious collinearity.
The purpose of the paper is to introduce various model establishment methods with variable selection capability, so that one could have more choices when establishing a similar model, and one could know how to select the most appropriate and effective method for a specific issue.
6. Discussion
The linear regression models are often used in quantitative remote sensing, but usually there are too many variables, and the correlation between variables is high, which brings difficulties to model development and model application. Among these applications, in addition to model accuracy, the ability of the estimation method in terms of variable selection also needs to be considered. This paper takes the quantitative estimation of biomass on the aboveground biomass as an example, and comprehensively considers the conventional precision indicators, PE, ME, model parameter stability, variable selection stability and variable selection ability, and conducts comparative study on the 10 common parameter estimation/variable selection methods. Research data includes Landsat TM data, its derived texture data, and field plot biomass data measured in the sample field. As an article that specially focuses on variable selection methods, the number of variables selected by each method is an important factor that needs consideration. Since the mean of variables selected is quite different, the analysis of adjustment of the degree of freedom was made in this paper.
(1) About OLS and RR. RR completely lacks variable selection ability, and OLS is not used in variable selecting generally. They are mainly used to compare with other methods that have variable selection ability in this paper. If the six indicators involving
R2, RMSE, RMSEr, PE, ME and ME/PE were taken into consideration, RR had the best performance among the ten methods and OLS was listed in the third before adjustment of the degree of freedom; and after adjustment, RR was listed 4th place and OLS took the 7th place. According to the significance test of
R2,
,
. RR has obvious advantages, while OLS lacks obvious advantages before we adjust the degree of freedom. After the adjustment of the degree of freedom,
,
. So, it can be found that after adjustment, RR’s advantages were weakened obviously, while OLS completely has no advantage, having only the same accuracy as the other two methods. In terms of parameter stability, RR takes the first place and OLS is ranked as No.7. Although RR has higher parameter stability, its precision performance is not outstanding, while OLS has no obvious advantages in any aspect. OLS is easily subject to collinearity effect, so it is not applied in the case of many variables and severe collinearity. Studies on other fields also show that OLS is inferior to the coefficient shrink method in the prediction accuracy, RMSE, etc. [
21,
22,
26]. Although RR has anti-collinearity ability, it completely lacks variable selection ability. Main variables among lots of variables can’t be found by the RR method, meanwhile, a model can’t be simplified, so RR is also not applicable. RR is far inferior to coefficient shrink and subset selection methods in reducing of complexity of the model. These issues have been demonstrated in the previous studies [
23,
24,
25,
26].
The following discussion doesn’t cover RR and OLS, and we only consider situations that involve the adjustment of the degree of freedom.
Conclusion on a general analysis of frequently-used evaluation indicators and PE. Through the comprehensive analysis of indicators including R2, RMSE, RMSEr, PE, ME, ME/PE, etc., it can be found that BIC> ADALASSO> LASSO> AIC> SCAD>SR>NNG>Cp; BIC is the best, and Cp, NNG and SR are relatively poor.
Significance test of the coefficient of determination difference. Here we see , the three former coefficients are significantly superior to the later four coefficients at the level of 0.01 or 0.05. There are no significant differences among the former three coefficients, and the same among the latter four coefficients. In addition, , .
Stability of model coefficients. Through the analysis of the ratio of variance within parameters to that among parameters based on the same method, a conclusion can be drawn that BIC > LASSO > ADALASSO > SR > SCAD > AIC > NNG > Cp. Stability of coefficients reflects changes of parameters found when models were established based on data having differences through a method. Higher stability means small changes, and lower stability means big changes. A good method should have high parameter stability.
Variable selection stability. Through the analysis of the ratio of variance of indicative data within parameters to that of indicative data among parameters based on the same method, it can be drawn that BIC > SR > LASSO > SCAD > ADALASSO > AIC > Cp > NNG. Variable selection stability reflects changes of explanatory variables selected when models were constructed based on data having differences through a method. Higher stability indicates higher possibility that the same variables are selected when models are constructed based on data having differences. Low stability indicates big changes in variable selecting. A good method should have high variable selection stability.
Variable selection ability. Through the analysis of the number and changes of explanatory variables used to construct models by different methods, and comparison of the mean, median, maximum, minimum, range and standard deviation of number of variables, these eight methods can be ranked as BIC > SR > Cp > ADALASSO > AIC > SCAD > LASSO > NNG. The mean of number of variables is between 2.32 and 10.06; the median is between two and 10; the maximum value is between three and 21; the minimum value is between two and six; the range is from one to 19; the standard deviation is between 0.4712 and 4.9132. All indicators under the BIC method are the best, number of variables is 2–3, and the range is one. The BIC method is the optimization of AIC. In terms of penalty, when n > 8, k ln(n) > 2k, so BIC gives more penalty to model parameters than AIC when there exists a large amount of data. This leads to that BIC tends to choose a simple model with a small number of variables. NNG has the worst performance. The number of variables selected by this method is up to 21, the minimum number is only two, and the range reaches 19. Overall, the variable selection ability of the subset selection method is stronger than the coefficient shrink method.
Comprehensive evaluation of the eight methods having variable selection ability. Sequence numbers of each method in each indicator are shown in
Table 10. According to the evaluation sequence number, BIC gives the best performance, and it takes the first place in terms of all indicators. Overall, NNG, Cp and AIC perform badly. Performance of other methods evaluated through various indicators is quite different. ADALASSO is good in terms of accuracy, but it is just Ok in the aspects of variable stability and variable selection ability. LASSO is particularly poor in terms of variable selecting, but it is not bad in other aspects. SCAD has a weak overall performance. SR has stronger ability to choose variables, but it has bad performance in terms of common performance. There are no significant differences in prediction accuracy and other indicators according to the study results. From this point of view, variable selection ability is a factor that should be given much more attention, so SR, as a common method, is used frequently due to its strong ability to choose variables. Among the eight methods, only BIC and AIC are both based on the Maximum Likelihood Estimation. AIC performs not as good as BIC does and the reason maybe the different penalty function. The best BIC performance may be related to the maximum likelihood estimate and its penalty function.
In 400 (8 × 5 × 10) experiments of eight methods with variable selection ability in five ten-fold cross validations, explanatory variables B7, B7_W9_CC and B7_W5_ME are mostly used, which are the short-wave infrared band and two texture features of the short-wave infrared band. From this, it can be known that the short-wave infrared band and its special texture features play an important role in the estimation of forest biomass. In the estimation model of biomass, a short-wave infrared band is more important than a visible-light band because the former is more sensitive to humidity and shadow information in the structure of forest, and atmospheric condition has a smaller influence on it, in comparison with other bands (e.g., visible light band and near infrared band).
7. Conclusions
By comparing four methods of subset selection and four methods of compression coefficients with variable selection ability, and OLS and RR without variable selection ability, the following conclusions are obtained:
RR has high parameter stability and anti-multicollinearity ability, but its accuracy performance is not outstanding, OLS has no obvious advantages in any aspect. Both methods lack the ability to select variables, so they are not applicable when there are many variables.
By comparing the R2, RMSE, RMSEr, PE, ME and ME/PE indicators, the order of performance is as follows: BIC> ADALASSO> LASSO> AIC> SCAD>SR>NNG>Cp.
By comparing the differences in the significance of coefficients of determination, the result is as follows, , and .
Comparing the stability of the coefficients of models, the following result is obtained: BIC > LASSO > ADALASSO > SR > SCAD > AIC > NNG > Cp.
Comparing the stability of variable selection, the following result is obtained, BIC > SR > LASSO > SCAD > ADALASSO > AIC > Cp > NNG.
Comparing the capability of variable selection, the following result is obtained: BIC>SR> Cp> ADALASSO> AIC> SCAD> LASSO> NNG.
Comprehensive evaluation of eight methods with variable selection ability. The BIC method has shown the best performance, while NNG, Cp, and AIC were generally poor. Other methods have a large difference in performance on each indicator. ADALASSO performs well in terms of accuracy, but performs not so bad in terms of variable stability and variable selection capability. LASSO is particularly poor in terms of variable selection, but relatively well in other aspects. SCAD is also weak overall; however, it is poor in common indicators. Variable selection ability is a factor that should be given much more attention, so SR, as a common method, is used frequently due to its strong ability to choose variables.
The most frequently selected variables are B7, B7_W9_CC and B7_W5_ME, which are the short-wave infrared and two texture features of short-wave infrared, respectively. It can be seen that the short-wave infrared band and its texture features are important in forest biomass estimation.
In this paper, the model construction methods are evaluated by five categories of indicators: Commonly used indicators, prediction error and model error, model parameter stability, variable selection stability and variable selection ability. For the same method, different indicators may have different performance, which brings difficulties to the method selection. Therefore, comprehensive consideration is needed. For one method, its advantage is particularly obvious on a certain indicator, or the disadvantage is particularly obvious. Such an indicator needs to be given more attention. You can give priority to this method or give up the method. On the contrary, there is no obvious advantage or disadvantage in a certain indicator, so one does not need to pay too much attention on such an indicator, that is, such an indicator has little effect on the selection of methods. In addition, we can consider the main indicators based on the needs. For example, when the main purpose is to choose a simpler model, we can pay more attention to variable selection ability, variable selection stability and model parameter stability, etc. The other indicators are only for reference.