Semantic Segmentation of SLAR Imagery with Convolutional LSTM Selectional AutoEncoders

Abstract

We present a method to detect maritime oil spills from Side-Looking Airborne Radar (SLAR) sensors mounted on aircraft in order to enable a quick response of emergency services when an oil spill occurs. The proposed approach introduces a new type of neural architecture named Convolutional Long Short Term Memory Selectional AutoEncoders (CMSAE) which allows the simultaneous segmentation of multiple classes such as coast, oil spill and ships. Unlike previous works using full SLAR images, in this work only a few scanlines from the beam-scanning of radar are needed to perform the detection. The main objective is to develop a method that performs accurate segmentation using only the current and previous sensor information, in order to return a real-time response during the flight. The proposed architecture uses a series of CMSAE networks to process in parallel each of the objectives defined as different classes. The output of these networks are given to a machine learning classifier to perform the final detection. Results show that the proposed approach can reliably detect oil spills and other maritime objects in SLAR sequences, outperforming the accuracy of previous state-of-the-art methods and with a response time of only 0.76 s.

1. Introduction

Oil spills are one of the main causes of marine pollution. In the past, major ecological disasters have occurred on the coasts and oceans around the world. Moreover, a large number of ships illegally clean their tanks at sea, worsening this problem. Early detection of oil slicks is very important to limit pollution and mitigate the environmental damage caused by accidents and illegal discharges.

Nowadays, research focuses on the detection of spills and the boats that cause them, as shown in recent works such as [1,2]. It is known that remote sensing technologies have been effective for oil spill monitoring and detection [3], reducing the emergency response time from authorities and governments. The European Maritime Safety Agency (EMSA) has an observation service called CleanSeaNet which uses satellite-based observation (e.g., ENVISAT, RADARSAT, SENTINEL, etc.) for oil spill monitoring and vessel detection. The Spanish Maritime Safety Agency (SASEMAR) also uses 3 EADS-CASA CN 235-300 aircraft to locate shipwrecks and vessels at sea, detect discharges into the marine environment, and identify the infringing ships. These airplanes are equipped with a Millimetre-Wave Radar (MWR) on each wing, and they are able to carry out maritime patrol missions with a maximal total range exceeding 3706 km, and up to more than 9 flight hours. The detection of possible targets is done manually, as the SLAR signal is digitized as an image and analyzed by expert operators. To confirm the detections, marine samples are also taken when necessary.

A variety of sensors are used for oil spill detection [4,5]. Among them, the best solution for wide area surveillance, during day or night and with rainy and cloudy weather, is Synthetic Aperture Radar (SAR) and Side-Looking Airborne Radar (SLAR), as shown in [6,7]. The main differences between them are that SAR in general is installed on satellites while SLAR is usually mounted on airplanes, assembling two SAR antennas under the wings. This implies that SLAR images, in contrast with SAR, contain artifacts caused by small differences in alignment between both antennas or by return signal loss (reflected signal), showing a higher complexity in the representation of ground scenes. Moreover, the size of these artifacts is variable and dependant on the flight altitude and the ascent/descent speed. However, SLAR has the advantage of being able to control an area with greater precision and at any time (without having to wait for the satellite to be positioned).

The basic principle on which the SAR and SLAR sensors are based to perform remote sensing is the emission of a microwave beam, where the received signal is the reflection by the object back scatter features. Based on this response the sensor builds a two dimensional image, where the brightness of the captured image is a function of the properties of the target-surface. This brightness is related to the normalized radar cross section (NRCS) representing the power of the backscattered radar signal. The possibility of detecting an oil spill in a SAR or SLAR image relies on the fact that the oil film decreases the backscattering of the sea surface resulting in a dark formation that contrasts with the brightness of the surrounding spill-free sea [8]. In addition, oil slick features, such as thickness, shape or size, which are mainly dependent on weather, sea or wind conditions, and the time since the spill, also determine the dark spot appearance observed in the image.

However, dark areas (or areas of reduced NRCS values) do not always originate from oil spills, because they can also be originated by other ocean phenomena, named “lookalikes”, such as very calm sea areas, currents, eddies, different weather conditions such as low wind, and may also have a biological origin such as shoals of fish, seaweed and plankton. For this reason it is very difficult to differentiate between mineral oil spills and effects caused by biogenic surface films.

Image processing techniques are commonly used for the extraction of textural, geometric and physical features along with segmentation methods in order to identify the regions of oil slicks within an image. Then, supervised machine learning classifiers can be applied to discriminate between oil slicks and lookalikes. They can produce false positives in the detection process due to the similarity in appearance with the regions that represent spills.

The statistical distributions of dark spots and background can also be modeled in order to differentiate between oil slicks and sea as in [9], applying a Generalized Likelihood Ratio Test (GLRT) [10], using spatial density features [11], using strategies based on energy minimization such as Region Scalable Fitting (RSF) methods [12], Global Minimization Active Contour Model (GMACM) [13] or Globally Statistical Active Contour Model (GSACM) [14], among others.

However, these approaches are very limited when there are environmental changes and SLAR images contain artifacts—such as that caused by aircraft maneuvers—which do not follow any statistical distribution and, therefore, it can be confused with oil slicks or other artifacts. To avoid this problem, Gil and Alacid [7] presented a method to identify oil slicks from SLAR imagery using an image processing technique to eliminate the artifacts regions caused by maneuvers. Other authors applied a segmentation process guided by a saliency map to identify the oil spills. For example, Li et al. [15] proposed a simplified graph-based visual saliency model to extract bottom-up saliency. The method is able to detect oil slicks and exclude other salient regions caused by other targets such as artifacts.

In general, the previously mentioned methods use image processing techniques to segment candidate regions representing oil spills and/or to extract features. Then, they feed these features into machine learning classifiers to detect oil slicks. Some of these methods (such as [16,17]) use the geometry of the image or the elements to be classified as features for oil spill detection. However, they are very dependent on the dataset used to select the most relevant features, failing as soon as the characteristics of the image change and therefore losing generalization capabilities.

Unlike with SAR, in SLAR it is not convenient to define descriptors using characteristics extracted from the whole image, as done in known state-of-art methods. SLAR data are obtained as a set of scanning lines and each of them represents a time observation. Therefore, it is very difficult to extract spatial characteristics in a representative neighborhood that allow to design robust descriptors for each target class.

Deep Learning and, in particular, Convolutional Neural Networks (CNN) are recently being used to perform classification without applying any hand-crafted feature extraction nor pre-processing techniques. They can also obtain reliable results in image segmentation and recognition tasks, in some cases showing a performance close (or even superior) to the human level when working with signals such as images, video, or audio [18]. Deep learning techniques are being applied to overcome the limitations from the traditional machine learning methods that require extracting hand-crafted features from the input data.

The kernels of the different convolutional layers of a CNN learn a numerical matrix which allows to transform the input image they receive. Therefore, each of these kernels learn to transform their input in a different way, highlighting different elements that are relevant for the detection of the target class. Low level features are learned in the first layers, since small kernels are applied over the entire image. These results are combined and passed through layer after layer, until the last layers of the network, that extract highest level features.

In the case of deep learning approaches, there is previous research using a CNN for oil spill detection task such as [19], or pixel-level segmentation techniques [20] to identify dark spots representing oil spills as in [21,22]. The latter work [23] successfully combined Resnet [24] and Googlenet [25] with Fully Convolutional Networks (FCN) [26] for this task.

Segmentation networks can be applied to SAR or SLAR images for the detection of spills or other classes, as in [27], where a Selectional Auto-Encoder (SAE) network was proposed. This architecture modifies the topology of a FCN to specialize it to the segmentation of one class (oil spills in this case) and to return a probability distribution after which a threshold is applied to select the pixels to segment.

Most existing methods for oil spill detection need to process the full image. Therefore, their usage in environments that require a quick response may not be feasible. In contrast with [27], which uses a SAE over the entire image of the flight sequence, in this work we present a new approach to segment SLAR images in real time. The proposed method uses a combination of Convolutional Long Short Term Memory (ConvLSTM) networks [28] with a variation of the SAE topology, in order to enable faster processing. The main reason for adding recurrent neurons (ConvLSTM) is to perform the segmentation using only the current reading of the sensor along with a small amount of the previous readings. In this way, it is possible to return a response during the flight time, without having to wait for more readings to complete an image or obtain a larger context of the area to be classified, which would generate a lag in the response. In addition, the proposed process simultaneously segments other elements of the image such as ships, coast or the artifacts generated by the aircraft sensors, and combines this information into a final classifier. The result obtained for these additional classes is used to improve the segmentation oil spills and ships. In this way, the final classifier can make a high-level decision by combining the result of the specialized classifiers, and thus discard, for example, the segmentation of a ship or an oil spill when they are surrounded by coast or noise.

In summary, the main contributions of this paper are:

• A method designed to work in real time (flight time), in contrast to previous techniques such as [27] which can only be used offline (once all the scanlines are available). For this, a SAE topology was modified in order to work directly with SLAR scanlines, and recurrent neurons were added to take advantage of the information in the previous readings.
• The proposed method uses a parallel set of specialized supervised classifiers for each of the classes, and finally combines their outputs to provide an answer. By combining the classifiers’ decisions, it is possible to consistently improve the results, as demonstrated with statistical tests in Section 3.
• The model was evaluated using 51 different flight sequences with a total of 5.4 flight hours, including a wide range of examples of the different elements to be classified as well as different meteorological and flight conditions (altitude, flight speed, wind speed, etc.).
• The proposed approach is compared with other state-of-the-art methods, reporting better results in both detection and segmentation tasks at the pixel level, as well as better processing time.

The rest of the paper is structured as follows. Section 2 describes the proposed method and the data used for evaluation, Section 3 shows the results obtained with the proposed method, Section 4 discusses the results and how they can be interpreted in perspective of previous studies, and finally, conclusions and future work are given in Section 5.

2. Materials and Methods

This section first describes the materials used for the experiments. Then, we introduce the proposed method, which uses a combination of ConvLSTM networks with SAE to process the SLAR signals during flight.

2.1. Materials

For the experiments with the proposed method, we have used a dataset composed of 51 flight sequences supplied by SASEMAR. SASEMAR is the public authority responsible for monitoring the Exclusive Economic Zones (EEZ) of Spain whose procedures are based on reports of EMSA.

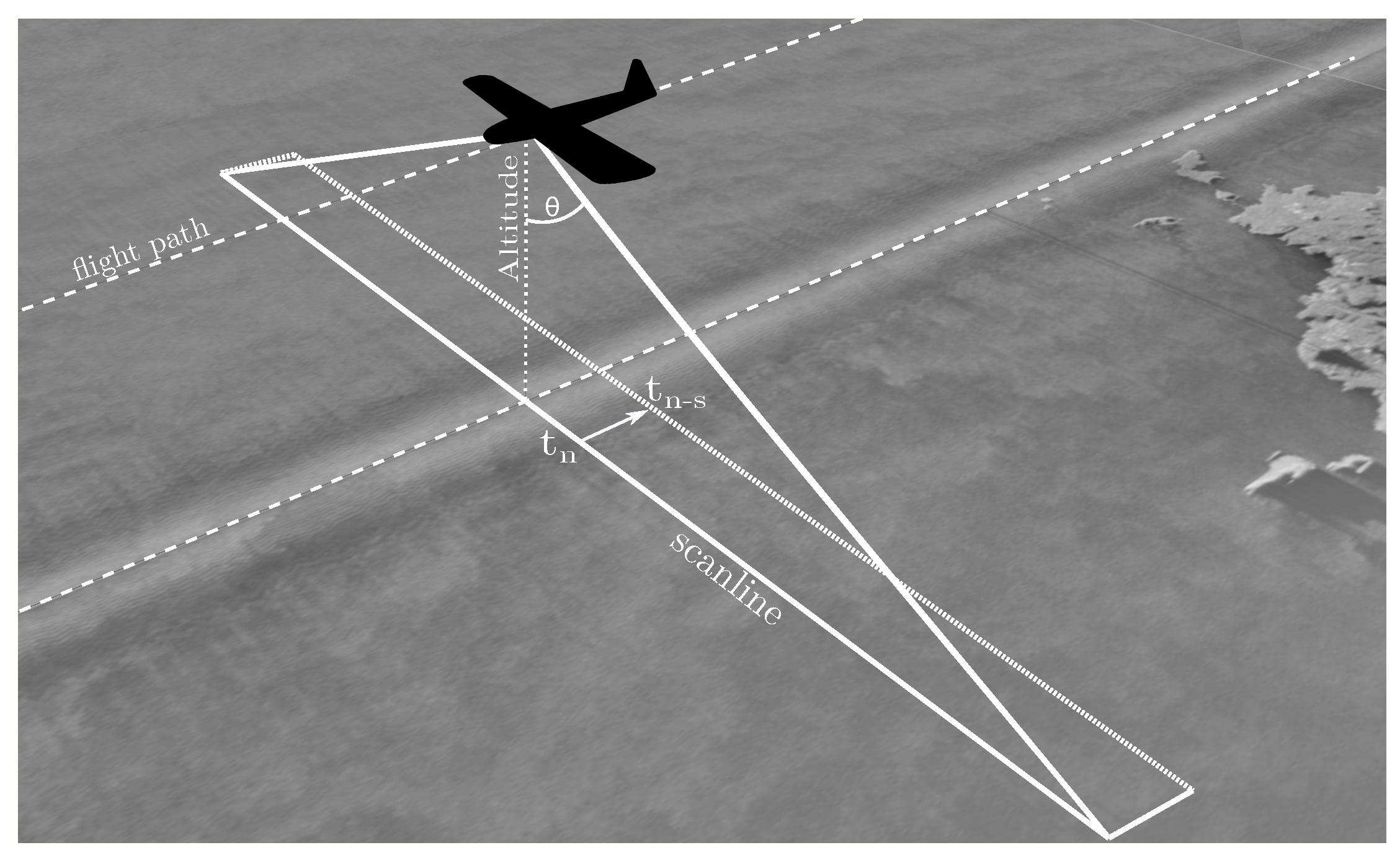
Figure 1 shows the scheme of the used EADS-CASA CN 235-300 aircraft with its data acquisition system. This aircraft has two TERMA SLAR-9000 antennas under both wings pointing in a perpendicular angle to the flight direction. At the average flight altitude of our dataset, they cover around 23 km on each side of the aircraft. Each antenna scans the surface with an angle $\theta$ (or so called off-nadir angle), returning two signals that are combined into a single scanline. This scanline is the data used as input at each time t for the proposed approach.

The flight sequences of the dataset have an average duration of 6.1 min ($\pm 0.9$ min), making a total of 5.4 h of flight and 24,582 scanlines. They were captured at an approximate altitude of 3100 feet ($\pm 1600$ ft), with a flight speed of about 183 Kn ($\pm 30$ Kn), and with a wind speed between 0 Kn and 32 Kn.

For each flight sequence, the raw data of the SLAR sensor was stored. Subsequently, these data were digitized as 8-bit integers (grayscale images) with an image resolution of $1157\times 482$ pixels due to the constraints of the monitoring equipment installed on the aircraft. A scanline, as used in the rest of the paper, is one row of this image, so each flight sequence consists of 482 scanlines. The area covered by each scanline on the ground depends on the altitude and on the flight speed, which, at the average values, means approximately 47.3 × 69.6 m per pixel. Therefore, a complete scanline (composed of 1157 pixels wide and 1 pixel high), at the average altitude, covers an average ground area of 54.8 km wide and 69.6 m high (27.4 km wide per antenna).

The scanlines of the 51 flight sequences were concatenated to give the 24,582 scanlines mentioned above. As ground truth, we have used a grayscale mask for each SLAR image delimiting the pixels of the target classes (ship, oil spill, lookalike, coast, central noise, lateral turns, and water) with a different gray value. It is important to note that this labeling has been performed at the pixel level since we want to evaluate both the detection and the precise location of the instances for each class in the digitized SLAR images.

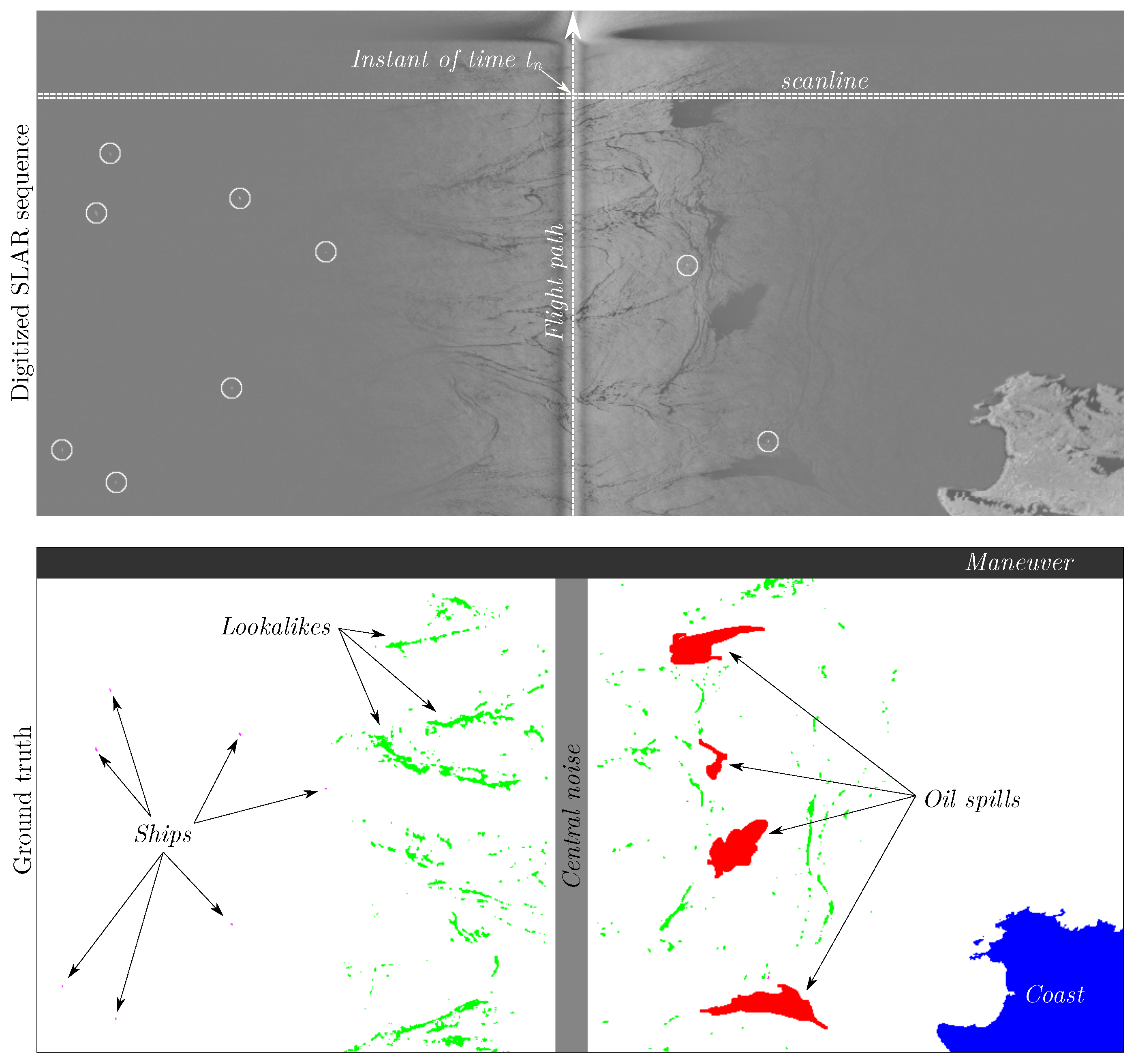
Figure 2 shows an example of a SLAR sequence (top) and its corresponding ground truth (bottom) with the seven classes labeled using different colors. This sample contains several instances of boats, coast, lookalikes, as well as the two types of noise generated by the sensor: The central noise, generated by the union of the radar signals, and the noise caused by the aircraft turning maneuvers. The central noise appears in the center of the image in light gray (coinciding with the trajectory of the plane) and the maneuver noise is in the top area of the image in dark gray. The instances of ships are marked with a circle in the left image. This image also contains some examples of lookalikes (in green color) around the central noise, with elongated shapes very similar to those of current instances of spills.

The lookalike class is very difficult to differentiate at first glance from an actual oil spill because sometimes they can have very similar shapes and intensity values. These classes were labeled by an expert flight operator (from SASEMAR) who was able to analyze the scene recorded in each sequence. Given the difficulty of distinguishing oil spills from lookalikes, in case of doubts, it is recommended (due to operational reasons) to notify an operator who can review the data.

Table 1. Statistics of the dataset including the number of instances of each class, the percentage of space they occupy, the average size (height × width) in pixels of the bounding box (BB) that contains them as well as the number of scanlines with information of each class.

Class	#Instances	#Scanlines/Class	% of Pixels ($\pm \mathit{\sigma }$)		Avg. BB in px. ($\pm \mathit{\sigma }$)
Central noise	51	24,582	6.06	$\pm 2.8$	$455.41\times 74.78$	$\pm 109.6\times 41.4$
Maneuvers	93	2091	8.18	$\pm 10.3$	$19.48\times 1115.58$	$\pm 15.7\times 170.8$
Ship	233	796	0.01	$\pm 0.0$	$3.91\times 3.17$	$\pm 2.2\times 1.9$
Spill	380	3732	0.22	$\pm 0.5$	$11.97\times 14.09$	$\pm 36.8\times 44.1$
Lookalike	3452	3351	0.38	$\pm 1.6$	$5.09\times 5.42$	$\pm 15.1\times 10.4$
Coast	493	4798	6.69	$\pm 13.9$	$13.99\times 66.33$	$\pm 43.9\times 172.8$
Water	51	22,635	79.89	$\pm 15.3$	$1157\times 482$	$\pm 0\times 0$

shows a summary with statistical information about the dataset, including the number of instances of each class, the percentage of pixels that each class occupies in total, the mean size of the samples considering the bounding box that contains them, and the number of scanlines with information of each class. As can be seen, the dataset has a significant number of samples of the main classes to be detected (ship and oil spills), whose sizes are also small with respect to the total size. The lookalike and coast classes also have many samples, although in this case they usually correspond to fragmented pieces of the same spot or small portions of land labeled separately due to the noise caused by the airplane maneuvers.

Based on these data, it may seem that certain classes are easy to differentiate simply by their size but, as can be seen, the standard deviation values are very high, so the area does not allow us to differentiate an oil spill from a lookalike and not even from a ship. The shapes of the different classes are also similar, for instance oil spills and lookalikes sometimes have similar shapes, as it happens with those of the ships and small islets. Therefore, it is not reliable to differentiate between different classes only according to their size or shape.

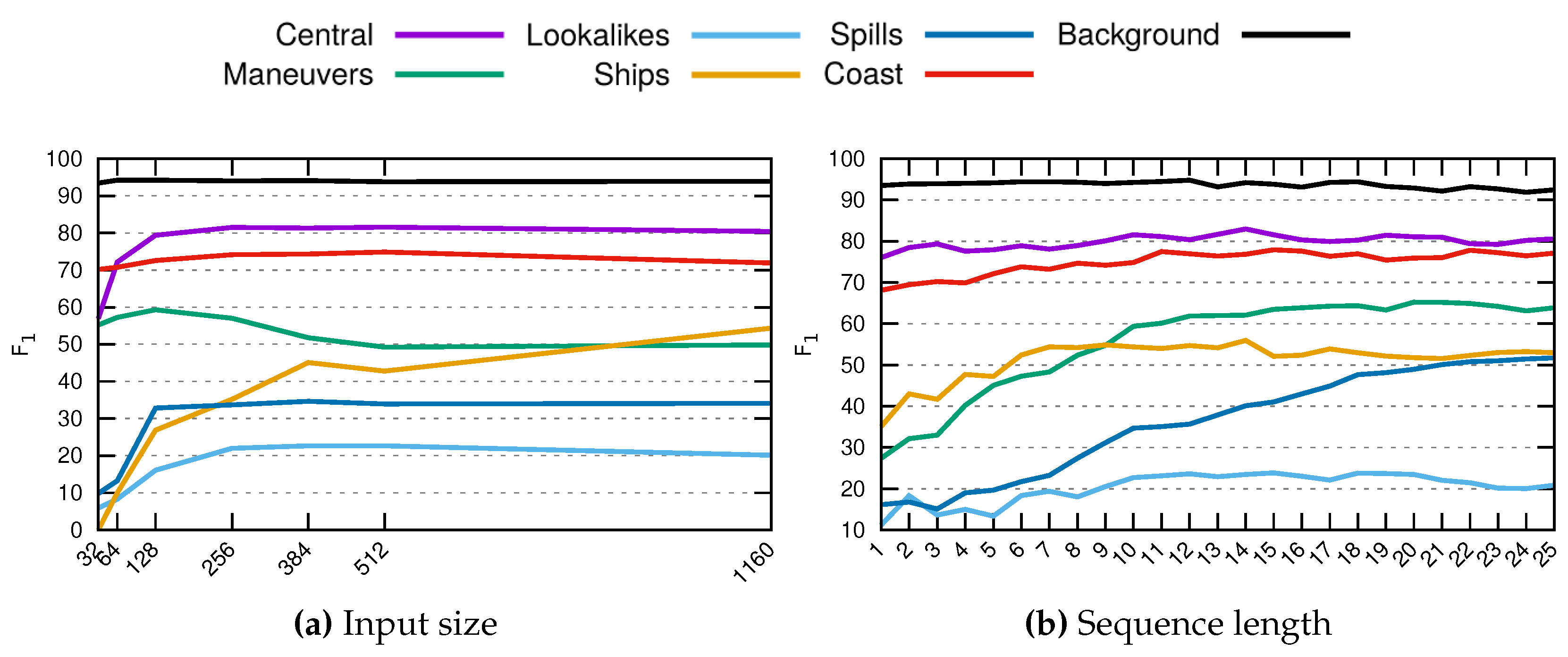
To train and evaluate the proposed method, we used sequences of SLAR scanlines with length s, hence we obtain a dataset containing a total of 24,582 −$51\times (s-1)$ scanlines (the algorithm cannot process the first $s-1$ scanlines of each flight since it still does not have a complete sequence, that is, it is necessary to have a minimum of s lines of context to return a response). For example, if the length of the sequence is 20 scanlines, we would obtain 24,582 −$51\times (20-1)=$ 23,613 sequences for which a prediction can be calculated.

2.2. Method

From the SLAR sensor signals, the aim of our method is to detect the presence of different objectives: ships, oil spills, lookalikes, coast, central noise, aircraft maneuvers (which causes image artifacts), and water (or background). Therefore, the proposed method receives as input a scanline digitalised from the sensor signal and returns as output the pixel-level segmentation with the labels of the considered classes.

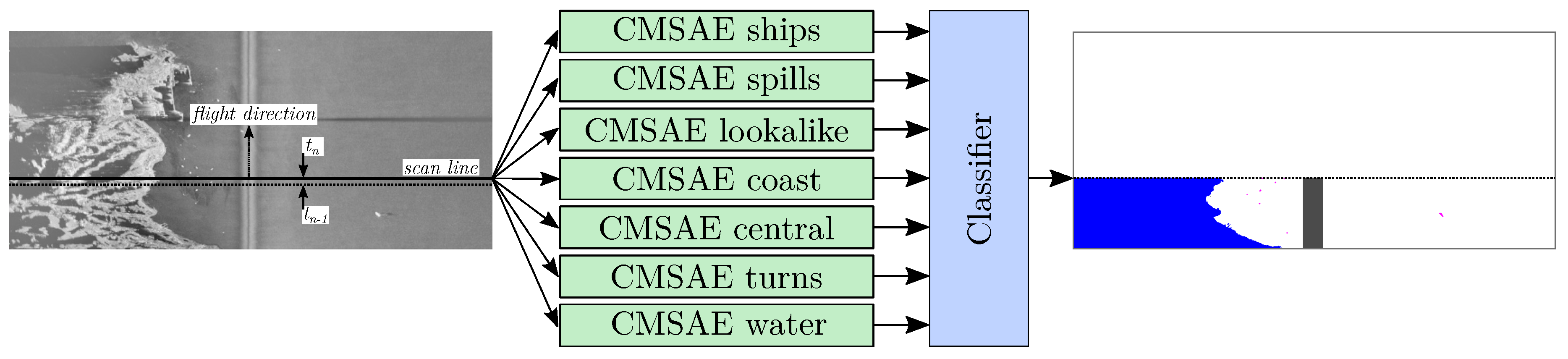
To perform this segmentation, we use an ensemble of ConvLSTM Selectional AutoEncoders (CMSAE), which are SAE networks with Convolutional LSTM layers as will be detailed in Section 2.2.1. This ensemble employs the strategy of one against all. For each class, a CMSAE is trained to specialize in the segmentation of that class (positive class), considering all the other classes (including water) as background (negative class). Then, we combine all the CMSAE results using another classifier to obtain the final segmentation. Figure 3 shows the proposed architecture. As can be seen, all CMSAE networks can be run in parallel. Therefore, in the inference stage the execution time will be equal to that of a single network.

We evaluated different topologies and parameter configurations for the CMSAE networks as well as different machine learning methods for the final classifier. The following sections describe in detail the architecture of the networks and the classifiers evaluated.

2.2.1. CMSAE

Autoencoders were proposed decades ago by Hinton and Zemel [29], and since then they have been actively researched [30]. They consist of feed-forward neural networks trained to reconstruct their input and are usually divided in two stages. The first part (called the encoder) receives the input and creates a latent representation of it, and the second part (the decoder) takes this intermediate representation and tries to reconstruct the input. Formally, given an input x, the network must minimize the loss $L(x,g(f\left(x\right)\left)\right)$, where f and g represent the encoder and decoder functions, respectively.

Some variations of autoencoders have been proposed in the literature to solve other kind of problems. For example, denoising autoencoders are an extension trained to reconstruct the input x from a corrupted version (usually generated using Gaussian noise) of it (denoted as $\widehat{x}$). Thus, these networks are trained to minimize the loss $L(x,g\left(f\left(\widehat{x}\right)\right))$, therefore they are not only focused on copying the input but also on removing the noise [31,32,33].

For the detection of each of the classes from the SLAR sensor data, we have based our approach on the SAE architecture introduced in Gallego et al. [27]. This type of architecture does not intend to learn the identity function as it happens with autoencoders, nor an underlying error as in denoising autoencoders. Instead, it learns a codification that maintains only those input pixels that we select as relevant (i.e., the class to be segmented). This goal is achieved by modifying the training function so that the input x is mapped to a ground truth classification image. For this, we use the ground truth y of the pixels from the input image that we want to select. Therefore, it is trained to minimize the loss $L(y,g(f\left(x\right)\left)\right)$, learning a function $\eta$ such that $\eta :{\mathbb{R}}^{(w\times h)}\to {[0,1]}^{(w\times h)}$, or in other words, a probability map over a $w\times h$ image that preserves the input shape and outputs the decision in the range of $[0,1]$ with the likelihood that each of the pixels from the input image belongs to the target class.

We modified this topology in order to use only one sensor scanline, so, in this case, w is the width of the image and h is set to 1. We also add a first layer with recurrent neurons to take advantage of the information from the previous $s-1$ (for various values of s) sensor readings (where s is the length of the input sequence). Recurrent neurons are a special type of artificial neurons that use an internal state to process sequences of inputs. These neurons process an input sequence one element at a time, maintaining a state (or memory) that implicitly contains information about the history of all the past elements of the sequence [18].

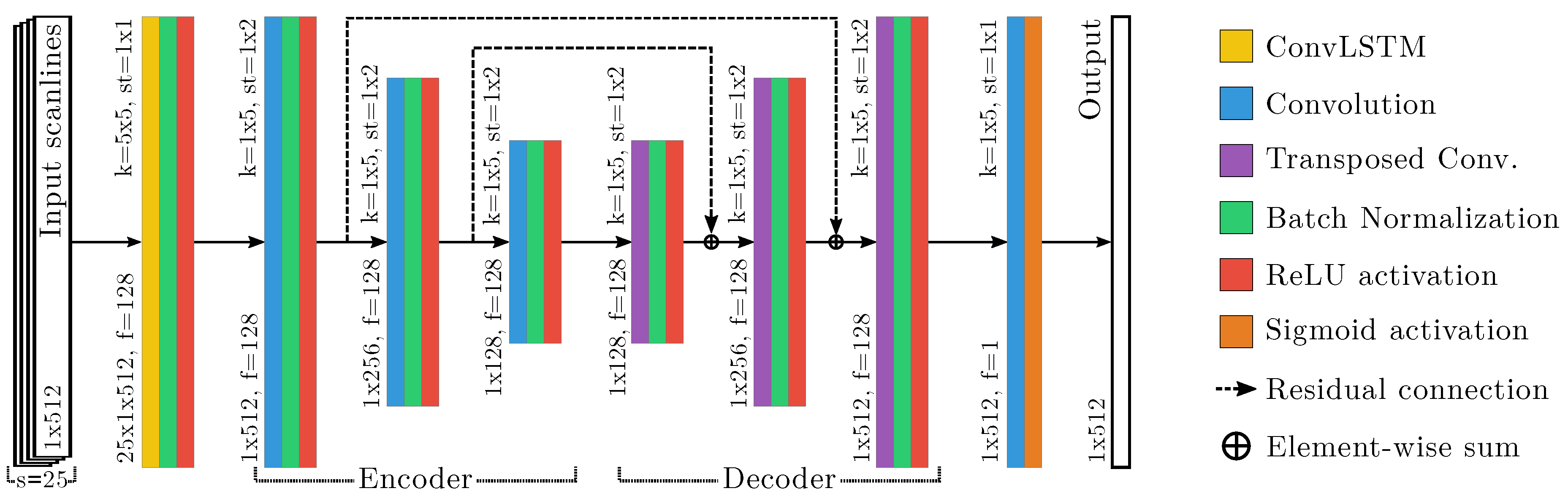
Figure 4 shows the scheme of the CMSAE network topology specialized for the segmentation of oil spills. As can be seen, the first layer uses the ConvLSTM recurrent neurons [28], followed by a Batch Normalization layer [34] and ReLU as the activation function [35]. The encoding part of the network consists of a series of layers with three elements: Convolutions, Batch Normalization and ReLU activation functions. These layers are replicated until the intermediate layer, in which the encoded representation of the input is attained. Then, this representation is followed by a series of transposed convolutions plus Batch Normalization layers, also with ReLU activation functions, which generate the output image with the same input size (that is, with the same size of the data that is supplied as input to the CMSAE network). In addition, we added residual connections from each encoding layer to its analogous decoding layer, which facilitate convergence and improve the results. The last layer consists of a unique convolution with a sigmoid activation to predict a value in the range of $[0,1]$, depending on the selectional level $\lambda$ for the corresponding input.

The downsampling in the network encoder part is performed by convolutions using stride, instead of resorting to pooling layers. Up-sampling is achieved through transposed convolution layers, which perform the inverse operation to a convolution, to increase rather than decrease the resolution of the output.

ConvLSTM neurons [28] are an extension of the fully connected LSTM (FC-LSTM) to contain convolutional structures in both the input-to-state and the state-to-state transitions. It is demonstrated that ConvLSTM neurons capture spatiotemporal correlations better, consistently outperforming the state of the art (FC-LSTM) in spatiotemporal data.

Batch Normalization layers [34] carry out a normalization process to the weights learned by the different layers after each training mini-batch. They help to perform faster training, reduce the overfitting, and improve the overall success rate. We have chosen the Rectified Linear Unit (ReLU) [35] as the activation function because it is computationally efficient and enhances the gradient propagation throughout the training phase, avoiding vanishing and exploding gradient problems.

The topology of this type of network can be easily varied since we can modify the number of layers, number of filters, kernel size, etc. In addition, it is expected that, depending on the class to be detected, the appropriate configuration may vary. For example, it is not the same to segment small ships, which are represented by only a few pixels in the image, as contrasted with a coastal area, whose size is significantly larger. To find the network architecture with the best configuration of layers and hyperparameters, we have applied a grid-search technique [36]. Results of this experimentation are included in Section 3.1, although we report the best topologies found for each network in

Table 2. Topology of each of the CMSAE networks used in the proposed algorithm.

Class	Input Size (px) height × width	Sequence Length (s)	# Encoder– Decoder Layers	# Filters (f)	Kernel Size (k)
Central noise	1 × 512	14	$2+2$	16	1 × 7
Maneuvers	1 × 128	20	$3+3$	128	1 × 7
Ships	1 × 1160	14	$3+3$	128	1 × 5
Spills	1 × 512	25	$3+3$	128	1 × 5
Lookalikes	1 × 512	15	$3+3$	64	1 × 7
Coast	1 × 512	15	$3+3$	64	1 × 7
Water	1 × 512	12	$3+3$	128	1 × 7

.

2.2.2. Classifier Integration

The segmentation result obtained from each of the networks is supplied to a classifier. To do this, we extract the feature vector (neural codes or NC) of the penultimate layer of each network, we normalize them using ${\ell }_2$ norm [37], and concatenate them with the others forming a single vector of features that can be supplied to a classifier. In previous experiments, we tried to use the intermediate encoding of the auto-encoder, but worse results were obtained possibly because the precision and position of the information was degraded or lost.

Since the input size of the auto-encoder used for each class (and its corresponding output size) is different (see Table 2), it is necessary to apply a process to normalize the sizes in order to combine this information. This process is performed on the NC extracted from each network, which form a matrix of $s\times w$, where we have set s to 12 scanlines (which is the minimum common sequence length used), and w is the width of the output size. To this matrix, we apply bi-cubic interpolation to adjust the network’s output size to obtain an $s\times 512$ matrix, which is the precision with which the result of the classification will be returned.

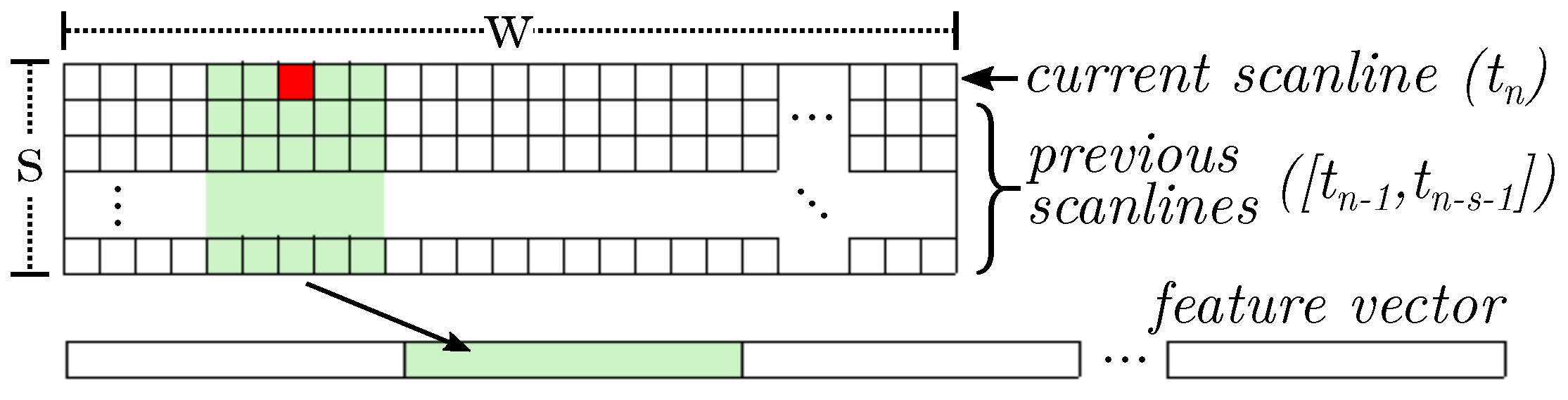
Once the sizes are normalized, we proceed to prepare the data to be supplied to the classifier, which has to predict one of the seven possible classes for each of the input pixels. For this, we create a feature vector by combining the NC in the neighborhood of each pixel. Specifically, a window of $s\times 5$ around each pixel is taken, adding zero padding for the edge pixels. This information is extracted for the NC of each of the seven networks, obtaining a vector of $s\times 5\times 7=420$ features (with $s=12$). Figure 5 shows a graphical representation of this process.

We evaluated different machine learning methods to choose the most suitable one for this task (that is, classify the red pixel in Figure 5). Specifically, we tested the following methods and parameter settings:

• k-Nearest-Neighbors (kNN) [38]: This classifier is one of the most widely used schemes for supervised learning tasks. It classifies a given input element by assigning the most common label among its k-nearest prototypes of the training set according to a similarity function. Different numbers of neighbors $k\in [1,9]$ have been evaluated in this work.
• Support-Vector Machines (SVM) [39]: It learns a hyperplane that tries to maximize the distance to the nearest samples (support vectors) of each class. In our case, we use the “one-against-rest” approach [40] for multi-class classification and a Radial Basis Function (or Gaussian) kernel to handle non-linear decision boundaries. Typically, an SVM also considers a parameter that measures the cost of learning a non-optimal hyperplane, which is usually referred to as parameter c. For these experiments, we tuned this parameter in the range $c\in [1,20]$.
• Random Forest (RaF) [41]: It builds an ensemble classifier by generating several random decision trees at the training stage. The final output is taken by combining the individual decisions of each tree. The number of random trees has been established by experimenting in the range $t\in [10,500]$.

As a result of this evaluation (which will be detailed in Section 3.2), we obtained the best results using a SVM with $c=15$. Therefore, we chose SVM as the final classifier of the proposed method.

2.3. Training Process

CMSAE can be trained using conventional optimization algorithms such as gradient descent. In this case, the network parameters were tuned by means of stochastic gradient descent [42] considering the adaptive learning rate proposed by Zeiler [43]. The loss function (usually called reconstruction loss in autoencoders) can be defined as the squared error between the ground truth and the generated output. In the proposed method, we use the cross-entropy loss function as the input is normalized to be in the range $[0,1]$.

In all of the experiments, we used an n-fold cross validation (with $n=5$), which yields a better Monte-Carlo estimation than when solely performing the tests with a single random partition [44]. Our dataset was consequently divided into n mutually exclusive sub-sets, using the data of each flight sequence only in one partition. For each fold, we used one of the partitions for test ($20\%$ of the samples) and the rest for training ($80\%$). Besides, a validation sub-set with 10% of the training samples was used in the grid search process (see Section 3.1). The training and testing processes were repeated $n=5$ times, using different partitions of the dataset and finally providing the average result along with its standard deviation.

The data supplied to the networks during both training and inference was normalized using standard normalization. For this, we apply the equation $Z=(X-\mu )/\sigma$, where X is the input matrix containing the raw pixel values from the training set, $\mu$ is the sample mean, and $\sigma$ the standard deviation. For the normalization of the test set we used the same mean and deviation calculated in the training set. As seen in Gallego et al. [27], this kind of normalization is suitable for this type of data, since in some cases the improvement reaches up to 25%.

In the dataset used for training and evaluation, nearly 80% of the pixels are water, and the most relevant targets (oil spills and ships) are represented by less than 0.25% of the pixels (see Table 1). As a consequence of that, the dataset is unbalanced. To solve this issue, we relied on data augmentation techniques to balance classes adding samples. Consequently, for training each of the CMSAE networks, the sequences of the positive and negative classes were counted and then, samples of the minority class were artificially generated by randomly applying different types of transformations to the original samples of that class. These transformations include horizontal and vertical flips and horizontal translations in the range [−10, 10]% of the sample width.

3. Results

In this section, the proposed CMSAE architecture and the different classification methods are evaluated. In order to quantitatively measure the obtained results, we use the F-measure ($F_1$) metric at the pixel level, which can be defined as:

$$F_1=\frac{2·TP}{2·TP+FN+FP}$$

(1)

where TP (True Positives) denotes the number of correctly detected pixels of the positive class (or targets), TN (True Negatives) the number of incorrectly detected targets, FN (False Negatives) the number of non-detected or missed targets, and FP (False Positives or false alarms) the number of incorrectly detected targets.

Using this metric, we first evaluate the hyper-parameters of the CMSAE networks. Then, we analyze the different classifiers considered for the last classification stage (described in Section 2.2.2).

3.1. Hyperparameters Evaluation

To choose both a good network topology and good hyperparameters, we performed a grid-search [36] using the training and validation sets. In addition, to better adjust the CMSAE networks, the obtained results are analyzed independently for each class. The appearance and size of the targets from the various classes is variable, therefore it is expected that the same network topology will not be the most suitable for all target classes.

First, we analyze the results when varying the input size of the network from $1\times 32$ pixels to $1\times 1160$ pixels, that is, digitizing the scanlines at different widths. To do this, we apply a bi-cubic interpolation, keeping the original labels for the ground truth. To carry out this experiment, we started with a basic network configuration with 6 layers with 64 filters each, using a kernel size of $1\times 5$ and a sequence length of 10 scanlines. Figure 6a shows the results of this experiment. In general, for all classes the results remain relatively stable for sizes of $1\times 256$ px or larger. Only the detection of the ship class seems to benefit from even larger sizes (perhaps because they are very small objects). The maneuvers class seems to be better with small input sizes. Maybe this is because they are objects that occupy the entire width of the SLAR image, and for small input sizes the information is summarized better. To reduce the loss obtained in the size normalization process, we decided to select the size $1\times 1160$ px for ships in order to increase precision, $1\times 128$ px for maneuvers (because they always occupy the entire width of the image, they do not suffer loss in normalization), and $1\times 512$ px for the rest of classes.

Another important variable to be analyzed is the number of SLAR scanlines used as input. The size of the input sequence has a direct impact on the result obtained since, on the one hand, by adding more scanlines to the sequence, the method is able to use more spatial information (or more context) to calculate the response, but on the other hand, to obtain a larger context in height it is necessary to wait more time to obtain those scanlines, which would slow down the method. For this reason, this variable is analyzed to determine the shortest sequence length with which good results are obtained.

To perform this experiment, we have started from the same base configuration, but using the best input size previously found, and only varying the length of the sequence used between 1 and 25 scanlines. Figure 6b shows the result of this experiment. Overall it seems that all classes benefit from the use of a longer sequence (more scanlines), especially the spills and the maneuvers classes, which need a greater context when dealing with more elongated or complex elements.

The optimum sequence length for LSTM is related to the size and direction of the targets. For example, if the spill is parallel to the scanline of the SLAR, it would be easier to detect and would require a shorter sequence length. However, given that it is not possible to know this information a priori, we selected the largest size with which a better overall result was obtained.

As can be seen in Figure 6b, the ship class improves up to a length of 14 scanlines, then stabilizes. The same happens with the lookalike class, which has a major increase at the beginning. Finally, a sequence of 12 scanlines for the background was selected, of 14 for ships and central noise, 15 for coast and lookalikes, 20 for maneuvers, and 25 for spills.

Next, we evaluated the rest of the parameters of the autoencoder topology. For this, we start from the base configuration but setting the input size and the sequence length to the previously found values, and then we introduce variations in the number of layers (from 2 to 6), the number of filters per layer (between 16 and 128), and in the kernel size of each filter (from $1\times 3$ to $1\times 7$). The results of this experiment are shown in

Table 3. Results ($F_1$%) of the grid-search process to determine the number of layers, filters and kernel size of each of the CMSAE networks. In addition, the average results obtained are included and the best result for each class is marked in bold.

			# Filters/Kernel Size
			16				32				64				128
Class	# Layers		3	5	7		3	5	7		3	5	7		3	5	7		Avg.
Central	2		82.0	83.7	86.0		82.3	85.4	86.0		81.9	85.6	86.2		83.8	85.4	86.0		84.5
	4		81.9	85.5	86.6		81.0	85.7	85.1		81.9	84.6	86.2		82.8	84.0	85.2		84.2
	6		79.2	80.7	81.0		78.3	80.0	80.5		75.7	83.0	83.4		76.6	81.4	82.5		80.2
	Avg. kernel		81.0	83.3	84.5		80.5	83.7	83.9		79.8	84.4	85.3		81.0	83.6	84.6
	Avg. filters		83.0				82.7				83.2				83.1
Maneuvers	2		47.9	48.3	58.8		49.1	54.4	59.0		52.5	53.4	58.9		50.0	55.3	54.8		53.5
	4		50.5	55.0	60.7		50.4	52.8	57.1		50.3	57.6	58.3		49.9	56.3	59.0		54.8
	6		52.6	58.8	64.9		52.9	54.6	62.5		53.0	65.2	65.4		53.5	65.4	65.4		59.5
	Avg. kernel		50.3	54.0	61.5		50.8	53.9	59.6		52.0	58.8	60.9		51.1	59.0	59.7
	Avg. filters		55.3				54.8				57.2				56.6
Ships	2		45.2	49.7	42.4		42.2	47.2	48.5		42.7	47.8	49.5		46.4	48.4	47.4		46.4
	4		42.8	45.2	45.5		42.4	44.7	48.0		47.1	48.7	51.0		47.1	47.2	48.1		46.5
	6		46.2	49.8	49.5		51.2	53.8	54.1		49.2	55.9	54.9		53.7	57.8	56.1		52.7
	Avg. kernel		44.7	48.2	45.8		45.3	48.6	50.2		46.3	50.8	51.8		49.0	51.1	50.5
	Avg. filters		46.3				48.0				49.7				50.2
Spills	2		17.4	18.4	17.9		18.1	18.6	18.0		18.9	19.6	20.1		21.6	23.7	23.0		19.6
	4		33.4	34.0	33.7		32.8	33.8	30.8		30.6	34.6	33.5		34.2	35.9	35.1		33.5
	6		49.1	50.9	51.6		50.9	51.1	50.0		50.6	51.7	50.9		51.5	52.6	52.1		51.1
	Avg. kernel		33.3	34.5	34.4		33.9	34.5	32.9		33.4	35.3	34.8		35.7	37.4	36.8
	Avg. filters		34.1				33.8				34.5				36.6
Lookalikes	2		21.2	21.7	21.8		21.8	21.9	20.8		22.0	22.0	21.4		23.0	19.8	19.3		21.4
	4		23.2	23.5	23.2		23.4	23.1	23.2		20.8	20.0	24.1		18.1	19.5	20.1		21.9
	6		23.8	23.1	23.8		23.5	23.1	23.2		23.7	23.8	24.5		23.0	23.2	23.2		23.5
	Avg. kernel		22.7	22.7	22.9		22.9	22.7	22.4		22.1	21.9	23.3		21.4	20.8	20.9
	Avg. filters		22.8				22.7				22.5				21.0
Coast	2		71.4	76.6	79.8		71.9	77.7	79.6		72.5	79.8	80.1		74.2	78.9	82.5		77.1
	4		72.3	77.6	79.8		72.7	75.6	80.5		72.6	78.0	81.6		73.4	77.5	79.7		76.8
	6		75.3	75.9	80.1		74.8	78.1	79.7		73.2	77.9	82.9		75.7	80.0	82.1		78.0
	Avg. kernel		73.0	76.7	79.9		73.1	77.1	79.9		72.8	78.6	81.5		74.4	78.8	81.5
	Avg. filters		76.5				76.7				77.6				78.2
Water	2		94.1	93.7	94.4		94.0	94.4	94.2		94.2	94.4	94.7		93.9	94.3	94.7		94.2
	4		94.0	94.3	94.6		94.1	94.5	94.5		94.1	94.5	94.9		94.1	94.4	94.7		94.4
	6		94.1	94.5	94.2		93.8	93.9	94.7		93.8	94.8	94.7		94.2	94.3	95.0		94.3
	Avg. kernel		94.1	94.2	94.4		94.0	94.2	94.5		94.0	94.6	94.8		94.0	94.3	94.8
	Avg. filters		94.2				94.2				94.5				94.4

. Overall, it seems that almost all networks benefit from the use of more layers, a greater number of filters and a larger kernel size. For this reason, we used 6 layers, 64 or 128 filters, and a kernel of $1\times 5$ or $1\times 7$ in most cases (see results marked in bold in Table 3). The only exception is the network used to process the central noise, which obtained better results using 4 layers, 16 filters with a kernel of $1\times 7$. The final selected configurations are shown in Table 2.

To analyze the results in depth, the confusion matrix among the different classes is calculated using the final selected configuration. Figure 7 shows the normalized confusion matrix at the pixel level for all classes. As can be seen, the oil spill class is frequently confused with the lookalike class (9.23%) and with the background (18.45%). The ship class is also confused with the background (9.24%) and coast (16.81%), perhaps due to the presence of small islets. In general, all classes are significantly confused with the background class, and some of them with the lookalike and coast classes. This result justifies the proposed method, since the final classifier takes advantage of the information of the other classes to improve the classification of the rest. For example, in this case, since the background classifier is highly reliable, that information could be used to reduce the error of the classifiers that are confused with the background class.

3.2. Final Classifier Evaluation

In this section, we evaluate the different types of classifiers used in the last stage of our pipeline. As explained in Section 2.2.2, we have compared three machine learning methods: k-Nearest-Neighbors (kNN) varying the number of neighbors $k\in [1,9]$, Support-Vector Machines (SVM) modifying the parameter $c\in [1,20]$, and Random Forests (RaF) evaluating different number of random trees $t\in [10,500]$.

Table 4. Best results ($F_1$%) obtained by the different classifiers considered for the last stage of the algorithm. The best result obtained for each class is marked in bold.

Class	CMSAE	CMSAE+kNN	CMSAE+SVM	CMSAE+RaF
Central noise	86.60	87.11	87.92	87.32
Maneuvers	65.44	65.37	65.45	65.43
Ships	57.79	57.53	58.03	58.17
Spills	52.58	53.12	54.36	53.91
Lookalikes	24.49	26.37	26.54	26.61
Coast	82.90	83.45	83.92	83.51
Water	94.97	95.12	95.49	95.35
Average	66.40	66.87	67.39	67.19

shows the results of this experiment. For each method, the result obtained with the best parameter settings is shown. As can be seen, the results for some of the classes improve by up to 2% with respect to the value obtained by the CMSAE network. However, for other classes such as turns and water, the result did not improve. For the kNN algorithm, the best results were obtained using a value of $k=7$, for SVM a value of $c=15$, and for RaF $t=300$. In general, the best results were obtained using SVM with a mean c value of 15, so this configuration was selected for the final setup.

Figure 8 shows the Receiver operating characteristic (ROC) curves calculated for oil spill and ship classes applying different threshold levels in order to see how it affects the sensitivity and the specificity of the model. The ROC curve is computed by plotting the True Positive Rate (TPR or sensitivity, equivalent to Recall) against the False Positive Rate (FPR, equivalent to 1-specificity) at various threshold settings. The Area Under the Curve (AUC) is also calculated using the trapezoidal rule to measure the goodness of discrimination. The higher the AUC index the better the discrimination performed by the method. Specifically, and using the traditional academic point system, the AUC for the oil spills curve is in the 0.8–0.9 range, showing a good accuracy, and the AUC for the ship curve is in the 0.9–1 range, so it has an excellent accuracy.

Figure 9 shows two examples of the prediction done by the proposed method for the spill class zooming in the area of interest. The first column shows the original input SLAR images and the second column shows the prediction. In the images of the second column, black areas depict correct detections of oil spills, red and blue pixels depict FP and FN of oil spills, respectively, and white areas depict correct detections of the negative class. These figures help to visualize the accuracy of the proposed approach and to understand where the errors of each target class occur. As can be seen, wrong detections are typically made only at the contours of the spills.

4. Discussion

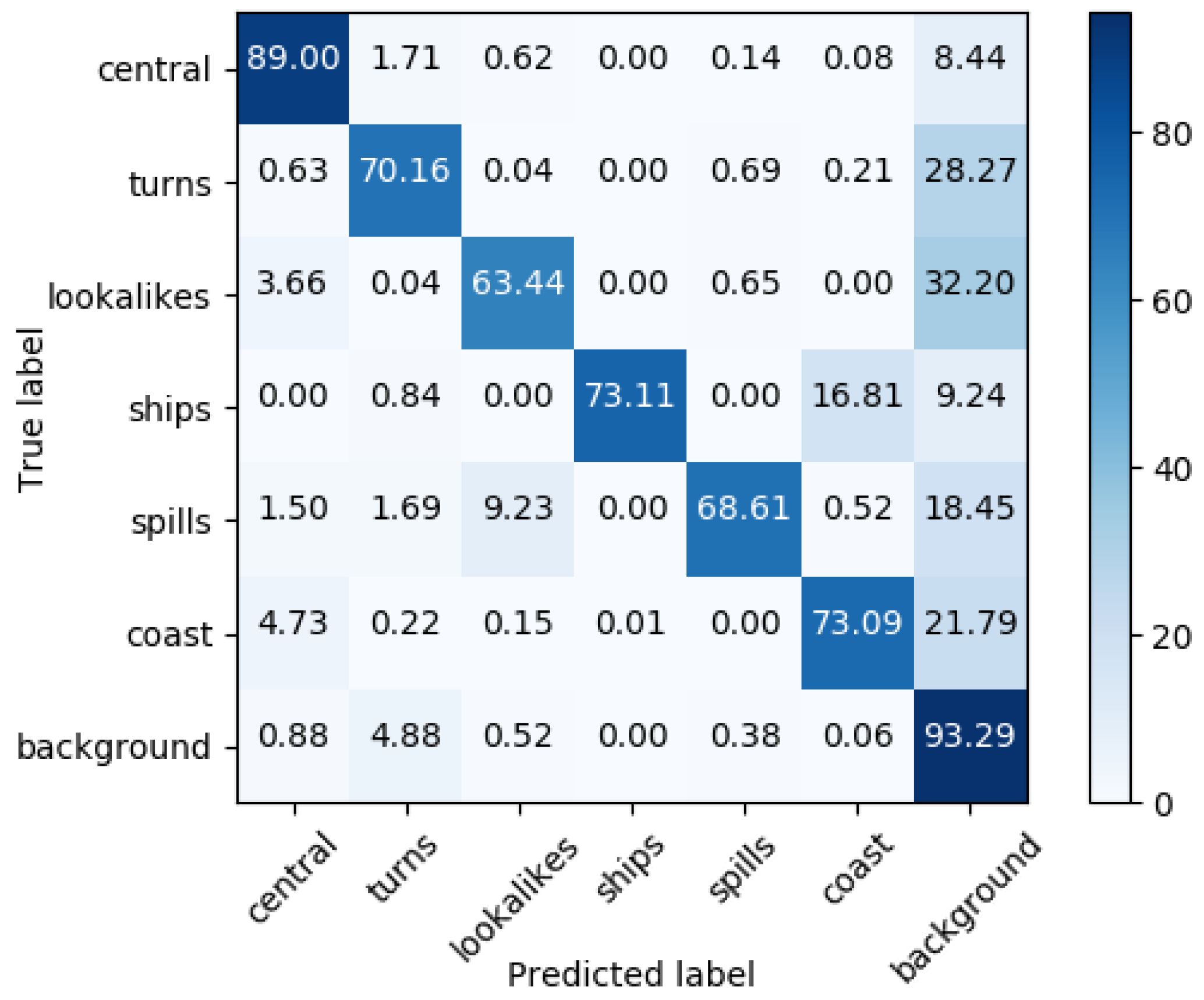
As shown in the previous section, the proposed method (CMSAE+SVM) obtains an average result of 67.39% for classifying the different targets at the pixel level. Some classes, such as central noise, coast or water, obtain accurate results, 87.92%, 83.92% and 95.45%, respectively. For the two most relevant classes, ships and spills, good results are also obtained (58.03% and 54.36%), especially considering that the discrimination is done at the pixel level. The worst result is obtained for the lookalikes class, since this class groups together different types of noise that can be confused with oil spills, and that even for a human expert are very difficult to distinguish.

To better discuss these results and analyze how they can be interpreted in perspective to other previous studies, we compare the results obtained using the proposed approach with other state-of-the-art methods, which are as follows:

• BiRNN [45]: The authors also proposed the use of recurrent neurons to process the sampling lines of the SLAR sensor in order to detect oil spills. In this case, they use Bidirectional RNNs [46], thus, in this model, the output at time t also depends on future elements.
• TSCNN [2]: This method employs a two-stage architecture composed of three pairs of CNNs. Each pair of networks is trained to recognize a single class (ship, oil spill, or coast) by following two steps: a first network performs a coarse detection, and then, a second CNN obtains the precise localization. After classification, a postprocessing stage is performed to improve the results.
• U-Net [47]: This CNN was developed for biomedical image segmentation. This network uses a FCN divided into two phases: a contracting path and an expansive path. The feature activations of the contracting path are concatenated with the corresponding layers from the expansive path. The last layer uses a 1x1 convolution with a Softmax activation function to output class labels.
• SegNet [20]: It uses a fully convolutional neural network architecture for semantic pixel-wise segmentation, containing an encoder network, a corresponding decoder network, and a pixel-wise multiclass classification layer. The architecture of the encoder network is topologically identical to the 13 convolutional layers in the VGG16 network [48].
• DeepLabv3 [49]: It uses atrous spatial pyramid pooling to robustly segment objects at multiple scales with filters at multiple sampling rates to explicitly control the resolution at which feature responses are computed within Deep Convolutional Neural Networks. It also includes a image-level feature to capture longer range information and uses batch normalization to facilitate the training.
• SelAE [27]: This approach uses a SAE network specialized in the segmentation of oil spills. It returns a probability distribution over which they apply a threshold to select the pixels to segment.

The BiRNN and SelAE methods were originally proposed for the detection of oil spills, however in this experiment they are also applied for the detection of the rest of the classes. For this, the originally proposed architectures were used with the same configuration, but training and evaluating a network model for each of the classes.

In the case of the U-Net, SegNet and DeepLabv3, we also used the original architectures but modifying the last layer to classify the seven classes from our dataset. The TSCNN method could only be used for the classification of ships, oil spills and coast, since this method proposed a specific architecture for these three classes and in addition then it applied post-processing that combined the information to improve the result. Therefore, it was not possible to extrapolate this method for the rest of the classes.

Table 5. Mean $F_1$ results of the 5-fold cross validation ($F_1$% $\pm \sigma$) obtained for each of the classes using the different methods evaluated. Best results per row are shown in bold.

Class	BiRNN	TSCNN	U-Net	SegNet	DeepLabv3	SelAE	Our Method
Central noise	75.37 ± 2.5	–	85.64 ± 1.5	84.19 ± 0.9	85.95 ± 1.1	87.84 ± 0.7	87.92 ± 0.7
Maneuvers	50.32 ± 2.2	–	62.47 ± 2.1	60.20 ± 1.0	65.71 ± 1.3	65.55 ± 0.9	65.45 ± 0.8
Ships	26.50 ± 3.1	50.35 ± 1.1	27.02 ± 2.9	2.53 ± 1.4	46.56 ± 1.0	57.29 ± 0.9	58.03 ± 0.8
Spills	32.38 ± 3.0	53.86 ± 1.0	33.39 ± 2.6	12.08 ± 1.3	49.33 ± 1.8	54.52 ± 0.9	54.36 ± 0.9
Lookalikes	14.90 ± 3.3	–	15.13 ± 3.1	1.67 ± 1.8	13.32 ± 2.3	17.74 ± 1.3	26.54 ± 1.0
Coast	65.41 ± 2.8	72.99 ± 1.3	68.25 ± 1.6	68.95 ± 1.2	84.57 ± 1.2	80.20 ± 1.0	83.92 ± 1.0
Water	90.39 ± 1.3	–	94.24 ± 1.2	94.79 ± 1.0	94.84 ± 1.1	95.37 ± 0.9	95.49 ± 0.7
Average	50.75 ± 2.5	–	55.16 ± 2.1	46.35 ± 1.2	62.90 ± 1.4	65.50 ± 1.0	67.39 ± 0.9

shows the results of this comparison, giving the accuracy for each of the classes as well as the average obtained by each method. In the case of TSCNN, the average is not shown since it does not contain all the results. However, it can be seen that this method performs worse for these classes than other methods, such as SelAE or our proposal (CMSAE+SVM). The SegNet network obtains the worst average result, because some classes have significantly low accuracy, especially those that have very small or thin elements, such as ships or lookalikes. The BiRNN, U-Net and DeepLabv3 methods obtain a slightly better result, however, difficulties to detect small objects are also observed.

Comparing the results obtained by SelAE for the detection of oil spills with those presented in the original paper [27], it can be observed that this method has significantly worse results here, decreasing from 93.01% with the previous dataset shown in [27] to 54.52% with the new dataset used in this work. However, it must be considered that many new sequences have been added in the new dataset, which include many examples of lookalikes, coast, more complex representations of oil spills, and also some of the images are very noisy.

On average, the proposed method CMSAE+SVM is the one that obtains the best results. The SelAE and DeepLabv3 algorithms obtain slightly better results for three of the classes. However, the difference is not significant, 0.26% for maneuvers, 0.16% for oil spills, and 0.65% for coast, less than 1% in all cases, with the standard deviation higher than this difference. Moreover, it should be considered that the proposed method works using only a few scanlines, so the execution time is much faster (as will be discussed in the next section).

To assess the significance of the result obtained by the proposed method in comparison with the second best result (the one obtained by SelAE), we performed a statistical significance comparison using the paired sample non-parametric Wilcoxon signed-rank test [50]. On average, the proposed method (CMSAE+SVM) obtains a p-value of $0.0005$, so this test reflects that this method significantly outperforms the results obtained by SelAE.

The results at the pixel level indicate the precision with which the method detects the position and shape of each class. However, this metric does not allow us to discern if all the objectives are actually being detected. For this reason, the Intersection over Union (IoU) metric is also calculated to evaluate if all the targets present in the image are correctly detected. In addition, we have also performed this process at the class level. To start, we calculate a binary mask with the output of the network using a threshold of 0.5, and setting the pixels of that class to 1 and the rest to 0. Then we apply a morphological opening filter and then a closing operation with a circular kernel of $3\times 3$ in order to eliminate small gaps as well as isolated pixels. Finally, we calculate the blobs (we define a blob as a group of connected pixels with value 1 in the binary mask) from the network prediction ($B_p$) and we pair them with those ground-truth blobs ($B_g$) with which they have a highest IoU using the following equation:

$$IoU=\frac{area(B_p\cap B_g)}{area(B_p\cup B_g)}$$

(2)

where $area(B_p\cap B_g)$ indicates the intersection between the object proposal and the ground truth blobs, and $area(B_p\cup B_g)$ depicts its union. The detection will be considered to be positive when the value of IoU exceeds a certain threshold $\lambda$, which is set to 0.5 since it is the value normally used for this type of tasks.

Table 6. Results of the object detection of each class using the Intersection over Union metric (IoU %). Best results per row are shown in bold.

Class	BiRNN	TSCNN	U-Net	SegNet	DeepLabv3	SelAE	Our Method
Central noise	100.00	–	100.00	100.00	100.00	100.00	100.00
Maneuvers	96.77	–	100.00	100.00	100.00	100.00	100.00
Ships	17.17	75.11	19.37	2.15	65.04	87.98	90.13
Spills	26.32	89.47	27.45	13.16	84.29	93.42	92.11
Lookalikes	43.45	–	45.63	1.30	41.12	56.49	59.39
Coast	76.06	86.21	80.21	81.14	95.67	93.31	94.32
Water	100.00	–	100.00	100.00	100.00	100.00	100.00
Average	65.68	–	67.52	56.82	83.73	90.17	90.85

shows the results of this experiment. As can be seen, the proposed method obtains the best result again, although using this metric the difference with respect to SelAE is not so significant since both methods perfectly detect the central noise, maneuvers and water. Therefore, we can conclude that the proposed method detects slightly better the presence of the different targets, but with greater precision for detecting their shape and in significantly less time (as will be seen in the next section).

All methods were trained and evaluated with the dataset described in Section 2.1. As stated before, this dataset is composed of more than 5 h of flight with varied missions, which allows an evaluation under different conditions. The weights learned by networks are dependant on the data used for training, however, to alleviate this fact, layers of Batch Normalization along with data augmentation were used, which increase the generalization capabilities of the method. Even so, it is possible that the proposed method would perform a wrong detection in a particular situation. In this case, this sample could be included in the training set so the weights will be updated to avoid a similar mistake. Therefore, unlike hand-crafted methods, it is easily adaptable to unseen data.

Runtime Analysis

It is also relevant to analyze the time required by each of the methods to give a prediction. The SelAE, SegNet, U-Net and DeepLabv3 algorithms use a complete image, so in principle it would be necessary to wait until a complete image (requiring 6.1 min of flight) is recorded before yielding a result. However, they could wait for that time at the beginning of the flight and then build new images incrementally as each scanline arrives. That is, add the new scanline to the top of the image and eliminate the oldest data from the bottom in order to always have a complete image and give results for every new scanline. This would imply that the prediction at each time instant would be for the last scanline, that is, the top row of the image. However, in the experiments carried out it has been observed that when using this technique the precision of the results is halved, as there is no context. To maintain the same precision using this technique, it would be necessary to wait 24 s to accumulate 32 scanlines preceding each prediction. That is, in order to give a result for the current scanline it is necessary to wait for the 32 future scanlines, which will produce a delay to get the current response (we will call this delay as “lag time”).

The TSCNN and BiRNN methods can be applied directly to a part of the sequence. Specifically, TSCNN uses a sliding window with different window sizes that can be applied horizontally to a set of scanlines. Since the largest window size used is 50 × 50, and that the result obtained is for the central pixel of the same, it would be necessary to wait 19 s (25 scanlines) for each answer. The BiRNN method, according to the specifications of the article, uses only 3 scanlines. However, as it is bidirectional, it would be necessary to wait 2.28 s, as it needs to wait for the next scanlines to get the current prediction. With the proposed method, it is possible to use only the previous information and obtain a response at each time frame, therefore the response time would be only 0.76 s. A summary of these results is shown in the column “lag time” of

Table 7. Comparison of runtimes (in seconds). The column lag time represents the time to wait until the current scanline is classified. This lag is because many algorithms need to use not only the current scanline and the previous ones, but also the following scanlines to have more context. The runtime column shows the time that the algorithm takes to yield a response once all the information is provided. The last column shows the sum of times, which corresponds to the time perceived by the user in getting a response.

Method	Lag Time	Runtime	Total Time
SegNet	24	0.2929	24.2929
DeepLabv3	24	0.1871	24.1871
U-Net	24	0.1044	24.1044
SelAE	24	0.0007	24.0007
TSCNN	19	0.0078	19.0078
BiRNN	2.28	0.0006	2.2806
Our approach	0.76	0.5259	1.2859

.

We have also added to this table the column “runtime” to compare the execution times once all the necessary data (scanlines) are available. These runtimes were obtained using a Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz with 16 GB DDR4 RAM and a Nvidia GeForce GTX 1070 GPU. The fastest methods are BiRNN, SelAE and TSCNN, since these are networks with few parameters and binary outputs. The processing time of our proposal is divided between the time used by the CMSAE networks, which is 0.0039 s. on average, and that used by the selected classifier, which for SVM with $c=15$ is 0.5220 s. Since the CMSAE networks can be run in parallel, the average time spent by the network with more parameters has been calculated. In this case these are the networks with 6 layers, 128 filters and a kernel of $1\times 7$. While our proposal has a slower runtime than the compared approaches, the perceived runtime (column “Total time”) would be the smallest by far, and since the runtime is less than both the lag time and the time needed by the sensor to return each scanline, the method could be used for the realtime detection of oil spills and ships during flight.

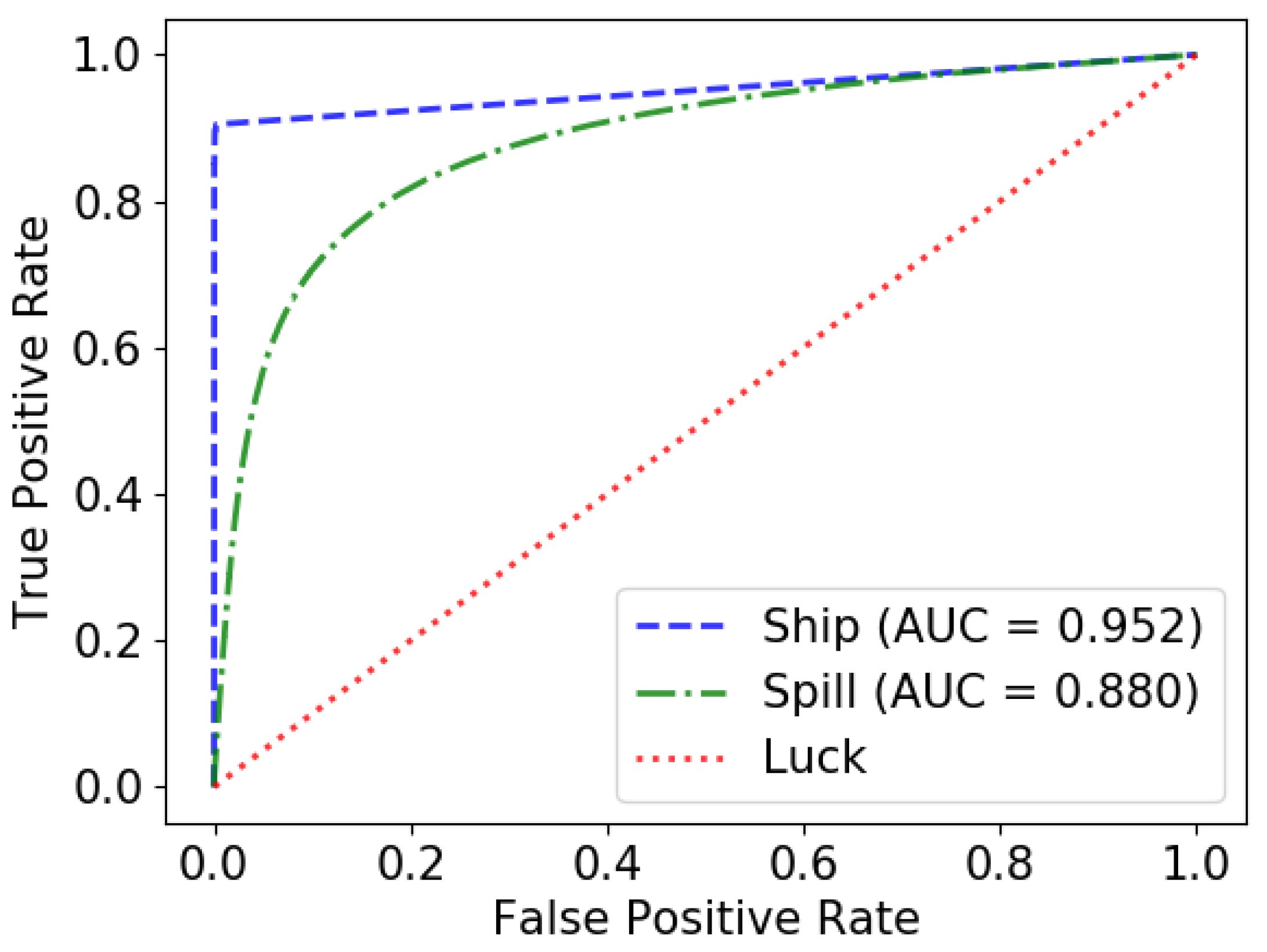
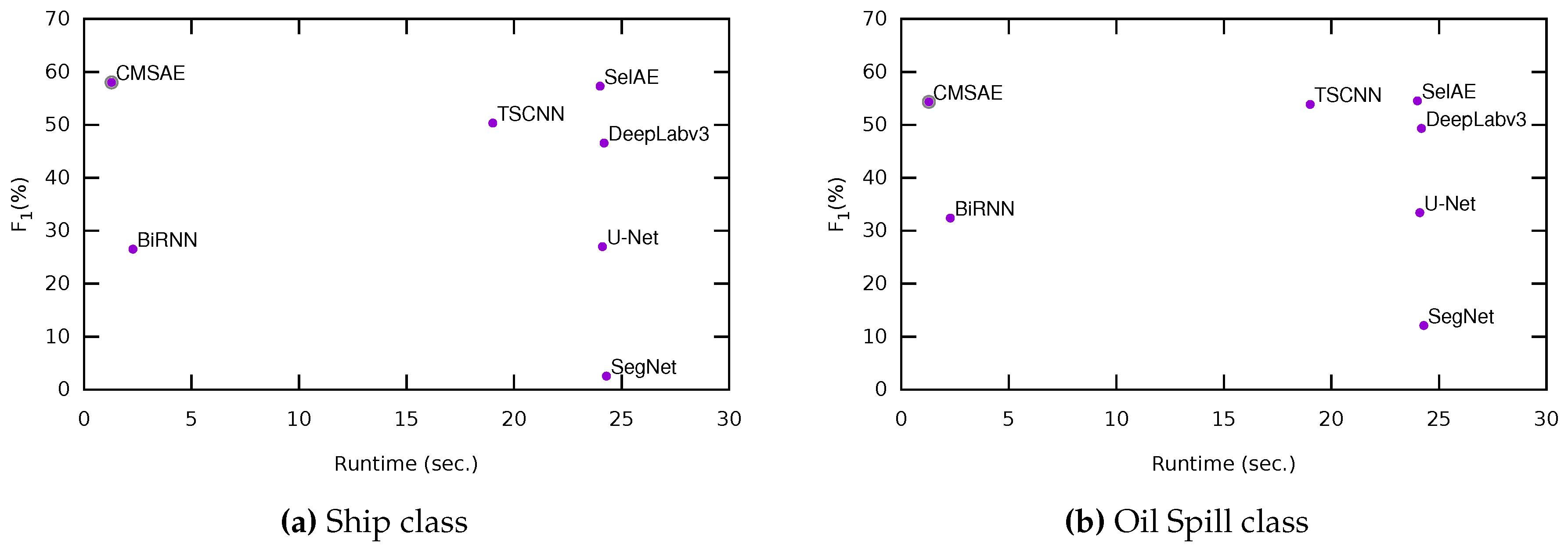
Having evaluated the classification performance and the runtime as stand-alone measures of merit, we will now analyze them jointly from a Multi-objective Optimization Problem (MOP) perspective. Note that classification performance and runtime could by opposing goals as improving one of them could deteriorate the other. Figure 10 compares these two variables graphically for the ship and oil spill classes. In this way, it can be clearly seen how the proposed method is much closer to the target, being much more efficient and also obtaining the best result for these two classes.

5. Conclusions

In this work we propose a new architecture called Convolutional LSTM Selectional AutoEncoders (CMSAE) to detect multiple targets such as coast, oil spill and ships from SLAR images. By running multiple CMSAE networks in parallel and combining their outputs using a machine learning classifier (SVM), the method can use only a few scanlines to obtain reliable results and also provide a quick response during live aircraft flights.

Different configurations of the networks and final classifier were evaluated. The best selected setup (CMSAE+SVM with $c=15$) was compared to previous methods from the state of the art (BiRNN, TSCNN, U-Net, SegNet, DeepLabv3, and SelAE) using a dataset with 51 flight sequences (with a total of 24,582 scanlines).

The proposed approach obtained the highest pixel level average $F_1$ (67.39%) with the lowest lag time. This result was validated using statistical significance tests, showing that the presented method significantly outperforms the results obtained by SelAE. In addition to the $F_1$ evaluation at the pixel level, the proposed approach also obtained the best results at blob level detection (90.85%) using the Intersection over Union metric.

One of the reasons why the proposed approach obtains better results than the rest of the state-of-the-art methods is because it uses specialized classifiers. This allows the networks to learn the particular characteristics of each class. Another reason is the use of a higher resolution for the scanline amplitude, which benefits the detection of ships and the more accurate detection of the edges for the different classes.

With respect to the time needed to process each scanline of the SLAR sensor during flight, the proposed method achieved the best result (1.28 s), far better than the second algorithm with best classification results (SelAE, which takes 20 s).

Therefore, we can summarize that the proposed method (CMSAE+SVM) obtains better average results when detecting the target objectives, with a higher precision for detecting their shape and requiring significantly less time.

With respect to the ship and spill classes, the proposed method detects 90.13% and 92.11% of these targets, respectively. It should be noted that SLAR sensors generate a large amount of noise and, in our case, the dataset used contains noise in all flight sequences. This noise prevents the detection of these classes and sometimes it can also be confused with them.

Based only on SLAR intensity data, the accuracy obtained from the state-of-the-art algorithms, including the proposed method, is still low to rely exclusively on them for ship and oil spill detection. However, they can be used to aid a human operator that can visually inspect the candidate targets.

Future work is intended to consider the metadata provided by the sensor and the aircraft to improve the results of the classification. Information such as flight altitude, airplane speed or wind speed could help to better discriminate between the true targets and the noise generated by the sensors.