Net Cloud Thinning, Low-Level Cloud Diminishment, and Hadley Circulation Weakening of Precipitating Clouds with Tropical West Pacific SST Using MISR and Other Satellite and Reanalysis Data
Abstract
1. Introduction
- (1)
- Use the TWP domain to test how SST distribution properties such as kurtosis change with domain-mean SST, and how these changes influence local cloud-precipitation-SST relationships and the local Hadley Circulation. Key TOA cloud effects examined are cloud albedo and net cloud forcing.
- (2)
- Quantify the importance of local SST gradients versus SST in determining total high cloud amount locally and away from the highest SSTs, as well as the convective SST onset as a function of large-scale mean SST.
- (3)
- As in Kubar et al. [2], investigate the cloud structure of precipitating systems by constructing Z-α histograms; how do these change with convective strength and domain-mean SST?
- (4)
- Investigate the extent to which local and domain-wide TWP high cloud changes can be attributed to associated ω500/large-scale dynamics changes, versus those that may be related to either an Iris Effect or thermodynamic effects associated with horizontal SST structure changes.
2. Observational and Reanalysis Datasets
2.1. MISR
2.2. CERES (Clouds and the Earth’s Radiant Energy System)
2.3. TRMM 3b42
2.4. ERA-Interim
3. Cloud Definitions and Domain-Choice
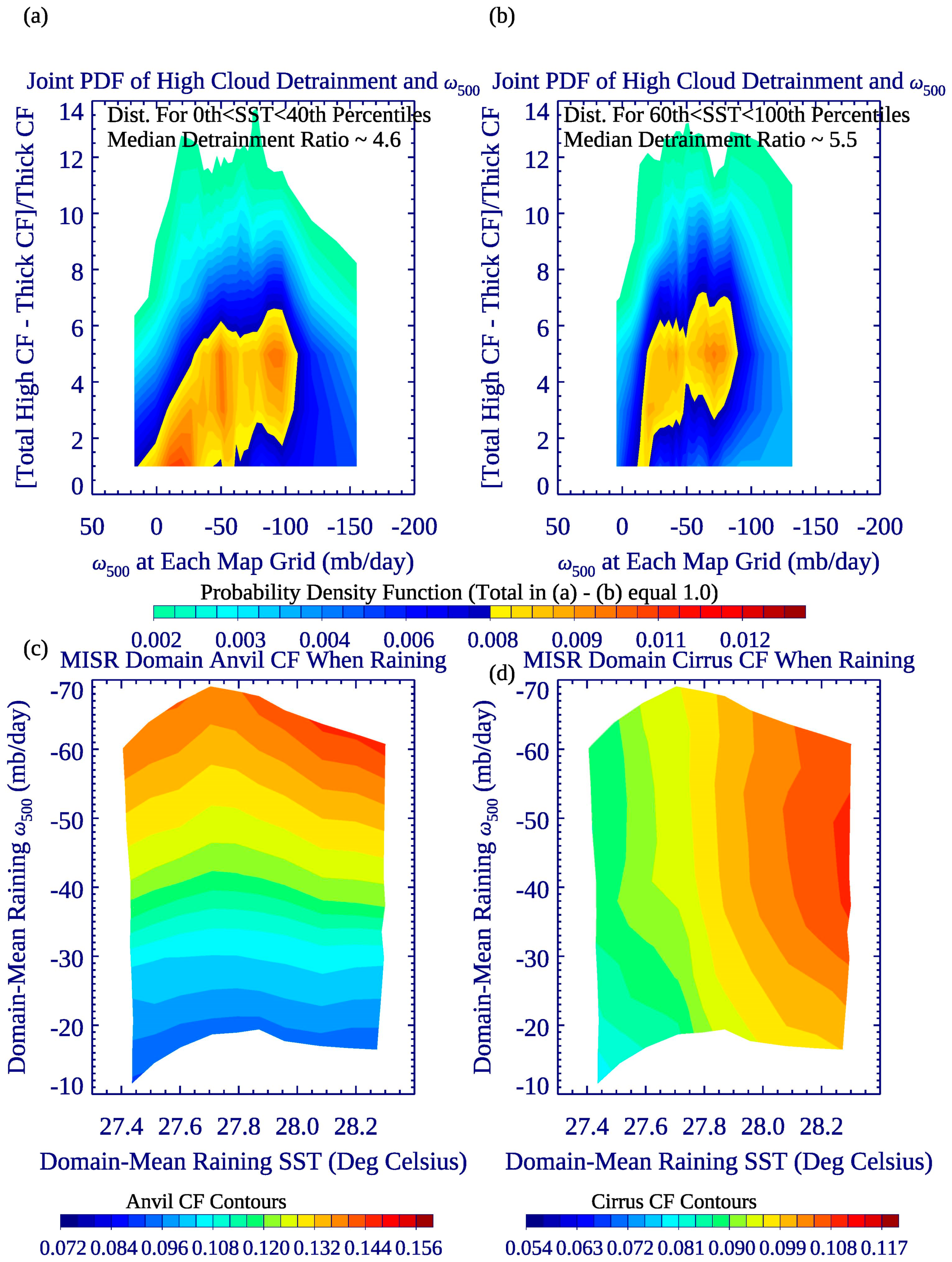
4. Results and Discussion
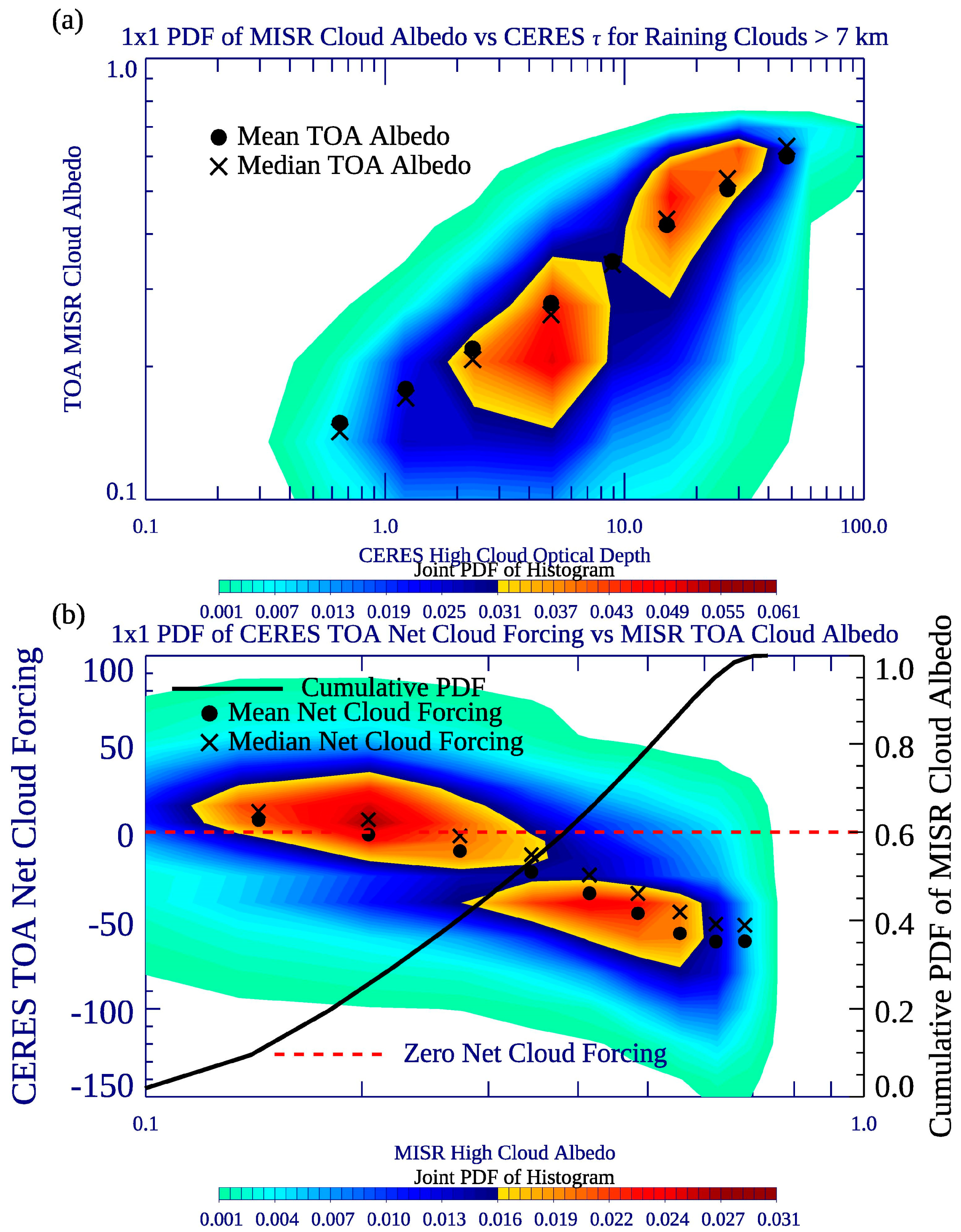
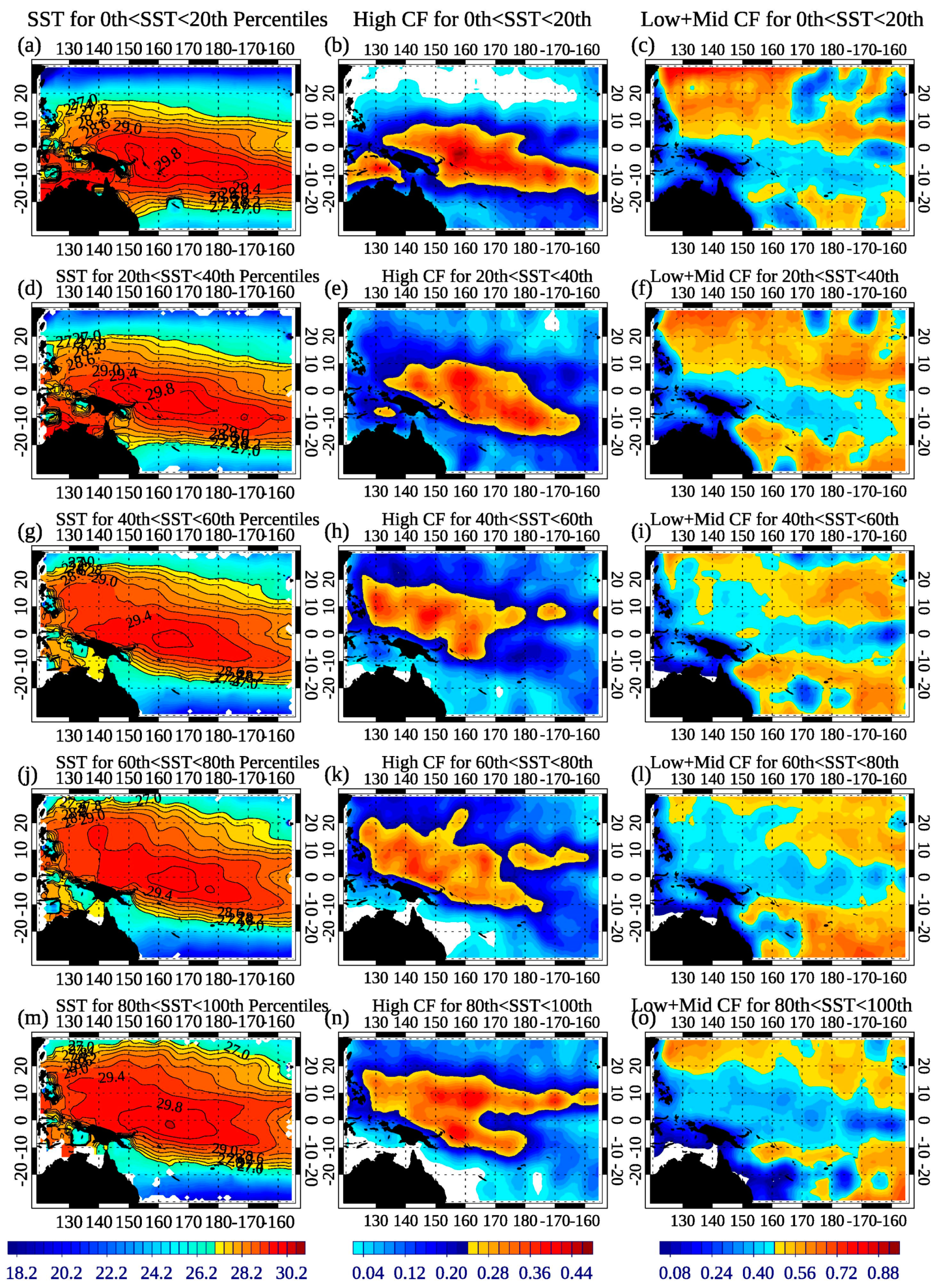
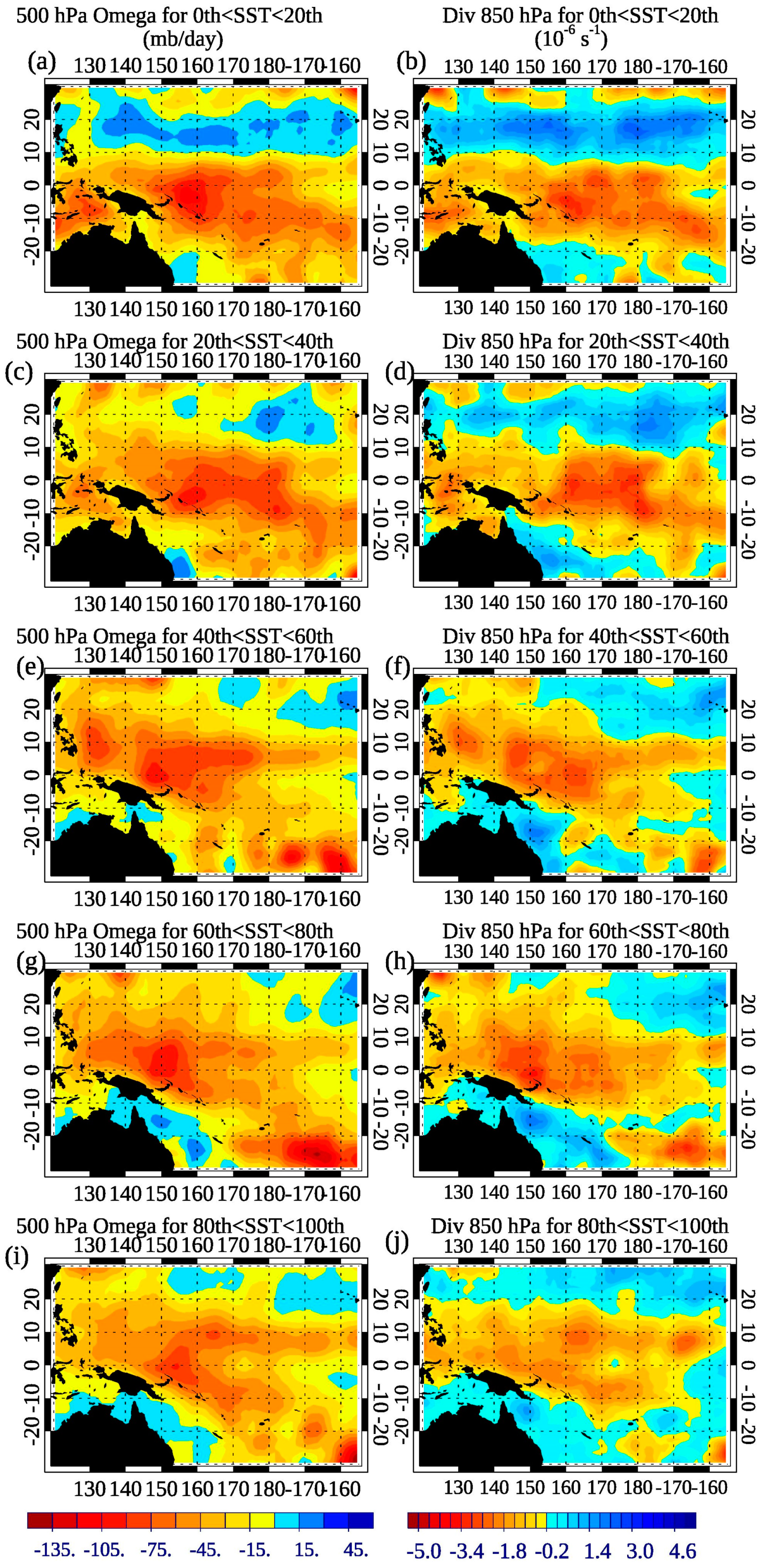
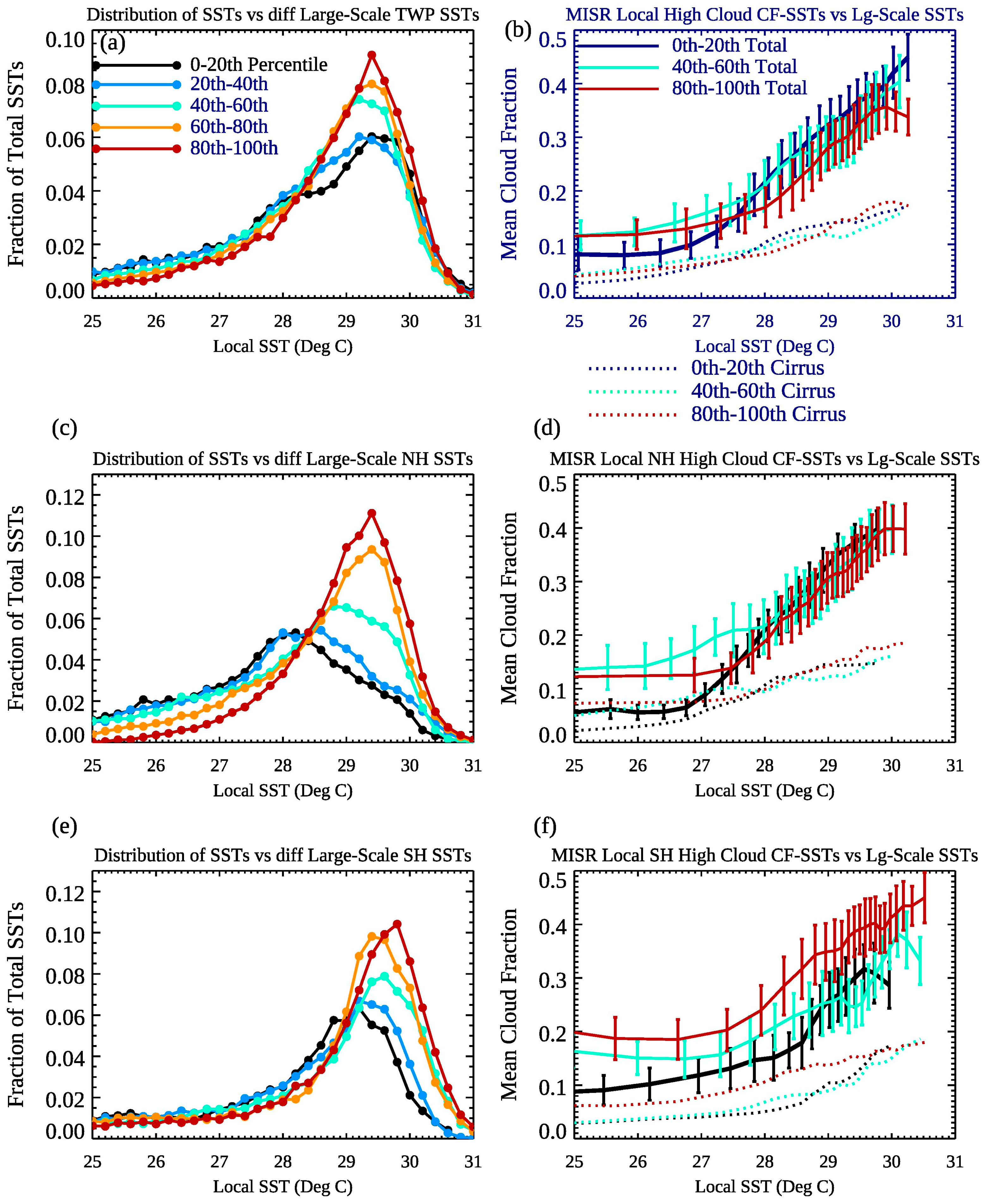
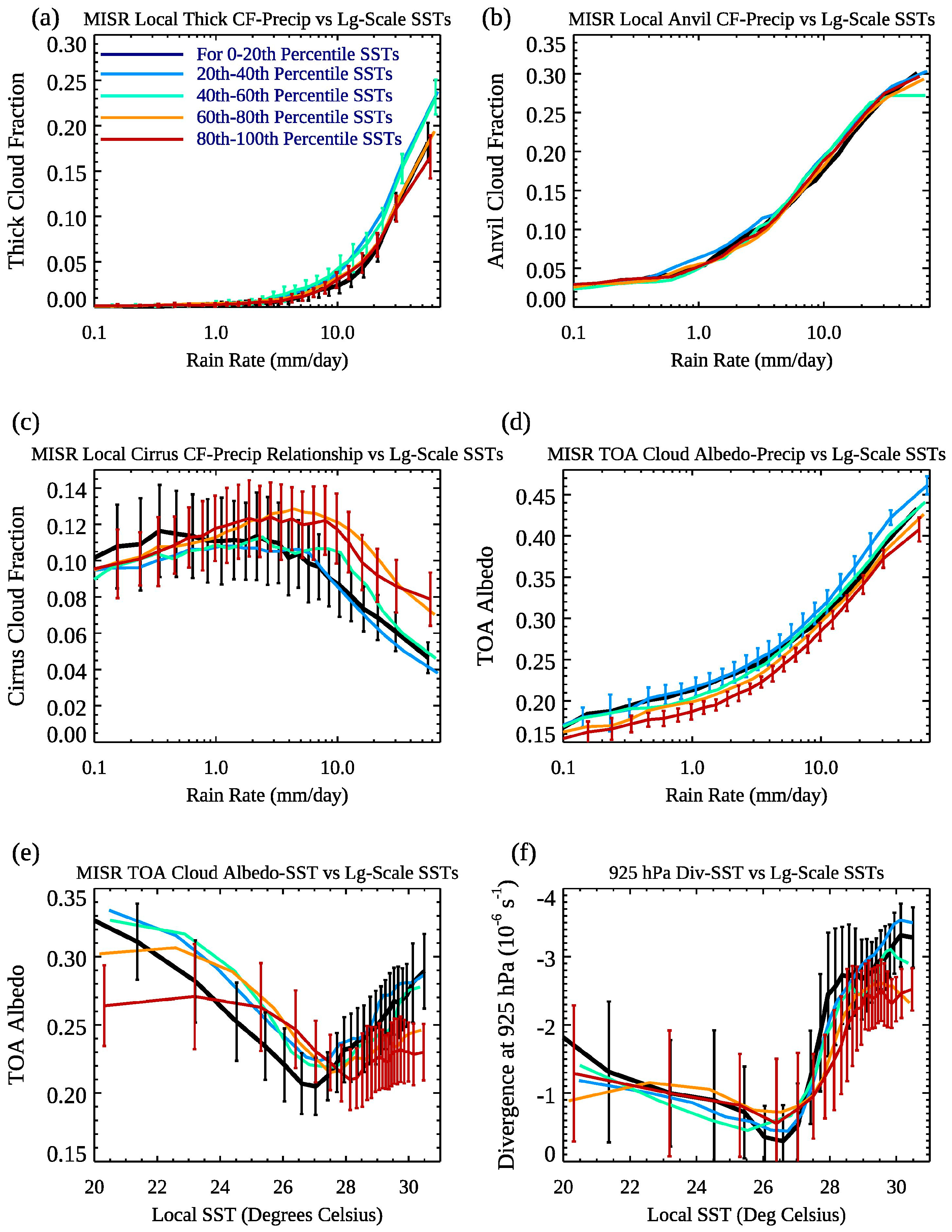
4.1. Distribution of SST, Clouds, Rain Fraction, Albedo, and Circulation vs. Large-Scale SST
4.2. Relationships vs. SSTlocal as a Function of Mean SSTTWP
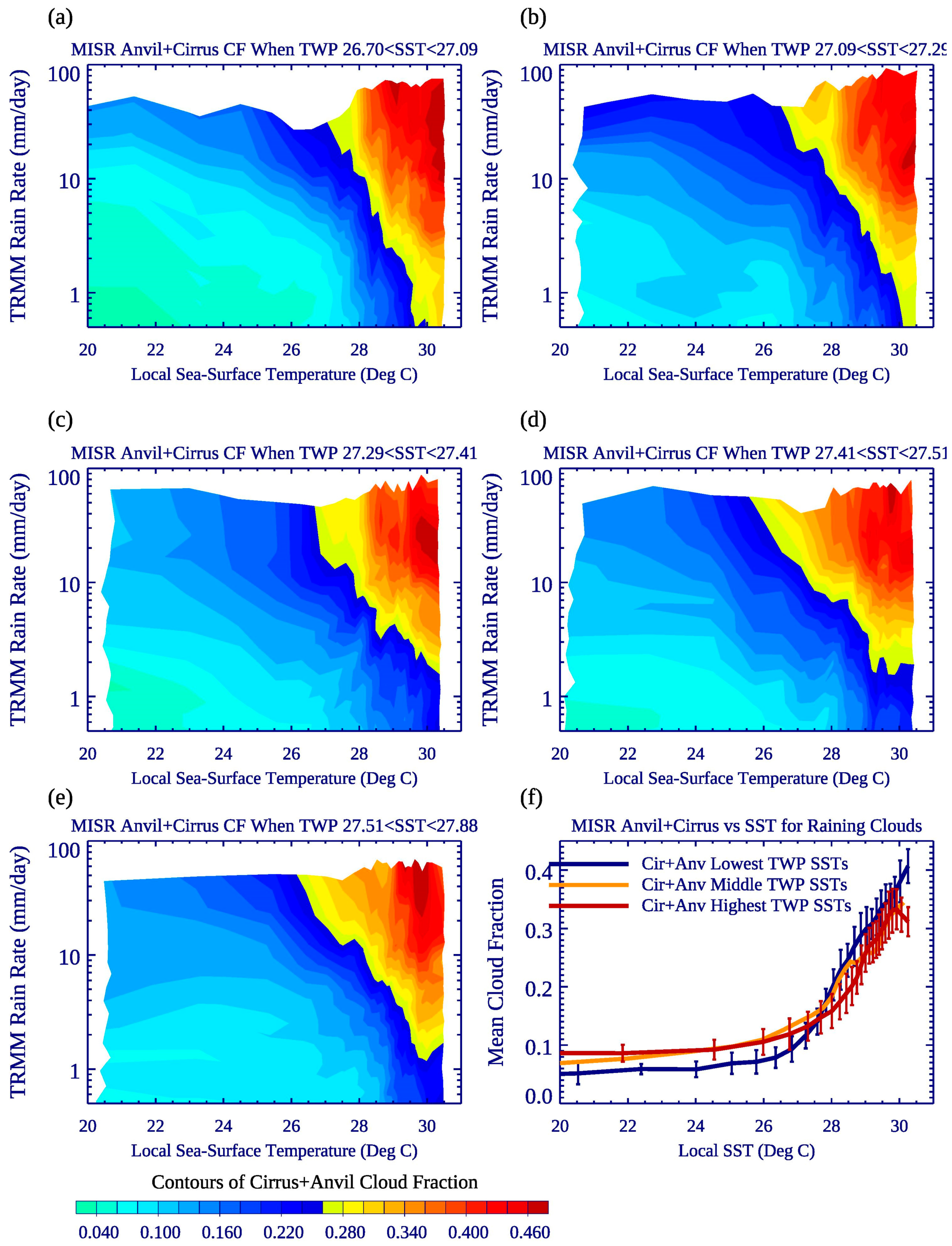
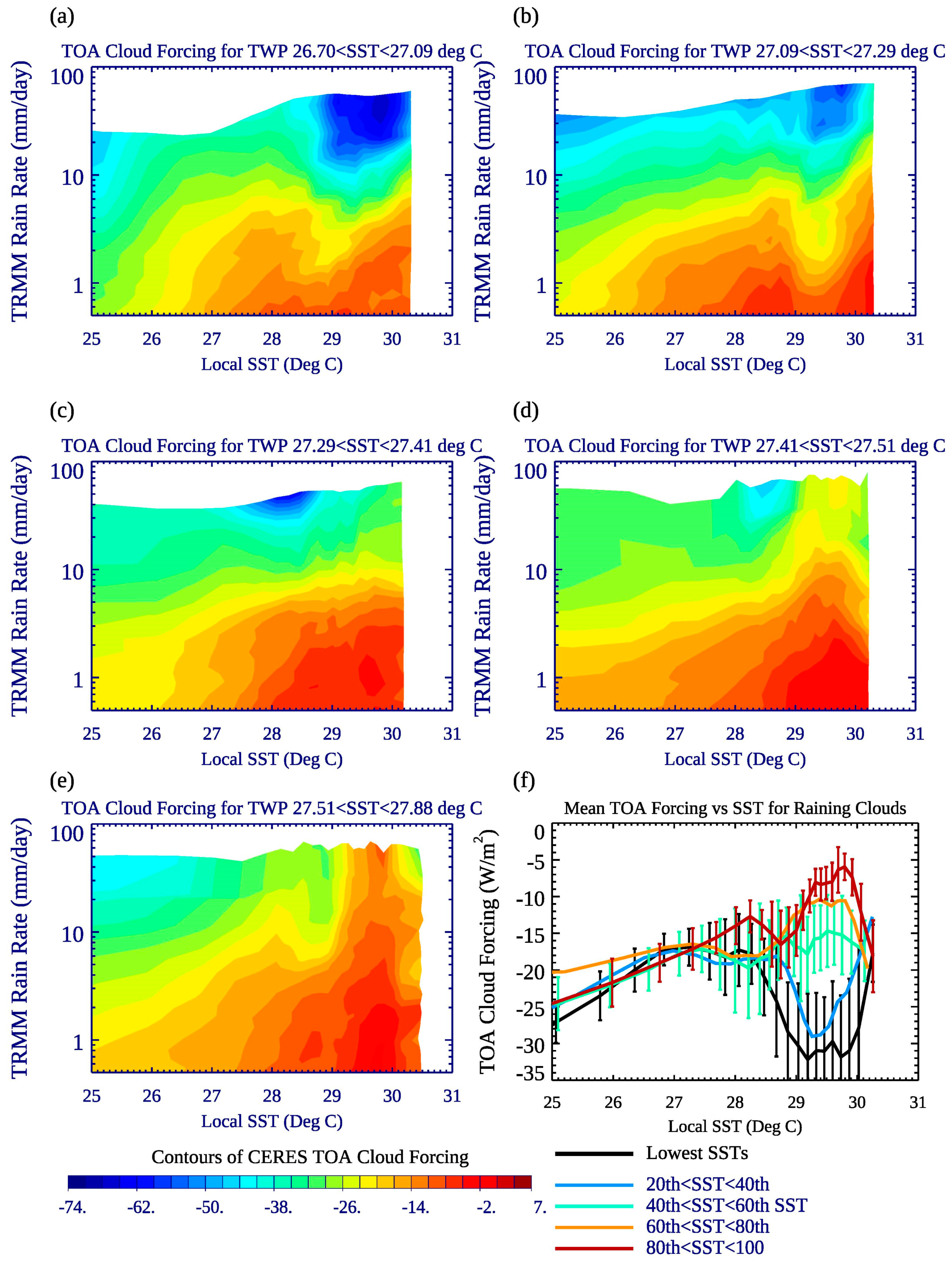
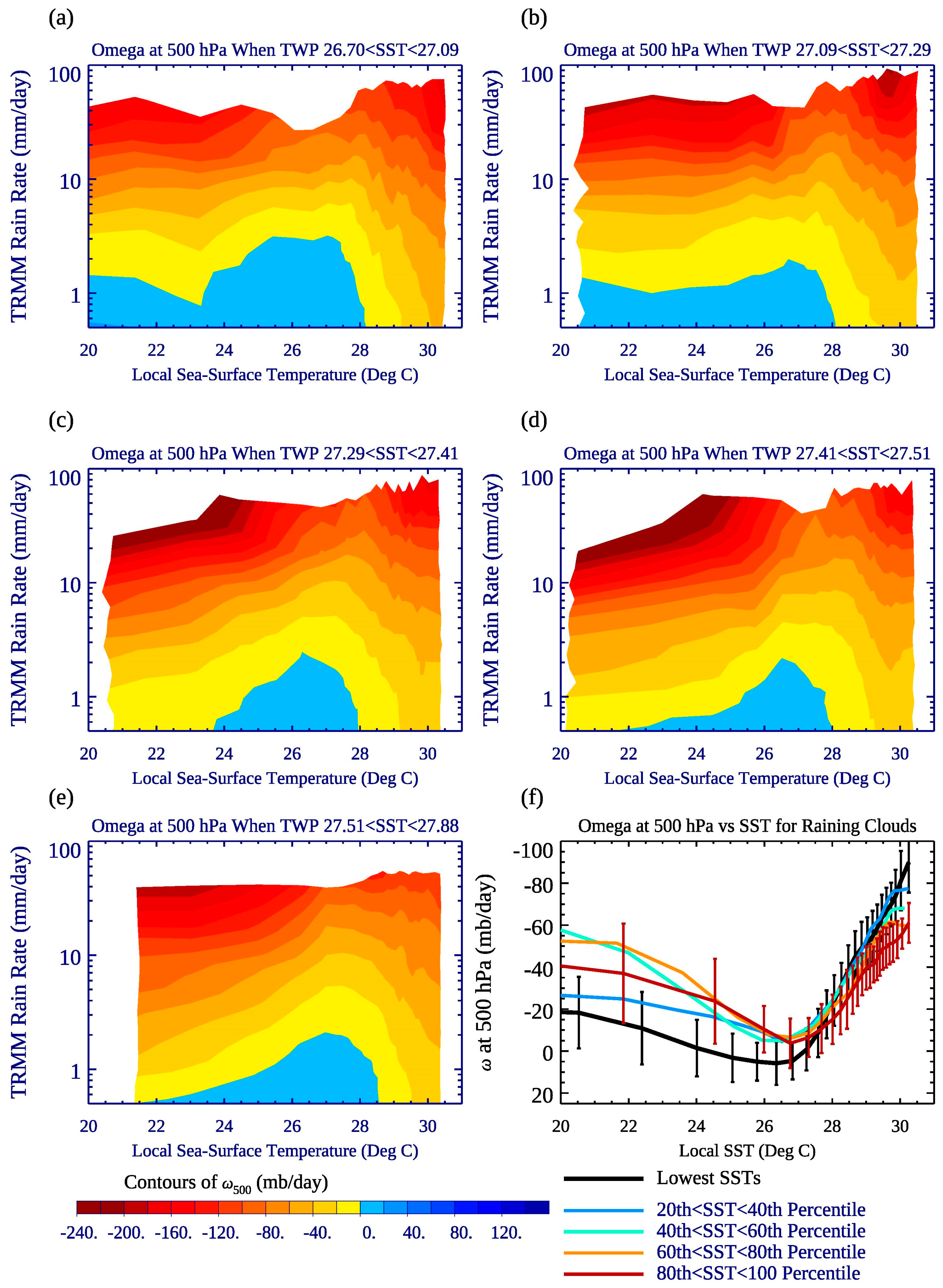
4.3. Local Cloud-Rain Rate Relationships for TWP SST Quintiles
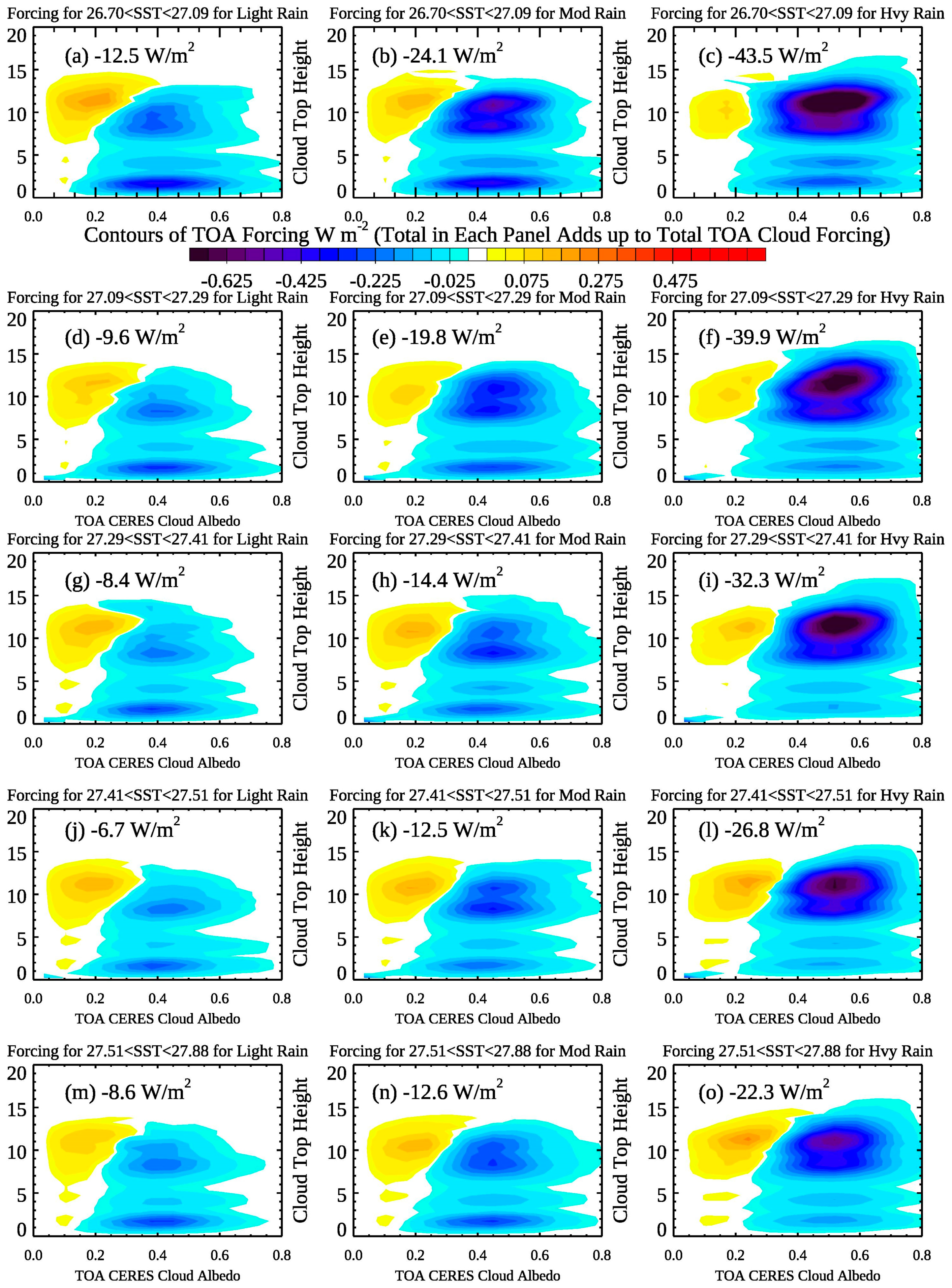
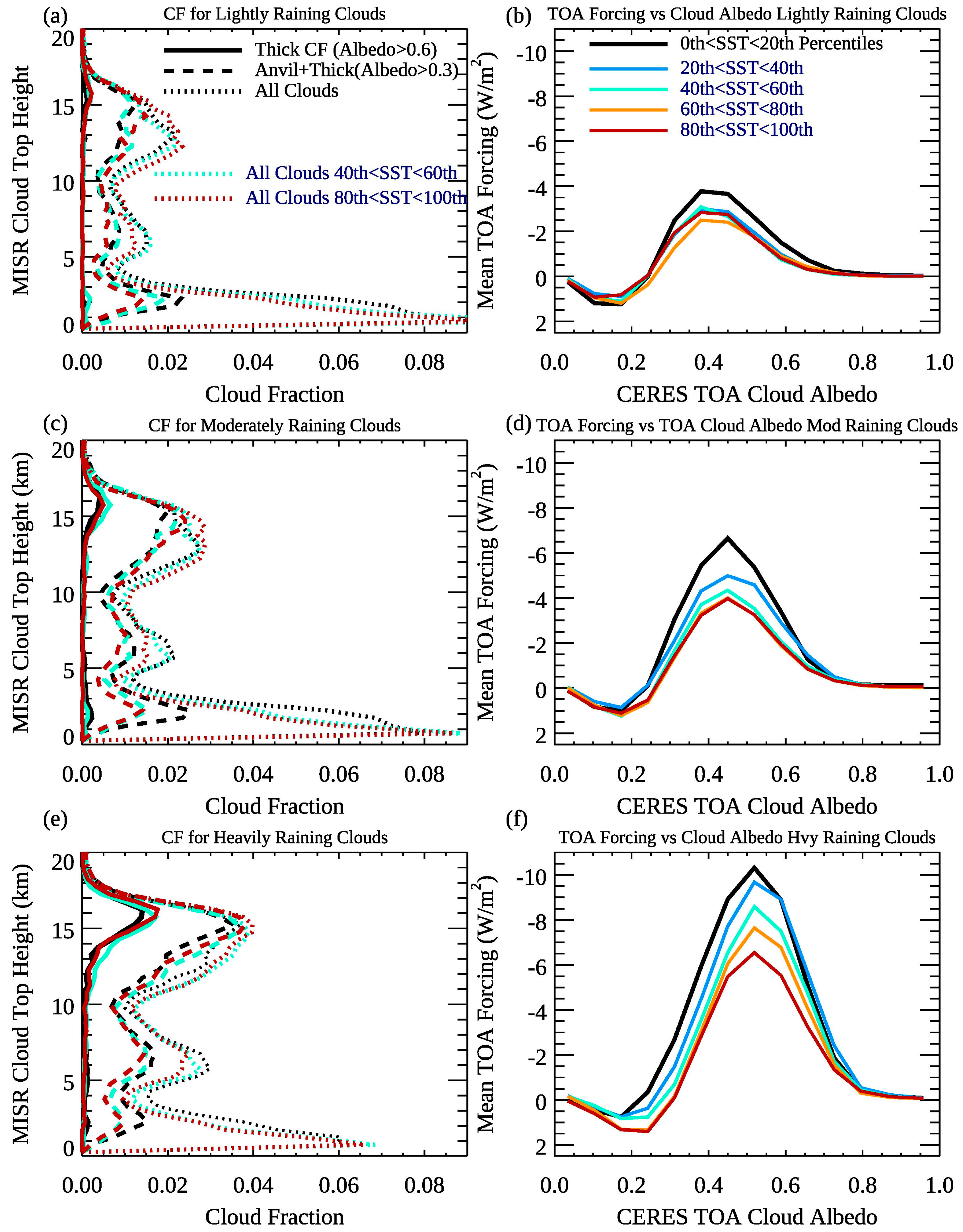
4.4. Z-α Histograms of Cloud Fraction and Net Cloud Forcing
- (1)
- Regardless of domain-mean-SST, as precipitation increases, high cloud fraction increases, with a shift towards brighter, more reflective clouds, with thick high clouds being more abundant during heavily raining systems. The highest TWP SST quintile also has slightly more thick anvil cloud than lower TWP SSTs for heavily raining systems. Regardless of SST, these clouds are very deep, with tops between 14–15 km.
- (2)
- With increasing rain rate, there is an increase, regardless of SST, of mid-level presumably congestus clouds, centered between 6–7 km. These are moderately reflective clouds, with a mean albedo of approximately 0.4. Thicker low clouds become less abundant with increasing precipitation category.
- (3)
- The most significant change from cool domain-mean SST to warm domain-mean SST is a decrease in mid-level clouds and a stronger decrease in low-level clouds, regardless of precipitation category. The results for the different cloud categories as a function of domain-mean SST and precipitation category are summarized in Table 1.
4.5. Tropical West Pacific Domain Mean Relationships
4.6. Robustness and Representativeness of Findings
5. Conclusions
- (1)
- For any domain-mean TWP SST, high cloud fraction of raining clouds increases both with local SST and rain rate, with maximum anvil+cirrus CF maximizing as local SSTs reach 30 °C, and slightly more anvil+cirrus clouds for lower domain-mean TWP periods (e.g., the 0th–20th domain-mean SST quintile versus the 80th–100th domain-mean SST quintile). This coincides with stronger ascent near SSTs of 29–30 °C during lower TWP SST quintiles, but weaker ascent over locally cooler SSTs off the equator compared to mean warm TWP periods.
- (2)
- The net domain-effect changes in the local SST/cloud/precipitation effects is a redistribution of high clouds as a function of domain-mean TWP SST, rather than a net change such that a zero-slope assumption for the regression between TWP SST and TWP high CF cannot be rejected. When only raining portions of the grid are considered, there is an increase of high CF per degree of TWP SST warming of 10% deg−1. When only the southern SST is indexed, however, there is a net increase of high cloud amount with SST.
- (3)
- As the TWP warms, the mean net cloud forcing increases (e.g., becomes less negative) by about 10 W m−2 per degree of TWP warming for mean raining grids, though locally cloud systems have even more profound differences as a function of mean TWP SST. Where high cloud systems are more prolific, at SSTs around 29°–30°, the TOA net forcing is much less negative for the fifth TWP SST quintile compared the lowest TWP SST quintile, at around -8 W m−2 compared to −30 W/m2, when averaged over all rain rates. This is due primarily to a greater portion of cirrus clouds, and somewhat less reflective anvil clouds, and fewer moderately thick low and middle clouds, perhaps due in part to the weaker low-level convergence over high SSTs by 0.5 – 1.0 × 10−6 s−1 (highest versus lowest TWP SST quintiles).
- (4)
- For a given local rain rate, local anvil cloud fraction is the same for all five TWP SST quintiles, making anvil cloud amount a ‘universal’ proxy for rain rates in the TWP. Since anvil clouds are defined as high clouds with albedos between 0.3 and 0.6, this relationship has ramifications for validation studies of precipitation sensors, as an albedo-based high cloud definition can quantify rain rates over a range of local and large-scale SSTs. In contrast, cirrus clouds are more abundant for a given heavy rain rate (> 10 mm day−1) as the entire domain warms, and this characteristic of convection, along with slightly less thick cloud, especially for the most heavily raining clouds, makes deep convective systems less reflective as the domain-mean SST warms.
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Tompkins, A.M. Organization of tropical convection in low vertical wind shears: The role of water vapor. J. Atmos. Sci. 2001, 58, 529–545. [Google Scholar] [CrossRef]
- Kubar, T.L.; Hartmann, D.L.; Wood, R. 2007: Radiative and convective driving of tropical high clouds. J. Clim. 2007, 20, 5510–5526. [Google Scholar] [CrossRef]
- Kubar, T.L.; Hartmann, D.L. Vertical structure of tropical oceanic convective clouds and its relation to precipitation. Geophys. Res. Lett. 2008, 35, L03804. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Nigam, S. On the role of sea surface temperature gradients in forcing low-level winds and convergence in the tropics. J. Atmos. Sci. 1987, 44, 2418–2436. [Google Scholar] [CrossRef]
- Back, L.E.; Bretherton, C.S. On the relationship between SST gradients, boundary layer winds, and convergence over the tropical oceans. J. Clim. 2009, 22, 4182–4196. [Google Scholar] [CrossRef]
- Back, L.E.; Bretherton, C.S. Geographic variability in the export of moist static energy and vertical motion profiles in the tropical Pacific. Geophys. Res. Lett. 2006, 33, L17810. [Google Scholar] [CrossRef]
- Wang, C. ENSO, Atlantic climate variability, and the Walker and Hadley circulations. In The Hadley Circulation: Present, Past and Future; Diaz, H.F., Bradley, R.S., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 173–202. [Google Scholar]
- Kubar, T.L.; Behrangi, A. The coupling of convection, westerly winds, and SST hot spots as characterized by satellite observations and reanalysis data, part I: Lagged relationships and the Predator-Prey model. J. Clim. under review.
- Kubar, T.L.; Behrangi, A. The coupling of convection, atmospheric dynamics, and SST hot spots as characterized by satellite observations and reanalysis data, part II: Horizontal structure, insights about the SPCZ, and cirrus-SST interactions. J. Clim. under review.
- Johnson, N.C.; Xie, S.-P. Changes in the sea surface temperature threshold for tropical convection. Nature Geosci. 2010, 3, 842–845. [Google Scholar] [CrossRef]
- Graham, N.E.; Barnett, T.P. Sea surface temperature, surface wind divergence, and convection over tropical oceans. Science 1987, 238, 657–659. [Google Scholar] [CrossRef] [PubMed]
- Neelin, J.D.; Held, I.M. Modeling tropical convergence based on the moist static energy budget. Mon. Wea. Rev. 1987, 115, 3–12. [Google Scholar] [CrossRef]
- Sud, Y.C.; Walker, G.K.; Lau, K.M. Mechansisms regulating sea-surface temperatures and deep convection in the tropics. Geophys. Res. Lett. 1999, 26, 1019–1022. [Google Scholar] [CrossRef]
- Su, H.; Read, W.G.; Jiang, J.H.; Waters, J.L.; Wu, D.L.; Fetzer, E.J. Enhanced positive water vapor feedback associated with tropical deep convection: New evidence from AURA MLS. Geophys. Res. Lett. 2006, 33, L05709. [Google Scholar] [CrossRef]
- Behrangi, A.; Kubar, T.L.; Lambrigtsen, B. Phenomenological Description of Tropical Clouds Using CloudSat Cloud Classification. Mon. Wea. Rev. 2012, 140, 3235–3249. [Google Scholar] [CrossRef]
- Kubar, T.L.; Waliser, D.E.; Li, J.-L. Boundary layer and cloud structure controls on tropical low cloud cover using A-Train satellite data and ECMWF analyses. J. Clim. 2011, 24, 194–215. [Google Scholar] [CrossRef]
- Waliser, D.E.; Graham, N.E. Convective cloud systems and warm-pool sea surface temperatures: Coupled interactions and self-regulation. J. Geophys. Res. Atmos. 1993, 98, 12881–12893. [Google Scholar] [CrossRef]
- Bjerknes, J.; Allison, L.J.; Kreins, E.R.; Godshall, F.A.; Warnecke, G. Satellite mapping of the Pacific tropical cloudiness. Bull. Amer. Met. Soc. 1969, 50, 313–322. [Google Scholar] [CrossRef][Green Version]
- Manabe, S.D.; Hahn, G.; Holloway, J.L. The seasonal variation of the tropical circulation as simulated by a global model of the atmosphere. J. Atmos. Sci. 1974, 31, 43–83. [Google Scholar] [CrossRef]
- Cornejo-Garrido, A.G.; Stone, P.H. On the heat balance of the Walker circulation. J. Atmos. Sci. 1977, 34, 1155–1162. [Google Scholar] [CrossRef]
- Liebmann, B.; Hartmann, D.L. Interannual variations of outgoing IR associated with tropical circulation changes during 1974–1978. J. Atmos. Sci. 1982, 39, 1153–1162. [Google Scholar]
- Jauregui, Y.R.; Takahashi, K. Simple physical-empirical model of the precipitation distribution based on a tropical sea surface temperature threshold and the effects of climate change. Clim. Dyn. 2018, 50, 2217–2237. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Chou, M.-D.; Hou, A.Y. Does the Earth have an adaptive infrared Iris? Bull. Amer. Meteor. Soc. 2001, 82, 417–432. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Michelsen, M.L. No Evidence for Iris. Bull. Amer. Meteor. Soc. 2002, 83, 249–254. [Google Scholar] [CrossRef]
- Fu, Q.; Baker, M.; Hartmann, D.L. Tropical cirrus and water vapor: An effective Earth infrared iris feedback? Atmos. Chem. Phys. 2002, 2, 31–37. [Google Scholar] [CrossRef]
- Kubar, T.L.; Waliser, D.E.; Li, J.-L.; Jiang, X. On the annual cycle variability and correlations of oceanic low-topped clouds with large-scale circulation using Aqua MODIS and ERA-Interim. J. Clim. 2012, 25, 6152–6174. [Google Scholar] [CrossRef]
- Ramanathan, V.; Collins, W. Thermodynamic regulation of ocean warming by cirrus clouds deduced from observations of the 1987 El Niño. Nature 1991, 351, 27–32. [Google Scholar] [CrossRef]
- Lin, B.; Wong, T.; Wielicki, B.A.; Hu, Y. Examination of the decadal tropical mean ERBS nonscanner radiation data for the Iris Hypothesis. J. Clim. 2004, 17, 1239–1246. [Google Scholar] [CrossRef]
- Rapp, A.D.; Kummerow, C.; Berg, W.; Griffith, B. An evaluation of the proposed mechanism of the adaptive Iris hypothesis using TRMM VIRS and PR measurements. J. Clim. 2005, 18, 4185–4194. [Google Scholar] [CrossRef]
- Dessler, A.E. A determination of the cloud feedback from climate variations over the past decade. Science 2010, 330, 1523–1527. [Google Scholar] [CrossRef]
- Igel, M.R.; Drager, A.J.; van den Heever, S.C. A CloudSat cloud object partitioning technique and assessment and integration of deep convective anvil sensitivities to sea surface temperature. J. Geophy. Res. Atmos. 2014, 119, 10515–10535. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Kim, W.; Yeh, S.-W.; Masunaga, H.; Kwon, M.-J.; Jo, H.S.; Huang, L. Revisiting the iris effect of tropical cirrus clouds with TRMM and A-Train satellite data. J. Geophys. Res. Atmos. 2017, 122, 5917–5931. [Google Scholar] [CrossRef]
- Chae, J.-H.; Sherwood, S.C. Insights into cloud-top height and dynamics from the seasonal cycle of cloud-top heights observed by MISR in the West Pacific Region. J. Atmos. Sci. 2010, 67, 248–261. [Google Scholar] [CrossRef]
- Sun, W.; Loeb, N.G.; Davies, R.; Loukachine, K.; Miller, W.F. Comparison of MISR and CERES top-of-atmosphere albedo. Geophys Res. Lett. 2006, 33, L23810. [Google Scholar] [CrossRef]
- Moroney, C.; Di Girolamo, L.; Zhao, G. MISR level 3 cloud fraction by altitude product quality statement 04 January 2018. Available online: http://eosweb.larc.nasa.gov (accessed on 22 May 2019).
- Davies, R.; Jovanovic, V.M.; Moroney, C.M. Cloud heights measured by MISR from 2000 to 2015. J. Geophys. Res. Atmos. 2017, 122, 3975–3986. [Google Scholar] [CrossRef]
- McPhaden, J.J. Evolution of the 2002/03 El Niño. Bull. Amer. Meteor. Soc. 2004, 85, 677–696. [Google Scholar] [CrossRef]
- Diner, D.J.; Davies, R.; Varnai, T.; Moroney, C.; Borel, C.; Gerstl, S.A.W.; Nelson, D.L. Multi-angle Imaging SpectroRadiometer (MISR): Level 2 top-of-atmosphere albedo algorithm theoretical basis. JPL Rep. 1999, 88, D-13401. [Google Scholar]
- Loeb, N.; Sun, W.; Miller, W.F.; Loukachine, K.; Davies, R. Fusion of CERES, MISR, and MODIS measurements for top-of-atmosphere radiative flux validation. J. Geophys. Res: Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Di Girolamo, L.; Menzies, A.; Zhao, G.; Mueller, K.; Moroney, C.; Diner, D.J. Multi-angle Imaging SpectroRadiometer (MISR) cloud fraction by altitude algorithm theoretical basis document. Available online: https://eospso.gsfc.nasa.gov/sites/default/files/atbd/MISR_CFBA_ATBD.pdf (accessed on 27 May 2019).
- Marchand, R.; Ackermand, T.; Smyth, M.; Rossow, W.B. A review of cloud top height and optical depth histograms from MISR, ISCCP, and MODIS. J. Geophys. Res. 2010, 111. [Google Scholar] [CrossRef]
- Stubenrauch, C.J.; Rossow, W.B.; Kinne, S.; Ackerman, S.; Cesana, G.; Chepfer, H.; Di Girolamo, L.; Getzewich, B.; Guignard, A.; Heidinger, A.; et al. Assessment of global cloud datasets from satellites. Bull. Amer. Meteor. Soc. 2013, 94, 1031–1049. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Smith, G.L.; Cooper, J.E. Clouds and the Earth’s radiant energy system (CERES): An Earth observing system experiment. Bull. Amer. Meteor. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Loeb, N.G.; Kato, S.; Loukachine, K.; Manalo-Smith, N. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Terra satellite, Part II: Methodology. J. Atmos. Ocean. Tech. 2005, 22, 338–351. [Google Scholar] [CrossRef]
- Loeb, N.G.; Kato, S.; Loukachine, K.; Manalo-Smith, N.; Doeeling, D.R. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Terra satellite. Part II: Validation. J. Atmos. Ocean. Techn. 2007, 24, 564–584. [Google Scholar] [CrossRef]
- Smith, G.L.; Mlynczak, P.E.; Potter, G.L. A technique using principal component analysis to compare seasonal cycles of Earth radiation from CERES and model computations. J. Geophys. Res. 2012, 117, D09116. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeor. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Hendon, H.; Woodberry, K. The diurnal cycle of tropical convection. J. Geophys. Res. 1993, 98, 16623–16637. [Google Scholar] [CrossRef]
- Behrangi, A.; Lebsock, M.; Wong, S.; Lambrigtsen, B. On the quantification of oceanic rainfall using space-borne sensors. J. Geophys. Res. 2012, 117, D20105. [Google Scholar] [CrossRef]
- Behrangi, A.; Stephens, G.; Adler, R.F.; Huffman, G.J.; Lambrigtsen, B.; Lebsock, M. An update on the oceanic precipitation rate and its zonal distribution in light of advanced observations from space. J. Clim. 2014, 27, 3957–3965. [Google Scholar] [CrossRef]
- Simmons, A.; Uppala, S.; Dee, D.; Kobayashi, S. ERA-Interim: New ECMWF reanalysis products from 1989 onwards. ECMWF Newsletter, No. 110, ECMWF, Reading United Kingdom. 2006. Available online: https://www.ecmwf.int/node/17713 (accessed on 27 May 2019).
- Waliser, D.E. Formation and limiting mechanisms for very high sea surface temperature: Linking the dynamics and the thermodynamics. J. Clim. 1996, 9, 161–188. [Google Scholar] [CrossRef]
- Johnson, R.H.; Rickenbach, T.M.; Rutledge, S.A.; Schubert, W.H. Trimodal characteristics of tropical convection. J. Clim. 1999, 12, 2397–2418. [Google Scholar] [CrossRef]
- Hamann, U.A.; Walther, B.; Baum, R.; Berrartz, L.; Bugliaro, M.; Derrien, P.N.; Francis, A.; Heidinger, S.; Joro, A.; Kniffka, H.; et al. Remote sensing of cloud top pressure/height from SEVIRI: Analysis of ten current retrieval algorithms. Atmos. Meas. Tech. 2014, 7, 2839–2867. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, G.; Li, J.-L.F. Assessing the radiative effects of global ice clouds based on CloudSat and CALIPSO measurements. J. Clim. 2016, 29, 7651–7674. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N. Parameterization of the solar radiative properties of cirrus clouds. J. Atmos. Sci. 1993, 50, 2008–2025. [Google Scholar] [CrossRef]
- Sohn, B.J.; Yeh, S.-W.; Schmetz, J.; Song, H.-J. Observational evidences of Walker circulation change over the last 30 years contrasting with GCM results. Clim. Dyn. 2013, 40, 1721–1732. [Google Scholar] [CrossRef]
| SST Range of Domain-Mean SST | Precipitation (0.0th–32nd Percentile) | Rain Rate (32nd–68th Percentile) | Rain Rate (68th–99.9th Percentile) |
|---|---|---|---|
| Cirrus, Anvil, Thick, (Total High CF) | Cirrus, Anvil, Thick, (Total High CF) | Cirrus, Anvil, Thick, (Total High CF) | |
| 26.70 °C < SST < 27.09 °C | 0.086, 0.116, 0.005, (0.207) | 0.081, 0.189, 0.025, (0.295) | 0.076, 0.240, 0.0893, (0.405) |
| 27.09 °C < SST < 27.29 °C | 0.077, 0.133, 0.009, (0.219) | 0.078, 0.205, 0.036, (0.319) | 0.076, 0.244, 0.120, (0.440) |
| 27.29 °C < SST < 27.41 °C | 0.076, 0.121, 0.012, (0.209) | 0.082, 0.196, 0.041, (0.320) | 0.084, 0.255, 0.115, (0.454) |
| 27.41 °C < SST < 27.51 °C | 0.089, 0.132, 0.013, (0.234) | 0.089, 0.211, 0.031, (0.331) | 0.096, 0.258, 0.107, (0.461) |
| 27.51 °C < SST < 27.88 °C | 0.096, 0.139, 0.011, (0.246) | 0.094, 0.216, 0.030, (0.340) | 0.093, 0.263, 0.108, (0.464) |
| Middle, Low Clouds, (Total Mid + Low CF) | Middle, Low Clouds, (Total Mid + Low CF) | Middle, Low Clouds, (Total Mid + Low CF) | |
| 26.70 °C < SST < 27.09 °C | 0.119, 0.356, (0.475) | 0.157, 0.346, (0.503) | 0.222, 0.263, (0.485) |
| 27.09 °C < SST < 27.29 °C | 0.118, 0.332, (0.450) | 0.166, 0.310, (0.476) | 0.234, 0.234, (0.468) |
| 27.29 °C < SST < 27.41 °C | 0.119, 0.333, (0.452) | 0.150, 0.296, (0.446) | 0.205, 0.228, (0.433) |
| 27.41 °C < SST < 27.51 °C | 0.105, 0.300, (0.405) | 0.145, 0.271, (0.416) | 0.201, 0.212, (0.413) |
| 27.51 °C < SST < 27.88 °C | 0.100, 0.295, (0.395) | 0.128, 0.272, (0.400) | 0.190, 0.216, (0.406) |
| TWP Variable Pairs | October 2002–September 2004 | October 2002–September 2003 (Mod. El Nino) | October 2003–September 2004 (Near-Neutral Year) |
|---|---|---|---|
| SSTTWP, TRMM (Raining Only) | Rain rate decreases by 4% deg−1 | Rain rate decreases by 8.5% deg−1 | Null Hypothesis of Zero Rain Rate Slope cannot be rejected |
| SSTTWP, MISR High CF (All) | Null Hypothesis of Zero High CF Slope with SST cannot be rejected | Null Hypothesis of Zero High CF Slope with SST cannot be rejected | High CF Decreases by 14% deg−1 |
| SSTTWP, MISR High CF (Raining Only) | High CF Increases by 10% deg−1 | High CF Increases by 15% deg−1 | Null Hypothesis of Zero High CF Slope with SST cannot be rejected |
| SSTTWP, MISR Cirrus (All) | Cirrus CF Increases by 14% deg−1 | Cirrus CF Increases by 17% deg−1 | Null Hypothesis of Zero Cirrus CF Slope cannot be rejected |
| SSTTWP, MISR Cirrus (Raining Only) | Cirrus CF Increases by 28% deg−1 | Cirrus CF Increases by 32% deg−1 | Cirrus CF Increases by 22% deg−1 |
| SSTTWP, Low+Middle CF (Raining Only) | Low+Mid CF Decreases by 10% deg−1 | Low+Mid CF Decreases by 11% deg−1 | Low+Mid CF Decreases by 8% deg−1 |
| SSTTWP, TOA Cloud Albedo (Raining Only) | Cloud Albedo Decreases by 14% deg−1 | Cloud Albedo Decreases by 12% deg−1 | Cloud Albedo Decreases by 17% deg−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubar, T.L.; Jiang, J.H. Net Cloud Thinning, Low-Level Cloud Diminishment, and Hadley Circulation Weakening of Precipitating Clouds with Tropical West Pacific SST Using MISR and Other Satellite and Reanalysis Data. Remote Sens. 2019, 11, 1250. https://doi.org/10.3390/rs11101250
Kubar TL, Jiang JH. Net Cloud Thinning, Low-Level Cloud Diminishment, and Hadley Circulation Weakening of Precipitating Clouds with Tropical West Pacific SST Using MISR and Other Satellite and Reanalysis Data. Remote Sensing. 2019; 11(10):1250. https://doi.org/10.3390/rs11101250
Chicago/Turabian StyleKubar, Terence L., and Jonathan H. Jiang. 2019. "Net Cloud Thinning, Low-Level Cloud Diminishment, and Hadley Circulation Weakening of Precipitating Clouds with Tropical West Pacific SST Using MISR and Other Satellite and Reanalysis Data" Remote Sensing 11, no. 10: 1250. https://doi.org/10.3390/rs11101250
APA StyleKubar, T. L., & Jiang, J. H. (2019). Net Cloud Thinning, Low-Level Cloud Diminishment, and Hadley Circulation Weakening of Precipitating Clouds with Tropical West Pacific SST Using MISR and Other Satellite and Reanalysis Data. Remote Sensing, 11(10), 1250. https://doi.org/10.3390/rs11101250







