A Multi-Primitive-Based Hierarchical Optimal Approach for Semantic Labeling of ALS Point Clouds
Abstract
1. Introduction
2. Related works
3. Semantic Labeling via a Multi-Primitive-Based Hierarchical Optimal Approach
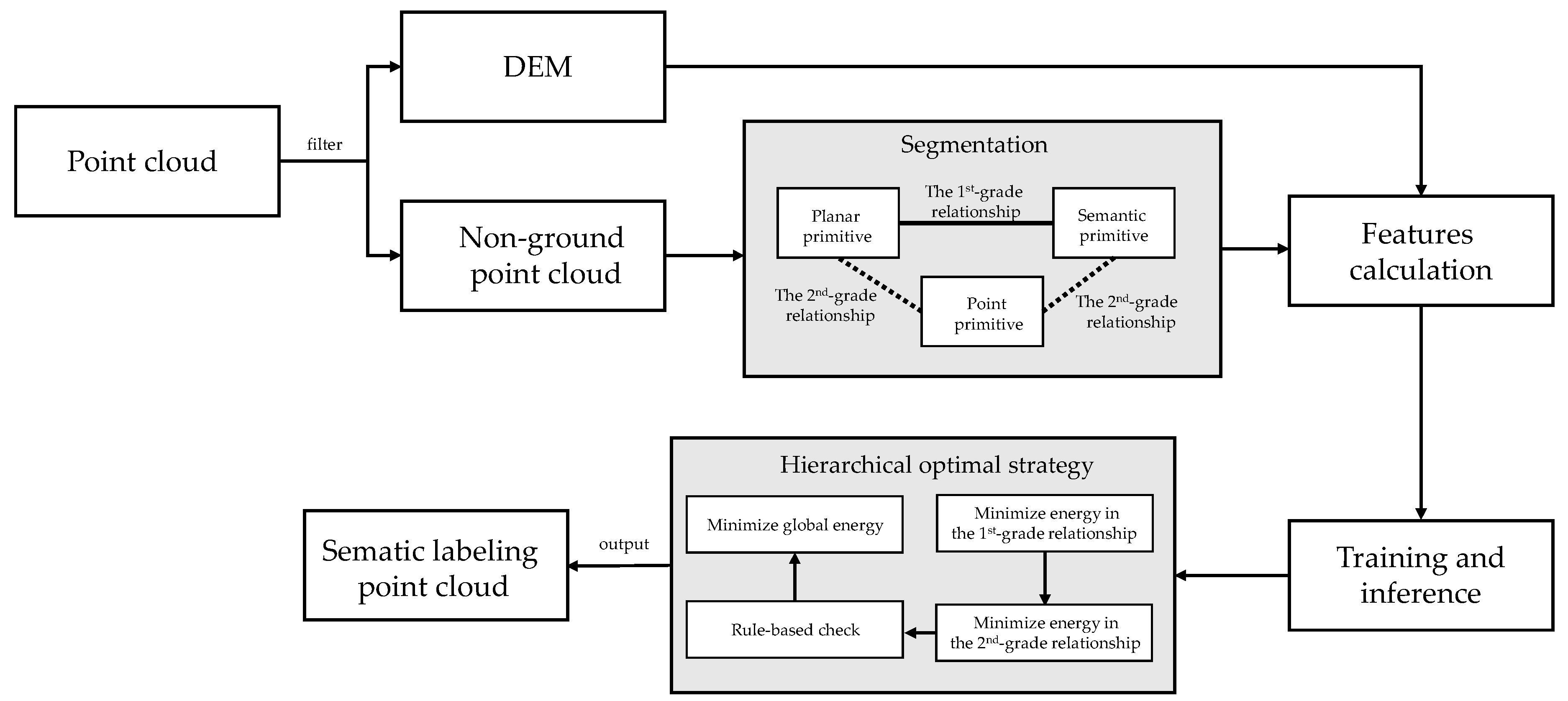
3.1. Overview of the Approach
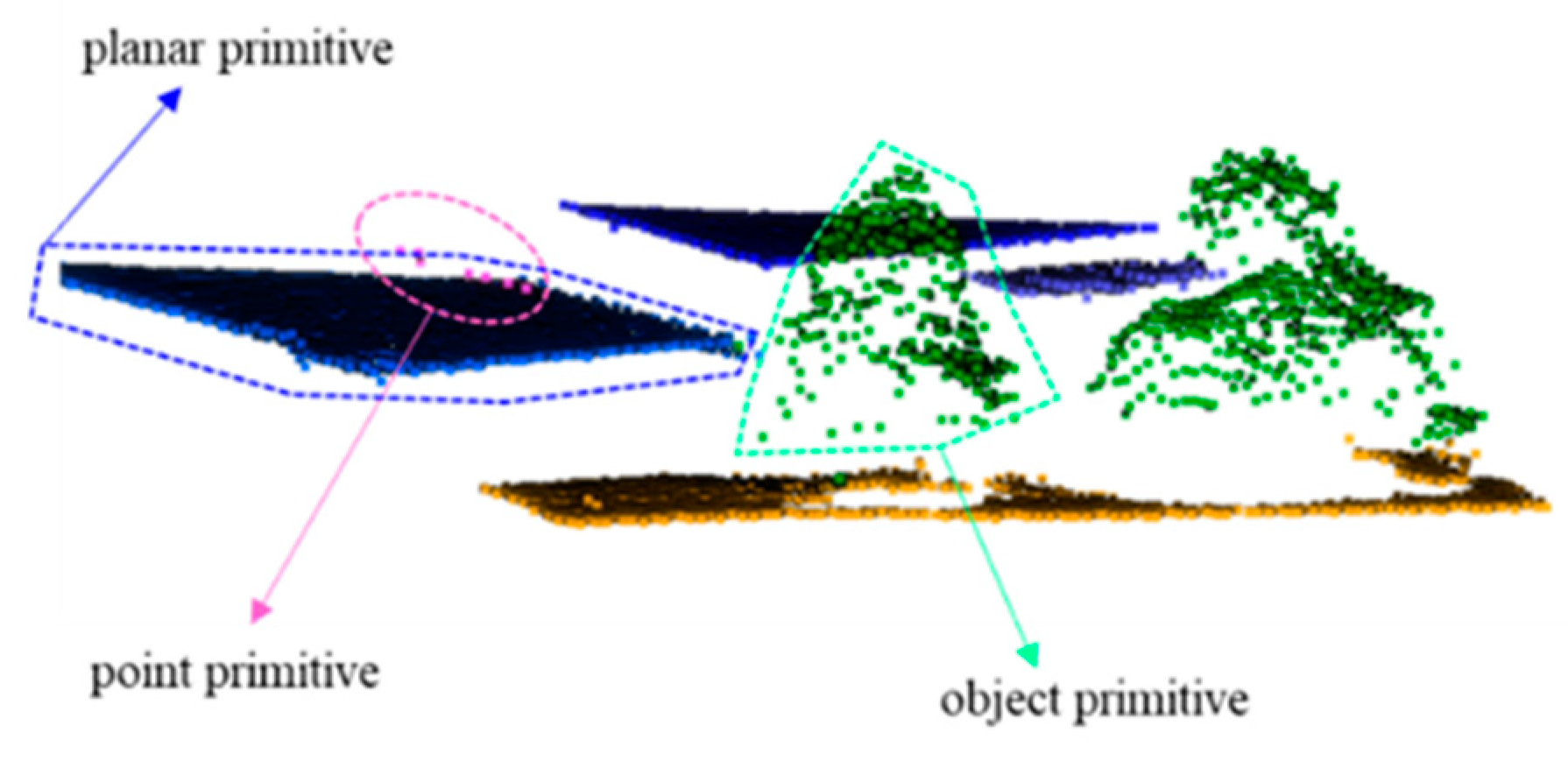
3.2. Multi-Primitive-Based Segmentation
3.2.1. Planar Segmentation
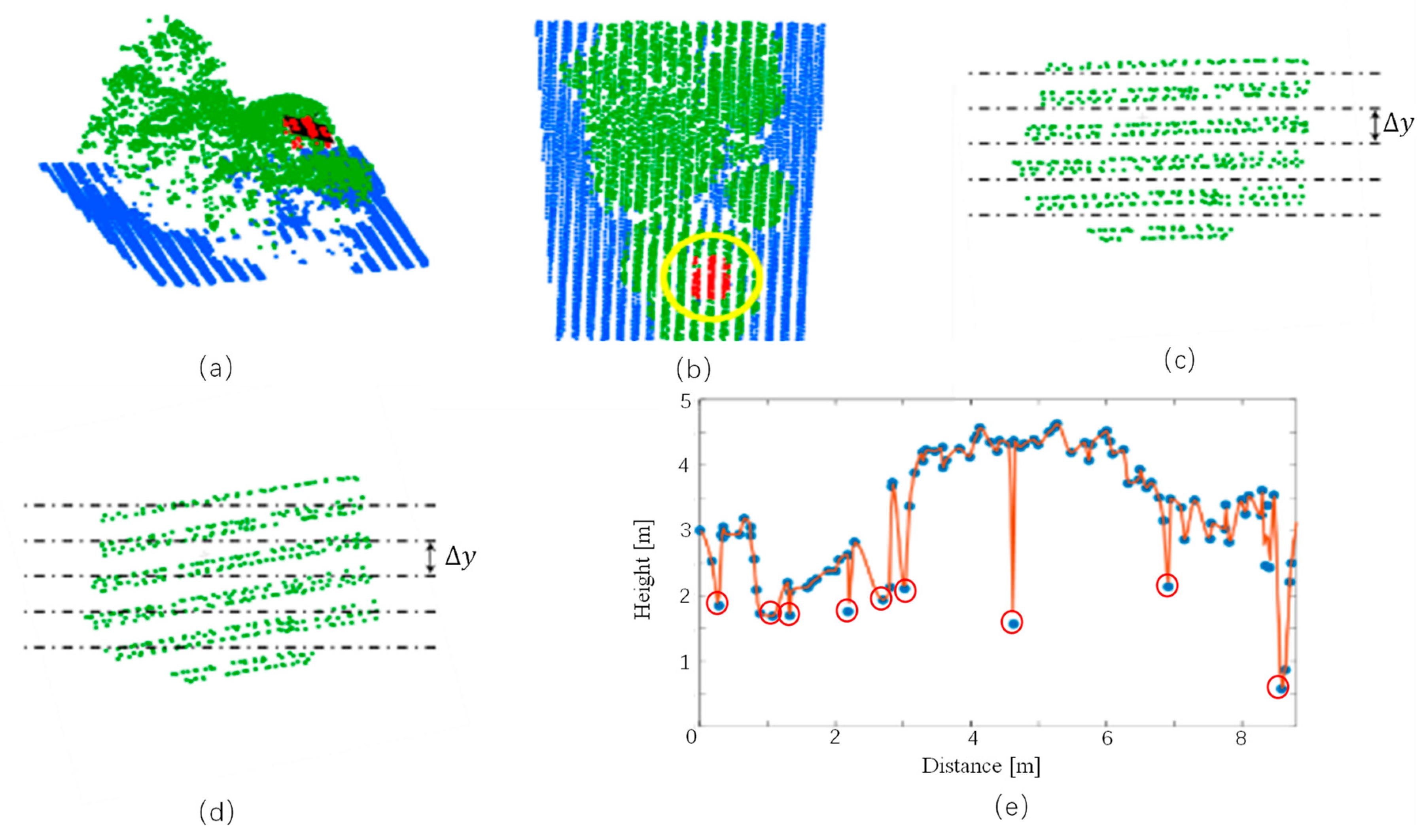
3.2.2. Object Segmentation
| Algorithm 1. Segmentation |
| Input: Point Cloud = {P}. 1. Grid P to subset point sets SP Calculate the normals of each and put in the corresponding Normal set . 2. For i = 0 to size (SP) 3. Obtain the planar set PS } from by a RANSAC-based algorithm. 4. Put the rest points into an outlier set OS. 5. For j = 0 to size (PS) 6. Generate a new object segment subset = . 7. For k = 0 to size ( ) 8. Find kn neighbors of pk Nk., pk . 9. If size (Nk ) > size () and oss = then 10. If Do OB is true then 11. (Nk ). 12. Remove points from original set, i.e., SP – , PS - and OS - . 13. End if 14. End if 15. If size (Nk ) > size () and then 16. Do RG to update oss, SP and OS. 17. End if 18. End for k 19. If = 20. Do planar RG to update , SP and OS. 21. Else 22. Put oss into the object segment set OSS. 23. End if 24. End for j 25. End for i 26. For i = 0 to size (PS)-1 27. If then 28. If merge conditions are true: with j = i + 1 to size (SP), . 29. For i = 0 to size (OSS)-1 30. If then 31. If merge conditions are true: with j = i + 1 to size (OSS), . 32. Output: PS, OSS, OS. |
3.3. Feature Description for Semantic Labeling
3.3.1. Unary Features
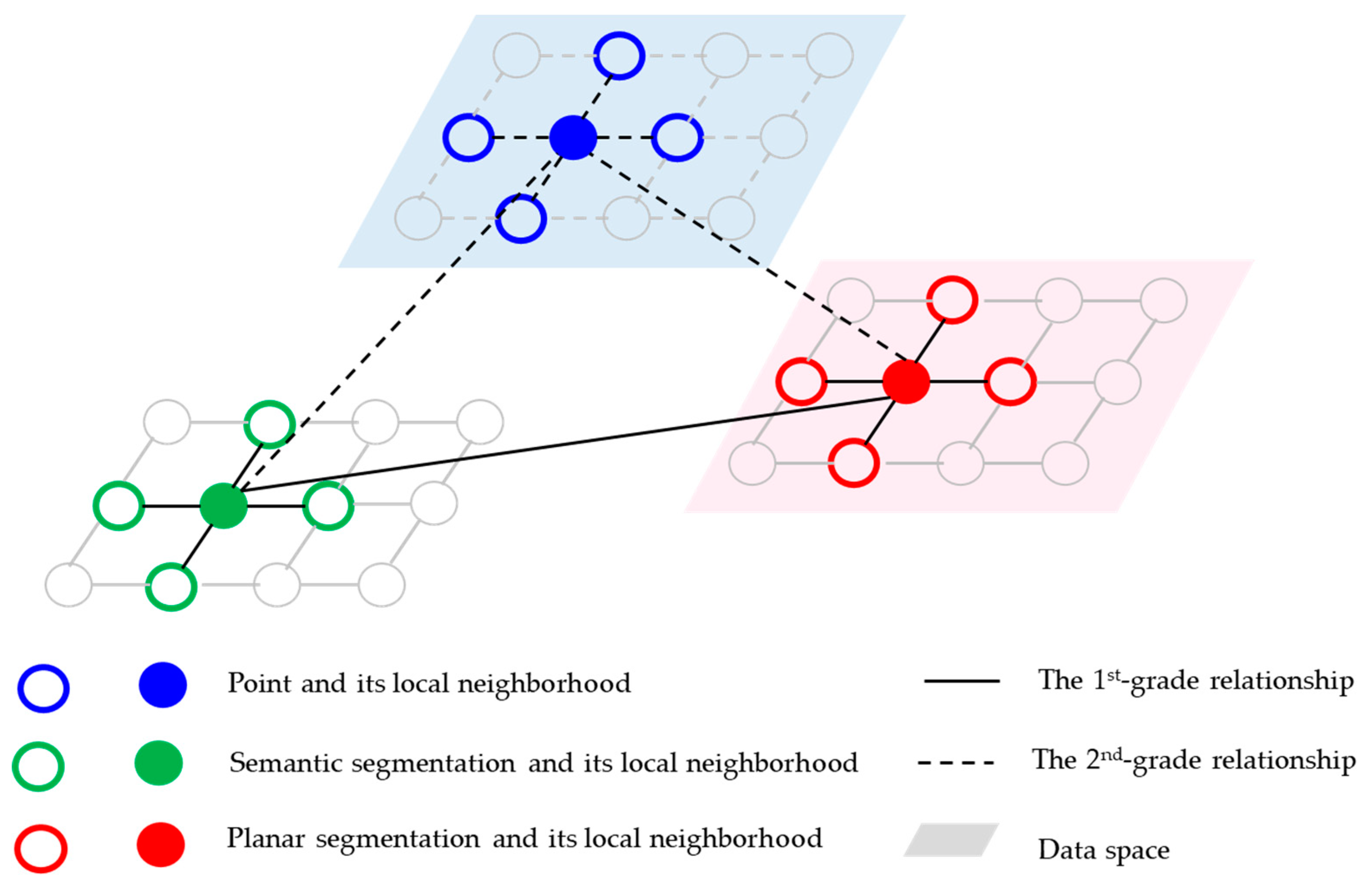
3.3.2. Pairwise Features
3.3.3. Heuristic Rule-Based Features
3.4. Hierarchical Labeling Strategy
3.4.1. Conditional Random Fields (CRFs)
3.4.2. Calculation of Local Energies
3.4.3. Hierarchical Strategy
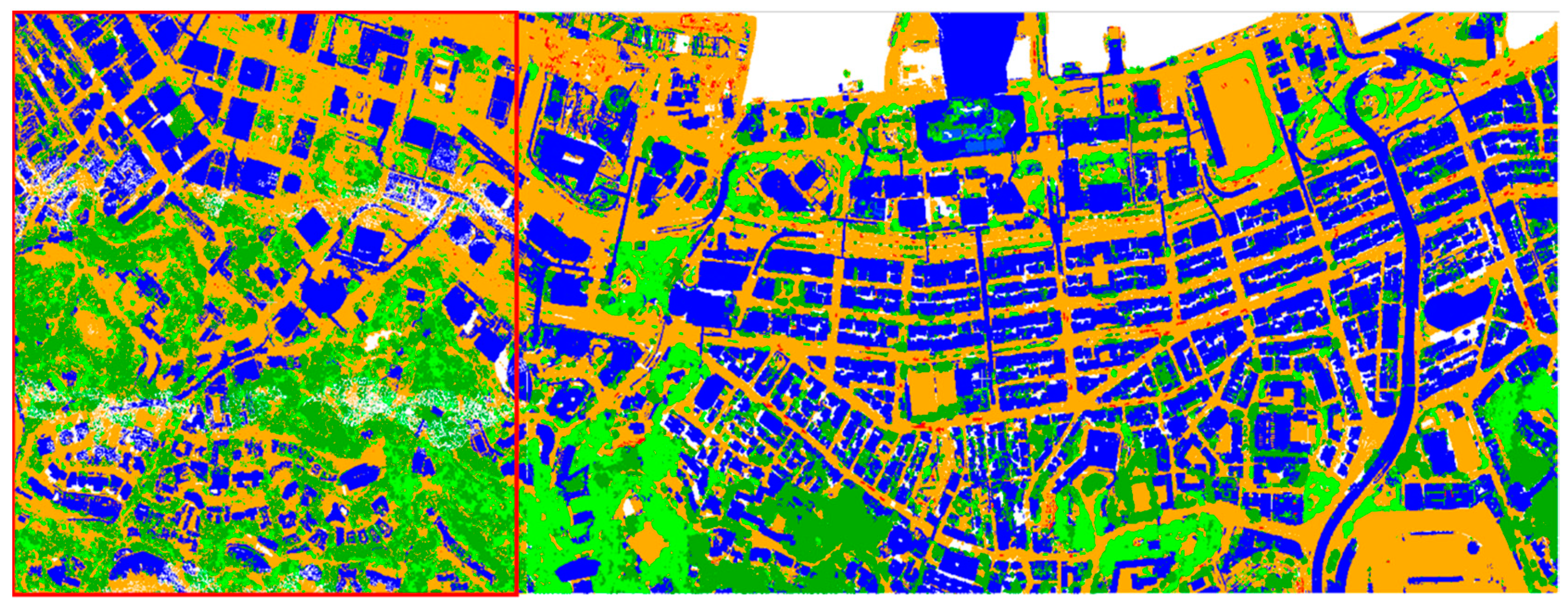
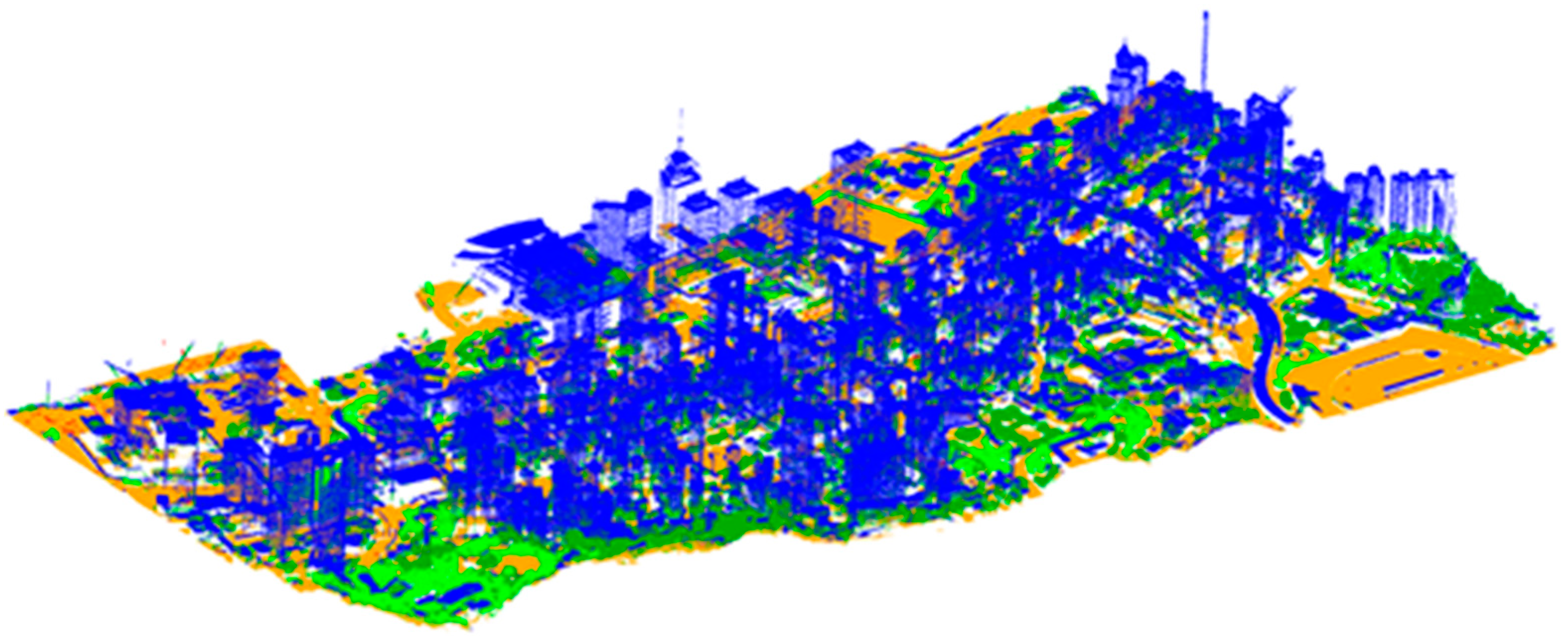
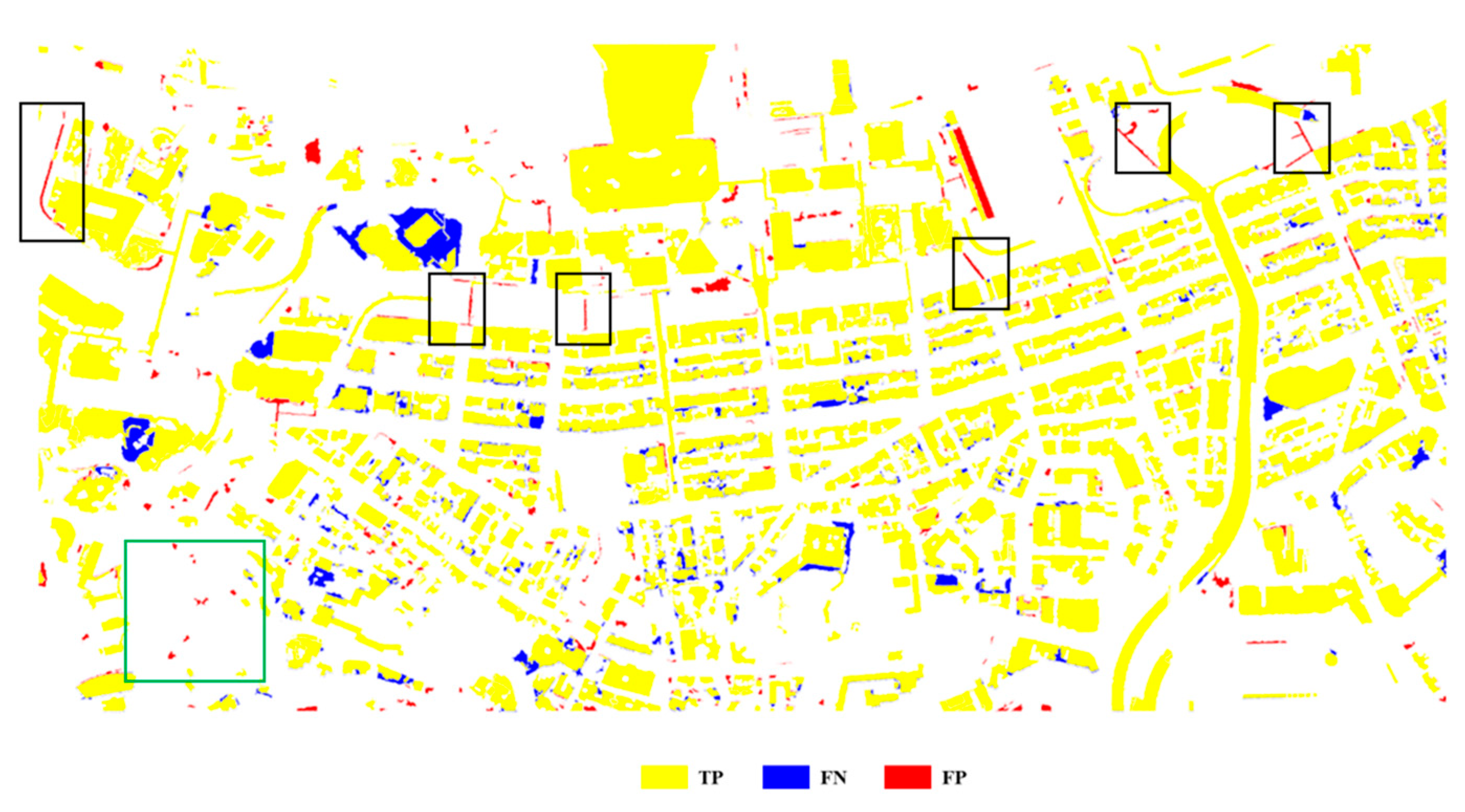
4. Experimental Analysis
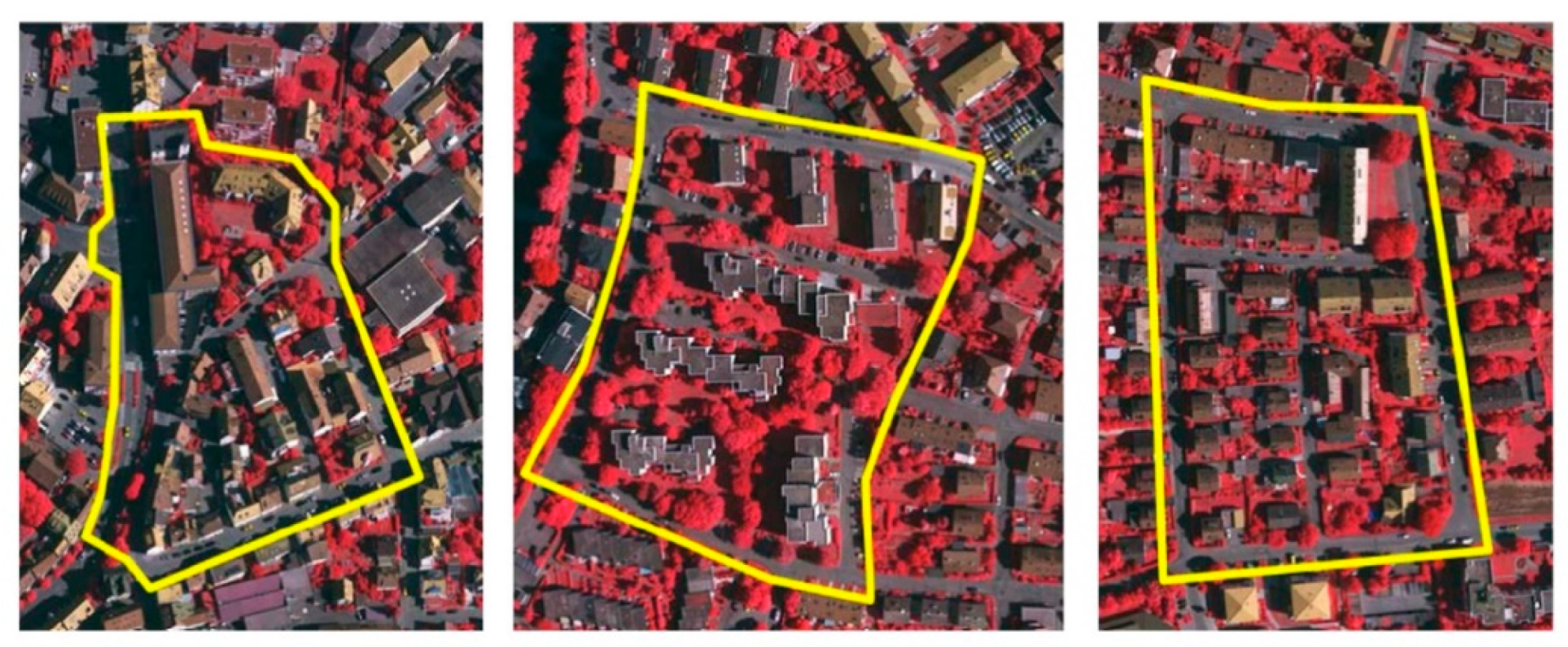
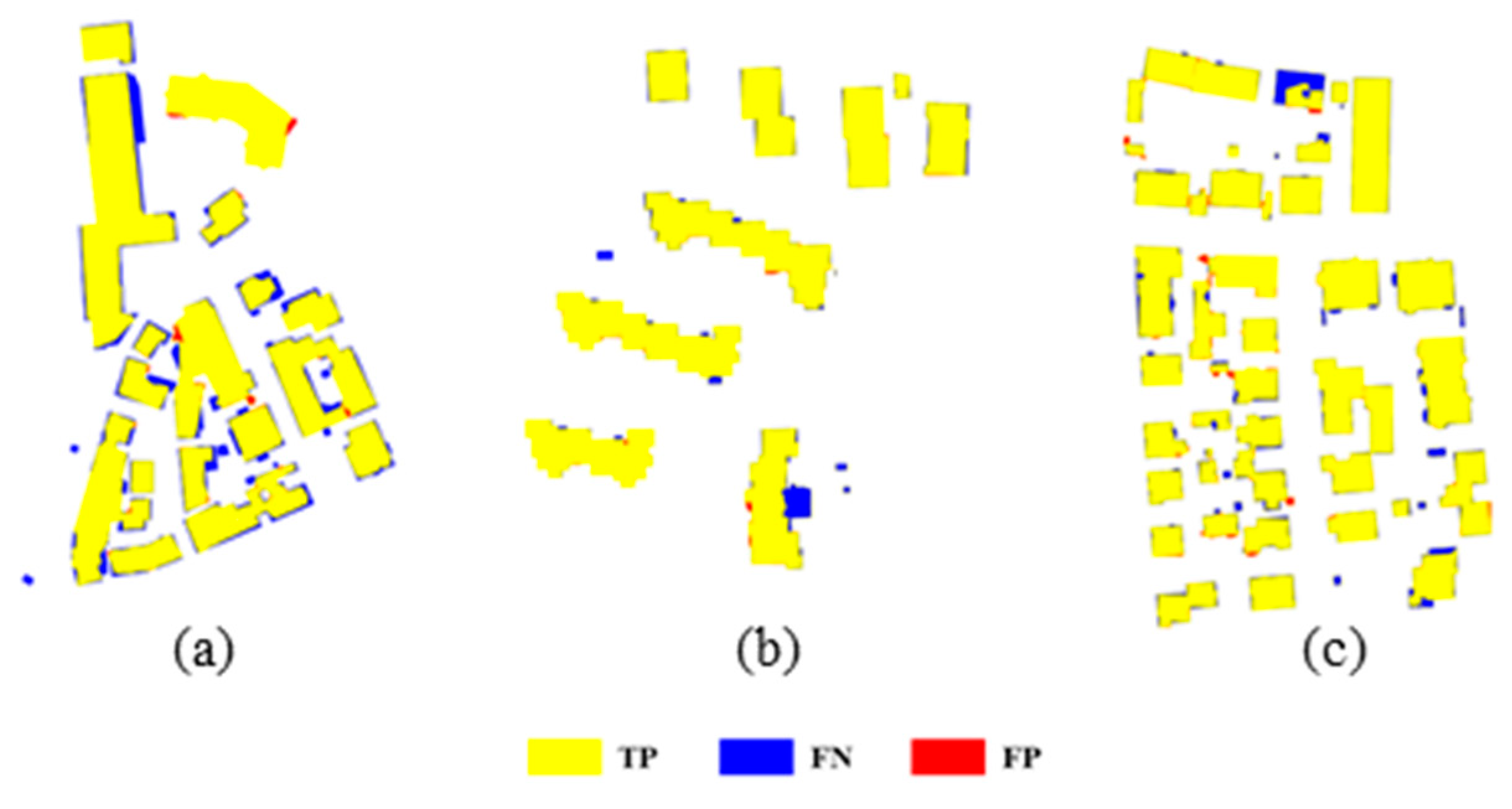
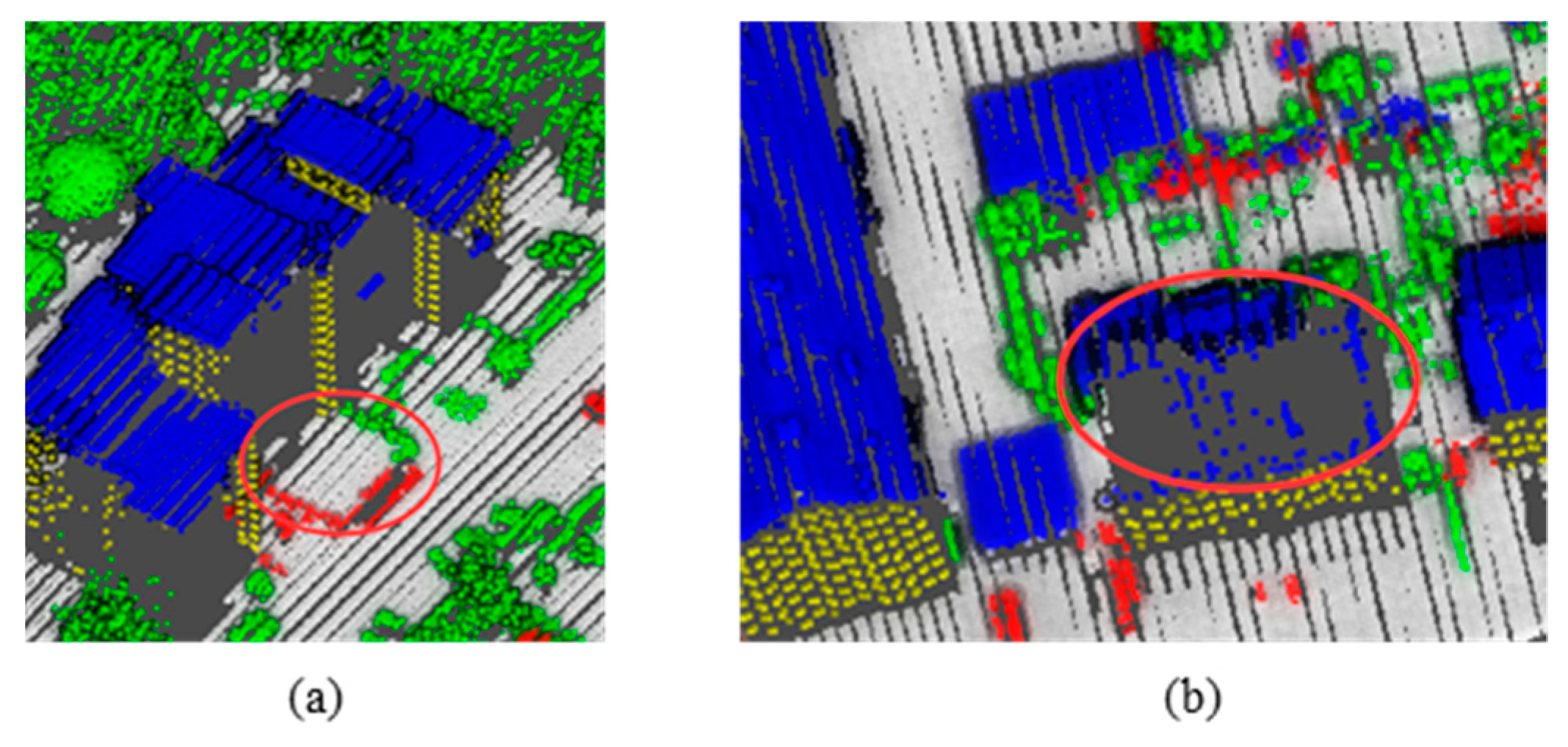
4.1. Vaihingen Dataset
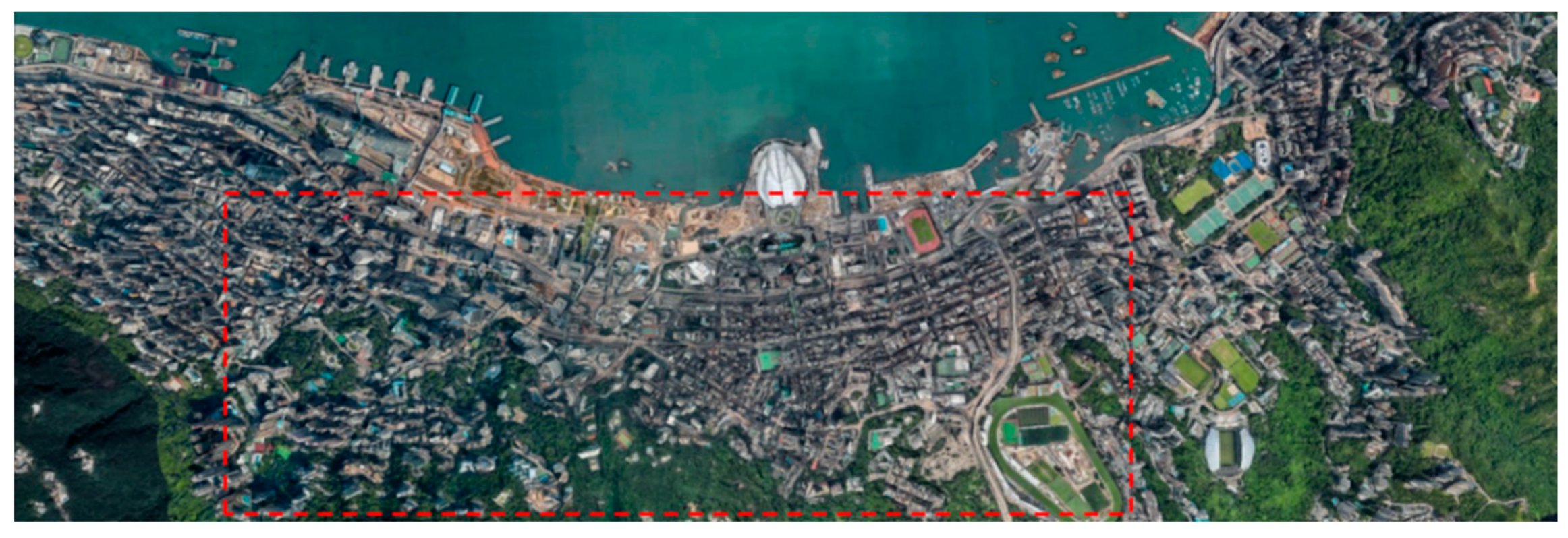
4.2. Hong Kong Dataset
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chehata, N.; Guo, L.; Mallet, C. Airborne lidar feature selection for urban classification using random forests. International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2009, 38(Part 3), W8. [Google Scholar]
- Vosselman, G.; Coenen, M.; Rottensteiner, F. Contextual segment-based classification of airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 354–371. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, Y.; Hu, H.; Wu, B. Robust point cloud classification based on multi-level semantic relationships for urban scenes. ISPRS J. Photogramm. Remote Sens. 2017, 129, 86–102. [Google Scholar] [CrossRef]
- Xu, S.; Vosselman, G.; Elberink, S.O. Multiple-entity based classification of airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 88, 1–15. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Gerke, M.; Xiao, J. Supervised and unsupervised MRF based 3D scene classification in multiple view airborne oblique images. ISPRS Annals of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2013, 2, 25–30. [Google Scholar]
- Frey, B.J.; MacKay, D.J. A Revolution: Belief Propagation in Graphs with cycles. In Proceedings of the 1997 Conference on Advances in Neural Information Processing Systems 10, Denver, CO, USA, 1997. [Google Scholar]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. Ieee Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Conditional random fields for lidar point cloud classification in complex urban areas. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 3, 263–268. [Google Scholar] [CrossRef]
- Weinmann, M.; Schmidt, A.; Mallet, C.; Hinza, S.; Rottensteinerb, F.; Jutzia, B. Contextual classification of point cloud data by exploiting individual 3D neigbourhoods. ISPRS annals of the photogrammetry. Remote Sens. Spat. Inf. Sci. 2015, 2, 271. [Google Scholar]
- Ni, H.; Lin, X.; Zhang, J. Classification of ALS point cloud with improved point cloud segmentation and random forests. Remote Sens. 2017, 9, 288. [Google Scholar] [CrossRef]
- Darmawati, A.T. Utilization of Multiple Echo Information for Classification of Airborne Laser Scanning Data; Master’s Thesis, International Institute for Geo-Information Science and Earth Observation (ITC), Enschede, The Netherlands, 2008. [Google Scholar]
- Luo, H.; Wang, C.; Wen, C.; Chen, Z.; Zai, D.; Yu, Y.; Li, J. Semantic Labeling of Mobile LiDAR Point Clouds via Active Learning and Higher Order MRF. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3631–3644. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Persello, C.; Vosselman, G. Optimizing multiple kernel learning for the classification of UAV data. Remote Sens. 2016, 8, 1025. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Sörgel, U.; Heipke, C. Hierarchical higher order crf for the classification of airborne lidar point clouds in urban areas. The International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2016, 41, 655. [Google Scholar]
- Mallet, C.; Bretar, F.; Roux, M.; Soergel, U.; Heipke, C. Relevance assessment of full-waveform lidar data for urban area classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, S71–S84. [Google Scholar] [CrossRef]
- Guo, B.; Huang, X.; Zhang, F.; Sohn, G. Classification of airborne laser scanning data using JointBoost. ISPRS J. Photogramm. Remote Sens. 2015, 100, 71–83. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Landrieu, L.; Raguet, H.; Vallet, B.; Mallet, C.; Weinmann, M. A structured regularization framework for spatially smoothing semantic labelings of 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 132, 102–118. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. arXiv 2016, arXiv:1612.00593. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. arXiv 2017, arXiv:1711.09869. [Google Scholar]
- Hackel, T.; Wegner, J.D.; Savinov, N.; Ladicky, L.; Schindler, K.; Pollefeys, M. Large-Scale Supervised Learning For 3D Point Cloud Labeling: Semantic3d. Net. Photogramm. Eng. Remote Sens. 2018, 84, 297–308. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.; Whitman, D.; Shyu, M.L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Liu, K.; Boehm, J. A new framework for interactive segmentation of point clouds: International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences-ISPRS Archives. Int. Soc. Photogramm. Remote Sens. 2014, 40, 357–362. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point-Cloud Shape Detection. Computer Graphics Forumn 26. 2007, 2, 214–226. [Google Scholar] [CrossRef]
- Xu, B.; Jiang, W.; Shan, J.; Zhang, J.; Li, L. Investigation on the weighted ransac approaches for building roof plane segmentation from lidar point clouds. Remote Sens. 2016, 8, 5. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Cheng, J.; Chen, B.; Jia, F.; Chen, Z.; Li, J. Line segment extraction for large scale unorganized point cloud. ISPRS J. Photogramm. Remote Sens. 2015, 102, 172–183. [Google Scholar] [CrossRef]
- Vosselman, G.; Klein, R. Visualisation and structuring of point clouds. In Airborne and Terrestrial Laser Scanning; Whittles Publishing: Dunbeath, UK, 2010; pp. 43–79. [Google Scholar]
- Mei, J.; Zhang, L.; Wang, Y.; Zhu, Z.; Ding, H. Joint Margin, Cograph, and Label Constraints for Semisupervised Scene Parsing From Point Clouds. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3800–3813. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Sörgel, U.; Heipke, C. Contextual classification of point clouds using a two-stage CRF. The International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2015, 40, 141. [Google Scholar]
- Wegner, J.D.; Montoya-Zegarra, J.A.; Schindler, K. A higher-order CRF model for road network extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1698–1705. [Google Scholar]
- Delong, A.; Osokin, A.; Isack, H.N.; Boykov, Y. Fast approximate energy minimization with label cost. Int. J. Comput. Vision 2012, 96, 1–27. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data; Technical Report 666; Statistics Department of University of California at Berkeley: Berkeley, CA, USA, 2004. [Google Scholar]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The ISPRS benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 293–298. [Google Scholar]
- Cramer, M.; Grenzdörffer, G.; Honkavaara, E. In-situ digital airborne camera validation and certification—The future standard? In Proceedings of the ISPRS 2010 Canadian Geomatics Conference and Symposium of Commission I, Calgargy, AB, Canada, 15–18 June 2010; Volume 38. [Google Scholar]
- Rutzinger, M.; Rottensteiner, F.; Pfeifer, N. A comparison of evaluation techniques for building extraction from airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 11–20. [Google Scholar] [CrossRef]
- Yang, B.; Xu, W.; Dong, Z. Automated extraction of building outlines from airborne laser scanning point clouds. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1399–1403. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Li, J.; Tian, M.; Dai, W.; Zhong, R. Automated reconstruction of building LoDs from airborne LiDAR point clouds using an improved morphological scale space. Remote Sens. 2016, 9, 14. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, Y.; Zhang, Y.; Cao, R. Extracting buildings from and regularizing boundaries in airborne lidar data using connected operators. Int. J. Remote Sens. 2016, 37, 889–912. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Lu, G.; Fraser, C. Automatic building extraction from LiDAR data covering complex urban scenes. The International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2014, 40, 25. [Google Scholar]
- Gilani, S.; Awrangjeb, M.; Lu, G. Fusion of LiDAR data and multispectral imagery for effective building detection based on graph and connected component analysis. The International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2015, 40, 65. [Google Scholar]
- Wei, Y.; Yao, W.; Wu, J.; Schmitt, M.; Stilla, U. Adaboost-based feature relevance assessment in fusing lidar and image data for classification of trees and vehicles in urban scenes. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 7, 323–328. [Google Scholar] [CrossRef]
- Dorninger, P.; Pfeifer, N. A comprehensive automated 3D approach for building extraction, reconstruction, and regularization from airborne laser scanning point clouds. Sensors 2008, 8, 7323–7343. [Google Scholar] [CrossRef]
- Mongus, D.; Lukač, N.; Žalik, B. Ground and building extraction from LiDAR data based on differential morphological profiles and locally fitted surfaces. ISPRS J. Photogramm. Remote Sens. 2014, 93, 145–156. [Google Scholar] [CrossRef]
- Moussa, A. Segmentation and Classification of Multi-Sensor Data Using Artificial Intelligence Techniques. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2014. [Google Scholar]
- Poznanska, A.M.; Bayer, S.; Bucher, T. Derivation of urban objects and their attributes for large-scale urban areas based on very high resolution UltraCam true orthophotos and nDSM: A case study. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications IV, Berlin, Germany, 24 October 2013; Volume 8893, p. 889303. [Google Scholar]


| No. | Domain | Feature’s Description |
|---|---|---|
| 1 | N | The number of points in segment i. |
| 2 | N | The perimeter and area of segment i in 2D space. |
| 3 | N | Feature derived from the height (calculated from spherical and cylindrical neighborhoods): average height above DTM; the difference between the maximum and minimum heights; the variance in height of segment i. |
| 4 | N | Features derived from the covariance matrix by principal component analysis, i.e., linearity, planarity, scattering, omnivariance, anisotropy, eigenentropy, and change of curvature. |
| 5 | N | The variances of planarity, omnivariance, and change of curvature within a cylindrical neighborhood are calculated for the point primitive only. |
| 6 | N | The number of extreme points for a cylindrical neighborhood of segment i. |
| 7 | [0, 360] | Features derived from the normal vector direction. |
| 8 | N | The point densities in spherical and cylindrical neighborhoods. |
| 9 | [0, 180] | The difference of normals of segment i using a multi-scale operator [21]. |
| No. | Domain | Feature’s Description |
|---|---|---|
| 1 | N | The number of the 2D border intersecting points. |
| 2 | [0, 1] | The linearity of the 2D border intersecting lines. |
| 3 | N | The average height difference of adjacent segments in the 2D overlapping part. |
| 4 | [0, 360] | The variance of the direction of the 2D border intersecting points in each segment. |
| 5 | N | The feature derives from point densities that are separately calculated using spherical and cylindrical neighborhoods. |
| 6 | {True, False} | For the point-to-point case, we define points i and j as connecting to each other if point j is in the neighborhood of point i and vice versa. The number of border points is a constant (i.e., = 1). |
| No. | Domain | Feature’s Description |
|---|---|---|
| 1 | {True, False} | The area and minimal height of a roof segment should be larger than given thresholds (e.g., 15 m2 and 1.5 m, respectively). |
| 2 | {True, False} | The edges of a roof segment should be larger than a given threshold (e.g., 1 m). |
| 3 | {True, False} | There is no isolated vegetation point in a roof segment. |
| 4 | {True, False} | A façade segment is always under a roof segment, and the angle of the normal vectors of such two segments should not be parallel. |
| Method | AREA 1 | AREA 2 | AREA 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Completeness % | Correctness % | Quality % | Completeness % | Correctness % | Quality % | Completeness % | Correctness % | Quality % | |
| Ours | 90.0 | 98.6 | 88.9 | 92.9 | 99.1 | 92.1 | 90.0 | 98.3 | 88.6 |
| HKP [3] | 92.0 | 97.4 | 89.8 | 93.0 | 98.4 | 91.6 | 89.2 | 97.7 | 87.4 |
| HANC3 [5] | 90.8 | 94.5 | 86.2 | 91.4 | 96.4 | 88.4 | 91.6 | 96.7 | 88.8 |
| WHUY2 [37] | 89.7 | 89.6 | 81.2 | 90.0 | 93.9 | 85.0 | 89.4 | 89.1 | 80.6 |
| WHU_YD [38] | 91.8 | 98.6 | 90.6 | 87.3 | 99.0 | 86.5 | 90.2 | 98.1 | 88.6 |
| WHU_ZZ [39] | 90.1 | 96.5 | 87.3 | 91.3 | 95.8 | 87.8 | 86.1 | 94.9 | 82.3 |
| MON2 [40] | 88.1 | 90.0 | 80.2 | 87.1 | 94.0 | 82.5 | 87.7 | 89.0 | 79.1 |
| FED_2 [41] | 85.4 | 86.6 | 75.4 | 88.8 | 84.5 | 76.4 | 89.9 | 84.7 | 77.3 |
| TUM [42] | 89.8 | 92.2 | 83.5 | 92.5 | 93.9 | 87.3 | 86.8 | 92.5 | 81.1 |
| VSK [43] | 85.7 | 98.1 | 84.3 | 85.4 | 98.4 | 84.2 | 86.3 | 98.7 | 85.3 |
| MAR2 [44] | 90.3 | 91.7 | 83.5 | 89.9 | 97.8 | 88.1 | 88.9 | 96.2 | 85.9 |
| ITCR [6] | 91.2 | 90.3 | 83.1 | 94.0 | 89.0 | 84.2 | 89.1 | 92.5 | 83.1 |
| CAL2 [45] | 87.7 | 97.2 | 85.5 | 90.7 | 96.7 | 88.0 | 89.2 | 97.7 | 87.4 |
| DLR [46] | 91.9 | 95.4 | 88.0 | 94.3 | 97.0 | 91.6 | 93.7 | 95.5 | 89.7 |
| Method | Completeness | Correctness | Quality |
|---|---|---|---|
| MPB+HS (the proposed method) | 89.2% | 95.6% | 85.7% |
| MPB | 80.5% | 88.4% | 72.8% |
| Multi-scaled point-based method | 75.9% | 86.6% | 67.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, X.; Wu, B.; Li, Y.; Hu, H. A Multi-Primitive-Based Hierarchical Optimal Approach for Semantic Labeling of ALS Point Clouds. Remote Sens. 2019, 11, 1243. https://doi.org/10.3390/rs11101243
Ge X, Wu B, Li Y, Hu H. A Multi-Primitive-Based Hierarchical Optimal Approach for Semantic Labeling of ALS Point Clouds. Remote Sensing. 2019; 11(10):1243. https://doi.org/10.3390/rs11101243
Chicago/Turabian StyleGe, Xuming, Bo Wu, Yuan Li, and Han Hu. 2019. "A Multi-Primitive-Based Hierarchical Optimal Approach for Semantic Labeling of ALS Point Clouds" Remote Sensing 11, no. 10: 1243. https://doi.org/10.3390/rs11101243
APA StyleGe, X., Wu, B., Li, Y., & Hu, H. (2019). A Multi-Primitive-Based Hierarchical Optimal Approach for Semantic Labeling of ALS Point Clouds. Remote Sensing, 11(10), 1243. https://doi.org/10.3390/rs11101243






