Reducing the Uncertainty of Lidar Measurements in Complex Terrain Using a Linear Model Approach
Abstract
1. Introduction
- Fluctuations in the flow field: Changes in terrain roughness upstream of the measurements cause large variations and changes in wind speed with height lead to uncertainty in the wind speed [6].
- Lidar technology: The weighting function of the lidar signal processing also leads to over- or under estimation of the wind speed.
- Is the length of the trajectory circulation time important in the comparisons with the met mast?
- Does the half opening-angle have an influence on the accuracy of the correlations?
- Is the local resolution of the measurement points important for the result?
2. Materials and Methods
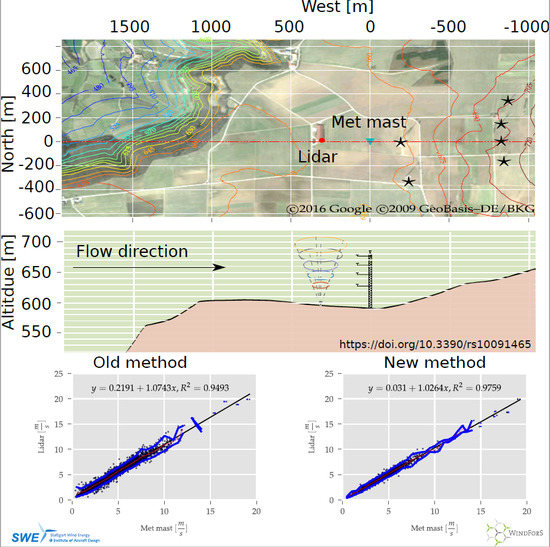
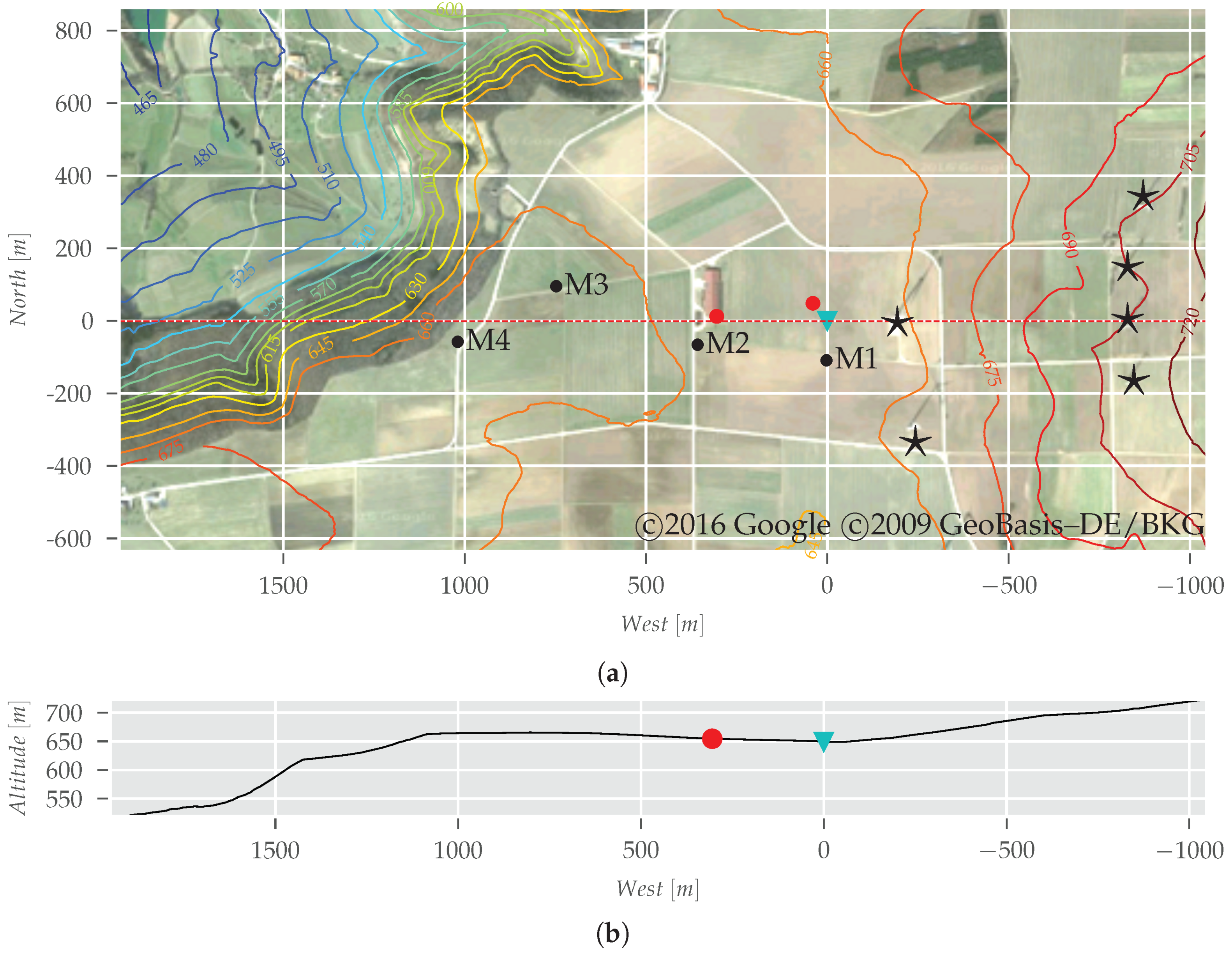
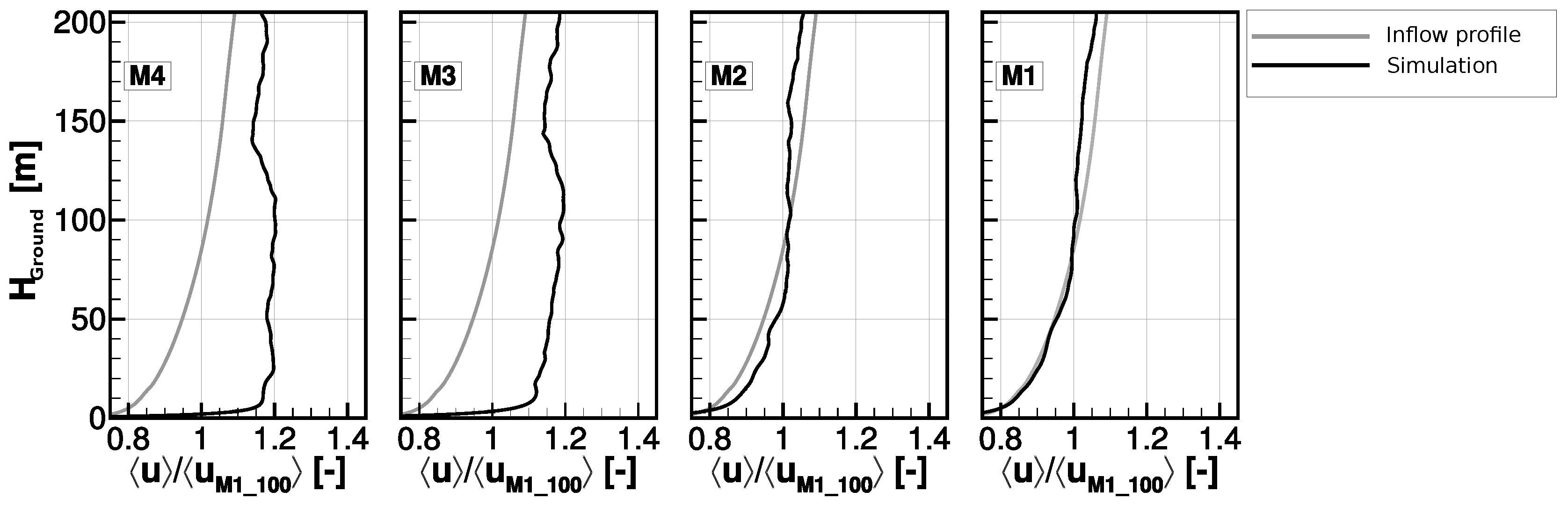
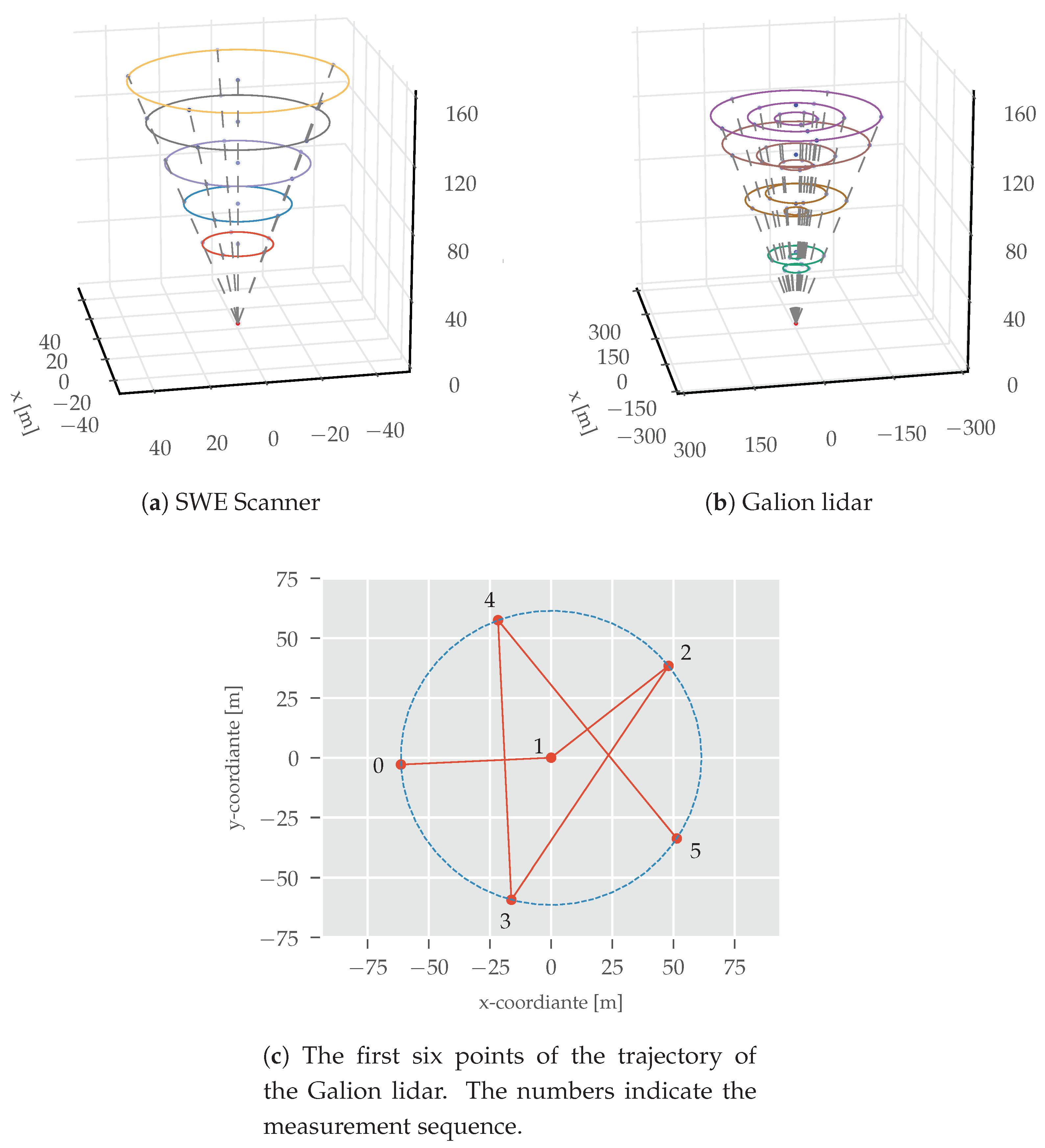
2.1. Test Site and Measurement Campaign
2.1.1. Local Conditions
2.1.2. Met Mast
2.1.3. Lidar
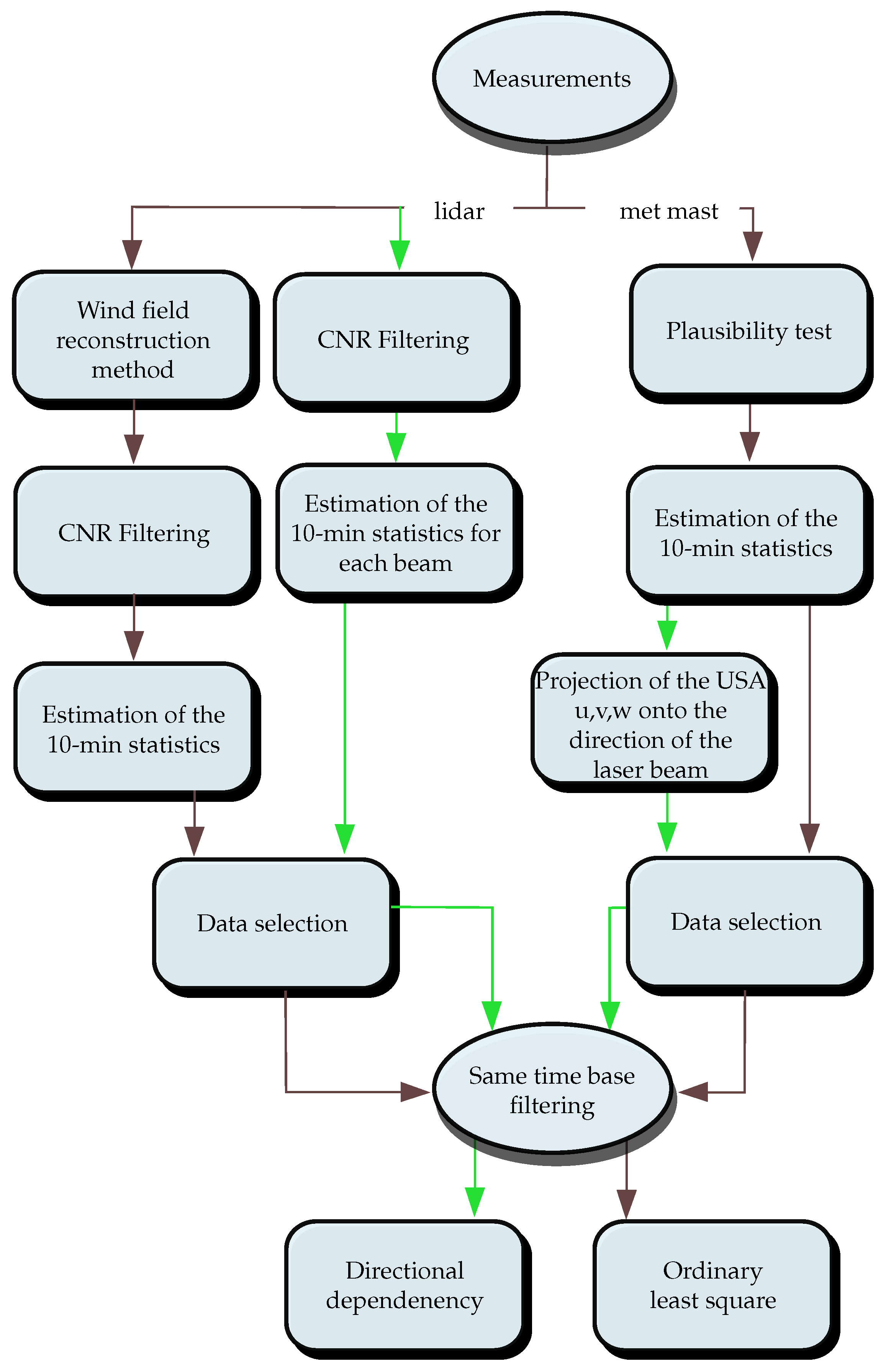
2.1.4. Data Filtering and Selection
2.2. Wind Field Reconstruction Methods
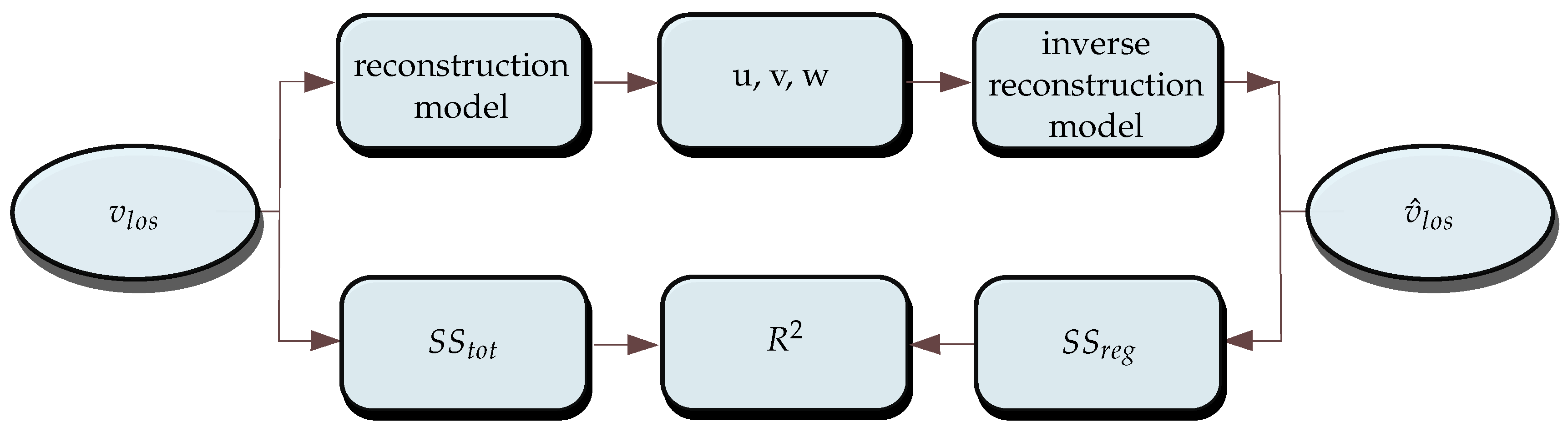
2.2.1. Continuous Least-Square
2.2.2. Predicted Residual Error Sum of Squares (PRESS)
2.2.3. Linear VAD Model
- with ( is the distance of the lidar measuring point).
- The components are only evaluated along the vertical axis of the lidar device (coordinate origin), which means that .
- The gradient of the vertical wind speed components in x- and y-direction and would be zero.
3. Results
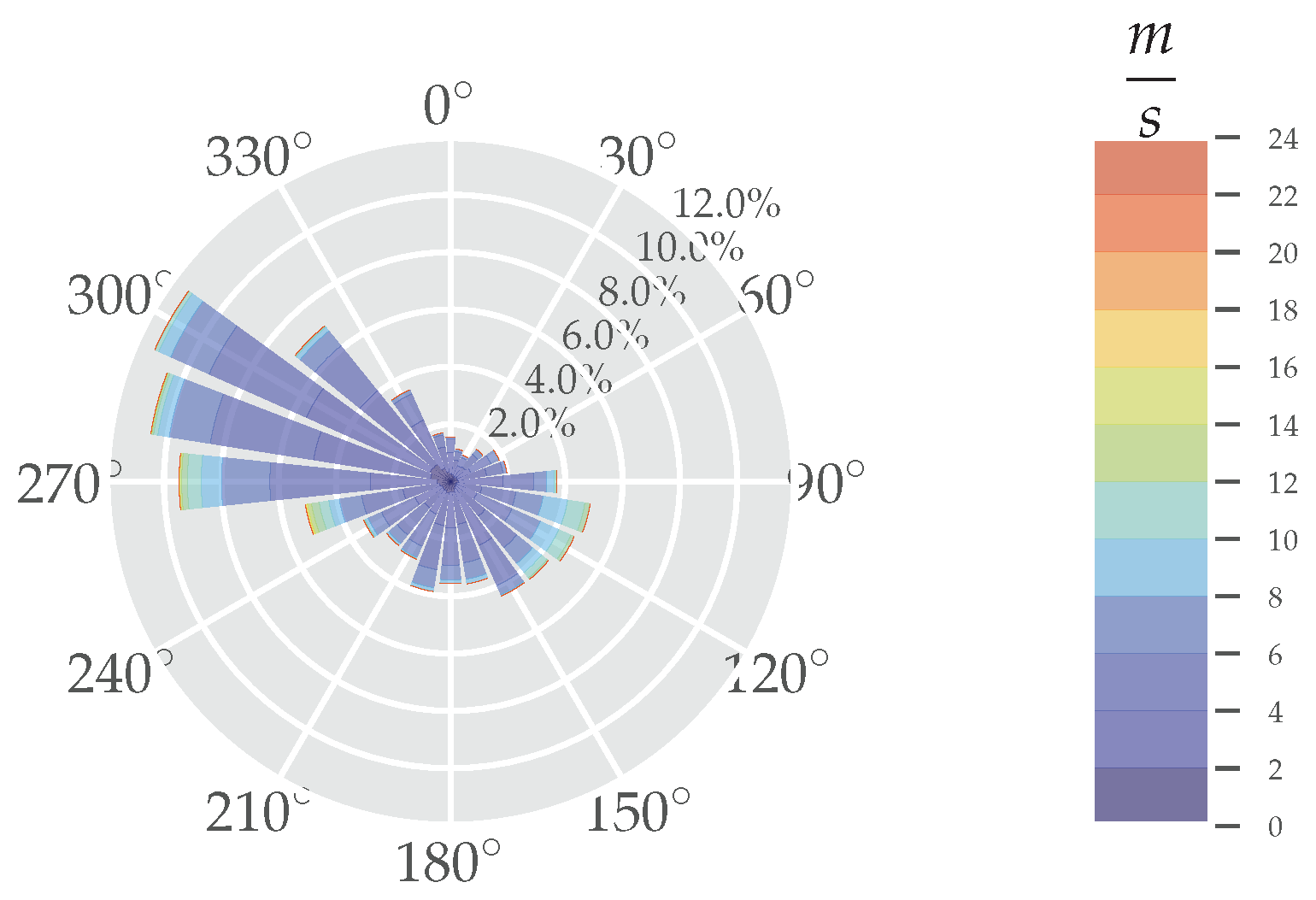
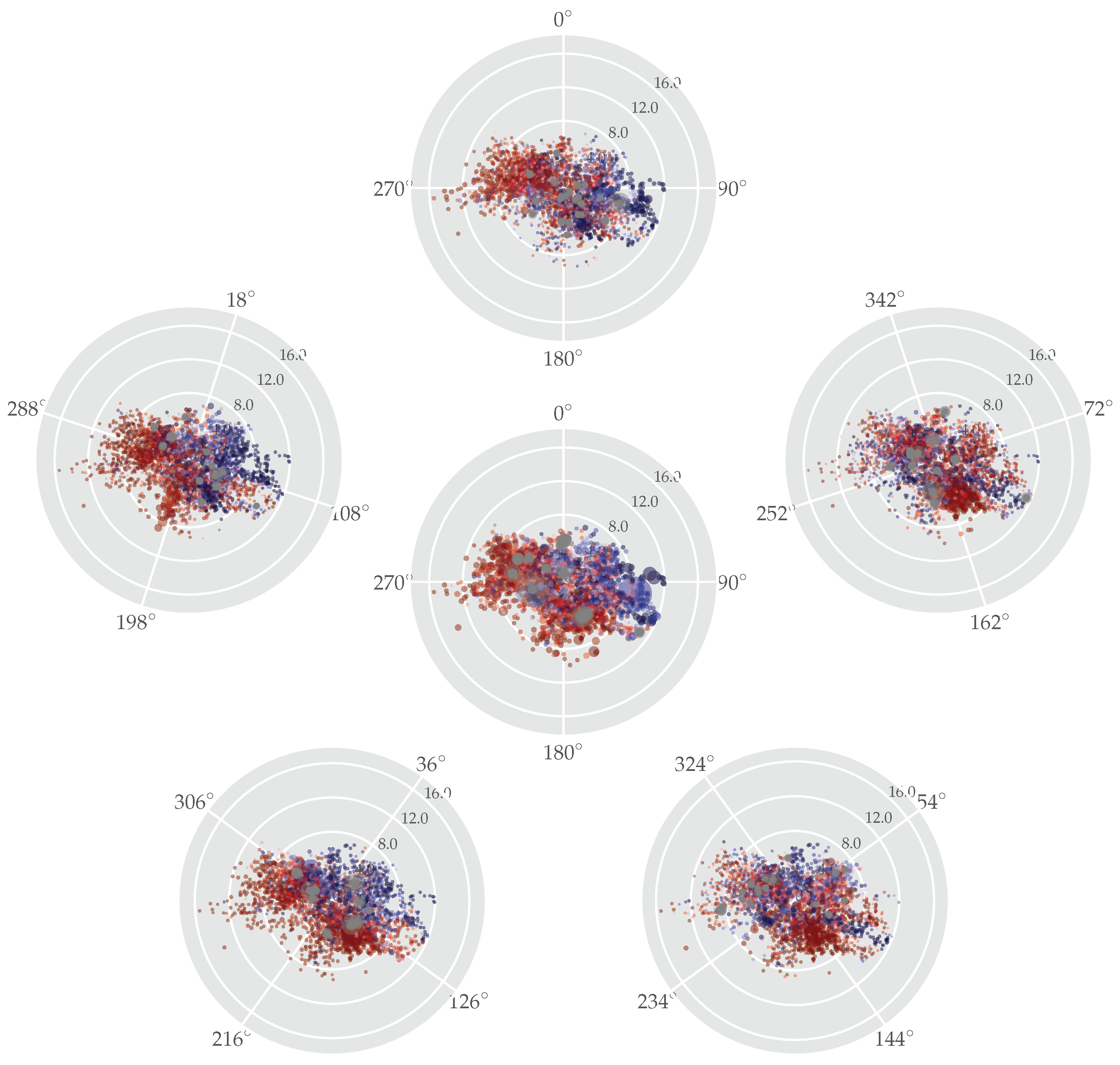
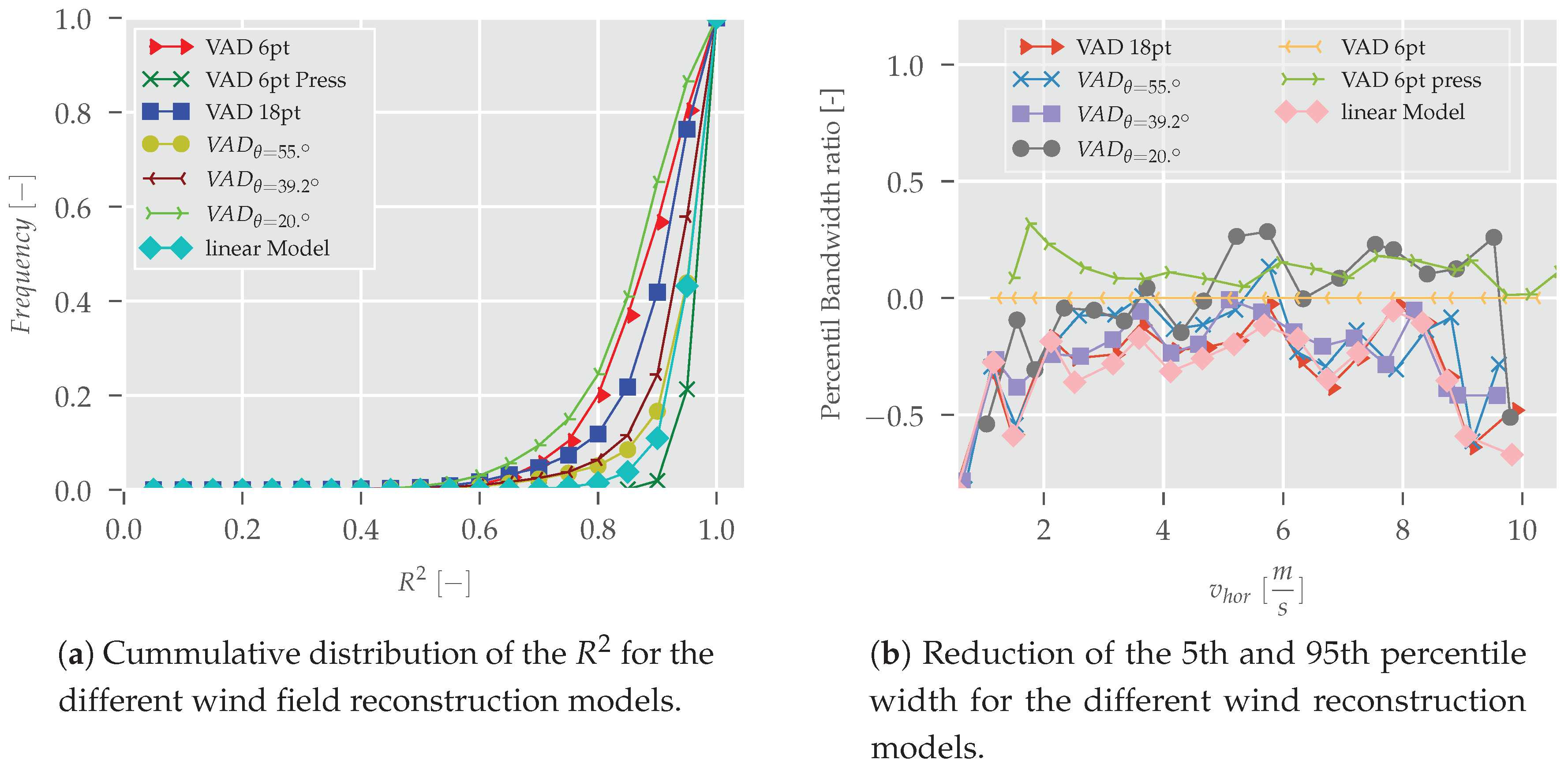
3.1. Directional Dependency
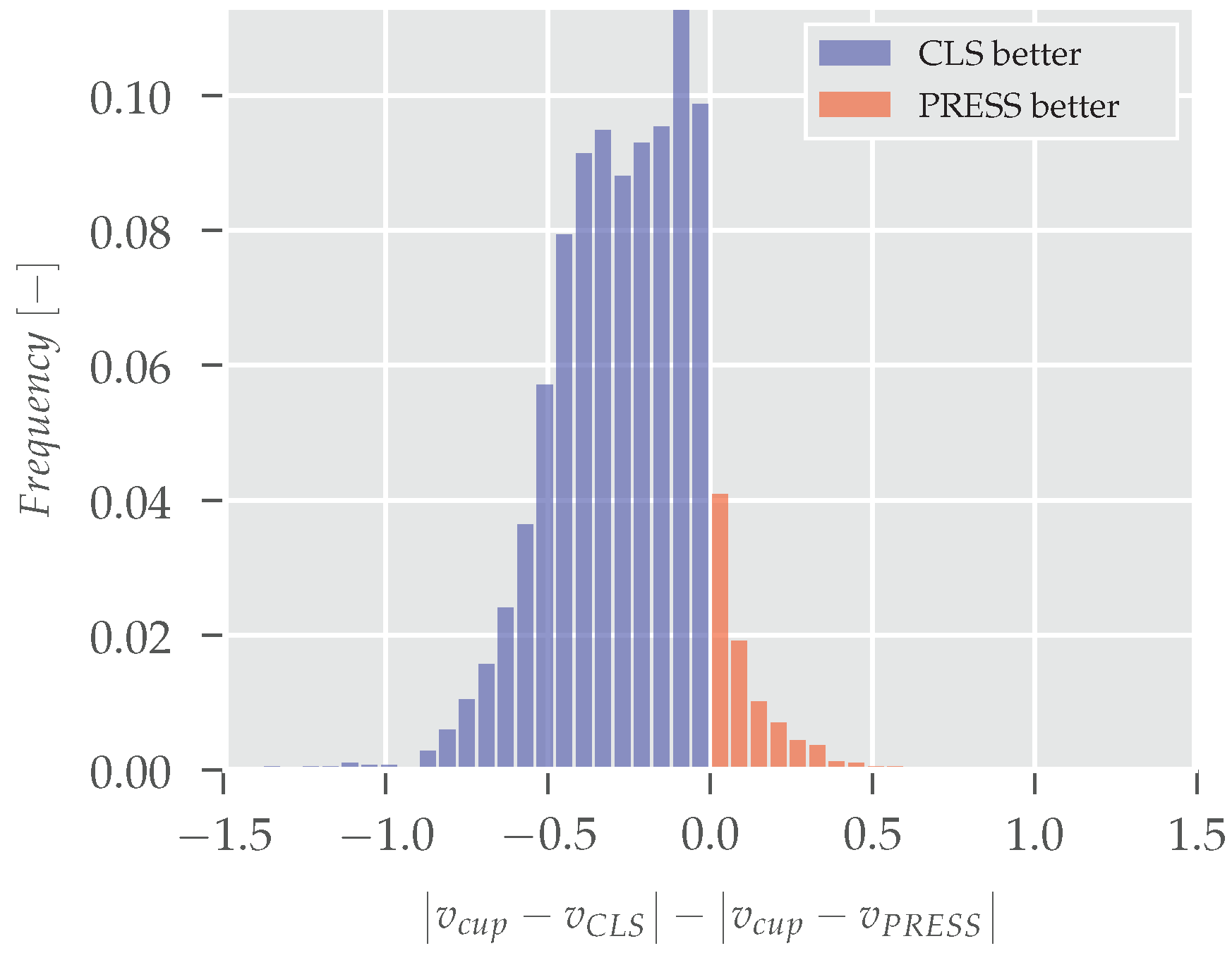
3.2. Wind Speed Comparisons
3.3. Comparison of the Statistical Parameters of Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weitkamp, C. Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Springer Science+Business Media Inc.: New York, NY, USA, 2005. [Google Scholar]
- Clifton, A.; Clive, P.; Gottschall, J.; Schlipf, D.; Simley, E.; Simmons, L.; Stein, D.; Trabucchi, D.; Vasiljevic, N.; Würth, I. IEA Wind Task 32: Wind Lidar Identifying and Mitigating Barriers to the Adoption of Wind Lidar. Remote Sens. 2018, 10, 406. [Google Scholar] [CrossRef]
- Courtney, M.; Wagner, R.; Lindelöw, P. Testing and comparison of lidars for profile and turbulence measurements in wind energy. IOP Conf. Ser. Earth Environ. Sci. 2008, 1, 012021. [Google Scholar] [CrossRef]
- Alberts, A.; Janssen, A.; Mander, J. German Test Station for Remote Wind Sensing Devices. EWEC, Marseille. 2009. Available online: https://www.researchgate.net/profile/Axel_Albers/publication/237616810_German_Test_Station_for_Remote_Wind_Sensing_Devices/links/568e2aee08ae78cc0514b121.pdf (accessed on 10 September 2018).
- Clifton, A.; Boquet, M.; Burin Des Roziers, E.; Westerhellweg, A.; Hofsäß, M.; Klaas, T.; Vogstad, K.; Clive, P.; Harris, M.; Wylie, S.; et al. Remote Sensing of Complex Flows by Doppler Wind Lidar: Issues and Preliminary Recommendations; Technical Report; NREL (National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2015.
- Clive, P.J.M. Compensation of bias in Lidar wind resource assessment. Wind Eng. 2008, 32, 415–432. [Google Scholar] [CrossRef]
- Bingöl, F.; Mann, J.; Foussekis, D. Conically scanning lidar error in complex terrain. Meteorol. Z. 2009, 18, 189–195. [Google Scholar] [CrossRef]
- Mikkelsen, T.; Mann, J.; Courtney, M.; Sjöholm, M. Windscanner: 3-D wind and turbulence measurements from three steerable doppler lidars. IOP Conf. Ser. Earth Environ. Sci. 2008, 1, 012018. [Google Scholar] [CrossRef]
- Pauscher, L.; Vasiljevic, N.; Callies, D.; Lea, G.; Mann, J.; Klaas, T.; Hieronimus, J.; Gottschall, J.; Schwesig, A.; Kühn, M.; et al. An Inter-Comparison Study of Multi- and DBS Lidar Measurements in Complex Terrain. Remote Sens. 2016, 8, 782. [Google Scholar] [CrossRef]
- Vasiljević, N.; Palma, J.M.; Angelou, N.; Carlos Matos, J.; Menke, R.; Lea, G.; Mann, J.; Courtney, M.; Frölen Ribeiro, L.; Gomes, V.M. Perdigão 2015: Methodology for atmospheric multi-Doppler lidar experiments. Atmos. Meas. Tech. 2017, 10, 3463–3483. [Google Scholar] [CrossRef]
- Mann, J.; Angelou, N.; Arnqvist, J.; Callies, D.; Cantero, E.; Arroyo, R.C.; Courtney, M.; Cuxart, J.; Dellwik, E.; Gottschall, J.; et al. Complex terrain experiments in the New European Wind Atlas. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160101. [Google Scholar] [CrossRef] [PubMed]
- Schlipf, D.; Rettenmeier, A.; Haizmann, F.; Hofsäß, M.; Courtney, M.; Cheng, P.W. Model based wind vector field reconstruction from lidar data. In Proceedings of the 11th German Wind Energy Conference DEWEK 2012, Bremen, Germany, 7–8 November 2012. [Google Scholar] [CrossRef]
- Bradley, S.; Strehz, A.; Emeis, S. Remote sensing winds in complex terrain—A review. Meteorol. Z. 2015, 24, 547–555. [Google Scholar] [CrossRef]
- Klaas, T.; Pauscher, L.; Callies, D. LiDAR-mast deviations in complex terrain and their simulation using CFD. Meteorol. Z. 2015, 24, 591–603. [Google Scholar] [CrossRef]
- Schulz, C.; Hofsäß, M.; Anger, J.; Rautenberg, A.; Lutz, T.; Cheng, P.W.; Bange, J. Comparison of Different Measurement Techniques and a CFD Simulation in Complex Terrain. J. Phys. Conf. Ser. 2016, 753, 082017. [Google Scholar] [CrossRef]
- Schulz, C. Numerische Untersuchung des Verhaltens von Windenergieanlagen in Komplexem Gelände unter Turbulenter AtmosphäRischer Zuströmung. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 2018. [Google Scholar]
- Rettenmeier, A.; Bischoff, O.; Hofsäß, M.; Schlipf, D.; Trujillo, J. Wind Field Analysis Using A Nacelle-Based LiDAR System. In Proceedings of the EWEC, Warsaw, Poland, 20–23 April 2010. [Google Scholar]
- Wildmann, N.; Bernard, S.; Bange, J. Measuring the local wind field at an escarpment using small remotely-piloted aircraft. Renew. Energy 2017, 103, 613–619. [Google Scholar] [CrossRef]
- Schulz, C.; Klein, L.; Weihing, P.; Lutz, T. Investigations into the Interaction of a Wind Turbine with Atmospheric Turbulence in Complex Terrain. J. Phys. Conf. Ser. 2016, 753, 032016. [Google Scholar] [CrossRef]
- Hofsäß, M.; Bergmann, D.; Bischoff, O.; Denzel, J.; Cheng, P.W.; Lutz, T.; Peters, B.; Schulz, C. Lidar Complex; Technical Report; Universität Stuttgart, Fakultät 6 Luft- und Raumfahrttechnik und Geodäsie, Institut für Flugzeugbau (IFB), Stuttgarter Lehrstuhl für Windenergie: Stuttgart, Germany, 2017. [Google Scholar] [CrossRef]
- Anger, J.; Bange, J.; Blick, C.; Brosz, F.; Emeis, S.; Fallmann, J. Erstellung einer Konzeption eines Windenergie-Testgeländes in bergig komplexem Terrain: Kurztitel: KonTest: Abschlussbericht des Forschungsprojektes: ein Vorhaben des WindForS Windenergie Forschungscluster Forschungsnetzwerks; Technical Report; Universität Stuttgart–Stuttgarter Lehrstuhl für Windenergie (SWE) am Institut für Flugzeugbau (IFB): Stuttgart, Germany, 2015. [Google Scholar] [CrossRef]
- IEC (International Electrotechnical Commission). Wind Turbines. Part 12-1, Power Performance Measurements of Electricity Producing Wind Turbines; Number 12, 1; IEC: Geneva, Switzerland, 2005. [Google Scholar]
- Sathe, A.; Mann, J.; Vasiljevic, N.; Lea, G. A six-beam method to measure turbulence statistics using ground-based wind lidars. Atmos. Meas. Tech. 2015, 8, 729–740. [Google Scholar] [CrossRef]
- Frisch, A.S. On the measurement of second moments of turbulent wind velocity with a single Doppler radar over non-homogeneous terrain. Bound.-Layer Meteorol. 1991, 54, 29–39. [Google Scholar] [CrossRef]
- Hofsäß, M.; Bischoff, O.; Cheng, P.W. Comparison of second moments between remote sensing devices in complex errain. In Proceedings of the 18th International Symposium for the Advancement of Boundary-Layer Remote Sensing, Varna, Bulgaria, 6–9 June 2016. [Google Scholar]
- Peña, A.; Hasager, C.B.; Badger, M.; Barthelmie, R.J.; Bingöl, F.; Cariou, J.P.; Emeis, S.; Frandsen, S.T.; Harris, M.; Karagali, I.; et al. Remote Sensing for Wind Energy; DTU Wind Energy: Roskilde, Denmark, 2015. [Google Scholar]
- Allen, D.M. Mean Square Error of Prediction as a Criterion for Selecting Variables. Technometrics 1971, 13, 469–475. [Google Scholar] [CrossRef]
- Allen, D.M. The Relationship Between Variable Selection and Data Agumentation and a Method for Prediction. Technometrics 1974, 16, 125–127. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley Series In Probability and Statistics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Teschke, G.; Lehmann, V. Mean wind vector estimation using the velocity–azimuth display (VAD) method: An explicit algebraic solution. Atmos. Meas. Tech. 2017, 10, 3265–3271. [Google Scholar] [CrossRef]
- IEC (International Electrotechnical Commission). Wind turbines. Part 1, Design Requirements; IEC: Geneva, Switzerland, 2014. [Google Scholar]
| Parameter | Acceptable Range | |
|---|---|---|
| Minimum | Maximum | |
| Lidar measurements | ||
| CNR (min, mean) [dB] | −22 | 10 |
| Weather conditions | ||
| Wind direction [] | 245 | 315 |
| Temperature [] | >2 | - |
| Mast function | ||
| Std. cup anemometer | >0.01 | - |
| Data availability | ||
| lidar [%] | 90 | 100 |
| met mast [%] | 100 | - |
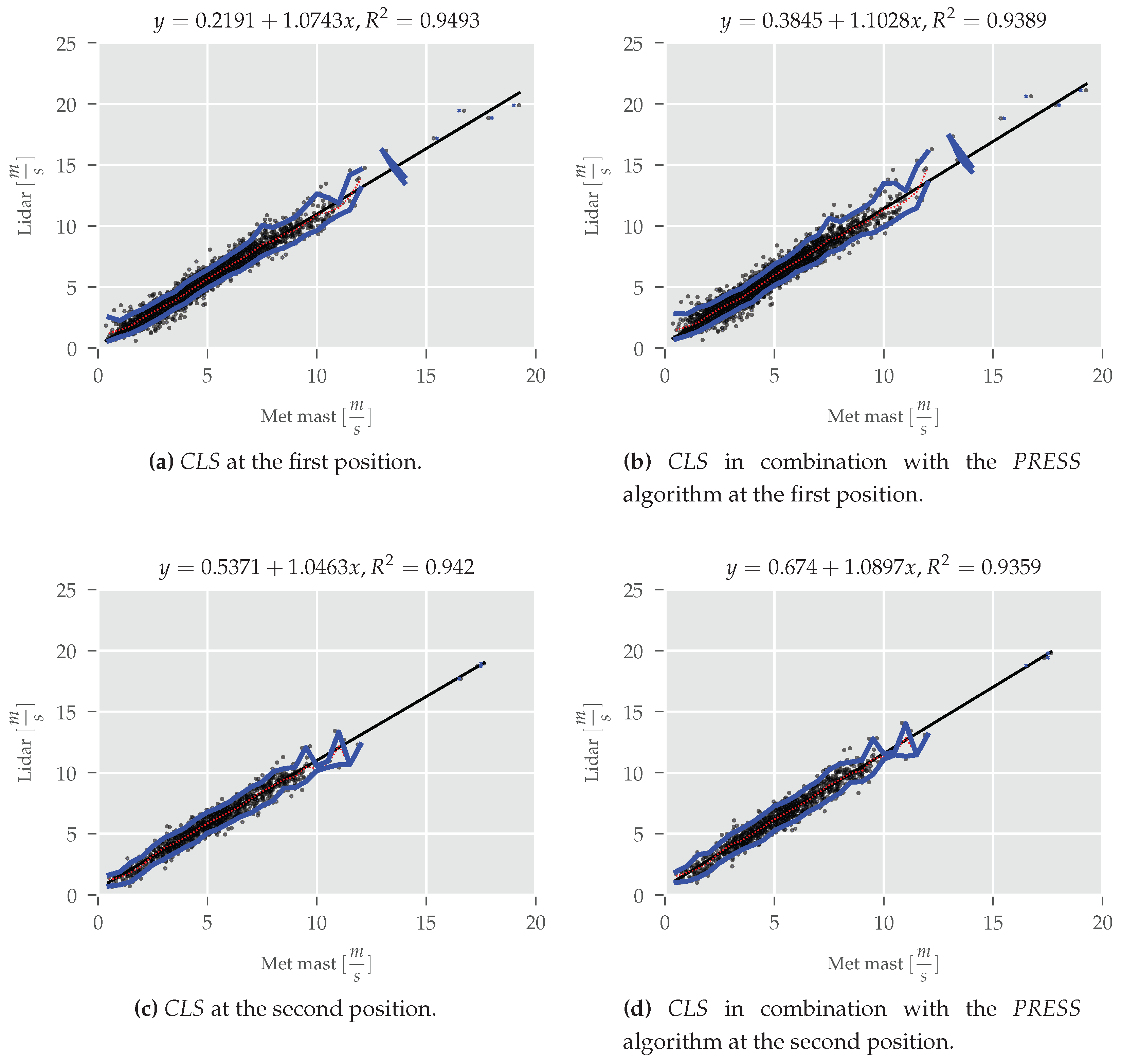
| Lidar System | Method | Slope [-] | Offset [m·s] | |
|---|---|---|---|---|
| SWE Scanner | CLS | 1.074 | 0.219 | 0.949 |
| SWE Scanner | PRESS | 1.103 | 0.385 | 0.938 |
| SWE Scanner 2nd position | CLS | 1.046 | 0.537 | 0.942 |
| SWE Scanner 2nd position | PRESS | 1.09 | 0.674 | 0.936 |
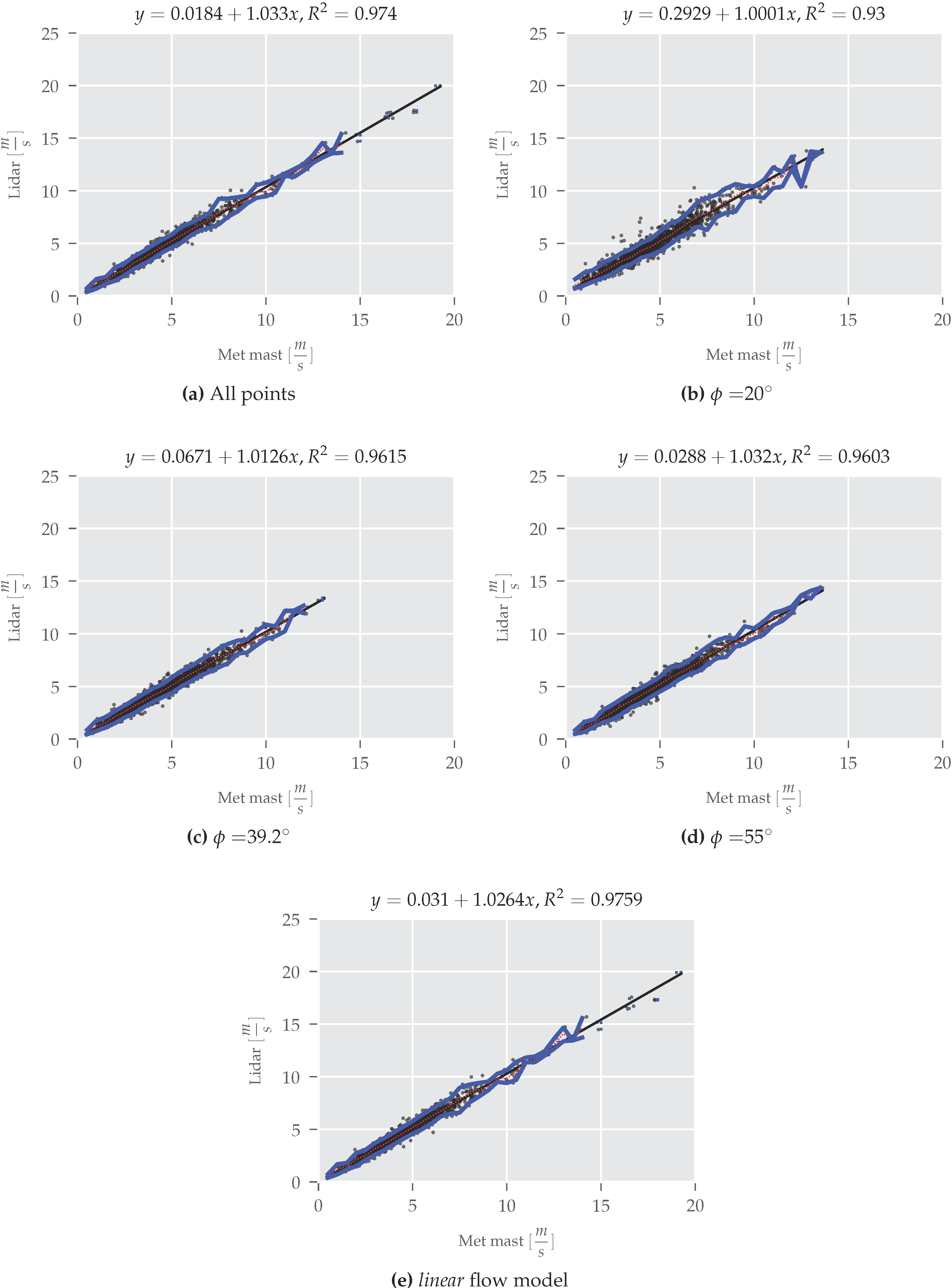
| Galion 18 Pts. | CLS | 1.033 | 0.02 | 0.974 |
| Galion 20 | CLS | 1.00 | 0.293 | 0.93 |
| Galion 39.2 | CLS | 1.013 | 0.067 | 0.962 |
| Galion 55 | CLS | 1.032 | 0.03 | 0.960 |
| Galion | linear | 1.026 | 0.03 | 0.976 |
| SWE Scanner | Galion | ||||||
|---|---|---|---|---|---|---|---|
| VAD 5+1 | VAD 18 | linear | |||||
| 15 | 15 | 20, 39.2, 55 | 20 | 39.2 | 55 | 20, 39.2, 55 | |
| scan duration [m·s] | 8.8 | 4.78 | 49 | 16.3 | 16.3 | 16.3 | 49 |
| [-] | 5.78 | 5.78 | 2.02 | 4.30 | 2.00 | 1.26 | 120.66 |
| Nb. of Points [-] | 6 | 6 | 18 | 6 | 6 | 6 | 18 |
| Location [-] | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofsäß, M.; Clifton, A.; Cheng, P.W. Reducing the Uncertainty of Lidar Measurements in Complex Terrain Using a Linear Model Approach. Remote Sens. 2018, 10, 1465. https://doi.org/10.3390/rs10091465
Hofsäß M, Clifton A, Cheng PW. Reducing the Uncertainty of Lidar Measurements in Complex Terrain Using a Linear Model Approach. Remote Sensing. 2018; 10(9):1465. https://doi.org/10.3390/rs10091465
Chicago/Turabian StyleHofsäß, Martin, Andrew Clifton, and Po Wen Cheng. 2018. "Reducing the Uncertainty of Lidar Measurements in Complex Terrain Using a Linear Model Approach" Remote Sensing 10, no. 9: 1465. https://doi.org/10.3390/rs10091465
APA StyleHofsäß, M., Clifton, A., & Cheng, P. W. (2018). Reducing the Uncertainty of Lidar Measurements in Complex Terrain Using a Linear Model Approach. Remote Sensing, 10(9), 1465. https://doi.org/10.3390/rs10091465