Hurricane Maria in the U.S. Caribbean: Disturbance Forces, Variation of Effects, and Implications for Future Storms
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
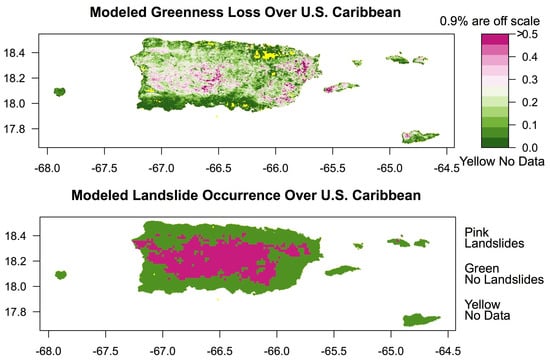
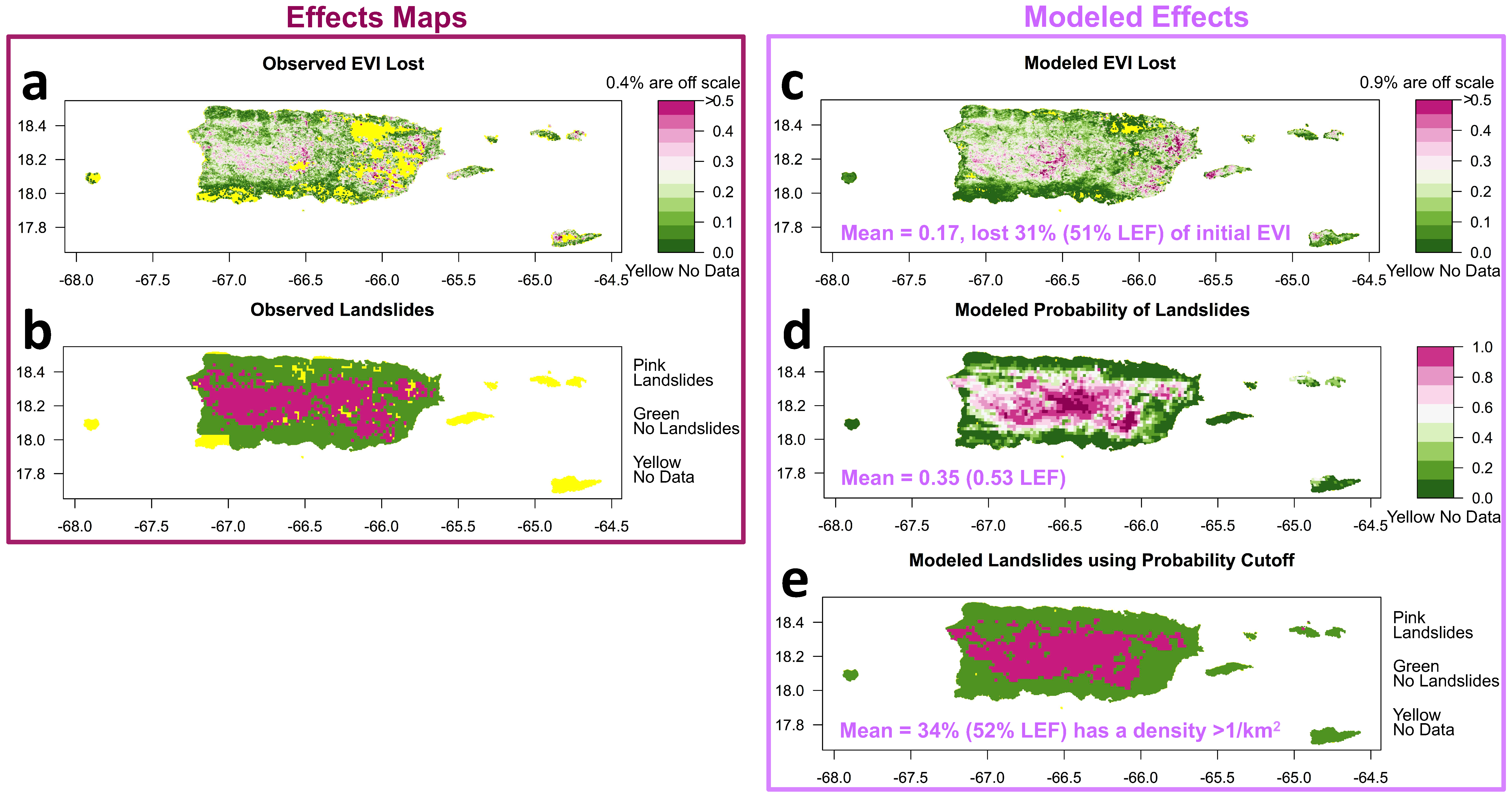
2.2. Effects Maps
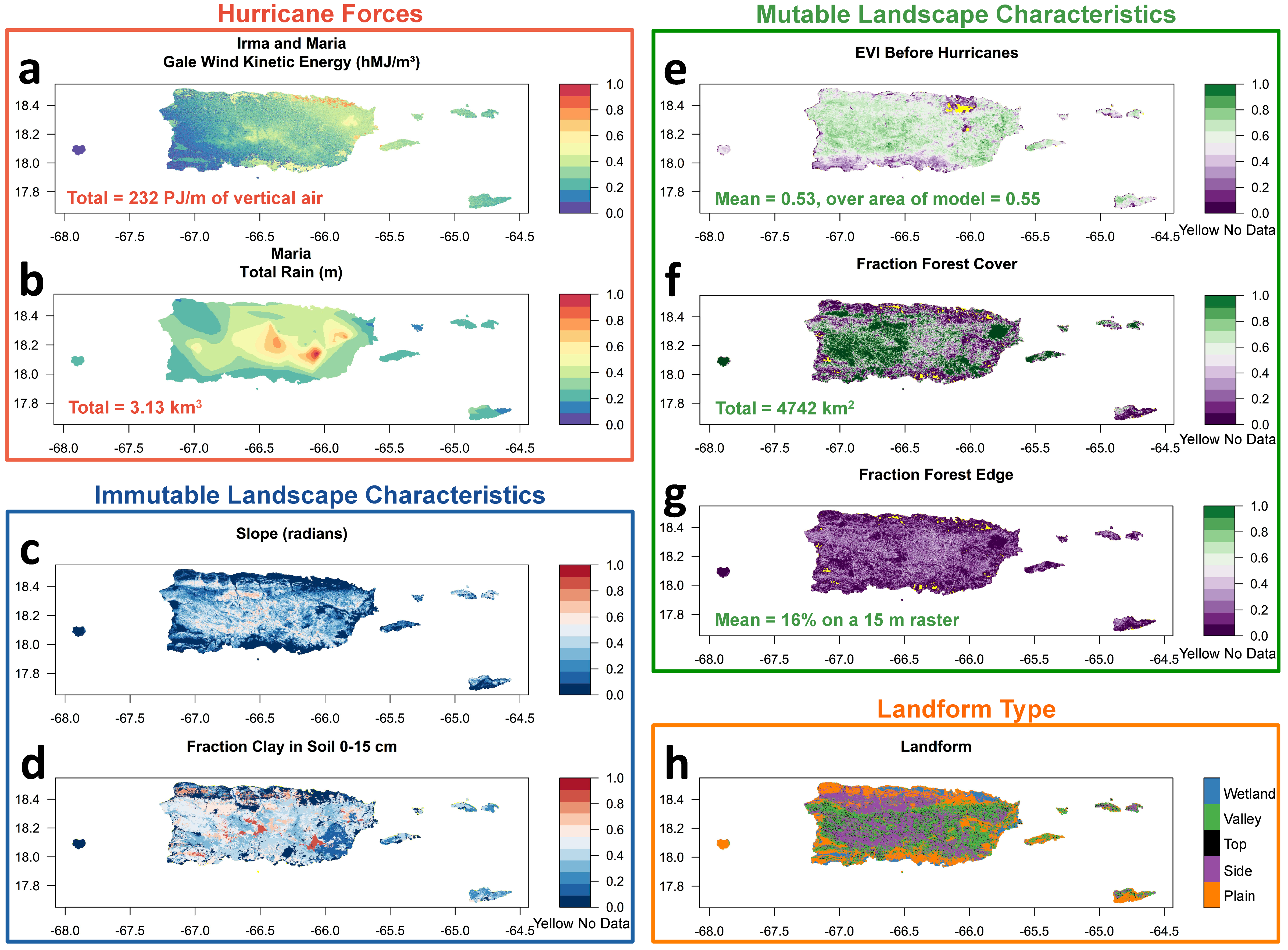
2.3. Hurricane Forces
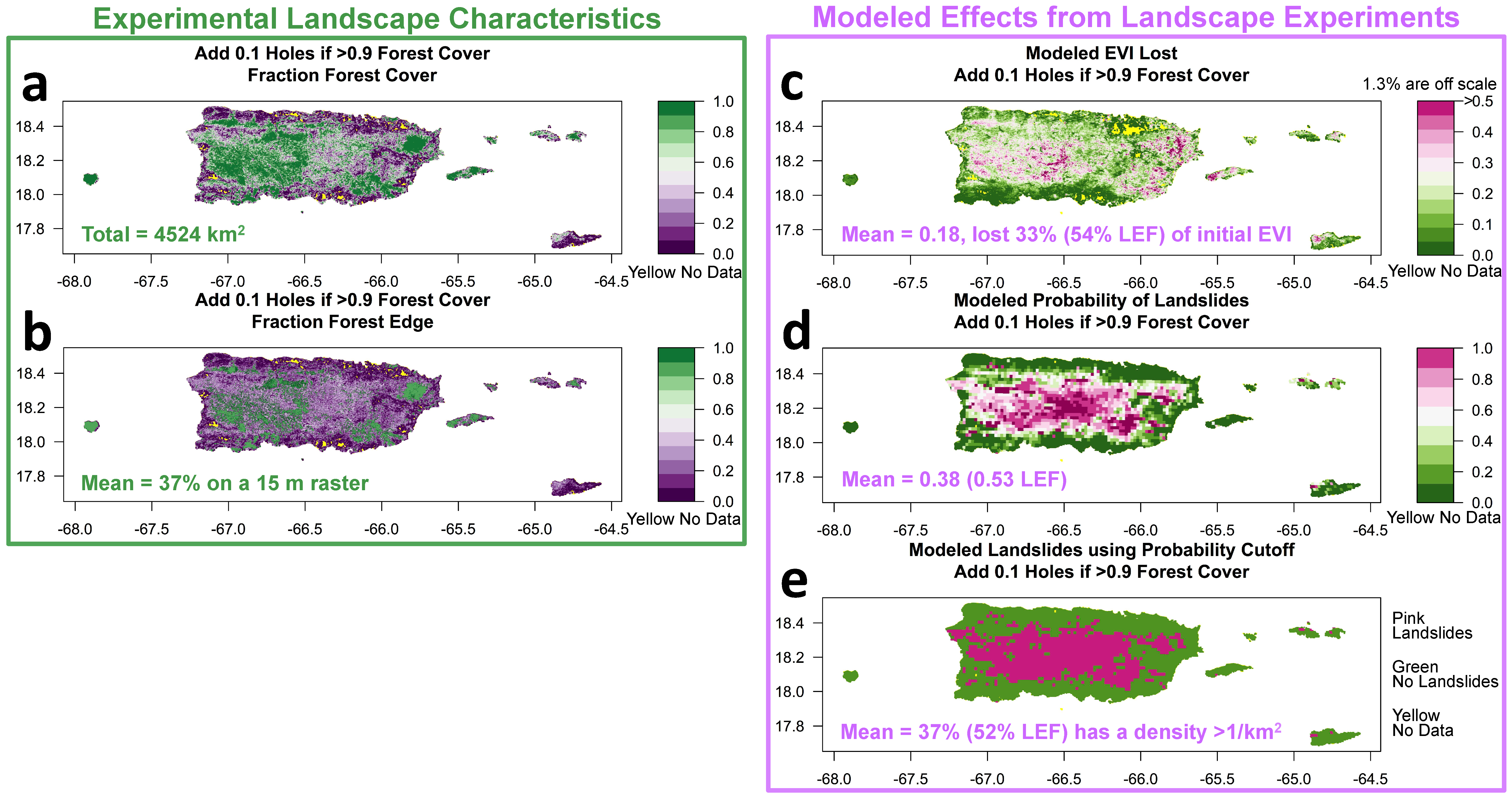
2.4. Landscape Characteristics
2.5. Generalized Linear Models
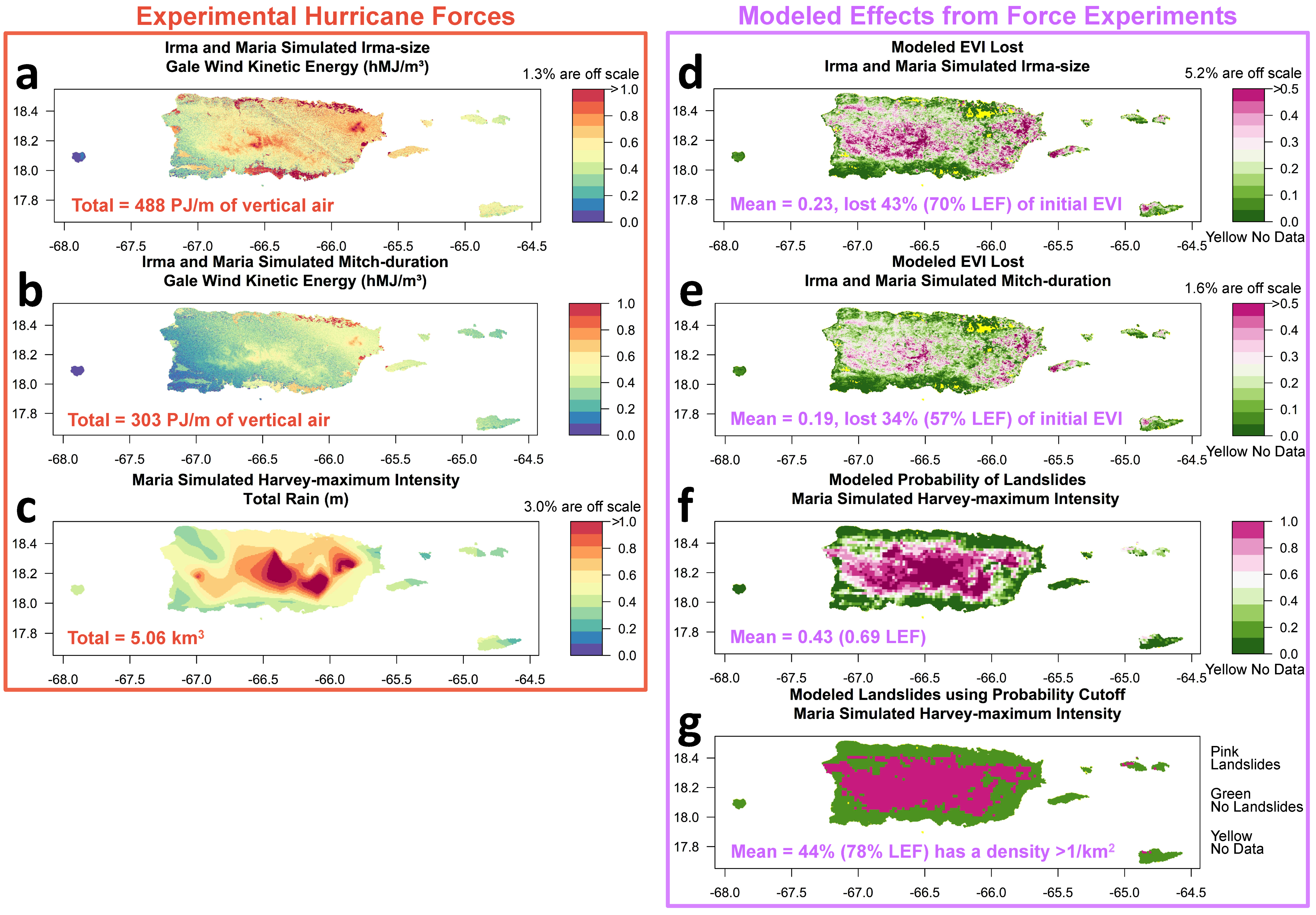
2.6. Stronger, Slower, Wetter Storm Events
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, Y.; Negron-Juarez, R.I.; Patricola, C.M.; Collins, W.D.; Uriarte, M.; Hall, J.S.; Clinton, N.; Chambers, J.Q. Rapid remote sensing assessment of impacts from Hurricane Maria on forests of Puerto Rico. PeerJ Inc. 2018, 6, e26597v1. [Google Scholar]
- Boose, E.R.; Foster, D.R.; Fluet, M. Hurricane impacts to tropical and temperate forest landscapes. Ecol. Monogr. 1994, 64, 369–400. [Google Scholar] [CrossRef]
- Anthes, R. Tropical cyclones: Their evolution, structure and effects. In Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 1982; ISBN 978-1-935704-28-7. [Google Scholar]
- Tanner, E.V.J.; Kapos, V.; Healey, J.R. Hurricane effects on forest ecosystems in the caribbean. Biotropica 1991, 23, 513–521. [Google Scholar] [CrossRef]
- Armentano, T.V.; Doren, R.F.; Platt, W.J.; Mullins, T. Effects of hurricane Andrew on coastal and interior forests of Southern Florida: Overview and synthesis. J. Coast. Res. 1995, 111–144. [Google Scholar]
- Schwartz, N.B.; Uriarte, M.; DeFries, R.; Bedka, K.M.; Fernandes, K.; Gutiérrez-Vélez, V.; Pinedo-Vasquez, M.A. Fragmentation increases wind disturbance impacts on forest structure and carbon stocks in a western Amazonian landscape. Ecol. Appl. 2017, 27, 1901–1915. [Google Scholar] [CrossRef] [PubMed]
- Boose, E.R.; Serrano, M.I.; Foster, D.R. Landscape and regional impacts of hurricanes in Puerto Rico. Ecol. Monogr. 2004, 74, 335–352. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Chambers, J.Q.; Hurtt, G.C.; Annane, B.; Cocke, S.; Powell, M.; Stott, M.; Goosem, S.; Metcalfe, D.J.; Saatchi, S.S. Remote sensing assessment of forest disturbance across complex mountainous terrain: The pattern and severity of impacts of tropical cyclone yasi on Australian rainforests. Remote Sens. 2014, 6, 5633–5649. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Y.J. Hurricane Katrina-induced forest damage in relation to ecological factors at landscape scale. Environ. Monit. Assess. 2009, 156, 491. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Smith, R.B. The impact of Hurricane Maria on the vegetation of Dominica and Puerto Rico using multispectral remote sensing. Remote Sens. 2018, 10, 827. [Google Scholar] [CrossRef]
- Philpott, S.M.; Lin, B.B.; Jha, S.; Brines, S.J. A multi-scale assessment of hurricane impacts on agricultural landscapes based on land use and topographic features. Agric. Ecosyst. Environ. 2008, 128, 12–20. [Google Scholar] [CrossRef]
- Stanley, T.; Kirschbaum, D.B. A heuristic approach to global landslide susceptibility mapping. Nat. Hazards 2017, 87, 145–164. [Google Scholar] [CrossRef]
- Wilde, M.; Günther, A.; Reichenbach, P.; Malet, J.-P.; Hervás, J. Pan-European landslide susceptibility mapping: ELSUS version 2. J. Maps 2018, 14, 97–104. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.; Huffman, G. Use of satellite remote sensing data in the mapping of global landslide susceptibility. Nat. Hazards 2007, 43, 245–256. [Google Scholar] [CrossRef]
- Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.K.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157–163. [Google Scholar] [CrossRef]
- Yoshida, K.; Sugi, M.; Mizuta, R.; Murakami, H.; Ishii, M. Future changes in tropical cyclone activity in high-resolution large-ensemble simulations. Geophys. Res. Lett. 2017, 44, 9910–9917. [Google Scholar] [CrossRef]
- Emanuel, K.A. The dependence of hurricane intensity on climate. Nature 1987, 326, 483–485. [Google Scholar] [CrossRef]
- Van Beusekom, A.E.; Hay, L.E.; Viger, R.J.; Gould, W.A.; Collazo, J.A.; Henareh Khalyani, A. The Effects of changing land cover on streamflow Simulation in Puerto Rico. J. Am. Water Resour. Assoc. 2014, 50, 1–19. [Google Scholar] [CrossRef]
- González, G.; Willig, M.R.; Waide, R.B. Ecological gradient analyses in a tropical landscape: Multiples perspectives and emerging themes. Ecol. Bull. 2013, 54, 13–20. [Google Scholar]
- Birdsey, R.A.; Weaver, P.L. Forest Area Trends in Puerto Rico; U.S. Department of Agriculture, Forest Service, Southern Forest Experiment Station: New Orleans, LA, USA, 1987; Volume 331, 5p.
- Gao, Q.; Yu, M. Discerning fragmentation dynamics of tropical forest and wetland during reforestation, urban sprawl, and policy shifts. PLoS ONE 2014, 9, e113140. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.; Didan, K.; van Leeuwen, W.; Miura, T.; Glenn, E. MODIS vegetation indices. In Land Remote Sensing and Global Environmental Change; Bhaskar, R., Christopher, O.J., Michael, J.A., Eds.; Springer: New York, NY, USA, 2010; pp. 579–602. ISBN 978-1-4419-6748-0. [Google Scholar]
- Justice, C.O.; Vermote, E.; Townshend, J.R.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Bessette-Kirton, E.K.; Coe, J.A.; Kean, J.W.; Godt, J.W.; Rengers, F.K.; Schulz, W.; Baum, R.L.; Jones, E.S.; Staley, D.M. Map Data Showing Concentration of Landslides Caused by Hurricane Maria in Puerto Rico; United States Geological Survey: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Lugo, A.E. Visible and invisible effects of hurricanes on forest ecosystems: An international review. Austral. Ecol. 2008, 33, 368–398. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Ryan, B.C. A Mathematical model for diagnosis and prediction of surface winds in mountainous terrain. J. Appl. Meteorol. 1977, 16, 571–584. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Phillips, D.L. A statistical-topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Gould, W.A.; Alarcón, C.; Fevold, B.; Jiménez, M.; Martinuzzi, S.; Potts, G.; Quiñones, M.; Solórzano, M.; Ventosa, E. The Puerto Rico Gap Analysis Project. Volume 1: Land Cover, Vertebrate Species Distributions, and Land Stewardship; General Technical Report IITF-GTR-39; USDA Forest Service: Washington, DC, USA, 2008; 165p. [Google Scholar]
- Laurance, W.F. Forest-climate interactions in fragmented tropical landscapes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Van Bloem, S.J.; Murphy, P.G.; Lugo, A.E.; Ostertag, R.; Costa, M.R.; Bernard, I.R.; Colon, S.M.; Mora, M.C. The influence of hurricane winds on Caribbean dry forest structure and nutrient pools. Biotropica 2005, 37, 571–583. [Google Scholar] [CrossRef]
- Larsen, M.C.; Torres-Sánchez, A.J. The frequency and distribution of recent landslides in three montane tropical regions of Puerto Rico. Geomorphology 1998, 24, 309–331. [Google Scholar] [CrossRef]
- Castro-Prieto, J.; Quiñones, M.; Gould, W. Characterization of the network of protected areas in Puerto Rico. Caribb. Nat. 2016, 29, 1–16. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nagelkerke, N.J. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Yang, Y. Prediction/Estimation with simple linear models: Is it really that simple? Econom. Theory 2007, 23, 1–36. [Google Scholar] [CrossRef]
- Pasch, R.J.; Avila, L.A.; Guiney, J.L. Atlantic hurricane season of 1998. Mon. Weather Rev. 2001, 129, 3085–3123. [Google Scholar] [CrossRef]
- Emanuel, K. Assessing the present and future probability of Hurricane Harvey’s rainfall. Proc. Natl. Acad. Sci. USA 2017. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zeng, X.; Zou, X.; González, G.; Wang, C.; Yang, S. Litterfall production prior to and during Hurricanes Irma and Maria in four Puerto Rican forests. Forests 2018, 9, 367. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, X.; Zou, X.; González, G.; Yang, S. Variation in tree-size and species dependency of hurricane damage between two Puerto Rican forests. For. Rev. 2018, 9, 1–14. [Google Scholar]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Holm, J.A.; Marra, D.M.; Rifai, S.W.; Riley, W.J.; Chambers, J.Q.; Koven, C.D.; Knox, R.G.; McGroddy, M.E.; Vittorio, A.V.D.; et al. Vulnerability of Amazon forests to storm-driven tree mortality. Environ. Res. Lett. 2018, 13, 054021. [Google Scholar] [CrossRef]
- Ramsay, H.A.; Leslie, L.M. The effects of complex terrain on severe landfalling Tropical Cyclone Larry (2006) over northeast Australia. Mon. Weather Rev. 2008, 136, 4334–4354. [Google Scholar] [CrossRef]
- Hergarten, S. Aspects of risk assessment in power-law distributed natural hazards. Nat. Hazards Earth Syst. Sci. 2004, 4, 309–313. [Google Scholar] [CrossRef]
- Prahl, B.F.; Kropp, J.P. Damage functions for climate-related hazards: Unification and uncertainty analysis. Nat. Hazards Earth Syst. Sci. 2016, 16, 1189. [Google Scholar] [CrossRef]
- Bellingham, P.J. Landforms influence patterns of hurricane damage: Evidence from jamaican montane forests. Biotropica 1991, 23, 427–433. [Google Scholar] [CrossRef]
- Brokaw, N.V.L.; Grear, J.S. Forest structure before and after Hurricane Hugo at three elevations in the Luquillo Mountains, Puerto Rico. Biotropica 1991, 23, 386–392. [Google Scholar] [CrossRef]
- Basnet, K.; Likens, G.E.; Scatena, F.N.; Lugo, A.E. Hurricane Hugo: Damage to a tropical rain forest in Puerto Rico. J. Trop. Ecol. 1992, 8, 47–55. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Beusekom, A.E.; Álvarez-Berríos, N.L.; Gould, W.A.; Quiñones, M.; González, G. Hurricane Maria in the U.S. Caribbean: Disturbance Forces, Variation of Effects, and Implications for Future Storms. Remote Sens. 2018, 10, 1386. https://doi.org/10.3390/rs10091386
Van Beusekom AE, Álvarez-Berríos NL, Gould WA, Quiñones M, González G. Hurricane Maria in the U.S. Caribbean: Disturbance Forces, Variation of Effects, and Implications for Future Storms. Remote Sensing. 2018; 10(9):1386. https://doi.org/10.3390/rs10091386
Chicago/Turabian StyleVan Beusekom, Ashley E., Nora L. Álvarez-Berríos, William A. Gould, Maya Quiñones, and Grizelle González. 2018. "Hurricane Maria in the U.S. Caribbean: Disturbance Forces, Variation of Effects, and Implications for Future Storms" Remote Sensing 10, no. 9: 1386. https://doi.org/10.3390/rs10091386
APA StyleVan Beusekom, A. E., Álvarez-Berríos, N. L., Gould, W. A., Quiñones, M., & González, G. (2018). Hurricane Maria in the U.S. Caribbean: Disturbance Forces, Variation of Effects, and Implications for Future Storms. Remote Sensing, 10(9), 1386. https://doi.org/10.3390/rs10091386