Next Article in Journal
An Empirical Algorithm to Retrieve Significant Wave Height from Sentinel-1 Synthetic Aperture Radar Imagery Collected under Cyclonic Conditions
Previous Article in Journal
Cross-Pol Transponder with Frequency Shifter for Bistatic Ground-Based Synthetic Aperture Radar
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 9
10.3390/rs10091365
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Statistical Machine Learning Methods and Remote Sensing for Sustainable Development Goals: A Review

by
Jacinta Holloway
* and
Kerrie Mengersen
School of Mathematical Sciences, Queensland University of Technology, 2 George Street, Brisbane 4001, Australia
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(9), 1365; https://doi.org/10.3390/rs10091365
Submission received: 9 July 2018 / Revised: 10 August 2018 / Accepted: 24 August 2018 / Published: 28 August 2018
Browse Figures
Versions Notes

Abstract

:
Interest in statistical analysis of remote sensing data to produce measurements of environment, agriculture, and sustainable development is established and continues to increase, and this is leading to a growing interaction between the earth science and statistical domains. With this in mind, we reviewed the literature on statistical machine learning methods commonly applied to remote sensing data. We focus particularly on applications related to the United Nations World Bank Sustainable Development Goals, including agriculture (food security), forests (life on land), and water (water quality). We provide a review of useful statistical machine learning methods, how they work in a remote sensing context, and examples of their application to these types of data in the literature. Rather than prescribing particular methods for specific applications, we provide guidance, examples, and case studies from the literature for the remote sensing practitioner and applied statistician. In the supplementary material, we also describe the necessary steps pre and post analysis for remote sensing data; the pre-processing and evaluation steps.

Graphical Abstract

1. Introduction

The development of Statistical Machine Learning (SML) methods and computational algorithms to analyse remote sensing data has been expanding for over half a century. An early example is the Laboratory for Applications of Remote Sensing (LARS), which was established in 1960. This centre produced crop identification based on the Apollo satellite spectral data and automated analysis as early as 1969, and machine implemented multispectral analysis in 1970 [1]. Since then, machine learning techniques applicable to remote sensing data have continued to develop and, as more data from quality sensors are becoming freely available, additional applications of these data are being explored.
A current key focus of remote sensing data analysis in the statistical research community is deriving environmental and agricultural statistics. Land use, land cover change, crop identification, deforestation, and water quality are some examples of statistics that are currently being derived from remote sensing data analysis. The use of remote sensing data for deriving these types of statistics and metrics is also topical internationally, as it conforms to the United Nations 2030 Agenda for Sustainable Development [2,3]. Use of remote sensing data for monitoring and supporting implementation of the Sustainable Development Goals, targets, and indicators is being explored and encouraged by the United Nations through global working groups [4], and National Statistical Organisations, such as Statistics Canada [5], are also producing these types of analyses. There is also growing interest internationally about using remote sensing data and other big data sources to examine the relationship between environmental and socio-economic indicators, such as poverty [6,7], and between environmental and economic indicators through ecosystem accounting, with the latter using the United Nations System of Environmental-Economic Accounting framework as the global standard [8].
This interest in measuring natural resources and official statistics from freely available big data sources has led to an interface between the statistical and remote sensing disciplines, and a growing number of useful resources and frameworks are being produced as a result. Examples include the Committee on Earth Observation Satellites (CEOS) 2018 handbook; Satellite earth observations in support of the sustainable development goals [9]; and the United Nations Satellite Imagery Task Team 2017 handbook on Earth Observations for Official Statistics [10]. Other useful guides for practitioners tailored to specific applications include the World Bank’s book; Earth Observation for Water Resources Management [11]; and the United Nations Food and Agriculture Organisation’s handbook on remote sensing for agricultural statistics. There is a growing body of literature from global institutes and in the research community from this multidisciplinary perspective, as we will describe further in this paper.
Given the established and increasing interest in these types of analyses and the wide range of tools and techniques available, it is timely to review the SML methods that have emerged as the most popular and appropriate approaches for remote sensing applications. Noting that there is usually no one true or correct approach, it is also of interest to consider approaches to selecting an appropriate method for a given problem. In this paper, we address these needs by providing the remote sensing and statistical practitioner with an overview of methods for analysing remote sensing data, guidance on how to select methods for particular problems, and how to evaluate the results of these analyses. We also provide references and case studies for further reading.

2. Remote Sensing for Environmental and Agricultural Statistics and SDG Indicators

Statistical analyses of remote sensing data to measure changes in natural and managed resources, such as water bodies, crops, and forests, over time has been in practice for decades. There is currently a focus on the use of remote sensing data analysis for deriving environmental and agricultural statistics.
A common example of environmental statistics that can be derived from remote sensing data is forest cover change and deforestation. Algorithms have been used to map afforestation and deforestation from Landsat satellite imagery data [12], and to assess patterns of deforestation and forest fragmentation over time using land cover maps derived from Landsat satellite imagery [13]. An example of monitoring forest change globally using satellite imagery data is the Global Forest Change map by Hansen, Potapov, Moore, Hancher et al. [14]. Forest loss, forest cover loss, and the gain and percentage of tree cover are identified from a time series analysis of Landsat images and depicted on an interactive global map in Google Earth Engine. For more information and to view the map, see https://earthenginepartners.appspot.com/science-2013-global-forest [14].
Examples of agricultural statistics that can be derived from remote sensing data include crop identification and crop yield. For example, [15] used high-temporal-resolution Geostationary Ocean Colour Imagery (GOCI) satellite data for monitoring the development of paddy rice in South Korea. For further information about using remote sensing data for crop identification and crop yield generally, refer to the FAO Handbook on Remote Sensing for Agriculture Statistics [16].
As mentioned in the introduction, the use of remote sensing data for monitoring and supporting implementation of the Sustainable Development Goals, targets, and indicators is being explored and encouraged by the United Nations through a range of avenues. The UN Committee of Experts on Global Geospatial Information Management (UN-GGIM) is leading the development of global geospatial information and encouraging its use to monitor the SDGs because these data are freely available, can enable more timely statistical outputs, and provide global data coverage [9]. CEOS have identified that remote sensing can supply high quality data about the condition and features of many natural resources, such as oceans, crops, forests, ecosystems, and snow, and man-made resources, such as built up areas and roads [9]. These, and many other environmental features relevant to the SDGs, can be measured and monitored through the use of remote sensing data. The applications of statistical machine learning methods to remote sensing data described in this review are related to a number of Sustainable Development Goals. These are briefly described in Table 1. A complete summary of all the SDGs that are measurable by remote sensing data is provided in Table S1 in the supplementary material. An extensive table of the SDG targets and indicators that can be directly or significantly measured by remote sensing is published by CEOS in their report, Satellite Earth Observations in Support of the Sustainable Development Goals [9] (pp. 13–19). For a review of the role that remote sensing data can contribute to the Sustainable Development Goals, see Anderson et al. (2017) [2].

3. Conducting SML Analyses

There are generally three main steps in the analysis of remote sensing data, namely, pre-processing, analysis, and evaluation [10]. The focus of this review is on the analysis step, although we include a short discussion of the pre-processing step in the supplementary material section 1. Included in the supplementary materials are Figure S1 which illustrates a range of free, analysis ready remote sensing data products, and Figure S2 which illustrates steps in an accuracy assessment process for map data.
The analysis step involves the following considerations:
Overall aim: Definition of the overall aim, such as producing a Sustainable Development Goal indicator; and definition of the corresponding statistical estimates, predictions, or inferences that are to be obtained from the analysis.
Data: Determination of which subset of the stored data will be used in the analysis, and whether the analysis will be based solely on the remote sensing data or in combination with other data sources.
Analytic method: Selection of a general approach and specific technique for extracting the required quantities, based on the aim and available data. This will be a focus of this review.

4. Analysis Step

Once pre-processing has been performed or an analysis ready dataset has been selected, the practitioner needs to determine their analytic approach and method (or methods) most appropriate to the specific problem. To assist in this process, the following questions should be considered:
  • Of what phenomena is knowledge required, and what measures are required to provide this knowledge?
  • what statistics will be used to estimate these measures? and
  • what data are required to obtain these statistics?
The answers to the first two questions will vary depending on the aim of the analysis. In addressing the third question, it is important to recognise that not all of the available data are necessarily required for a particular analysis. A good data management structure will allow either the aggregation of relevant data for analysis, or alternatively provide the tools to access datasets from different databases stored in different (virtual) locations. There are advantages and disadvantages of both of these approaches. Identifying only relevant data for the analysis helps to guard against the generation of spurious results due to the inclusion of superfluous information.
In addition to identifying the type of analytic problem, it is necessary to choose an analytic approach or combination of approaches. Analytic approaches can be broadly categorised as statistical machine learning methods, informed statistical machine learning methods, physics based methods, and object based methods.
Statistical machine learning methods are methods that can be used to establish statistical relationships between remotely sensed covariates and a variable of interest without there necessarily being a causal or even known relationship. Informed statistical machine learning methods are similar, however, there is some knowledge about the relationship or the covariates involved. Physics based methods require detailed knowledge about the relationship being modelled. Object based methods can be used as a pre-analysis step to segment satellite images into homogenous groups or as a method of analysis, without requiring knowledge of the relationship being modelled.
The choice of analytic approach depends on the available data and degree of understanding of the physical processes underlying the relationship between the remote sensing inputs and the target estimates. For example, if there is a strong understanding of the biological or physical processes, then a physics-based approach is appropriate, otherwise a statistical machine learning approach may be more suitable. If data are available and there is knowledge of the process, then informed statistical machine learning methods can be used. There are a number of ways methods can be categorised, and this is just one approach based on a collaboration between members of the remote sensing, statistical, and machine learning communities [10].
The methods described in the paper are under the first three categories; statistical machine learning, informed statistical machine learning, and physics based methods are all pixel based, that is, applied at a per pixel level. These methods could also be applied to objects, for example, using a boosted regression tree to classify objects made up of many pixels into land cover type. However, in this review, a selection of object based methods are only described in the relevant sections. There are benefits to performing object based methods to cluster pixels prior to analysis to cope with finer resolution satellite imagery and reduce the dimensionality of the data i.e., analysing 50 objects or clusters rather than thousands of individual pixels. It is important to recognise and account for the fact that any choice of method, at any level of resolution, will introduce some error in measurement and/or uncertainty.

4.1. Statistical Machine Learning Methods

Statistical machine learning methods, also referred to as empirical methods, can be defined as cases where a statistical relationship is established between the spectral bands or frequencies used and the variable measured (field-based) without there necessarily being a causal relationship. This relationship can be parametric, semi-parametric, or nonparametric [10].
The main advantages of SML approaches are that they provide a mathematically rigorous way of describing sampling and model error, estimating and predicting outcomes of interest and relationships between variables, and quantifying the uncertainty associated with these estimates and predictions. They can also be used to test hypotheses under specified assumptions, and some models, such as decision trees, have few assumptions. Disadvantages are the required ground truth data to train the model or verify model results (unlike the physics-based models). This reliance on ground truth data also means they may be difficult to extrapolate or transfer to other contexts [18,19].
There are many statistical machine learning algorithms that perform different tasks. Some of the algorithms that are relevant to remote sensing data as applied to Sustainable Development Goal targets are grouped according to four main analytic aims: Classification, clustering, regression, and dimension reduction (Figure 1). An overview of these methods and their applications, including references for further reading, is provided in Table 2, Section 8.

4.2. Informed Statistical Machine Learning Methods

Informed statistical machine learning methods, also referred to as semi-empirical methods, combine knowledge about the process with SML or empirical models. This knowledge can be about the process itself or about the variables that are included in the process. These methods have been used for remote sensing data analysis for over a decade [10]. For example, [20] used Landsat 7 Enhanced Thematic Mapper image data to map selected water quality and substrate cover type parameters. Dekker et al. [19] describe a semi-empirical approach to water quality detection, in which knowledge about the spectral characteristics of some of the parameters is used to refine the statistical model. In their example, only a subset of variables is used in the model, with well-chosen spectral areas and appropriate wavebands or combinations of wavebands. The authors highlight the popularity and utility of these approaches, but also caution they still require ground truth data. While semi-empirical methods are arguably more transferable than purely empirical models (since they contain information about the process), they can still be limited by the generality of the data used to build them.
Tripathy et al. (2014) also use a semi-empirical method, which incorporates physiological measures, spectral measures, and spatial features for estimating wheat yield [21]. The authors note that while spectral (empirical) and physics-based (mechanistic) models based on vegetation indices are widely used, they are respectively limited by being data-intensive and complex. Their semi-empirical approach is proposed as an intermediate method.

4.3. Physics Based Methods

Physics based models are based on detailed knowledge of the system that is being modelled. They can be built without data, or data can be used to calibrate the model parameters. This method is suitable for automation across large areas provided that the model is appropriately and accurately parameterised [10].
Biophysical and geophysical models that utilise remote sensing data have been developed and applied to a wide range of problems for over 15 years. An early example is the extension of a PHYSGROW plant growth model to include NOAA and NASA satellite data products to create forage production maps for a large landscape. The remote sensing derived inputs were gridded to daily temperature, rainfall, and a normalised difference vegetation index (NDVI), with cokriging to take advantage of spatial autocorrelation [22]. The authors concluded that the mapped surfaces of the cokriging output could successfully identify areas of drought and argued these maps could be used as part of a geographic information system (GIS), ‘which could then be linked to economic models, natural resource management assessments, or used for drought early warning systems’ [22].
Phinn et al. (2005) pioneered the use of these methods in a marine context, using Landsat 7 Enhanced Thematic Mapper image data to map selected water quality and substrate cover type parameters [20]. There are now many examples of these types of models. For instance, Watts et al. (2014) [23] extended a terrestrial flux model that allows for satellite data as primary inputs to estimate CO2 and CH4 fluxes, and Gow (2016) combined satellite observations of land surface temperature with a surface energy balance model to estimate groundwater use by vegetation [24]. These physics-based approaches are typically based on sophisticated algorithms that consider sensor performance and multiple environmental impacts from the atmosphere and sea surface, as well as the optical properties of the water body and seafloor. For more information, see Wettle et al. (2013) [25].

4.4. Object Based Image Analysis

Object based image analysis for remote sensing data involves grouping pixels into homogenous segments or objects which can be analysed instead of analysing individual pixels. These segments have additional information to individual pixels, such as mean, variance, and mean ratio values per band [26]. Aggregating pixels into segments also makes it less computationally expensive to work with finer resolution satellite imagery, which is becoming available as the quality of sensors increases. The algorithms that perform this type of image segmentation are divided into four categories: Point-based, edge-based, region-based, and combined [26] (p. 3). Some examples of region-based object based image analysis are [27,28], which employed region-based segmentation for modelling cyclone impacts, with the latter paper evaluating cyclone risks for present and future climate change scenarios. The authors of reference [29] implemented an Object Based Image Analysis (OBIA) approach to segment QuickBird satellite imagery, classifying segments based on spatial, spectral (brightness and colour), and texture characteristics to identify new buildings in Ghana.
Geographic Object Based Image Analysis (GEOBIA) is an extension of object based image analysis, which, in the remote sensing field, involves classifying segments of pixels based on geographical information, topology, relative, and absolute locations in addition to their spectral information [30].

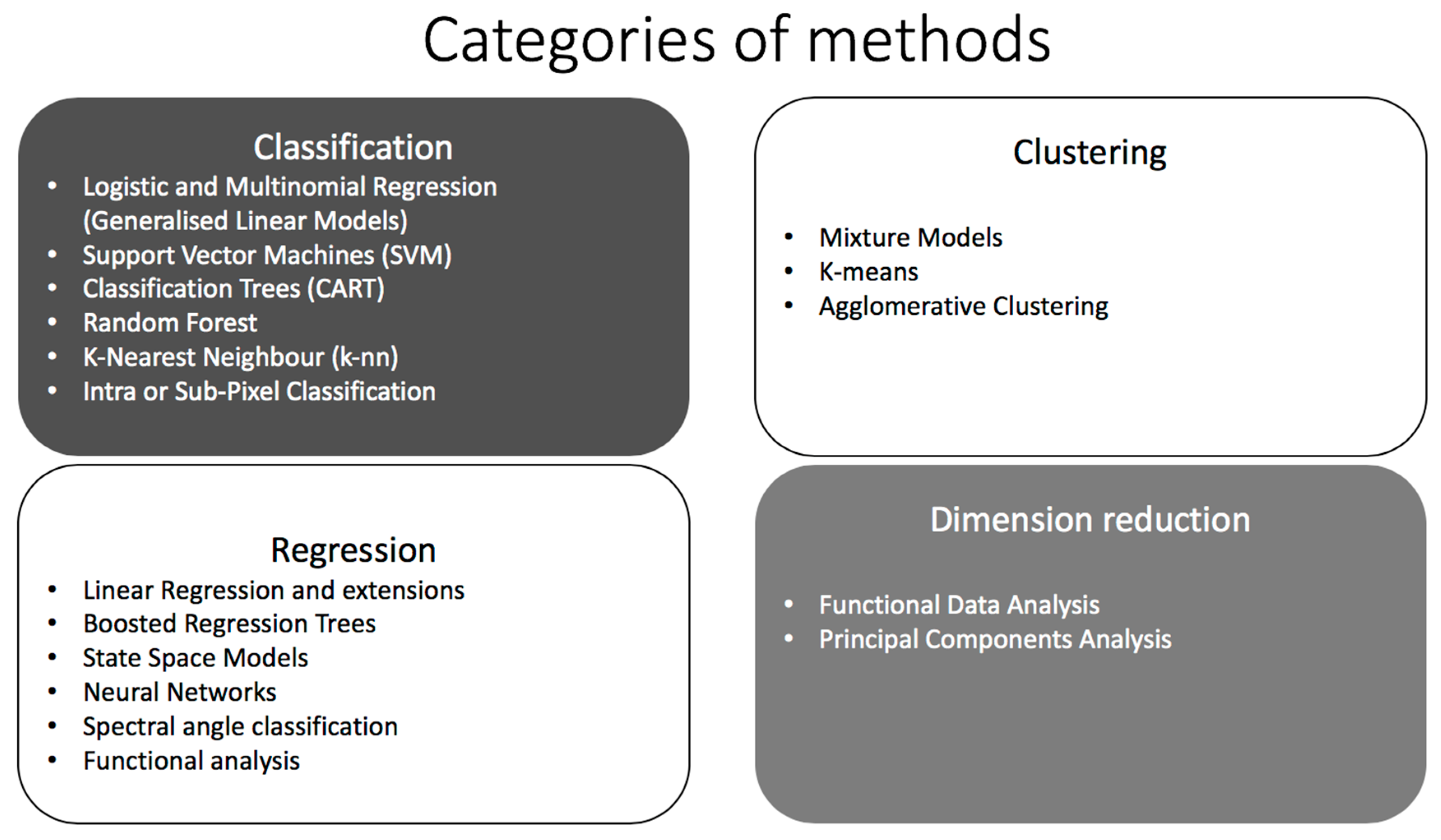
5. Categories of Statistical Machine Learning Methods

As indicated in Figure 1, four of the most common aims of remote sensing data analyses are classification, clustering, regression, and dimension reduction. The four categories of methods, as applied to remote sensing data, can be described as follows.

5.1. Classification

A classification method is applicable if the overall aim is to accurately allocate objects to a discrete (usually small) set of known classes or groups. This allocation is based on a set of input variables. In the literature, these are also called explanatory variables, factors, predictor variables, independent variables, covariates, or attributes. In this review, we will refer to these as the input variables or covariates. A set of data containing input variables and the response variable, also called the output variable, are used to develop or ‘train’ the model. This model can then be applied to test datasets that contain only the input variables. An example is the categorisation of pixels in an image into crop types based on a training dataset that contains variables extracted from the images (the input variables) and ground truth crops (the output variable) at a set of sites. The crop classification model that is developed can then be applied to the rest of the image where ground truth data are not available to classify the crop type.

5.2. Clustering

A clustering method is applicable if the aim is to combine objects into groups or classes based on a set of input variables. Clustering is an unsupervised learning method, which does not require a training data set [31]. Unlike classification, we do not know the output variable or classes. Therefore, we need to work out a measure of similarity between the objects and a way of grouping them according to these similarities. We can specify the number of groups (clusters), or also make this unknown and estimate the number of groups as part of the analysis. The analysis can be used to make decisions about the objects that were clustered or to predict cluster membership for new objects. An example is the allocation of pixels into groups based on a set of input variables extracted from an image. These groupings can then be inspected, described, and compared in terms of their characteristics.

5.3. Regression

A regression method is applicable if the aim is estimation or prediction of a response variable based on a set of covariates. This is similar to classification methods, but the response is continuous instead of categorical. Like classification methods, the regression model is developed or trained based on a set of input variables for which the response is known. An example of regression is accurately estimating or predicting crop yield based on variables extracted from a remote sensing image. In this case, crop yield is a continuous variable, rather than the crop type classes described as in the above classification example.
As shown in Figure 1, there is a wide range of regression methods, ranging from simple linear regression and logistic regression to currently popular methods, such as neural networks. For example, the neural networks category of methods includes artificial neural networks, convolutional neural networks, and deep neural networks. Of these, convolutional neural networks and deep neural networks (deep learning) are commonly used for imagery applications, such as classifying satellite images on a pixel level to improve maps [32] and integrate multiple types of remote sensing data spectrally to monitor land surface changes [33]. Other examples of neural networks for land use/land cover classification include [34,35,36,37,38]. Recently, Mayfield, Smith, Gallagher, and Hockings (2017) [39] used artificial neural networks to produce deforestation risk maps for Madagascar and Mexico.
Deep learning is becoming a method of choice for remote sensing analysis due to its predictive capability, although this accuracy comes at the cost of explanatory capacity. An example is the long short term memory neural network (LSTM), which is trained on historical satellite images, then used to predict new time series data (see Table 2). The LSTM is one of many neural network algorithms that now exist, and there are many others, including recurrent neural networks, VGG networks, and autoencoder models. These deep learning neural networks have been applied to remote sensing data in a number of ways, including classifying hyperspectral images, detecting anomalies in images, classifying terrain in synthetic aperture radar (SAR) images, and extracting features and classifying satellite images [40]. We describe neural networks in Table 2, Section 8. For a detailed review of deep learning for remote sensing, see Zhu et al. (2017) [40].

5.4. Dimension Reduction

A dimension reduction method is applicable if there are many variables that can be extracted from remote sensing data (and other data sources), and the aim is to construct a small set of new variables that contain all (or most) of the information contained in the original (large) set of input variables. These new variables can be used as inputs into other analyses or they can be end products in their own right. For example, they may be inspected to gain a better understanding of important variables or interpreted as ‘features’ or ‘indices’ (e.g., two satellite reflectance variables are combined to give a single vegetation index variable, VI). This is an unsupervised learning process since there is no response variable to estimate.

6. Statistical Machine Learning Methods for Time Series Data

The above methods can be used for analysis at a point in time or over time. Remote sensing data is often collected at regular intervals, for example, new satellite images are captured every 16 days by the Landsat 7 and 8 satellites [10], which means there is a time series of remote sensing data available. Performing analyses over time is important for measuring progress of the Sustainable Development Goals. The number of time periods considered might be small or large, depending on the analytic aim. Examples of these aims are comparisons of before-after outcomes, for example, comparing water quality or forest cover as a result of an extreme weather event and estimation; and comparison of trends over time, for example, monitoring annual land use change over decades or crop growth over a number of seasons.
If the aim is comparison of before-after outcomes, then it is typical to have a small number of remote sensing datasets corresponding to a small number of time periods. For these types of data, common approaches are to analyse the data for each time period using the methods described in Section 7; for example [12], take the difference in pixel or object values between the satellite imagery data for two periods of interest and analyse the differences using methods described in Section 7, and another example [41] is to include the time period as a covariate in the methods, as described in Section 7 [42].
If the aim is to estimate or compare trends over time, then it is typical to have a larger time series of datasets. For example, the aim may be to monitor land use changes or urban expansion over a decade, changes in water bodies during and after an extreme weather event, and so on.
Many forms of remotely sensed data, particularly from satellites, are collected over time. Although adding a temporal dimension increases the data size substantially, this can be managed by careful selection of data. For example, based on a priori knowledge regarding particular crop growth cycles. Including a temporal dimension in the analysis can add a wealth of useful insights, such as substantially more accurate crop classification as well as estimation and prediction of crop yield.
There are many approaches to analysing time series data. Fulcher et al. (2013) [43] analysed over 9000 time-series analysis algorithms and annotated collections of over 35,000 real-world and model generated time series. They developed a resource which automates the selection of useful methods for time-series classification and regression tasks and connects methods based on their empirical behavior. This can sometimes result in novel recommendations about model choice for the practitioner by drawing similarities between seemingly unrelated methods or methods outside those commonly used in their discipline that are suited to their data and problem. Some examples of the types of questions that can be answered using this resource are:
  • how do scientific methods relate to one another?
  • is there any structure in my time-series dataset? and
  • which methods will be helpful to classify time series in a particular dataset?
A useful diagram of these and other questions that can be answered by using Fulcher et al.’s tool is available via the blog Systems and Signals Group [44].
The different methods for analysing remote sensing data collected over time can also be classified according to whether the aim is classification, clustering, regression, or dimension reduction.

6.1. Classification

To classify time series data, it is necessary to establish how to compare them. A common approach to comparing curves is through alignment matching. Two methods for alignment matching are instance-based comparison, which involves computing the distance between the series at a set of points along the series [45], and feature-based comparison [45,46], which involves comparing a set of features, such as those obtained by principal components analysis. Other approaches for classifying curves can be categorised as comparative approaches, such as clustering and principal components analysis, and model-based approaches, such as cubic splines, harmonic analysis, and state space models.

6.2. Clustering

As previously described in Section 5.2, the overall aim is to combine objects into groups or classes based on a set of input variables. Three main groups of methods for clustering time series data are as follows [47]:
1.
Work directly on time series data either in frequency or time domain.
The most common similarity measures used for direct comparison of time series include correlation, distance between data points, and information measures. Hierarchical clustering and k-means methods are then applied to these measures.
2.
Work indirectly with features extracted from time series.
The most common features extracted from time series data include points identified visually, via transformations of the data, or via dimension reduction. The most common distance measure is the Euclidean distance, although Kullback-Liebler and geometric distances are also used.
3.
Work with models built from the time series.
The most common time series models include moving average (MA), autoregressive (AR) and autoregressive moving average (ARMA) models and variants, State Space Models (SSM) which are a form of hidden Markov models (HMM), and fuzzy set methods.

6.3. Regression

Time series regression aims to predict a future response based on the response history from relevant predictors. Common methods that are used for this purpose are parametric time series models that capture temporal dynamics, which are listed above (MA, AR, ARMA, and HMM), and nonparametric convolutional neural networks, which are an extension of static neural networks, adapted to describe data over time. Another common aim for time series regression is interpolation of missing data within the spatial and temporal span of the data. For example, cloud cover is a common reason for missing data in remote sensing images [48]. Splines are widely used for both spatial and temporal interpolation.

6.4. Dimension Reduction

A common approach to dimension reduction of temporal data is principal components analysis (PCA). One application is to perform PCA to reduce dimensionality of satellite imagery prior to further statistical analysis. McCord et al. [49] used PCA after pre-processing Landsat and RedEye remote sensing data and before fitting a Bayesian additive regression tree model to classify landcover. This approach is also used to classify remote sensing data into output classes, such as land cover and crop types. An example of PCA applied to a time series of enhanced vegetation index (EVI) values is described in [50]. Another approach to dimension reduction of temporal data is factor analysis. An example of factor analysis applied to vegetation indices over time is described in Liu et al. [51].

7. Ensemble Approaches

Recent trends in machine learning and remote sensing analyses centre on the combination of multiple SML methods to form hybrid approaches. These ensemble approaches are also known by other names, such as multiple classifier systems for classification problems [52,53]. Ensemble methods fall into two categories: Serial (or concatenation) and parallel.
Serial combination refers to the methods being combined in a serial fashion—the results of the first analysis are used as inputs into the next analysis, and so on [54]. The final output (classification, estimate, clustering, dimension reduction, etc.) is determined by the output of the final method in the series.
Parallel combination refers to the approach that applies multiple methods to the data simultaneously; with the final output determined using some kind of decision rule [54]. The most popular decision rule for continuous outcomes is the simple average of all of the methods. For multiple classifier systems, the most popular rule is the majority vote, whereby the final class membership is the one which the majority of classifiers predict. The output of the methods can also be weighted by its estimated accuracy using a training set. Other decision rules include Bayesian averaging, fuzzy integration, and consensus theory [52].
An example of the combination of different methods for improved classification is given by [55]. The authors combined probabilistic modelling, in the form of logistic regression, with traditional remote sensing approaches to obtain maps of small-scale cropland. While the various methods are well established, the authors argued that the novelty of their approach is in the sequence of their application and the way in which they are combined. An example of the combination of different methods for improved clustering in remotely sensed images is given by [56]. In this paper, the authors propose a merger of K-means and Gaussian mixture models, whereby the former method is used to identify starting points for the latter method and EM (expectation maximisation) is employed for analysis.
Other examples of recent work in the remote sensing literature utilising a multiple classifier systems approach include Huang and Zhang (2013) [57], Li et al. (2012) [58], Roy et al. (2014) [59], Bigdeli et al. (2015) [60], Samat et al. (2014) [61], and Clinton et al. (2015) [62].

8. Overview of Methods

In Table 2, we describe types of methods that are useful for remote sensing data analysis and provide references to examples of their application in the remote sensing literature. The methods are listed by analytic aim category as described in Figure 1.

9. Conclusions

This review has shown there is clearly an interface between the earth science and statistical domains, as remote sensing data continues to become more freely available and interest in deriving key environmental, social, and agricultural metrics continues to grow at the researcher, institute, and country level. We have described four key categories of statistical machine learning methods for analysing remote sensing data; namely, regression, classification, clustering, and dimension reduction. Following a discussion about the type of estimates that can be obtained from remote sensing data, the focus turned to two of the three broad steps in analysing remote sensing data, techniques for analysing the data, and the critical evaluation of the analysis results.
A range of references has been provided to demonstrate the relevance of the methods described and their practical application to these data. The areas of application focused on those relevant to monitoring the Sustainable Development Goals, and range across agricultural and environmental statistics to other fields, such as water quality detection and urban growth. We also provide references for the technical details of the methods described here.
The choice of method used for analysis of remote sensing data depends on a number of factors; the nature and amount of training data, amount of ground truth data, type of estimates and inferences required, and availability of software and computing power for modelling.
The following overall statements can be made. SML methods are useful if there is sufficient training and calibration data, if a model-based approach is required, and if the assumptions of the models are tenable. Some machine learning methods are non-parametric and, therefore, do not require the traditional regression assumptions, which makes them useful in many cases. Informed statistical machine learning methods are useful if the conditions for statistical machine learning methods are fulfilled and, additionally, if there is some expert knowledge about the input variables and system. Physics-based methods are useful if there is a deep knowledge about the system under consideration and/or if there is a lack of calibration or training data.
Comparisons between various SML methods are often made, as multiple methods can be applied to the same data. Advantages and disadvantages of the different methods depend on the nature of the problem. Some examples of these comparisons are Hogland et al. [95], Shao and Lunetta [36], Otukei and Blaschke [68], Szuster et al. [65], Yang et al. [96], and Melgani and Bruzzone [97].
As the use of remote sensing data for measuring the Sustainable Development Goals and producing official statistics increases, the need for practitioners to have an understanding of both the earth science and statistical side of producing these metrics will continue to increase. Research using remotely sensed data is also increasing, and as available sensors change and more data sources become freely available, future work will likely include more ensemble methods and new approaches to performing these remote sensing analyses.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/10/9/1365/s1. These materials describe the pre-processing and evaluation steps referred to in section 3, and the application of remote sensing data to sustainable development goals referred to in section 2. Figure S1: CEOS Data Cube products by status, Figure S2: Adapted process for processing map data from raw form to interpreting statistical outputs, Table S1: Earth observation and geospatial information resources for SDG monitoring.

Author Contributions

J.H. and K.M. conceived the concept for the review and wrote the paper in collaboration.

Funding

This research received no external funding.

Acknowledgments

This paper is motivated by a United Nations Report the authors contributed a methodology chapter to as part of their role in the United Nations Satellite Imagery and Geospatial Data Task Team. The authors would like to thank and acknowledge the other main authors of the Task Team report (in chapter order) Hannes I. Reuter (Eurostat), Arnold Dekker, Flora Kerblat, Alex Held and Robert Woodcock (Commonwealth Science and Industrial Research Organisation), Alexis McIntyre (Geoscience Australia) and Sandra Yaneth Rodriquez (Departamento Administrativo Nacional de Estadistica). The authors also thank and acknowledge Siu-Ming Tam for comments and guidance on the report, as Chair of the Task Team at the time the report was written.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Landgrebe, D. Early History of LARS. Available online: https://www.lars.purdue.edu/home/LARSHistory.html (accessed on 2 August 2018).
  2. Anderson, K.; Ryan, B.; Sonntag, W.; Kavvada, A.; Friedl, L. Earth observation in service of the 2030 Agenda for Sustainable Development. Geo-Spat. Inf. Sci. 2017, 20, 77–96. [Google Scholar] [CrossRef]
  3. European Space Agency Earth Observation for Sustainable Development. Available online: http://eo4sd.esa.int/ (accessed on 10 April 2018).
  4. United Nations United Nations Global Working Group on Big Data for Official Statistics. Available online: https://unstats.un.org/bigdata/ (accessed on 10 April 2018).
  5. Statistics Canada Integrated Crop Yield Modelling Using Remote Sensing, Agroclimatic Data and Survey Data. Available online: http://www23.statcan.gc.ca/imdb-bmdi/document/5225_D1_T9_V1-eng.htm (accessed on 10 April 2018 ).
  6. Imran, M.; Stein, A.; Zurita-Milla, R. Investigating rural poverty and marginality in Burkina Faso using remote sensing-based products. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 322–334. [Google Scholar] [CrossRef]
  7. Xie, M.; Jean, N.; Burke, M.; Lobell, D.; Ermon, S. Transfer Learning from Deep Features for Remote Sensing and Poverty Mapping. Available online: https://arxiv.org/abs/1510.00098 (accessed on 10 April 2018).
  8. United Nations SEEA Experimental Ecosystem Accounting. Available online: https://unstats.un.org/unsd/envaccounting/eea_project/default.asp (accessed on 10 April 2018).
  9. Committee on Earth Observation Satellites. Ceos eo Handbook Special 2018 Edition. Available online: http://eohandbook.com/sdg/index.html (accessed on 10 April 2018).
  10. Earth Observations for Official Statistics: Satellite Imagery and Geospatial Data Task Team Report. 2017. Available online: https://unstats.un.org/bigdata/taskteams/satellite/UNGWG_Satellite_Task_Team_Report_WhiteCover.pdf (accessed on 10 April 2018).
  11. García, L.; Rodríguez, J.D.; Wijnen, M.; Pakulski, I. Earth Observation for Water Resources. In Management: Current Use and Future Opportunities for the Water Sector; García, L., Rodríguez, D., Wijnen, M., Pakulski, I., Eds.; The World Bank: Washington, DC, USA, 2016; Available online: http://elibrary.worldbank.org/doi/book/10.1596/978-1-4648-0475-5 (accessed on 10 April 2018).
  12. Liu, L.; Tang, H.; Caccetta, P.; Lehmann, E.A.; Hu, Y.; Wu, X. Mapping afforestation and deforestation from 1974 to 2012 using Landsat time-series stacks in Yulin District, a key region of the Three-North Shelter region, China. Environ. Monit. Assess. 2013, 185, 9949–9965. [Google Scholar] [CrossRef] [PubMed]
  13. Echeverria, C.; Coomes, D.; Salas, J.; Rey-Benayas, J.M.; Lara, A.; Newton, A. Rapid deforestation and fragmentation of Chilean Temperate Forests. Biol. Conserv. 2006, 130, 481–494. [Google Scholar] [CrossRef]
  14. Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
  15. Yeom, J.-M.; Kim, H.-O. Comparison of NDVIs from GOCI and MODIS Data towards Improved Assessment of Crop Temporal Dynamics in the Case of Paddy Rice. Remote Sens. 2015, 7, 11326–11343. [Google Scholar] [CrossRef] [Green Version]
  16. FAO. Handbook on Remote Sensing for Agricultural Statistics. 2016. Available online: http://gsars.org/wp-content/uploads/2017/09/GS-REMOTE-SENSING-HANDBOOK-FINAL-04.pdf (accessed on 10 April 2018).
  17. Nations, U. Sustainable Development Goals: Sustainable Development Knowledge Platform. Available online: https://sustainabledevelopment.un.org/?menu=1300 (accessed on 29 June 2018).
  18. Wikle, C.K. A Kernel-Based Spectral Model for Non-Gaussian Spatio-Temporal Processes. Available online: http://journals.sagepub.com/doi/abs/10.1191/1471082x02st036oa?journalCode=smja (accessed on 19 April 2018).
  19. Dekker, A.G.; Peters, S.; Vos, R.; Rijkeboer, M. Remote sensing for inland water quality detection and monitoring: State-of-the-art application in Friesland waters. In GIS and Remote Sensing Techniques in Land- and Water-Management; Springer: Dordrecht, The Netherland, 2001; pp. 17–38. [Google Scholar]
  20. Phinn, S.R.; Dekker, A.G.; Brando, V.E.; Roelfsema, C.M. Mapping water quality and substrate cover in optically complex coastal and reef waters: An integrated approach. Mar. Pollut. Bull. 2005, 51, 459–469. [Google Scholar] [CrossRef] [PubMed]
  21. Tripathy, R.; Chaudhary, K.N.; Nigam, R.; Manjunath, K.R.; Chauhan, P.; Ray, S.S.; Parihar, J.S. Operational semi-physical spectral-spatial wheat yield model development. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-8, 977–982. [Google Scholar] [CrossRef]
  22. Angerer, J.P.; Stuth, J.W.; Wandera, F.P.; Kaitho, R.J. Use of Satellite-Derived Data to Improve Biophysical Model Output: An Example from Southern Kenya. 2005. Available online: https://vtechworks.lib.vt.edu/handle/10919/65682 (accessed on 13 April 2018).
  23. Watts, J.D.; Kimball, J.S.; Parmentier, F.J.W.; Sachs, T.; Rinne, J.; Zona, D.; Oechel, W.; Tagesson, T.; Jackowicz-Korcz nski, M.; Aurela, M.; et al. A satellite data driven biophysical modeling approach for estimating northern peatland and tundra CO2 and CH4 fluxes. Biogeosciences 1961, 11. [Google Scholar] [CrossRef]
  24. Gow, L. A Land Surface Temperature Model-Data Differencing Approach to Quantifying Subsurface Water Use by Vegetation: Application in the Condamine Region, South-Eastern Queensland; University of Queensland: Brisbane, Australia, 2016; Available online: https://espace.library.uq.edu.au/view/UQ:603403 (accessed on 16 April 2018).
  25. Wettle, M.; Hartmann, K.; Heege, T.; Mittal, A.S. Satellite Derived Bathymetry Using Physics-Based Algorithms and Multispectral Satellite Imagery. Available online: http://a-a-r-s.org/acrs/index.php/acrs/acrs-overview/proceedings-1?view=publication&task=show&id=1369 (accessed on 16 April 2018).
  26. Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
  27. Hoque, M.A.-A.; Phinn, S.; Roelfsema, C.; Childs, I. Assessing tropical cyclone impacts using object-based moderate spatial resolution image analysis: A case study in Bangladesh. Int. J. Remote Sens. 2016, 37, 5320–5343. [Google Scholar] [CrossRef]
  28. Hoque, M.A.-A.; Phinn, S.; Roelfsema, C.; Childs, I. Modelling tropical cyclone risks for present and future climate change scenarios using geospatial techniques. Int. J. Digit. Earth 2018, 11, 246–263. [Google Scholar] [CrossRef]
  29. Tsai, Y.H.; Stow, D.; Weeks, J. Comparison of Object-Based Image Analysis Approaches to Mapping New Buildings in Accra, Ghana Using Multi-Temporal QuickBird Satellite Imagery. Remote Sens. 2011, 3, 2707–2726. [Google Scholar] [CrossRef] [Green Version]
  30. Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Queiroz Feitosa, R.; van der Meer, F.; van der Werff, H.; van Coillie, F.; et al. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
  31. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: Berlin, Germany, 2008; ISBN 978-0-387-84857-0. [Google Scholar]
  32. Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef]
  33. Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal Satellite Image Fusion Using Deep Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
  34. Kavzoglu, T.; Mather, P.M. The use of backpropagating artificial neural networks in land cover classification. J. Int. J. Remote Sens. 2003, 2423, 143–1161. [Google Scholar] [CrossRef]
  35. Kavzoglu, T.; Reis, S. Performance Analysis of Maximum Likelihood and Artificial Neural Network Classifiers for Training Sets with Mixed Pixels. GISci. Remote Sens. 2008, 45, 330–342. [Google Scholar] [CrossRef]
  36. Shao, Y.; Lunetta, R.S. Comparison of support vector machine, neural network, and CART algorithms for the land-cover classification using limited training data points. ISPRS J. Photogramm. Remote Sens. 2012, 70, 78–87. [Google Scholar] [CrossRef]
  37. Wang, L.; Shi, C.; Diao, C.; Ji, W.; Yin, D. A survey of methods incorporating spatial information in image classification and spectral unmixing. Int. J. Remote Sens. 2016, 37, 3870–3910. [Google Scholar] [CrossRef] [Green Version]
  38. Wang, Q.; Shi, W.; Atkinson, P.M.; Li, Z. Land Cover Change Detection at Subpixel Resolution with a Hopfield Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 1–14. [Google Scholar] [CrossRef]
  39. Mayfield, H.; Smith, C.; Gallagher, M.; Hockings, M. Use of freely available datasets and machine learning methods in predicting deforestation. Environ. Model. Softw. 2017, 87, 17–28. [Google Scholar] [CrossRef]
  40. Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
  41. Espinoza-Molina, D.; Bahmanyar, R.; Datcu, M.; Diaz-Delgado, R.; Bustamante, J. Land-cover evolution class analysis in Image Time Series of Landsat and Sentinel-2 based on Latent Dirichlet Allocation. In Proceedings of the 2017 9th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp), Brugge, Belgium, 27–29 June 2017; pp. 1–4. [Google Scholar]
  42. Vance, C.; Geoghegan, J. Temporal and spatial modelling of tropical deforestation: A survival analysis linking satellite and household survey data. Agric. Econ. 2002, 27, 317–332. [Google Scholar] [CrossRef]
  43. Fulcher, B.D.; Little, M.A.; Jones, N.S. Highly comparative time-series analysis: The empirical structure of time series and their methods. J. R. Soc. Interface 2013, 10, 20130048. [Google Scholar] [CrossRef] [PubMed]
  44. Signals and Systems Group. A Compound Methodological Eye on Nature’s Signals. Available online: http://systems-signals.blogspot.com.au/2013/04/a-compound-methodological-eye-on.html (accessed on 16 April 2018).
  45. Nanopoulos, A.; Alcock, R.; Manolopoulos, Y. Feature-Based Classiication of Time-Series Data; Nova Science Publishers, Inc.: Commack, NY, USA, 2001; pp. 49–61. [Google Scholar]
  46. James, G.M. Curve Alignments by Moments. Ann. Appl. Stat. 2007, 1, 480–501. [Google Scholar] [CrossRef]
  47. Rani, S.; Sikka, G. Recent Techniques of Clustering of Time Series Data: A Survey. Int. J. Comput. Appl. 2012, 52, 975–8887. [Google Scholar] [CrossRef]
  48. Tahsin, S.; Medeiros, S.; Hooshyar, M.; Singh, A. Optical Cloud Pixel Recovery via Machine Learning. Remote Sens. 2017, 9, 527. [Google Scholar] [CrossRef]
  49. McCord, S.E.; Buenemann, M.; Karl, J.W.; Browning, D.M.; Hadley, B.C. Integrating Remotely Sensed Imagery and Existing Multiscale Field Data to Derive Rangeland Indicators: Application of Bayesian Additive Regression Trees. Rangel. Ecol. Manag. 2017, 70, 644–655. [Google Scholar] [CrossRef]
  50. Potgieter, A.B.; Apan, A.; Dunn, P.; Hammer, G. Estimating crop area using seasonal time series of Enhanced Vegetation Index from MODIS satellite imagery. Aust. J. Agric. Res. 2007, 58, 316. [Google Scholar] [CrossRef]
  51. Liu, C.; Ray, S.; Hooker, G.; Friedl, M. Functional Factor Analysis for Periodic Remote Sensing Data. Ann. Appl. Stat. 2012, 6, 601–624. [Google Scholar] [CrossRef]
  52. Du, P.; Xia, J.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple Classifier System for Remote Sensing Image Classification: A Review. Sensors 2012, 12, 4764–4792. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Woźniak, M.; Graña, M. A survey of multiple classifier systems as hybrid systems. Inf. Fusion 2014, 16, 3–17. [Google Scholar] [CrossRef]
  54. Ponti, M.P. Combining Classifiers: From the creation of ensembles to the decision fusion. In Proceedings of the 2011 24th SIBGRAPI Conference on Graphics, Patterns, and Images Tutorials, Alagoas, Brazil, 28–30 August 2011. [Google Scholar]
  55. Sweeney, S.; Ruseva, T.; Estes, L.; Evans, T. Mapping Cropland in Smallholder-Dominated Savannas: Integrating Remote Sensing Techniques and Probabilistic Modeling. Remote Sens 2015, 7, 15295–15317. [Google Scholar] [CrossRef] [Green Version]
  56. Neagoe, V.-E.; Chirila-Berbentea, V. A novel approach for semi-supervised classification of remote sensing images using a clustering-based selection of training data according to their GMM responsibilities. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4730–4733. [Google Scholar]
  57. Huang, X.; Zhang, L. An SVM Ensemble Approach Combining Spectral, Structural, and Semantic Features for the Classification of High-Resolution Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
  58. Li, X.; Liu, X.; Yu, L. Aggregative model-based classifier ensemble for improving land-use/cover classification of Landsat TM Images. Int. J. Remote Sens. 2014, 35, 1481–1495. [Google Scholar] [CrossRef]
  59. Roy, M.; Ghosh, S.; Ghosh, A. A novel approach for change detection of remotely sensed images using semi-supervised multiple classifier system. Inf. Sci. 2014, 269, 35–47. [Google Scholar] [CrossRef]
  60. Bigdeli, B.; Samadzadegan, F.; Reinartz, P. Fusion of hyperspectral and LIDAR data using decision template-based fuzzy multiple classifier system. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 309–320. [Google Scholar] [CrossRef]
  61. Samat, A.; Du, P.; Baig, M.H.A.; Chakravarty, S.; Cheng, L. Ensemble Learning with Multiple Classifiers and Polarimetric Features for Polarized SAR Image Classification. Photogramm. Eng. Remote Sens. 2014, 80, 239–251. [Google Scholar] [CrossRef]
  62. Clinton, N.; Yu, L. Geographic stacking: Decision fusion to increase global land cover map accuracy. ISPRS J. Photogramm. Remote Sens. 2015, 103, 57–65. [Google Scholar] [CrossRef]
  63. Bavaghar, P.M. Deforestation modelling using logistic regression and GIS. J. For. Sci. 2015, 61, 193–199. [Google Scholar] [CrossRef]
  64. Hyandye, C.; Mandara, C.G.; Safari, J. GIS and Logit Regression Model Applications in Land Use/Land Cover Change and Distribution in Usangu Catchment. Am. J. Remote Sens. 2015, 3, 6–16. [Google Scholar] [CrossRef]
  65. Szuster, B.W.; Chen, Q.; Borger, M. A comparison of classification techniques to support land cover and land use analysis in tropical coastal zones. Appl. Geogr. 2011, 31, 525–532. [Google Scholar] [CrossRef]
  66. Mathur, A.; Foody, G.M. Crop classification by support vector machine with intelligently selected training data for an operational application. Int. J. Remote Sens. 2008, 29, 2227–2240. [Google Scholar] [CrossRef] [Green Version]
  67. Wu, K.-P.; Wang, S.-D. Choosing the kernel parameters for support vector machines by the inter-cluster distance in the feature space. Pattern Recognit. 2009, 42, 710–717. [Google Scholar] [CrossRef]
  68. Otukei, J.R.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
  69. Sharma, R.; Ghosh, A.; Joshi, P.K. Decision tree approach for classification of remotely sensed satellite data using open source support. J. Earth Syst. Sci. 2013, 122, 1237–1247. [Google Scholar] [CrossRef]
  70. Al-Obeidat, F.; Al-Taani, A.T.; Belacel, N.; Feltrin, L.; Banerjee, N. A Fuzzy Decision Tree for Processing Satellite Images and Landsat Data. Procedia Comput. Sci. 2015, 52, 1192–1197. [Google Scholar] [CrossRef]
  71. Chasmer, L.; Hopkinson, C.; Veness, T.; Quinton, W.; Baltzer, J. A decision-tree classification for low-lying complex land cover types within the zone of discontinuous permafrost. Remote Sens. Environ. 2014, 143, 73–84. [Google Scholar] [CrossRef]
  72. Dos Reis, A.A.; Carvalho, M.C.; de Mello, J.M.; Gomide, L.R.; Ferraz Filho, A.C.; Acerbi Junior, F.W. Spatial prediction of basal area and volume in Eucalyptus stands using Landsat TM data: An assessment of prediction methods. N. Z. J. For. Sci. 2018, 48, 1. [Google Scholar] [CrossRef]
  73. Schmidt, M.; Pringle, M.; Devadas, R.; Denham, R.; Tindall, D. A Framework for Large-Area Mapping of Past and Present Cropping Activity Using Seasonal Landsat Images and Time Series Metrics. Remote Sens. 2016, 8, 312. [Google Scholar] [CrossRef]
  74. McRoberts, R.E.; Tomppo, E.O.; Finley, A.O.; Heikkinen, J. Estimating areal means and variances of forest attributes using the k-Nearest Neighbors technique and satellite imagery. Remote Sens. Environ. 2007, 111, 466–480. [Google Scholar] [CrossRef]
  75. Ver Hoef, J.M.; Temesgen, H. A Comparison of the Spatial Linear Model to Nearest Neighbor (k-NN) Methods for Forestry Applications. PLoS ONE 2013, 8, e59129. [Google Scholar] [CrossRef] [PubMed]
  76. Blanzieri, E.; Melgani, F. Nearest Neighbor Classification of Remote Sensing Images With the Maximal Margin Principle. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1804–1811. [Google Scholar] [CrossRef]
  77. Zhang, J.; Wei, F.; Sun, P.; Pan, Y.; Yuan, Z.; Yun, Y. A Stratified Temporal Spectral Mixture Analysis Model for Mapping Cropland Distribution through MODIS Time-Series Data. J. Agric. Sci. 2015, 7, 95. [Google Scholar] [CrossRef]
  78. Thenkabail, P.S. Remotely Sensed Data Characterization, Classification, and Accuracies; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9781482217865. [Google Scholar]
  79. De Melo, A.C.O.; de Moraes, R.M.; dos Santos Machado, L. Gaussian Mixture Models for Supervised Classification of Remote Sensing Multispectral Images. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; pp. 440–447. [Google Scholar]
  80. Walsh, S.J.; Shao, Y.; Mena, C.F.; McCleary, A.L. Integration of Hyperion Satellite Data and A Household Social Survey to Characterize the Causes and Consequences of Reforestation Patterns in the Northern Ecuadorian Amazon. Photogramm. Eng. Remote Sens. 2008, 74, 725–735. [Google Scholar] [CrossRef]
  81. Tao, J.; Shu, N.; Wang, Y.; Hu, Q.; Zhang, Y. A study of a Gaussian mixture model for urban land-cover mapping based on VHR remote sensing imagery. Int. J. Remote Sens. 2016, 37, 1–13. [Google Scholar] [CrossRef]
  82. Usman, B. Satellite Imagery Land Cover Classification using K-Means Clustering Algorithm Computer Vision for Environmental Information Extraction. Elixir Comput. Sci. Eng. 2013, 63, 18671–18675. [Google Scholar]
  83. Kamarudin, M.K.A.; Toriman, M.E.; Wahab, N.A.; Juahir, H.; Endut, A.; Umar, R.; Gasim, M.B. Development of stream classification system on tropical areas with statistical approval in Pahang River basin, Malaysia. Desalin. WATER Treat. 2017, 96, 237–254. [Google Scholar] [CrossRef]
  84. Liao, W.; Liu, X.; Wang, D.; Sheng, Y.; Yu, B.; Zhou, Y.; He, C.; Li, X.; Myint, S.; Thenkabail, P.S. The Impact of Energy Consumption on the Surface Urban Heat Island in China’s 32 Major Cities. Remote Sens. 2017, 9, 250. [Google Scholar] [CrossRef]
  85. Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  86. Safari, A.; Sohrabi, H.; Powell, S.; Shataee, S. A comparative assessment of multi-temporal Landsat 8 and machine learning algorithms for estimating aboveground carbon stock in coppice oak forests. Int. J. Remote Sens. 2017, 38, 6407–6432. [Google Scholar] [CrossRef]
  87. Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
  88. Wendroth, O.; Reuter, H.I.; Kersebaum, K.C. Predicting yield of barley across a landscape: A state-space modeling approach. J. Hydrol. 2003, 272, 250–263. [Google Scholar] [CrossRef]
  89. Schneibel, A.; Frantz, D.; Röder, A.; Stellmes, M.; Fischer, K.; Hill, J. Using Annual Landsat Time Series for the Detection of Dry Forest Degradation Processes in South-Central Angola. Remote Sens. 2017, 9, 905. [Google Scholar] [CrossRef]
  90. Srivastava, P.K.; Han, D.; Rico-Ramirez, M.A.; Bray, M.; Islam, T. Selection of classification techniques for land use/land cover change investigation. Adv. Sp. Res. 2012, 50, 1250–1265. [Google Scholar] [CrossRef]
  91. Kong, Y.-L.; Huang, Q.; Wang, C.; Chen, J.; Chen, J.; He, D. Long Short-Term Memory Neural Networks for Online Disturbance Detection in Satellite Image Time Series. Remote Sens. 2018, 10, 452. [Google Scholar] [CrossRef]
  92. Reddy, D.S.; Prasad, P.R.C. Prediction of vegetation dynamics using NDVI time series data and LSTM. Model. Earth Syst. Environ. 2018, 4, 409–419. [Google Scholar] [CrossRef]
  93. Mia, B.; Fujimitsu, Y. Mapping hydrothermal altered mineral deposits using Landsat 7 ETM+ image in and around Kuju volcano, Kyushu, Japan. J. Earth Syst. Sci. 2012, 121, 1049–1057. [Google Scholar] [CrossRef]
  94. Escabias, M.; Aguilera, A.M.; Valderrama, M.J. Modeling environmental data by functional principal component logistic regression. Environmetrics 2005, 16, 95–107. [Google Scholar] [CrossRef]
  95. Hogland, J.; Billor, N.; Anderson, N. Comparison of standard maximum likelihood classification and polytomous logistic regression used in remote sensing. Eur. J. Remote Sens. 2013, 46, 623–640. [Google Scholar] [CrossRef]
  96. Yang, C.; Everitt, J.H.; Murden, D. Evaluating high resolution SPOT 5 satellite imagery for crop identification. Comput. Electron. Agric. 2011, 75, 347–354. [Google Scholar] [CrossRef]
  97. Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 10 01365 g001 550
Figure 1. Statistical machine learning methods for analysis of remote sensing and other data, collated according to the analytic aim.
Figure 1. Statistical machine learning methods for analysis of remote sensing and other data, collated according to the analytic aim.
Remotesensing 10 01365 g001
Table
Table 1. Remote sensing data, as used to measure UN Sustainable Development Goals.
Table 1. Remote sensing data, as used to measure UN Sustainable Development Goals.
Sustainable Development GoalSustainable Development Target DescriptionRemote Sensing Application and Indicator
Goal 2: End Hunger
Remotesensing 10 01365 i001		End hunger, achieve food security and improved nutrition, and promote sustainable agriculture.
By 2030, ensure sustainable food production systems and implement resilient agricultural practices that increase productivity and production, that help maintain ecosystems, that strengthen capacity for adaptation to climate change, extreme weather, drought, flooding, and other disasters, and that progressively improve land and soil quality.		Crop area estimation, crop yield, land cover classification, extreme weather event detection.
Indicator 2.4.1 Proportion of agricultural area under productive and sustainable agriculture.
Goal 6: Clean water and sanitation
Remotesensing 10 01365 i002		Ensure availability and sustainable management of water and sanitation for all.
By 2020, protect and restore water-related ecosystems, including mountains, forests, wetlands, rivers, aquifers, and lakes.		Water quality monitoring.
Indicator 6.6.1 Change in the extent of water-related ecosystems over time.
Indicator 6.3.2 Proportion of bodies of water with good ambient water quality.
Goal 15: Life on land
Remotesensing 10 01365 i003		Protect, restore, and promote sustainable use of terrestrial ecosystems, sustainably manage forests, combat desertification, halt and reverse land degradation, and halt biodiversity loss.
By 2020, ensure the conservation, restoration, and sustainable use of terrestrial and inland freshwater ecosystems and their services, in particular forests, wetlands, mountains, and drylands, in line with obligations under international agreements.		Forest cover monitoring, deforestation detection.
Indicator 15.1.1
Forest area as a proportion of total land area.
Indicator 15.3.1 Proportion of land that is degraded over total land area.
Indicator 15.4.2 Mountain Green Cover Index.
Source: [9,17].
Table
Table 2. Summary of methods for remote sensing data analysis and applications.
Table 2. Summary of methods for remote sensing data analysis and applications.
Method DescriptionApplications
Analytic Aim: Classification
Logistic and Multinomial Regression
Types of generalised linear models (glm). Logistic regression is used when the response variable is categorical with two levels (vegetation/not vegetation, high/low, present/absent). Multinomial logistic regression is used when the response variable has more than two levels (trees/grass/bare ground/crop/water, high/medium/low).		Bavaghar (2015) [63] used logistic regression on satellite imagery data to estimate the location and extent of deforestation based on variables, such as slope, distance to roads, and residential areas, and highlights in particular the ability to quantify the uncertainty in predictions as a strength of the approach. An overall 75% correct classification rate was obtained, with an estimate of 12% deforestation of the total study site over the 27 years from 1967 to 1994.
Hyandye et al. (2015) [64] used multinomial logistic regression to determine how land use/land cover class in Usangu, Tanzania was influenced by a set of covariates; slope, elevation, distance from roads, distance from rivers, population density, annual rainfall, Normalized Difference Vegetation Index (NDVI), and soil types. The authors used the multinomial model, run on Landsat of data across multiple years, to obtain the probable change in land use/land cover given a one unit change in these covariates.
Support Vector Machines (SVM)
SVMs are a class of non-parametric supervised classification techniques. In their simplest form, 2-class SVMs are linear binary classifiers. The term, “support vector”, refers to the points lying on the separation margin between the data groups or classes. SVMs can be used to map the support vectors in higher dimensional feature spaces to make them more separable, and then classified in the original input space. Kernel functions are used to define this mapping from the input space to the feature space.		Some papers that examine the use of SVMs for analysis of remote sensing data include Szuster (2011) [65] for land use and land cover classification in tropical coastal zones; Mathur and Foody (2008) [66] for crop classification; and Shao and Lunetta (2012) [36] for land classification.
Wu and Wang (2009) [67] and Hastie, Tibshirani, and Friedman (2008) [31] provide helpful explanations of kernels and guidance on how to select an appropriate kernel for SVMs.
Classification and Regression Trees (CART)
A supervised classification technique that represents class memberships as “leaves” and input variables are “nodes”. Branches are formed from these nodes based on splitting the values of the input variables to best group the data.
A classification tree is a member of the family of decision tree methods, which include regression trees, boosted trees, bagged trees, and so on.
The main advantage of classification trees in particular, and decision trees in general, is they are simple and easy to understand. Due to their computational simplicity they can be applied to large amounts of data.		Lawrence and Wright (2001) employed this method to classify land cover in the Yellowstone ecosystem in the USA, based on Landsat TM imagery. Otukei and Blaschke (2010) [68] used a maximum likelihood classifier, support vector machine, and decision trees to identify land cover change in satellite imagery. They found decision trees generally outperformed the other two methods and had an accuracy of over 85%.
More recent references to decision trees and remote sensing include Sharma et al. (2013) [69], Al-Obeidat et al. (2015) [70], and Chasmer et al. (2014) [71].
Random forest
A type of classification tree method, which is a set of ‘shallow’ trees constructed from many random samples. The method combines the results of these trees to classify or predict values.		dos Reis et al. (2018) [72] applied a number of methods to mapping the basal area and volume of Eucalyptus forest in Brazil, and found random forest was the best method for this spatial prediction, compared with multiple linear regression, SVM, and artificial neural network methods.
Schmidt et al. (2016) [73] compared a number of methods for classifying crop/no crop in Australia using Landsat imagery, and found that random forests provided the best accuracy and robustness.
K nearest neighbour (K-nn)
A well-known and popular nonparametric classification technique due to their relative simplicity. In their simplest form, an observation is classified according to a majority vote of its k nearest neighbours. That is, an object’s class is assigned to it by the most common class among its k nearest neighbours, where k is generally a small positive integer.
Although nearest neighbour methods are conceptually appealing and computationally fast, they are not always the best model for remote sensing data and are sometimes combined with other methods in this context.		McRoberts et al. (2007) [74] employed k-nn methodology for forest inventory mapping and estimation using Landsat imagery to derive 12 satellite image-based predictor variables, NDVI, and the Tassel Cap (TC) transformations (brightness, greenness, wetness).
Ver Hoef and Temesgen (2013) [75] compared k-nn and spatial linear models for forestry applications and preferred the spatial model. However, their accuracy and predictive capability can be improved by combining them with other models. For example, Blanzieri and Melgani (2008) [76] preferred a combination of k-nn and SVM methods for classification of remote sensing images.
Intra or sub-pixel classification
These methods can be used to address the issue of so-called “mixed” pixels; pixels that display characteristics of more than one group. Mixed pixels are mainly a concern in coarse (e.g., MODIS) or moderate (e.g., Landsat) resolution remotely sensed data.
The two most common approaches in the remote sensing literature to the mixed pixel classification problem are spectral mixture analysis (SMA) and soft, or fuzzy, classifiers.		Zhang et al. (2015) [77] propose a stratified temporal spectral mixture analysis (STSMA) for cropland area estimation using MODIS time-series data.
Discussion of advantages and disadvantages of SMA for analysis of remotely sensed data are given by Thenkabail [78].
Analytic Aim: Clustering
Mixture models
Models based on the premise that observed data arise from various sources or groups. Each group is assumed to have a particular distribution. The mixture model is then a weighted sum of these distributions, where the weights correspond to the proportion of observations in the population that belong to that group; this can also be interpreted as the probability that an observation belongs to that particular group. These methods are also known as soft, or fuzzy, classifiers. 		de Melo et al. (2003) [79] used mixture models for supervised classification of remote sensing multispectral images in an area of Tapajós River in Brazil, and Walsh (2008) [80], who combine secondary forest estimates derived from remote sensing data and a household survey to characterise causes and consequences of reforestation in an area in the Northern Ecuadorian Amazon.
More recently, Tao et al. (2016) [81] employed a Gaussian mixture model to estimate and map urban land cover using remote sensing images with very high resolution.
K-means
One of the most common clustering approaches used in machine learning. The algorithm assumes the data is drawn from K different clusters and assigns each unlabeled point to the closest group centre, which are recalculated until no changes occur.
K-means can also be used for dimension reduction; a value of k is chosen, which is large, but much smaller than the original number of pixels, and the resultant clusters are then used for further classification, regression or other analysis. 		Usman (2013) [82] used a k-means approach to classify high resolution satellite imagery data into classes, which were then determined to farmland, bare land, and built up areas. Yuan et al. (2015) used k-means to cluster land use in remotely sensed data that had already been pre-processed using functional analysis.
Agglomerative clustering
A popular clustering method. The algorithm starts with each point as its own cluster and iteratively merges the closest clusters until a stopping rule is reached. 		Kamarudin et al. (2017) [83] used hierarchical agglomerative cluster analysis on remote sensing, GIS, and a river hydrographic survey to develop a stream classification system for tropical areas in Peninsular Malaysia.
Analytic Aim: Regression
Linear regression
One of the most common empirical models. The response variable is used in its natural form or it is transformed to be more symmetric, for example, through a log transformation if the distribution is very skew. The response is then estimated by a linear combination of covariates. These covariates can take their original form or be transformed to describe non-linear relationships between the response variable and covariates e.g., polynomial transformation to describe nonlinear relationships with the response or combinations of covariates to describe interactions.		Liao (2017) [84] used linear regression to determine the impact of energy consumption on surface temperature in urban areas. The focus of the study was on 32 major cities in China and used the sum of nighttime lights in each province.
Schmidt et al. (2016) [73] used linear regression to predict reflectance at t0 in synthetic spectral images based on archived satellite images.
Boosted Regression Trees
A boosted regression tree is a combination of single decision trees. This provides the added benefit of boosting, which improves the predictive performance by combining simple tree models. Elith et al. (2008) [85] describe benefits of boosted regression trees, including the ability to fit complex nonlinear relationships and handle interaction effects between predictors. These models can also accommodate missing data and do not require data transformation or the removal of outliers. 		Safari et al. (2017) [86] used boosted regression trees to estimate carbon stocks in forests based on Landsat 8 satellite images and field data. They found this method was outperformed by random forest and support vector machine algorithms in terms of R2 and root mean square error (RMSE), but produced less biased results than the support vector machine.
Youssef et al. (2016) [87] applied boosted regression tree algorithms to satellite images to produce landslide susceptibility maps.
State Space Models
A common form of spatio-temporal model that can provide a natural setting for analysing time series of remote sensing data, particularly if the process to be modelled can be viewed as one that is spatially evolving through time.		State space models have been employed for crop estimation and prediction for over 15 years. For example, Wendroth et al. (2003) [88] used this approach to predict the yield of barley across a landscape. More recently, Schneibel et al. (2017) [89] applied the method to annual Landsat time series data, with the aim of detecting dry forest degradation processes in South-Central Angola.
Neural Networks
Popular classification methods and can also be used for regression. When represented graphically, a neural network is arranged in a number of layers; an input layer of predictor variables, one or more layers of hidden nodes, which each represent an activation function acting on a weighted input of the previous layers’ outputs, and an output layer. The output layer may be a single layer in the case of regression or in the case of classification, will consist of a node for each possible output category.
They are typically ‘trained’ or quantified via a back-propagation algorithm, which is similar to gradient descent, and iteratively adjust the weights of the graph after seeing each new data point. This updating of the weights moves the neural network toward some local minima in the parameter space in relation to the training accuracy.		Kavzoglu and Mather (2003) [90] used artificial neural networks to identify land use/land cover for remote sensing data in England, and provide a set of guidelines for practitioners for designing and using artificial neural networks in remote sensing image classification.
Recent examples of classification using neural networks for remote sensing data are given by Srivastava et al. (2012) [90], Shao and Lunetta (2012) [36], and Wang et al. (2014) [38].
Kong et al. (2018) [91] apply a long short-term memory (LSTM) neural network to predict forest fire based on a time series of Modis satellite images. To detect fire events, the authors applied the method to a composite time series instead of a single-pixel time series and examined changes in the vegetation index, GEMI (Global Environment Monitoring Index). Reddy and Prasad (2018) [92] use LSTM to predict NDVI across different terrains, including coastal and inland regions.
Analytic Aim: Dimension Reduction
Principal Components Analysis (PCA)
This method creates linear combinations of covariates, such that the new combinations (termed components) encapsulate a large amount of the information or variation in the data. Each component has an eigenvalue (‘eigen’ means ‘own’ or ‘specific’) that indicates the proportion of variation explained by the component, and a set of weights attached to each input variable (the eigenvector) that indicates the relative importance of each variable in the component.		Bodruddoza and Fujimitsu (2012) applied PCA to Landsat satellite imagery to identify mineral deposits in and around the Kuju volcano in Japan [93]
An example of PCA applied to a time series of enhanced vegetation index (EVI) values is described in Potgieter et al. (2007) [52]. EVI from 16-day MODIS satellite imagery within the cropping period (i.e., April–November) was investigated to estimate the crop area for wheat, barley, chickpea, and total winter cropped area for a case study region in North East Australia.
Functional Data Analysis (FDA)
FDA is a nonparametric method for describing and classifying curves, in which each sample point in the time series is considered to be a function observed along an underlying continuum (e.g., time). This provides great flexibility in describing the underlying curve.		Escabias et al. (2005) [94] used an FDA method for logistic regression. In this paper, the authors modelled the relationship between the risk of drought and curves of temperatures.
Cardot et al. (2003) also used a functional logistic regression model to predict land use based on the temporal evolution of coarse-resolution remote sensing data.
Liu et al. (2012) [51] used rotating functional factor analyses to improve estimation of periodic temporal trends in remote sensing data, applied to a six-year time series at eight-day intervals of vegetation index measurements obtained from remote sensing images.

Share and Cite

MDPI and ACS Style

Holloway, J.; Mengersen, K. Statistical Machine Learning Methods and Remote Sensing for Sustainable Development Goals: A Review. Remote Sens. 2018, 10, 1365. https://doi.org/10.3390/rs10091365

AMA Style

Holloway J, Mengersen K. Statistical Machine Learning Methods and Remote Sensing for Sustainable Development Goals: A Review. Remote Sensing. 2018; 10(9):1365. https://doi.org/10.3390/rs10091365

Chicago/Turabian Style

Holloway, Jacinta, and Kerrie Mengersen. 2018. "Statistical Machine Learning Methods and Remote Sensing for Sustainable Development Goals: A Review" Remote Sensing 10, no. 9: 1365. https://doi.org/10.3390/rs10091365

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop