Effects of Forest Canopy Vertical Stratification on the Estimation of Gross Primary Production by Remote Sensing
Abstract
1. Introduction
2. Materials
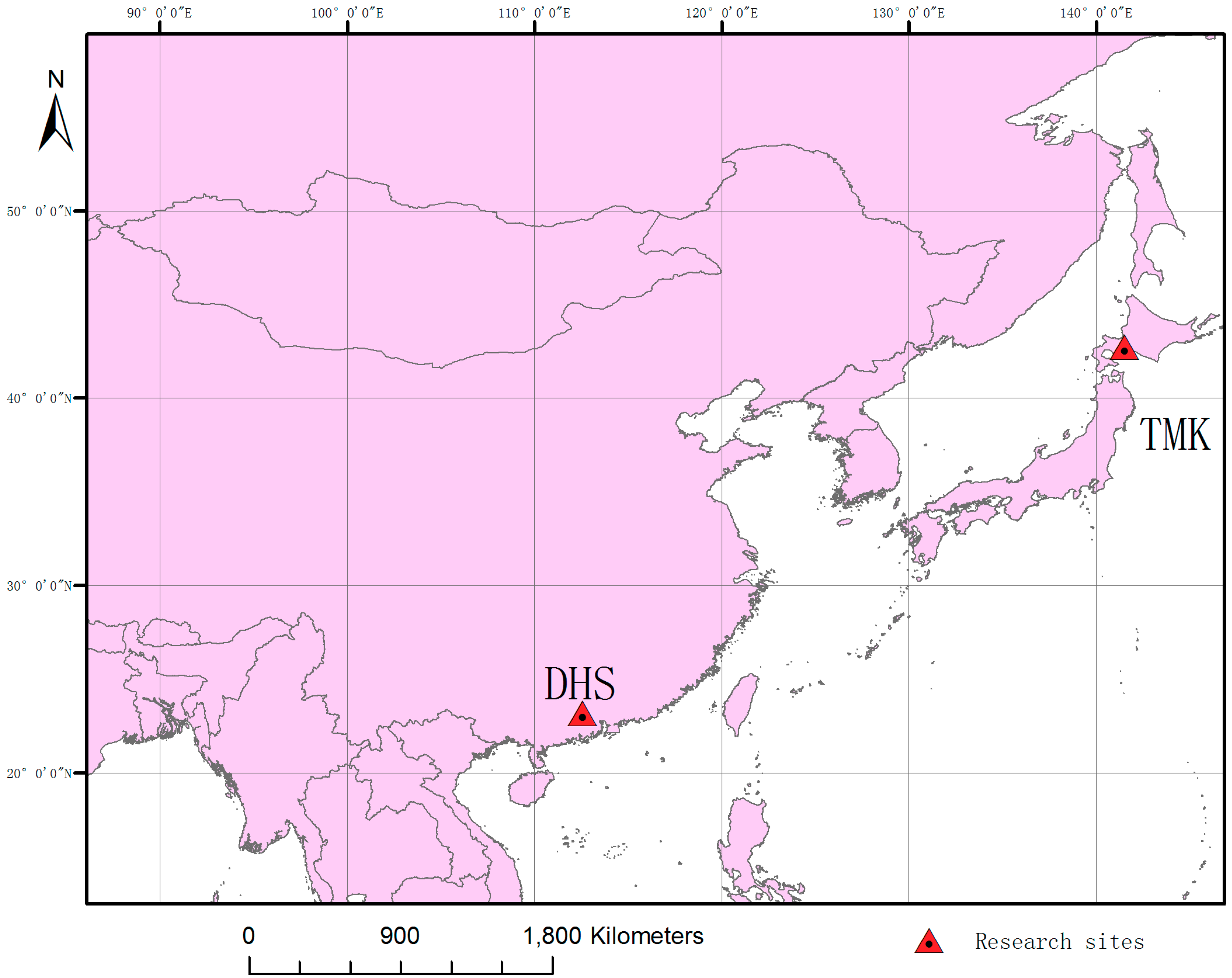
2.1. Study Sites
2.1.1. Dinghushan (DHS)
2.1.2. Tomakomai (TMK)
2.2. Vertical Data Measurements in the Forest
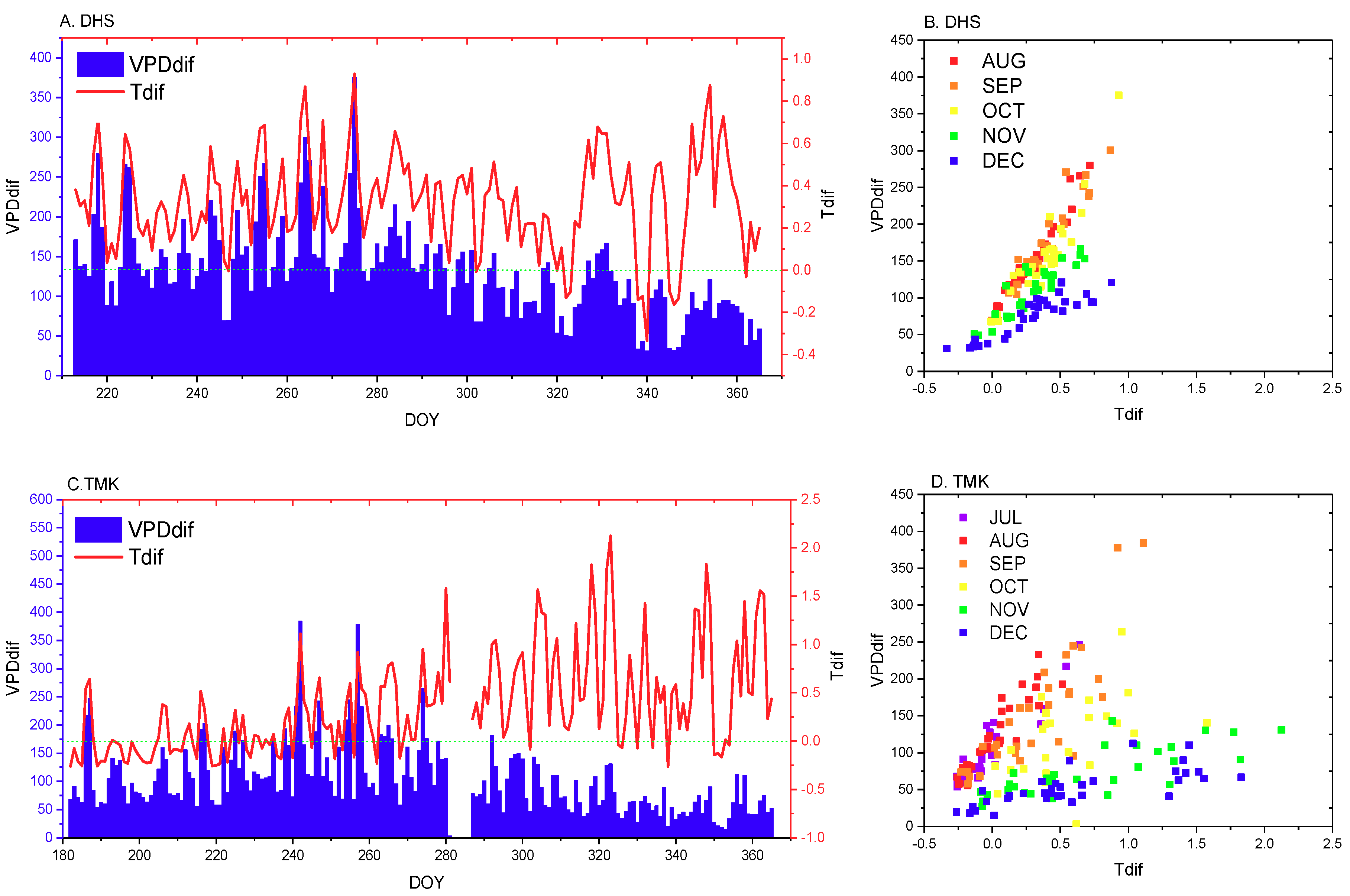
2.2.1. Temperature and VPD Data Preprocessing
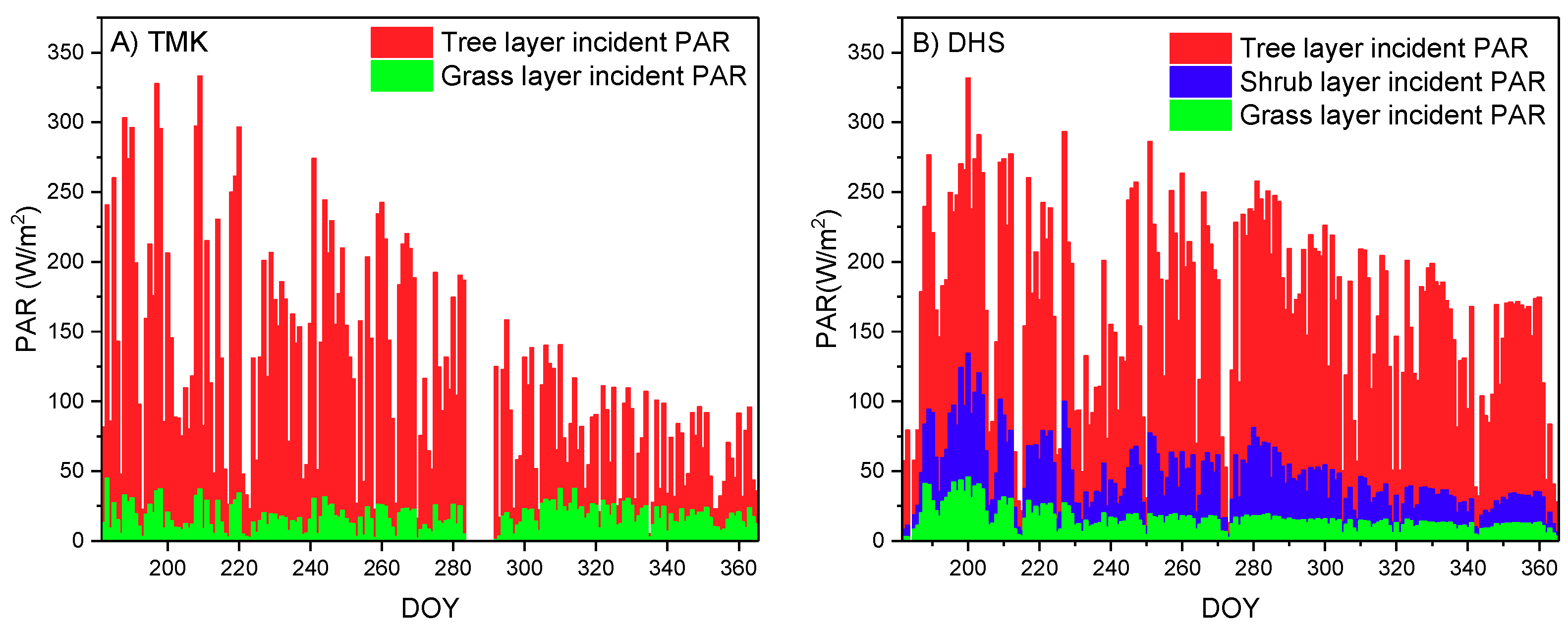
2.2.2. PPFD Data Preprocessing
2.3. GPP Data Processing
3. Methods
3.1. Theoretical Background of the GPP Model
3.2. GPP Estimation Considering the Vertical Structure
3.3. Modeling Vertical PAR with a Radiative Transfer Model
3.4. Statistical Indicators
4. Results and Analysis
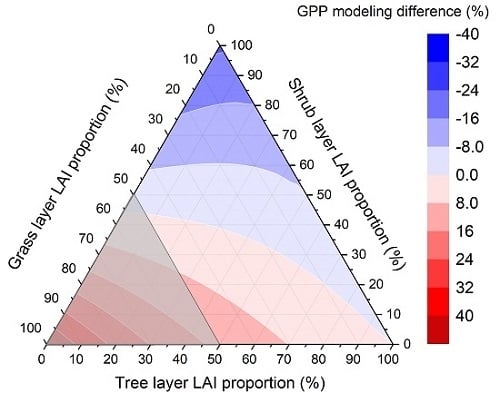
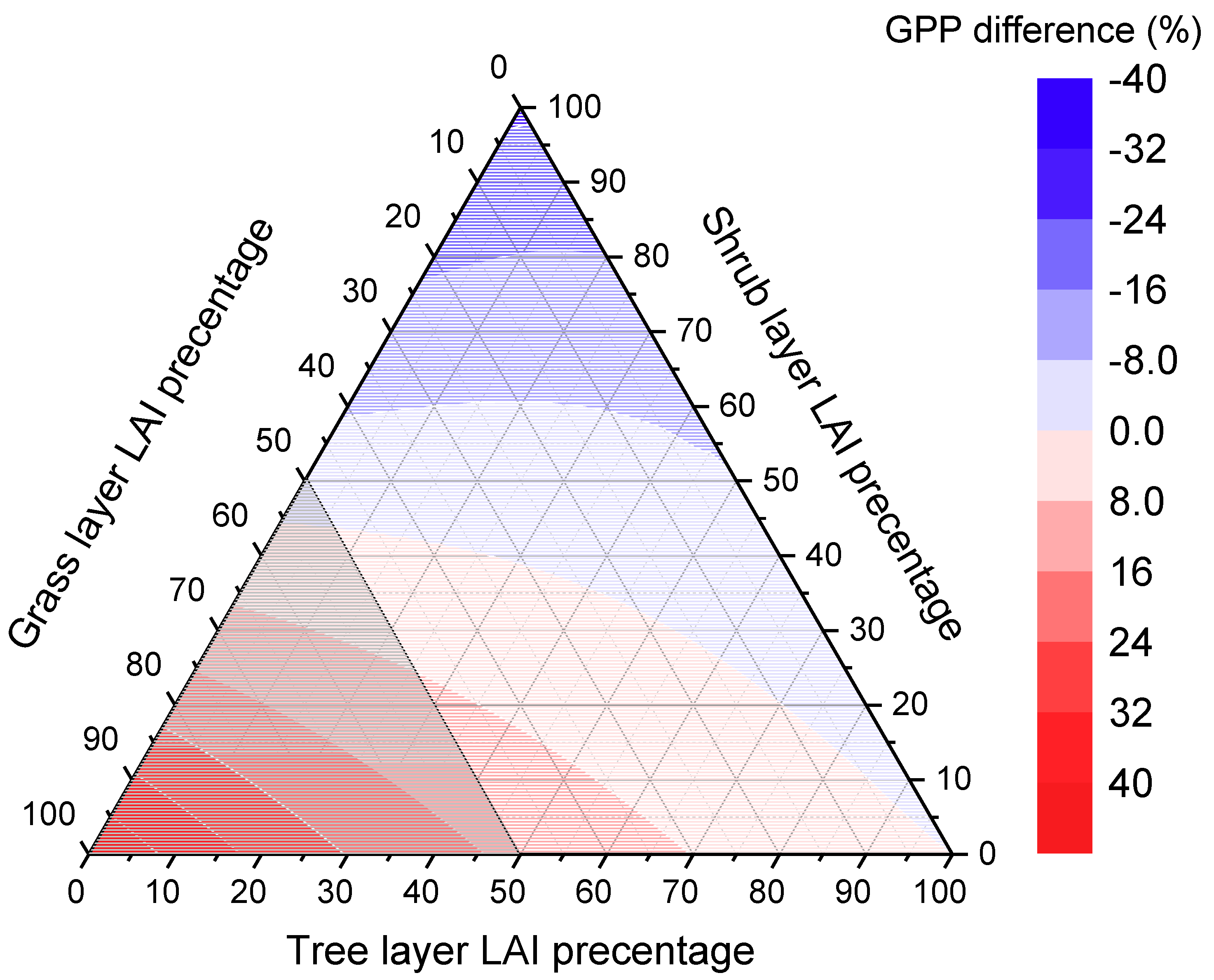
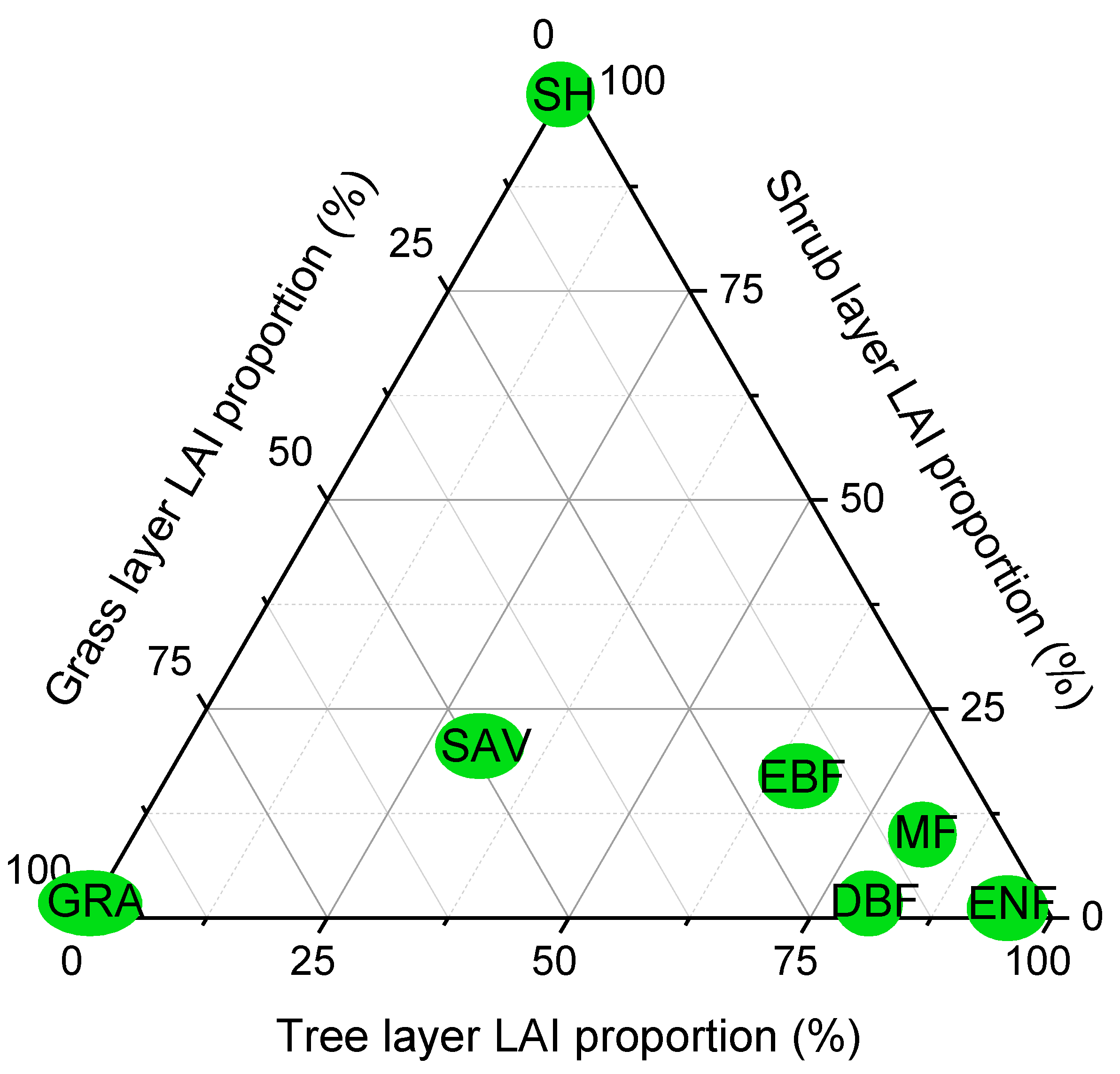
4.1. Analysis of Variance in Forest Canopy Vertical Stratification
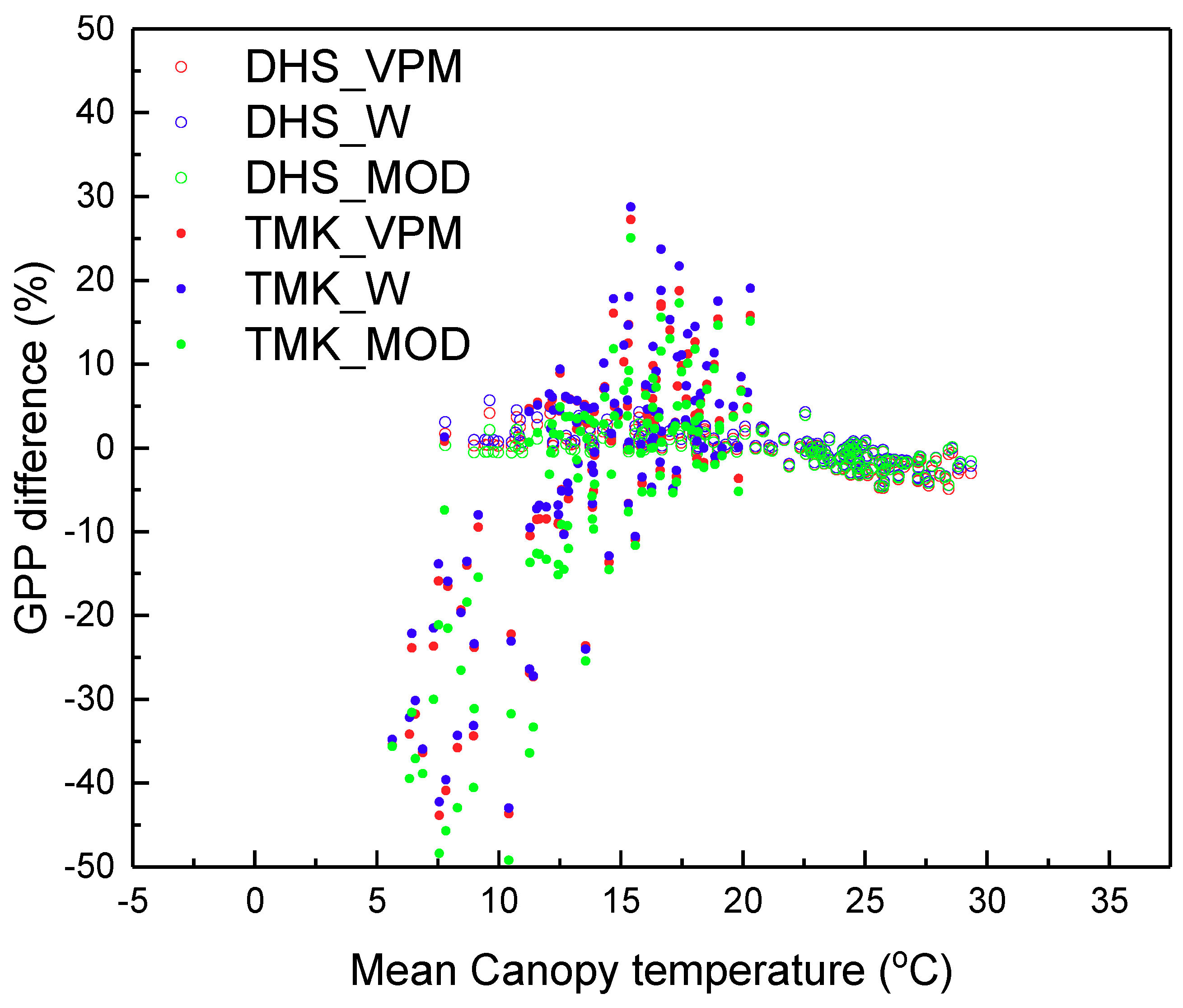
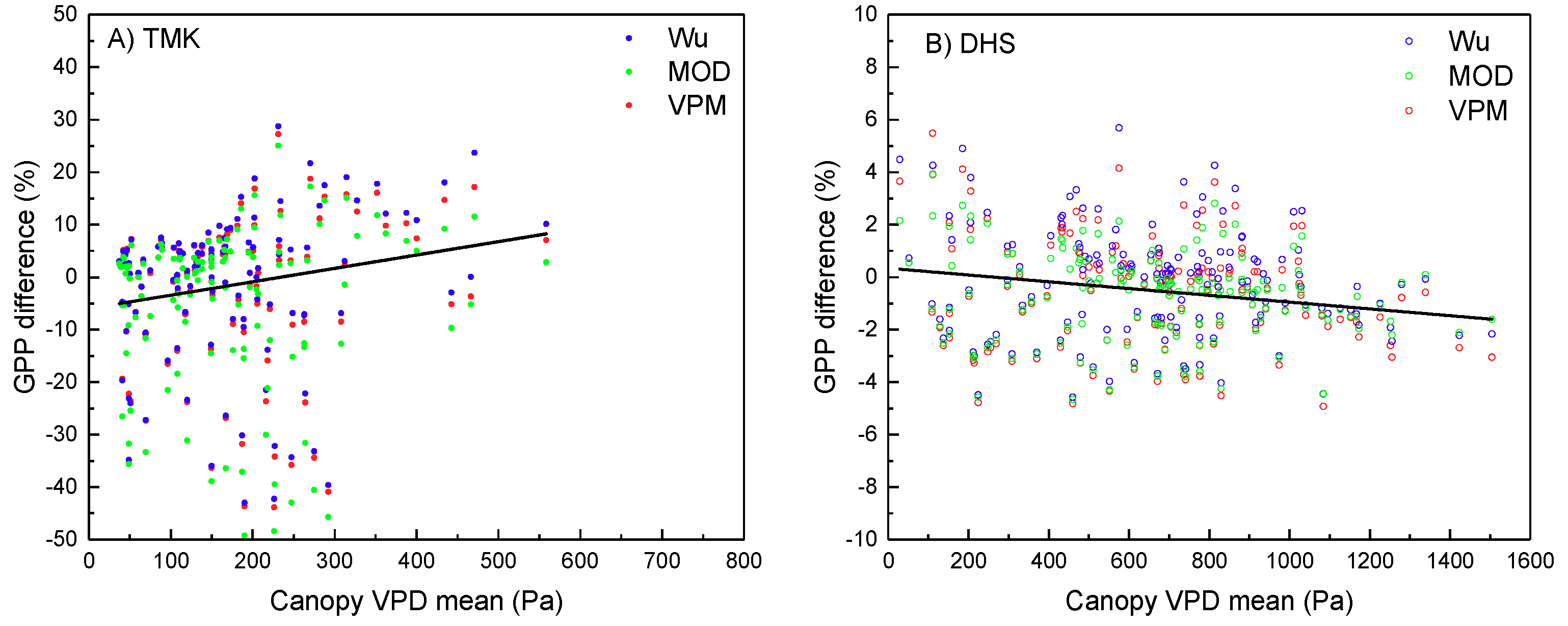
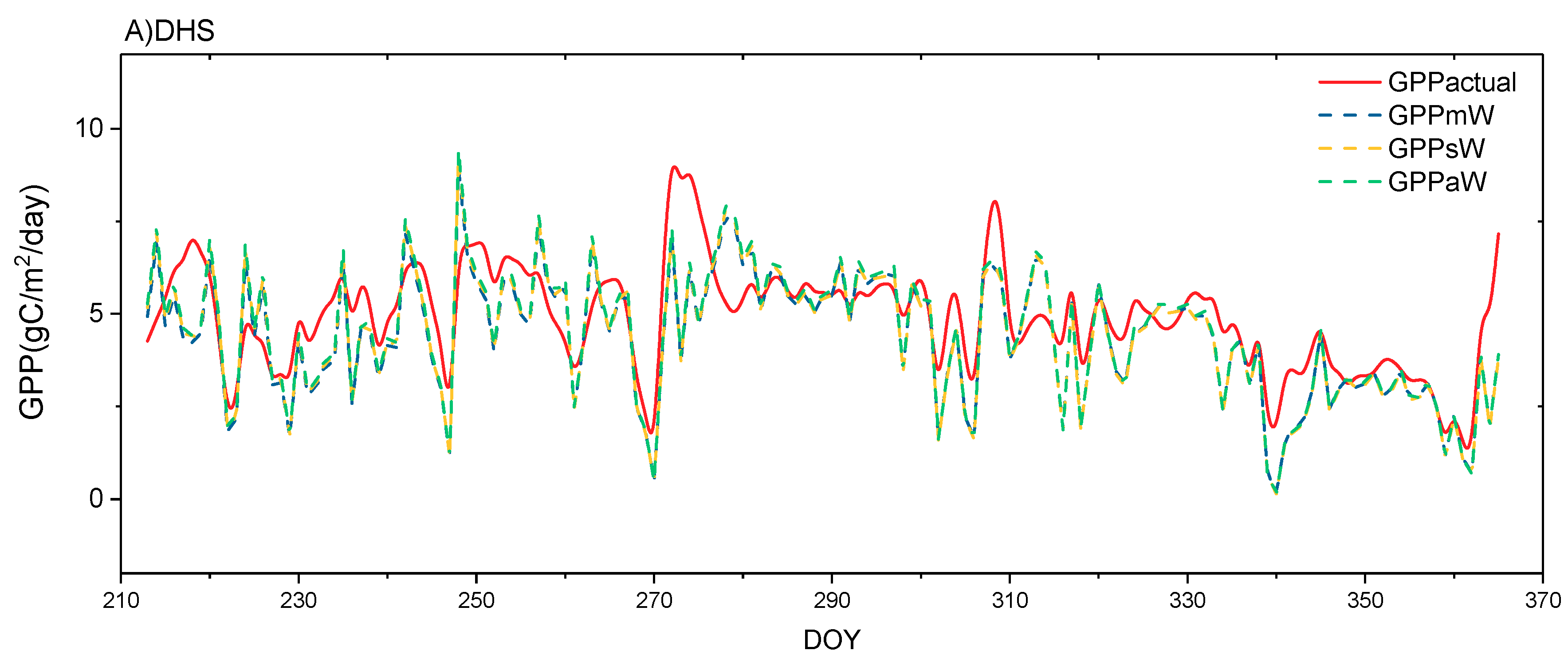
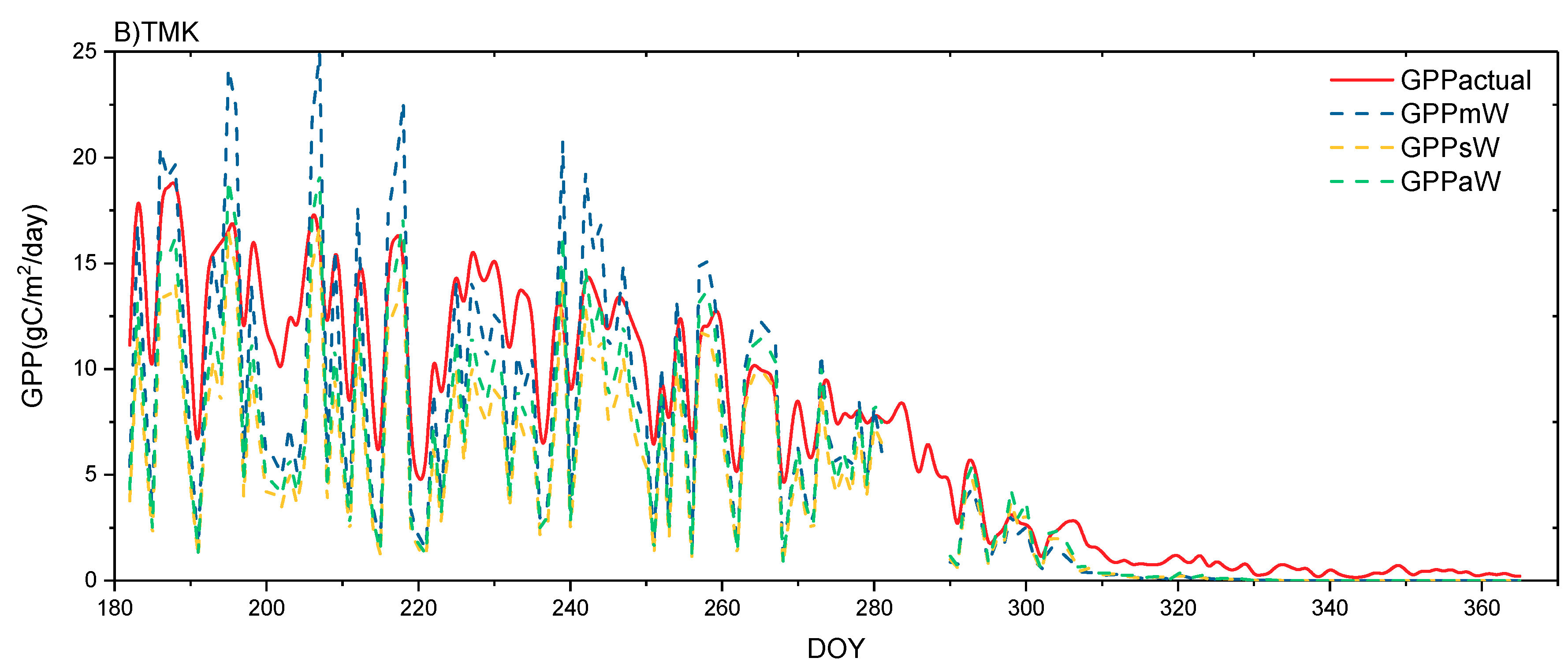
4.2. Influence of Vertical Stratification on GPP Estimation
4.2.1. LUE in Different Sub-Ecosystems Is Influenced by the Vertical Stratification of Temperature, VPD, and LUEmax
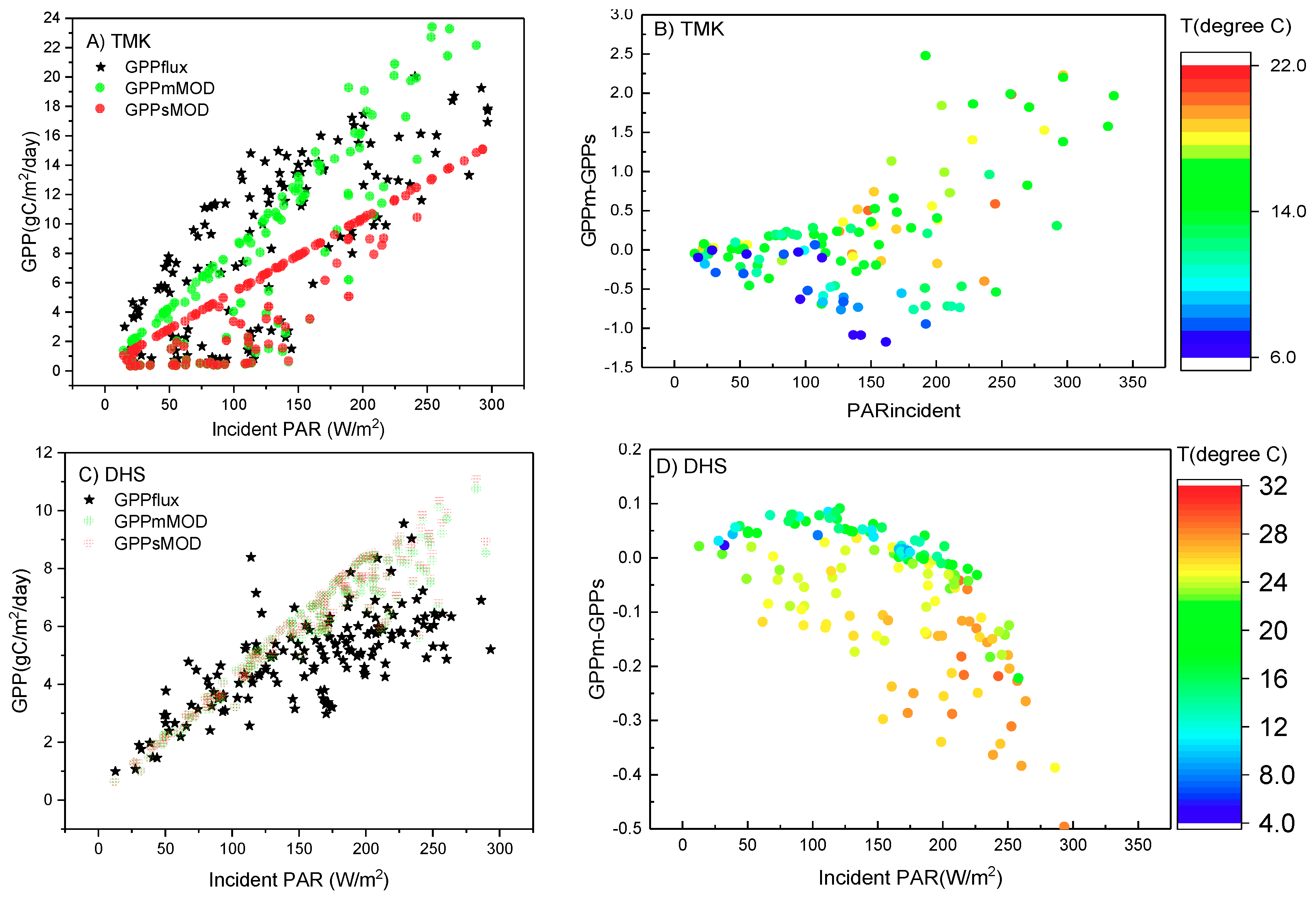
4.2.2. Vertical Stratification of APAR Influenced GPP Estimation by the Multilayer Model
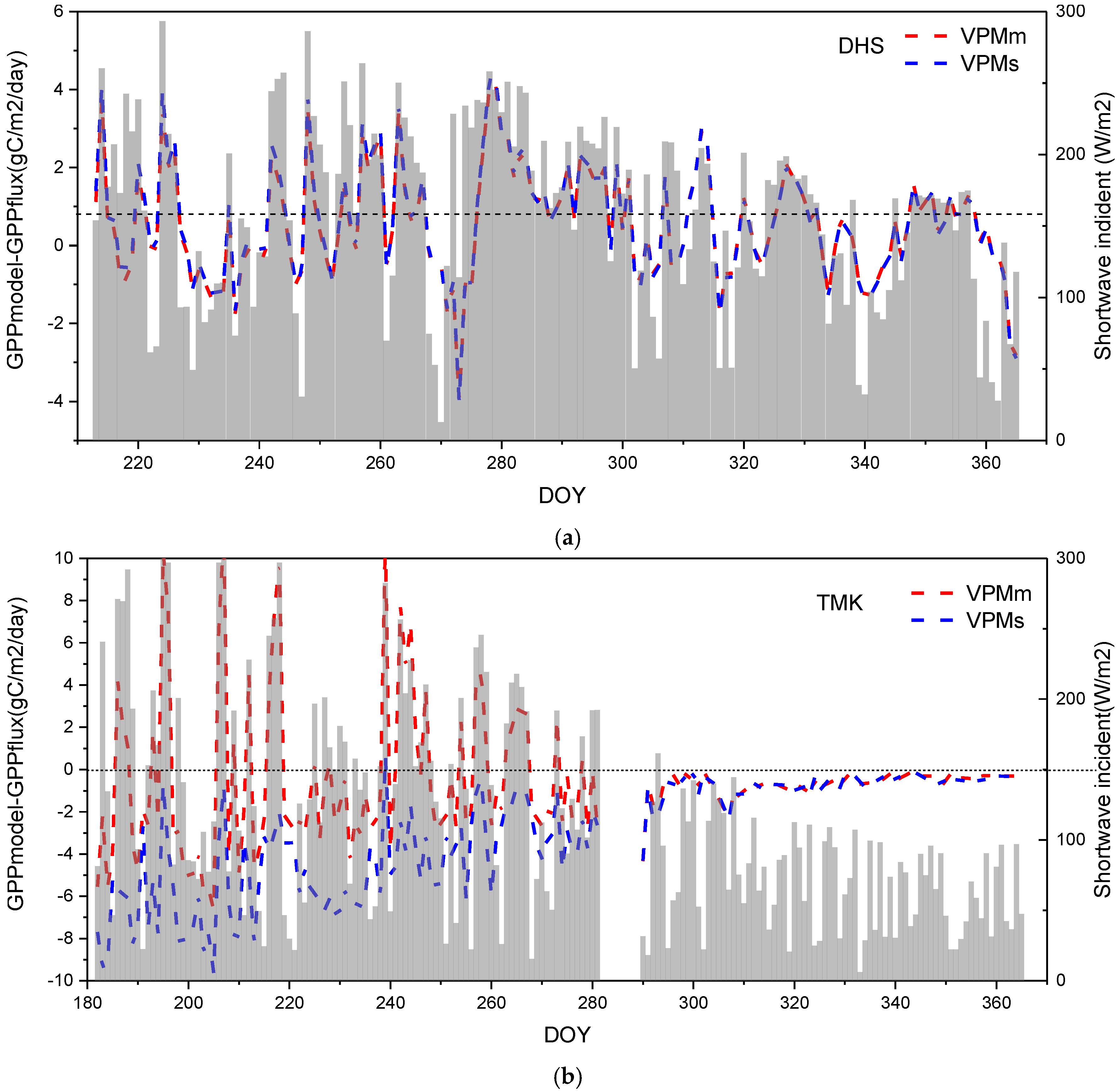
4.3. Performance of GPP Estimation Results Based on Flux Tower-Based GPP
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Litton, C.M.; Raich, J.W.; Ryan, M.G. Carbon allocation in forest ecosystems. Glob. Chang. Boil. 2007, 13, 2089–2109. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444. [Google Scholar] [CrossRef] [PubMed]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Baldocchi, D.D.; Turner, D.P.; Gower, S.T.; Bakwin, P.S.; Hibbard, K.A. A Global Terrestrial Monitoring Network Integrating Tower Fluxes, Flask Sampling, Ecosystem Modeling and EOS Satellite Data. Remote Sens. Environ. 1999, 70, 108–127. [Google Scholar] [CrossRef]
- Andrewd, F.; Almut, A.; Nancyy, K.; Mark, L.; Jérôme, O.; Christian, R.; Stevenw, R.; Jeandiego, S.; Stephen, S.; Nicolas, V. FLUXNET and modelling the global carbon cycle. Glob. Chang. Boil. 2007, 13, 610–633. [Google Scholar]
- Campbell, J.E.; Berry, J.A.; Seibt, U.; Smith, S.J.; Montzka, S.A.; Launois, T.; Belviso, S.; Bopp, L.; Laine, M. Large historical growth in global terrestrial gross primary production. Nature 2017, 544, 84. [Google Scholar] [CrossRef] [PubMed]
- Vitousek, P.M.; Aber, J.D.; Howarth, R.W.; Likens, G.E.; Matson, P.A.; Schindler, D.W.; Schlesinger, W.H.; Tilman, D.G. Human Alteration of the global nitrogen cycle: sources and consequences. Ecol. Appl. 1997, 7, 737–750. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2015, 116, 245–255. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Alton, P.B.; North, P.R.; Los, S.O. The impact of diffuse sunlight on canopy light-use efficiency, gross photosynthetic product and net ecosystem exchange in three forest biomes. Glob. Chang. Boil. 2007, 13, 776–787. [Google Scholar] [CrossRef]
- Harper, A.B.; Cox, P.M.; Friedlingstein, P.; Wiltshire, A.J.; Jones, C.D.; Sitch, S.; Mercado, L.M.; Groenendijk, M.; Robertson, E.; Kattge, J. Improved representation of plant functional types and physiology in the Joint UK Land Environment Simulator (JULES v4.2) using plant trait information. Geosci. Model Dev. 2016, 9, 1–64. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- Ju, W.; Chen, J.; Liu, R.; Liu, Y. Changes of global terrestrial carbon budget and major drivers in recent 30 years simulated using the remote sensing driven BEPS model. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2013; B23A-0535. [Google Scholar]
- Keenan, R.J.; Reams, G.A.; Achard, F.; Freitas, J.V.D.; Grainger, A.; Lindquist, E. Dynamics of global forest area: Results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 2015, 352, 9–20. [Google Scholar] [CrossRef]
- Malhi, Y.; Baldocchi, D.D.; Jarvis, P.G. The carbon balance of tropical, temperate and boreal forests. Plant Cell Environ. 1999, 22, 715–740. [Google Scholar] [CrossRef]
- Nilsson, M.C.; Wardle, D.A. Understory vegetation as a forest ecosystem driver: Evidence from the northern Swedish boreal forest. Front. Ecol. Environ. 2005, 3, 421–428. [Google Scholar] [CrossRef]
- Thiffault, N.; Fenton, N.J.; Munson, A.D.; Hébert, F.; Fournier, R.A.; Valeria, O.; Bradley, R.L.; Bergeron, Y.; Grondin, P.; Paré, D. Managing Understory Vegetation for Maintaining Productivity in Black Spruce Forests: A Synthesis within a Multi-Scale Research Model. Forests 2013, 4, 613–631. [Google Scholar] [CrossRef]
- Kolari, P.; Pumpanen, J.; Kulmala, L.; Ilvesniemi, H.; Nikinmaa, E.; Gronholm, T.; Hari, P. Forest floor vegetation plays an important role in photosynthetic production of boreal forests. For. Ecol. Manag. 2006, 221, 241–248. [Google Scholar] [CrossRef]
- Kim, D.; Oren, R.; Qian, S.S. Response to CO2 enrichment of understory vegetation in the shade of forests. Glob. Chang. Boil. 2016, 22, 944. [Google Scholar] [CrossRef] [PubMed]
- Misson, L.; Baldocchi, D.D.; Black, T.A.; Blanken, P.D.; Brunet, Y.; Curiel, Y.J.; Dorsey, J.R.; Falk, M.; Granier, A.; Irvine, M.R. Partitioning forest carbon fluxes with overstory and understory eddy-covariance measurements: A synthesis based on FLUXNET data. Agric. For. Meteorol. 2007, 144, 14–31. [Google Scholar] [CrossRef]
- Moore, C.E.; Beringer, J.; Evans, B.; Hutley, L.B.; Mchugh, I.; Tapper, N.J. The contribution of trees and grasses to productivity of an Australian tropical savanna. Biogeosci. Discuss. 2016, 12, 19307–19350. [Google Scholar] [CrossRef]
- Sakai, T.; Akiyama, T.; Saigusa, N.; Yamamoto, S.; Yasuoka, Y. The contribution of gross primary production of understory dwarf bamboo, Sasa senanensis, in a cool-temperate deciduous broadleaved forest in central Japan. For. Ecol. Manag. 2007, 236, 259–267. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Gonsamo, A.; Luo, X.; Wang, R.; Liu, Y.; Liu, R. Changes in the Shadow: The Shifting Role of Shaded Leaves in Global Carbon and Water Cycles under Climate Change. Geophys. Res. Lett. 2018, 45, 5052–5061. [Google Scholar] [CrossRef]
- Black, T.A.; Hartog, G.D.; Neumann, H.H.; Blanken, P.D.; Yang, P.C.; Russell, C.; Nesic, Z.; Lee, X.; Chen, S.G.; Staebler, R. Annual cycles of water vapour and carbon dioxide fluxes in and above a boreal aspen forest. Glob. Chang. Boil. 1996, 2, 219–229. [Google Scholar] [CrossRef]
- Landhäusser, S.M.; Lieffers, V.J. Photosynthesis and carbon allocation of six boreal tree species grown in understory and open conditions. Tree Physiol. 2001, 21, 243–250. [Google Scholar] [CrossRef] [PubMed]
- Pons, T.L.; Westbeek, M.H.M. Analysis of differences in photosynthetic nitrogen-use efficiency between four contrasting species. Physiol. Plant. 2004, 122, 68–78. [Google Scholar] [CrossRef]
- Mielke, M.S.; Almeida, A.A.F.D.; Gomes, F.P. Photosynthetic traits of five neotropical rainforest tree species: Interactions between light response curves and leaf-to-air vapour pressure deficit. Braz. Arch. Boil. Technol. 2005, 48, 815–824. [Google Scholar] [CrossRef]
- Xue, B.L.; Kumagai, T.O.; Iida, S.I.; Nakai, T.; Matsumoto, K.; Komatsu, H.; Otsuki, K.; Ohta, T. Influences of canopy structure and physiological traits on flux partitioning between understory and overstory in an eastern Siberian boreal larch forest. Ecol. Model. 2011, 222, 1479–1490. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, X.; Ju, W.; Chen, J.M.; Wang, S.; Wang, H.; Yuan, W.; Andrew Black, T.; Jassal, R.; Ibrom, A. Global parameterization and validation of a two-leaf light use efficiency model for predicting gross primary production across FLUXNET sites. J. Geophys. Res. 2016, 121, 1045–1072. [Google Scholar] [CrossRef]
- Gebremichael, M.; Barros, A.P. Evaluation of MODIS Gross Primary Productivity (GPP) in tropical monsoon regions. Remote Sens. Environ. 2006, 100, 150–166. [Google Scholar] [CrossRef]
- He, M.; Zhou, Y.; Ju, W.; Chen, J.; Li, Z.; Wang, S.; Saigusa, N.; Hirata, R.; Murayama, S.; Liu, Y. Evaluation and improvement of MODIS gross primary productivity in typical forest ecosystems of East Asia based on eddy covariance measurements. J. For. Res. 2013, 18, 31–40. [Google Scholar] [CrossRef]
- Propastin, P.; Ibrom, A.; Knohl, A.; Erasmi, S. Effects of canopy photosynthesis saturation on the estimation of gross primary productivity from MODIS data in a tropical forest. Remote Sens. Environ. 2012, 121, 252–260. [Google Scholar] [CrossRef]
- Wolf, A.; Akshalov, K.; Saliendra, N.; Johnson, D.A.; Laca, E.A. Inverse estimation of Vcmax, leaf area index, and the Ball-Berry parameter from carbon and energy fluxes. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Bonan, G.B.; Oleson, K.W.; Fisher, R.A.; Lasslop, G.; Reichstein, M. Reconciling leaf physiological traits and canopy flux data: Use of the TRY and FLUXNET databases in the Community Land Model version 4. J. Geophys. Res. Biogeosci. 2015, 117, 313–325. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global clumping index map derived from the MODIS BRDF product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Govind, A.; Guyon, D.; Roujean, J.L.; Yauschew-Raguenes, N.; Kumari, J.; Pisek, J.; Wigneron, J.P. Effects of canopy architectural parameterizations on the modeling of radiative transfer mechanism. Ecol. Model. 2013, 251, 114–126. [Google Scholar] [CrossRef]
- Brooks, J.R.; Flanagan, L.B.; Varney, G.T.; Ehleringer, J.R. Vertical gradients in photosynthetic gas exchange characteristics and refixation of respired CO2 within boreal forest canopies. Tree Physiol. 1997, 17, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Beaumont, S.; Burns, K.C. Vertical gradients in leaf trait diversity in a New Zealand forest. Trees 2009, 23, 339–346. [Google Scholar] [CrossRef]
- Coble, A.P.; Vanderwall, B.; Mau, A.; Cavaleri, M.A. How vertical patterns in leaf traits shift seasonally and the implications for modeling canopy photosynthesis in a temperate deciduous forest. Tree Physiol. 2016, 36, 1077. [Google Scholar] [CrossRef] [PubMed]
- Slot, M.; Winter, K. Photosynthetic acclimation to warming in tropical forest tree seedlings. J. Exp. Bot. 2017, 68, 2275–2284. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.H.; Zeng, J.; Zhang, Y.J.; Slot, M.; Gamo, M.; Hirano, T.; Kosugi, Y.; Rocha, H.R.D.; Saleska, S.R.; Goulden, M.L. Optimum air temperature for tropical forest photosynthesis: Mechanisms involved and implications for climate warming. Environ. Res. Lett. 2017, 12, 054022. [Google Scholar] [CrossRef]
- Man, R.; Yang, H.; Schnare, J.W. Data on overstory and understory trees in aspen-dominated boreal mixedwood stands over 20 years after partial harvesting. Data Brief 2018, 17, 284–287. [Google Scholar] [CrossRef] [PubMed]
- Ames, G.M.; Anderson, S.M.; Ungberg, E.A.; Wright, J.P. Functional traits of the understory plant community of a pyrogenic longleaf pine forest across environmental gradients. Ecology 2017, 98, 2225. [Google Scholar] [CrossRef] [PubMed]
- Jagodziński, A.M.; Horodecki, P.; Rawlik, K.; Dyderski, M.K. Do understory or overstory traits drive tree encroachment on a drained raised bog? Plant Boil. 2017, 19, 571–583. [Google Scholar] [CrossRef] [PubMed]
- Sterck, F.; Schieving, F. Modelling functional trait acclimation for trees of different height in a forest light gradient: Emergent patterns driven by carbon gain maximization. Tree Physiol. 2011, 31, 1024–1037. [Google Scholar] [CrossRef] [PubMed]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Chang. Boil. 2015, 21, 1762. [Google Scholar] [CrossRef] [PubMed]
- Alsaidi, A.; Fukuzawa, Y.; Furukawa, N.; Ueno, M.; Baba, S.; Kawamitsu, Y. A system for the measurement of vertical gradients of CO2, H2O and air temperature within and above the canopy of plant. Plant Prod. Sci. 2009, 12, 139–149. [Google Scholar] [CrossRef]
- Lantinga, E.A.; Nassiri, M.; Kropff, M.J. Modelling and measuring vertical light absorption within grass-clover mixtures. Agric. For. Meteorol. 1999, 96, 71–83. [Google Scholar] [CrossRef]
- Ohkubo, S.; Kosugi, Y.; Takanashi, S.; Matsuo, N.; Tani, M.; Nik, A.R. Vertical profiles and storage fluxes of CO2, heat and water in a tropical rainforest at Pasoh, Peninsular Malaysia. Tellus 2008, 60, 569–582. [Google Scholar] [CrossRef]
- Kenlonishida, N.; Hiroyuki, M.; Shin, N.; Hiroaki, M. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agric. For. Meteorol. 2008, 148, 1136–1146. [Google Scholar]
- Kobayashi, H.; Baldocchi, D.D.; Ryu, Y.; Chen, Q.; Ma, S.; Osuna, J.L.; Ustin, S.L. Modeling energy and carbon fluxes in a heterogeneous oak woodland: A three-dimensional approach. Agric. For. Meteorol. 2012, 152, 83–100. [Google Scholar] [CrossRef]
- Poorter, L.; Oberbauer, S.F.; Clark, D.B. Leaf Optical Properties Along a Vertical Gradient in a Tropical Rain Forest Canopy in Costa Rica. Am. J. Bot. 1995, 82, 1257–1263. [Google Scholar] [CrossRef]
- Gallego, H.A.; Rico, M.; Moreno, G.; Santa, R.I. Leaf water potential and stomatal conductance in Quercus pyrenaica Willd. forests: Vertical gradients and response to environmental factors. Tree Physiol. 1994, 14, 1039–1047. [Google Scholar] [CrossRef] [PubMed]
- Flerchinger, G.N.; Reba, M.L.; Link, T.E.; Marks, D. Modeling temperature and humidity profiles within forest canopies. Agric. For. Meteorol. 2015, 213, 251–262. [Google Scholar] [CrossRef]
- Kuusk, A. Absorption profiles of shortwave radiation in a vegetation canopy. Agric. For. Meteorol. 1992, 62, 191–204. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Pinty, B.; Lopatka, M.; Atzberger, C.; Buzica, D.; Chelle, M.; Disney, M.; Gastellu-Etchegorry, J.P.; Gerboles, M.; Gobron, N. The fourth radiation transfer model intercomparison (RAMI-IV): Proficiency testing of canopy reflectance models with ISO-13528. J. Geophys. Res. Atmos. 2013, 118, 6869–6890. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Swatantran, A.; Hofton, M.; Sheldon, S.; Clark, D.B.; Blair, B. Retrieval of vertical LAI profiles over tropical rain forests using waveform lidar at La Selva, Costa Rica. Remote Sens. Environ. 2012, 124, 242–250. [Google Scholar] [CrossRef]
- Coops, N.C.; Hermosilla, T.; Hilker, T.; Black, T.A. Linking stand architecture with canopy reflectance to estimate vertical patterns of light-use efficiency. Remote Sens. Environ. 2017, 194, 322–330. [Google Scholar] [CrossRef]
- Wu, J.; Guan, K.; Hayek, M.; Restrepocoupe, N.; Wiedemann, K.T.; Xu, X.; Wehr, R.; Christoffersen, B.O.; Miao, G.; Da, S.R. Partitioning controls on Amazon forest photosynthesis between environmental and biotic factors at hourly to inter-annual time scales. Glob. Chang. Boil. 2017, 23, 1240. [Google Scholar] [CrossRef] [PubMed]
- Kosugi, Y.; Takanashi, S.; Tani, M.; Ohkubo, S.; Matsuo, N.; Itoh, M.; Noguchi, S.; Nik, A.R. Effect of inter-annual climate variability on evapotranspiration and canopy CO2 exchange of a tropical rainforest in Peninsular Malaysia. J. For. Res. 2012, 17, 227–240. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Iii, B.M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, G.; Tang, X.; Wang, X.; Zhou, C.; Yu, G.; Tang, L.; Meng, Z. Ecosystem respiration and its controlling factors in a coniferous and broad-leaved mixed forest in Dinghushan, China. Acta Ecol. Sin. 2007, 27, 2659–2668. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, G.; Wang, X.; Tang, X.; Zhou, C.; Yu, G. Below-canopy CO2 flux and its environmental response characteristics in a coniferous and broad-leaved mixed forest in Dinghushan, China. Acta Ecol. Sin. 2007, 27, 846–853. [Google Scholar] [CrossRef]
- Zhang, L.M.; Yu, G.R.; Sun, X.M.; Wen, X.F.; Ren, C.Y.; Fu, Y.L.; Li, Q.K.; Li, Z.Q.; Liu, Y.F.; Guanc, D.X. Seasonal variations of ecosystem apparent quantum yield (alpha) and maximum photosynthesis rate (P-max) of different forest ecosystems in China. Agric. For. Meteorol. 2006, 137, 176–187. [Google Scholar] [CrossRef]
- Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.; Chen, J.Y. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Hirata, R.; Hirano, T.; Saigusa, N.; Fujinuma, Y.; Inukai, K.; Kitamori, Y.; Takahashi, Y. Seasonal and interannual variations in carbon dioxide exchange of a temperate larch forest. Agric. For. Meteorol. 2007, 147, 110–124. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the köppen-geiger climate classification. Hydrol. Earth Sys. Sci. 2007, 11, 259–263. [Google Scholar] [CrossRef]
- Ueyama, M.; Hirata, R.; Mano, M.; Hamotani, K. Influences of various calculation options on heat, water and carbon fluxes determined by open- and closed-path eddy covariance methods. Tellus Ser. B-Chem. Phys. Meteorol. 2011, 64, 91–102. [Google Scholar] [CrossRef]
- Jakubauskas, M.E. Harmonic analysis of time-series avhrr ndvi data. Photogr. Eng. Remote Sens. 2001, 67, 461–470. [Google Scholar]
- Madani, N.; Kimball, J.S.; Affleck, D.L.R.; Kattge, J.; Graham, J.; Bodegom, P.M.; Reich, P.B.; Running, S.W. Improving ecosystem productivity modeling through spatially explicit estimation of optimal light use efficiency. J. Geophys. Res. Biogeosci. 2015, 119, 1755–1769. [Google Scholar] [CrossRef]
- Maselli, F.; Barbati, A.; Chiesi, M.; Chirici, G.; Corona, P. Use of remotely sensed and ancillary data for estimating forest gross primary productivity in Italy. Remote Sens. Environ. 2006, 100, 563–575. [Google Scholar] [CrossRef]
- Maselli, F.; Papale, D.; Puletti, N.; Chirici, G.; Corona, P. Combining remote sensing and ancillary data to monitor the gross productivity of water-limited forest ecosystems. Remote. Sens. Environ. 2009, 113, 657–667. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. Radiation Fluxes in Natural Environments; Springer: New York, NY, USA, 1998; pp. 167–184. [Google Scholar]
- Gastellu-Etchegorry, J.P.; Trichon, V. A modeling approach of PAR environment in a tropical rain forest in Sumatra: Application to remote sensing. Ecol. Model. 1998, 108, 237–264. [Google Scholar] [CrossRef]
- Gastelluetchegorry, J.P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.B.; Lopes, M.; Guilleux, J.; Dedieu, G. Discrete Anisotropic Radiative Transfer (DART 5) for Modeling Airborne and Satellite Spectroradiometer and LIDAR Acquisitions of Natural and Urban Landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Montgomery, R.A.; Chazdon, R.L. Forest structure, canopy architecture, and light transmittance in tropical wet forests. Ecology 2001, 82, 2707–2718. [Google Scholar] [CrossRef]
- Pettigrew, C.A.; Breen, A.; Corcoran, C.; Sayler, G.S. Chlorinated biphenyl mineralization by individual populations and consortia of freshwater bacteria. Appl. Environ. Microbiol. 1990, 56, 2036–2045. [Google Scholar] [PubMed]
- Nepstad, D.C.; Carvalho, C.R.D.; Davidson, E.A.; Jipp, P.H.; Lefebvre, P.A.; Negreiros, G.H.; Silva, E.D.D.; Stone, T.A.; Trumbore, S.E.; Vieira, S. The role of deep roots in the hydrological and carbon cycles of Amazonian forests and pastures. Nature 1994, 372, 666–669. [Google Scholar] [CrossRef]
- Onoda, Y.; Saluñga, J.B.; Akutsu, K.; Aiba, S.I.; Yahara, T.; Anten, N.P.R. Trade-off between light interception efficiency and light use efficiency: Implications for species coexistence in one-sided light competition. J. Ecol. 2014, 102, 167–175. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, R.; Pisek, J.; Chen, J.M. Separating overstory and understory leaf area indices for global needleleaf and deciduous broadleaf forests by fusion of MODIS and MISR data. Biogeosciences 2017, 14, 1–32. [Google Scholar] [CrossRef]
- Pisek, J.; Chen, J.; Kobayashi, H.; Rautiainen, M.; Schaepman, M.; Karnieli, A.; Sprintsin, M.; Ryu, Y.; Nikopensius, M.; Raabe, K. Retrieval of seasonal dynamics of forest understory reflectance from semi-arid to boreal forests using MODIS BRDF data. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Pisek, J.; Rautiainen, M.; Heiskanen, J.; Mõttus, M. Retrieval of seasonal dynamics of forest understory reflectance in a Northern European boreal forest from MODIS BRDF data. Remote Sens. Environ. 2012, 117, 464–468. [Google Scholar] [CrossRef]
- Pisek, J.; Rautiainen, M.; Nikopensius, M.; Raabe, K. Estimation of seasonal dynamics of understory NDVI in northern forests using MODIS BRDF data: Semi-empirical versus physically-based approach. Remote Sens. Environ. 2015, 163, 42–47. [Google Scholar] [CrossRef]
- Hutyra, L.R.; Munger, J.W.; Saleska, S.R.; Gottlieb, E.; Daube, B.C.; Dunn, A.L.; Amaral, D.F.; De Camargo, P.B.; Wofsy, S.C. Seasonal controls on the exchange of carbon and water in an Amazonian rain forest. J. Geophys. Res. Biogeosci. 2015, 112, 488–497. [Google Scholar] [CrossRef]
- Falk, M.; Kyaw, T.P.U.; Wharton, S.; Schroeder, M. Is soil respiration a major contributor to the carbon budget within a Pacific Northwest old-growth forest? Agric. For. Meteorol. 2005, 135, 269–283. [Google Scholar] [CrossRef]
- Lamaud, E.; Ogee, J.; Brunet, Y.; Berbigier, P. Validation of eddy flux measurements above the understorey of a pine forest. Agric. For. Meteorol. 2001, 106, 187–203. [Google Scholar] [CrossRef]
- Biudes, M.S.; Machado, N.G.; Danelichen, V.H.D.M.; Souza, M.C.; Vourlitis, G.L.; Nogueira, J.D.S. Ground and remote sensing-based measurements of leaf area index in a transitional forest and seasonal flooded forest in Brazil. Int. J. Biometeorol. 2014, 58, 1181–1193. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Ganguly, S.; Zhang, G.; Hofton, M.A.; Nelson, R.F.; Dubayah, R. Characterizing Leaf Area Index (LAI) and Vertical Foliage Profile (VFP) over the United States. Biogeosci. Discuss. 2016, 12, 13675–13710. [Google Scholar] [CrossRef]
- Oppelt, N.M. Vertical profiling of chlorophyll within wheat canopies using multi-angular remote sensing data. Can. J. Remote Sens. 2008, 34, S314–S325. [Google Scholar] [CrossRef]
- Verónica, C.; Anatoly, G.; James, S. Vertical Profile and Temporal Variation of Chlorophyll in Maize Canopy: Quantitative “Crop Vigor” Indicator by Means of Reflectance-Based Techniques. Agron. J. 2008, 100, 1409–1417. [Google Scholar]

| DHS | TMK | |
|---|---|---|
| Location | 23.1733 N, 112.5361 E | 42.7333 N, 141.5167 E |
| Elevation (m, above sea level) | 240 | 115–140 |
| Canopy height (m) | 15 | 18–20 |
| Period of data collection | July to December 2005 | July to December 2003 |
| LAI overstory (m2/m2) 1 | August 2.5 | July 5.6 |
| November 4.6 | September 5.0 | |
| November 0.4 | ||
| LAI understory (m2/m2) | August 1.25 | July 3.6 |
| November 1.25 | September 3.0 | |
| November 0.2 | ||
| KGCC (Köppen-Geiger climate classification [73]) | Warm temperate, fully humid with hot summer | Snowy, fully humid warm summer |
| IGBP (International Geosphere-Biosphere Programme, a land cover classification system) | EBF (evergreen broadleaf forest) | DNF 2 (Deciduous needle leaf; cropland after destruction) |
| Height of EC measurement (m) | 27 | 27 |
| Heights of temperature and humidity measurements (m) | 4, 9, 15, 21, 27, 31, 36 | 2, 5, 8, 14, 18, 22, 27, 40 |
| Heights of PPFD measurements (m) | 2, 9, 21, 36 | 2, 5, 14, 18, 40 |
| Dominant species | Cleistocalyx operculatus, Syzygium jambos, Castanopsis chinensis, etc. Many understory herb species | Overstory: Japanese larch (Larix kaempferi Sarg.) Birch (Betula ermanii and Betula platyphylla) Japanese elm (Ulmus japonica) Spruce (Picea jezoensis) Understory: Fern (Dryopteris crassirhizoma, Dryopteris austriaca) and Pachysandra terminalis |
| Tree (DHS) | Overstory (TMK) | Shrub | Grass | |
|---|---|---|---|---|
| Zhou [32] | 1.120 | 1.180 | 0.930 | 1.520 |
| MODIS [67] | 1.268 | 1.051 | 0.841 | 0.860 |
| Yuan [31] | 1.680 | 1.640 | 0.660 | 1.520 |
| Madani [76] | 0.980 | 1.171 | 0.631 | 1.294 |
| TMK | DHS | |
|---|---|---|
| Input parameters | ||
| Overstory LAI | 5.4 | 2.6 |
| X (leaf angle distribution in spherical distribution) | 1 | 1 |
| Daytime zenith angle (mean) | 31 | 45 |
| Output results | ||
| Direct PAR % | 4.2 | 15.9 |
| Diffuse PAR % | 1.6 | 9.3 |
| Understory simulation % | 5.6 | 25.2 |
| Understory in situ % | 8.2 | 27.5 |
| DHS_s | DHS_m | DHS_adjust | TMK_s | TMK_m | TMK_adjust | ||
|---|---|---|---|---|---|---|---|
| VPM | R2 | 0.587 | 0.588 | 0.589 | 0.738 | 0.769 | 0.753 |
| RMSE | 0.99 | 0.99 | 0.99 | 2.51 | 2.36 | 2.43 | |
| mean bias | −1.15 | −1.08 | −0.55 | 4.16 | 1.85 | 0.59 | |
| Wu | R2 | 0.595 | 0.599 | 0.595 | 0.726 | 0.771 | 0.754 |
| RMSE | 0.98 | 0.97 | 0.96 | 2.57 | 2.35 | 2.44 | |
| mean bias | 0.53 | 0.49 | 0.09 | 3.84 | 1.5 | 0.21 | |
| MOD | R2 | 0.491 | 0.489 | 0.491 | 0.777 | 0.801 | 0.786 |
| RMSE | 1.1 | 1.1 | 1.1 | 2.32 | 2.19 | 2.27 | |
| mean bias | −1.67 | −1.57 | −1.05 | 3.96 | 1.68 | 0.47 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Li, J.; Liu, Q.; Huete, A.; Li, L. Effects of Forest Canopy Vertical Stratification on the Estimation of Gross Primary Production by Remote Sensing. Remote Sens. 2018, 10, 1329. https://doi.org/10.3390/rs10091329
Lin S, Li J, Liu Q, Huete A, Li L. Effects of Forest Canopy Vertical Stratification on the Estimation of Gross Primary Production by Remote Sensing. Remote Sensing. 2018; 10(9):1329. https://doi.org/10.3390/rs10091329
Chicago/Turabian StyleLin, Shangrong, Jing Li, Qinhuo Liu, Alfredo Huete, and Longhui Li. 2018. "Effects of Forest Canopy Vertical Stratification on the Estimation of Gross Primary Production by Remote Sensing" Remote Sensing 10, no. 9: 1329. https://doi.org/10.3390/rs10091329
APA StyleLin, S., Li, J., Liu, Q., Huete, A., & Li, L. (2018). Effects of Forest Canopy Vertical Stratification on the Estimation of Gross Primary Production by Remote Sensing. Remote Sensing, 10(9), 1329. https://doi.org/10.3390/rs10091329