Radiative Transfer Modeling of Phytoplankton Fluorescence Quenching Processes
Abstract
:1. Introduction
2. Methods
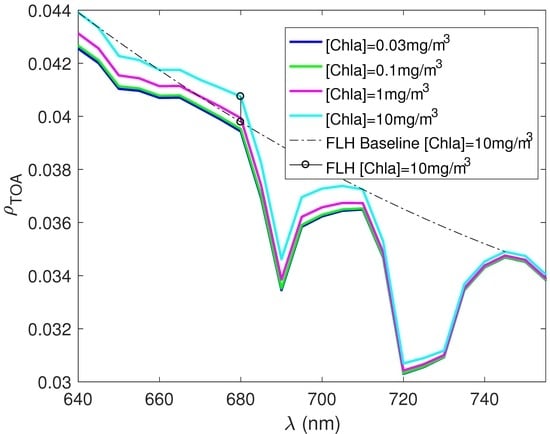
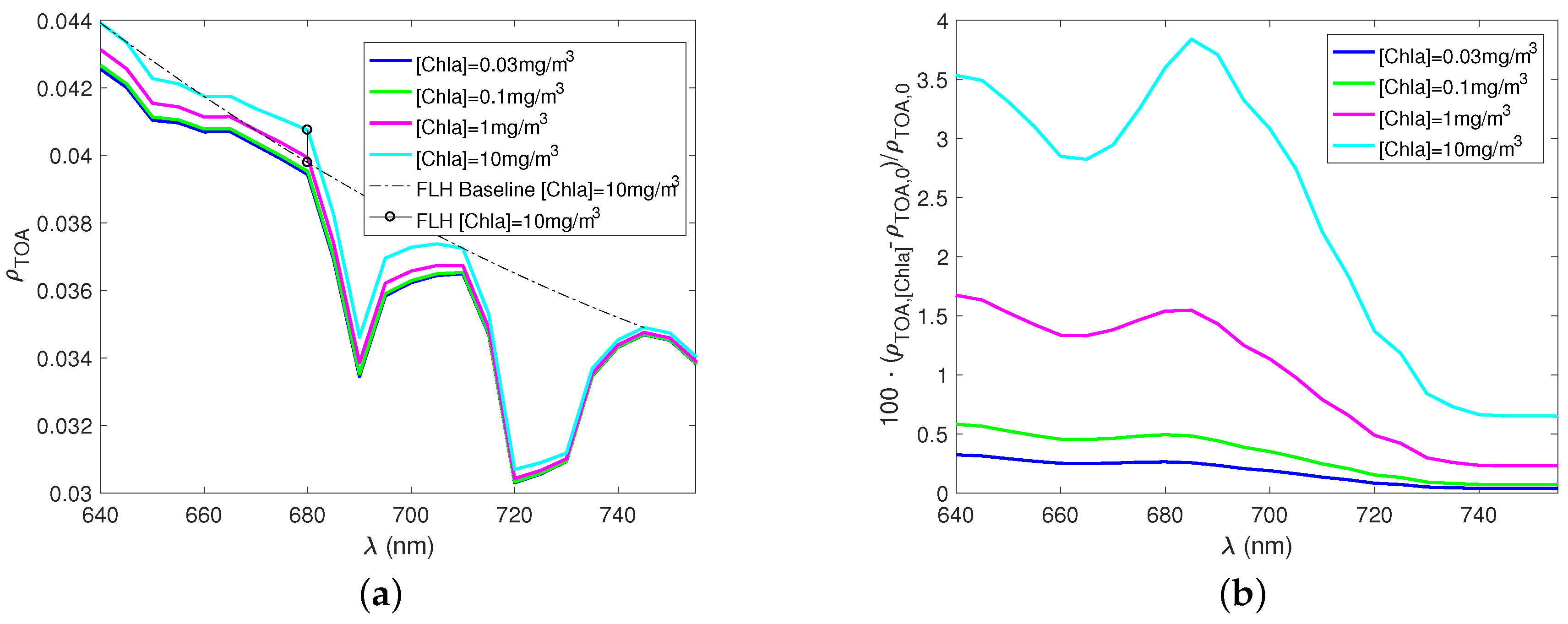
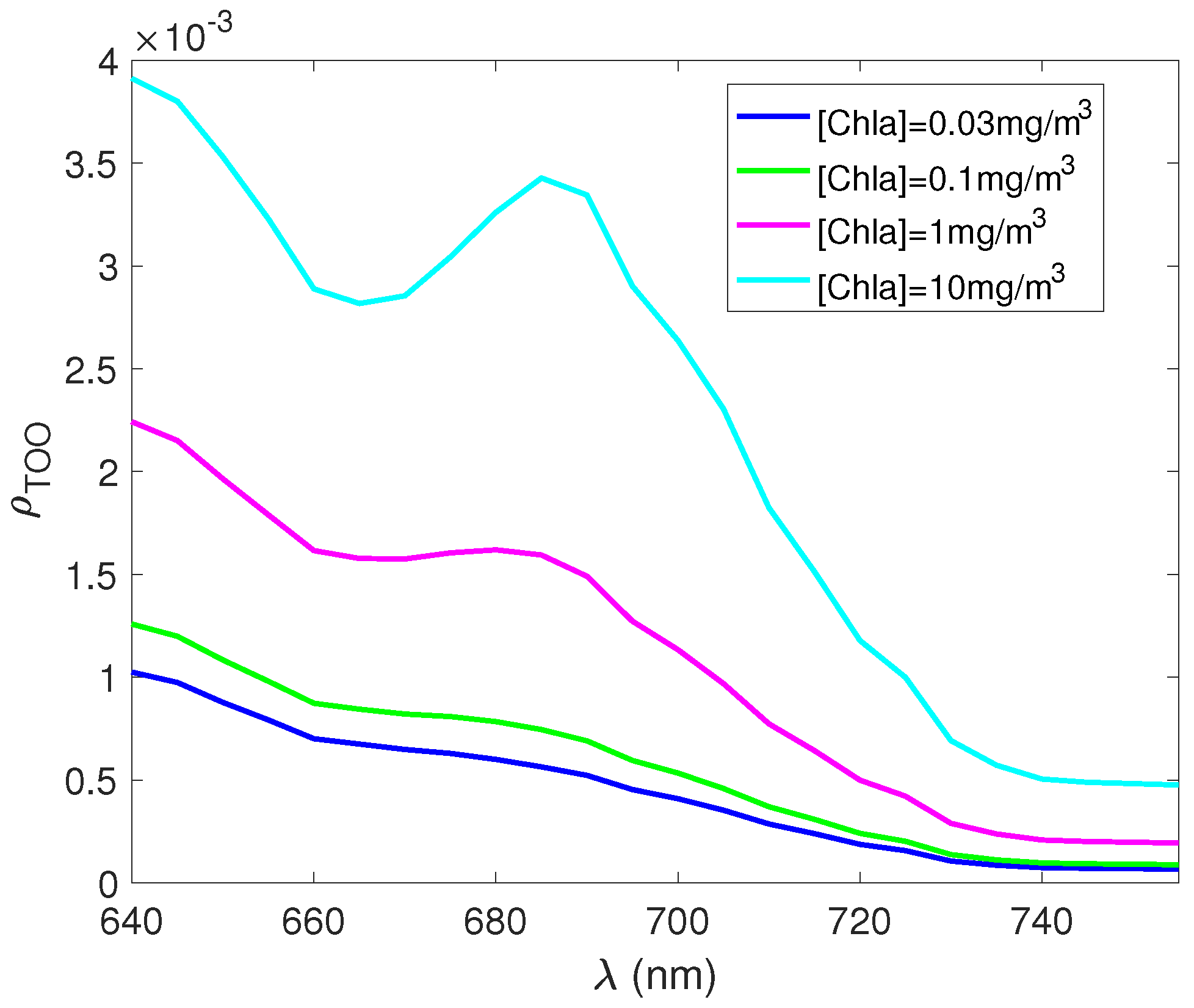
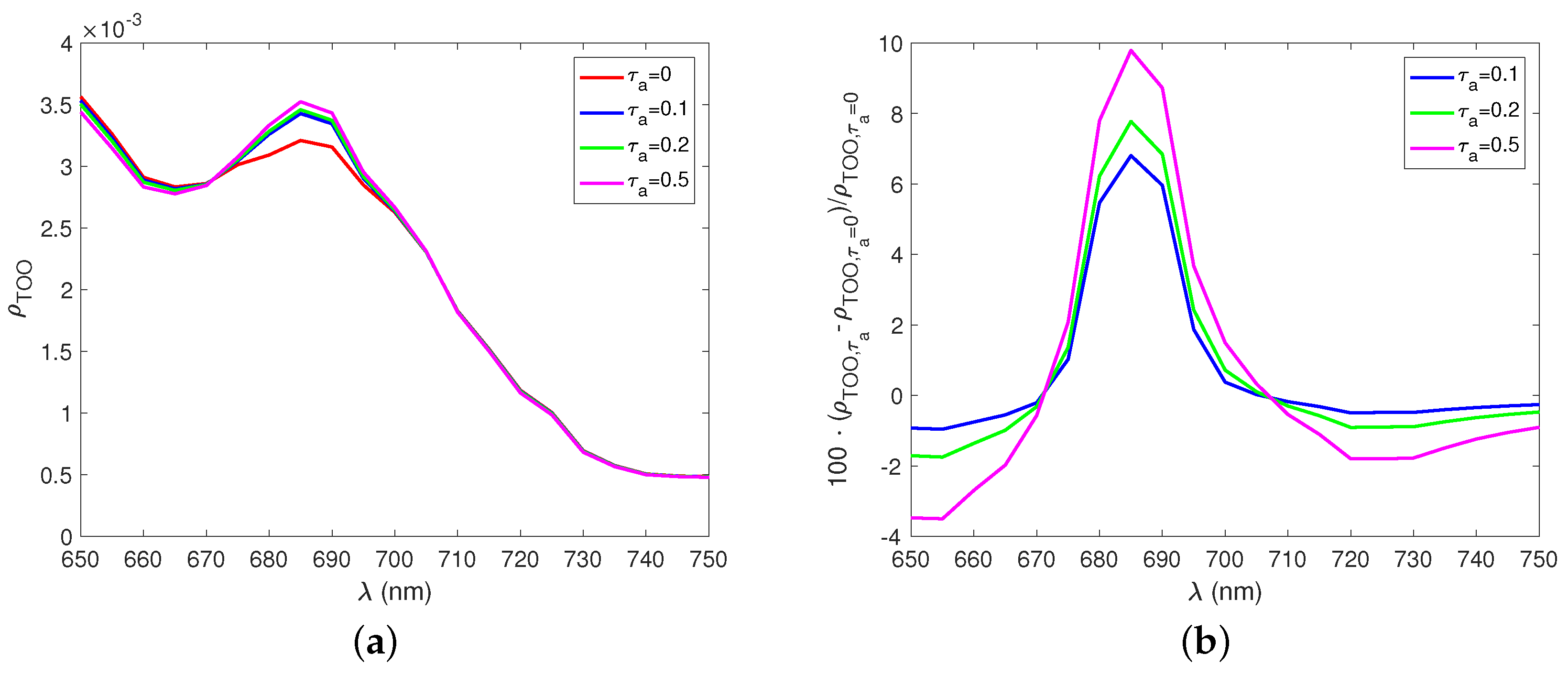
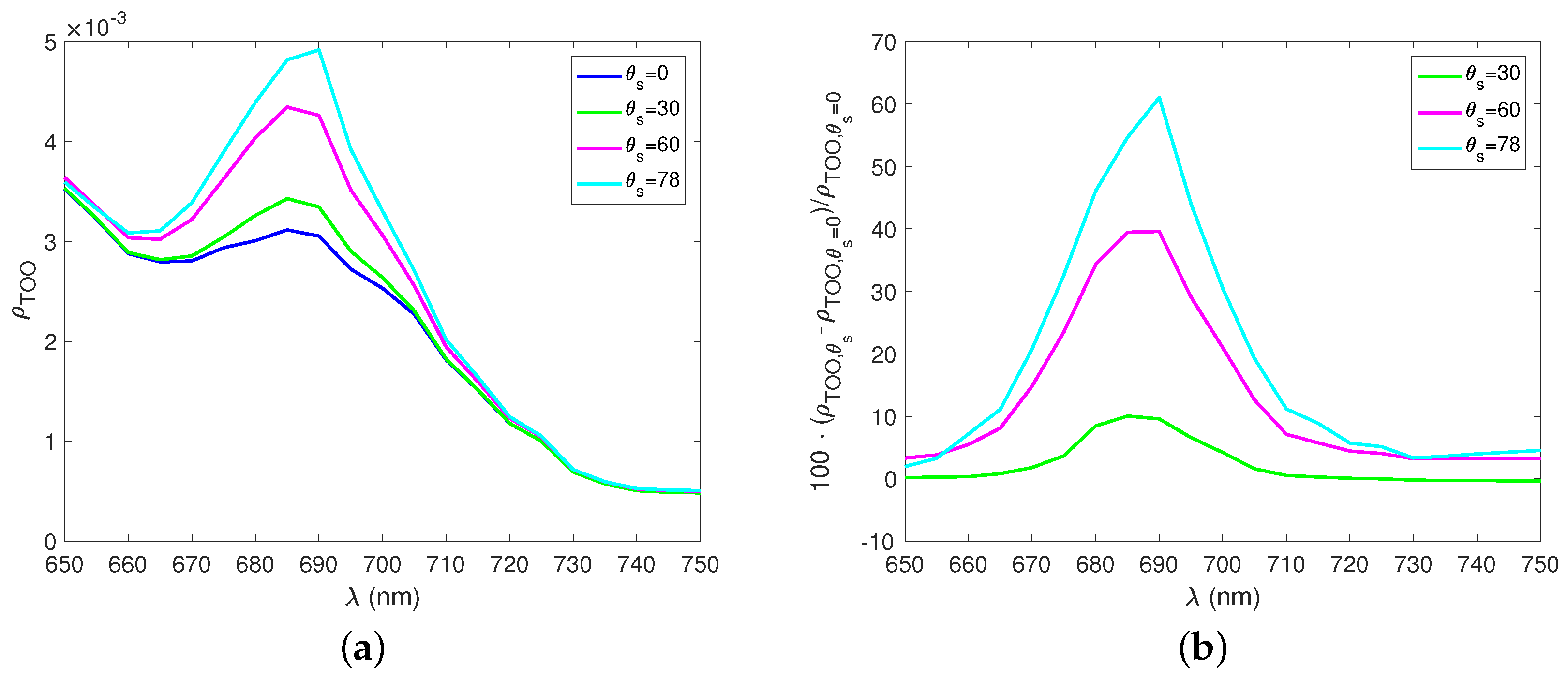
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Morrison, R.J. In situ determination of the quantum yield of phytoplankton chlorophyll a fluorescence: A simple algorithm, observations, and a model. Limnol. Oceanogr. 2003, 48, 618–631. [Google Scholar] [CrossRef] [Green Version]
- Gower, J.F.R. Observations of in situ fluorescence of chlorophyll-a in Saanich Inlet. Bound.-Lay. Meteorol. 1980, 18, 235–245. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Westberry, T.K.; Boss, E.S.; O’Malley, R.T.; Siegel, D.A.; Wiggert, J.D.; Franz, B.A.; McClain, C.R.; Feldman, G.C.; Doney, S.C.; et al. Satellite-detected fluorescence reveals global physiology of ocean phytoplankton. Biogeosciences 2009, 6, 779–794. [Google Scholar] [CrossRef] [Green Version]
- Proctor, C.W.; Roesler, C.S. New insights on obtaining phytoplankton concentration and composition from in situ multispectral Chlorophyll fluorescence. Limnol. Oceanogr. Methods 2010, 8, 695–708. [Google Scholar] [CrossRef] [Green Version]
- O’Malley, R.T.; Behrenfeld, M.J.; Westberry, T.K.; Milligan, A.J.; Shang, S.; Yan, J. Geostationary satellite observations of dynamic phytoplankton photophysiology. Geophys. Res. Lett. 2014, 41, 5052–5059. [Google Scholar] [CrossRef] [Green Version]
- Gilerson, A.; Zhou, J.; Hlaing, S.; Ioannou, I.; Gross, B.; Moshary, F.; Ahmed, S. Fluorescence component in the reflectance spectra from coastal waters. II. Performance of retrieval algorithms. Opt. Express 2008, 16, 2446–2460. [Google Scholar] [CrossRef] [PubMed]
- Huot, Y.; Franz, B.A.; Fradette, M. Estimating variability in the quantum yield of Sun-induced chlorophyll fluorescence: A global analysis of oceanic waters. Remote Sens. Environ. 2013, 132, 238–253. [Google Scholar] [CrossRef]
- Morrison, R.J.; Goodwin, D.S. Phytoplankton photocompensation from space based fluorescence measurements. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- El-Habashi, A.; Foster, R.; Carrizo, C.; Legbandt, T.; Ahmed, S. Impact of fluorescence on the underwater polarized light field: Comparison of theory and field measurements. Proc. SPIE 2017, 10402. [Google Scholar] [CrossRef]
- Pozdnyakov, D.; Grassl, H. Color of Inland and Coastal Waters: A Methodology for Its Interpretation; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Vigneshwaran, J.; Shanmugam, P.; Gokul, E. Simulating the effects of inelastic scattering on upwelling radiance in coastal and inland waters: Implications for hyperspectral remote sensing. Curr. Sci. 2015, 108, 903–914. [Google Scholar]
- Kattawar, G.W.; Xu, X. Filling in of Fraunhofer lines in the ocean by Raman scattering. Appl. Opt. 1992, 31, 6491–6500. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Gordon, H.R.; Voss, K.J. Simulation of inelastic-scattering contributions to the irradiance field in the ocean: variation in Fraunhofer line depths. Appl. Opt. 1993, 32, 4028–4036. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Schroeder, M.; Barth, H.; Reuter, R. Effect of inelastic scattering on underwater daylight in the ocean: Model evaluation, validation, and first results. Appl. Opt. 2003, 42, 4244–4260. [Google Scholar] [CrossRef] [PubMed]
- Zhai, P.W.; Hu, Y.; Winker, D.M.; Franz, B.A.; Boss, E. Contribution of Raman scattering to polarized radiation field in ocean waters. Opt. Express 2015, 23, 23582–23596. [Google Scholar] [CrossRef] [PubMed]
- Zhai, P.W.; Hu, Y.; Winker, D.M.; Franz, B.A.; Werdell, J.; Boss, E. Vector radiative transfer model for coupled atmosphere and ocean systems including inelastic sources in ocean waters. Opt. Express 2017, 25, A223–A239. [Google Scholar] [CrossRef] [PubMed]
- Wolanin, A.; Rozanov, V.; Dinter, T.; Bracher, A. Detecting CDOM Fluorescence Using High Spectrally Resolved Satellite Data: A Model Study. In Towards an Interdisciplinary Approach in Earth System Science: Advances of a Helmholtz Graduate Research School; Springer International Publishing: Cham, Switzerland, 2015; pp. 109–121. [Google Scholar] [CrossRef] [Green Version]
- Rozanov, V.; Dinter, T.; Rozanov, A.; Wolanin, A.; Bracher, A.; Burrows, J. Radiative transfer modeling through terrestrial atmosphere and ocean accounting for inelastic processes: Software package SCIATRAN. J. Quant. Spectrosc. Radiat. Transf. 2017, 194, 65–85. [Google Scholar] [CrossRef] [Green Version]
- Zhai, P.W.; Hu, Y.; Trepte, C.R.; Lucker, P.L. A vector radiative transfer model for coupled atmosphere and ocean systems based on successive order of scattering method. Opt. Express 2009, 17, 2057–2079. [Google Scholar] [CrossRef] [PubMed]
- Zhai, P.W.; Hu, Y.; Chowdhary, J.; Trepte, C.R.; Lucker, P.L.; Josset, D.B. A vector radiative transfer model for coupled atmosphere and ocean systems with a rough interface. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1025–1040. [Google Scholar] [CrossRef]
- Zhai, P.W.; Knobelspiesse, K.; Ibrahim, A.; Franz, B.A.; Hu, Y.; Gao, M.; Frouin, R. Water-leaving contribution to polarized radiation field over ocean. Opt. Express 2017, 25, A689–A708. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D.; Boss, E.S. Improved irradiances for use in ocean heating, primary production, and photo-oxidation calculations. Appl. Opt. 2012, 51, 6549–6560. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Diffuse reflectance of the ocean: the theory of its augmentation by chlorophyll a fluorescence at 685 nm. Appl. Opt. 1979, 18, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Werdell, J. The NASA Plankton, Aerosol, Cloud, Ocean Ecosystem (PACE) Mission. 2016. Available online: https://pace.gsfc.nasa.gov (accessed on 26 June 2018).
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Wei, J.; Voss, K.; Lewis, M.; Bricaud, A.; Huot, Y. Hyperspectral absorption coefficient of “pure” seawater in the range of 350–550 nm inverted from remote sensing reflectance. Appl. Opt. 2015, 54, 546–558. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, L. Scattering by pure seawater at high salinity. Opt. Express 2009, 17, 12685–12691. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Gentili, B. A simple band ratio technique to quantify the colored dissolved and detrital organic material from ocean color remotely sensed data. Remote Sens. Environ. 2009, 113, 998–1011. [Google Scholar] [CrossRef]
- IOCCG Ocean Color Algorithm Working Group. Models, Parameters, and Approaches that Used to Generate Wide Range of Absorption and Backscattering Spectra. 2003. Available online: http://www.ioccg.org/groups/lee_data.pdf (accessed on 26 June 2018).
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for biooptical models. J. Geophys. Res. Oceans 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Voss, K.J. A spectral model of the beam attenuation coefficient in the ocean and coastal areas. Limnol. Oceanogr. 1992, 37, 501–509. [Google Scholar] [CrossRef] [Green Version]
- Voss, K.J.; Fry, E.S. Measurement of the Mueller matrix for ocean water. Appl. Opt. 1984, 23, 4427–4439. [Google Scholar] [CrossRef] [PubMed]
- Committee on Extension to the Standard Atmosphere. U.S. Standard Atmosphere; Technical Report; U.S. Government Printing Office: Washington, DC, USA, 1976.
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Shettle, E.P.; Fenn, R.W. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties; Technical Report, No. AFGL-TR-79-0214; U.S. Air Force Geophysics Laboratory: Hanscom AFB, MA, USA, 1979.
- Braslau, N.; Dave, J.V. Effect of Aerosols on the Transfer of Solar Energy Through Realistic Model Atmospheres. Part II: Partly-Absorbing Aerosols. J. Appl. Meteorol. 1973, 12, 601–615. [Google Scholar] [CrossRef]
- Mukherjee, L.; Zhai, P.W.; Hu, Y.; Winker, D.M. Equivalence of internal and external mixture schemes of single scattering properties in vector radiative transfer. Appl. Opt. 2017, 56, 4105–4112. [Google Scholar] [CrossRef] [PubMed]
- Buehler, S.A.; Eriksson, P.; Lemke, O. Absorption lookup tables in the radiative transfer model ARTS. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1559–1567. [Google Scholar] [CrossRef] [Green Version]
- Rothman, L.; Gordon, I.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef] [Green Version]
- Daumont, D.; Brion, J.; Charbonnier, J.; Malicet, J. Ozone UV spectroscopy I: Absorption cross-sections at room temperature. J. Atmos. Chem. 1992, 15, 145–155. [Google Scholar] [CrossRef]
- Bogumil, K.; Orphal, J.; Homann, T.; Voigt, S.; Spietz, P.; Fleischmann, O.; Vogel, A.; Hartmann, M.; Kromminga, H.; Bovensmann, H.; et al. Measurements of molecular absorption spectra with the SCIAMACHY pre-flight model: instrument characterization and reference data for atmospheric remote-sening in the 230–2380 nm region. J. Photochem. Photobiol. A Chem. 2003, 157, 167–184. [Google Scholar] [CrossRef]
- Duan, M.; Min, Q.; Li, J. A fast radiative transfer model for simulating high-resolution absorption bands. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.; Mandel, H. The Solar Spectral Irradiance from 200 to 2400 nm as Measured by the SOLSPEC Spectrometer from the Atlas and Eureca Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Meister, G.; McClain, C.R.; Ahmad, Z.; Bailey, S.W.; Barnes, R.A.; Brown, S.; Eplee, R.E.; Franz, B.; Holmes, A.; Monosmith, W.B.; et al. Requirements for an Advanced Ocean Radiometer. 2011. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20110023620.pdf (accessed on 26 June 2018).
- Letelier, R.M.; Abbott, M.R. An analysis of chlorophyll fluorescence algorithms for the moderate resolution imaging spectrometer (MODIS). Remote Sens. Environ. 1996, 58, 215–223. [Google Scholar] [CrossRef]
- Abbott, M.R.; Letelier, R.M. Algorithm Theoretical Basis Document Chlorophyll Fluorescence, MODIS Product Number 20; Technical Report; NASA: Washington, DC, USA, 1999. Available online: https://eospso.nasa.gov/sites/default/files/atbd/atbd_mod22.pdf (accessed on 26 June 2018).
- Werdell, P.J.; Roesler, C.S.; Goes, J.I. Discrimination of phytoplankton functional groups using an oceanreflectance inversion model. Appl. Opt. 2014, 53, 4833–4849. [Google Scholar] [CrossRef] [PubMed]
- Chowdhary, J.; Cairns, B.; Mishchenko, M.I.; Hobbs, P.V.; Cota, G.F.; Redemann, J.; Rutledge, K.; Holben, B.N.; Russell, E. Retrieval of Aerosol Scattering and Absorption Properties from Photopolarimetric Observations over the Ocean during the CLAMS Experiment. J. Atmos. Sci. 2005, 62, 1093–1117. [Google Scholar] [CrossRef]
- Xu, F.; Dubovik, O.; Zhai, P.W.; Diner, D.J.; Kalashnikova, O.V.; Seidel, F.C.; Litvinov, P.; Bovchaliuk, A.; Garay, M.J.; van Harten, G.; et al. Joint retrieval of aerosol and water-leaving radiance from multispectral, multiangular and polarimetric measurements over ocean. Atmos. Meas. Tech. 2016, 9, 2877–2907. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.; Zhai, P.W.; Franz, B.; Hu, Y.; Knobelspiesse, K.; Werdell, P.J.; Ibrahim, A.; Xu, F.; Cairns, B. Retrieval of aerosol properties and water-leaving reflectance from multi-angular polarimetric measurements over coastal waters. Opt. Express 2018, 26, 8968–8989. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, C. Inverse Methods for Atmospheric Sounding: Theory and Practice; Series on Atmospheric, Oceanic and planetary Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Oceans 2001, 106, 7163–7180. [Google Scholar] [CrossRef] [Green Version]
- Bricaud, A.; Claustre, H.; Ras, J.; Oubelkheir, K. Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal populations. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef] [Green Version]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, P.-W.; Boss, E.; Franz, B.; Werdell, P.J.; Hu, Y. Radiative Transfer Modeling of Phytoplankton Fluorescence Quenching Processes. Remote Sens. 2018, 10, 1309. https://doi.org/10.3390/rs10081309
Zhai P-W, Boss E, Franz B, Werdell PJ, Hu Y. Radiative Transfer Modeling of Phytoplankton Fluorescence Quenching Processes. Remote Sensing. 2018; 10(8):1309. https://doi.org/10.3390/rs10081309
Chicago/Turabian StyleZhai, Peng-Wang, Emmanuel Boss, Bryan Franz, P. Jeremy Werdell, and Yongxiang Hu. 2018. "Radiative Transfer Modeling of Phytoplankton Fluorescence Quenching Processes" Remote Sensing 10, no. 8: 1309. https://doi.org/10.3390/rs10081309
APA StyleZhai, P.-W., Boss, E., Franz, B., Werdell, P. J., & Hu, Y. (2018). Radiative Transfer Modeling of Phytoplankton Fluorescence Quenching Processes. Remote Sensing, 10(8), 1309. https://doi.org/10.3390/rs10081309