Building Detection from VHR Remote Sensing Imagery Based on the Morphological Building Index
Abstract
1. Introduction
2. Proposed Method
2.1. Local Feature Points Detection and Optimization
2.1.1. Local Feature Points Detection
2.1.2. Local Feature Points Optimization
2.2. Built-Up Areas Extraction
- (1)
- Superpixel segmentation: The simple linear iterative clustering (SLIC) method is used here to partition the input VHR image into superpixels [37]. Given the number parameter and the compactness parameter , the input image will be partitioned into homogeneous objects. In order to automatically handle different images, we set and use the width and height of the input image to calculate the parameter with the expression .
- (2)
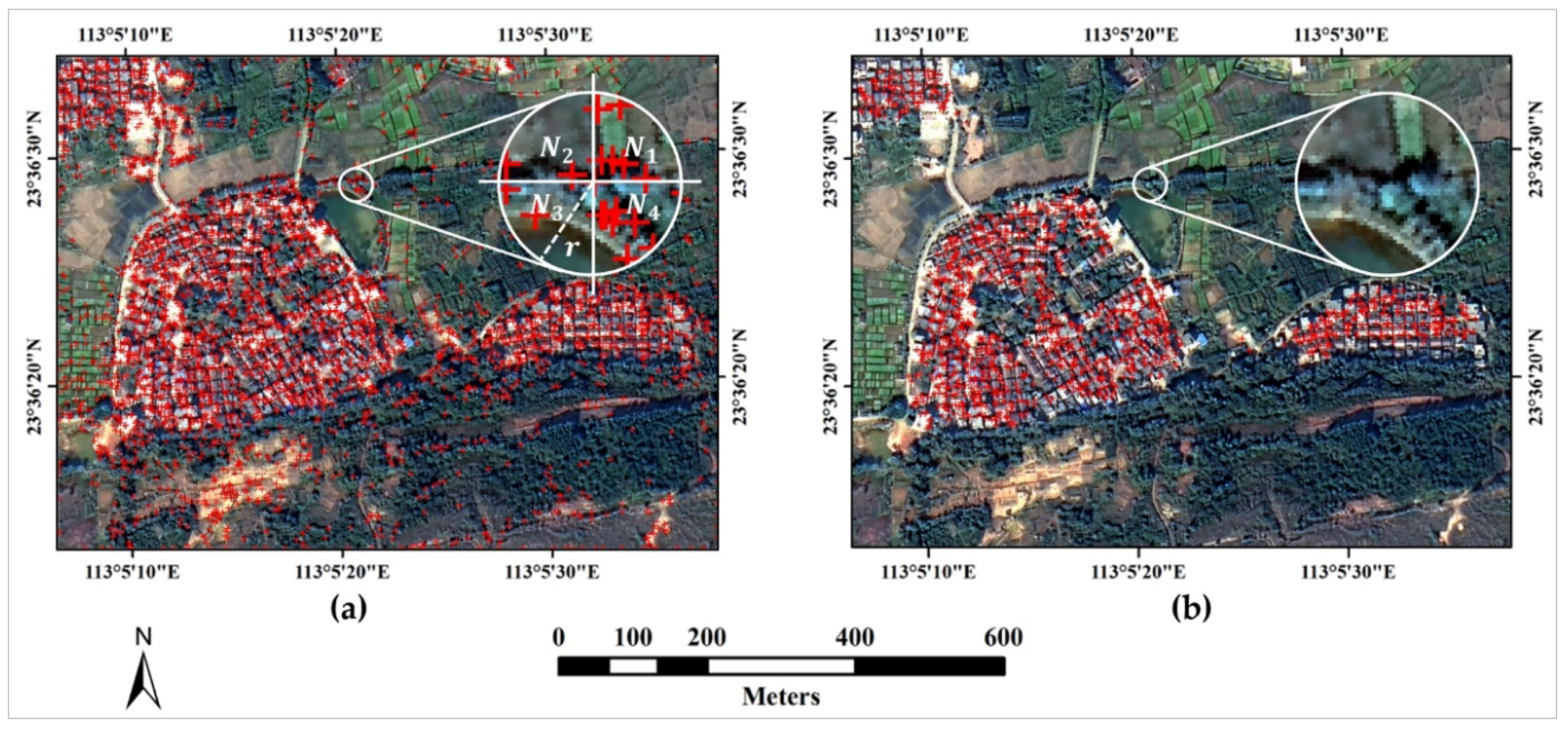
- Local feature point sparse representation: This method first searches for the connected components in , and then uses the centroid of the connected component to represent all the local feature points it contains. In this way, the optimized local feature point set can be represented by a sparse local feature point set, noted as , where denotes the centroid coordinate of the th connected component , and denotes the number of connected components. The centroid coordinate of is defined aswhere represents the coordinate of the th local feature point in , and represents the number of the local feature points belonging to .
- (3)
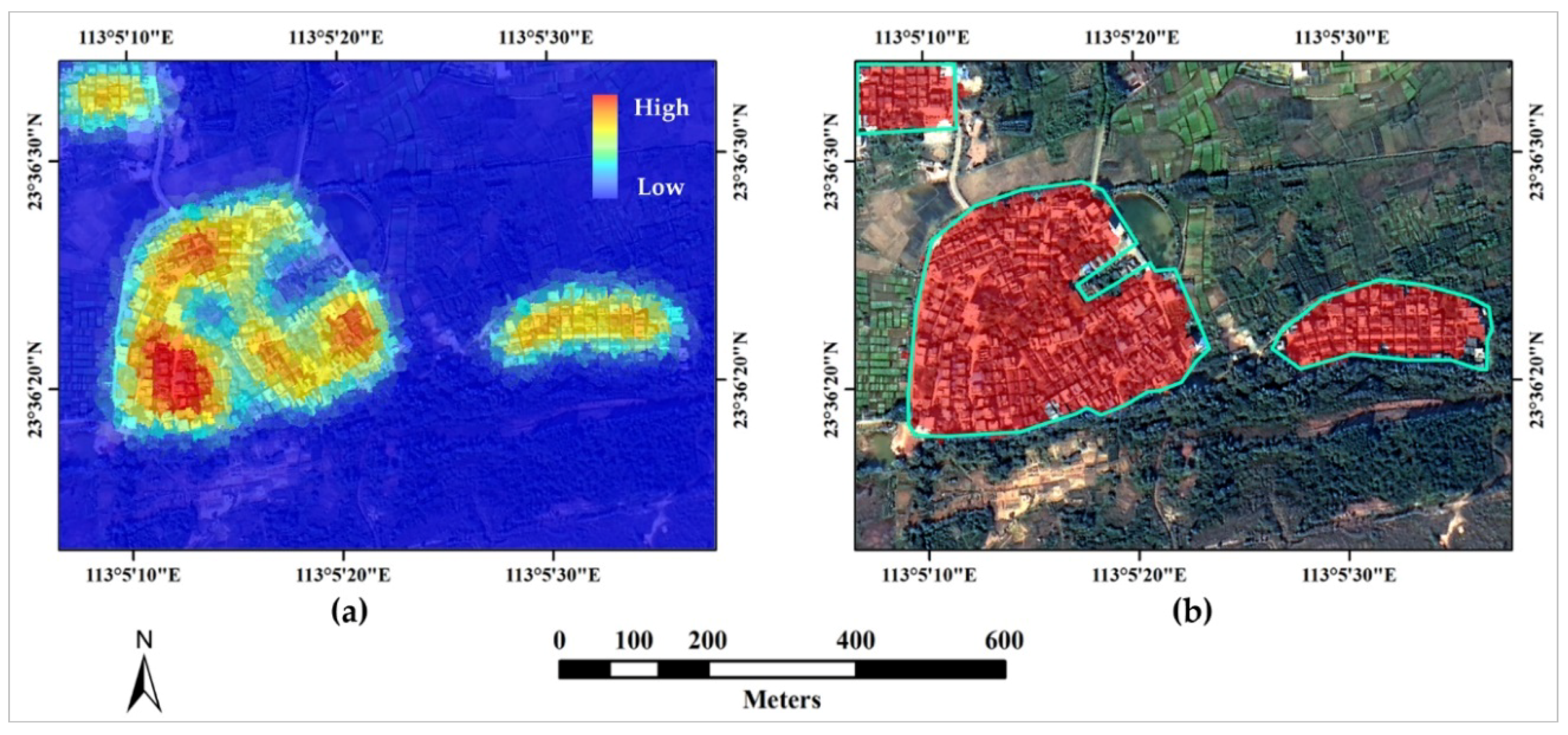
- Calculation of the voting matrix: In order to improve the computational efficiency and extraction accuracy, our improved spatial voting method uses the homogeneous objects as the basic calculation units and combines them with the sparse local feature point set to calculate the voting matrix, which is defined aswhere represents the voting value of the homogeneous object , represents the tolerance parameter of the th connected component , which is calculated by the expression , represents the centroid coordinate of , and represents the centroid coordinate of . Figure 3a shows the voting matrix calculated by the improved spatial voting method. As shown in Figure 3a, the calculated voting matrix can clearly indicate the location of the built-up areas. The high voting value (marked in red) in the voting matrix corresponds to the built-up area, while the low voting value (marked in blue) corresponds to the non-built-up area.
- (4)
- Built-up areas extraction: Since the voting value of the built-up area is higher than that of the non-built-up area, we use the Otsu’ method [35] to segment the voting matrix to extract built-up areas. Figure 3b shows the built-up areas (marked with red-colored area) extracted using the voting matrix shown in Figure 3a. As shown in Figure 3b, the extracted built-up areas match very well with the reference data (marked with cyan-colored polygons), which demonstrates the effectiveness of our improved spatial voting method.
2.3. Building Detection via the MBI Algorithm
THEN β should be removed,
3. Experiments
3.1. Data Set Description
3.2. Accuracy Assessment Metrics and Parameter Settings
3.2.1. Accuracy Assessment Metrics
3.2.2. Parameter Settings
- (1)
- Local feature points detection and optimization parameters: A large number of experiments show that when the scale number and the direction number of the Gabor wavelets are set to 5 and 4, respectively, most of the local feature points in the image can be detected. Therefore, in this study, the values of and are fixed as 5 and 4, respectively. Meanwhile, for the radius of the local circle window, the suggested value is twice the average size of buildings in the image, so it should be tuned according to different test images.
- (2)
- MBI parameters: As analyzed in [23], the four-directional MBI is sufficient to estimate the presence of buildings, and the accuracy of building extraction does not improve significantly as increases. Therefore, in this study, the value of is fixed as 4. For the scale parameter , the suggested value of it is calculated by the expression , where and represent the maximum and minimum sizes of buildings in the image, respectively. Therefore, it needs to be changed according to the test image. For the threshold , its recommended range is [1,6], and a large value will result in a large omission error and a small commission error. This parameter should also be adjusted for different test images.
- (3)
- Postprocessing parameters: For the threshold , according to the author’s experience, its appropriate range is between 0.1 and 0.3, and we can adjust it within this range according to the test images to obtain the best performance. In this study, the parameter is fixed as 0.2. For the thresholds and , since they are relevant to the geometric characteristics of the building, we should also adjust them according to different test images. The appropriate value of should be less than the area of the smallest building in the image to avoid erroneous removal of the building. In this study, the value of is fixed as 20. In addition, after many trials, we determined that the appropriate value of should be greater than 3. In this study, the values of for R1–R5 are 5, 4, 3.5, 4, and 3.5, respectively. Since the postprocessing of the building detection results is to further eliminate some small errors, it does not play a pivotal role in our method. Therefore, these postprocessing parameters (, , and ) are also not critical to our method.
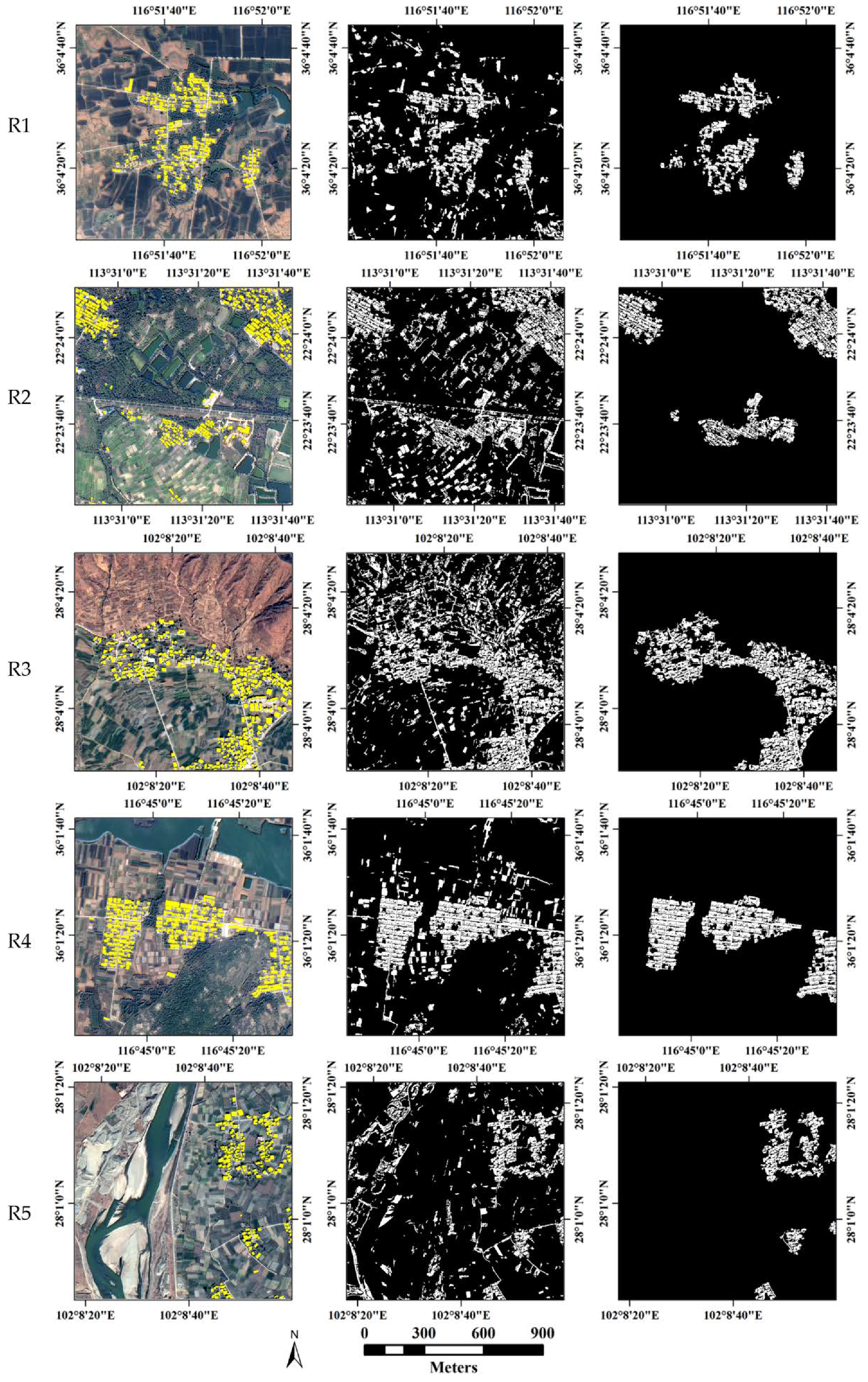
3.3. Results and Analysis
3.3.1. Built-Up Areas Extraction Results and Analysis
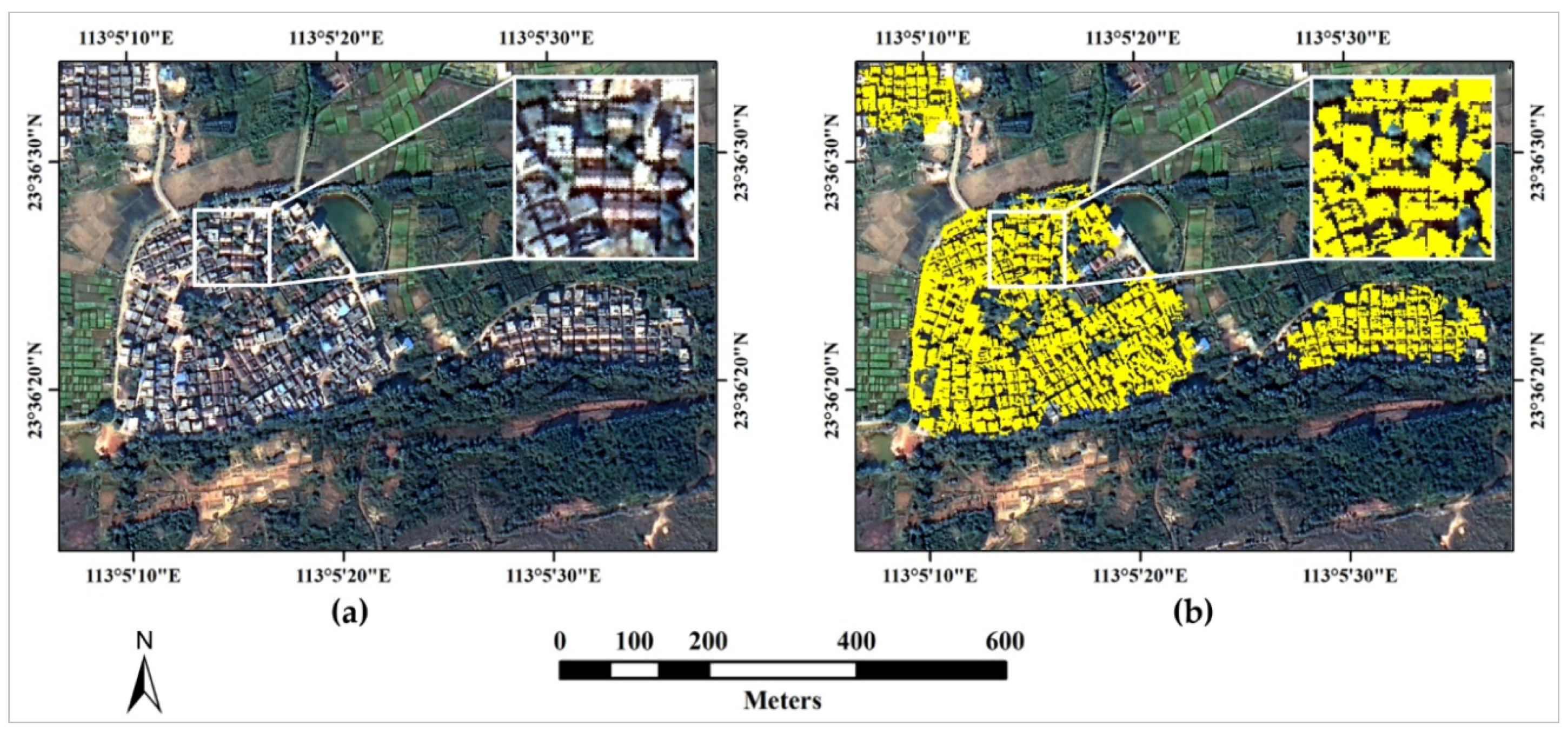
3.3.2. Building Detection Results and Analysis
4. Discussion
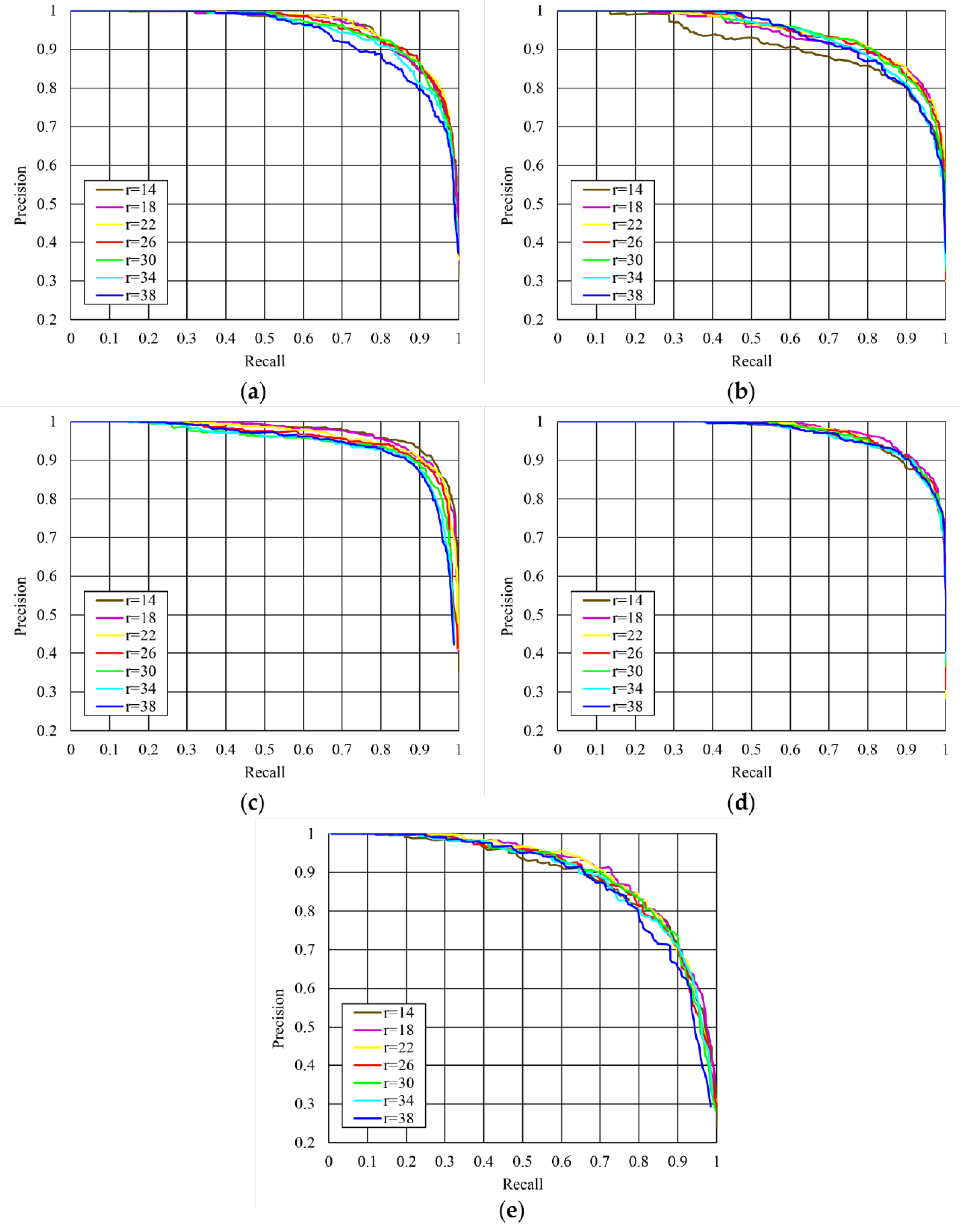
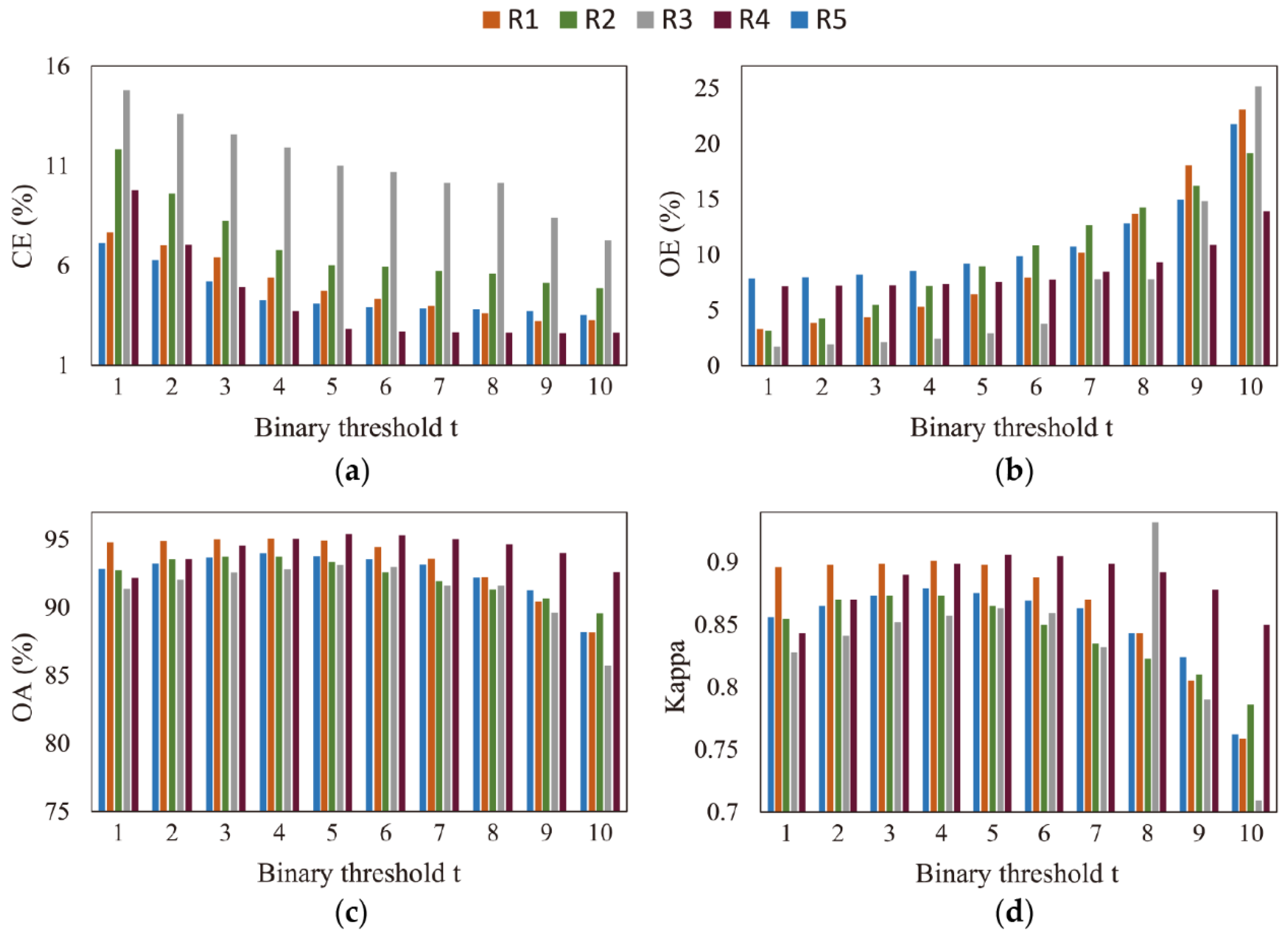
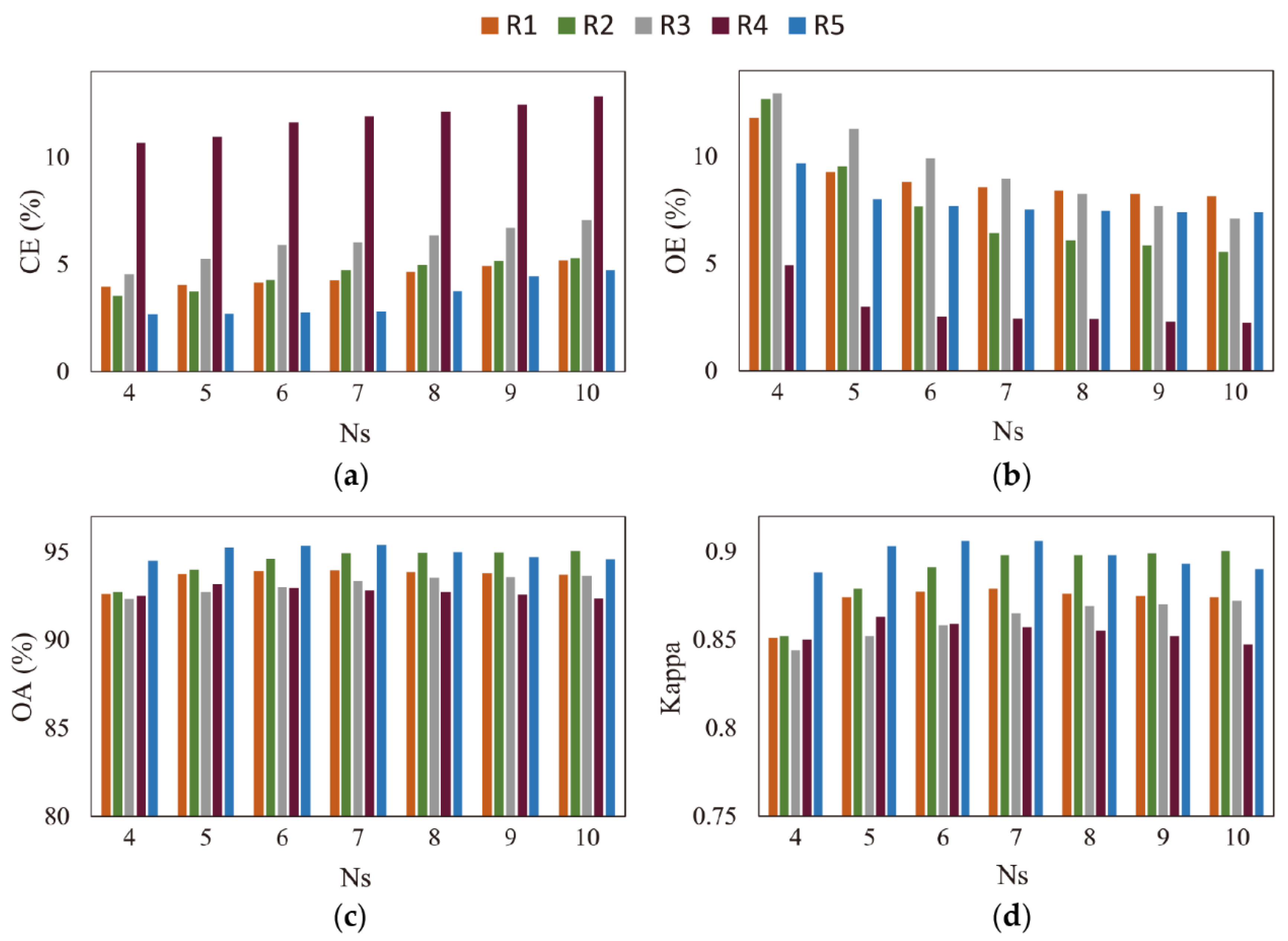
4.1. Parameter Sensitivity Analysis
4.1.1. Sensitivity Analysis of the Parameter
4.1.2. Sensitivity Analysis of the Binary Threshold
4.1.3. Sensitivity Analysis of the Parameter
4.2. Merits, Limitations, and Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MBI | morphological building index |
| ISODATA | iterative self-organizing data analysis technique algorithm |
| CNN | convolutional neural network |
| SIFT | scale invariant feature transform |
| DRV | discrimination by ratio of variance |
| SLIC | simple linear iterative clustering |
| WTH | white top-hat |
| DMP | differential morphological profiles |
| IBR | initial building results |
| NDVI | normalized difference vegetation index |
| LWR | length–width ratio |
| CE | commission error |
| OE | omission error |
| OA | overall accuracy |
References
- Ridd, M.K.; Hipple, J.D.; Photogrammetry, A.S.f.; Sensing, R. Remote Sensing of Human Settlements; American Society for Photogrammetry and Remote Sensing: Las Vegas, NV, USA, 2006. [Google Scholar]
- Pesaresi, M.; Guo, H.; Blaes, X.; Ehrlich, D.; Ferri, S.; Gueguen, L.; Halkia, M.; Kauffmann, M.; Kemper, T.; Lu, L. A Global Human Settlement Layer From Optical HR/VHR RS Data: Concept and First Results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2102–2131. [Google Scholar] [CrossRef]
- Florczyk, A.J.; Ferri, S.; Syrris, V.; Kemper, T.; Halkia, M.; Soille, P.; Pesaresi, M. A New European Settlement Map From Optical Remotely Sensed Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1978–1992. [Google Scholar] [CrossRef]
- Konstantinidis, D.; Stathaki, T.; Argyriou, V.; Grammalidis, N. Building Detection Using Enhanced HOG–LBP Features and Region Refinement Processes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 1–18. [Google Scholar] [CrossRef]
- Solano-Correa, Y.T.; Bovolo, F.; Bruzzone, L. An Approach for Unsupervised Change Detection in Multitemporal VHR Images Acquired by Different Multispectral Sensors. Remote Sens. 2018, 10, 533. [Google Scholar] [CrossRef]
- Mayer, H. Automatic object extraction from aerial imagery—A survey focusing on buildings. Comput. Vis. Image Underst. 1999, 74, 138–149. [Google Scholar] [CrossRef]
- Unsalan, C.; Boyer, K.L. A system to detect houses and residential street networks in multispectral satellite images. Comput. Vis. Image Underst. 2005, 98, 423–461. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Object extraction and revision by image analysis using existing geodata and knowledge: Current status and steps towards operational systems. ISPRS-J. Photogramm. Remote Sens. 2004, 58, 129–151. [Google Scholar] [CrossRef]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS-J. Photogramm. Remote Sens. 2010, 65, 570–580. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.W. A survey on object detection in optical remote sensing images. ISPRS-J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Lee, D.S.; Shan, J.; Bethel, J.S. Class-guided building extraction from Ikonos imagery. Photogramm. Eng. Remote Sens. 2003, 69, 143–150. [Google Scholar] [CrossRef]
- Inglada, J. Automatic recognition of man-made objects in high resolution optical remote sensing images by SVM classification of geometric image features. ISPRS-J. Photogramm. Remote Sens. 2007, 62, 236–248. [Google Scholar] [CrossRef]
- Senaras, C.; Ozay, M.; Vural, F.T.Y. Building Detection With Decision Fusion. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 1295–1304. [Google Scholar] [CrossRef]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Dalla Mura, M. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS-J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Sirmacek, B.; Unsalan, C. Urban-Area and Building Detection Using SIFT Keypoints and Graph Theory. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1156–1167. [Google Scholar] [CrossRef]
- Ok, A.O.; Senaras, C.; Yuksel, B. Automated Detection of Arbitrarily Shaped Buildings in Complex Environments From Monocular VHR Optical Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1701–1717. [Google Scholar] [CrossRef]
- Ok, A.O. Automated detection of buildings from single VHR multispectral images using shadow information and graph cuts. ISPRS-J. Photogramm. Remote Sens. 2013, 86, 21–40. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Y.C. Model and context-driven building extraction in dense urban aerial images. Int. J. Remote Sens. 2005, 26, 1289–1307. [Google Scholar] [CrossRef]
- Ahmadi, S.; Zoej, M.J.V.; Ebadi, H.; Moghaddam, H.A.; Mohammadzadeh, A. Automatic urban building boundary extraction from high resolution aerial images using an innovative model of active contours. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 150–157. [Google Scholar] [CrossRef]
- Liasis, G.; Stavrou, S. Building extraction in satellite images using active contours and colour features. Int. J. Remote Sens. 2016, 37, 1127–1153. [Google Scholar] [CrossRef]
- Pesaresi, M.; Gerhardinger, A.; Kayitakire, F. A Robust Built-Up Area Presence Index by Anisotropic Rotation-Invariant Textural Measure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2008, 1, 180–192. [Google Scholar] [CrossRef]
- Lhomme, S.; He, D.C.; Weber, C.; Morin, D. A new approach to building identification from very-high-spatial-resolution images. Int. J. Remote Sens. 2009, 30, 1341–1354. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.P. A Multidirectional and Multiscale Morphological Index for Automatic Building Extraction from Multispectral GeoEye-1 Imagery. Photogramm. Eng. Remote Sens. 2011, 77, 721–732. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, X.; Zhang, G.X. A Morphological Building Detection Framework for High-Resolution Optical Imagery Over Urban Areas. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1388–1392. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. Morphological Building/Shadow Index for Building Extraction From High-Resolution Imagery Over Urban Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 161–172. [Google Scholar] [CrossRef]
- Huang, X.; Yuan, W.L.; Li, J.Y.; Zhang, L.P. A New Building Extraction Postprocessing Framework for High-Spatial-Resolution Remote-Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 654–668. [Google Scholar] [CrossRef]
- Sirmacek, B.; Unsalan, C. Urban Area Detection Using Local Feature Points and Spatial Voting. IEEE Geosci. Remote Sens. Lett. 2010, 7, 146–150. [Google Scholar] [CrossRef]
- Xu, W.; Huang, X.; Zhang, W. A multi-scale visual salient feature points extraction method based on Gabor wavelets. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Guilin, China, 19–23 December 2009; pp. 1205–1208. [Google Scholar]
- Kovacs, A.; Sziranyi, T. Improved Harris Feature Point Set for Orientation-Sensitive Urban-Area Detection in Aerial Images. IEEE Geosci. Remote Sens. Lett. 2013, 10, 796–800. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Q.; Zhang, Q.; Wu, G. Representation of Block-Based Image Features in a Multi-Scale Framework for Built-Up Area Detection. Remote Sens. 2016, 8, 155. [Google Scholar] [CrossRef]
- Shi, H.; Chen, L.; Bi, F.K.; Chen, H.; Yu, Y. Accurate Urban Area Detection in Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1948–1952. [Google Scholar] [CrossRef]
- Li, Y.S.; Tan, Y.H.; Deng, J.J.; Wen, Q.; Tian, J.W. Cauchy Graph Embedding Optimization for Built-Up Areas Detection From High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2078–2096. [Google Scholar] [CrossRef]
- Tao, C.; Tan, Y.H.; Zou, Z.R.; Tian, J.W. Unsupervised Detection of Built-Up Areas From Multiple High-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1300–1304. [Google Scholar] [CrossRef]
- Lee, T.S. Image representation using 2D gabor wavelets. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 959–971. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Hu, X.Y.; Shen, J.J.; Shan, J.; Pan, L. Local Edge Distributions for Detection of Salient Structure Textures and Objects. IEEE Geosci. Remote Sens. Lett. 2013, 10, 466–470. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2281. [Google Scholar] [CrossRef] [PubMed]
- Teke, M.; Başeski, E.; Ok, A.Ö.; Yüksel, B.; Şenaras, Ç. Multi-spectral False Color Shadow Detection. In Photogrammetric Image Analysis; Springer: Berlin/Heidelberg, Germany, 2011; pp. 109–119. [Google Scholar]
- Sun, W.; Messinger, D. Nearest-neighbor diffusion-based pan-sharpening algorithm for spectral images. Opt. Eng. 2013, 53, 013107. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]


| Sensor Specification | Panchromatic | Multispectral |
|---|---|---|
| Spatial Resolution | 1 m | 4 m |
| Swath Width | 45 km | 45 km |
| Repetition Cycle | 5 days | 5 days |
| Spectral Range | 450~900 nm | Blue: 450~520 nm Green: 520~590 nm Red: 630~690 nm Near-infrared: 770~890 nm |
| Scene ID | Acquisition Date and Time (UTC) | Image Locations | Image Patches |
|---|---|---|---|
| 3609415 | 30 April 2017, 11:27:58 | Tai’an City, China | R1, R4 |
| 3131139 | 18 December 2016, 11:31:01 | Zhongshan City, China | R2 |
| 2097076 | 14 February 2016, 12:11:49 | Xichang City, China | R3, R5 |
| Image | Number of Samples | Major Error Sources | |
|---|---|---|---|
| Building | Background 1 | ||
| R1 | 11218 | 11814 | bright barren land, impervious roads |
| R2 | 12989 | 14816 | impervious roads, open areas, farmland |
| R3 | 10334 | 12115 | bright barren land, impervious roads, farmland |
| R4 | 11028 | 12395 | bright barren land, impervious roads, farmland |
| R5 | 7120 | 7986 | bright barren land, farmland, mudflats |
| Image | |||
|---|---|---|---|
| R1 | 26 | 7 | 4 |
| R2 | 26 | 7 | 5 |
| R3 | 24 | 7 | 5 |
| R4 | 26 | 7 | 4 |
| R5 | 24 | 7 | 5 |
| Image | With the Saliency Index 1 | Without the Saliency Index 2 | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | F-Measure | Precision | Recall | F-Measure | |
| R1 | 0.925 | 0.901 | 0.913 | 0.605 | 0.989 | 0.751 |
| R2 | 0.812 | 0.930 | 0.867 | 0.435 | 0.998 | 0.606 |
| R3 | 0.849 | 0.978 | 0.909 | 0.720 | 0.996 | 0.836 |
| R4 | 0.857 | 0.940 | 0.896 | 0.458 | 0.998 | 0.628 |
| R5 | 0.762 | 0.931 | 0.838 | 0.335 | 0.993 | 0.501 |
| Average | 0.841 | 0.936 | 0.885 | 0.511 | 0.995 | 0.664 |
| Image | Accuracy Assessment | |||||||
|---|---|---|---|---|---|---|---|---|
| The Original MBI Algorithm | Our Proposed Method | |||||||
| CE (%) | OE (%) | OA (%) | Kappa | CE (%) | OE (%) | OA (%) | Kappa | |
| R1 | 28.82 | 7.50 | 78.11 | 0.565 | 4.33 | 8.60 | 93.79 | 0.876 |
| R2 | 32.02 | 3.96 | 77.02 | 0.549 | 4.58 | 6.57 | 94.84 | 0.896 |
| R3 | 37.86 | 8.30 | 70.46 | 0.426 | 6.29 | 9.01 | 93.05 | 0.860 |
| R4 | 32.92 | 1.92 | 76.43 | 0.539 | 11.58 | 2.36 | 92.87 | 0.858 |
| R5 | 28.64 | 3.48 | 80.10 | 0.608 | 2.74 | 7.36 | 95.29 | 0.905 |
| Average | 32.05 | 5.03 | 76.42 | 0.537 | 5.90 | 6.78 | 93.97 | 0.879 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.; Wang, S.; Ma, Y.; Chen, G.; Wang, B.; Shen, M.; Liu, W. Building Detection from VHR Remote Sensing Imagery Based on the Morphological Building Index. Remote Sens. 2018, 10, 1287. https://doi.org/10.3390/rs10081287
You Y, Wang S, Ma Y, Chen G, Wang B, Shen M, Liu W. Building Detection from VHR Remote Sensing Imagery Based on the Morphological Building Index. Remote Sensing. 2018; 10(8):1287. https://doi.org/10.3390/rs10081287
Chicago/Turabian StyleYou, Yongfa, Siyuan Wang, Yuanxu Ma, Guangsheng Chen, Bin Wang, Ming Shen, and Weihua Liu. 2018. "Building Detection from VHR Remote Sensing Imagery Based on the Morphological Building Index" Remote Sensing 10, no. 8: 1287. https://doi.org/10.3390/rs10081287
APA StyleYou, Y., Wang, S., Ma, Y., Chen, G., Wang, B., Shen, M., & Liu, W. (2018). Building Detection from VHR Remote Sensing Imagery Based on the Morphological Building Index. Remote Sensing, 10(8), 1287. https://doi.org/10.3390/rs10081287







