Influence of Spatial Aggregation on Prediction Accuracy of Green Vegetation Using Boosted Regression Trees
Abstract
1. Introduction
2. Material and Methods
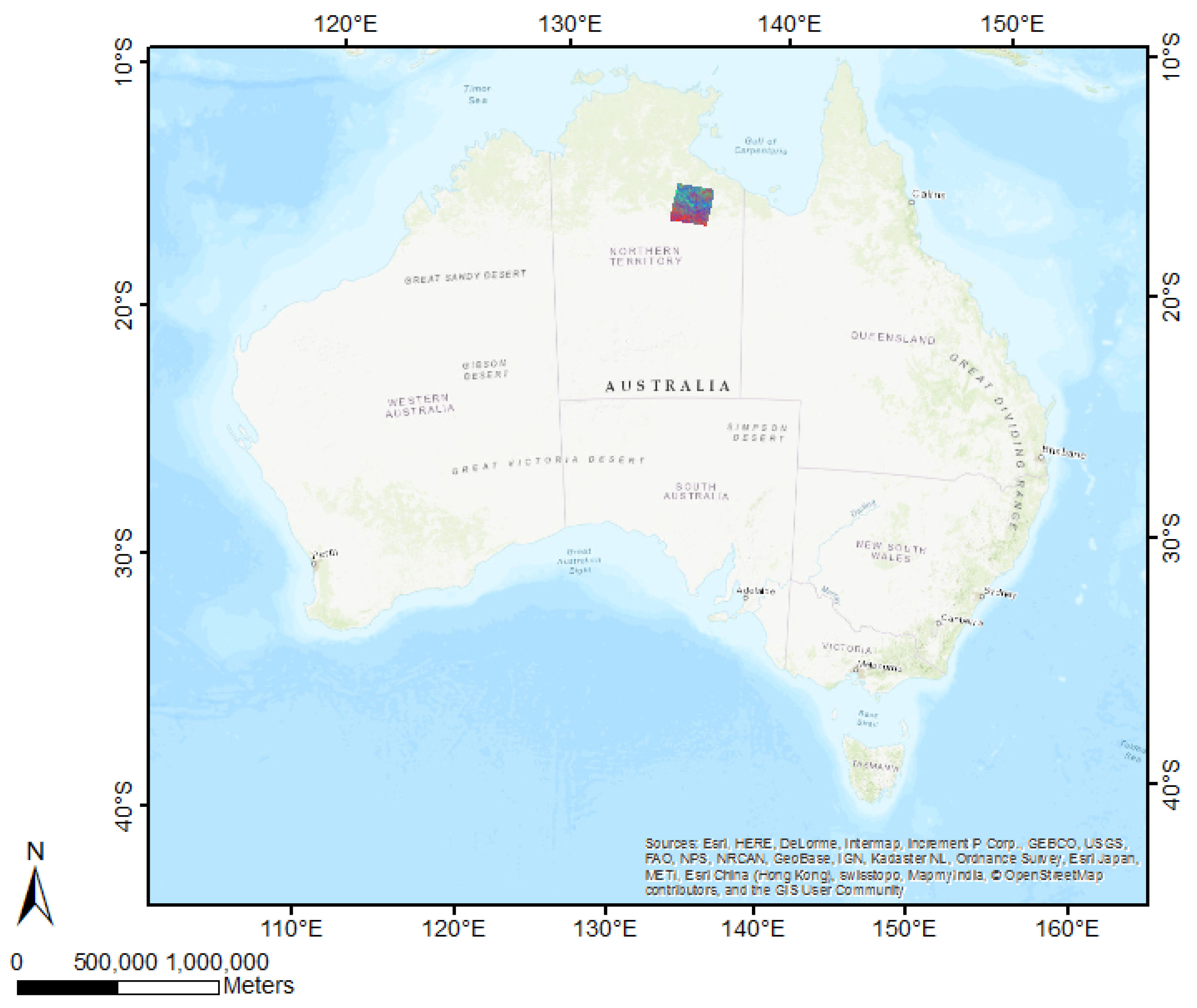
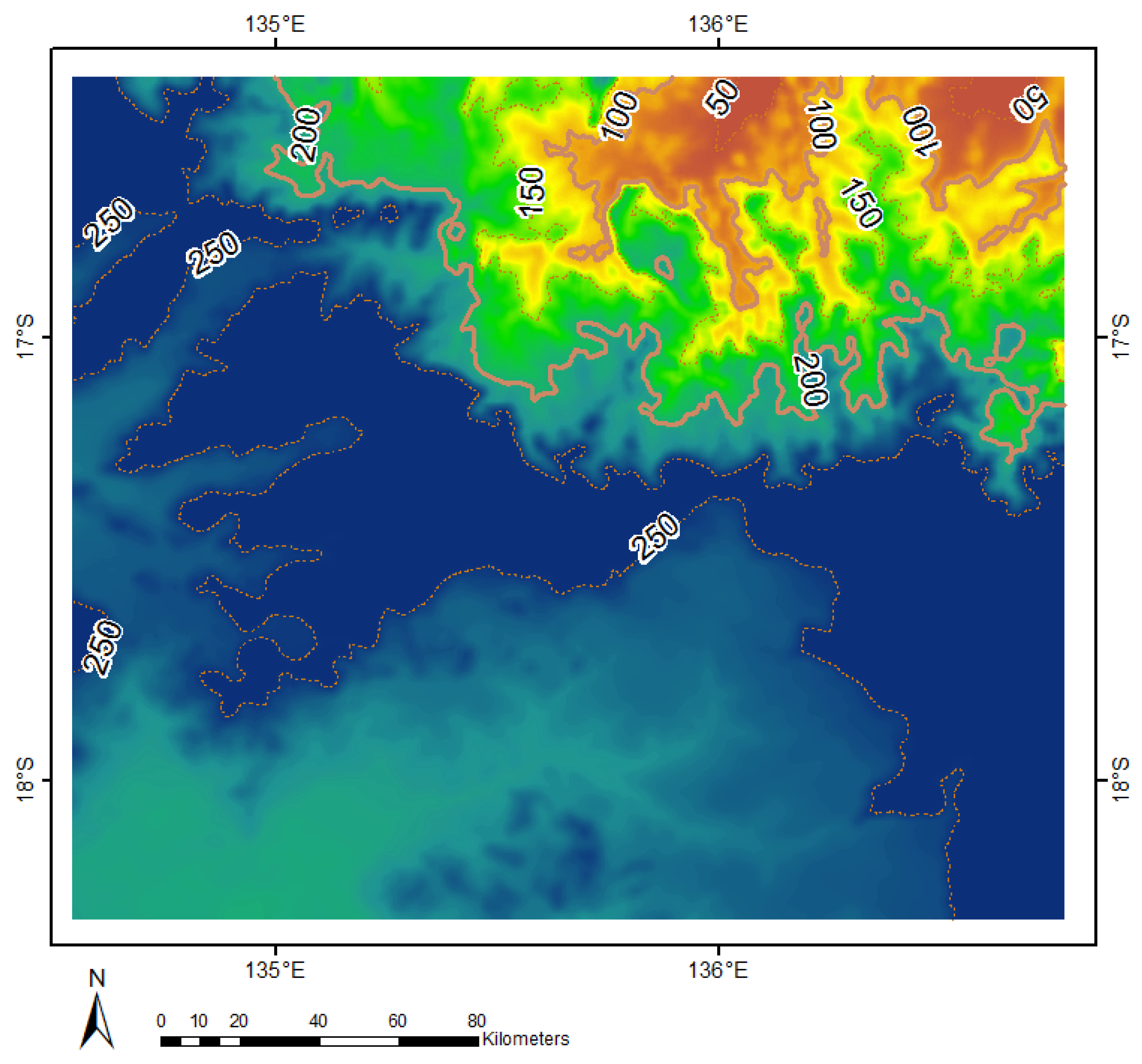
2.1. Case Study
2.2. Data
Spectral Unmixing Approach
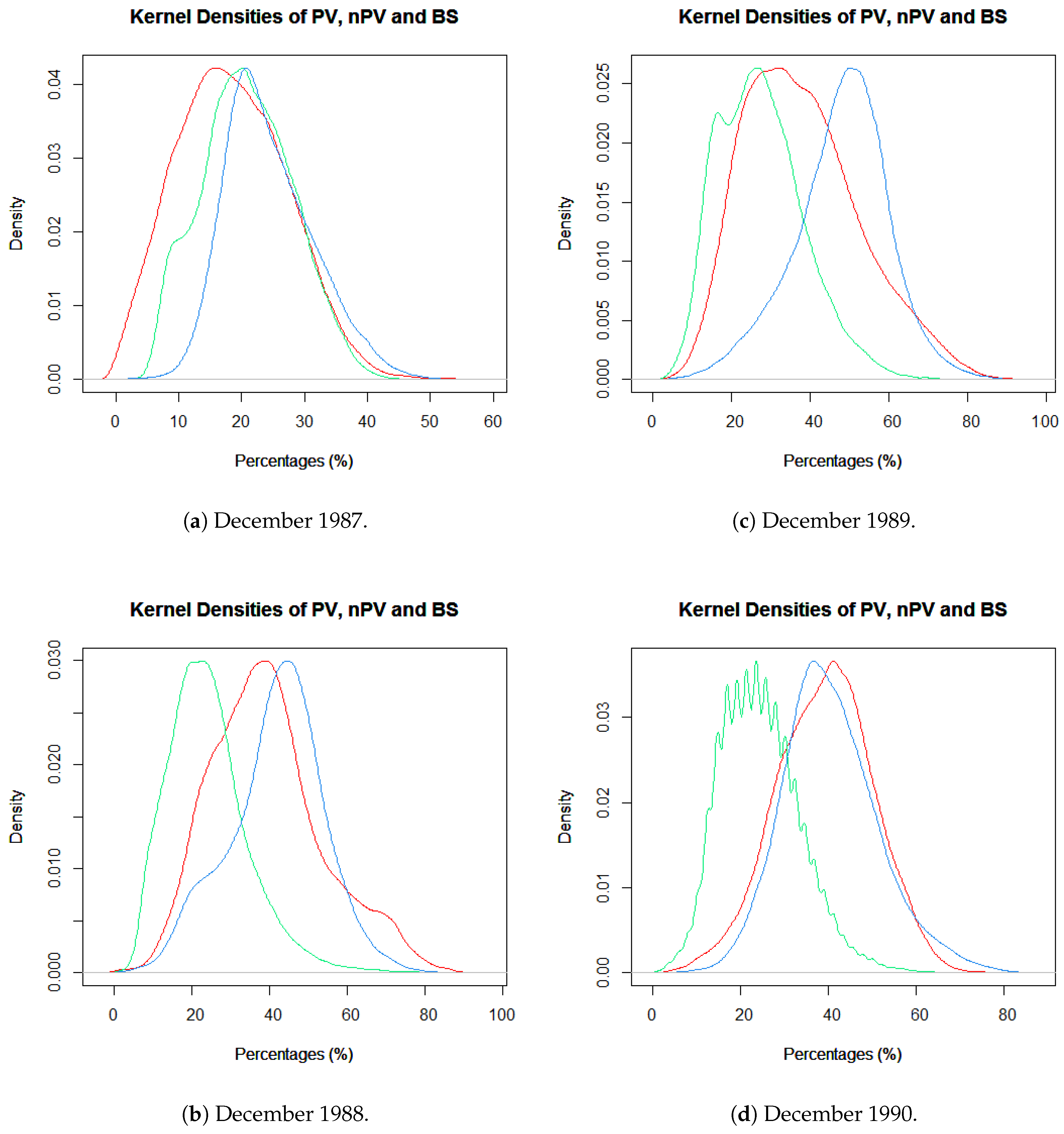
2.3. Data Exploration for FCover Imagery
2.4. Data Pre-Processing and Spatial Aggregation
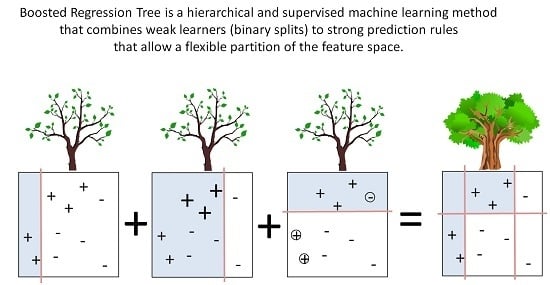
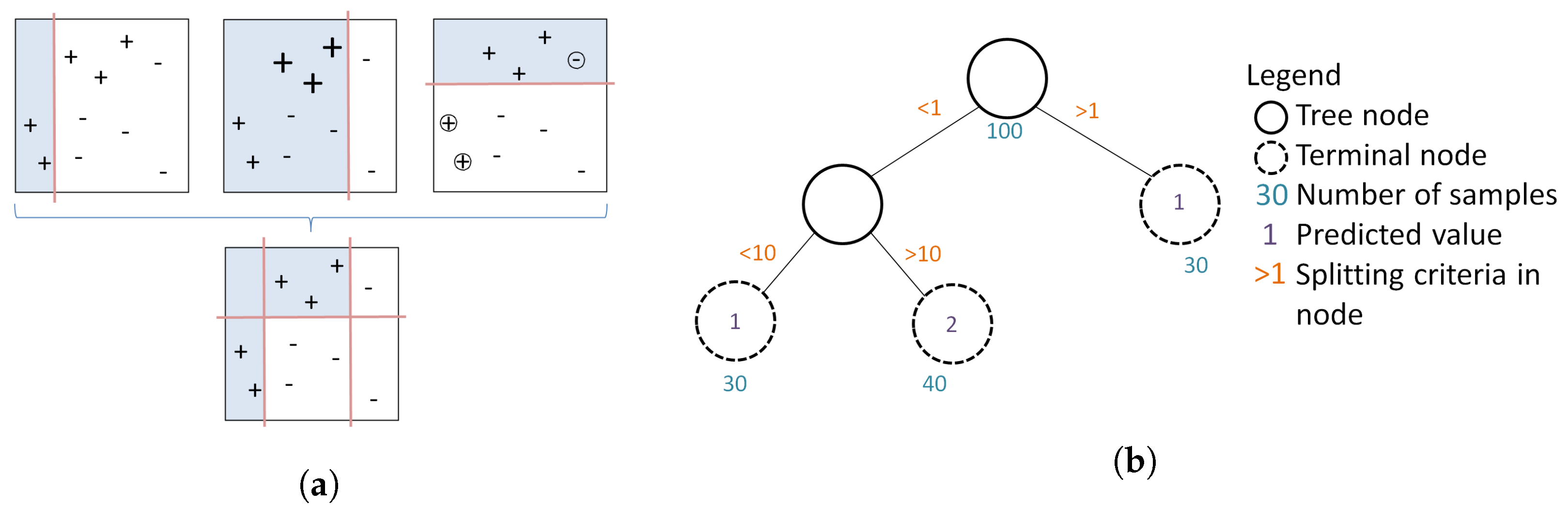
2.5. Boosted Regression Trees
| Algorithm 1 Stochastic Gradient Boosting algorithm. |
|
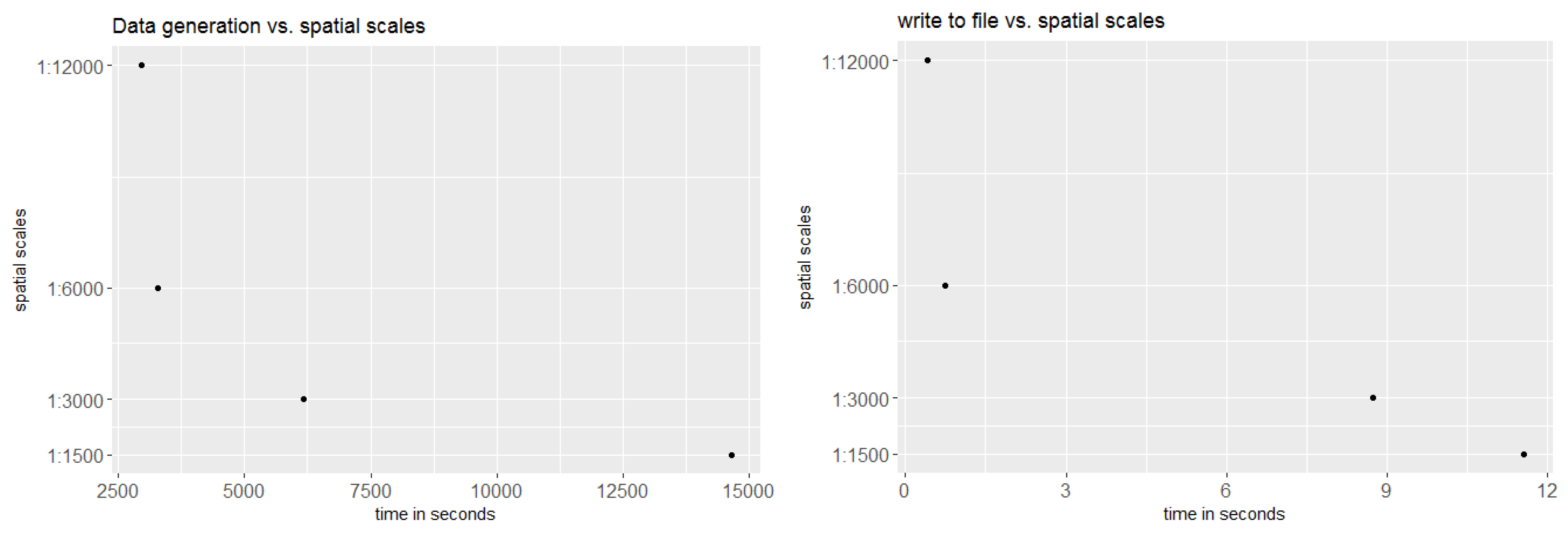
2.6. Implementation
- shrinkage; (how quickly the algorithm adapts)
- tree complexity; the total number of trees in the final model (number of iterations)
- interaction depth; interaction between different nodes along the branch
- minimum observations in node; minimum number of training set samples in a node to commence splitting.
2.7. Quantitative Assessment of the Model Fit
3. Results
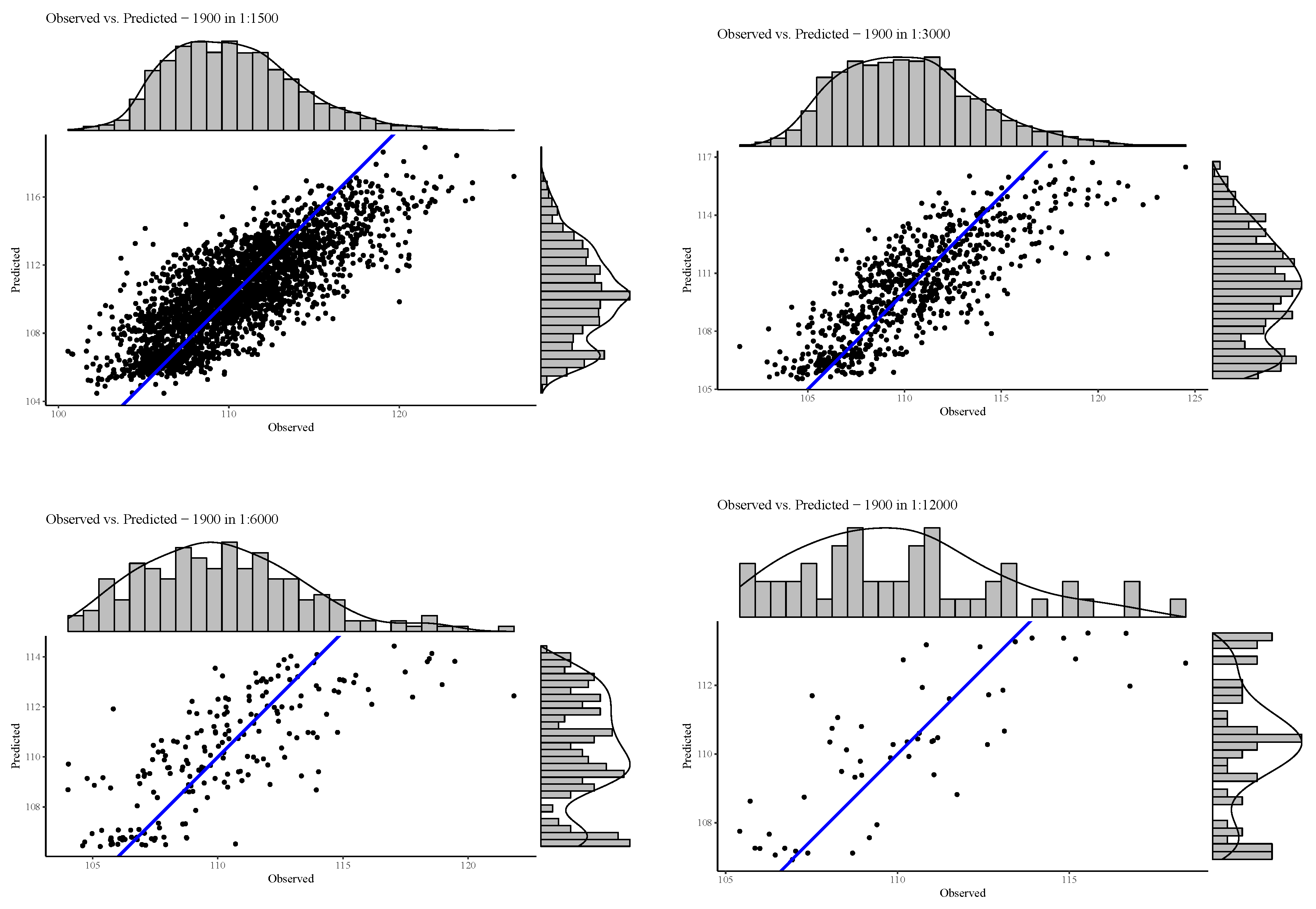
3.1. Comparison of Model Fit at Different Spatial Resolutions
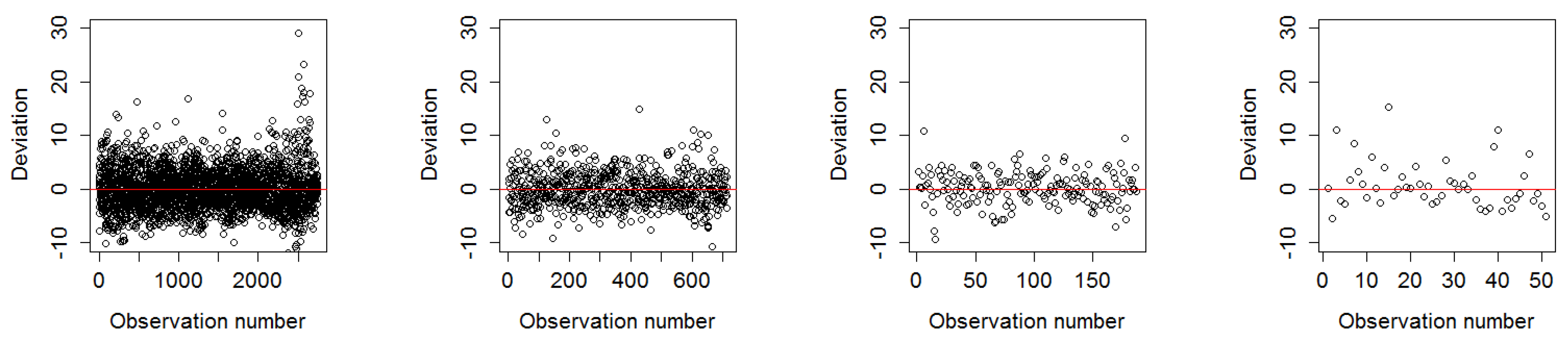
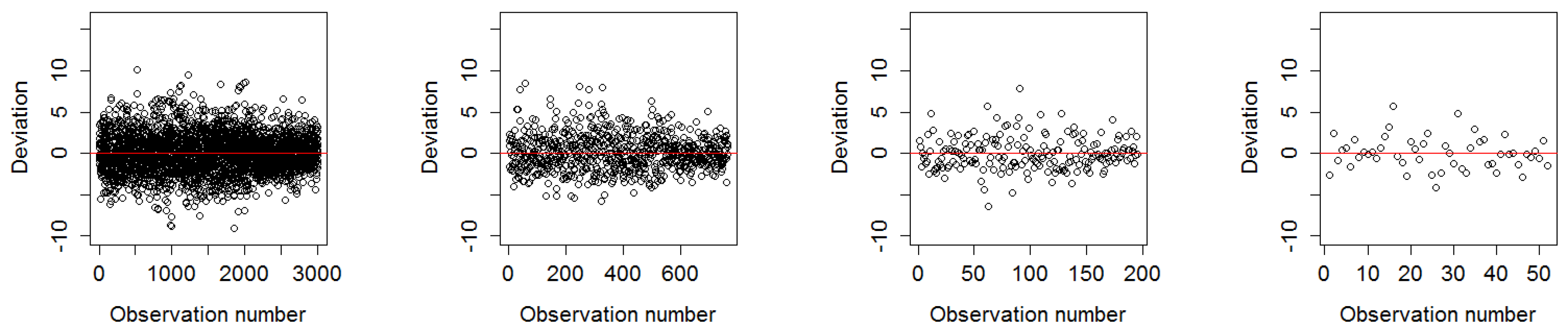
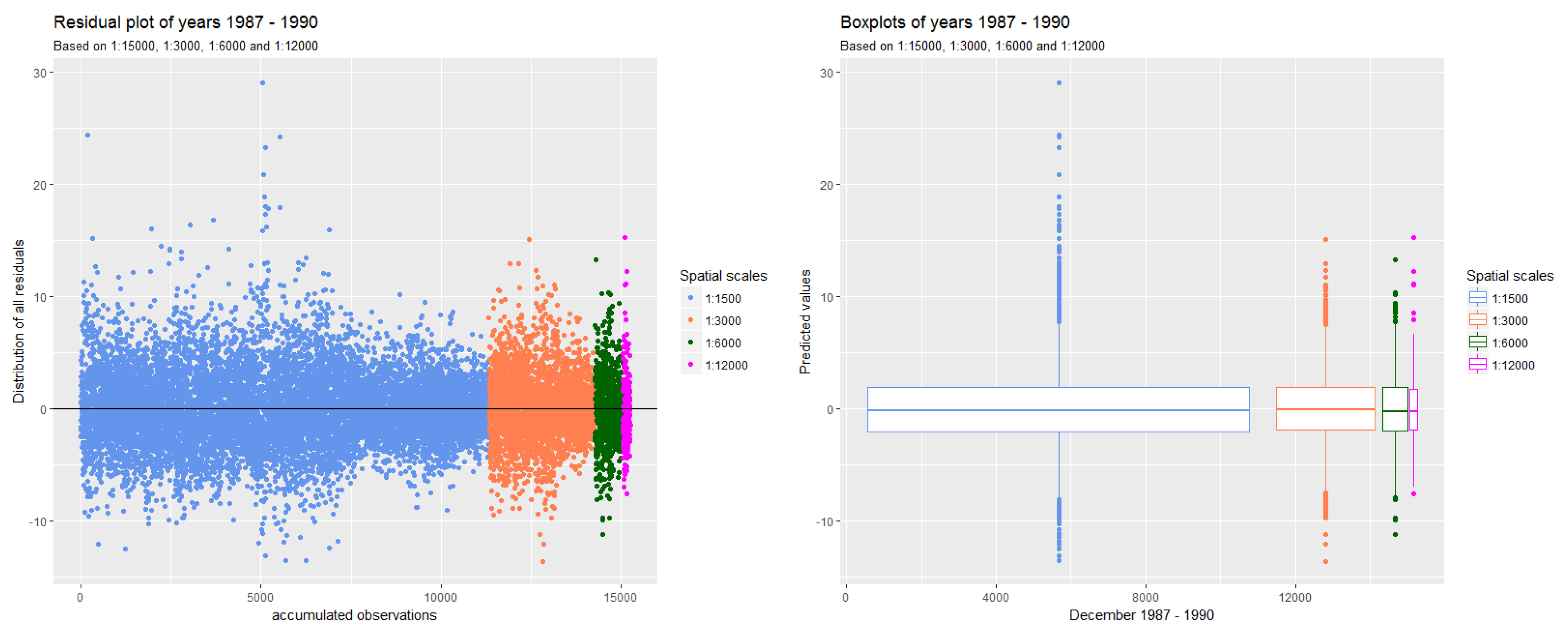
3.1.1. Deviation of Residuals Around the Mean
3.1.2. RMSE Comparisons between BRT and Linear Model (LM)
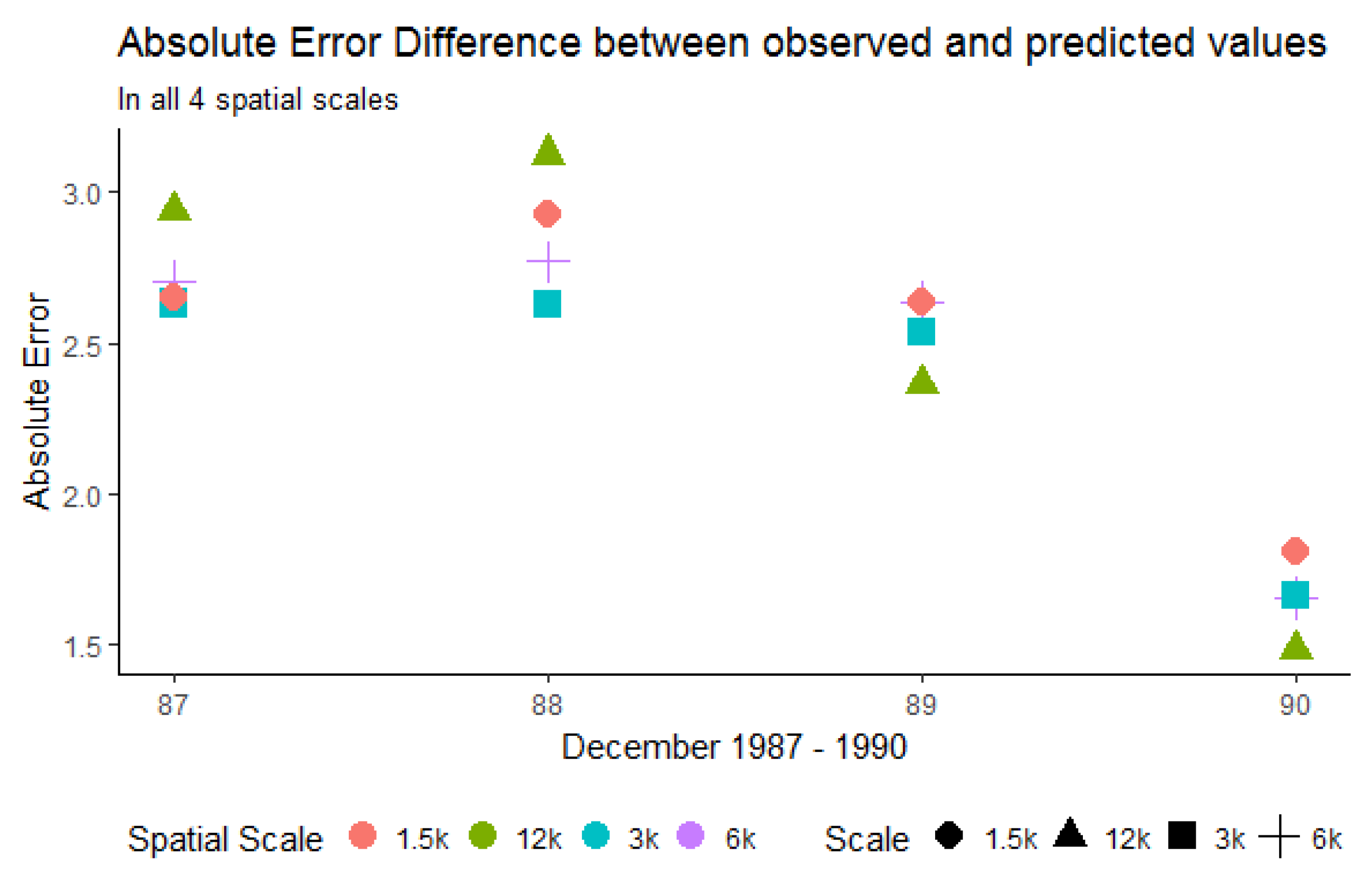
3.1.3. Mean Absolute Error (MAE) and Median Absolute Error (MDAE)
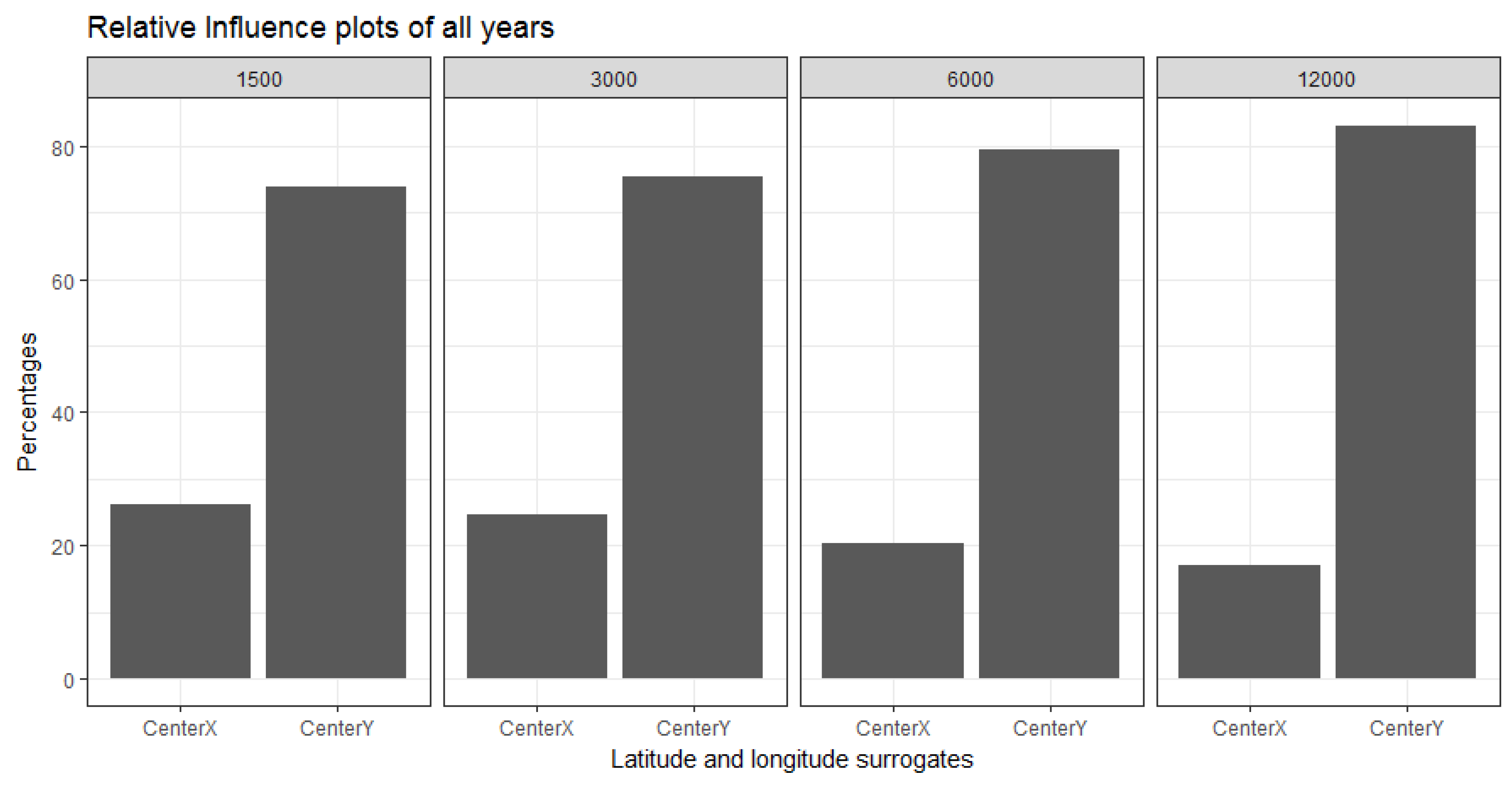
3.2. Variable Importance
3.2.1. Relative Influence of Covariates at Different Resolutions
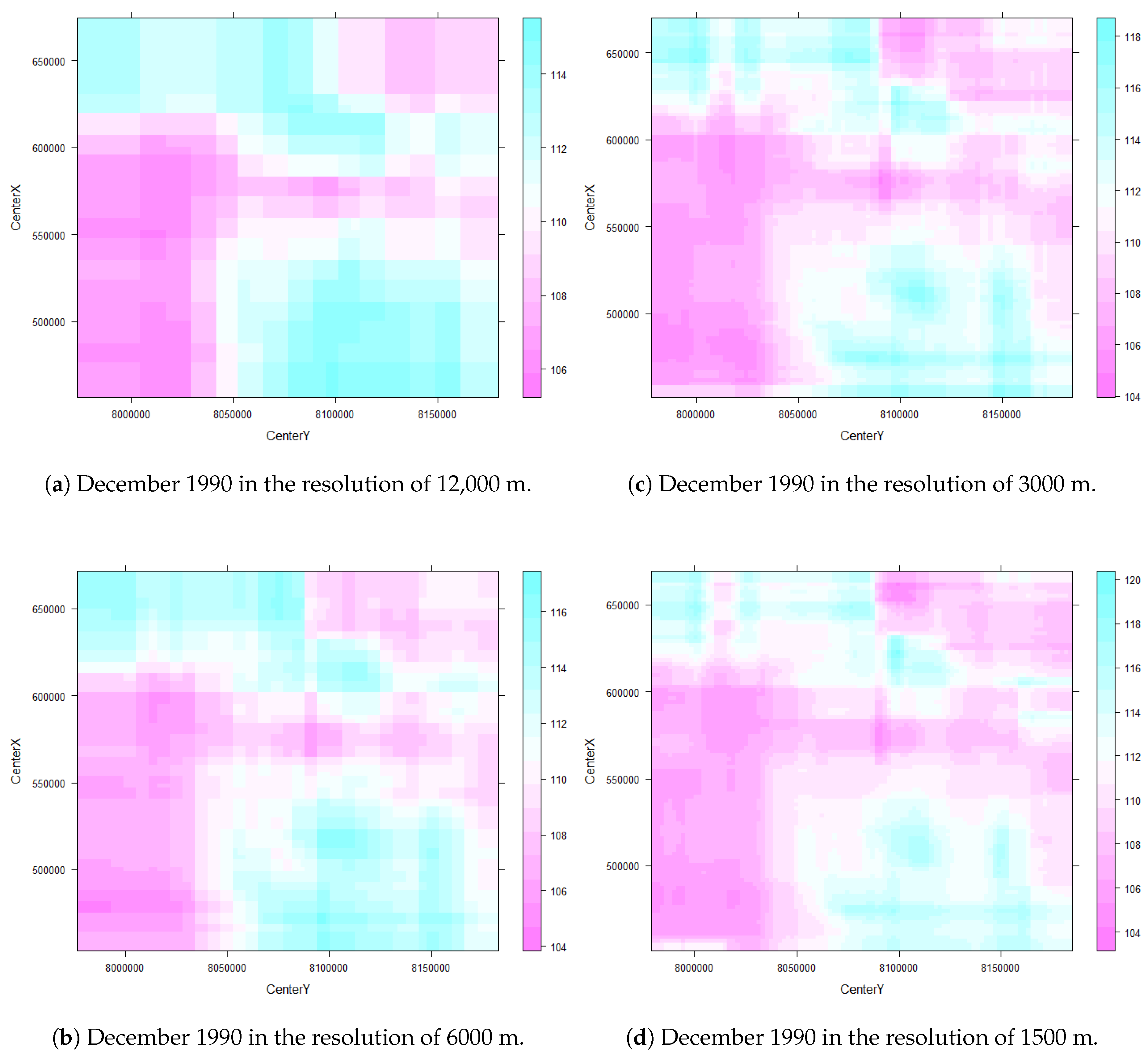
3.2.2. Prediction Raster Maps
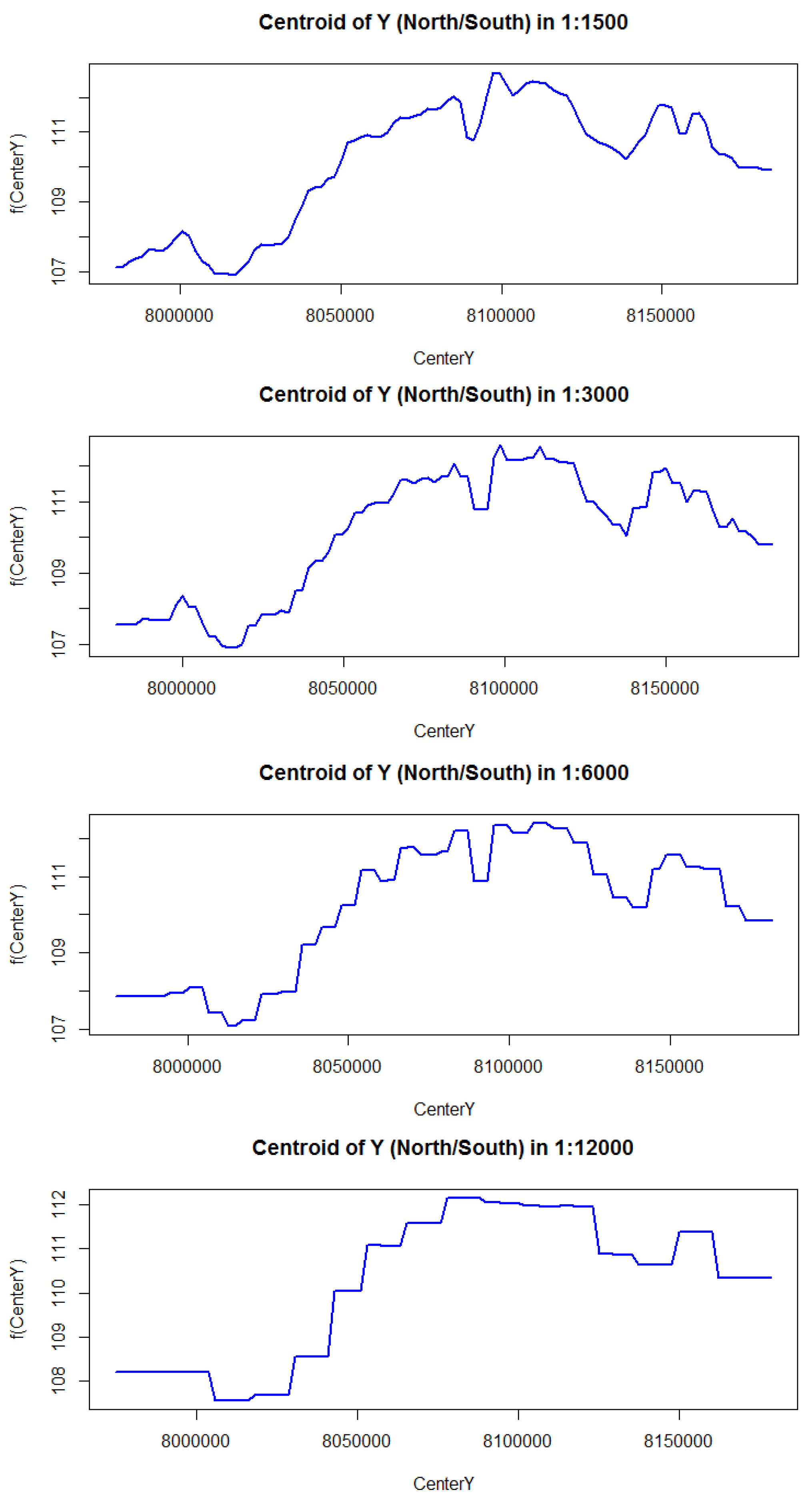
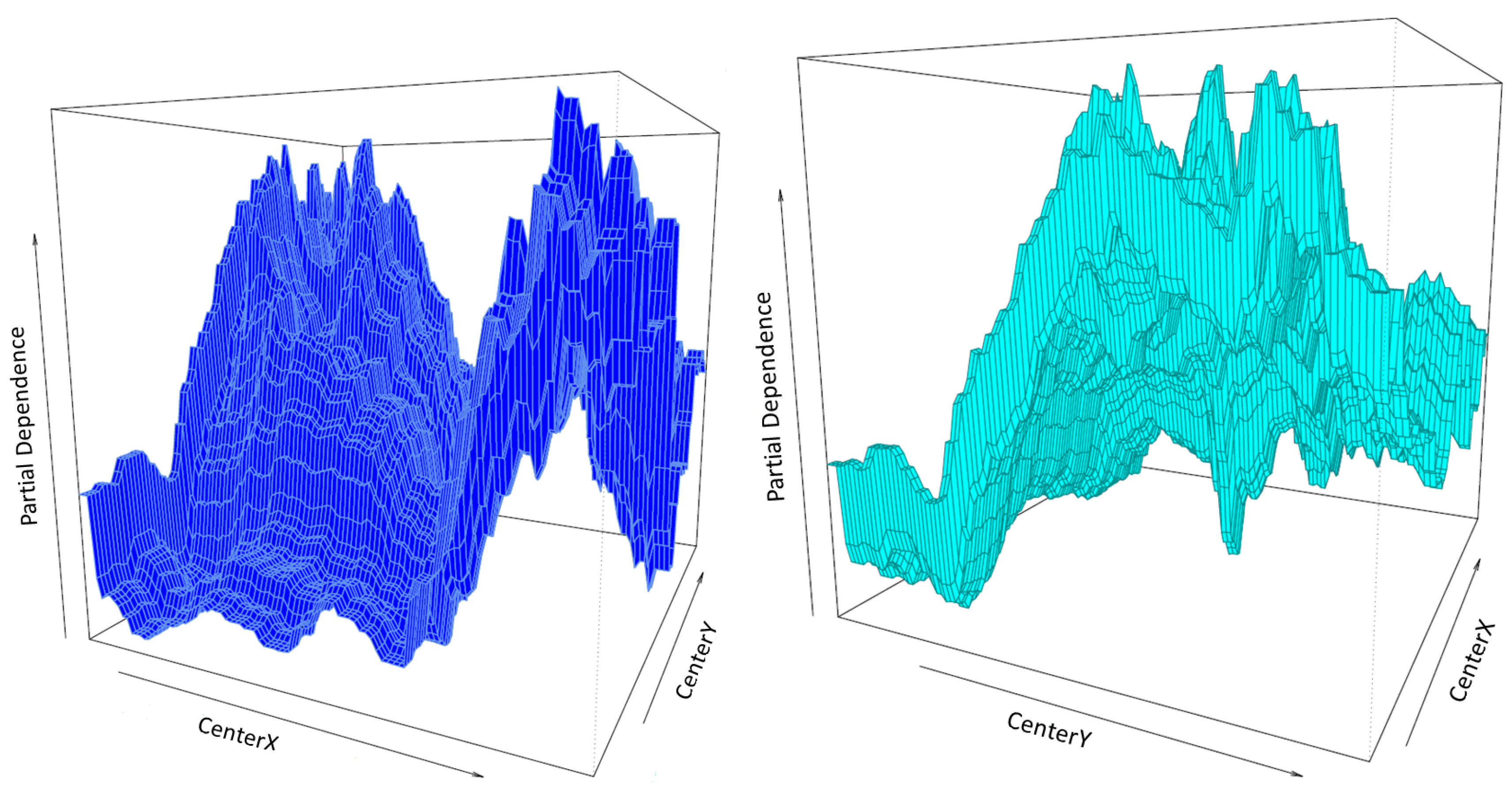
3.2.3. Prediction Surface Plots
3.2.4. Marginal Influence Plots
3.3. Aggregation and Scaling Error
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A.
Appendix A.1. Mathematical Explanation of the BRT Method
Appendix A.2. Partial Dependency Plots
References
- Datt, B. A New Reflectance Index for Remote Sensing of Chlorophyll Content in Higher Plants: Tests using Eucalyptus Leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Schmidt, M.; Thamm, H.-P.; Menz, G.; Bénes, T. (Eds.) Long term vegetation change detection in an and environment using LANDSAT data. In Geoinformation for European–Wide Integration; Millpress: Rotterdam, The Netherlands, 2003; pp. 145–154. [Google Scholar]
- Marsett, R.C.; Qi, J.; Heilman, P.; Biedenbender, S.H.; Watson, M.C.; Amer, S.; Weltz, M.; Goodrich, D.; Marsett, R. Remote Sensing for Grassland Management in the Arid Southwest. Rangel. Ecol. Manag. 2006, 59, 530–540. [Google Scholar] [CrossRef]
- Huete, A.; Ponce-Campos, G.; Zhang, Y.; Restrepo-Coupe, N.; Ma, X.; Susan Moran, M. Monitoring Photosynthesis From Space. In Land Resources Monitoring, Modeling, and Mapping with Remote Sensing; CRC Press: Boca Raton, FL, USA, 2015; pp. 3–22. [Google Scholar]
- Jafari, A.; Khademi, H.; Finke, P.A.; Van de Wauw, J.; Ayoubi, S. Spatial prediction of soil great groups by boosted regression trees using a limited point dataset in an arid region, southeastern Iran. Geoderma 2014, 232–234, 148–163. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Washington-Allen, R.; Van Niel, T.; Ramsey, R.; West, N. Remote Sensing-Based Piosphere Analysis. GISci. Remote Sens. 2004, 41, 136–154. [Google Scholar] [CrossRef]
- Stohlgren, T.J.; Ma, P.; Kumar, S.; Rocca, M.; Morisette, J.T.; Jarnevich, C.S.; Benson, N. Ensemble habitat mapping of invasive plant species. Risk Anal. 2010, 30, 224–235. [Google Scholar] [CrossRef] [PubMed]
- Lowell, K. A socio-environmental monitoring system for a UNESCO biosphere reserve. Environ. Monit. Assess. 2017, 189, 601. [Google Scholar] [CrossRef] [PubMed]
- Sarker, C.; Alvarez, L.M.; Woodley, A. Integrating Recursive Bayesian Estimation with Support Vector Machine to Map Probability of Flooding from Multispectral Landsat Data. In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications, DICTA 2016, Gold Coast, Australia, 30 November–2 December 2016. [Google Scholar] [CrossRef]
- Walsh, S.J.; Crawford, T.W.; Welsh, W.F.; Crews-Meyer, K.A. A multiscale analysis of LULC and NDVI variation in Nang Rong district, northeast Thailand. Agric. Ecosyst. Environ. 2001, 85, 47–64. [Google Scholar] [CrossRef]
- Gallo, K.P.; Easterling, D.R.; Peterson, T.C. The Influence of Land Use/Land Cover on Climatological Values of the Diurnal Temperature Range. J. Clim. 1996, 9, 2941–2944. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q.Z.; Lei, F.; Du, X.; Wei, J.D. Research on rice acreage estimation in fragmented area based on decomposition of mixed pixels. Remote Sens. Spat. Inf. Sci. 2015, 40, 133. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Scarth, P.F.; McVicar, T.R.; Renzullo, L.J.; Malthus, T.J.; Stewart, J.B.; Rickards, J.E.; Trevithick, R. Assessing the effects of site heterogeneity and soil properties when unmixing photosynthetic vegetation, non-photosynthetic vegetation and bare soil fractions from Landsat and MODIS data. Remote Sens. Environ. 2015, 161, 12–26. [Google Scholar] [CrossRef]
- Adams, J.B.; Sabol, D.E.; Kapos, V.; Almeida Filho, R.; Roberts, D.A.; Smith, M.O.; Gillespie, A.R. Classification of Multispectral Images Based on Fractions of Endmembers: Application to Land-Cover Change in the Brazilian Amazon. Remote Sens. Environ. 1995, 52, 137–154. [Google Scholar] [CrossRef]
- Roberts, D.A.; Smith, M.A.J. Green vegetation, nonphotosynthetic vegetation, and soils in AVIRIS data. Remote Sens. Environ. 1993, 44, 255–269. [Google Scholar] [CrossRef]
- Tane, Z.; Roberts, D.; Veraverbeke, S.; Casas, Á.; Ramirez, C.; Ustin, S. Evaluating Endmember and Band Selection Techniques for Multiple Endmember Spectral Mixture Analysis using Post-Fire Imaging Spectroscopy. Remote Sens. 2018, 10, 389. [Google Scholar] [CrossRef]
- Scarth, P.F.; Röder, A.; Schmidt, M. Tracking Grazing pressure and climate interaction—The Role of Landsat Fractional Cover in time series analysis. In Proceedings of the 15th Australasian Remote Sensing and Photogrammetry Conference, Alice Springs, Australia, 13–17 September 2010; p. 13. [Google Scholar] [CrossRef]
- Scanlon, T.M.; Albertson, J.D.; Caylor, K.K.; Williams, C.A. Determining land surface fractional cover from NDVI and rainfall time series for a savanna ecosystem. Remote Sens. Environ. 2002, 82, 376–388. [Google Scholar] [CrossRef]
- Held, A.; Phinn, S.; Soto-Berelov, M.; Jones, S. AusCover Good Practice Guidelines: A Technical Handbook Supporting Calibration and Validation Activities of Remotely Sensed Data Product; Version 1.2; TERN AusCover: Taipei, Taiwan, 2015. [Google Scholar]
- Trevithick, R.; Soto-Berelov, M.; Jones, S.; Held, A.; Phinn, S.; Armston, J.; Bradford, M.; Broomhall, M.; Cabello, A.; Chisholm, L.; et al. AusCover Good Practice Guidelines: A Technical Handbook Supporting Calibration and Validation Activities of Remotely Sensed Data Products; Version 1.1; TERN AusCover: Taipei, Taiwan, 2015. [Google Scholar]
- Muir, J.; Schmidt, M.; Tindall, D.; Trevithick, R.; Scarth, P.; Stewart, J. Field Measurement of Fractional Ground Cover: A Technical Handbook Supporting Ground Cover Monitoring for Australia; Queensland Department of Environment and Resource Management for the Australian Bureau of Agricultural and Resource Economics and Sciences: Brisbane, Australia, 2011.
- Bastin, G.; Scarth, P.; Chewings, V.S.A.; Denham, R.; Schmidt, M.; O’Reagain, P.; Shepherd, R.; Abbot, B. Dynamic reference cover method to separate grazing and rainfall effects on rangeland ground cover. Remote Sens. Environ. 2012, 121, 443–457. [Google Scholar] [CrossRef]
- Carroll, C.; Waters, D.; Vardy, S.; Silburn, M.; Attard, S.; Thorburn, P.; Davis, A.; Halpin, N.; Schmidt, M.; Wilson, B.; et al. A Paddock to reef monitoring and modelling framework for the Great Barrier Reef: Paddock and catchment component. Mar. Pollut. Bull. 2012, 65, 136–149. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Amler, E.; Guerschmann, J.P.; Scarth, P.B.K.; Thonfeld, F. Fractional Vegetation Cover of East African Wetlands Observed on Ground and from Space; European Space Agency: Paris, France, 2016. [Google Scholar]
- Cressie, N.A. Change of Support and The Modifiable Areal Unit Problem. Geogr. Syst. 1996, 3, 159–180. [Google Scholar]
- Ershadi, A.; McCabe, M.; Evans, J.; Walker, J. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Schucknecht, A.; Meroni, M.; Kayitakire, F.; Boureima, A. Phenology-Based Biomass Estimation to Support Rangeland Management in Semi-Arid Environments. Remote Sens. 2017, 9, 463. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Paruelo, J.M.; Lauenroth, W.K. Relative Abundance of Plant Functional Types in Grasslands and Shrublands of North America. Ecol. Appl. 1996, 6, 1212–1224. [Google Scholar] [CrossRef]
- McNab, W.H.; Lloyd, F.T. Testing Ecoregions in Kentucky and Tennessee with Satellite Imagery and Forest Inventory Data. In Proceedings of the Forest Inventory and Analysis (FIA) Symposium, Fort Collins, CO, USA, 21–23 October 2008. [Google Scholar]
- Chen, H. Köppen Climate Classification. Available online: http://hanschen.org/koppen (accessed on 10 August 2018).
- Bureau of Meteorology. Climate Classification of Australia; Bureau of Meteorology: Melbourne, Australia, 2016.
- Australia, G. Fractional Cover (FC25) Product Description; Technical Report; Australian Government: Canberra, Australia, 2015.
- Scarth, P.; Byrne, M.; Danaher, T.; Henry, B.; Hassett, R.; Carter, J.; Timmers, P. State of the paddock: monitoring condition and trend in groundcover across Queensland. In Proceedings of the 13th Australasian Remote Sensing and Photogrammetry Conference (ARSPC), Canberra, Australia, 21–24 November 2006; p. 11. [Google Scholar]
- Friedman, J.H. Recent Advances in Predictive ( Machine) Learning. J. Classif. 2001, 23, 175–197. [Google Scholar] [CrossRef]
- Ridgeway, G. Generalized Boosted Models: A Guide to the Gbm Package. Available online: https://pdfs.semanticscholar.org/a3f6/d964ac323b87d2de3434b23444cb774a216e.pdf (accessed on 10 August 2018).
- Robinzonov, N. Advances in Boosting of Temporal and Spatial Models. Ph.D. Thesis, Ludwig -Maximilians-Universität München, Munich, Germany, 2013. [Google Scholar]
- Tarling, R. Statistical Modelling for Social Researchers: Principles and Practice; Taylor & Francis Group: London, UK; New York, NY, USA, 2009. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 103, pp. 856–875. [Google Scholar]
- Breiman, L. Arcing classifiers. Ann. Stat. 1998, 26, 801–849. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer Series in Statistics: New York, NY, USA, 2009; pp. 337–387. [Google Scholar]
- Matteson, A. Boosting the accuracy of your Machine Learning Models. Available online: https://www.datasciencecentral.com/profiles/blogs/boosting-the-accuracy-of-your-machine-learning-models (accessed on 10 August 2018).
- Kuhn, M. The caret Package. J. Stat. Softw. 2008, 5, 1–10. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Adams, M. Generalized Boosted Models: A Guide to the Gbm Package. Available online: https://cran.r-project.org/web/packages/lm.br/index.html (accessed on 10 August 2018).
- Colin, B.; Clifford, S.; Wu, P.; Rathmanner, S.; Mengersen, K. Using Boosted Regression Trees and Remotely Sensed Data to Drive Decision-Making. Open J. Stat. 2017, 7, 859–875. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Landslide susceptibility mapping using a modified decision tree classifier in the Xanthi Perfection, Greece. Landslides 2016, 13, 305–320. [Google Scholar] [CrossRef]
- Kotta, J.; Kutser, T.; Teeveer, K.; Vahtmäe, E.; Pärnoja, M. Predicting Species Cover of Marine Macrophyte and Invertebrate Species Combining Hyperspectral Remote Sensing, Machine Learning and Regression Techniques. PLoS ONE 2013, 8, e63946. [Google Scholar] [CrossRef] [PubMed]
- Pittman, S.J.; Costa, B.M.; Battista, T.A. Using Lidar Bathymetry and Boosted Regression Trees to Predict the Diversity and Abundance of Fish and Corals. J. Coast. Res. 2009, 10053, 27–38. [Google Scholar] [CrossRef]
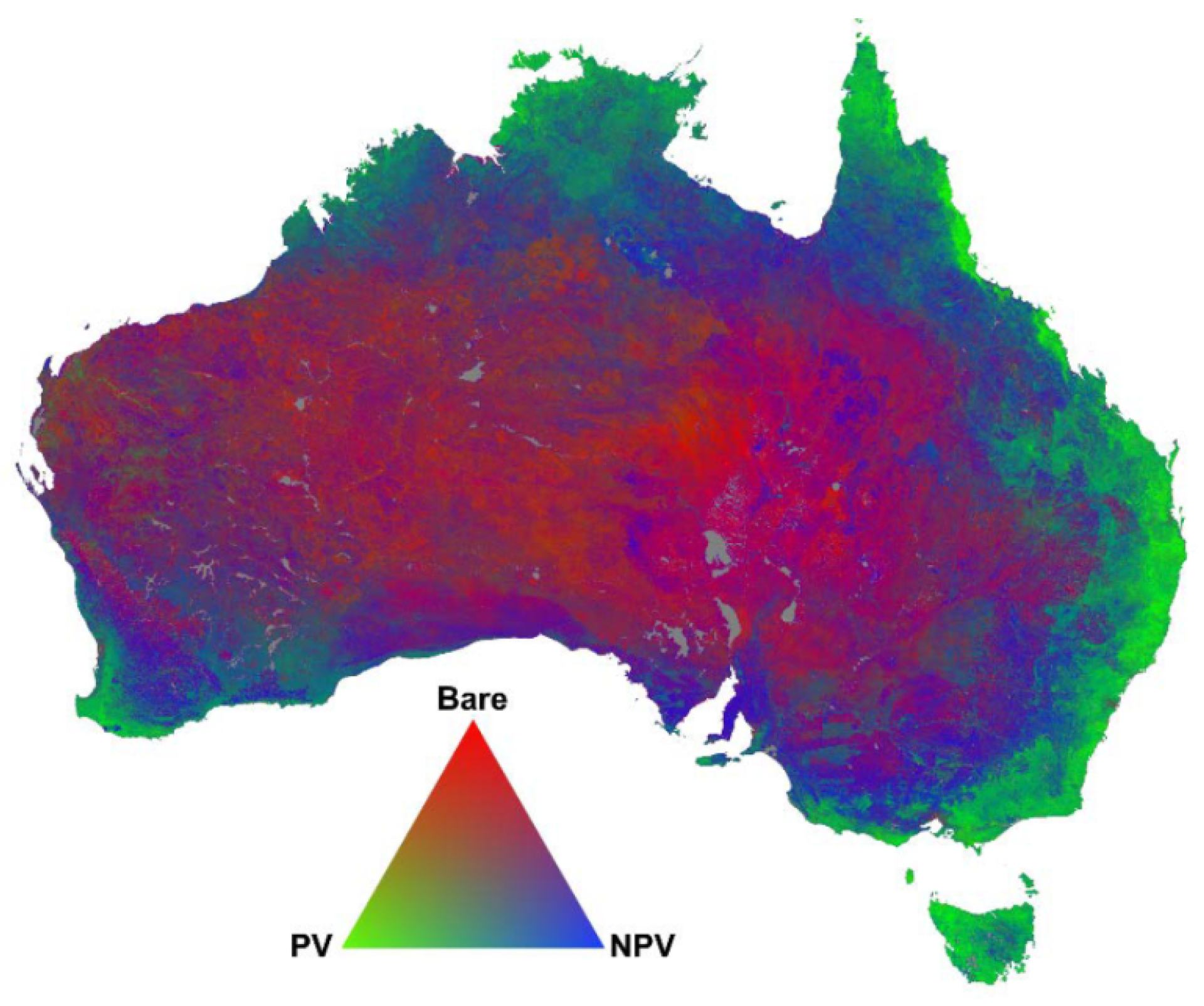
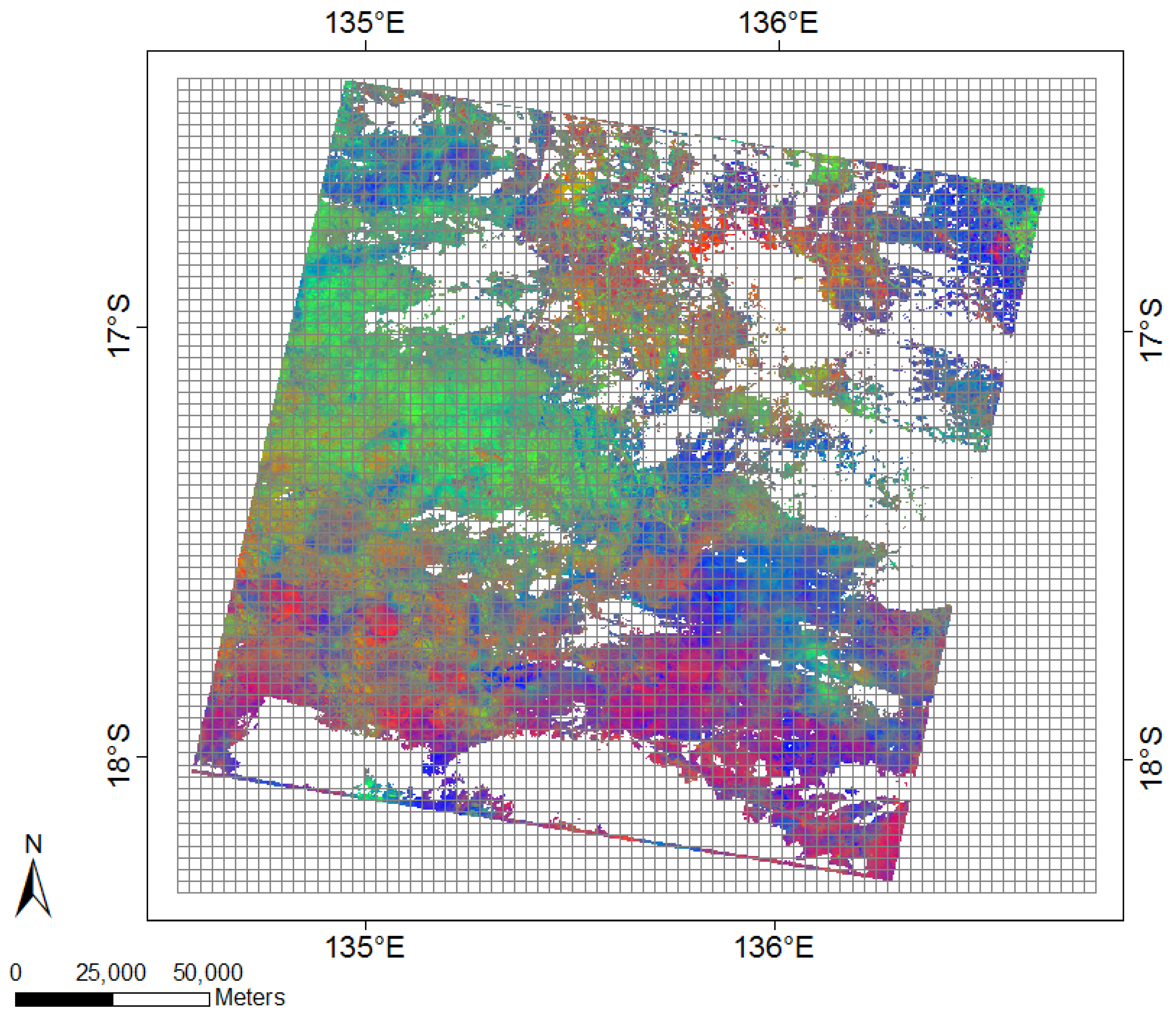
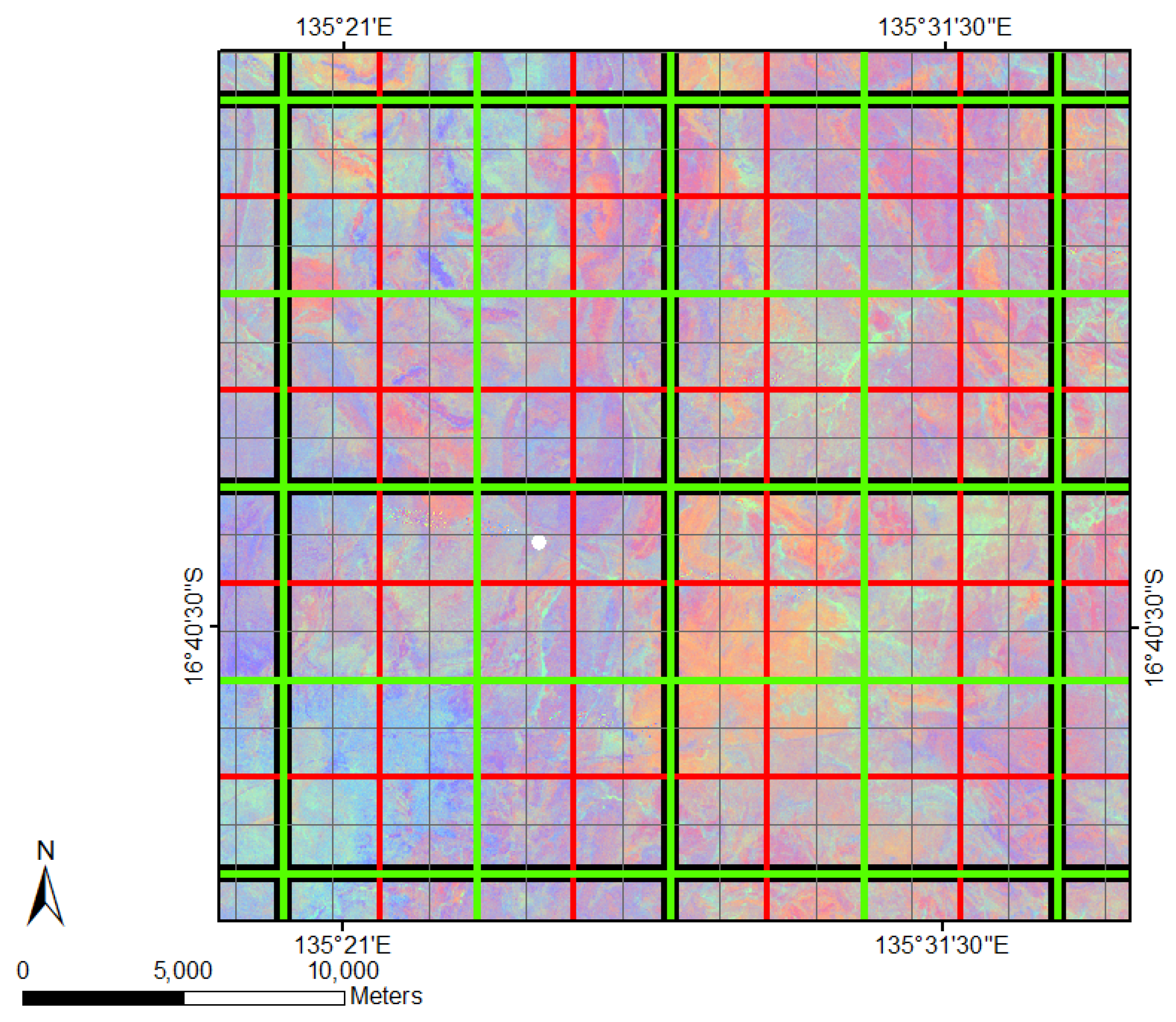
| Spatial Resolution (m) | Number of Pixels in Grid Each Cell | Ground Covered by Each Grid Cell (m) | Total Number of Grid Cells | Coloured Outline of Spatial Grids |
|---|---|---|---|---|
| original | 1 × 1 | 30 × 30 | 54 million | FCover pixel |
| 12,000 | 400 × 400 | 12,000 × 12,000 | 360 | black |
| 6000 | 200 × 200 | 6000 × 6000 | 1400 | green |
| 3000 | 100 × 100 | 3000 × 3000 | 5530 | red |
| 1500 | 50 × 50 | 1500 × 1500 | 21,980 | grey |
| Spatial Resolution (m) | Number of Grid Cells in Overlay | Length of Aggregated Response Variable |
|---|---|---|
| 12,000 | 360 | 360 |
| 6000 | 1400 | 1400 |
| 3000 | 5530 | 5530 |
| 1500 | 21,980 | 21,980 |
| Spatial Resolution (m) | Year | RMSE |
|---|---|---|
| 12,000 | 1987 | 3.0583 |
| 1988 | 3.9691 | |
| 1989 | 3.0056 | |
| 1990 | 1.6151 | |
| 6000 | 1987 | 2.8583 |
| 1988 | 3.1428 | |
| 1989 | 3.1591 | |
| 1990 | 1.9577 | |
| 3000 | 1987 | 3.1120 |
| 1988 | 3.2134 | |
| 1989 | 3.1543 | |
| 1990 | 2.0731 | |
| 1500 | 1987 | 3.4241 |
| 1988 | 3.8306 | |
| 1989 | 3.4500 | |
| 1990 | 2.3348 |
| Spatial Resolution (m) | 1988 | 1990 | ||
|---|---|---|---|---|
| Linear Model | BRT | Linear Model | BRT | |
| 12,000 | 4.0551 | 3.9691 | 2.7933 | 1.6151 |
| 6000 | 4.9710 | 3.1428 | 3.0449 | 1.9577 |
| 3000 | 5.3688 | 3.2134 | 3.3028 | 2.0731 |
| 1500 | 5.5863 | 3.8306 | 3.5676 | 2.3348 |
| Spatial Resolution (m) | Mean Absolute Error (Worst/Best) | Median Absolute Error (Worst/Best) |
|---|---|---|
| 12,000 | 2.752/1.236 | 2.236/0.836 |
| 6000 | 2.370/1.500 | 1.909/1.185 |
| 3000 | 2.489/1.613 | 2.053/1.305 |
| 1500 | 2.925/1.808 | 2.398/1.467 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colin, B.; Schmidt, M.; Clifford, S.; Woodley, A.; Mengersen, K. Influence of Spatial Aggregation on Prediction Accuracy of Green Vegetation Using Boosted Regression Trees. Remote Sens. 2018, 10, 1260. https://doi.org/10.3390/rs10081260
Colin B, Schmidt M, Clifford S, Woodley A, Mengersen K. Influence of Spatial Aggregation on Prediction Accuracy of Green Vegetation Using Boosted Regression Trees. Remote Sensing. 2018; 10(8):1260. https://doi.org/10.3390/rs10081260
Chicago/Turabian StyleColin, Brigitte, Michael Schmidt, Samuel Clifford, Alan Woodley, and Kerrie Mengersen. 2018. "Influence of Spatial Aggregation on Prediction Accuracy of Green Vegetation Using Boosted Regression Trees" Remote Sensing 10, no. 8: 1260. https://doi.org/10.3390/rs10081260
APA StyleColin, B., Schmidt, M., Clifford, S., Woodley, A., & Mengersen, K. (2018). Influence of Spatial Aggregation on Prediction Accuracy of Green Vegetation Using Boosted Regression Trees. Remote Sensing, 10(8), 1260. https://doi.org/10.3390/rs10081260