Maximizing the Information Content of Ill-Posed Space-Based Measurements Using Deterministic Inverse Method
Abstract
1. Introduction
2. Methodology
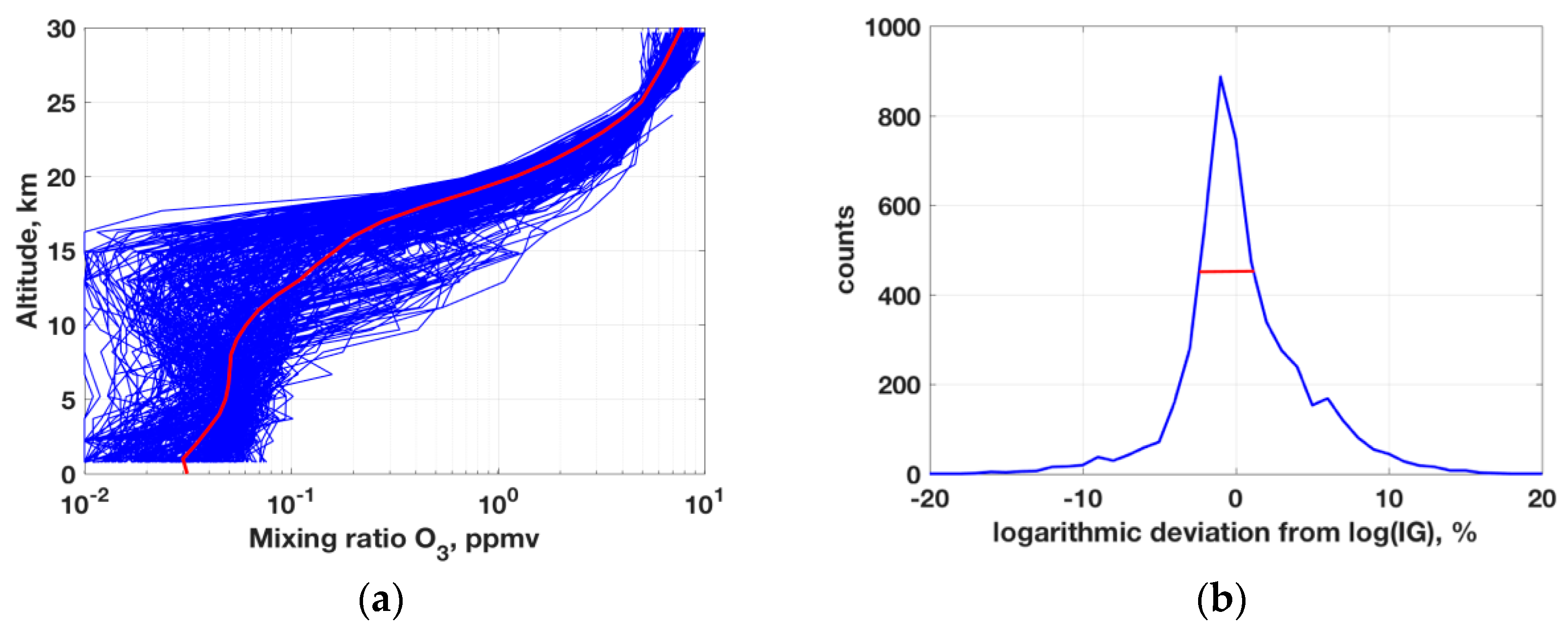
3. Simulated Theoretical Smooth Profile Retrieval
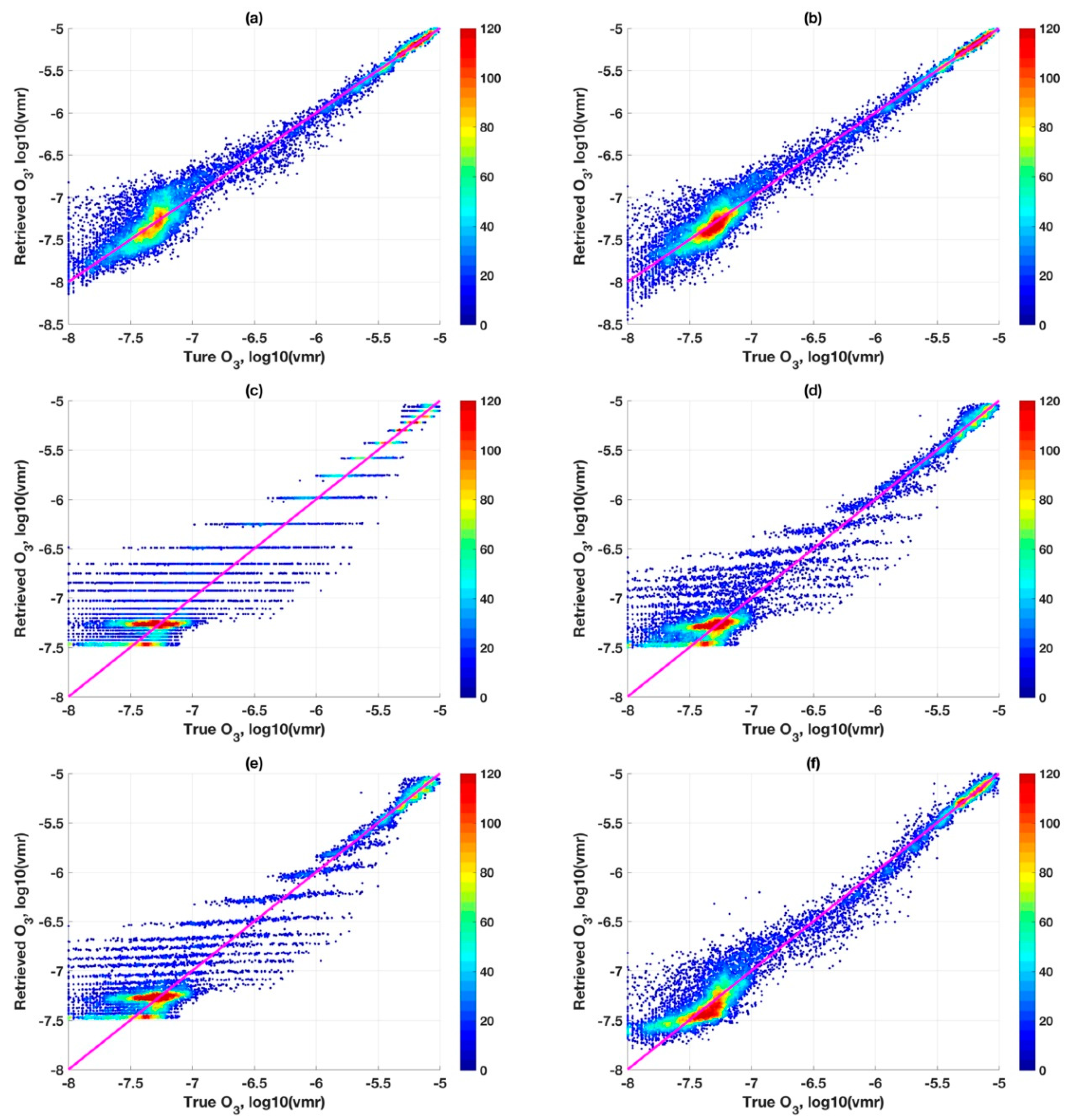
3.1. Profile Retrievals from Simulated CrIS Measuremts
3.2. Profile Retrievals from Simulated TES Measuremts
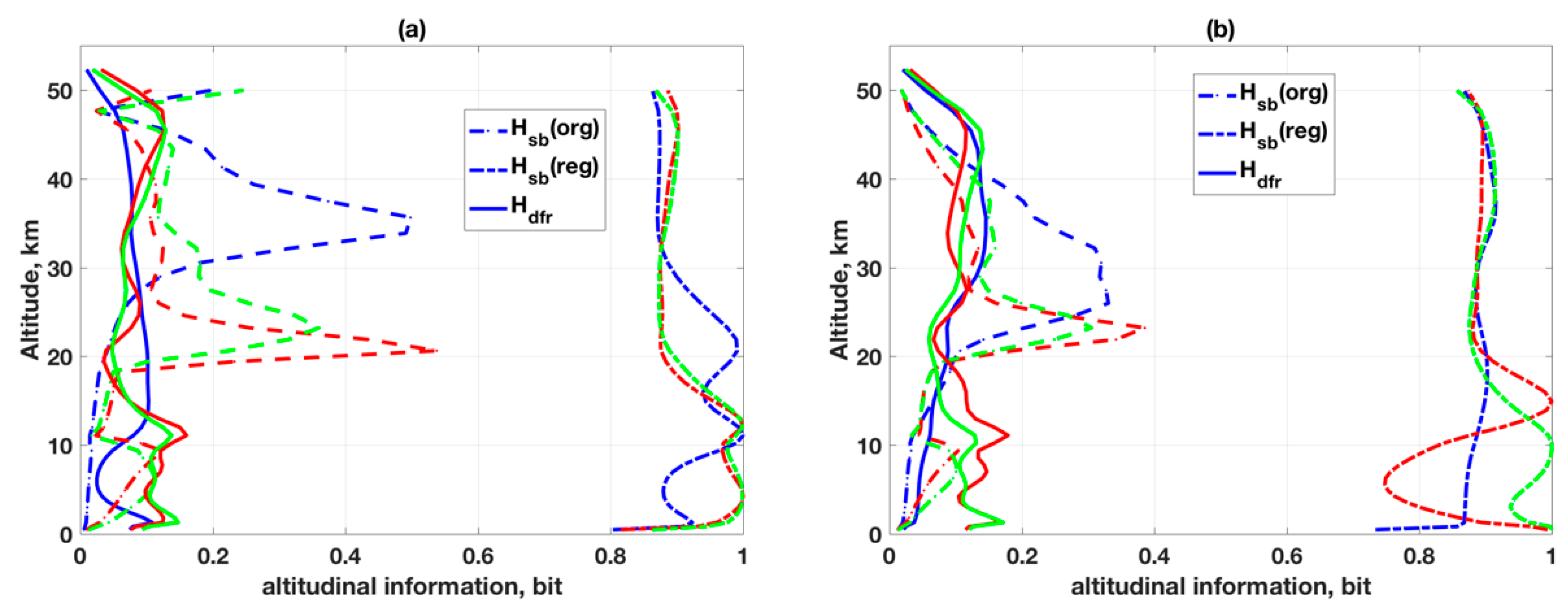
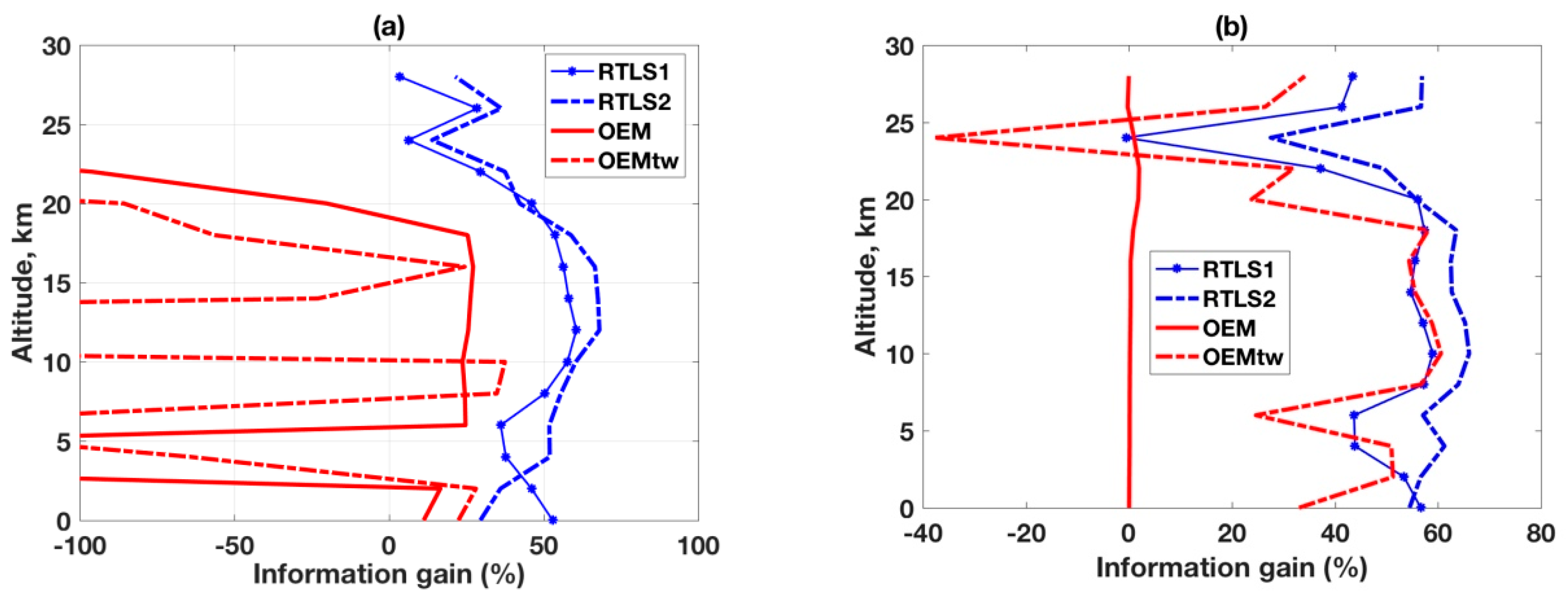
3.3. Information Content Analysis Using Subspace
4. Simulated Profile Retrievals Using Radiosonde Data
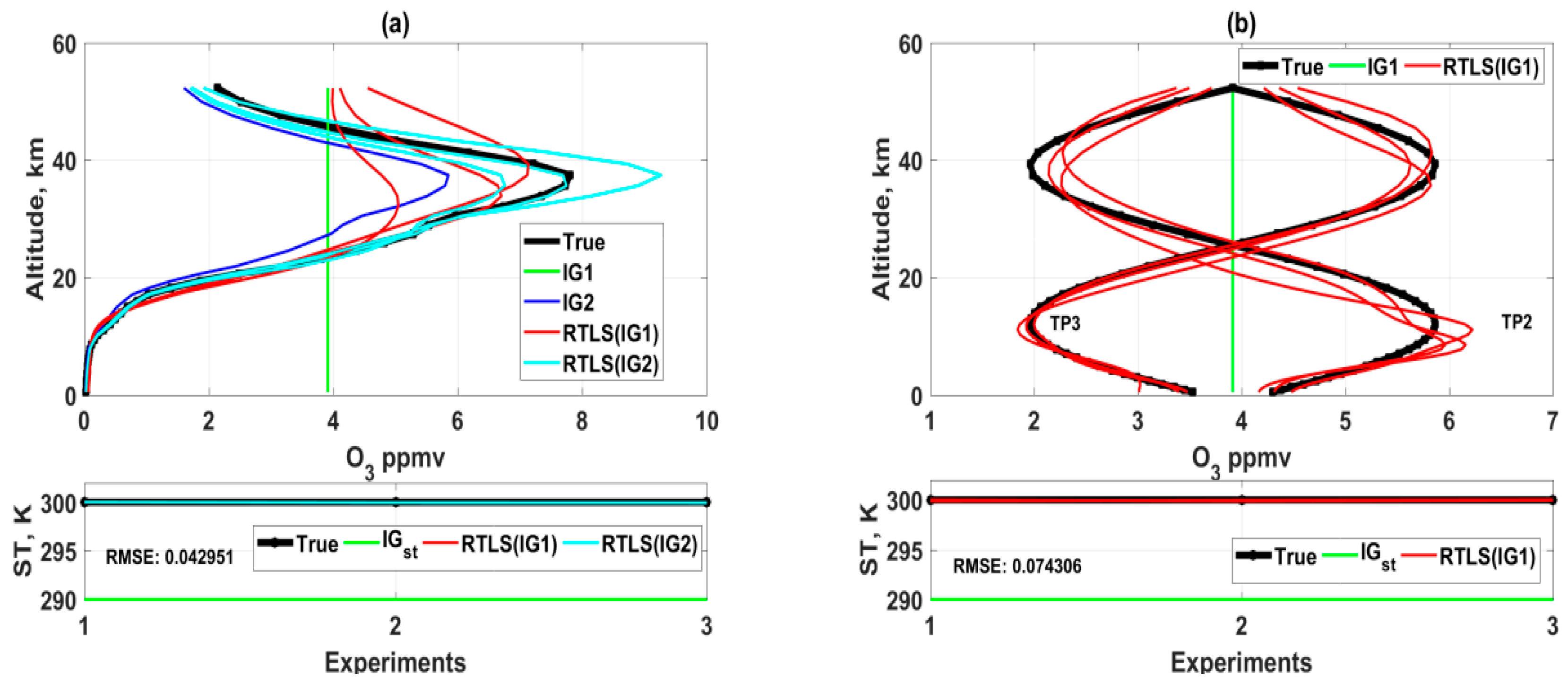
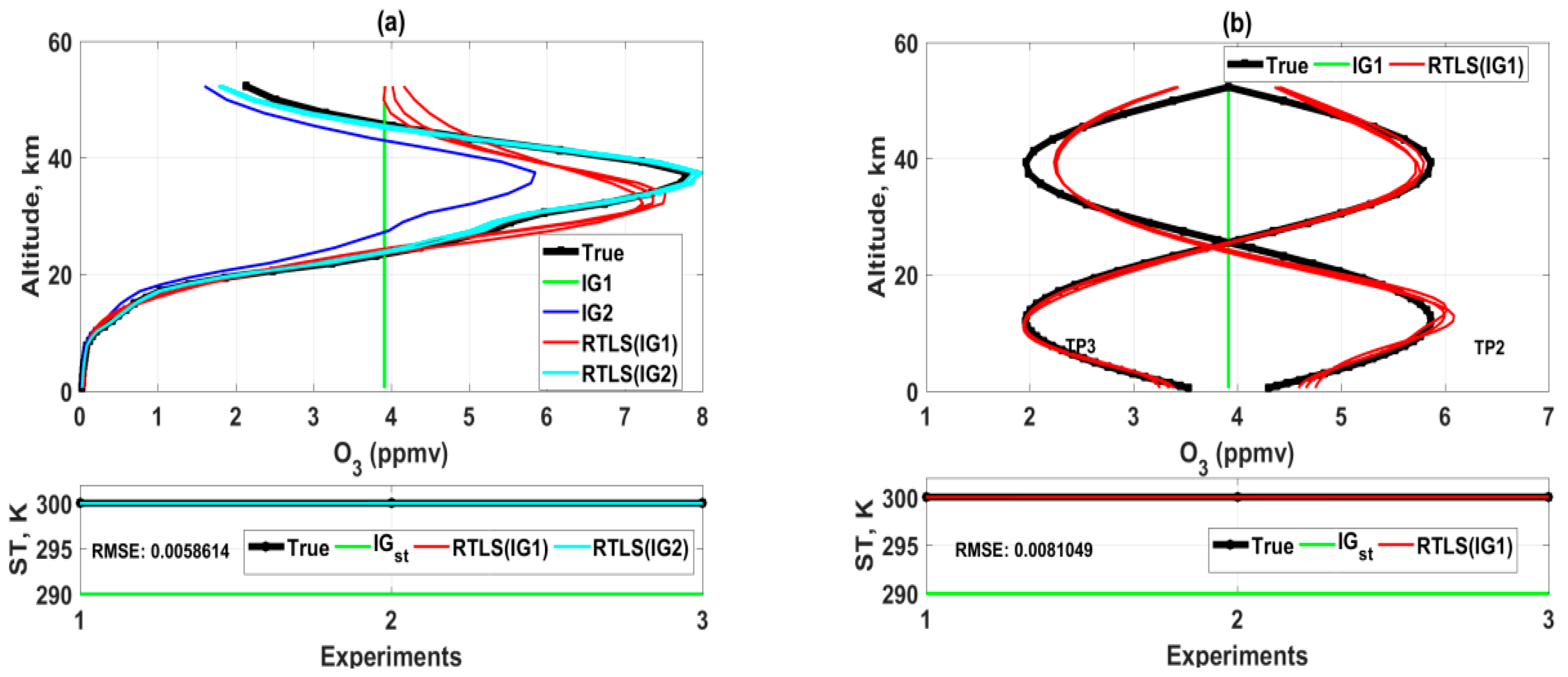
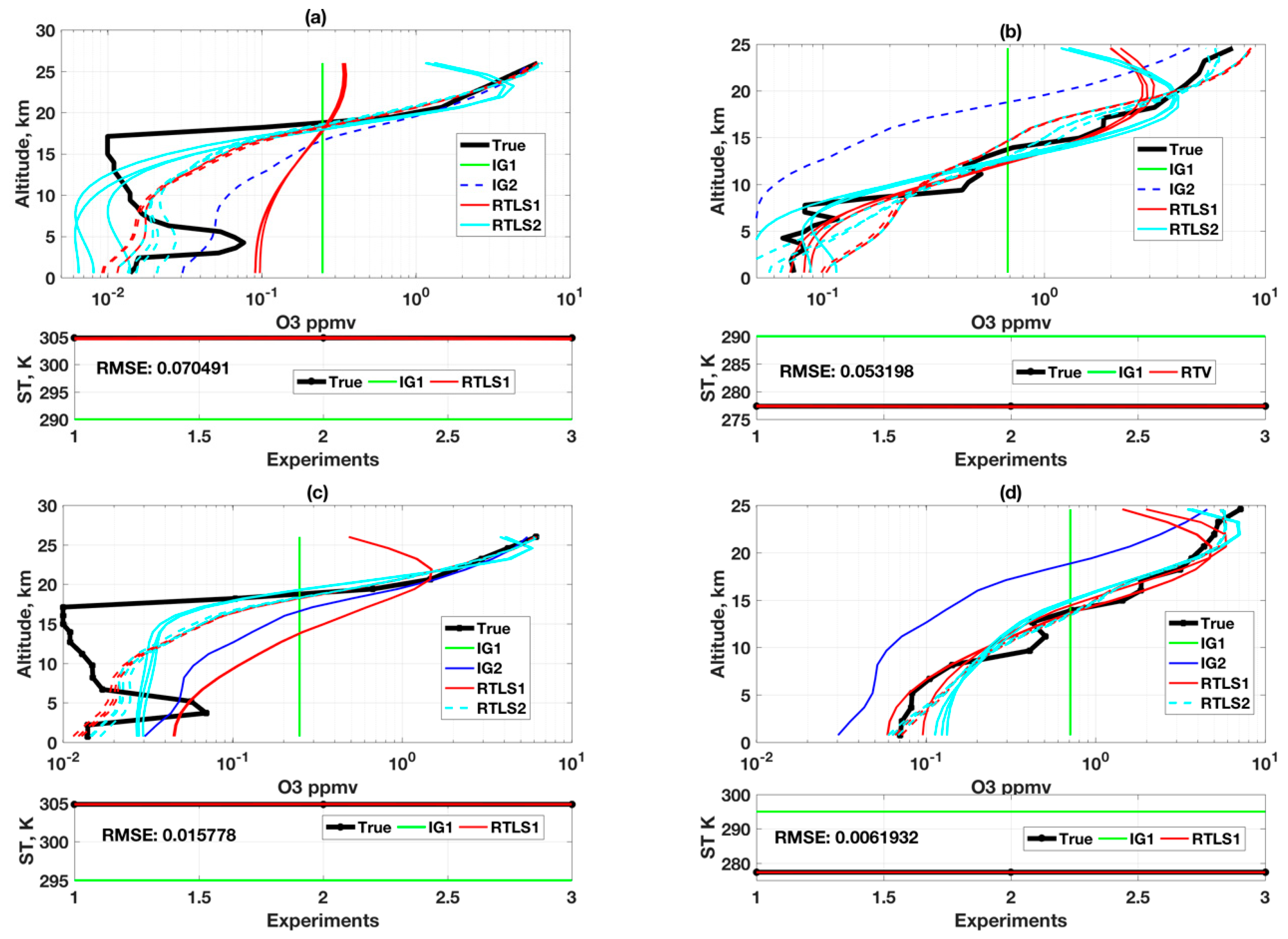
4.1. Profile Retrievals Using RTLS
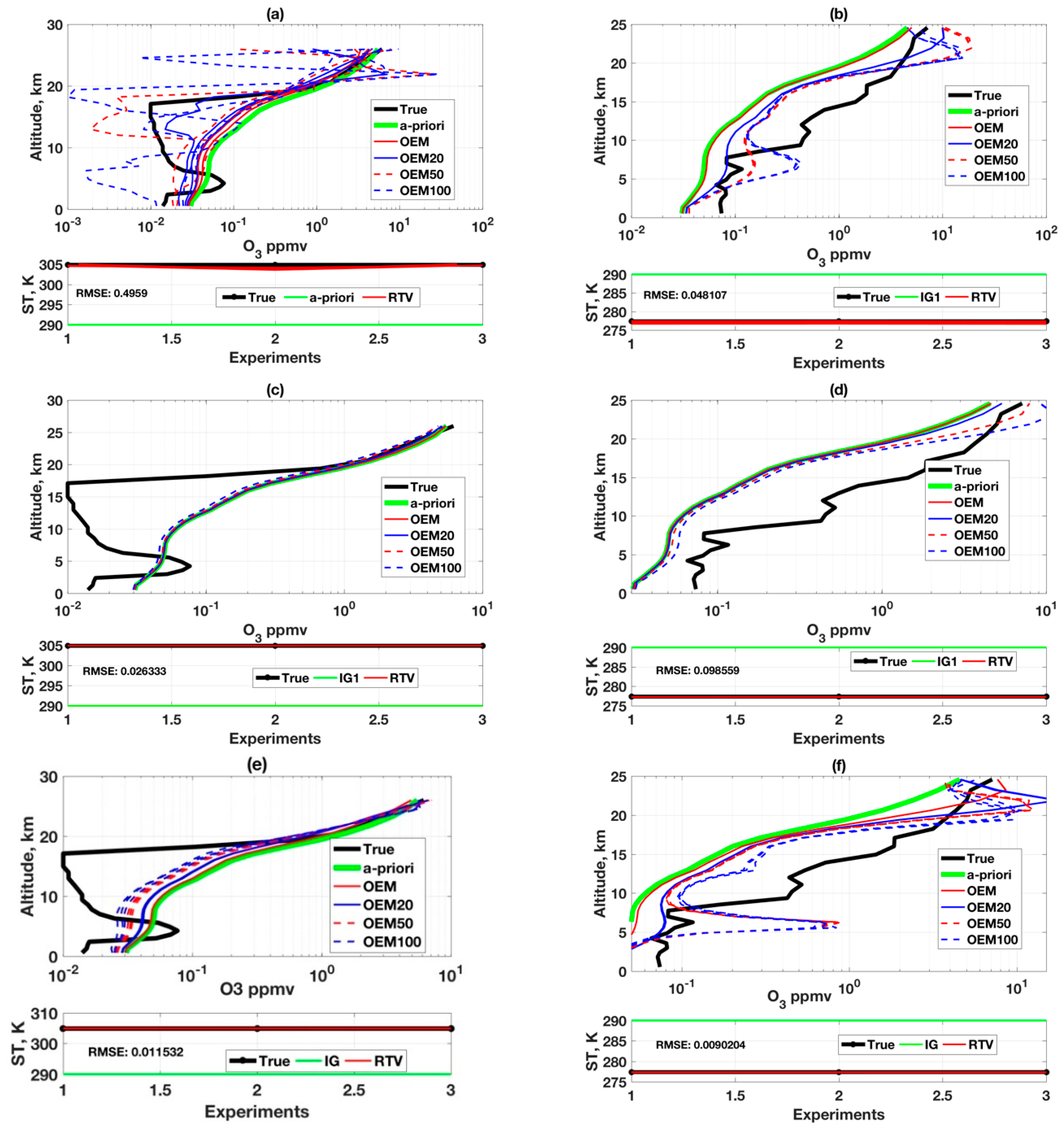
4.2. Profile Retrievals Using OEM
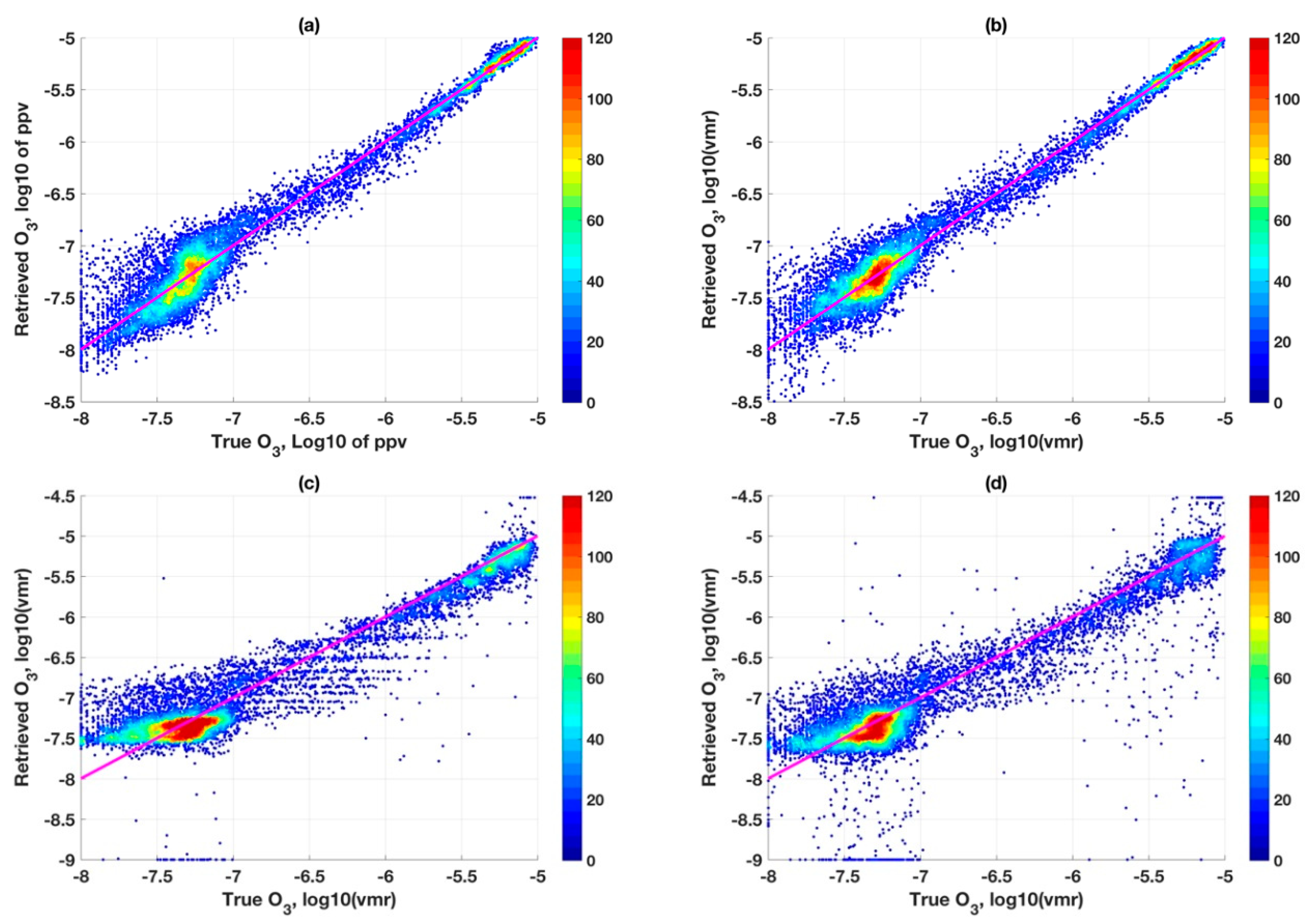
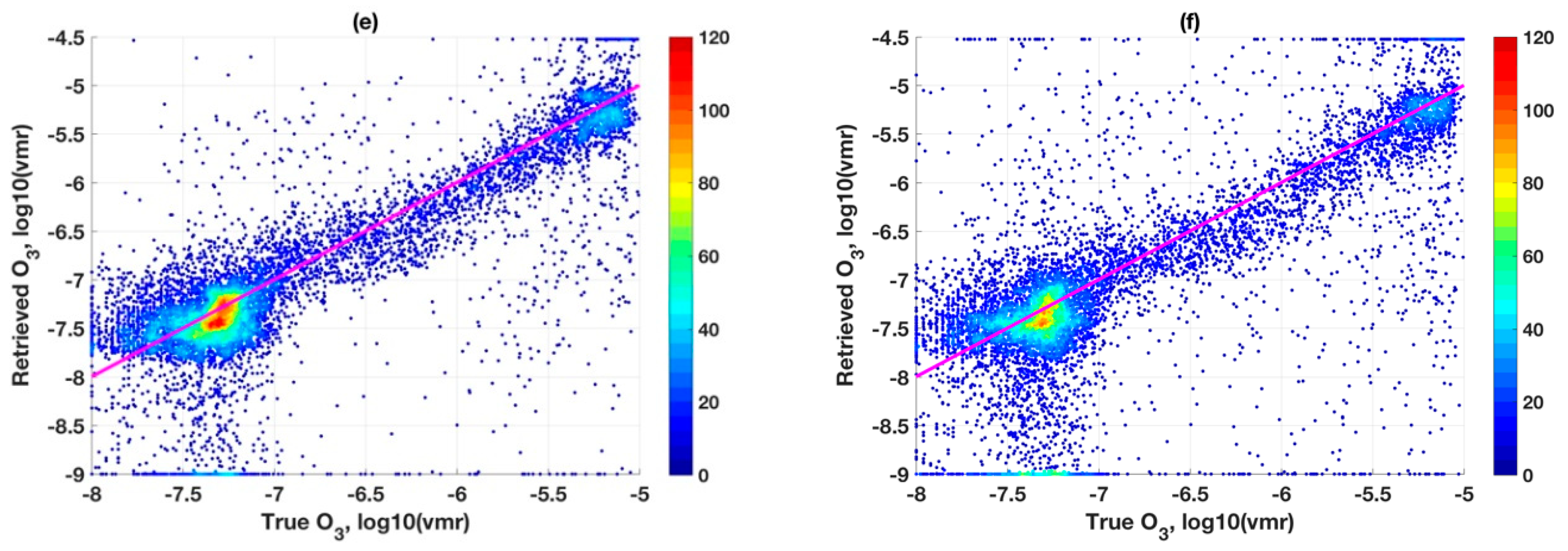
4.3. Comparative Retrievals for CrIS
4.4. Comparative Retrievals Results for TES
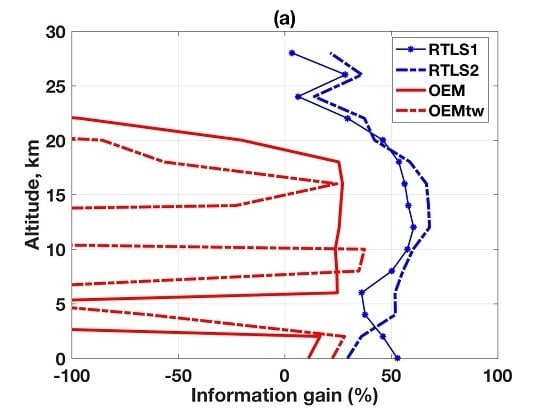
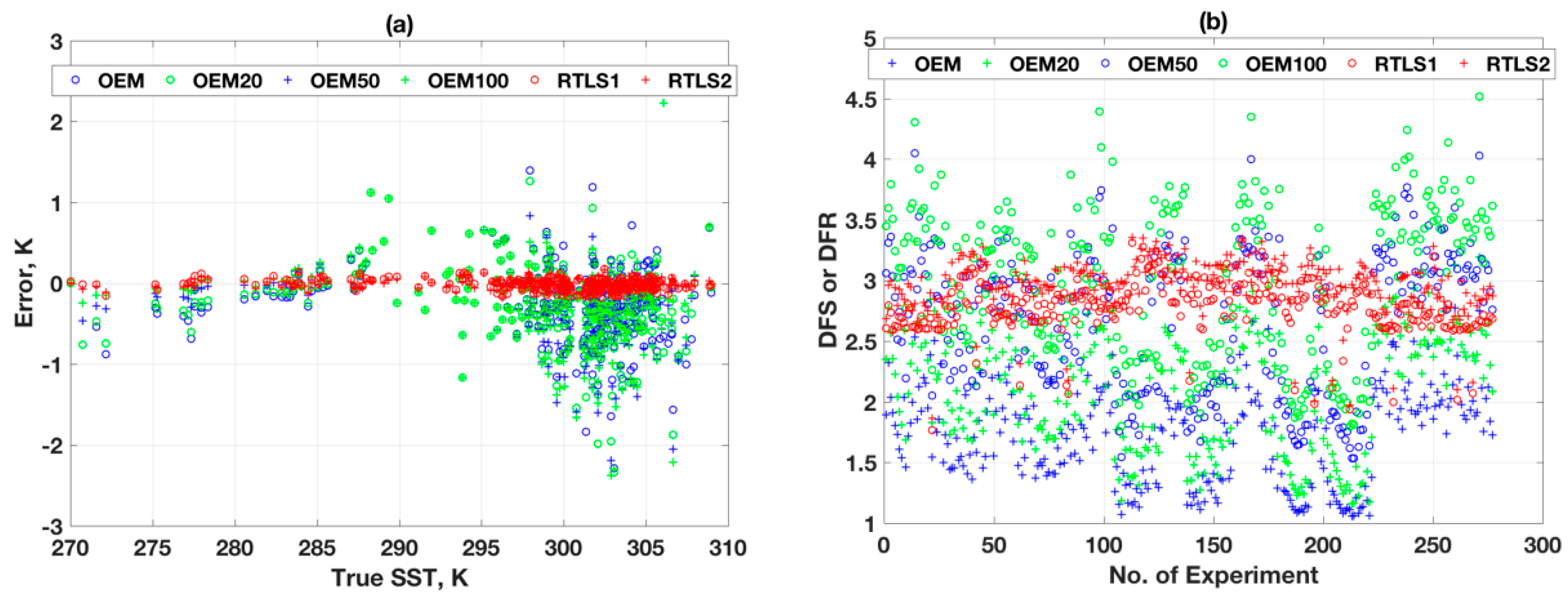
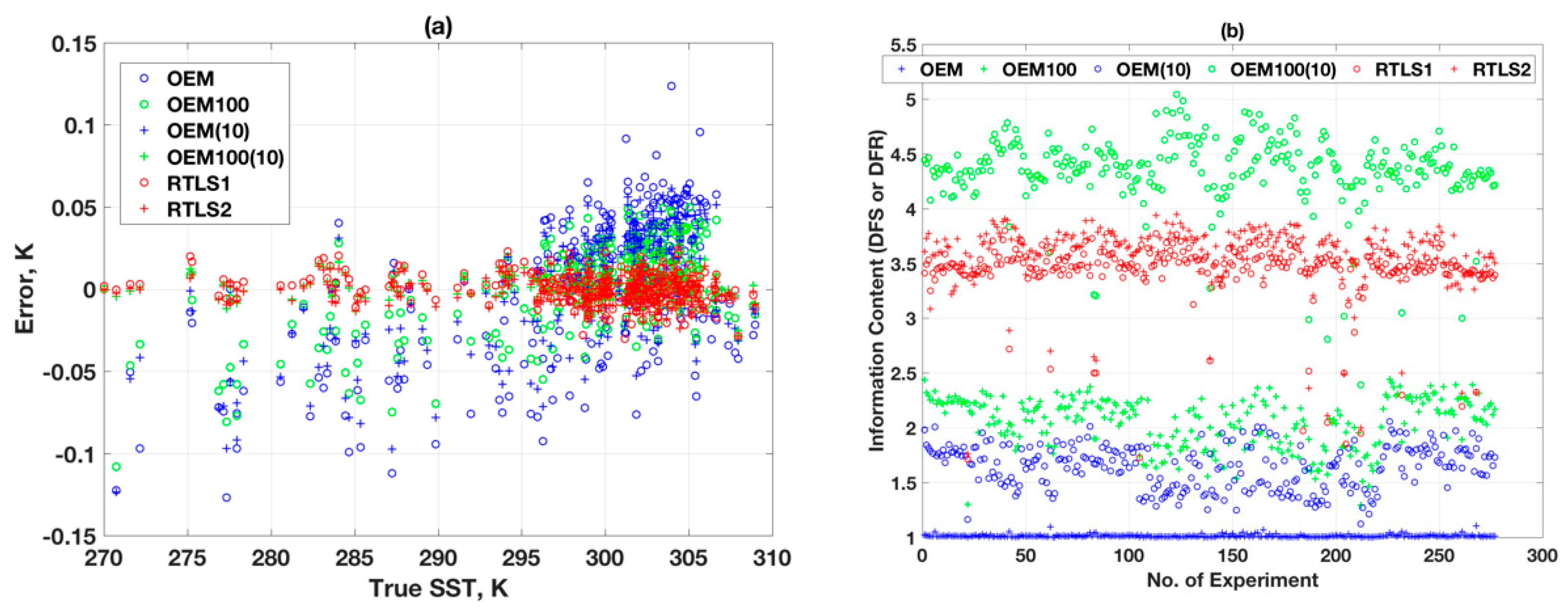
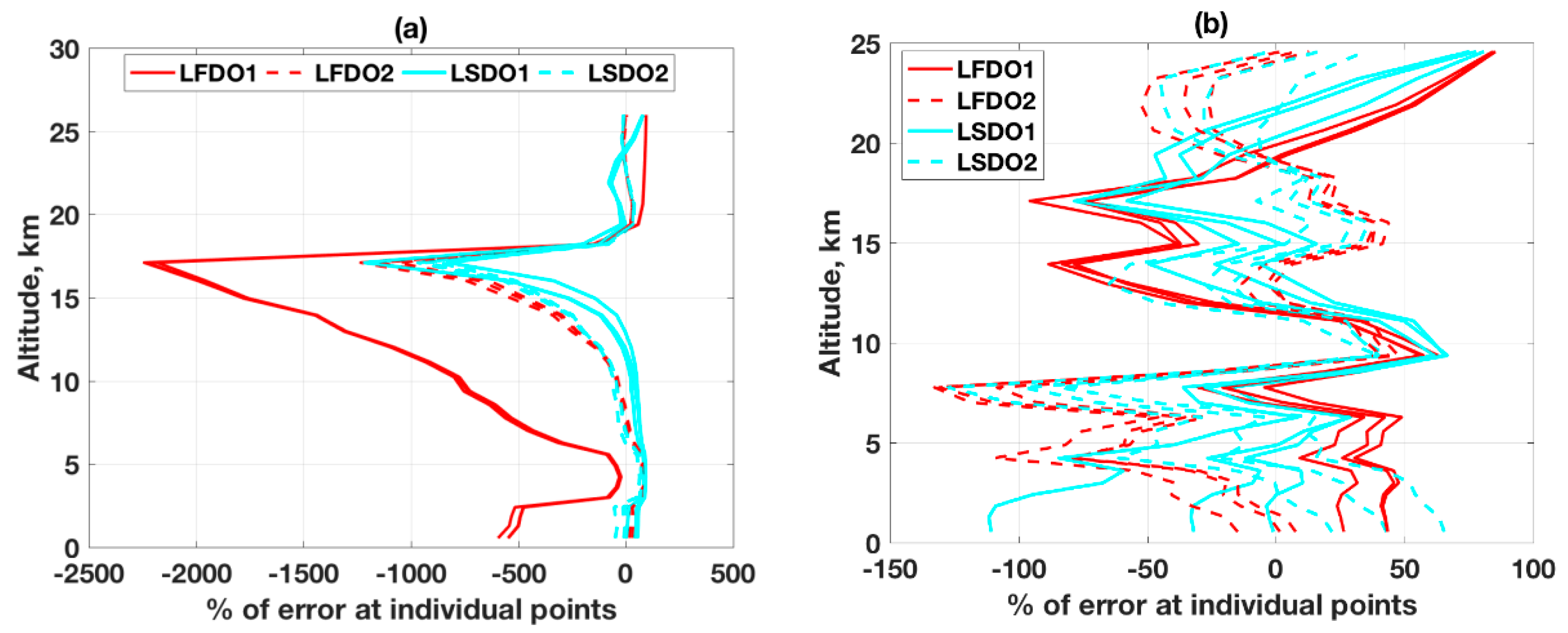
4.5. Comparative Error Analysis between Both Sensors and Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| ACE-FTS | Atmospheric Chemistry Experiment-Fourier Transform Spectrometer. |
| AIRS | Atmospheric InfraRed Sounder. |
| GOME | Global Ozone Monitoring Experiment. |
| IASI | Infrared Atmospheric Sounding Interferometer. |
| MIPAS | Michelson Interferometer for Passive Atmospheric Sounding. |
| MLS | Microwave Limb Sounder. |
| OMI | Ozone Monitoring Instrument. |
| OMPS | Ozone Mapping Profiler Suite. |
| TOMS | Total Ozone Mapping Spectrometer. |
| SBUV | Solar Backscatter Ultraviolet Radiometer. |
| SCIAMACHY | SCanning Imaging Absorption SpectroMeter for Atmospheric CHartographY. |
References
- Van Peet, J.C.; van der, A.R.J.; Wolfram, E.; Salvador, J.; Levelt, P.F.; Kelder, H.M. Ozone ProfilE Retrieval Algorithm (OPERA) for nadir-looking satellite instruments in the UV–VIS. Atmos. Meas. Tech. 2014, 7, 859–876. [Google Scholar] [CrossRef]
- Pittman, J.V.; Pan, L.L.; Wei, J.C.; Irion, F.W.; Liu, X.; Maddy, E.S.; Barnet, C.D.; Chance, K.; Gao, R.S. Evaluation of AIRS, IASI, and OMI ozone profile retrievals in the extratropical tropopause region using in situ aircraft measurements. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- McPeters, R.D.; Labow, G.J.; Logan, J.A. Ozone climatological profiles for satellite retrieval algorithms. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Arosio, C.; Rozanov, A.; Malinina, E.; Eichmann, K.U.; von Clarmann, T.; Burrows, J.P. Retrieval of ozone profiles from OMPS limb scattering observations. Atmos. Meas. Tech. 2018, 11, 2135–2149. [Google Scholar] [CrossRef]
- Boynard, A.; Clerbaux, C.; Coheur, P.F.; Hurtmans, D.; Turquety, S.; George, M.; Hadji-Lazaro, J.; Keim, C.; Meyer-Arnek, J. Measurements of total and tropospheric ozone from IASI: Comparison with correlative satellite, ground-based and ozonesonde observations. Atmos. Chem. Phys. 2009, 9, 6255–6271. [Google Scholar] [CrossRef]
- Oetjen, H.; Payne, V.H.; Kulawik, S.S.; Eldering, A.; Worden, J.; Edwards, D.P.; Francis, G.L.; Worden, H.M.; Clerbaux, C.; Hadji-Lazaro, J.; et al. Extending the satellite data record of tropospheric ozone profiles from Aura-TES to MetOp-IASI: Characterisation of optimal estimation retrievals. Atmos. Meas. Tech. 2014, 7, 4223–4236. [Google Scholar] [CrossRef]
- Ebojie, F.; von Savigny, C.; Ladstätter-Weißenmayer, A.; Rozanov, A.; Weber, M.; Eichmann, K.U.; Bötel, S.; Rahpoe, N.; Bovensmann, H.; Burrows, J.P. Tropospheric column amount of ozone retrieved from SCIAMACHY limb–nadir-matching observations. Atmos. Meas. Tech. 2014, 7, 2073–2096. [Google Scholar] [CrossRef]
- Hasekamp, O.P.; Landgraf, J. Ozone profile retrieval from backscattered ultraviolet radiances: The inverse problem solved by regularization. J. Geophys. Res. Atmos. 2001, 106, 8077–8088. [Google Scholar] [CrossRef]
- Worden, H.M.; Logan, J.A.; Worden, J.R.; Beer, R.; Bowman, K.; Clough, S.A.; Eldering, A.; Fisher, B.M.; Gunson, M.R.; Herman, R.L.; et al. Comparisons of Tropospheric Emission Spectrometer (TES) ozone profiles to ozonesondes: Methods and initial results. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Mead, J.L. Parameter estimation: A new approach to weighting a priori information. J. Inverse Ill-Posed Probl. 2007, 15, 1–21. [Google Scholar]
- Zhang, R.; Sen, M.K.; Phan, S.; Srinivasan, S. Stochastic and deterministic seismic inversion methods for thin-bed resolution. J. Geophys. Eng. 2012, 9, 611–618. [Google Scholar] [CrossRef]
- Aguilo, M.A.; Swiler, L.P.; Urbina, A. An overview of inverse material identification within the frameworks of deterministic and stochastic parameter estimation. Int. J. Uncertain. Quantif. 2013, 3, 289–319. [Google Scholar] [CrossRef]
- Koner, P.K.; Harris, A.R.; Dash, P. A Deterministic Method for Profile Retrievals from Hyperspectral Satellite Measurements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5657–5670. [Google Scholar] [CrossRef]
- Koner, P.K.; Battaglia, A.; Simmer, C. A rain-rate retrieval algorithm for attenuated radar measurements. J. Appl. Meteorol. Climatol. 2010, 49, 381–393. [Google Scholar] [CrossRef]
- Koner, P.K.; Drummond, J.R. A comparison of regularization techniques for atmospheric trace gases retrievals. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 514–526. [Google Scholar] [CrossRef]
- Koner, P.K.; Drummond, J.R. Atmospheric trace gases profile retrievals using the nonlinear regularized total least squares method. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 2045–2059. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the solution of ill-posed problems and the method of regularization. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Xu, J.; Schreier, F.; Doicu, A.; Trautmann, T. Assessment of Tikhonov-type regularization methods for solving atmospheric inverse problems. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 274–286. [Google Scholar] [CrossRef]
- Beck, A.; Ben-Tal, A. On the solution of the Tikhonov regularization of the total least squares problem. SIAM J. Optim. 2006, 17, 98–118. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Golub, G.H.; Hansen, P.C.; O’Leary, D.P. Tikhonov regularization and total least squares. SIAM J. Matrix Anal. Appl. 1999, 21, 185–194. [Google Scholar] [CrossRef]
- Mesarovic, V.Z.; Galatsanos, N.P.; Katsaggelos, A.K. Regularized constrained total least squares image restoration. IEEE Trans. Image Process. 1995, 4, 1096–1108. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Chen, M.; Zhou, J. Adaptively regularized constrained total least-squares image restoration. IEEE Trans. Image Process. 2000, 9, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Mastronardi, N.; Lemmerling, P.; Kalsi, A.; O’Leary, D.P.; Van Huffel, S. Implementation of the regularized structured total least squares algorithms for blind image deblurring. Linear Algebra Appl. 2004, 391, 203–221. [Google Scholar] [CrossRef]
- Fu, H.; Ng, M.K.; Barlow, J.L. Structured total least squares for color image restoration. SIAM J. Sci. Comput. 2006, 28, 1100–1119. [Google Scholar] [CrossRef]
- Lei, J.; Liu, S.; Li, Z.; Schlaberg, H.I.; Sun, M. An image reconstruction algorithm based on the regularized total least squares method for electrical capacitance tomography. Flow Meas. Instrum. 2008, 19, 325–330. [Google Scholar] [CrossRef]
- Koner, P.K.; Harris, A.R.; Maturi, E. A Physical Deterministic Inverse Method for Operational Satellite Remote Sensing: An Application for Sea SurfaceTemperature Retrievals. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5872–5888. [Google Scholar] [CrossRef]
- Koner, P.K.; Harris, A.R.; Maturi, E. Hybrid cloud and error masking to improve the quality of deterministic satellite sea surface temperature retrieval and data coverage. Remote Sens. Environ. 2016, 174, 266–278. [Google Scholar] [CrossRef]
- Koner, P.K.; Harris, A.R. Improved quality of MODIS sea surface temperature retrieval and data coverage using physical deterministic methods. Remote Sens. 2016, 8, 454. [Google Scholar] [CrossRef]
- Koner, P.K.; Harris, A.R. Sea Surface Temperature Retrieval from MODIS Radiances Using Truncated Total Least Squares with Multiple Channels and Parameters. Remote Sens. 2016, 8, 725. [Google Scholar] [CrossRef]
- Liou, K.N. An Introduction to Atmospheric Radiation; Elsevier: San Diego, CA, USA, 2002. [Google Scholar]
- Quine, B.M.; Drummond, J.R. GENSPECT: A line-by-line code with selectable interpolation error tolerance. J. Quant. Spectrosc. Radiat. Transf. 2002, 74, 147–165. [Google Scholar] [CrossRef]
- Lampe, J.; Voss, H. On a quadratic eigenproblem occurring in regularized total least squares. Comput. Stat. Data Anal. 2007, 52, 1090–1102. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. An analysis of the total least squares problem. SIAM J. Numer. Anal. 1980, 17, 883–893. [Google Scholar] [CrossRef]
- Golub, G.H. Some modified matrix eigenvalue problems. SIAM Rev. 1973, 15, 318–334. [Google Scholar] [CrossRef]
- Fierro, R.D.; Golub, G.H.; Hansen, P.C.; O’Leary, D.P. Regularization by truncated total least squares. SIAM J. Sci. Comput. 1997, 18, 1223–1241. [Google Scholar] [CrossRef]
- Norton, R.H.; Beer, R. New apodizing functions for Fourier spectrometry. J. Opt. Soc. Am. 1976, 66, 259–264. [Google Scholar] [CrossRef]
- Tobin, D.; Revercomb, H.; Knuteson, R.; Taylor, J.; Best, F.; Borg, L.; DeSlover, D.; Martin, G.; Buijs, H.; Esplin, M.; et al. Suomi-NPP CrIS radiometric calibration uncertainty. J. Geophys. Res. Atmos. 2013, 118, 10589–10600. [Google Scholar] [CrossRef]
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L.; et al. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 12734–12748. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar]
- Menke, W. Geophysical Data Analysis: Discrete Inverse Theory; Academic Press: San Diego, CA, USA, 1989. [Google Scholar]
- Steck, T. Methods for determining regularization for atmospheric retrieval problems. Appl. Opt. 2002, 41, 1788–1797. [Google Scholar] [CrossRef] [PubMed]
- Björck, Ȧ.; Golub, G.H. Numerical methods for computing angles between linear subspaces. Math. Comput. 1973, 27, 579–594. [Google Scholar] [CrossRef]
- Sato, T.O.; Sato, T.M.; Sagawa, H.; Noguchi, K.; Saitoh, N.; Irie, H.; Kita, K.; Mahani, M.E.; Zettsu, K.; Imasu, R.; et al. Vertical profile of tropospheric ozone derived from synergetic retrieval using three different wavelength ranges, UV, IR, and microwave: Sensitivity study for satellite observation. Atmos. Meas. Tech. 2018, 11, 1653–1668. [Google Scholar] [CrossRef]
- Steinwagner, J.; Schwarz, G. Shape-dependent regularization for the retrieval of atmospheric state parameter profiles. Appl. Opt. 2006, 45, 1000–1009. [Google Scholar] [CrossRef] [PubMed]
- Ridolfi, M.; Sgheri, L. Iterative approach to self-adapting and altitude-dependent regularization for atmospheric profile retrievals. Opt. Express 2011, 19, 26696–26709. [Google Scholar] [CrossRef] [PubMed]
- Bowman, K.W.; Rodgers, C.D.; Kulawik, S.S.; Worden, J.; Sarkissian, E.; Osterman, G.; Steck, T.; Lou, M.; Eldering, A.; Shephard, M.; et al. Tropospheric emission spectrometer: Retrieval method and error analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1297–1307. [Google Scholar] [CrossRef]
- Eremenko, M.; Dufour, G.; Foret, G.; Keim, C.; Orphal, J.; Beekmann, M.; Bergametti, G.; Flaud, J.M. Tropospheric ozone distributions over Europe during the heat wave in July 2007 observed from infrared nadir spectra recorded by IASI. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Divakarla, M.; Barnet, C.; Liu, X.; Gu, D.; Wilson, M.; Kizer, S.; Xiong, X.; Maddy, E.; Ferraro, R.; Knuteson, R.; et al. The CrIMSS EDR algorithm: Characterization, optimization, and validation. J. Geophys. Res. Atmos. 2014, 119, 4953–4977. [Google Scholar] [CrossRef]
- Ohyama, H.; Kawakami, S.; Shiomi, K.; Morino, I.; Uchino, O. Atmospheric temperature and water vapor retrievals from GOSAT thermal infrared spectra and initial validation with coincident radiosonde measurements. SOLA 2013, 9, 143–147. [Google Scholar] [CrossRef]
- Nalli, N.R.; Barnet, C.D.; Reale, A.; Tobin, D.; Gambacorta, A.; Maddy, E.S.; Joseph, E.; Sun, B.; Borg, L.; Mollner, A.K.; et al. Validation of satellite sounder environmental data records: Application to the Cross-track Infrared Microwave Sounder Suite. J. Geophys. Res. Atmos. 2013, 118, 628–643. [Google Scholar] [CrossRef]
- Pougatchev, N.; August, T.; Calbet, X.; Hultberg, T.; Oduleye, O.; Schlüssel, P.; Stiller, B.; Germain, K.S.; Bingham, G. IASI temperature and water vapor retrievals–error assessment and validation. Atmos. Chem. Phys. 2009, 9, 6453–6458. [Google Scholar] [CrossRef]
- Lopez, J.P.; Luo, M.; Christensen, L.E.; Loewenstein, M.; Jost, H.; Webster, C.R.; Osterman, G. TES carbon monoxide validation during two AVE campaigns using the Argus and ALIAS instruments on NASA’s WB-57F. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koner, P.K.; Dash, P. Maximizing the Information Content of Ill-Posed Space-Based Measurements Using Deterministic Inverse Method. Remote Sens. 2018, 10, 994. https://doi.org/10.3390/rs10070994
Koner PK, Dash P. Maximizing the Information Content of Ill-Posed Space-Based Measurements Using Deterministic Inverse Method. Remote Sensing. 2018; 10(7):994. https://doi.org/10.3390/rs10070994
Chicago/Turabian StyleKoner, Prabhat K., and Prasanjit Dash. 2018. "Maximizing the Information Content of Ill-Posed Space-Based Measurements Using Deterministic Inverse Method" Remote Sensing 10, no. 7: 994. https://doi.org/10.3390/rs10070994
APA StyleKoner, P. K., & Dash, P. (2018). Maximizing the Information Content of Ill-Posed Space-Based Measurements Using Deterministic Inverse Method. Remote Sensing, 10(7), 994. https://doi.org/10.3390/rs10070994