Spectral-Spatial Classification of Hyperspectral Images: Three Tricks and a New Learning Setting
Abstract
1. Introduction
Related Work
2. Materials and Methods
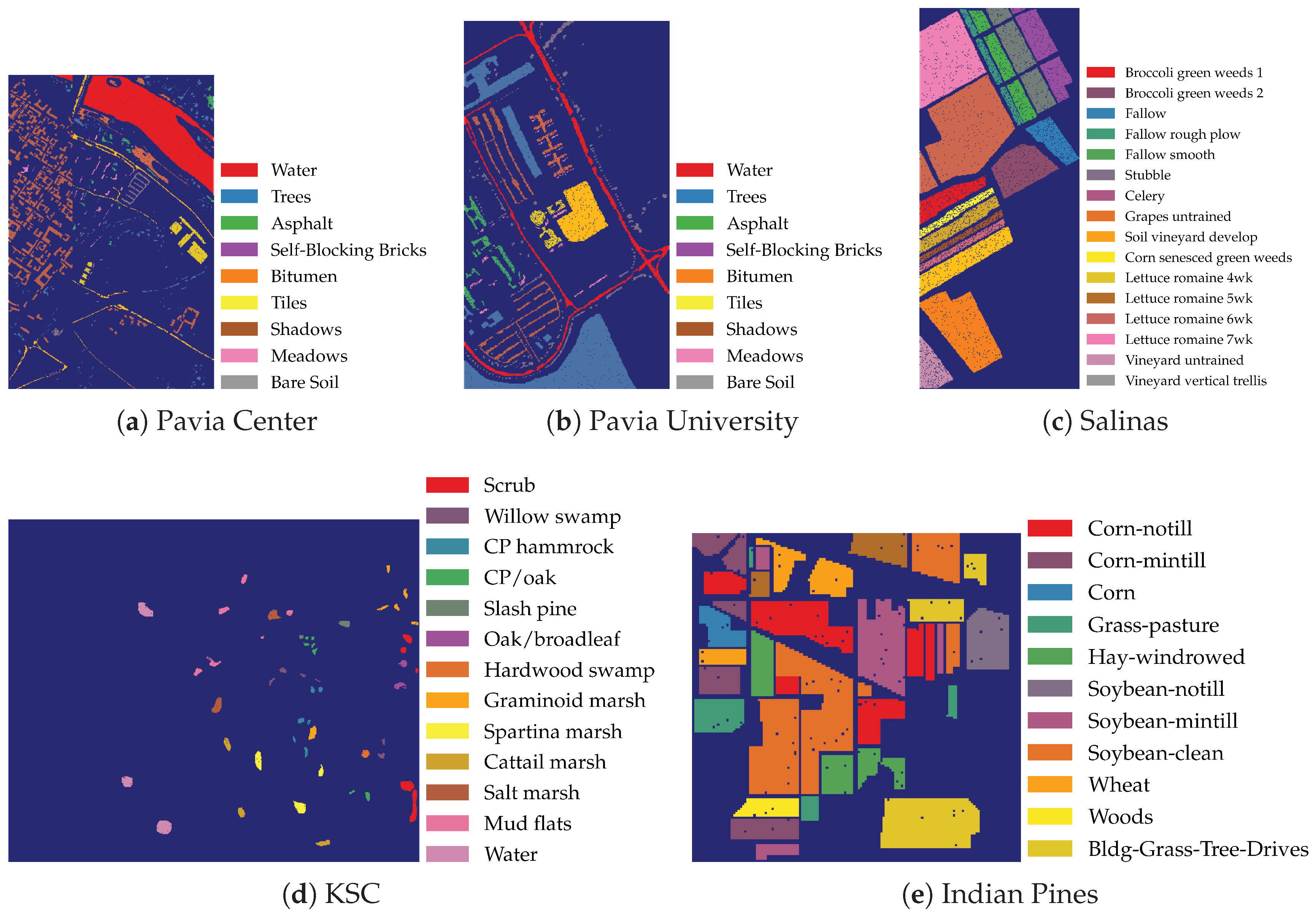
2.1. Data
- Pavia Center: obtained with a Reflective Optics System Imaging Spectrometer (ROSIS) sensor during a flight campaign over Pavia, Northern Italy
- Pavia University: scanned using the ROSIS sensor during a flight campaign over Pavia, Northern Italy
- Kennedy Space Center (KSC): obtained with the Airborne/Visible Infrared Imaging Spectrometer (AVIRIS) sensor over the Kennedy Space Center, Florida (USA)
- Indian Pines: scanned using the AVIRIS sensor over the Indian Pines test site in north-western Indiana (USA)
- Salinas: scanned using the AVIRIS sensor over Salinas Valley, California (USA)
2.2. Learning Settings
2.2.1. Transductive Learning Setting
2.2.2. Non-Overlapping Learning Setting
| Algorithm 1: CNN-RSL. |
|
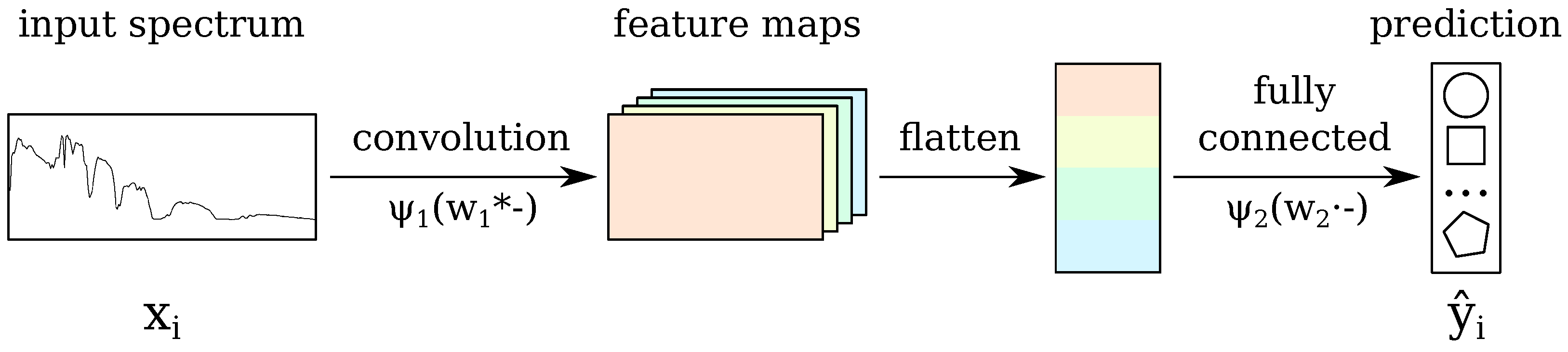
2.3. The Baseline CNN
- learning rate ();
- momentum (default value used in experiments: );
- number of convolutional kernels ();
- size of the convolutional kernels (N);
- stride for the convolution (s);
- L2 regularization constant ().
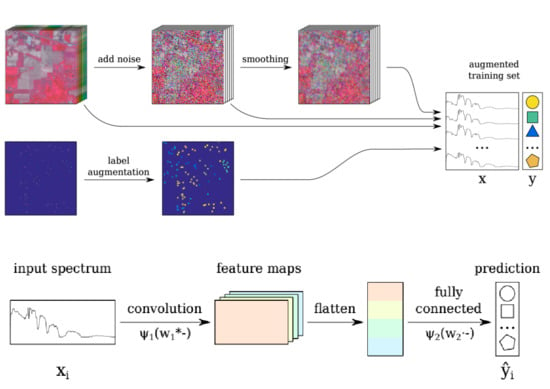
- by constraining weights of the neural network corresponding to nearby wavelengths to assume similar values (see Section 2.4);
- by generating pixels with smoothed spectra from neighbors of labeled pixels (see Section 2.5);
- by propagating the label of a pixel to its neighbors and adding them to the training set (see Section 2.6).
2.4. Trick 1: Locality-Aware Regularization
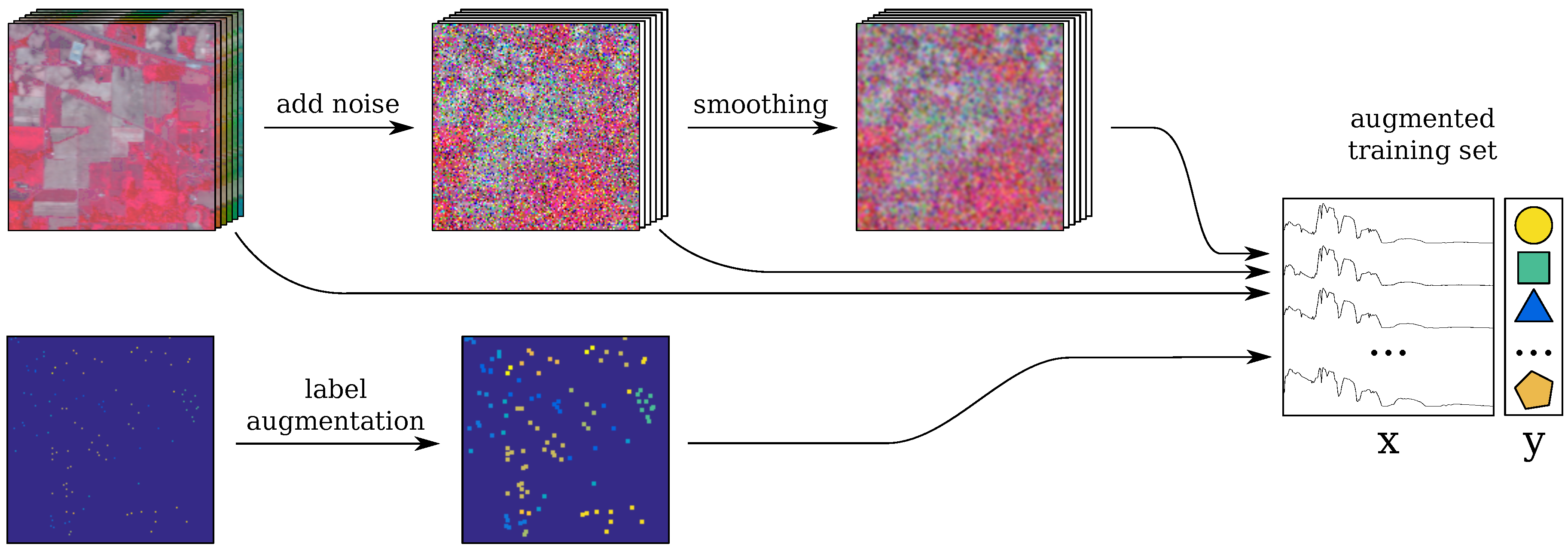
2.5. Trick 2: Smoothing-Based Data Augmentation
2.6. Trick 3: Label-Based Data Augmentation
- find its Moore neighborhood;
- select a subset of pixels in the neighborhood; see Equation (5);
- propagate the label of i to the selected neighbor pixels;
- insert the selected pixels into the training set.
2.7. Incorporating the Tricks into the Baseline CNN: CNN-RSL
- the original image is perturbed with random Gaussian noise Equation (2) (see Section 2.3);
- the resulting image is spatially smoothed (S step);
- label augmentation is applied (L step);
- the spectra for the labeled pixels are selected from the original, noisy and smoothed images; these are combined to form the training set;
- the spectra are rescaled between , which is a common practice for artificial neural networks. Note that this rescaling retains the original distribution of the features, while helping the CNN training to converge faster.
3. Experiments
3.1. Algorithms
- R: spectral-locality-aware regularization term (see Section 2.4);
- S: smoothing-based data augmentation (see Section 2.5);
- L: label-based data augmentation (see Section 2.6).
- SVM-RBF: a support vector machine with the Radial Basis Function (RBF) kernel;
- HL-ELM: a deep convolutional neural network for hyperspectral image labeling for which we were able to retrieve the source code. HL-ELM has two convolutional and two max pooling hidden layers arranged one after the other (see [28]).
3.2. Parameter Setting
- the number of kernels of the convolutional layer, ;
- the size of kernels of the convolutional layer, ;
- the stride for the convolution, ;
- the parameters in the regularization terms, for ;
- the learning rate, for .
- the Gaussian exponent constant where ,
- the regularization constant where .
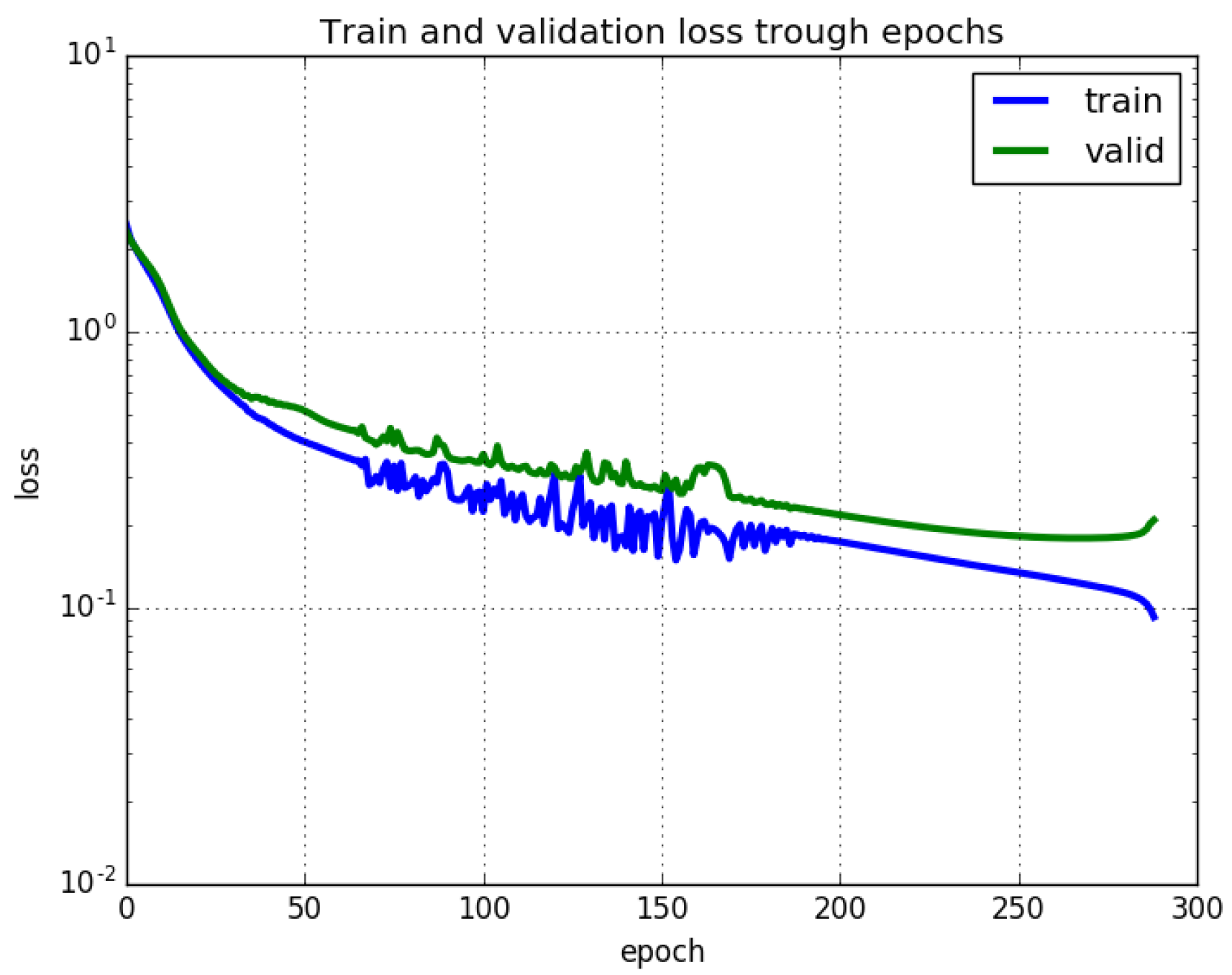
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, C.I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification; Springer: Berlin, Germany, 2003; Volume 1. [Google Scholar]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Sign. Proc. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Hoekman, D.H.; Vissers, M.A.M.; Tran, T.N. Unsupervised Full-Polarimetric SAR Data Segmentation as a Tool for Classification of Agricultural Areas. IEEE J. STARS 2011, 4, 402–411. [Google Scholar] [CrossRef]
- Tran, T.N.; Wehrens, R.; Buydens, L.M. Clustering multispectral images: A tutorial. Chemom. Intell. Lab. Syst. 2005, 77, 3–17. [Google Scholar] [CrossRef]
- Tran, T.N.; Wehrens, R.; Hoekman, D.H.; Buydens, L.M.C. Initialization of Markov random field clustering of large remote sensing images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1912–1919. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Sveinsson, J.R. Automatic spectral—Spatial classification framework based on attribute profiles and supervised feature extraction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5771–5782. [Google Scholar] [CrossRef]
- Falco, N.; Benediktsson, J.A.; Bruzzone, L. Spectral and spatial classification of hyperspectral images based on ICA and reduced morphological attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6223–6240. [Google Scholar] [CrossRef]
- He, L.; Li, Y.; Li, X.; Wu, W. Spectral—Spatial classification of hyperspectral images via spatial translation-invariant wavelet-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2696–2712. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Wang, Z.; Huang, X.; Zhang, L.; Sun, H. Unsupervised feature learning via spectral clustering of multidimensional patches for remotely sensed scene classification. IEEE J. STARS 2015, 8. [Google Scholar] [CrossRef]
- Yang, W.; Yin, X.; Xia, G.S. Learning high-level features for satellite image classification with limited labeled samples. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4472–4482. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Plaza, A.; Li, Y. Discriminative Low-Rank Gabor Filtering for Spectral—Spatial Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1381–1395. [Google Scholar] [CrossRef]
- Veganzones, M.A.; Tochon, G.; Dalla-Mura, M.; Plaza, A.J.; Chanussot, J. Hyperspectral image segmentation using a new spectral unmixing-based binary partition tree representation. IEEE Trans. Image Process. 2014, 23, 3574–3589. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Li, S.; Fang, L.; Jia, X.; Benediktsson, J.A. From Subpixel to Superpixel: A Novel Fusion Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4398–4411. [Google Scholar] [CrossRef]
- Sun, B.; Kang, X.; Li, S.; Benediktsson, J.A. Random-walker-based collaborative learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 212–222. [Google Scholar] [CrossRef]
- Wang, Z.; Du, B.; Zhang, L.; Zhang, L.; Jia, X. A Novel Semisupervised Active-Learning Algorithm for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3071–3083. [Google Scholar] [CrossRef]
- Kemker, R.; Kanan, C. Self-taught feature learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2693–2705. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Contextual Deep CNN Based Hyperspectral Classification. arXiv, 2016; arXiv:1604.03519. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep Supervised Learning for Hyperspectral Data Classification through Convolutional Neural Networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Slavkovikj, V.; Verstockt, S.; Neve, W.D.; Hoecke, S.V.; Walle, R.V.D. Hyperspectral Image Classification with Convolutional Neural Networks. In Proceedings of the 23rd ACM international conference on Multimedia, Brisbane, Australia, 26–30 October 2015; pp. 1159–1162. [Google Scholar]
- Liang, H.; Li, Q. Hyperspectral imagery classification using sparse representations of convolutional neural network features. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Amini, S.; Homayouni, S.; Safari, A.; Darvishsefat, A.A. Object-based classification of hyperspectral data using Random Forest algorithm. Geo-Spat. Inf. Sci. 2018, 21, 127–138. [Google Scholar] [CrossRef]
- O’Neil-Dunne, J.; Pelletier, K.; MacFaden, S.; Troy, A.; Grove, J.M. Object-based high-resolution land-cover mapping. In Proceedings of the 2009 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009. [Google Scholar]
- Blaschke, T.; Lang, S.; Hay, G.J. Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Lecture Notes in Geoinformation and Cartography; Springer: Berlin, Germany, 2008. [Google Scholar]
- Lv, Q.; Niu, X.; Dou, Y.; Xu, J.; Lei, Y. Classification of Hyperspectral Remote Sensing Image Using Hierarchical Local-Receptive-Field-Based Extreme Learning Machine. IEEE Geosci. Remote Sens. Lett. 2016, 13, 434–438. [Google Scholar] [CrossRef]
- Gu, Y.; Chanussot, J.; Jia, X.; Benediktsson, J.A. Multiple Kernel Learning for Hyperspectral Image Classification: A Review. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6547–6565. [Google Scholar] [CrossRef]
- Pan, L.; Li, H.C.; Meng, H.; Li, W.; Du, Q.; Emery, W.J. Hyperspectral Image Classification via Low-Rank and Sparse Representation With Spectral Consistency Constraint. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2117–2121. [Google Scholar] [CrossRef]
- Shao, Y.; Sang, N.; Gao, C.; Ma, L. Probabilistic class structure regularized sparse representation graph for semi-supervised hyperspectral image classification. Pattern Recognit. 2017, 63, 102–114. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral-Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1579–1597. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Member, S.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. STARS 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification via kernel sparse representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef]
- Zhang, G.; Jia, X.; Hu, J. Superpixel-based graphical model for remote sensing image mapping. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5861–5871. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Geng, J. Spectral-Spatial Classification of Hyperspectral Image Based on Deep Auto-Encoder. IEEE J. STARS 2016, 9, 4073–4085. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper With Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Zhou, J.; Qian, Y.; Wen, L.; Bai, X.; Gao, Y. On the sampling strategy for evaluation of spectral-spatial methods in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 862–880. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS 2010), Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the 19th International Conference on Computational Statistics, COMPSTAT’2010, Paris, France, 22–27 August 2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Salenstein, Switzerland, 2010; pp. 177–186. [Google Scholar]
- Acquarelli, J.; van Laarhoven, T.; Gerretzen, J.; Tran, T.N.; Buydens, L.M.; Marchiori, E. Convolutional neural networks for vibrational spectroscopic data analysis. Anal. Chim. Acta 2017, 954, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Forero, S.; Manian, V. Improving Hyperspectral Image Classification Using Spatial Preprocessing. IEEE Geosci. Remote Sens. Lett. 2009, 6, 297–301. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-parameter Optimization. J. Machine Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Salzberg, S.L. On Comparing Classifiers: Pitfalls to Avoid and a Recommended Approach. Data Min. Knowl. Discov. 1997, 1, 317–328. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature Extraction of Hyperspectral Images With Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar] [CrossRef]
- Cope, B. Implementation of 2D Convolution on FPGA, GPU and CPU; Imperial College Report: London, UK, 2006; pp. 2–5. [Google Scholar]

| Image | Size | # Features | # Foreground Pixels | # Classes |
|---|---|---|---|---|
| Pavia Center | 102 | 148,152 | 09 | |
| Pavia University | 103 | 42,776 | 09 | |
| KSC | 176 | 5211 | 13 | |
| Indian Pines | 220 | 10,062 | 12 | |
| Salinas | 224 | 54,129 | 16 |
| Dataset | N | s | |||||
|---|---|---|---|---|---|---|---|
| Pavia Center | 32 | 47 | 1 | 0.001 | 0.1 | 0.001 | 2.33 |
| Pavia University | 32 | 35 | 1 | 0.010 | 0.1 | 0.001 | 2.33 |
| KSC | 16 | 51 | 1 | 0.010 | 0.1 | 0.001 | 3.00 |
| Indian Pines | 16 | 53 | 1 | 0.001 | 0.1 | 0.001 | 3.67 |
| Salinas | 32 | 49 | 1 | 0.001 | 0.1 | 0.001 | 4.33 |
| Train % | 1% 165211 | 2% 329422 | 3% 494633 | 4% 658845 | 5% 8231056 | |
|---|---|---|---|---|---|---|
| Method | ||||||
| CNN | 97.790.22 * | 97.980.20 * | 98.140.25 * | 98.570.29 * | 98.690.25 * | |
| CNN-S | 99.230.16 * | 99.260.15 * | 99.240.12 * | 99.280.11 * | 99.350.22 * | |
| CNN-L | 98.480.18 * | 98.810.20 * | 99.000.27 * | 99.090.14 * | 99.200.22 * | |
| CNN-R | 98.010.28 * | 98.320.25 * | 98.410.22 * | 98.630.30 * | 98.790.22 * | |
| CNN-RS | 99.210.88 * | 99.280.68 * | 99.280.51 * | 99.330.58* | 99.410.35 * | |
| CNN-SL | 98.110.96 * | 98.590.85 * | 98.840.74 * | 98.960.59 * | 99.120.54 * | |
| CNN-RL | 98.760.39 * | 98.860.45 * | 98.950.41 * | 99.200.43 * | 99.340.29 * | |
| CNN-RSL | 99.52 ± 0.07 | 99.67 ± 0.15 | 99.72 ± 0.04 | 99.76 ± 0.07 | 99.82 ± 0.05 | |
| SVM-RBF | 84.312.51 * | 85.411.77 * | 85.891.65 * | 87.041.83 * | 87.191.67 * | |
| SVM-RBF-S | 99.050.52 * | 99.210.51 * | 99.500.34 * | 99.600.38 * | 99.640.33 * | |
| SVM-RBF-L | 90.125.24 * | 92.144.26 * | 92.251.85 * | 92.840.95 * | 92.800.82 * | |
| SVM-RBF-SL | 98.950.51 * | 99.090.57 * | 99.250.62 * | 99.360.41 * | 99.450.49 * | |
| HL-ELM | 96.220.08 * | 97.270.11 * | 97.780.08 * | 98.090.11 * | 98.220.10 * | |
| HL-ELM-S | 98.750.17 * | 98.920.18 * | 99.170.13 * | 99.280.12 * | 99.300.09 * | |
| HL-ELM-L | 96.320.15 * | 97.540.22 * | 97.870.17 * | 98.120.22 * | 98.290.14 * | |
| HL-ELM-SL | 99.050.23 * | 99.270.25 * | 99.400.10 * | 99.430.06 * | 99.520.07 * | |
| Train % | 1% 4852 | 2% 95104 | 3% 143157 | 4% 190209 | 5% 238261 | |
|---|---|---|---|---|---|---|
| Method | ||||||
| CNN | 88.760.20 * | 89.040.26 * | 90.160.27 * | 91.520.23 * | 92.790.21 * | |
| CNN-S | 95.01 ± 0.74 | 95.550.68 * | 95.870.59 * | 95.980.46 * | 96.250.72* | |
| CNN-L | 88.770.13 * | 89.510.02 * | 88.790.49 * | 89.050.81 * | 89.200.83 * | |
| CNN-R | 89.040.51 * | 89.860.45 * | 90.290.50 * | 91.500.36 * | 92.650.45 * | |
| CNN-RS | 94.250.49* | 95.610.52* | 95.920.47* | 96.150.53* | 96.510.29* | |
| CNN-SL | 91.121.15 * | 92.170.95 * | 92.530.87 * | 93.100.61 * | 93.320.41 * | |
| CNN-RL | 88.510.55 * | 88.910.58 * | 89.130.49 * | 89.620.52 * | 89.980.77 * | |
| CNN-RSL | 94.740.25 | 96.36 ± 0.68 | 96.54 ± 0.46 | 96.65 ± 0.31 | 96.70 ± 0.44 | |
| SVM-RBF | 75.962.56 * | 74.850.78 * | 74.921.41 * | 75.431.26 * | 75.981.96 * | |
| SVM-RBF-S | 89.184.23 * | 91.773.59 * | 93.203.57 * | 93.744.21 * | 94.353.68 * | |
| SVM-RBF-L | 57.512.67 * | 79.061.47 * | 82.562.86 * | 82.820.86 * | 90.511.24 * | |
| SVM-RBF-SL | 91.682.28 * | 93.891.23 * | 95.000.78 * | 95.482.59 * | 95.560.59 * | |
| HL-ELM | 75.772.02 * | 78.902.13 * | 82.262.55 * | 83.272.18 * | 86.512.27 * | |
| HL-ELM-S | 90.750.75 * | 92.910.81 * | 93.850.57 * | 94.370.26 * | 95.230.19 * | |
| HL-ELM-L | 75.961.76 * | 81.412.31 * | 83.981.95 * | 85.591.72 * | 86.811.63 * | |
| HL-ELM-SL | 92.790.91 * | 94.740.79 * | 95.560.58 * | 96.210.36 * | 96.340.18* | |
| Train % | 1% 42 | 2% 85 | 3% 127 | 4% 169 | 5% 2011 | |
|---|---|---|---|---|---|---|
| Method | ||||||
| CNN | 78.090.99 * | 83.980.92 * | 85.371.21 * | 87.061.25 * | 88.271.75 * | |
| CNN-S | 84.741.32 * | 85.950.78 * | 86.480.72 * | 88.610.66 * | 90.180.52 * | |
| CNN-L | 84.651.85 * | 88.021.70 * | 91.940.99 * | 93.580.36 * | 94.210.15 * | |
| CNN-R | 80.241.44 * | 84.000.82 * | 85.410.94 * | 88.560.81 * | 90.190.59 * | |
| CNN-RS | 84.951.14 * | 85.860.70 * | 86.500.85 * | 88.950.91 * | 90.090.32 * | |
| CNN-SL | 87.070.85 * | 90.240.78 * | 92.850.71 * | 95.050.66 * | 97.280.53 * | |
| CNN-RL | 84.781.83 * | 88.530.80 * | 92.650.77 * | 93.660.80 * | 94.090.42 * | |
| CNN-RSL | 90.340.97 | 95.360.02 | 97.220.37 | 98.800.60 | 99.790.20 | |
| SVM-RBF | 67.851.97 * | 76.172.85 * | 79.872.59 * | 79.173.25 * | 82.452.62 * | |
| SVM-RBF-S | 89.032.04 * | 90.873.16 * | 93.513.05 * | 95.362.53 * | 96.761.98 * | |
| SVM-RBF-L | 81.102.81 * | 87.141.59 * | 87.662.51 * | 91.151.95 * | 92.472.06 * | |
| SVM-RBF-SL | 89.143.15 * | 90.741.65 * | 91.122.54 * | 96.001.56 * | 97.380.85 * | |
| HL-ELM | 79.210.65 * | 81.881.36 * | 82.790.95 * | 83.871.23 * | 86.210.92 * | |
| HL-ELM-S | 81.522.42 * | 86.951.24 * | 90.581.12 * | 92.170.87 * | 93.460.51 * | |
| HL-ELM-L | 79.601.54 * | 83.140.98 * | 83.560.64 * | 85.350.53 * | 86.480.45 * | |
| HL-ELM-SL | 88.112.52 * | 91.311.14 * | 93.641.26 * | 95.720.82 * | 96.770.58 * | |
| Train % | 1% 86 | 2% 1712 | 3% 2518 | 4% 3424 | 5% 4230 | |
|---|---|---|---|---|---|---|
| Method | ||||||
| CNN | 54.830.23 * | 60.830.87 * | 64.560.74 * | 67.580.67 * | 70.830.77 * | |
| CNN-S | 70.930.40 * | 78.590.54 * | 83.880.65 * | 87.770.70 * | 90.510.53 * | |
| CNN-L | 65.790.51 * | 71.830.42 * | 76.340.46 * | 78.540.27 * | 80.360.88 * | |
| CNN-R | 56.240.39 * | 61.120.45 * | 64.890.55 * | 67.640.50 * | 71.030.83 * | |
| CNN-RS | 72.630.38 * | 78.630.44 * | 84.010.58 * | 88.320.57 * | 90.830.49 * | |
| CNN-SL | 68.110.54 * | 72.670.38 * | 76.710.53 * | 78.760.57 * | 80.850.38 * | |
| CNN-RL | 66.020.43 * | 72.000.53 * | 76.140.37 * | 78.820.46 * | 80.780.61 * | |
| CNN-RSL | 86.420.66 | 92.700.80 | 94.450.92 | 96.000.38 | 96.420.24 | |
| SVM-RBF | 58.750.49 * | 60.580.36 * | 61.470.28 * | 63.810.47 * | 64.450.32 * | |
| SVM-RBF-S | 77.232.90 * | 83.232.46 * | 86.443.01 * | 88.912.78 * | 89.522.67 * | |
| SVM-RBF-L | 65.742.92 * | 69.471.43 * | 70.381.35 * | 77.181.77 * | 77.901.59 * | |
| SVM-RBF-SL | 85.142.53 * | 90.121.91 * | 92.951.57 * | 93.241.72 * | 94.170.86 * | |
| HL-ELM | 66.290.51 * | 71.691.24 * | 74.280.79 * | 76.600.64 * | 78.040.52 * | |
| HL-ELM-S | 73.880.54 * | 82.480.96 * | 86.510.74 * | 88.490.68 * | 90.580.55 * | |
| HL-ELM-L | 66.340.14 * | 73.150.11 * | 73.190.21 * | 76.850.16 * | 78.270.19 * | |
| HL-ELM-SL | 82.050.96 * | 88.120.54 * | 91.390.49 * | 93.370.53 * | 94.410.45 * | |
| Train % | 1% 3427 | 2% 6854 | 3% 10181 | 4% 135107 | 5% 169134 | |
|---|---|---|---|---|---|---|
| Method | ||||||
| CNN | 87.130.42 * | 88.210.37 * | 88.540.22 * | 89.460.57 * | 91.140.17 * | |
| CNN-S | 96.870.35 * | 97.050.29 * | 97.170.31 * | 97.210.17 * | 97.520.54 * | |
| CNN-L | 87.130.59 * | 87.930.52 * | 88.290.37 * | 88.450.36 * | 89.560.75 * | |
| CNN-R | 88.190.37 * | 89.150.45 * | 89.980.40 * | 90.560.32 * | 91.270.22 * | |
| CNN-RS | 94.930.65 * | 97.020.51 * | 97.140.57 * | 97.300.72 * | 97.570.60 * | |
| CNN-SL | 93.150.84 * | 93.960.73 * | 94.230.68 * | 95.170.52 * | 96.250.43 * | |
| CNN-RL | 86.820.77 * | 87.020.65 * | 87.870.60 * | 88.020.54 * | 88.360.46 * | |
| CNN-RSL | 96.930.55 | 97.160.69 | 97.680.78 | 98.210.41 | 99.030.17 | |
| SVM-RBF | 72.381.85 * | 73.512.67 * | 73.782.54 * | 74.362.16 * | 74.842.04 * | |
| SVM-RBF-S | 93.353.41 * | 94.682.87 * | 96.182.26 * | 96.872.59 * | 97.161.85 * | |
| SVM-RBF-L | 84.292.85 * | 85.362.16 * | 85.872.14 * | 86.682.27 * | 87.161.55 * | |
| SVM-RBF-SL | 96.230.47 * | 96.310.36 * | 97.380.52 * | 97.470.75 * | 97.680.48 * | |
| HL-ELM | 87.500.53 * | 88.950.74 * | 89.380.45 * | 91.020.40 * | 91.360.25 * | |
| HL-ELM-S | 92.160.78 * | 94.640.89 * | 95.360.45 * | 96.170.41 * | 96.420.48 * | |
| HL-ELM-L | 87.770.56 * | 89.560.46 * | 90.160.37 * | 91.110.32 * | 91.870.40 * | |
| HL-ELM-SL | 93.510.92 * | 95.440.83 * | 96.490.35 * | 97.410.26 * | 97.810.20 * | |
| Method | Pavia Center | Pavia University | KSC | Indian Pines | Salinas |
|---|---|---|---|---|---|
| CNN | 92.210.56 * | 85.511.65 * | 90.892.83 * | 76.750.56 * | 88.582.15 * |
| CNN-S | 97.440.38 * | 89.121.10 * | 93.622.74 * | 80.590.10 * | 91.310.79 * |
| CNN-L | 96.570.48 * | 88.361.39 * | 92.912.54 * | 79.770.52 * | 90.661.42 * |
| CNN-R | 92.840.44 * | 86.111.22 * | 91.312.14 * | 77.500.49 * | 89.011.54 * |
| CNN-RS | 97.870.29 * | 90.302.11 * | 94.412.03 * | 81.250.12 * | 91.680.84 * |
| CNN-SL | 97.250.41 * | 88.671.02 * | 93.101.95 * | 80.030.46 * | 92.810.79 * |
| CNN-RL | 96.880.43 * | 88.391.18 * | 93.042.11 * | 82.920.41 * | 91.750.93 * |
| CNN-RSL | 98.650.37 | 95.761.14 | 97.851.35 | 83.960.60 | 93.011.44 |
| SVM-RBF | 90.040.64 * | 83.271.80 * | 88.712.76 * | 76.490.73 * | 87.592.81 * |
| SVM-RBF-S | 90.820.72 * | 89.491.46 * | 80.861.94 * | 78.320.91 * | 85.191.61 * |
| SVM-RBF-L | 90.650.79 * | 89.051.65 * | 80.161.88 * | 78.021.14 * | 84.781.82 * |
| SVM-RBF-SL | 91.080.58 * | 89.791.37 * | 81.471.85 * | 78.960.83 * | 85.691.62 * |
| HL-ELM | 90.890.85 * | 83.471.92 * | 85.102.74 * | 76.220.68 * | 84.191.69 * |
| HL-ELM-S | 78.440.51 * | 88.591.80 * | 91.121.74 * | 78.330.61 * | 84.791.55 * |
| HL-ELM-L | 77.810.61 * | 86.191.85 * | 90.961.83 * | 77.530.75 * | 84.581.73 * |
| HL-ELM-SL | 91.200.67 * | 90.071.77 * | 92.501.53 * | 79.310.66 * | 85.711.33 * |
| Method | Pavia Center | Pavia University | KSC | Indian Pines | Salinas |
|---|---|---|---|---|---|
| CNN-RSL | 99.520.11 | 97.850.07 | 99.870.17 | 97.730.22 | 98.540.41 |
| SVM-RBF | 96.262.38 * | 78.319.59 * | 92.963.81 * | 71.185.56 * | 87.362.18 * |
| SVM-RBF-SL | 98.670.14 * | 90.020.19 * | 98.920.09 * | 95.123.58 * | 97.292.01 * |
| Hu et al. [19] | — | 92.56 | — | — | 92.60 |
| Lee & Kwon [18] | — | — | — | 92.06 | — |
| HL-ELM-SL [28] | 98.040.09 * | 95.740.49 * | 93.080.66 * | 95.400.54 * | 97.840.09 * |
| MH-KELM [36] | — | 80.070.01 * | — | 91.750.29 * | — |
| Dataset | Train % | Methods | ||||||
|---|---|---|---|---|---|---|---|---|
| LRSRC-SCC [30] | PCSSR [31] | MKL [29] | DLRGF [12] | KSR [34] | IFRF [46] | CNN-RSL | ||
| Pavia University | 1% | 94.150.56 | — | 96.87 | — | — | 87.881.19* | 94.740.25* |
| Pavia University | 5% | — | — | — | — | — | 97.581.51 | 96.700.44* |
| KSC | 1% | — | — | 79.80 | 89.400.88* | — | 84.011.76* | 90.340.97 |
| KSC | 5% | — | 88.48 | — | 98.730.99* | — | 93.461.23* | 99.790.20 |
| Indian Pines | 1% | — | — | — | 83.590.81* | — | 84.501.24* | 86.420.66 |
| Indian Pines | 5% | — | — | — | 95.160.24* | — | 95.310.85* | 96.420.24 |
| Indian Pines | 10% | 95.180.58* | — | — | — | 98.47 | 96.270.34* | 97.620.17* |
| Salinas | 1% | — | — | 95.31 | — | — | 96.360.51* | 96.930.55 |
| Salinas | 5% | — | — | 97.98 | — | — | 98.360.51* | 99.030.17 |
| Method | Pavia Center | Pavia University | KSC | Indian Pines | Salinas |
|---|---|---|---|---|---|
| CNN | 92.682.35 * | 51.038.40 * | 66.765.58 * | 39.105.15 * | 75.663.82 * |
| CNN-RS | 93.383.69 | 52.745.82 | 74.864.24 | 49.223.20 | 77.903.73 |
| SVM-RBF | 80.916.52 * | 32.4311.35 * | 65.926.53 * | 24.135.99 * | 76.893.78 * |
| SVM-RBF-S | 81.463.53 * | 48.449.97 * | 68.958.23 * | 36.4810.97 * | 78.293.64 * |
| HL-ELM | 84.722.54 * | 49.013.97 * | 53.144.65 * | 43.855.49 * | 71.875.07 * |
| HL-ELM-S | 88.821.79 * | 50.283.86 * | 64.231.81 * | 45.124.76 * | 75.841.59 * |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acquarelli, J.; Marchiori, E.; Buydens, L.M.C.; Tran, T.; Van Laarhoven, T. Spectral-Spatial Classification of Hyperspectral Images: Three Tricks and a New Learning Setting. Remote Sens. 2018, 10, 1156. https://doi.org/10.3390/rs10071156
Acquarelli J, Marchiori E, Buydens LMC, Tran T, Van Laarhoven T. Spectral-Spatial Classification of Hyperspectral Images: Three Tricks and a New Learning Setting. Remote Sensing. 2018; 10(7):1156. https://doi.org/10.3390/rs10071156
Chicago/Turabian StyleAcquarelli, Jacopo, Elena Marchiori, Lutgarde M.C. Buydens, Thanh Tran, and Twan Van Laarhoven. 2018. "Spectral-Spatial Classification of Hyperspectral Images: Three Tricks and a New Learning Setting" Remote Sensing 10, no. 7: 1156. https://doi.org/10.3390/rs10071156
APA StyleAcquarelli, J., Marchiori, E., Buydens, L. M. C., Tran, T., & Van Laarhoven, T. (2018). Spectral-Spatial Classification of Hyperspectral Images: Three Tricks and a New Learning Setting. Remote Sensing, 10(7), 1156. https://doi.org/10.3390/rs10071156