1. Introduction
Ships navigating in ice-covered sea areas need ice information to support their operations. In the Baltic Sea, operative ice information includes daily ice charts, ice model forecasts, and ice thickness charts provided by the national ice services, in our case by the Finnish Ice Service (FIS). The production of the information relies strongly on synthetic aperture radar (SAR) imagery, both Sentinel-1 and Radarsat-2 imagery, typically obtained once or twice a day from each sea area. Experts of the Ice Service prepare the daily ice chart using the chart of the preceding day and other satellite images, in addition to using observations from icebreakers and coastal stations. The charts divide the ice cover into regions characterized by a set of parameters that comprises the concentration; typical, maximum and minimum thicknesses of level ice types; and a five-degree numeral for the degree of ice ridging (DIR). On the other hand, the level ice thickness chart is a supporting operative SAR-based product [
1]. The product refines the level ice thickness information of the ice charts using SAR-based segmentation. The product has been operative for several years. It is validated annually using ship reports and more extensively in reference [
2].
The difficulty of ice navigation is mainly due to ice ridges. Additionally, when assisted by an icebreaker, the ships must be able to proceed through the thick ice channel rubble that remains from the ridges broken by the icebreaker. The traffic restrictions to Northern Baltic ports are set in terms of the Finnish–Swedish ice classes where class IA ships may navigate to all ports throughout the winter season. Ships in the more powerful subclass IA Super are capable of independent navigation unless the conditions are exceptionally difficult. This may be due to very difficult ridging conditions, brash barriers or ice compression. A brash barrier (windrow) is a band of ice rubble at the ice margin that is typically 2 nautical miles wide and 10 m thick. It is created when thin ice is broken by waves and then compressed by wind against thicker ice. During compression, the ice cover is in a prevailing stress state that may manifest as channel closing, added resistance or even pileup of ice against the ship hull.
During normal conditions, ridge fields complicate the navigation system, especially the icebreaker assistance, by inducing performance variations between ships of different capabilities as well as speed variation for each individual ship. This includes occasional besetting, which, in convoy operations, increases collision risks and causes delays and disorder in port logistics. Better information about the distribution of ridged ice would improve the predictability of arrival times and make the winter navigation system generally more efficient and economical. For this reason, the detection and quantification of ridging from SAR imagery has been investigated from different aspects since the late 1980s. For Baltic Sea studies, see, for example, references [
3,
4,
5,
6,
7,
8].
On the surface, ridge rubble is usually arranged into narrow, elongated sails. The usual surface parameters to describe ridging are the sail height and ridge density, which is the number of ridge sails along a linear transect (e.g., a linear ship track). These surface parameters can be linked to the statistics of the subsurface ridge keels, which can, in turn, be used to estimate ship speed reduction. The ridge sail height and density are related to the horizontal coverage of the fraction of the surface area covered by ridge rubble [
9], a parameter which contributes to the magnitude of
in SAR images. Consequently, a connection exists between the backscattering intensity and the difficulty of navigation. Field campaigns carried out in the Baltic Sea ice have shown that variation in the C-band
is mainly due to large-scale surface roughness (e.g., ridge rubble) [
5,
10,
11,
12]. Based on the SAR studies, it has been observed that, on average, the C-band
increases when the intensity of ridging increases. Some figures can be found in [
11,
12]. The relationship is not unambiguous, as small-scale roughness, salinity and the incidence angle also contribute to the backscattering coefficient (e.g., new thin ice types can produce strong backscattering) [
13].
Thus, results that are sufficiently reliable for operational implementation are still lacking, and attempts to derive the ridge height or surface rubble volume per unit area have been inconclusive [
14], although the coverage of individual sails increases with the sail height. The same surface rubble coverage can result from shallow sails and a high ridge density or from high sails and a low ridge density. If the resolution of SAR imagery is too coarse (like 500 m) to allow ridge sails to be visible, the ridging parameters can barely be obtained from the aggregated contribution of ridges to
in the pixel area. Recently, learning methods, such as the random forest classification of feature statistics [
8], have shown promise in the determination of DIR from SAR images.
Another line in the utilization of SAR in winter navigation has been to provide the imagery to ships navigating in polar ice-covered seas [
15,
16,
17]. Ships can use the images as an aid in route selection and tactical navigation by identifying leads, areas of low concentration or areas with low degree of ice ridging. The ice conditions ahead can be anticipated from SAR based on what has been experienced in the near past when navigating through ice fields with similar SAR texture. This can be supported by state-of-the-art SAR classifications and other ice information products supplied by the land base. The main problems are a limited communication bandwidth and the fact that in the presence of ice drift, it can be impossible to pinpoint the ship’s location in reference to the image, even when the image is only a few hours old.
Finnish and Swedish icebreakers in the Baltic Sea provide a working example of SAR-based operation planning. The SAR images used to prepare ice charts are also received by a geographic information system–type terminal software on icebreaker bridges and presented with other selectable layers of navigational and environmental information [
16].
As the icebreakers may operate for weeks or months in the same sea area, the crew learns to link the SAR texture with degrees of navigational difficulty. This is facilitated by the fact that a large part of the SAR texture remains largely unchanged between two images, and the ice drift patterns are not too complicated in the semi-enclosed Baltic basins. However, this personal understanding is not easily expressed quantitatively or communicated to others (e.g., to the FIS). The two-way communication between the FIS and the icebreakers was discussed in [
18].
The idea that a ship’s observed response to an image texture and features is used to interpret the image is inherent in all SAR-assisted navigation. We seek to develop this idea into a consistent methodology of SAR classification that can also be used to complement other methods to extract navigationally-relevant information from the images. The ship response is extracted from the AIS (automatic identification system), which is a messaging system for broadcasting navigational information from a ship to other ships and to onshore authorities. Among other things, the AIS messages report the location and speed of the ships. Since the AIS system became mandatory in 2002, the data has been used extensively to study maritime traffic and its impacts.
AIS data are particularly applicable in the Baltic Sea, with its intense and steadily growing ship traffic. There are approximately 2000 ships for which the AIS is mandatory at sea at any given moment heading to or from its 200 commercial ports. The annual amount of cargo is about 1 billion tonnes, and the ferries carry approximately 100 million passengers. The main research applications have been general spatiotemporal characterization and statistical analyses of the traffic systems in some sea areas [
19] and the quantification of ship encounters and associated collision risks (e.g., [
20]).
The cargo and passenger flow continue without interruption throughout the ice season, when, on average, half of the Baltic area becomes covered with ice. Icebreakers are also used to keep the ports open in the northernmost parts of the sea. The presence of ice modifies both the traffic patterns and risks, but also introduces traffic system features that are not present in open water conditions—especially icebreaker assistance and speed reduction and besetting due to ice conditions. AIS data have been used to assess the winter navigation system [
16], navigation risks [
21], icebreakers and convoy operations [
22], ship ice performance [
23,
24], ice resistance modeling [
25] and route selection [
26].
We widen this domain of applications with a new approach where AIS data are used to interpret the SAR images in terms of attainable ship speed and locations of difficult navigation. As a first-order approach, the speed reductions observed at certain locations of the SAR image are taken to indicate that the location is navigationally difficult, and if several ships show a similar response, this is almost certainly so. As such, this would be valuable information along frequently-operated ice channels, and it is easily obtained if the ice is not drifting. However, we aim for a SAR-based classification of whole sea areas by studying the ship responses to SAR feature vectors constructed for this purpose. The methodology is based on random forest regression, the demonstration is conducted in ice-covered part of the Gulf of Bothia in March 2013, and the response is described in terms of the relative speed of independently navigating IA Super ships.
This paper is organized as follows. The data sets comprising AIS, SAR and ice chart data are described in
Section 2. The random forest tree ensemble method to estimate ship speeds using SAR features and sea ice parameters extracted from the manual ice charts is presented in
Section 3.
Section 4 presents the results and the quantitative analyses of their accuracy, and the concluding
Section 5 and
Section 6 discuss the results and the future potential of the approach.
2. Data Sets and Processing
2.1. Ice Conditions during the Ice Season and Study Period
The time period of our study was March 2013, and the area studied was the Baltic Sea northward from the latitude of N. This covers the entire Bay of Bothnia and largely, the Sea of Bothnia, and the areal extent is about 92,000 . In the Bay of Bothnia, ice formation in the open sea started during the first week of December and the bay was fully ice-covered on 26 December. After a few days, winds decreased the coverage to 20% of the bay area. Full coverage was attained again on 17 January, after which the pack ice developed in phases of opening, ridging and refreezing. In the Sea of Bothnia, there was ice pack only close to the coast. At the end of February, the temperatures started to decrease and the extent of ice grew rapidly. The whole of March was extremely cold. The maximum ice extent covered 177,000 of the Baltic area of 422,000 , and was attained on 15 March. The extent was close to climatological average, but the date was later than usual. The Sea of Bothnia became fully ice-covered for the first time at the end of the month. In April, the ice retreated rapidly because the ice types formed in March did not have large thicknesses.
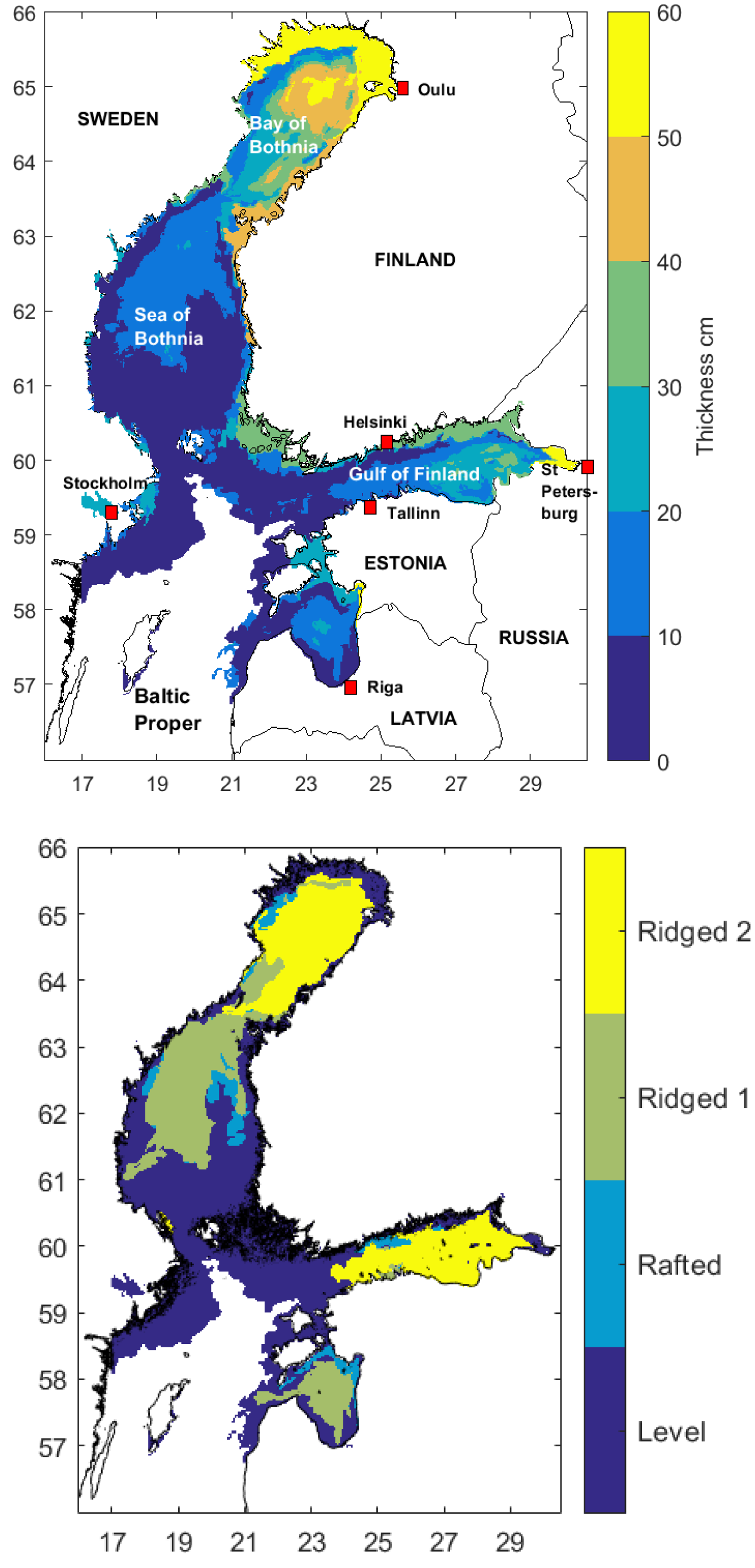
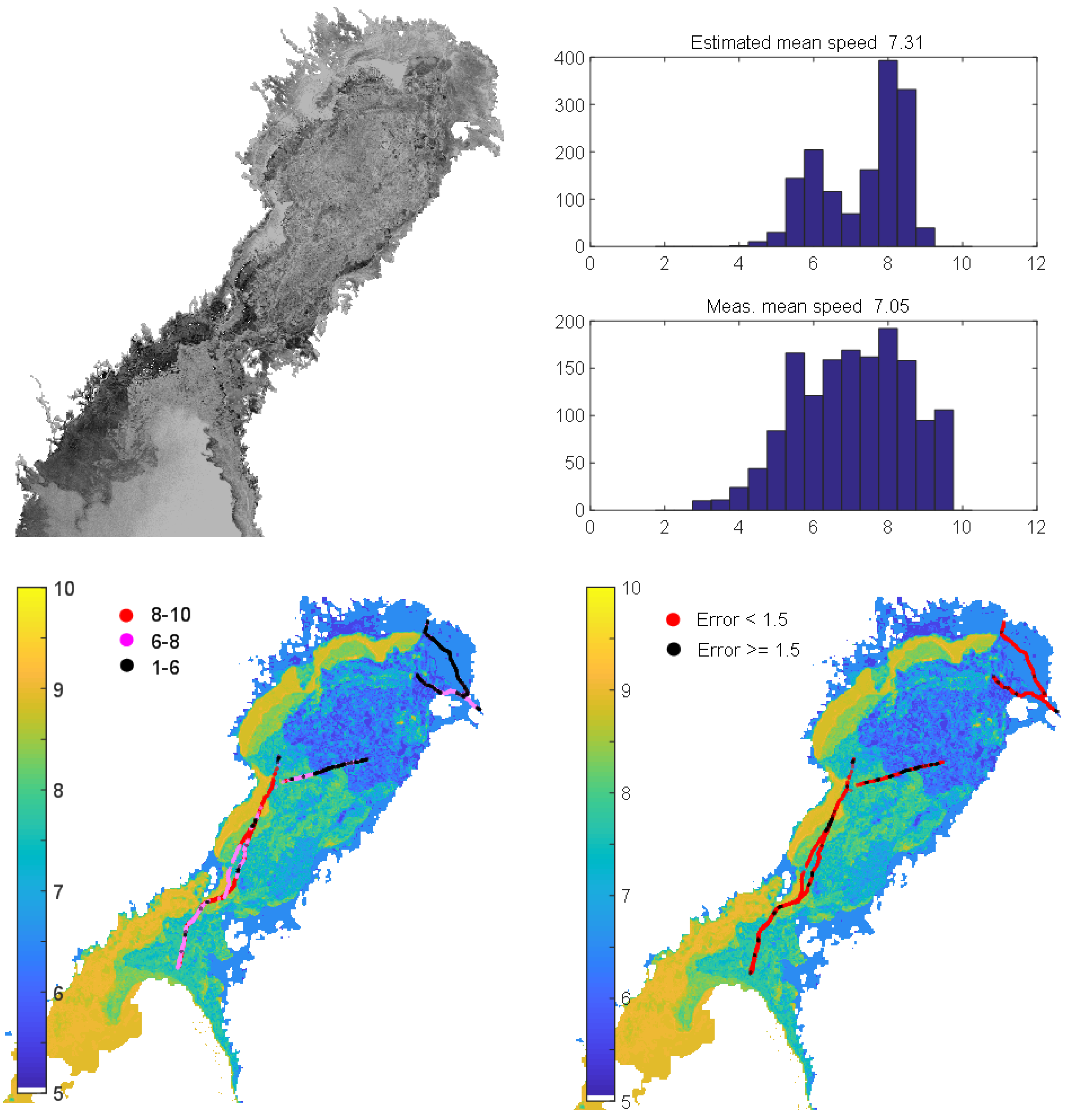
During the study period, the maximum average thicknesses of level ice types was greater than 50 cm in the Bay of Bothnia (see
Figure 1 (upper panel)). Although the ice pack was mobile throughout the month, the winds were not particularly strong. The wind speeds fluctuated during the first week and settled at around 5 m/s with occasional spikes reaching 10 m/s. However, the wind direction varied greatly. In the Bay of Bothnia, this resulted in the opening of a lead and the formation of new thin ice alternatingly along the Finnish and Swedish coasts. This is shown in
Figure 1 as lower monthly averages. The main pack of older and thicker ice suffered few changes, but rather, was shuffled back and forth. In the Sea of Bothnia, the ice cover started to expand more rapidly after the first week of March, and during the last ten days, southward ice drift accelerated the freezing of remaining open water areas. Ice ridging conditions were not difficult. The highest degree of ice ridging (i.e., Ridged 3 in
Figure 1 (lower panel)) was atypically not present even in the Bay of Bothnia, and the Sea of Bothnia became only slightly ridged due to the moderate winds.
2.2. AIS Data
The AIS is a very high frequency system used for broadcasting information on ship state, and it has been mandatory for vessels over 300 gross tonnage and for all passenger vessels since 2002. The Finnish Traffic Administration (FTA) receives Baltic AIS data on terrestrial stations, conducts a quality check and redirects the data to the vessel traffic service (VTS) centers and other civil end users. The AIS data consist of different types of messages, many of which are optional. However, the basic navigational data are automatically coded in position reports (Type 1–3 messages) which include the ship identifier, location, speed, heading and course.
This AIS data stream has been received at the Finnish Meteorological Institute since 2007, arranged into a database and used for research purposes. The database links the position reports with marine environmental data and ship particulars data and provides search utilities that can be conditioned by time, geographic area, environmental parameters and ship particulars. The Type 1–3 message interval for a steaming ship is about 10 s, and the number of position reports for years 2007–2016 amounts to 6 billion. The main use of the database has been winter navigation research, in which the environmental data consists of gridded ice charts and ice model forecasts.
The main shortcoming of the AIS data is that the changes in propulsion power are not known. When studying a ship’s response to ice conditions, there is no guarantee that the observed speed reduction is due to the increased difficulty of ice conditions and not due to a change in the power setting. The power setting may be reduced when a safe encounter with other ships requires a slower speed, increased if the ice conditions ahead pose a besetting risk or changed either way in order to adjust to convoy speed. To minimize this uncertainty, we selected the group of independently navigating ships of the Finnish–Swedish ice class IA Super. The criterion of independency was that there were no ships within 3 nautical miles and none expected to come within 3 miles during the following 10 min. On the other hand, IA Super ships are able to navigate without icebreaker assistance unless the ice conditions are exceptionally difficult. They also usually do not change their power setting much when navigating independently [
23].
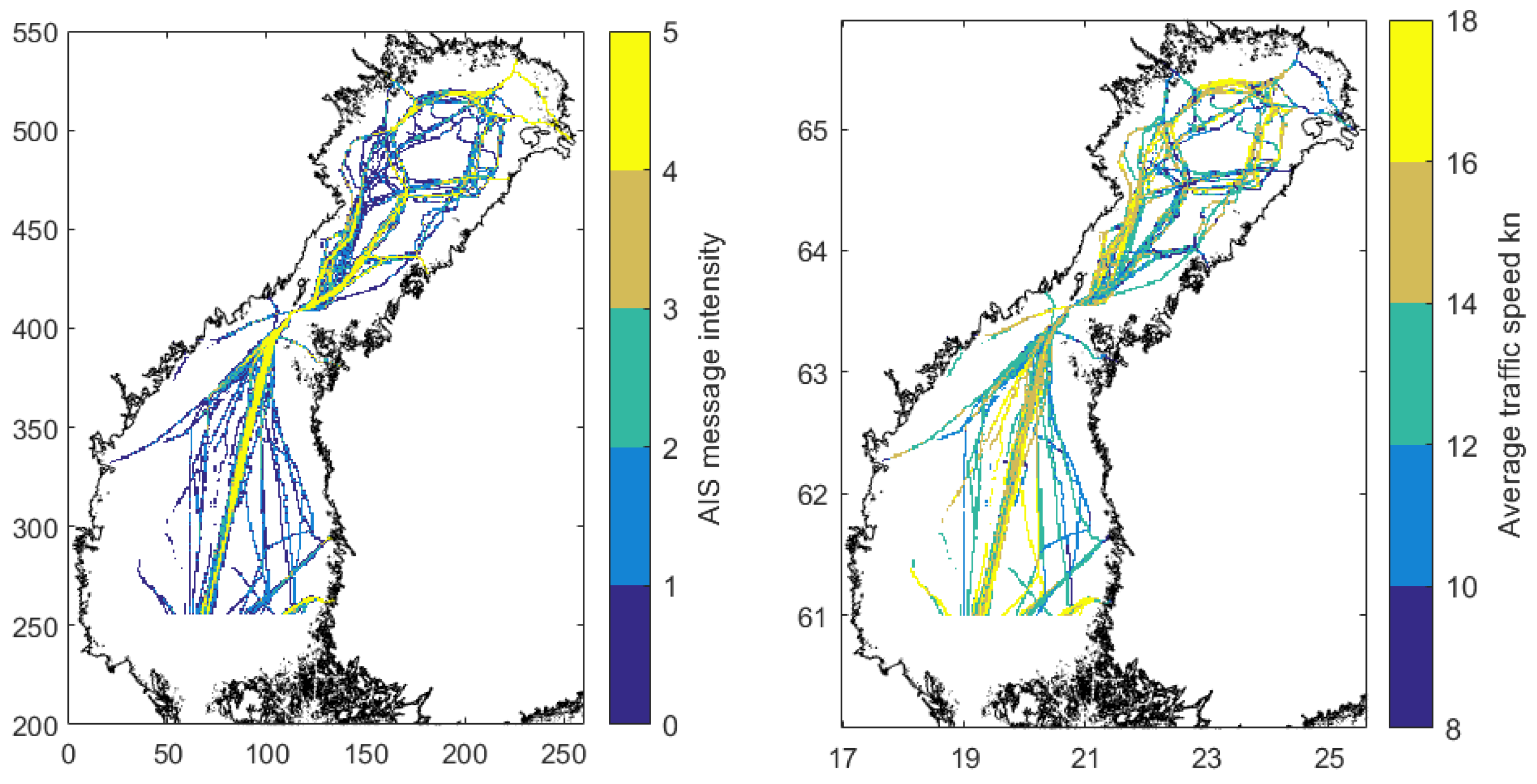
The range of FTA terrestrial stations is limited. The coverage of the data decreases when moving close to the Western coastline of the Sea of Bothnia. For the Bay of Bothnia, the coverage is complete and the AIS message intensity (
Figure 2) is measured by the number of position reports from
square nautical miles per day for the IA Super ship class. The concentration of traffic to the main ice channels in the Bay of Bothnia is discernible. Outside these routes, the ships visited almost all locations within the pack ice except for an area in the middle of Bay of Bothnia where the ice was very thick (
Figure 1). In the fast ice zone, the traffic is constrained to narrow channels leading to ports. The average traffic speed is the monthly average of speed records from a
square nautical miles for the ship class IA Super. It is a summarizing descriptor that also includes ships that have been idling. It was observed that the traffic speed generally increased with a decreasing intensity in the Bay of Bothnia. This is due to powerful ships selecting routes outside the main ice channels occupied by the convoys of weaker ships led by icebreakers.
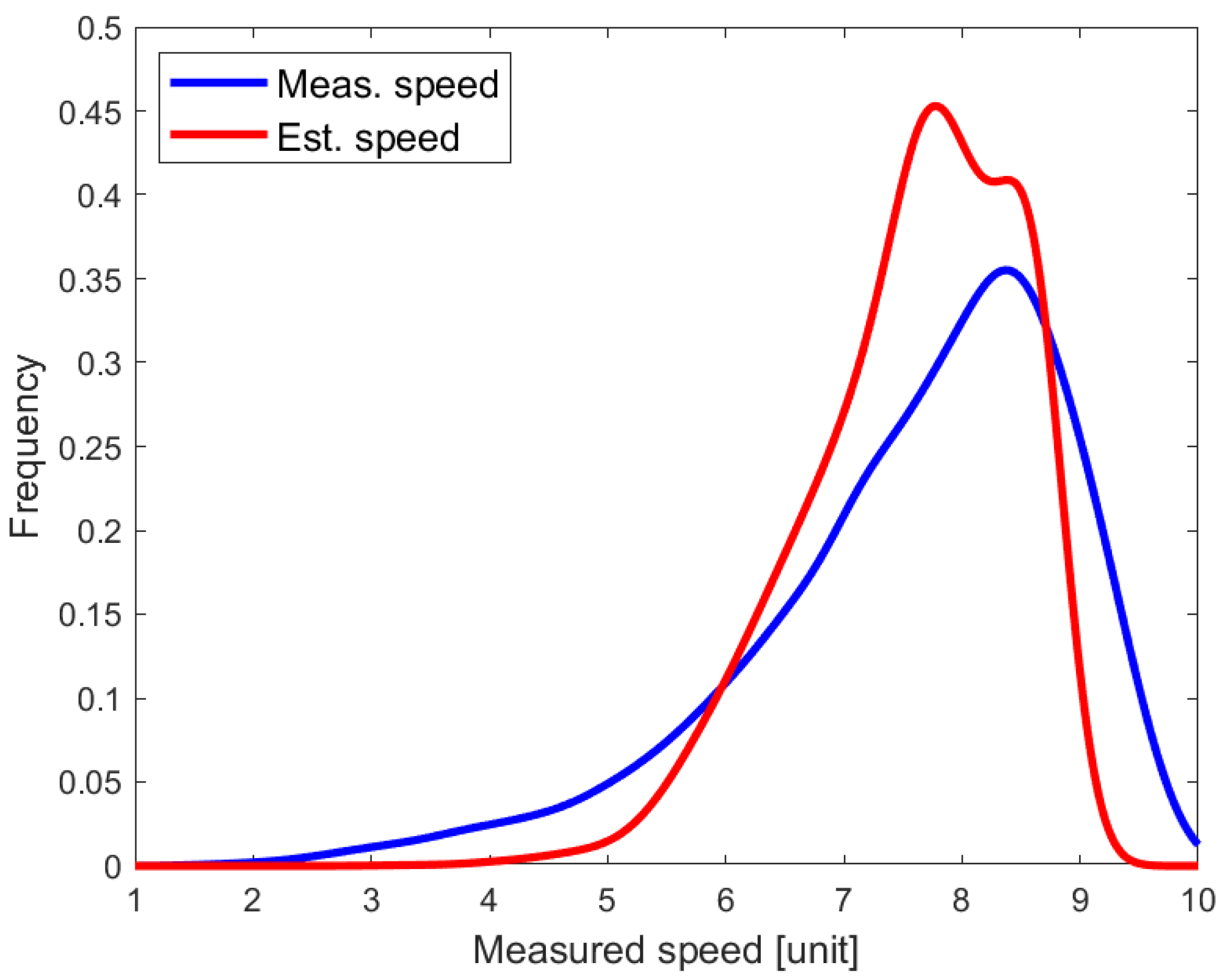
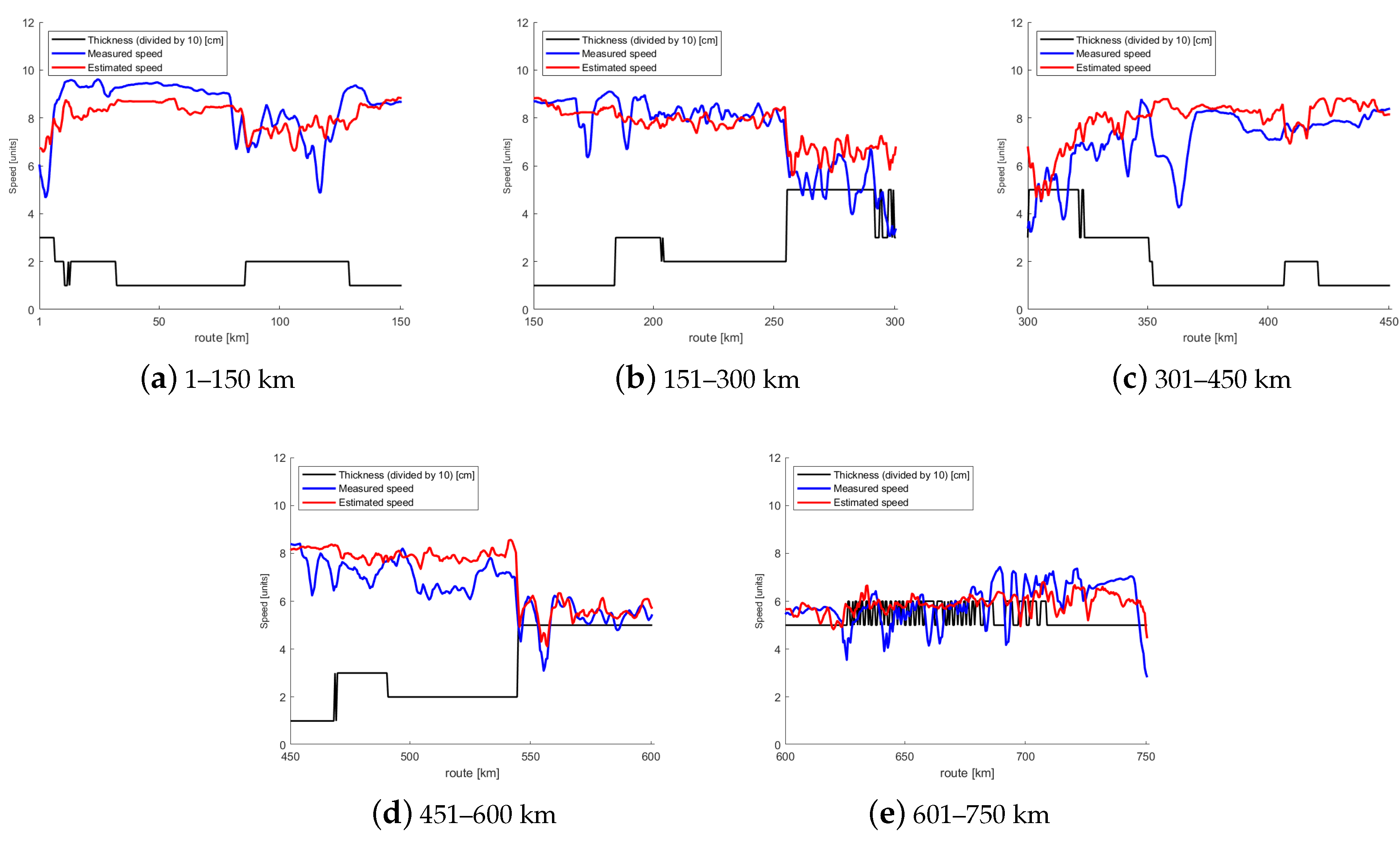
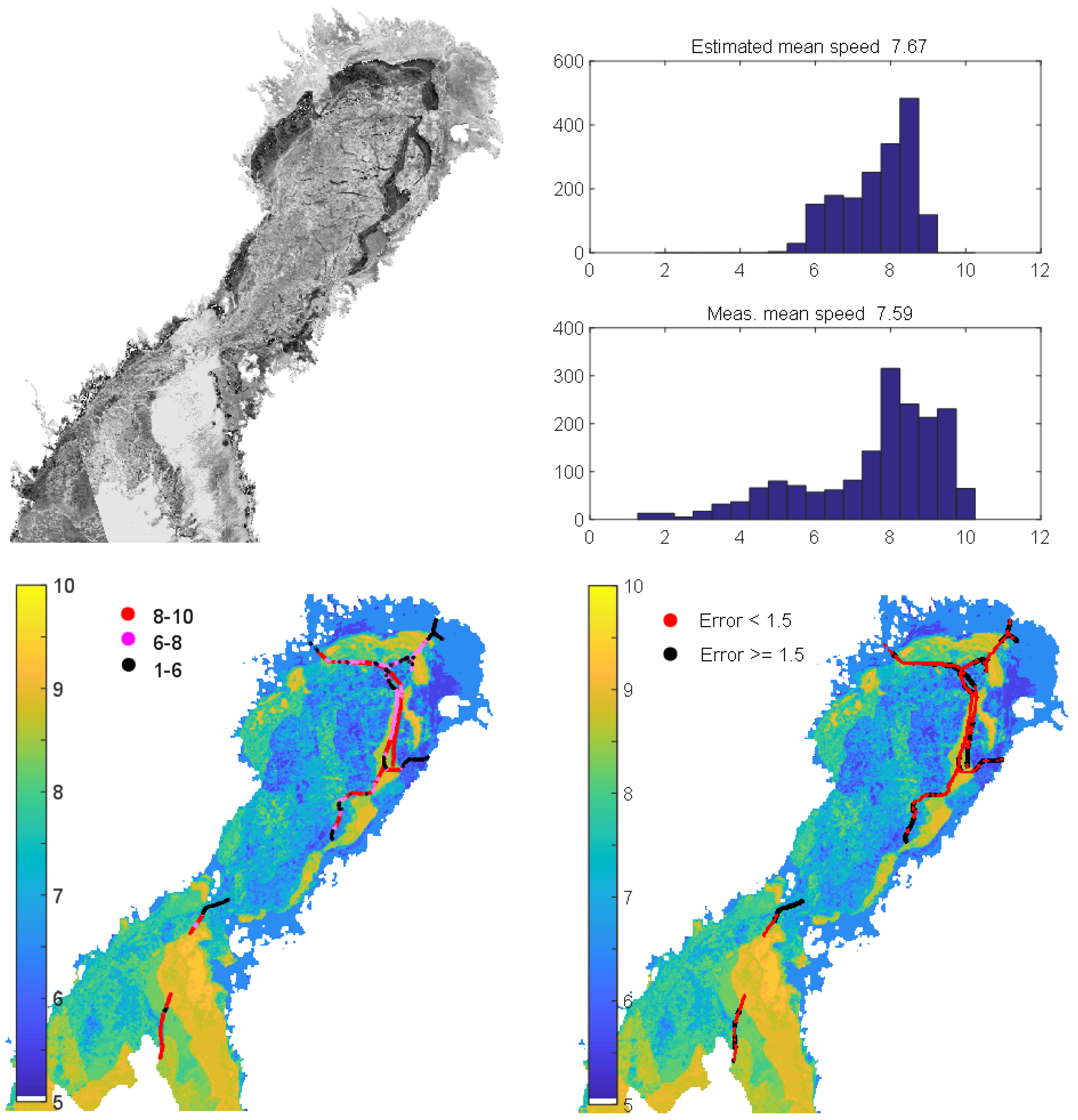
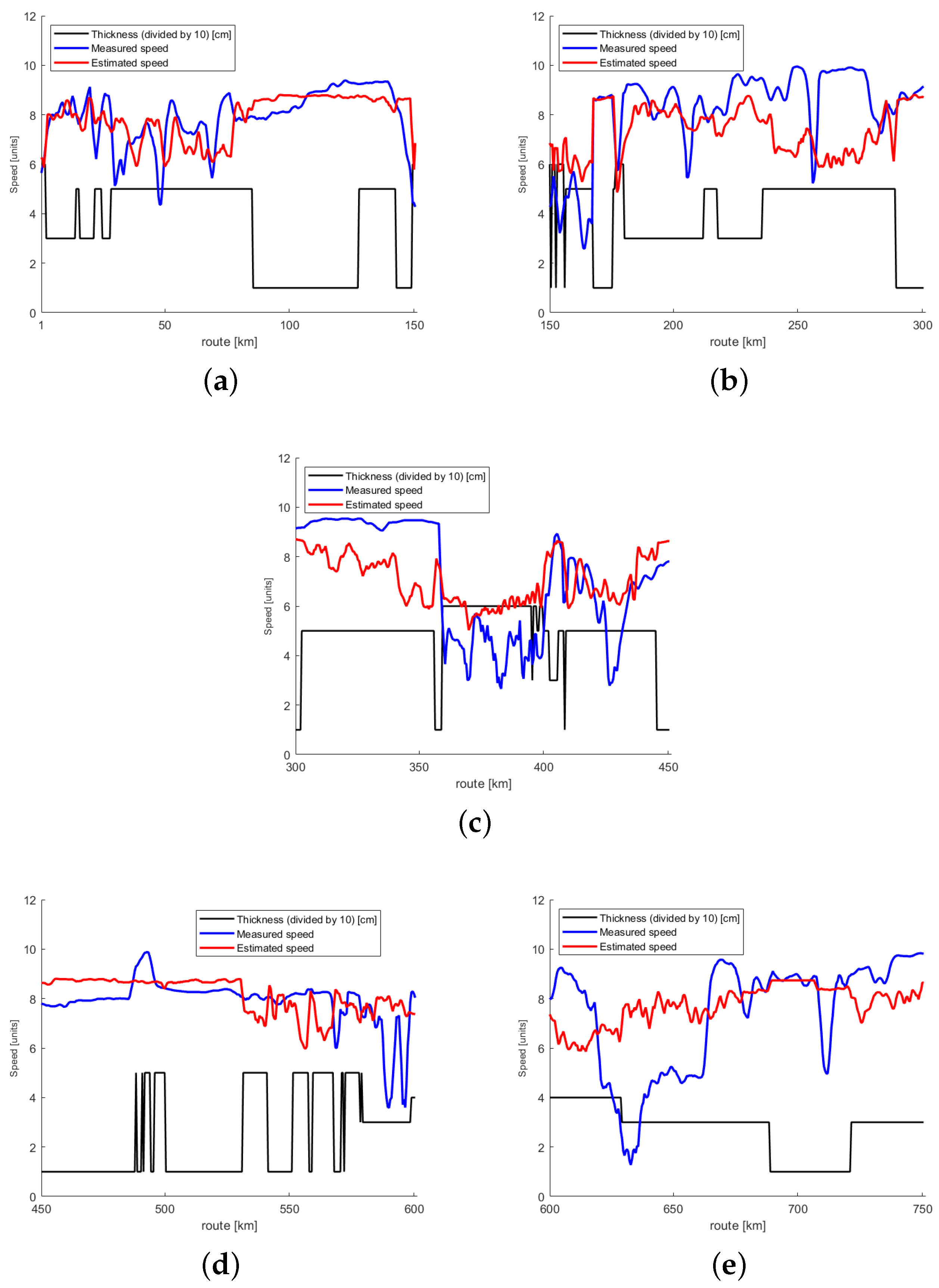
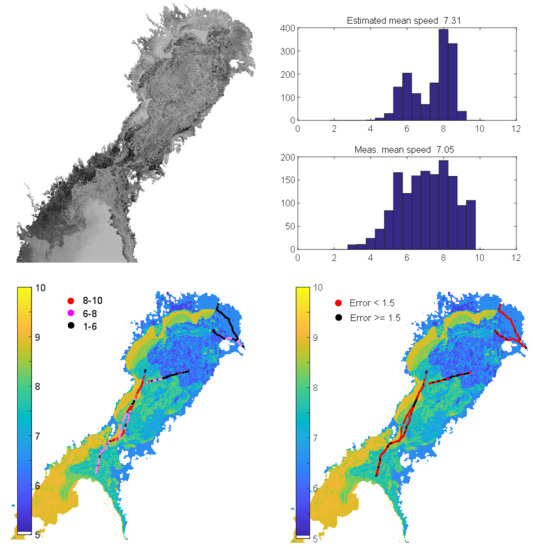
In total, 21 IA Super cargo ships operated in March 2013 in our test area north of latitude 61 N. There were sister ships, and the number of ships with different particulars was 13. They comprised 700,000 position reports of independent navigation, and made up a total of 55 voyages. The size ranged from 4000 to 28,000 gross tonnage, and the length of vessels ranged from 105 to 215 m. We imposed a threshold speed of 1 knot to eliminate data of idling ships drifting in the ice. From the voyages, we further selected continuous test routes that constituted the basic data for our analysis. If a voyage took place on more than one calendar day, the track covered during each different day was regarded as a different route. The data for the ships contained gaps whenever the independency condition did not hold any longer, and less frequently if the AIS messages were not received from the Western part of the Sea of Bothnia. To eliminate short AIS records, it was required that only such transects for which at least 2000 AIS measurements were recorded consecutively during one day were included in the analysis. Finally, there were 139 routes in the data set, with a total length of 38,500 km. The fraction of the data used in the training of the regression model was about 23%, and the rest of the data was used in the testing. The training data were created by randomly selecting 30 routes from the AIS data set.
The ships generally had different icebreaking capabilities and ice transit speeds. It is possible to establish comparability by considering their speed relative to their maximum speed, which is often also their open water speed. Thus, in the analysis, we normalized the speed for each ship to a dimensionless unit of 0–10, where 10 indicates a high speed for each particular vessel. Speeds over 20 knots were considered to be outliers, and their normalised speed was set was set to 10 units. Hence, the formula from knots to units was
where
v is the speed of an individual ship in knots and
is the maximum speed recorded for the ship during March. We call the unit of the normalized speed
simply “unit”. Approximately 2% of all AIS speeds in the training were set to 10 units. After the normalization, the relatively few recorded extreme speeds over 20 knots did not affect the estimation process as outliers.
2.3. RADARSAT-2 SAR Imagery
The SAR imagery used in this study was RADARSAT-2 ScanSAR Wide (RS-2 SCWA) dual-polarized imagery with the HH/HV polarization combination. The nominal size of an RS-2 SCWA image was approximately 500 × 500 km, and the pixel size was 50 m. The spatial resolution was approximately 73–163 m × 100 m (range by azimuth). The incidence angle (
) varied from
to
. The equivalent number of looks (ENL) was larger than six. The noise equivalent,
, at both HH- and HV-polarizations was around −28 ± 2.5 dB, and the absolute accuracy of
was better than 1 dB [
27].
The preprocessing of the RS-2 SCWA images consisted of the calibration of
and
according to information included in the SAR images, georectification with Geospatial Data Abstraction Library (GDAL) software and calculation of the incidence angle,
. The incidence angle correction and land masking was performed using in-house-developed software. First, the data were rectified into the Mercator projection with a pixel size of 100 m and a reference latitude of
N. This georectification is compatible with the FIS ice charts and the navigation systems of the Finnish and Swedish icebreakers. During HV-polarization, the SAR
values are close to the instrument noise floor (around −28 dB for RS-2 SCWA mode), and the noise floor (noise equivalent
) varies along the across-track direction. The calculation of the incidence angle correction was described in detail in reference [
28] for the HH channel and in reference [
29] for the HV channel.
A SAR mosaic covering the whole Baltic Sea was formed each day by employing enough processed RS-2 SAR images that there were no holes in the coverage of sea areas. The Baltic Sea SAR images were used to update the SAR mosaic twice daily. The number of images used to update the SAR mosaic over the study area varied from 0 to 1 SAR images per day. On average, the study area was partly covered by one new SAR image each day. For a specific location in the study area the SAR imagery was 0–2 days old, depending on the last acquisition time. The daily information from the acquisition of SAR data during the test period is shown in Table 2 in
Section 4.6. Due to the large size of the SAR images in the SAR mosaics, the resolution was downsampled to 500 m.
2.4. Ice Charts
In our analysis, we also used the daily manual ice charts provided by the FIS over the Baltic Sea. The ice charting software divides the ice cover into polygons described by quantitative parameters and qualitative characterizations. The polygons and their quantitative parameters in ice charts were also saved as numerical latitude–longitude grids using the ice charting software. The usual grid resolution was degree of latitude and degree of longitude, which is approximately 1 nautical mile in both directions at N. Parameters in the grid format included the typical, minimum and maximum thicknesses of the ice level, ice concentration and the degree of ice ridging. These grids were converted to the Mercator projection used in the rectification of the SAR imagery. When combining the ice chart grids with the SAR mosaic, the nearest neighbor interpolation was used to find the chart value for the SAR pixels.
The information in the FIS ice charts was typically reported for rather large areas (hundreds of square kilometers). The level ice thickness values are based on the observations made by the operating icebreakers. According to the annual surveys where in-situ level ice thicknesses and typical level ice thicknesses by manual ice charts were compared, the mean difference was less than 10 cm (private communication by Alexandru Gegiuc). In the graphic FIS charts, the thickness values are given as a variation range between the minimum and maximum thicknesses. The gridded charts also include the typical thickness, which is the mean of the range. This value is also rounded to the nearest 5 cm if the result is at least 15 cm. We chose to use the mean value without rounding in order to have a denser gradation of thickness. The sea-ice concentration at FIS is based mainly on the SAR imagery, and—if the conditions allow—also optical data. This variable has an uncertainty of approximately 10% according to the ice experts at FIS.
5. Discussion
5.1. Uncertainties
Our approach was developed from the basic idea that ship speeds change with ce conditions in a consistent manner. The starting assumption was that average speed and speed variation correlate with the average ice thickness and thickness variation. However, there are missing pieces that make the implementation of this idea problematic when relying on AIS data alone. Firstly, without propulsion power it is not known for sure what speed changes are due to ice conditions. There are also engineering models that derive speeds for specific ship types from propulsion power, hull particulars, and ice conditions. These would provide a basis for predicting the ice performance of some ship types from the observed performance of another ship type. The lacking uniformity of icegoing capabilities of ships is the second missing piece in an approach relying solely on AIS data. The third is that most ships follow frequently navigated ice channels. For the channels, not only the ice resistance but also dynamic and thermal evolution are different from the surrounding intact ice cover.
We sought to minimize these problems by restricting the analysis to independently navigating IA Super ships. These are mostly able to make steady progress in Baltic Sea ice conditions and do not change their power setting much. For the IA Super class, the ice performance also varies much less between different ship types than is the case for lower ice classes. Finally, the IA Super ships often select routes outside the main channels in order to bypass convoys. On the other hand, although the progress in the channels is easier, they still display thickness variation in the surrounding ice cover; in particular, there are thick channel rubble sections remaining from broken ridges.
The uncertainties from channel navigation, a lack of propulsion power and different performance capabilities could be further reduced by also considering the variation in speed over short time scales corresponding to few ship lengths of transit. As such, variation is induced by the ridges. The speed should drop at the same locations for all ships. Adding the speed variation to the present approach could not only improve the results, but provide a method to quantify ice ridging from SAR images.
The inclusion of lower ice classes generally greatly increases the amount of data. The present results intended to demonstrate the soundness of the approach using a limited dataset, scratching the surface of the data comprising billions of AIS position reports from ten years and covering a wide range of ice conditions. Apart from increasing the amount of data, there are several possible future lines of research that are addressed in the next section.
5.2. Future Prospects of the Approach
To the best knowledge of the authors, this is the first attempt to generate ice navigation information from the direct classification of SAR imagery with ship data. Similar methods have great application potential. Approaches seeking to generate navigationally relevant information by linking SAR signatures with ship performance can be divided into three types: data-driven, classification-oriented and hybrid. In the Baltic Sea, more than 60 million position reports from ice-going ships are obtained every month, and it is perfectly feasible to generate maps of navigational difficulty from this data alone. A primitive approach would simply identify the SAR locations where several ships have difficulty. This cumulating information could be transferred to the next image for the part that has remained similar. In the first instance, this could be done by the charting experts of the Finnish Ice Service, as a similar task is already a daily routine for standard ice chart variables. This is helped by the fact that most traffic is constrained to ice channels which are rather easily identified. Channels also make the problem essentially one-dimensional, as along-track conditions are sufficient. Although navigation outside the main channels is common (see
Figure 2), providing SAR-based navigability indices for them would be very useful for ships.
On the other hand, our approach is oriented towards SAR classification. Such methods seek to extrapolate the information gained from ship responses to certain SAR features to the whole image area. The extrapolated parameter can be speed (as in the present case), some numeral for navigational difficulty, or the load level experienced by the ship. There are also options for partial but more reliable extrapolation. The areas with difficult ice conditions are often discernible band-like formations created by previous stormy periods. The difficulty experienced when transsecting the band is likely to be close to the truth when extrapolated to the whole band. This is especially true for brash barriers (windrows) which usually have homogeneous properties in the along-band direction.
The present approach also has application potential in ice routing, where the objective is to optimize the route with respect to travel time or fuel consumption. The bottleneck has been that ice information has lacked the necessary detail for the calculation of ship speed from ice conditions. Our approach, in fact, indirectly demonstrates that routing is feasible in the Baltic Sea. Approximately one-quarter of the AIS speeds in our data set were used for training, and the rest were used for validation. In a similar manner, the ship data collected during the first quarter of some time period could be used to generate a speed map used in routing during the remaining period. The data from the routed ships could, in turn, be used to update the speed maps for the ships arriving later. The applied regression method works better the more comprehensive its training data set is. Therefore, such an incremental increase of the training data set should constantly improve the estimates.
In a hybrid approach, the AIS-based SAR classification is combined with other classification methods, especially those seeking to retrieve ice thickness, ice concentration and ridging parameters. Our approach applied the thickness and concentration from ice charts, but it could also have used parameters from SAR-based products that are used in FIS ice charting [
1]. A promising direction of research is integrating AIS-based SAR classification with methods seeking to retrieve ridging for SAR. In reference [
8], we introduced a method to retrieve the degree of ice ridging used in ice charts. Thus, one evident step would be to add the degree of ice ridging as one categorical variable to the current regression model. Further developments could also utilize ice forecast models and kinematic algorithms for ice drift. Additionally, engineering models describing how ship performance depends on ice conditions could be used to theoretically connect the AIS-based SAR methods with the existing methods of ice parameter retrieval from SAR.