Fast Semi-Supervised Unmixing of Hyperspectral Image by Mutual Coherence Reduction and Recursive PCA
Abstract
1. Introduction
- Some algorithms require high computational time.
- These algorithms tend to perform poorly when the mutual coherence of library is high.
2. Signal Model for Linear Unmixing
2.1. Semi-Supervised Unmixing
2.1.1. Dictionary Pruning
- Some algorithms require high computational time.
- These algorithms tend to perform poorly when the mutual coherence of library is high.
3. Proposed Dictionary Pruning Method
3.1. Noise Removal by Multi Linear Regression
3.2. Estimation of the Number of Endmembers
3.3. Mutual Coherence Reduction
| Algorithm 1: Reduction of Mutual Coherence Reduction of Spectral Library |
| Input: Spectral library with high mutual coherence |
| Output: Spectral library with relatively lower mutual coherence |
| Initialization: Select a random initial projection matrix |
| 1: Compute the transformed library |
| 2: Compute the Gram matrix |
| 3: Set the threshold value t |
| 4: Compute t-averaged mutual coherence according to Equation (17) |
| 5: while The optimization problem Equation (20) not converged do |
| 6: Normalize M to unit length |
| 7: Shrink the elements of G according to
|
| 8: Obtain the square root of the Gram matrix M according to |
| 9: Apply SVD on M and reduce the rank of M to m |
| 10: end while |
3.4. Dictionary Pruning by Recursive PCA
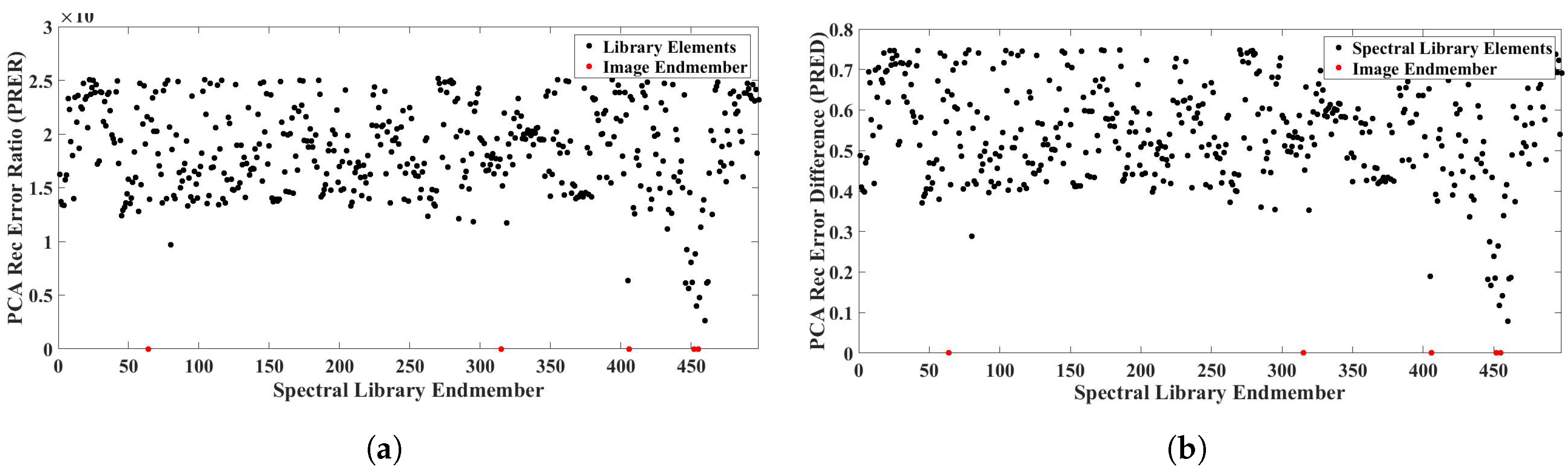
3.4.1. Proposed PCA Reconstruction Error Ratio Criteria (PRER)
3.4.2. Proposed PCA Reconstruction Error Difference Criteria (PRED)
| Algorithm 2: PCA Reconstruction Error Ratio Criteria (PRER) for Dictionary Pruning |
| Input: Hyperspectral image data , Spectral library , Number of endmembers |
| Output: Index of the pruned library , Pruned library |
| Initialization: |
| 1: Transform the data into -dimension by PCA. Record PCA reconstruction error . |
| 2: for and do |
| 3: Append each library element with the data matrix according to |
| 4: Calculate the reconstruction error by transforming the appended data into -dimension by PCA. Obtained reconstruction error |
| 5: Calculate PCA reconstruction error ratio criteria |
| 6:end for |
| 7: Consider the -elements corresponding to the minimum reconstruction error ratio as endmembers. Index of pruned library . |
| 8: Pruned library |
| 9: return Index of the pruned library elements , pruned library |
| Algorithm 3: Dictionary Pruning by PCA Reconstruction Error Difference Criteria (PRED) for Dictionary Pruning |
| Input: Hyperspectral image data , Spectral library , Number of endmembers P |
| Output: Index of the pruned library , Pruned library |
| Initialization: |
| Transform the data into -dimension by PCA. PCA reconstruction error |
| 2: for and do |
| Append each library element with the data matrix |
| 4: Transform the data into -dimension by PCA and record the reconstruction error |
| Calculate the difference in reconstruction error |
| 6: end for |
| Consider the P-elements corresponding to the minimum reconstruction error difference as image endmember index . |
| 8: Obtain pruned library by |
| return Index of the pruned library elements and Pruned library |
3.5. Recursive Principal Component Analysis
3.6. Abundance Computation
4. Results
4.1. Performance Measures
- Signal to Reconstruction Error (SRE)Signal to reconstruction error (SRE) denotes the relative power of reconstructed data with respect to the actual data.where, is the hyperspectral data reconstructed by the unmixing or dictionary pruning algorithm. Better unmixing leads to lower reconstruction error, which in turn increases SRE.
- Probability of DetectionThe probability of detection defines the number of spectral library endmembers accurately selected according to the formulawhere is the indices corresponding to the actual spectral library elements present in the image and is the indices corresponding to the estimated spectral library elements of the pruned library.
4.2. Description of Data
4.2.1. Synthetic Image Experiments
4.2.2. Real Image Experiments
4.3. Algorithms Compared
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Van der Meer, F.D.; Van der Werff, H.M.; Van Ruitenbeek, F.J.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Van Der Meijde, M.; Carranza, E.J.M.; De Smeth, J.B.; Woldai, T. Multi-and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Chi, J.; Crawford, M.M. Spectral unmixing-based crop residue estimation using hyperspectral remote sensing data: A case study at Purdue university. IEEE J. Sel. Top. App. Earth Obs. Remote Sens. 2014, 7, 2531–2539. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Kruse, F.A.; Boardman, J.W.; Huntington, J.F. Comparison of airborne hyperspectral data and EO-1 Hyperion for mineral mapping. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1388–1400. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Soc. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Chang, C.I. Hyperspectral Data Exploitation: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Ma, W.K.; Bioucas-Dias, J.M.; Chan, T.H.; Gillis, N.; Gader, P.; Plaza, A.J.; Ambikapathi, A.; Chi, C.Y. A signal processing perspective on hyperspectral unmixing: Insights from remote sensing. IEEE Signal Process. Mag. 2014, 31, 67–81. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Dictionary pruning in sparse unmixing of hyperspectral data. In Proceedings of the 2012 4th Workshop on Hyperspectral Image and Signal Processing (WHISPERS), Shanghai, China, 4–7 June 2012; pp. 1–4. [Google Scholar]
- Zou, J.; Lan, J.; Shao, Y. A Hierarchical Sparsity Unmixing Method to Address Endmember Variability in Hyperspectral Image. Remote Sens. 2018, 10, 738. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Chang, C.I.; Plaza, A. A fast iterative algorithm for implementation of pixel purity index. IEEE Geosci. Remote Sens. Lett. 2006, 3, 63–67. [Google Scholar] [CrossRef]
- Ifarraguerri, A.; Chang, C.I. Multispectral and hyperspectral image analysis with convex cones. IEEE Trans. Geosci. Remote Sens. 1999, 37, 756–770. [Google Scholar] [CrossRef]
- Chan, T.H.; Chi, C.Y.; Huang, Y.M.; Ma, W.K. A convex analysis-based minimum-volume enclosing simplex algorithm for hyperspectral unmixing. IEEE Trans. Signal Process. 2009, 57, 4418–4432. [Google Scholar] [CrossRef]
- Ambikapathi, A.; Chan, T.H.; Ma, W.K.; Chi, C.Y. Chance-constrained robust minimum-volume enclosing simplex algorithm for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4194–4209. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M. Minimum volume simplex analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2008, 3, 250–253. [Google Scholar]
- Berman, M.; Kiiveri, H.; Lagerstrom, R.; Ernst, A.; Dunne, R.; Huntington, J.F. ICE: A statistical approach to identifying endmembers in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2085–2095. [Google Scholar] [CrossRef]
- Chang, C.I.; Wu, C.C.; Liu, W.; Ouyang, Y.C. A new growing method for simplex-based endmember extraction algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2804–2819. [Google Scholar] [CrossRef]
- Wang, J.; Chang, C.I. Applications of independent component analysis in endmember extraction and abundance quantification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2601–2616. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M. Does independent component analysis play a role in unmixing hyperspectral data? IEEE Trans. Geosci. Remote Sens. 2005, 43, 175–187. [Google Scholar] [CrossRef]
- Chiang, S.S.; Chang, C.I.; Ginsberg, I.W. Unsupervised hyperspectral image analysis using independent component analysis. IEEE Trans. Geosci. Remote Sens. 2000, 7, 3136–3138. [Google Scholar]
- Wang, N.; Du, B.; Zhang, L.; Zhang, L. An abundance characteristic-based independent component analysis for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 416–428. [Google Scholar] [CrossRef]
- Huang, R.; Li, X.; Zhao, L. Nonnegative Matrix Factorization with Data-Guided Constraints for Hyperspectral Unmixing. Remote Sens. 2017, 9, 1074. [Google Scholar] [CrossRef]
- Wang, N.; Du, B.; Zhang, L. An endmember dissimilarity constrained non-negative matrix factorization method for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Trans. Earth Obs. Remote Sens. 2013, 6, 554–569. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Rontogiannis, A.A.; Berberidis, K. Distributed blind hyperspectral unmixing via joint sparsity and low-rank constrained non-negative matrix factorization. IEEE Trans. Comput. Imaging 2017, 3, 160–174. [Google Scholar] [CrossRef]
- Arngren, M.; Schmidt, M.N.; Larsen, J. Unmixing of hyperspectral images using Bayesian non-negative matrix factorization with volume prior. J. Signal Process. Syst. 2011, 65, 479–496. [Google Scholar] [CrossRef]
- Jia, S.; Qian, Y. Constrained nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2009, 47, 161–173. [Google Scholar] [CrossRef]
- Huck, A.; Guillaume, M.; Blanc-Talon, J. Minimum dispersion constrained nonnegative matrix factorization to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2590–2602. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, S.; Zhang, H.; Wang, S.; Wang, Y. Bilateral Filter Regularized L2 Sparse Nonnegative Matrix Factorization for Hyperspectral Unmixing. Remote Sens. 2018, 10, 816. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Wang, D.; Shi, Z.; Cui, X. Robust Sparse Unmixing for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1348–1359. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Sparse unmixing of hyperspectral data with noise level estimation. Remote Sens. 2017, 9, 1166. [Google Scholar] [CrossRef]
- Rizkinia, M.; Okuda, M. Joint Local Abundance Sparse Unmixing for Hyperspectral Images. Remote Sens. 2017, 9, 1224. [Google Scholar] [CrossRef]
- Gong, M.; Li, H.; Luo, E.; Liu, J.; Liu, J. A multiobjective cooperative coevolutionary algorithm for hyperspectral sparse unmixing. IEEE Trans. Evol. Comput. 2017, 21, 234–248. [Google Scholar] [CrossRef]
- Feng, R.; Zhong, Y.; Zhang, L. Adaptive spatial regularization sparse unmixing strategy based on joint MAP for hyperspectral remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5791–5805. [Google Scholar] [CrossRef]
- Themelis, K.E.; Rontogiannis, A.A.; Koutroumbas, K.D. A novel hierarchical Bayesian approach for sparse semisupervised hyperspectral unmixing. IEEE Trans. Signal Process. 2012, 60, 585–599. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, Y.; Fang, F. Framelet-based sparse unmixing of hyperspectral images. IEEE Trans. Image Process. 2016, 25, 1516–1529. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Halimi, A.; Honeine, P.; Chen, B.; Zheng, N. Correntropy Maximization via ADMM: Application to Robust Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4944–4955. [Google Scholar] [CrossRef]
- Feng, R.; Wang, L.; Zhong, Y.; Zhang, L. Differentiable sparse unmixing based on Bregman divergence for hyperspectral remote sensing imagery. In Proceedings of the 2017 International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 598–601. [Google Scholar]
- Mei, S.; Du, Q.; He, M. Equivalent-sparse unmixing through spatial and spectral constrained endmember selection from an image-derived spectral library. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2665–2675. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Futuristic greedy approach to sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2157–2174. [Google Scholar] [CrossRef]
- Shi, Z.; Tang, W.; Duren, Z.; Jiang, Z. Subspace matching pursuit for sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3256–3274. [Google Scholar] [CrossRef]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M.J. Simultaneous sparse approximation via greedy pursuit. In Proceedings of the 2005 IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23–23 March 2005; Volume 5, p. v-721. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A.; Somers, B. MUSIC-CSR: Hyperspectral unmixing via multiple signal classification and collaborative sparse regression. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4364–4382. [Google Scholar] [CrossRef]
- Fu, X.; Ma, W.K.; Bioucas-Dias, J.M.; Chan, T.H. Semiblind hyperspectral unmixing in the presence of spectral library mismatches. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5171–5184. [Google Scholar] [CrossRef]
- Tang, W.; Shi, Z.; Wu, Y.; Zhang, C. Sparse unmixing of hyperspectral data using spectral a priori information. IEEE Trans. Geosci. Remote Sens. 2015, 53, 770–783. [Google Scholar] [CrossRef]
- Wang, R.; Li, H.C.; Liao, W.; Huang, X.; Philips, W. Centralized collaborative sparse unmixing for hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1949–1962. [Google Scholar] [CrossRef]
- Zhao, X.L.; Wang, F.; Huang, T.Z.; Ng, M.K.; Plemmons, R.J. Deblurring and sparse unmixing for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4045–4058. [Google Scholar] [CrossRef]
- Tang, W.; Shi, Z.; Wu, Y. Regularized simultaneous forward–backward greedy algorithm for sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5271–5288. [Google Scholar] [CrossRef]
- Das, S.; Routray, A.; Deb, A.K. Hyperspectral Unmixing by Nuclear Norm Difference Maximization based Dictionary Pruning. arXiv, 2018; arXiv:1806.00864. [Google Scholar]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral unmixing with robust collaborative sparse regression. Remote Sens. 2016, 8, 588. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Chang, C.I.; Du, Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2004, 42, 608–619. [Google Scholar] [CrossRef]
- Acito, N.; Diani, M.; Corsini, G. Hyperspectral signal subspace identification in the presence of rare vectors and signal-dependent noise. IEEE Trans. Geosci. Remote Sens. 2013, 51, 283–299. [Google Scholar] [CrossRef]
- Das, S.; Routray, A.; Deb, A.K. Noise robust estimation of number of endmembers in a hyperspectral image by Eigenvalue based gap index. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 19 October 2017; pp. 1–5. [Google Scholar]
- Das, S.; Kundu, J.N.; Routray, A. Estimation of number of endmembers in a Hyperspectral image using Eigen thresholding. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–5. [Google Scholar]
- Sumarsono, A.; Du, Q. Low-rank subspace representation for estimating the number of signal subspaces in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6286–6292. [Google Scholar] [CrossRef]
- Asadi, H.; Seyfe, B. Source number estimation via entropy estimation of eigenvalues (EEE) in Gaussian and non-Gaussian noise. arXiv 2013, arXiv:1311.6051. [Google Scholar]
- Chang, C.I.; Xiong, W.; Chen, H.M.; Chai, J.W. Maximum orthogonal subspace projection approach to estimating the number of spectral signal sources in hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 504–520. [Google Scholar] [CrossRef]
- Chang, C.I.; Xiong, W.; Wen, C.H. A theory of high-order statistics-based virtual dimensionality for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 188–208. [Google Scholar] [CrossRef]
- Rasti, B.; Ulfarsson, M.O.; Sveinsson, J.R. Hyperspectral subspace identification using SURE. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2481–2485. [Google Scholar] [CrossRef]
- Ambikapathi, A.; Chan, T.H.; Chi, C.Y. Convex geometry based estimation of number of endmembers in hyperspectral images. In Proceedings of the 2012 IEEE International Conference onAcoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 1233–1236. [Google Scholar]
- Heylen, R.; Parente, M.; Scheunders, P. Estimation of the number of endmembers in a hyperspectral image via the hubness phenomenon. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2191–2200. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Xia, P.; Zhou, S.; Giannakis, G.B. Achieving the Welch bound with difference sets. IEEE Trans. Inf. Theory 2005, 51, 1900–1907. [Google Scholar] [CrossRef]
- Elad, M. Optimized projections for compressed sensing. IEEE Trans. Signal Process. 2007, 55, 5695–5702. [Google Scholar] [CrossRef]
- Liu, H.; Song, B.; Qin, H.; Qiu, Z. An adaptive-ADMM algorithm with support and signal value detection for compressed sensing. IEEE Signal Process. Lett. 2013, 20, 315–318. [Google Scholar] [CrossRef]
- Craig, M.D. Minimum-volume transforPArlettms for remotely sensed data. IEEE Trans. Geosci. Remote Sens. 1994, 32, 542–552. [Google Scholar] [CrossRef]
- Zhu, F. Hyperspectral Unmixing: Ground Truth Labeling, Datasets, Benchmark Performances and Survey. arXiv, 2017; arXiv:1708.05125. [Google Scholar]
- Gu, M.; Eisenstat, S.C. A divide-and-conquer algorithm for the symmetric tridiagonal eigenproblem. SIAM J. Matrix Anal. Appl. 1995, 16, 172–191. [Google Scholar] [CrossRef]
- Parlett, B.M. The Symmetric Eigenvalue Problem; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Li, W.; Yue, H.H.; Valle-Cervantes, S.; Qin, S.J. Recursive PCA for adaptive process monitoring. J. Process Control 2000, 10, 471–486. [Google Scholar] [CrossRef]
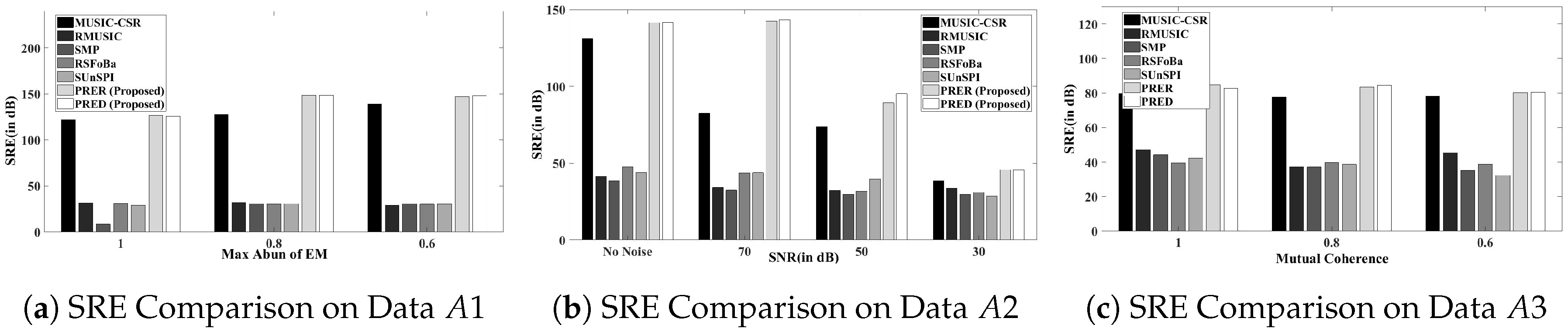




| nEm | Max Abun | MUSIC-CSR | RMUSIC | SMP | RSFoBa | SUnSPI | PRER | PRED |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.6 | 0.8 | 0.1724 | 0.2083 | 1 | 1 | |
| 1000 | 0.8 | 0.9 | 0.3 | 0.8 | 0.1724 | 0.2 | 1 | 1 |
| 0.6 | 0.9 | 0.4 | 0.6 | 0.1613 | 0.1852 | 1 | 1 | |
| 1 | 1 | 0.6 | 0.5 | 0.1563 | 0.2381 | 1 | 1 | |
| 500 | 0.8 | 0.9 | 0.4 | 0.5 | 0.1926 | 0.2083 | 1 | 1 |
| 0.6 | 0.9 | 0.2 | 0.5 | 0.1852 | 0.1926 | 1 | 0.9 |
| nEm | SNR (in dB) | MUSIC-CSR | RMUSIC | SMP | RSFoBa | SUnSPI | PRER | PRED |
|---|---|---|---|---|---|---|---|---|
| No Noise | 1 | 0.6 | 0.8 | 0.1923 | 0.1724 | 1 | 1 | |
| 70 | 1 | 0.3 | 0.8 | 0.1613 | 0.1563 | 1 | 1 | |
| 50 | 1 | 0.3 | 0.8 | 0.1515 | 0.1563 | 1 | 1 | |
| 5 | 30 | 1 | 0.2 | 0.6 | 0.1471 | 0.1429 | 1 | 1 |
| 20 | 0.8333 | 0.2 | 0.4166 | 0.1428 | 0.1351 | 1 | 0.8333 | |
| 10 | 0.625 | 0.1851 | 0.3846 | 0.1388 | 0.1351 | 0.8333 | 0.8333 | |
| 0 | 0.555 | 0.1786 | 0.3571 | 0.1315 | 0.1282 | 0.625 | 0.625 | |
| No Noise | 1 | 0.3 | 0.5 | 0.303 | 0.2381 | 1 | 1 | |
| 70 | 1 | 0.2 | 0.5 | 0.2703 | 0.222 | 1 | 1 | |
| 50 | 0.8 | 0.3 | 0.5 | 0.2632 | 0.1961 | 0.9 | 0.8 | |
| 10 | 30 | 0.8 | 0.2 | 0.5 | 0.2326 | 0.1887 | 0.9 | 0.9 |
| 20 | 0.7 | 0.2 | 0.3 | 0.1923 | 0.1785 | 0.9 | 0.8 | |
| 10 | 0.6 | 0.1923 | 0.2 | 0.1923 | 0.1724 | 0.8 | 0.8 | |
| 0 | 0.4 | 0.1887 | 0.1887 | 0.1724 | 0.1724 | 0.7 | 0.7 |
| Mutual Coherence | MUSIC-CSR | RMUSIC | SMP | RSFoBa | SUnSPI | PRER | PRED |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.6 | 0.5 | 0.1563 | 0.2381 | 1 | 1 |
| 0.8 | 0.8 | 0.5 | 0.6 | 0.1926 | 0.2083 | 1 | 1 |
| 0.6 | 0.9 | 0.2 | 0.5 | 0.1852 | 0.1926 | 0.9 | 0.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.; Routray, A.; Deb, A.K. Fast Semi-Supervised Unmixing of Hyperspectral Image by Mutual Coherence Reduction and Recursive PCA. Remote Sens. 2018, 10, 1106. https://doi.org/10.3390/rs10071106
Das S, Routray A, Deb AK. Fast Semi-Supervised Unmixing of Hyperspectral Image by Mutual Coherence Reduction and Recursive PCA. Remote Sensing. 2018; 10(7):1106. https://doi.org/10.3390/rs10071106
Chicago/Turabian StyleDas, Samiran, Aurobinda Routray, and Alok Kanti Deb. 2018. "Fast Semi-Supervised Unmixing of Hyperspectral Image by Mutual Coherence Reduction and Recursive PCA" Remote Sensing 10, no. 7: 1106. https://doi.org/10.3390/rs10071106
APA StyleDas, S., Routray, A., & Deb, A. K. (2018). Fast Semi-Supervised Unmixing of Hyperspectral Image by Mutual Coherence Reduction and Recursive PCA. Remote Sensing, 10(7), 1106. https://doi.org/10.3390/rs10071106






