Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows
Abstract
1. Introduction
2. Spectral UAV Sensors
2.1. Point Spectrometers
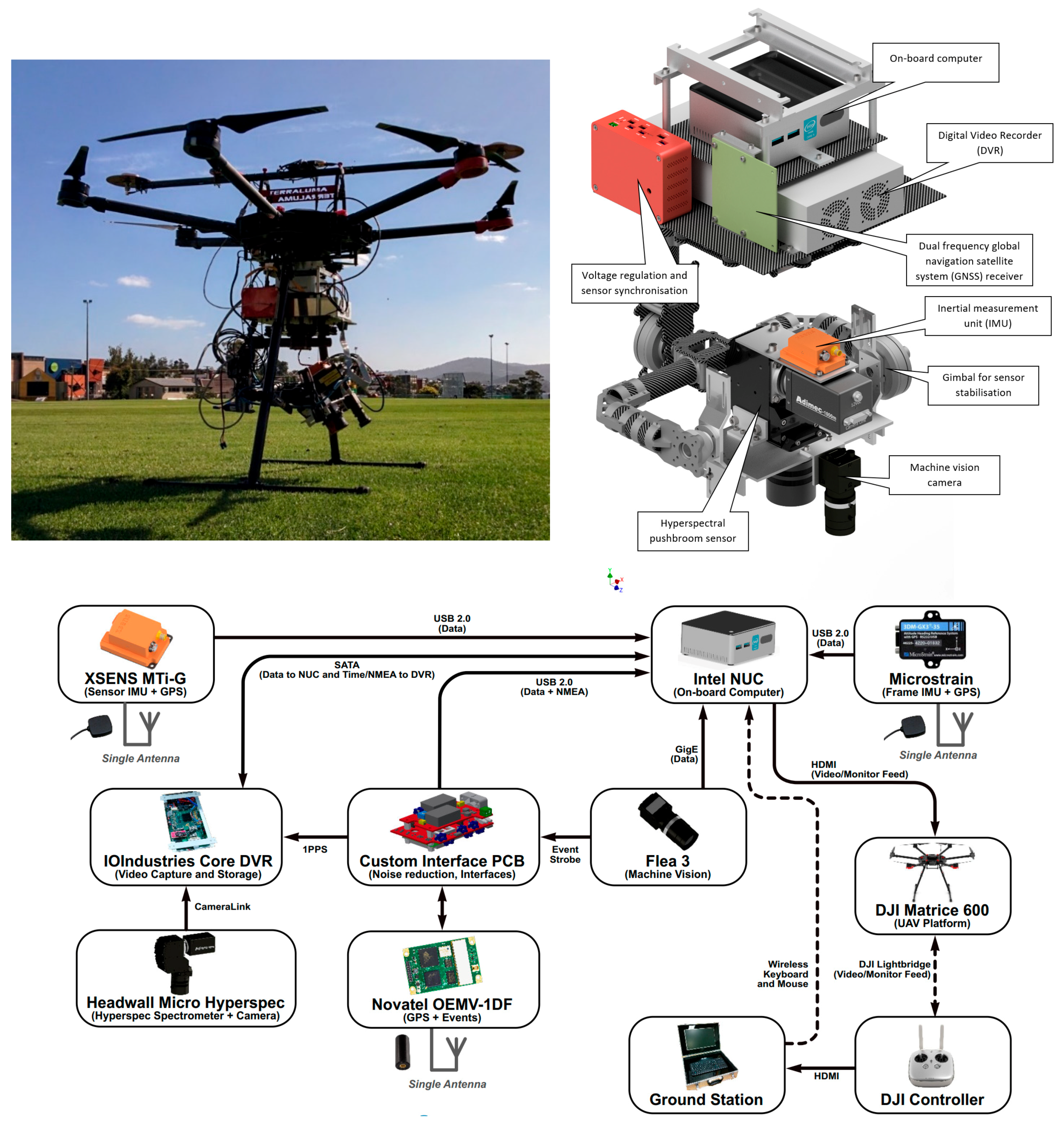
2.2. Pushbroom Spectrometers
2.3. Spectral 2D Imagers
2.3.1. Multi-Camera 2D Imagers
2.3.2. Sequential 2D Imagers
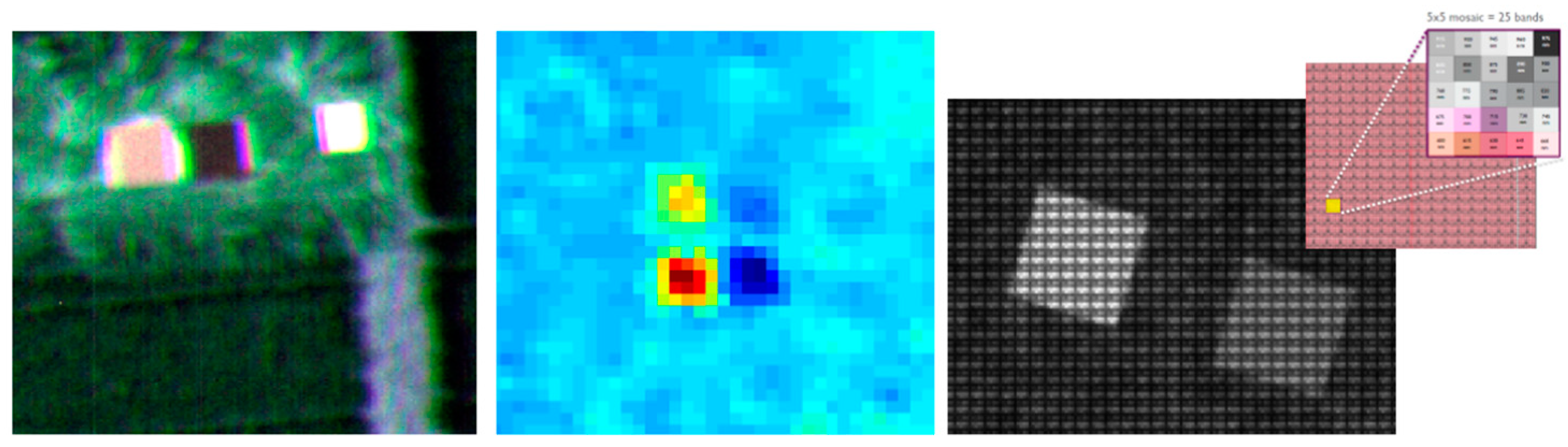
2.3.3. Snapshot 2D Imagers
Multi-point spectrometer
Mosaic filter-on-chip cameras
Spatiospectral filter-on-chip cameras
Characterized (modified) RGB cameras
3. Integration of Sensors and Geometric Processing
3.1. Georeferencing of Point Spectrometer Data
3.2. Georeferencing of Pushbroom Scanner Data
3.3. Georeferencing of 2D Imager Data
3.3.1. Snapshot 2D Imagers
3.3.2. Georeferencing of Sequential and Multi-Camera 2D Imagers
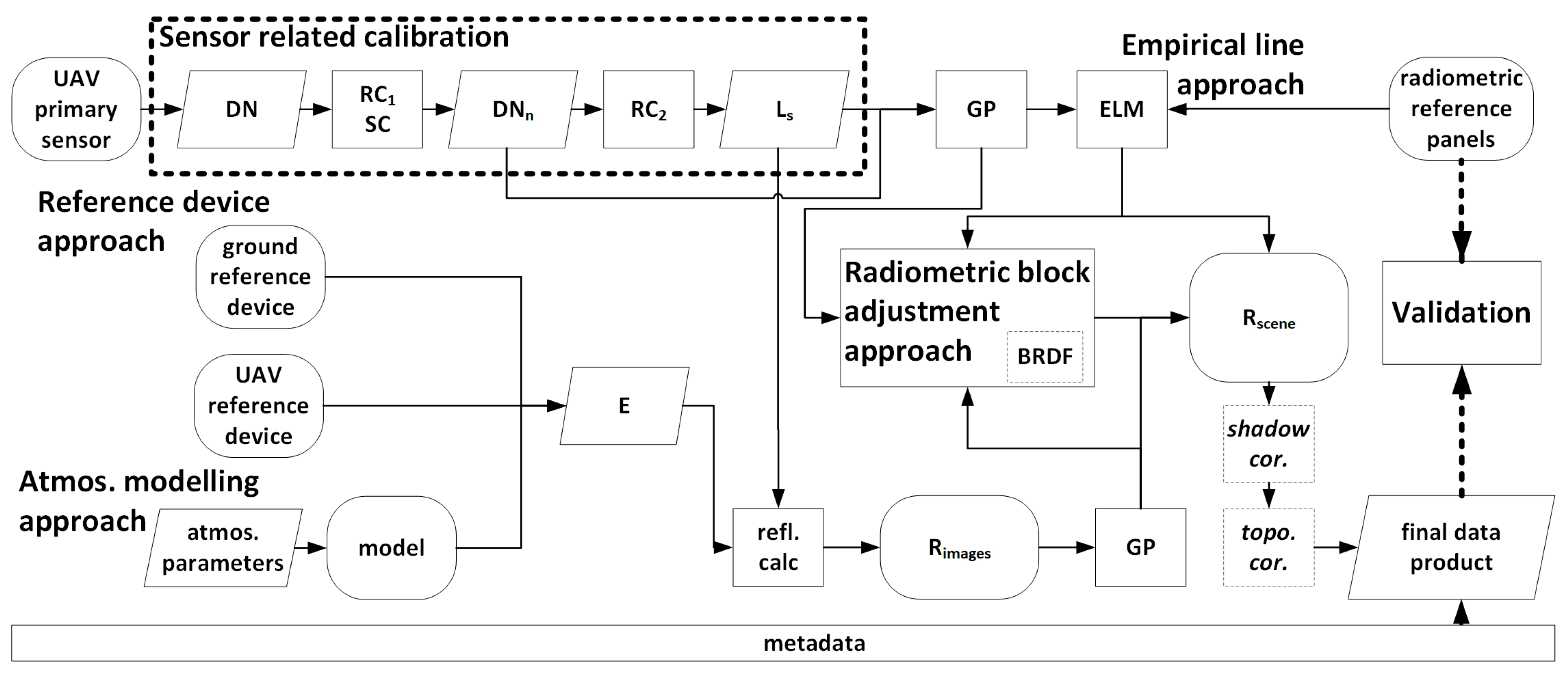
4. Radiometric Processing Workflow
4.1. General Procedure for Generating Reflectance Maps from UAVs
4.2. Sensor-Related Calibration
4.2.1. Relative Radiometric Calibration
4.2.2. Spectral Calibration
4.2.3. Absolute Radiometric Calibration
4.3. Scene Reflectance Generation
4.3.1. Reflectance Generation Based on Incident Irradiance
4.3.2. Empirical Line Method (ELM)
4.3.3. Atmospheric Correction
4.4. Scene Reflectance Correction
4.4.1. BRDF Correction
4.4.2. Topographic Correction
4.4.3. Shadow Correction
4.5. Radiometric Block Adjustment
5. Discussion and Best Practice
5.1. Sensors
5.2. Geometric Processing
Ground control points (GCPs)
On-board GNSS/IMU (direct georeferencing)
Structure from Motion (SfM)
Co-registration
5.3. Radiometric Processing
5.4. Data Products from UAV Sensing Systems
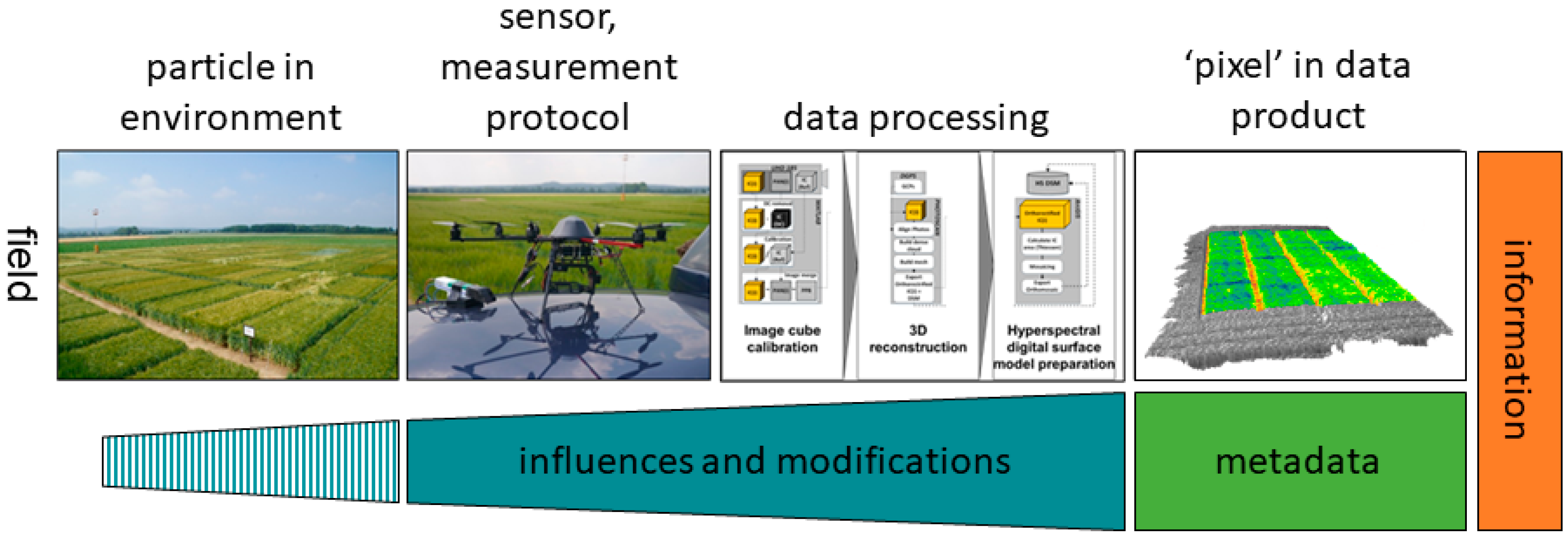
5.5. Quality Assurance and Metadata Information
5.6. Comparability between Sensing Systems
6. Conclusions—From Revolution to Maturity of UAV Spectral Remote Sensing
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zarco-Tejada, P.J. A new era in remote sensing of crops with unmanned robots. SPIE Newsroom 2008. [Google Scholar] [CrossRef]
- Sanchez-Azofeifa, A.; Antonio Guzmán, J.; Campos, C.A.; Castro, S.; Garcia-Millan, V.; Nightingale, J.; Rankine, C. Twenty-first century remote sensing technologies are revolutionizing the study of tropical forests. Biotropica 2017, 49, 604–619. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E.; et al. The future of Earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Rango, A.; Anderson, C.A.; Pierini, N.A.; Schreiner-McGraw, A.P.; Saripalli, S.; Laliberte, A.S. Ecohydrology with unmanned aerial vehicles. Ecosphere 2014, 5, art130. [Google Scholar] [CrossRef]
- Warner, T.A.; Cracknell, A.P. Unmanned aerial vehicles for environmental applications. Int. J. Remote Sens. 2017, 38, 2029–2036. [Google Scholar] [CrossRef]
- Toth, C.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Pajares, G. Overview and Current Status of Remote Sensing Applications Based on Unmanned Aerial Vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar] [CrossRef]
- Salamí, E.; Barrado, C.; Pastor, E. UAV Flight Experiments Applied to the Remote Sensing of Vegetated Areas. Remote Sens. 2014, 6, 11051–11081. [Google Scholar] [CrossRef]
- Rango, A.; Laliberte, A.S.; Herrick, J.E.; Winters, C.; Havstad, K.; Steele, C.; Browning, D. Unmanned aerial vehicle-based remote sensing for rangeland assessment, monitoring, and management. J. Appl. Remote Sens. 2009, 3, 033542. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Congalton, R.G.; Fenstermaker, L.K.; Jensen, J.R.; McGwire, K.C.; Tinney, L.R. Remote sensing and geographic information system data integration: Error sources and research issues. Photogramm. Eng. Remote Sens. 1991, 57, 677–687. [Google Scholar]
- Schaepman, M.E. Spectrodirectional remote sensing: From pixels to processes. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 204–223. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Pádua, L.; Vanko, J.; Hruška, J.; Adão, T.; Sousa, J.J.; Peres, E.; Morais, R. UAS, sensors, and data processing in agroforestry: A review towards practical applications. Int. J. Remote Sens. 2017, 38, 2349–2391. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Goetz, A.F.H.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Goetz, A.F.H. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Sellar, R.G.; Boreman, G.D. Classification of imaging spectrometers for remote sensing applications. Opt. Eng. 2005, 44, 013602. [Google Scholar] [CrossRef]
- Schickling, A.; Matveeva, M.; Damm, A.; Schween, J.; Wahner, A.; Graf, A.; Crewell, S.; Rascher, U. Combining Sun-Induced Chlorophyll Fluorescence and Photochemical Reflectance Index Improves Diurnal Modeling of Gross Primary Productivity. Remote Sens. 2016, 8, 574. [Google Scholar] [CrossRef]
- Burkart, A.; Cogliati, S.; Schickling, A.; Rascher, U. A Novel UAV-Based Ultra-Light Weight Spectrometer for Field Spectroscopy. IEEE Sens. J. 2014, 14, 62–67. [Google Scholar] [CrossRef]
- Ocean Optics, Inc. STS Series. Available online: https://oceanoptics.com/product-category/sts-series/ (accessed on 13 October 2017).
- Burkart, A.; Aasen, H.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, U. Angular Dependency of Hyperspectral Measurements over Wheat Characterized by a Novel UAV Based Goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar] [CrossRef]
- Garzonio, R.; Mauro, B.D.; Colombo, R.; Cogliati, S. Surface Reflectance and Sun-Induced Fluorescence Spectroscopy Measurements Using a Small Hyperspectral UAS. Remote Sens. 2017, 9, 472. [Google Scholar] [CrossRef]
- Zeng, C.; Richardson, M.; King, D.J. The impacts of environmental variables on water reflectance measured using a lightweight unmanned aerial vehicle (UAV)-based spectrometer system. ISPRS J. Photogramm. Remote Sens. 2017, 130, 217–230. [Google Scholar] [CrossRef]
- Burkhart, J.F.; Kylling, A.; Schaaf, C.B.; Wang, Z.; Bogren, W.; Storvold, R.; Solbø, S.; Pedersen, C.A.; Gerland, S. Unmanned aerial system nadir reflectance and MODIS nadir BRDF-adjusted surface reflectances intercompared over Greenland. Cryosphere 2017, 11, 1575–1589. [Google Scholar] [CrossRef]
- Zeng, C.; King, D.J.; Richardson, M.; Shan, B. Fusion of Multispectral Imagery and Spectrometer Data in UAV Remote Sensing. Remote Sens. 2017, 9, 696. [Google Scholar] [CrossRef]
- Link, J.; Senner, D.; Claupein, W. Developing and evaluating an aerial sensor platform (ASP) to collect multispectral data for deriving management decisions in precision farming. Comput. Electron. Agric. 2013, 94, 20–28. [Google Scholar] [CrossRef]
- Shang, S.; Lee, Z.; Lin, G.; Hu, C.; Shi, L.; Zhang, Y.; Li, X.; Wu, J.; Yan, J. Sensing an intense phytoplankton bloom in the western Taiwan Strait from radiometric measurements on a UAV. Remote Sens. Environ. 2017, 198, 85–94. [Google Scholar] [CrossRef]
- Uto, K.; Seki, H.; Saito, G.; Kosugi, Y.; Komatsu, T. Development of a Low-Cost Hyperspectral Whiskbroom Imager Using an Optical Fiber Bundle, a Swing Mirror, and Compact Spectrometers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3909–3925. [Google Scholar] [CrossRef]
- Jones, H.G.; Vaughan, R.A. Remote Sensing of Vegetation: Principles, Techniques, and Applications; Oxford University Press: Oxford, UK; New York, NY, USA, 2010; ISBN 978-0-19-920779-4. [Google Scholar]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Headwall Photonics Inc. Micro-Hyperspec Airborne Sensors. Available online: http://www.headwallphotonics.com/spectral-imaging/hyperspectral/micro-hyperspec (accessed on 16 April 2016).
- Calderón, R.; Navas-Cortés, J.A.; Lucena, C.; Zarco-Tejada, P.J. High-resolution airborne hyperspectral and thermal imagery for early detection of Verticillium wilt of olive using fluorescence, temperature and narrow-band spectral indices. Remote Sens. Environ. 2013, 139, 231–245. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Morales, A.; Testi, L.; Villalobos, F.J. Spatio-temporal patterns of chlorophyll fluorescence and physiological and structural indices acquired from hyperspectral imagery as compared with carbon fluxes measured with eddy covariance. Remote Sens. Environ. 2013, 133, 102–115. [Google Scholar] [CrossRef]
- Sankey, T.; Donager, J.; McVay, J.; Sankey, J.B. UAV lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Lucieer, A.; Malenovský, Z.; Veness, T.; Wallace, L. HyperUAS-Imaging Spectroscopy from a Multirotor Unmanned Aircraft System: HyperUAS-Imaging Spectroscopy from a Multirotor Unmanned. J. Field Robot. 2014, 31, 571–590. [Google Scholar] [CrossRef]
- Malenovský, Z.; Lucieer, A.; King, D.H.; Turnbull, J.D.; Robinson, S.A. Unmanned aircraft system advances health mapping of fragile polar vegetation. Methods Ecol. Evol. 2017, 8, 1842–1857. [Google Scholar] [CrossRef]
- Suomalainen, J.; Anders, N.; Iqbal, S.; Roerink, G.; Franke, J.; Wenting, P.; Hünniger, D.; Bartholomeus, H.; Becker, R.; Kooistra, L. A Lightweight Hyperspectral Mapping System and Photogrammetric Processing Chain for Unmanned Aerial Vehicles. Remote Sens. 2014, 6, 11013–11030. [Google Scholar] [CrossRef]
- HySpex. HySpex Mjolnir V-1240. Available online: https://www.hyspex.no/products/mjolnir.php (accessed on 15 November 2017).
- Aasen, H.; Bolten, A. Multi-temporal high-resolution imaging spectroscopy with hyperspectral 2D imagers—From theory to application. Remote Sens. Environ. 2018, 205, 374–389. [Google Scholar] [CrossRef]
- Aasen, H.; Burkart, A.; Bolten, A.; Bareth, G. Generating 3D hyperspectral information with lightweight UAV snapshot cameras for vegetation monitoring: From camera calibration to quality assurance. ISPRS J. Photogramm. Remote Sens. 2015, 108, 245–259. [Google Scholar] [CrossRef]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Pölönen, I.; Hakala, T.; Litkey, P.; Mäkynen, J.; Pesonen, L. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Fereres, E.; Villalobos, F. Mapping canopy conductance and CWSI in olive orchards using high resolution thermal remote sensing imagery. Remote Sens. Environ. 2009, 113, 2380–2388. [Google Scholar] [CrossRef]
- Stagakis, S.; González-Dugo, V.; Cid, P.; Guillén-Climent, M.L.; Zarco-Tejada, P.J. Monitoring water stress and fruit quality in an orange orchard under regulated deficit irrigation using narrow-band structural and physiological remote sensing indices. ISPRS J. Photogramm. Remote Sens. 2012, 71, 47–61. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Berni, J.A.J.; González-Dugo, V.; Fereres, E. Modelling PRI for water stress detection using radiative transfer models. Remote Sens. Environ. 2009, 113, 730–744. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Peña, J.M. An automatic object-based method for optimal thresholding in UAV images: Application for vegetation detection in herbaceous crops. Comput. Electron. Agric. 2015, 114, 43–52. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Peña, J.M.; Gutiérrez, P.A.; Torres-Sánchez, J.; Hervás-Martínez, C.; López-Granados, F. A semi-supervised system for weed mapping in sunflower crops using unmanned aerial vehicles and a crop row detection method. Appl. Soft Comput. 2015, 37, 533–544. [Google Scholar] [CrossRef]
- Kelcey, J.; Lucieer, A. Sensor Correction of a 6-Band Multispectral Imaging Sensor for UAV Remote Sensing. Remote Sens. 2012, 4, 1462–1493. [Google Scholar] [CrossRef]
- MicaSense. Parrot Sequoia. Available online: https://www.micasense.com/parrotsequoia/ (accessed on 14 December 2017).
- MicaSense. RedEdge-M. Available online: https://www.micasense.com/rededge-m/ (accessed on 14 December 2017).
- SAL. Engineering MAIA—The Multispectral Camera. Available online: http://www.spectralcam.com/ (accessed on 14 December 2017).
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Li, X.; Gong, H.; Shi, C.; Zhong, R.; Liu, X. Comparison of UAV and WorldView-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Albetis, J.; Duthoit, S.; Guttler, F.; Jacquin, A.; Goulard, M.; Poilvé, H.; Féret, J.-B.; Dedieu, G. Detection of Flavescence dorée Grapevine Disease Using Unmanned Aerial Vehicle (UAV) Multispectral Imagery. Remote Sens. 2017, 9, 308. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suárez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A PRI-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Geipel, J.; Link, J.; Wirwahn, J.; Claupein, W. A Programmable Aerial Multispectral Camera System for In-Season Crop Biomass and Nitrogen Content Estimation. Agriculture 2016, 6, 4. [Google Scholar] [CrossRef]
- Honkavaara, E.; Arbiol, R.; Markelin, L.; Martinez, L.; Cramer, M.; Bovet, S.; Chandelier, L.; Ilves, R.; Klonus, S.; Marshal, P.; et al. Digital Airborne Photogrammetry—A New Tool for Quantitative Remote Sensing?—A State-of-the-Art Review On Radiometric Aspects of Digital Photogrammetric Images. Remote Sens. 2009, 1, 577–605. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-Based Photogrammetry and Hyperspectral Imaging for Mapping Bark Beetle Damage at Tree-Level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- SENOP. Optronics Hyperspectral. Available online: http://senop.fi/en/optronics-hyperspectral (accessed on 11 October 2017).
- Mäkynen, J.; Holmlund, C.; Saari, H.; Ojala, K.; Antila, T. Unmanned aerial vehicle (UAV) operated megapixel spectral camera. In International Society for Optics and Photonics; Kamerman, G.W., Steinvall, O., Bishop, G.J., Gonglewski, J.D., Lewis, K.L., Hollins, R.C., Merlet, T.J., Eds.; SPIE: Bellingham, WA, USA, 2011; p. 81860Y. [Google Scholar]
- De Oliveira, R.A.; Tommaselli, A.M.G.; Honkavaara, E. Geometric Calibration of a Hyperspectral Frame Camera. Photogramm. Rec. 2016, 31, 325–347. [Google Scholar] [CrossRef]
- Näsilä, A. Aalto-1 -satelliitin spektrikamerateknologian validointi avaruusympäristöön Validation of Aalto-1 Spectral Imager Technology to Space Environment; G2 Pro gradu, diplomityö, Aalto University: Helsinki, Finland, 2013. [Google Scholar]
- Honkavaara, E.; Eskelinen, M.A.; Polonen, I.; Saari, H.; Ojanen, H.; Mannila, R.; Holmlund, C.; Hakala, T.; Litkey, P.; Rosnell, T.; et al. Remote Sensing of 3-D Geometry and Surface Moisture of a Peat Production Area Using Hyperspectral Frame Cameras in Visible to Short-Wave Infrared Spectral Ranges Onboard a Small Unmanned Airborne Vehicle (UAV). IEEE Trans. Geosci. Remote Sens. 2016, 54, 5440–5454. [Google Scholar] [CrossRef]
- Mannila, R.; Holmlund, C.; Ojanen, H.J.; Näsilä, A.; Saari, H. Short-Wave Infrared (SWIR) Spectral Imager Based on Fabry-Perot Interferometer for Remote Sensing; Meynart, R., Neeck, S.P., Shimoda, H., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; p. 92411M. [Google Scholar]
- Honkavaara, E.; Rosnell, T.; Oliveira, R.; Tommaselli, A. Band registration of tuneable frame format hyperspectral UAV imagers in complex scenes. ISPRS J. Photogramm. Remote Sens. 2017, 134, 96–109. [Google Scholar] [CrossRef]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The Need for Accurate Geometric and Radiometric Corrections of Drone-Borne Hyperspectral Data for Mineral Exploration: MEPHySTo—A Toolbox for Pre-Processing Drone-Borne Hyperspectral Data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Moriya, E.A.S.; Imai, N.N.; Tommaselli, A.M.G.; Miyoshi, G.T. Mapping Mosaic Virus in Sugarcane Based on Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 740–748. [Google Scholar] [CrossRef]
- Roosjen, P.; Suomalainen, J.; Bartholomeus, H.; Kooistra, L.; Clevers, J. Mapping Reflectance Anisotropy of a Potato Canopy Using Aerial Images Acquired with an Unmanned Aerial Vehicle. Remote Sens. 2017, 9, 417. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Brede, B.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G.P.W. Improved estimation of leaf area index and leaf chlorophyll content of a potato crop using multi-angle spectral data—Potential of unmanned aerial vehicle imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 14–26. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.; et al. Individual Tree Detection and Classification with UAV-Based Photogrammetric Point Clouds and Hyperspectral Imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Saarinen, N.; Vastaranta, M.; Näsi, R.; Rosnell, T.; Hakala, T.; Honkavaara, E.; Wulder, M.; Luoma, V.; Tommaselli, A.; Imai, N.; et al. Assessing Biodiversity in Boreal Forests with UAV-Based Photogrammetric Point Clouds and Hyperspectral Imaging. Remote Sens. 2018, 10, 338. [Google Scholar] [CrossRef]
- Tuominen, S.; Balazs, A.; Honkavaara, E.; Pölönen, I.; Saari, H.; Hakala, T.; Viljanen, N. Hyperspectral UAV-imagery and photogrammetric canopy height model in estimating forest stand variables. Silva Fenn. 2017, 51, 7721. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Blomqvist, M.; Lyytikäinen-Saarenmaa, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Holopainen, M. Remote sensing of bark beetle damage in urban forests at individual tree level using a novel hyperspectral camera from UAV and aircraft. Urban For. Urban Green. 2018, 30, 72–83. [Google Scholar] [CrossRef]
- Hagen, N.; Kester, R.T.; Gao, L.; Tkaczyk, T.S. Snapshot advantage: A review of the light collection improvement for parallel high-dimensional measurement systems. Opt. Eng. 2012, 51, 111702. [Google Scholar] [CrossRef] [PubMed]
- Hagen, N.; Kudenov, M.W. Review of snapshot spectral imaging technologies. Opt. Eng. 2013, 52, 090901. [Google Scholar] [CrossRef]
- Jung, A.; Michels, R.; Graser, R. Hyperspectral camera with spatial and spectral resolution and method EP2944930A3. 23 December 2015. [Google Scholar]
- Cubert. GmbH UHD 185—Firefly. Available online: http://cubert-gmbh.de/uhd-185-firefly/ (accessed on 21 April 2016).
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- IMEC. Hyperspectral Imaging. Available online: https://www.imec-int.com/en/hyperspectral-imaging (accessed on 11 October 2017).
- Lambrechts, A.; Gonzalez, P.; Geelen, B.; Soussan, P.; Tack, K.; Jayapala, M. A CMOS-compatible, integrated approach to hyper- and multispectral imaging. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Cubert. GmbH Butterfly X2 Announced. Available online: http://cubert-gmbh.de/2016/02/11/butterfly-x2-announced/ (accessed on 10 April 2016).
- Photon Focus. AG Hyperspectral Cameras. Available online: http://www.photonfocus.com/de/produkte/kamerafinder/?no_cache=1&cid=9&pfid=2 (accessed on 11 October 2017).
- Constantin, D.; Rehak, M.; Akhtman, Y.; Liebisch, F. Detection of Crop Properties by Means of Hyperspectral Remote Sensing from a Micro UAV. Available online: https://www.researchgate.net/publication/301920193_Detection_of_crop_properties_by_means_of_hyperspectral_remote_sensing_from_a_micro_UAV (accessed on 9 July 2018).
- Khanna, R.; Sa, I.; Nieto, J.; Siegwart, R. On Field Radiometric Calibration for Multispectral Cameras. Available online: https://ieeexplore.ieee.org/document/7989768/ (accessed on 9 July 2018).
- Mihoubi, S.; Losson, O.; Mathon, B.; Macaire, L. Multispectral Demosaicing Using Pseudo-Panchromatic Image. IEEE Trans. Comput. Imaging 2017, 3, 982–995. [Google Scholar] [CrossRef]
- IMEC. Imec Demonstrates Shortwave Infrared (SWIR) Range Hyperspectral Imaging Camera. Available online: https://www.imec-int.com/en/articles/imec-demonstrates-shortwave-infrared-swir-range-hyperspectral-imaging-camera (accessed on 1 March 2018).
- Delaure, B. Cubert and VITO Remote Sensing Introduced Compact Hyperspectral COSI-cam at EGU 2016. Available online: https://vito.be/en/news-events/news/cubert-and-vito-remote-sensing-introduced-compact-hyperspectral-cosi-cam-at-egu-2016 (accessed on 14 December 2017).
- Livens, S.; Pauly, K.; Baeck, P.; Blommaert, J.; Nuyts, D.; Zender, J.; Delauré, B. A spatio-spectral camera for high resolution hyperspectral imaging. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W6, 223–228. [Google Scholar] [CrossRef]
- Sima, A.A.; Baeck, P.; Nuyts, D.; Delalieux, S.; Livens, S.; Blommaert, J.; Delauré, B.; Boonen, M. Compact Hyperspectral Imaging System (cosi) for Small Remotely Piloted Aircraft Systems (rpas)—System Overview and First Performance Evaluation Results. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 1157–1164. [Google Scholar] [CrossRef]
- Berra, E.F.; Gaulton, R.; Barr, S. Commercial Off-the-Shelf Digital Cameras on Unmanned Aerial Vehicles for Multitemporal Monitoring of Vegetation Reflectance and NDVI. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4878–4886. [Google Scholar] [CrossRef]
- Adobe Systems Incorporated. Digital Negative (DNG), Adobe DNG Converter | Adobe Photoshop CC. Available online: https://helpx.adobe.com/photoshop/digital-negative.html (accessed on 1 March 2018).
- Harwin, S.; Lucieer, A.; Osborn, J. The Impact of the Calibration Method on the Accuracy of Point Clouds Derived Using Unmanned Aerial Vehicle Multi-View Stereopsis. Remote Sens. 2015, 7, 11933–11953. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Jagt, B.; Lucieer, A.; Wallace, L.; Turner, D.; Durand, M. Snow Depth Retrieval with UAS Using Photogrammetric Techniques. Geosciences 2015, 5, 264–285. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Wallace, L. Direct Georeferencing of Ultrahigh-Resolution UAV Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2738–2745. [Google Scholar] [CrossRef]
- Gautam, D.; Lucieer, A.; Malenovský, Z.; Watson, C. Comparison of MEMS-Based and FOG-Based IMUs to Determine Sensor Pose on an Unmanned Aircraft System. J. Surv. Eng. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Remondino, F.; El-Hakim, S. Image-based 3D Modelling: A Review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision; Texts in Computer Science; Springer: London, UK, 2011; ISBN 978-1-84882-934-3. [Google Scholar]
- Mac Arthur, A.; MacLellan, C.J.; Malthus, T. The Fields of View and Directional Response Functions of Two Field Spectroradiometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3892–3907. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; McCabe, M.; Parkes, S.; Clarke, I. PUSHBROOM HYPERSPECTRAL IMAGING FROM AN UNMANNED AIRCRAFT SYSTEM (UAS)—GEOMETRIC PROCESSINGWORKFLOW AND ACCURACY ASSESSMENT. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W6, 379–384. [Google Scholar] [CrossRef]
- Baiocchi, V.; Dominici, D.; Milone, M.V.; Mormile, M. Development of a software to optimize and plan the acquisitions from UAV and a first application in a post-seismic environment. Eur. J. Remote Sens. 2014, 47, 477–496. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An Automated Technique for Generating Georectified Mosaics from Ultra-High Resolution Unmanned Aerial Vehicle (UAV) Imagery, Based on Structure from Motion (SfM) Point Clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Weiss, S.; Scaramuzza, D.; Siegwart, R. Monocular-SLAM-based navigation for autonomous micro helicopters in GPS-denied environments. J. Field Robot. 2011, 28, 854–874. [Google Scholar] [CrossRef]
- Habib, A.; Han, Y.; Xiong, W.; He, F.; Zhang, Z.; Crawford, M. Automated Ortho-Rectification of UAV-Based Hyperspectral Data over an Agricultural Field Using Frame RGB Imagery. Remote Sens. 2016, 8, 796. [Google Scholar] [CrossRef]
- Ramirez-Paredes, J.-P.; Lary, D.J.; Gans, N.R. Low-altitude Terrestrial Spectroscopy from a Pushbroom Sensor. J. Field Robot. 2016, 33, 837–852. [Google Scholar] [CrossRef]
- Dawn, S.; Saxena, V.; Sharma, B. Remote Sensing Image Registration Techniques: A Survey. In Image and Signal Processing; Elmoataz, A., Lezoray, O., Nouboud, F., Mammass, D., Meunier, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6134, pp. 103–112. ISBN 978-3-642-13680-1. [Google Scholar]
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; Wiley: New York, NY, USA, 2001; ISBN 978-0-471-30924-6. [Google Scholar]
- Jhan, J.-P.; Rau, J.-Y.; Huang, C.-Y. Band-to-band registration and ortho-rectification of multilens/multispectral imagery: A case study of MiniMCA-12 acquired by a fixed-wing UAS. ISPRS J. Photogramm. Remote Sens. 2016, 114, 66–77. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Goforth, M.A.; Steele, C.M.; Rango, A. Multispectral Remote Sensing from Unmanned Aircraft: Image Processing Workflows and Applications for Rangeland Environments. Remote Sens. 2011, 3, 2529–2551. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; De Castro, A.I.; Peña-Barragán, J.M. Configuration and Specifications of an Unmanned Aerial Vehicle (UAV) for Early Site Specific Weed Management. PLoS ONE 2013, 8, e58210. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.; Lucieer, A.; Malenovský, Z.; King, D.; Robinson, S. Spatial Co-Registration of Ultra-High Resolution Visible, Multispectral and Thermal Images Acquired with a Micro-UAV over Antarctic Moss Beds. Remote Sens. 2014, 6, 4003–4024. [Google Scholar] [CrossRef]
- Vakalopoulou, M.; Karantzalos, K. Automatic Descriptor-Based Co-Registration of Frame Hyperspectral Data. Remote Sens. 2014, 6, 3409–3426. [Google Scholar] [CrossRef]
- Schott, J.R. Remote sensing: The Image Chain Approach, 2nd ed.; Oxford University Press: New York, NY, USA, 2007; ISBN 978-0-19-517817-3. [Google Scholar]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical Considerations and Nomenclature for Reflectance; National Bureau of Standards: Washington DC, WA, USA, 1977; p. 67.
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R.; Feingersh, T. Operational BRDF Effects Correction for Wide-Field-of-View Optical Scanners (BREFCOR). IEEE Trans. Geosci. Remote Sens. 2015, 53, 1855–1864. [Google Scholar] [CrossRef]
- Gege, P.; Fries, J.; Haschberger, P.; Schötz, P.; Schwarzer, H.; Strobl, P.; Suhr, B.; Ulbrich, G.; Jan Vreeling, W. Calibration facility for airborne imaging spectrometers. ISPRS J. Photogramm. Remote Sens. 2009, 64, 387–397. [Google Scholar] [CrossRef]
- Sandau, R. (Ed.) Digital Airborne Camera: Introduction and Technology; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2010; ISBN 978-1-4020-8877-3. [Google Scholar]
- Schowengerdt, R.A. Remote Sensing, Models, and Methods for Image Processing, 3rd ed.; Academic Press: Burlington, MA, USA, 2007; ISBN 978-0-12-369407-2. [Google Scholar]
- Jablonski, J.; Durell, C.; Slonecker, T.; Wong, K.; Simon, B.; Eichelberger, A.; Osterberg, J. Best Practices in Passive Remote Sensing VNIR Hyperspectral System Hardware Calibrations; Bannon, D.P., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; p. 986004. [Google Scholar]
- Yoon, H.W.; Kacker, R.N. Guidelines for Radiometric Calibration of Electro-Optical Instruments for Remote Sensing; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015.
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Büttner, A.; Röser, H.-P. Hyperspectral Remote Sensing with the UAS “Stuttgarter Adler”—System Setup, Calibration and First Results. Photogramm. Fernerkund. Geoinf. 2014, 2014, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Aasen, H.; Bendig, J.; Bolten, A.; Bennertz, S.; Willkomm, M.; Bareth, G. Introduction and preliminary results of a calibration for full-frame hyperspectral cameras to monitor agricultural crops with UAVs. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-7, 1–8. [Google Scholar] [CrossRef]
- Brachmann, J.F.S.; Baumgartner, A.; Lenhard, K. Calibration Procedures for Imaging Spectrometers: Improving Data Quality from Satellite Missions to UAV Campaigns; Meynart, R., Neeck, S.P., Kimura, T., Shimoda, H., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; p. 1000010. [Google Scholar]
- Yang, G.; Li, C.; Wang, Y.; Yuan, H.; Feng, H.; Xu, B.; Yang, X. The DOM Generation and Precise Radiometric Calibration of a UAV-Mounted Miniature Snapshot Hyperspectral Imager. Remote Sens. 2017, 9, 642. [Google Scholar] [CrossRef]
- Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and Narrowband Multispectral Remote Sensing for Vegetation Monitoring from an Unmanned Aerial Vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Del Pozo, S.; Rodríguez-Gonzálvez, P.; Hernández-López, D.; Felipe-García, B. Vicarious Radiometric Calibration of a Multispectral Camera on Board an Unmanned Aerial System. Remote Sens. 2014, 6, 1918–1937. [Google Scholar] [CrossRef]
- Goldman, D.B. Vignette and Exposure Calibration and Compensation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2276–2288. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.J.; Pollefeys, M. Robust Radiometric Calibration and Vignetting Correction. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 562–576. [Google Scholar] [CrossRef] [PubMed]
- Wonpil Yu Practical anti-vignetting methods for digital cameras. IEEE Trans. Consum. Electron. 2004, 50, 975–983. [CrossRef]
- Nocerino, E.; Dubbini, M.; Menna, F.; Remondino, F.; Gattelli, M.; Covi, D. GEOMETRIC CALIBRATION AND RADIOMETRIC CORRECTION OF THE MAIA MULTISPECTRAL CAMERA. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-3/W3, 149–156. [Google Scholar] [CrossRef]
- Beisl, U. Absolute spectroradiometric calibration of the ADS40 sensor. In Proceedings of the ISPRS Commission I Symposium “From Sensors to Imagery”, Marne-la-Vallée, Paris, 4–6 July 2006; pp. 3–6. [Google Scholar]
- D’Odorico, P.; Schaepman, M. Monitoring the Spectral Performance of the APEX Imaging Spectrometer for Inter-Calibration of Satellite Missions; Remote Sensing Laboratories, Department of Geography, University of Zurich: Zurich, Switzerland, 2012. [Google Scholar]
- Liu, Y.; Wang, T.; Ma, L.; Wang, N. Spectral Calibration of Hyperspectral Data Observed From a Hyperspectrometer Loaded on an Unmanned Aerial Vehicle Platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2630–2638. [Google Scholar] [CrossRef]
- Busetto, L.; Meroni, M.; Crosta, G.F.; Guanter, L.; Colombo, R. SpecCal: Novel software for in-field spectral characterization of high-resolution spectrometers. Comput. Geosci. 2011, 37, 1685–1691. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN 5: A Reformulated Atmospheric Band Model with Auxiliary Species and Practical Multiple Scattering Options: Update; Shen, S.S., Lewis, P.E., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; p. 662. [Google Scholar]
- Ryan, R.E.; Pagnutti, M. Enhanced absolute and relative radiometric calibration for digital aerial cameras. In Photogrammetric Week ’09: Keynote and Invited Papers of the 100th Anniversary of the Photogrammetric Week Series (52nd Photogrammetric Week) held at Universitaet Stuttgart, September 7 to 11, 2009; Woche, P., Fritsch, D., Eds.; Wichmann: Heidelberg, Germany, 2009; pp. 81–90. ISBN 978-3-87907-483-9. [Google Scholar]
- Jehle, M.; Hueni, A.; Lenhard, K.; Baumgartner, A.; Schaepman, M.E. Detection and Correction of Radiance Variations During Spectral Calibration in APEX. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1023–1027. [Google Scholar] [CrossRef]
- Gueymard, C. SMARTS2, A Simple Model of the Atmospheric Radiative Transfer of Sunshine: Algorithms and performance assessment; Florida Solar Energy Ce nter/University of Central Florida: Cocoa, FL, USA, 1995; p. 84. [Google Scholar]
- Suomalainen, J.; Hakala, T.; Peltoniemi, J.; Puttonen, E. Polarised Multiangular Reflectance Measurements Using the Finnish Geodetic Institute Field Goniospectrometer. Sensors 2009, 9, 3891–3907. [Google Scholar] [CrossRef] [PubMed]
- Julitta, T. Optical Proximal Sensing for Vegetation Monitoring; University of Milano—Bicocca: Milano, Italy, 2015. [Google Scholar]
- Pacheco-Labrador, J.; Martín, M. Characterization of a Field Spectroradiometer for Unattended Vegetation Monitoring. Key Sensor Models and Impacts on Reflectance. Sensors 2015, 15, 4154–4175. [Google Scholar] [CrossRef] [PubMed]
- Bais, A.F.; Kazadzis, S.; Balis, D.; Zerefos, C.S.; Blumthaler, M. Correcting global solar ultraviolet spectra recorded by a Brewer spectroradiometer for its angular response error. Appl. Opt. 1998, 37, 6339. [Google Scholar] [CrossRef] [PubMed]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Bogren, W.S.; Burkhart, J.F.; Kylling, A. Tilt error in cryospheric surface radiation measurements at high latitudes: A model study. Cryosphere 2016, 10, 613–622. [Google Scholar] [CrossRef]
- Anderson, K.; Milton, E.J.; Rollin, E.M. Calibration of dual-beam spectroradiometric data. Int. J. Remote Sens. 2006, 27, 975–986. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Wang, C.; Myint, S.W. A Simplified Empirical Line Method of Radiometric Calibration for Small Unmanned Aircraft Systems-Based Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1876–1885. [Google Scholar] [CrossRef]
- Lu, B.; He, Y. Species classification using Unmanned Aerial Vehicle (UAV)-acquired high spatial resolution imagery in a heterogeneous grassland. ISPRS J. Photogramm. Remote Sens. 2017, 128, 73–85. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; Peña, J.M.; de Castro, A.I.; López-Granados, F. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV. Comput. Electron. Agric. 2014, 103, 104–113. [Google Scholar] [CrossRef]
- Markelin, L.; Honkavaara, E.; Schläpfer, D.; Bovet, S.; Korpela, I. Assessment of Radiometric Correction Methods for ADS40 Imagery. Photogramm. Fernerkund. Geoinf. 2012, 2012, 251–266. [Google Scholar] [CrossRef] [PubMed]
- Moran, M.S.; Ross, B.B.; Clarke, T.R.; Qi, J. Deployment and calibration of reference reflectance tarps for use with airborne imaging sensors. Photogramm. Eng. Remote Sens. 2001, 67, 273–286. [Google Scholar]
- Miura, T.; Huete, A.R. Performance of Three Reflectance Calibration Methods for Airborne Hyperspectral Spectrometer Data. Sensors 2009, 9, 794–813. [Google Scholar] [CrossRef] [PubMed]
- Beisl, U.; Telaar, J.; von Schönermark, M. Atmospheric Correction, Reflectance Calibration and BRDF Correction for ADS40 Image Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 7–12. [Google Scholar]
- Sabater, N.; Vicent, J.; Alonso, L.; Cogliati, S.; Verrelst, J.; Moreno, J. Impact of Atmospheric Inversion Effects on Solar-Induced Chlorophyll Fluorescence: Exploitation of the Apparent Reflectance as a Quality Indicator. Remote Sens. 2017, 9, 622. [Google Scholar] [CrossRef]
- Aasen, H. Influence of the viewing geometry on hyperspectral data retrieved from UAV snapshot cameras. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-7, 257–261. [Google Scholar] [CrossRef]
- Honkavaara, E.; Markelin, L.; Hakala, T.; Peltoniemi, J.I. The Metrology of Directional, Spectral Reflectance Factor Measurements Based on Area Format Imaging by UAVs. Photogramm. Fernerkund. Geoinf. 2014, 2014, 175–188. [Google Scholar] [CrossRef]
- Honkavaara, E.; Khoramshahi, E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sens. 2018, 10, 256. [Google Scholar] [CrossRef]
- Beisl, U. Correction of Bidirectional Effects in Imaging Spectrometer Data; Remote Sensing Series; Remote Sensing Laboratories, Department of Geography: Zurich, Switzerland, 2001; ISBN 978-3-03703-001-1. [Google Scholar]
- Von Schönermark, M.; Geiger, B.; Röser, H.-P. (Eds.) Reflection Properties of Vegetation and Soil: With a BRDF Data Base; 1. Aufl.; Wissenschaft und Technik Verlag: Berlin, Germany, 2004; ISBN 978-3-89685-565-7. [Google Scholar]
- Weyermann, J.; Damm, A.; Kneubuhler, M.; Schaepman, M.E. Correction of Reflectance Anisotropy Effects of Vegetation on Airborne Spectroscopy Data and Derived Products. IEEE Trans. Geosci. Remote Sens. 2014, 52, 616–627. [Google Scholar] [CrossRef]
- Hueni, A.; Damm, A.; Kneubuehler, M.; Schlapfer, D.; Schaepman, M.E. Field and Airborne Spectroscopy Cross Validation—Some Considerations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 1117–1135. [Google Scholar] [CrossRef]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple equation to approximate the bidirectional reflectance from vegetative canopies and bare soil surfaces. Appl. Opt. 1985, 24, 383. [Google Scholar] [CrossRef] [PubMed]
- Nilson, T.; Kuusk, A. A reflectance model for the homogeneous plant canopy and its inversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Richter, R.; Kellenberger, T.; Kaufmann, H. Comparison of Topographic Correction Methods. Remote Sens. 2009, 1, 184–196. [Google Scholar] [CrossRef]
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the Slope-Aspect Correction of Multispectral Scanner Data. Can. J. Remote Sens. 1982, 8, 84–106. [Google Scholar] [CrossRef]
- Shepherd, J.D.; Dymond, J.R. Correcting satellite imagery for the variance of reflectance and illumination with topography. Int. J. Remote Sens. 2003, 24, 3503–3514. [Google Scholar] [CrossRef]
- Minnaert, M. The reciprocity principle in lunar photometry. Astrophys. J. 1941, 93, 403. [Google Scholar] [CrossRef]
- Adeline, K.R.M.; Chen, M.; Briottet, X.; Pang, S.K.; Paparoditis, N. Shadow detection in very high spatial resolution aerial images: A comparative study. ISPRS J. Photogramm. Remote Sens. 2013, 80, 21–38. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R.; Kellenberger, T. Atmospheric and Topographic Correction of Photogrammetric Airborne Digital Scanner Data (ATCOR-ADS); EuroSDR—EUROCOW 2012. Barcelona, Spain, 2012. Available online: http://www.geo.uzh.ch/microsite/rsl-documents/research/publications/other-sci-communications/Schlaepfer_eurocow2012_ATCOR-ADS-1512234752/Schlaepfer_eurocow2012_ATCOR-ADS.pdf (accessed on 9 July 2018).
- Richter, R.; Müller, A. De-shadowing of satellite/airborne imagery. Int. J. Remote Sens. 2005, 26, 3137–3148. [Google Scholar] [CrossRef]
- Chandelier, L.; Martinoty, G. A Radiometric Aerial Triangulation for the Equalization of Digital Aerial Images and Orthoimages. Photogramm. Eng. Remote Sens. 2009, 75, 193–200. [Google Scholar] [CrossRef]
- Collings, S.; Caccetta, P.; Campbell, N.; Wu, X. Empirical Models for Radiometric Calibration of Digital Aerial Frame Mosaics. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2573–2588. [Google Scholar] [CrossRef]
- Gehrke, S.; Beshah, B.T. RADIOMETRIC NORMALIZATION OF LARGE AIRBORNE IMAGE DATA SETS ACQUIRED BY DIFFERENT SENSOR TYPES. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI–B1, 317–326. [Google Scholar] [CrossRef]
- Hernández López, D.; Felipe García, B.; González Piqueras, J.; Alcázar, G.V. An approach to the radiometric aerotriangulation of photogrammetric images. ISPRS J. Photogramm. Remote Sens. 2011, 66, 883–893. [Google Scholar] [CrossRef]
- ITRES. Imagers | ITRES. Available online: http://www.itres.com/imagers/ (accessed on 9 March 2018).
- Schaepman, M.E.; Jehle, M.; Hueni, A.; D’Odorico, P.; Damm, A.; Weyermann, J.; Schneider, F.D.; Laurent, V.; Popp, C.; Seidel, F.C.; et al. Advanced radiometry measurements and Earth science applications with the Airborne Prism Experiment (APEX). Remote Sens. Environ. 2015, 158, 207–219. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-induced fluorescence—A new probe of photosynthesis: First maps from the imaging spectrometer HyPlant. Glob. Change Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef] [PubMed]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Cook, B.; Corp, L.; Nelson, R.; Middleton, E.; Morton, D.; McCorkel, J.; Masek, J.; Ranson, K.; Ly, V.; Montesano, P. NASA Goddard’s LiDAR, Hyperspectral and Thermal (G-LiHT) Airborne Imager. Remote Sens. 2013, 5, 4045–4066. [Google Scholar] [CrossRef]
- Specim, Spectral Imaging Ltd. Hyperspectral Imaging System AisaKESTREL. Available online: http://www.specim.fi/products/aisakestrel-hyperspectral-imaging-system/ (accessed on 30 January 2018).
- Roosjen, P.; Suomalainen, J.; Bartholomeus, H.; Clevers, J. Hyperspectral Reflectance Anisotropy Measurements Using a Pushbroom Spectrometer on an Unmanned Aerial Vehicle—Results for Barley, Winter Wheat, and Potato. Remote Sens. 2016, 8, 909. [Google Scholar] [CrossRef]
- Uto, K.; Seki, H.; Saito, G.; Kosugi, Y.; Komatsu, T. Development of a Low-Cost, Lightweight Hyperspectral Imaging System Based on a Polygon Mirror and Compact Spectrometers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 861–875. [Google Scholar] [CrossRef]
- Meng, Z.; Petrov, G.I.; Cheng, S.; Jo, J.A.; Lehmann, K.K.; Yakovlev, V.V.; Scully, M.O. Lightweight Raman spectroscope using time-correlated photon-counting detection. Proc. Natl. Acad. Sci. USA 2015, 112, 12315–12320. [Google Scholar] [CrossRef] [PubMed]
- Lelong, C.C.D.; Burger, P.; Jubelin, G.; Roux, B.; Labbé, S.; Baret, F. Assessment of Unmanned Aerial Vehicles Imagery for Quantitative Monitoring of Wheat Crop in Small Plots. Sensors 2008, 8, 3557–3585. [Google Scholar] [CrossRef] [PubMed]
- Harwin, S.; Lucieer, A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- Grenzdörffer, G.J. Crop height determination with UAS point clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-1, 135–140. [Google Scholar] [CrossRef]
- Eltner, A.; Schneider, D. Analysis of Different Methods for 3D Reconstruction of Natural Surfaces from Parallel-Axes UAV Images. Photogramm. Rec. 2015, 30, 279–299. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; de Sanjosé-Blasco, J.; de Matías-Bejarano, J.; Berenguer-Sempere, F. Comparing Two Photo-Reconstruction Methods to Produce High Density Point Clouds and DEMs in the Corral del Veleta Rock Glacier (Sierra Nevada, Spain). Remote Sens. 2014, 6, 5407–5427. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Puliti, S.; Olerka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Van der Wal, T.; Abma, B.; Viguria, A.; Prévinaire, E.; Zarco-Tejada, P.J.; Serruys, P.; van Valkengoed, E.; van der Voet, P. Fieldcopter: Unmanned aerial systems for crop monitoring services. In Precision agriculture ’13; Stafford, J., Ed.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2013; pp. 169–175. [Google Scholar]
- Hakala, T.; Suomalainen, J.; Peltoniemi, J.I. Acquisition of Bidirectional Reflectance Factor Dataset Using a Micro Unmanned Aerial Vehicle and a Consumer Camera. Remote Sens. 2010, 2, 819–832. [Google Scholar] [CrossRef]
- Anderson, K.; Dungan, J.L.; MacArthur, A. On the reproducibility of field-measured reflectance factors in the context of vegetation studies. Remote Sens. Environ. 2011, 115, 1893–1905. [Google Scholar] [CrossRef]
- Anderson, K.; Milton, E.J. On the temporal stability of ground calibration targets: Implications for the reproducibility of remote sensing methodologies. Int. J. Remote Sens. 2006, 27, 3365–3374. [Google Scholar] [CrossRef]
- Miyoshi, G.T.; Imai, N.N.; Tommaselli, A.M.G.; Honkavaara, E.; Näsi, R.; Moriya, É.A.S. Radiometric block adjustment of hyperspectral image blocks in the Brazilian environment. Int. J. Remote Sens. 2018, 1–21. [Google Scholar] [CrossRef]
- Hakala, T.; Honkavaara, E.; Saari, H.; Mäkynen, J.; Kaivosoja, J.; Pesonen, L.; Pölönen, I. Spectral imaging from UAVs under varying illumination conditions. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013. [Google Scholar] [CrossRef]
- Walter, A.; Finger, R.; Huber, R.; Buchmann, N. Opinion: Smart farming is key to developing sustainable agriculture. Proc. Natl. Acad. Sci. USA 2017, 114, 6148–6150. [Google Scholar] [CrossRef] [PubMed]
- Hunt, E.R.; Daughtry, C.S.T. What good are unmanned aircraft systems for agricultural remote sensing and precision agriculture? Int. J. Remote Sens. 2017, 1–32. [Google Scholar] [CrossRef]
- Araus, J.L.; Cairns, J.E. Field high-throughput phenotyping: The new crop breeding frontier. Trends Plant Sci. 2014, 19, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Fiorani, F.; Schurr, U. Future Scenarios for Plant Phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives. Front. Plant Sci. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Queiroz Feitosa, R.; van der Meer, F.; van der Werff, H.; van Coillie, F.; et al. Geographic Object-Based Image Analysis – Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Aasen, H.; Bareth, G. Ground and UAV sensing approaches for spectral and 3D crop trait estimation. In Hyperspectral Remote Sensing of Vegetation—Volume II: Advanced Approaches and Applications in Crops and Plants; Thenkabail, P., Lyon, J.G., Huete, A., Eds.; Taylor and Francis Inc.: Abingdon, UK, 2018. [Google Scholar]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Tilly, N.; Aasen, H.; Bareth, G. Fusion of Plant Height and Vegetation Indices for the Estimation of Barley Biomass. Remote Sens. 2015, 7, 11449–11480. [Google Scholar] [CrossRef]
- Hueni, A.; Nieke, J.; Schopfer, J.; Kneubühler, M.; Itten, K.I. The spectral database SPECCHIO for improved long-term usability and data sharing. Comput. Geosci. 2009, 35, 557–565. [Google Scholar] [CrossRef]
- Duarte, L.; Teodoro, A.C.; Moutinho, O.; Gonçalves, J.A. Open-source GIS application for UAV photogrammetry based on MicMac. Int. J. Remote Sens. 2017, 38, 3181–3202. [Google Scholar] [CrossRef]
- Itten, K.I.; Dell’Endice, F.; Hueni, A.; Kneubühler, M.; Schläpfer, D.; Odermatt, D.; Seidel, F.; Huber, S.; Schopfer, J.; Kellenberger, T.; et al. APEX—The Hyperspectral ESA Airborne Prism Experiment. Sensors 2008, 8, 6235–6259. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.P.; Borak, J.S.; Devadiga, S.; Wolfe, R.E.; Zheng, M.; Descloitres, J. The MODIS land product quality assessment approach. Remote Sens. Environ. 2002, 83, 62–76. [Google Scholar] [CrossRef]
- Bareth, G.; Aasen, H.; Bendig, J.; Gnyp, M.L.; Bolten, A.; Jung, A.; Michels, R.; Soukkamäki, J. Low-weight and UAV-based Hyperspectral Full-frame Cameras for Monitoring Crops: Spectral Comparison with Portable Spectroradiometer Measurements. Photogramm. Fernerkund. Geoinf. 2015, 2015, 69–79. [Google Scholar] [CrossRef]
- Domingues Franceschini, M.; Bartholomeus, H.; van Apeldoorn, D.; Suomalainen, J.; Kooistra, L. Intercomparison of Unmanned Aerial Vehicle and Ground-Based Narrow Band Spectrometers Applied to Crop Trait Monitoring in Organic Potato Production. Sensors 2017, 17, 1428. [Google Scholar] [CrossRef] [PubMed]
- Von Bueren, S.K.; Burkart, A.; Hueni, A.; Rascher, U.; Tuohy, M.P.; Yule, I.J. Deploying four optical UAV-based sensors over grassland: Challenges and limitations. Biogeosciences 2015, 12, 163–175. [Google Scholar] [CrossRef]

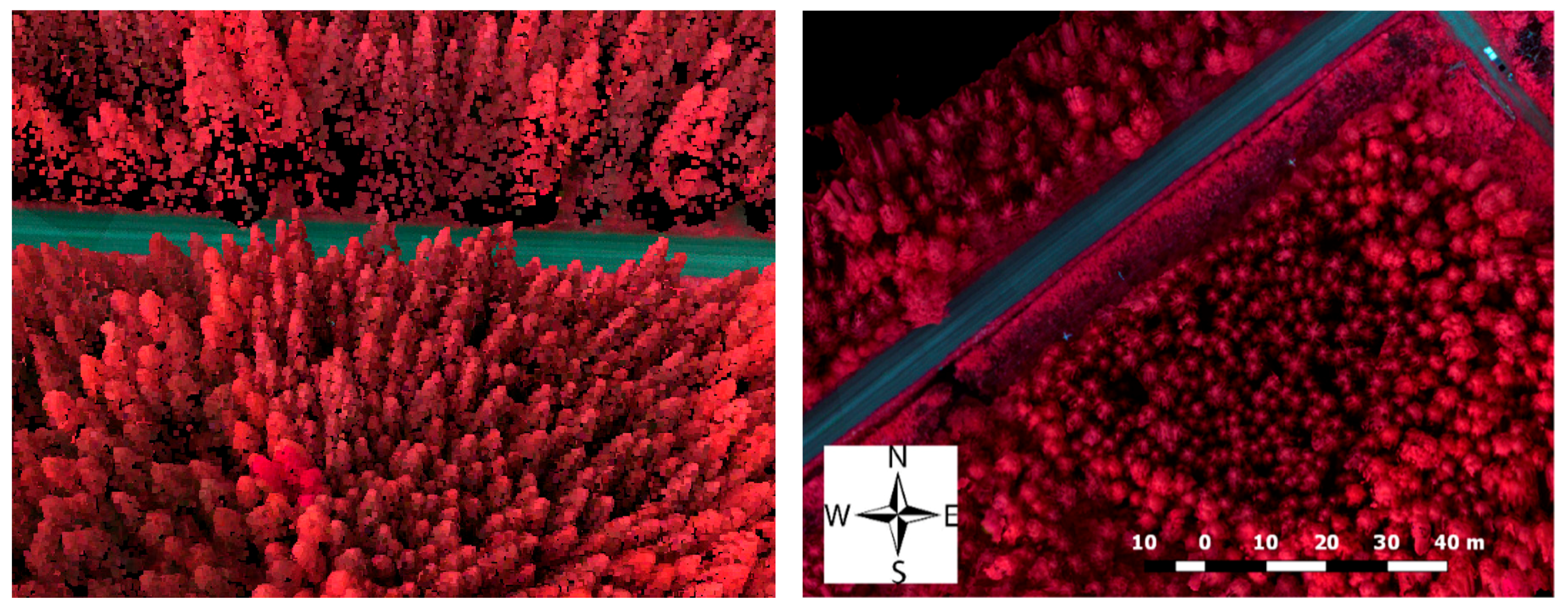
| Data Cube Slice | Scanning Dimension | Spatial Resolution | Spectral Bands ** | Spectral Resolution (FWHM) | Bit Depth | Example Sensors | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Point | 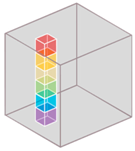 | spatial | none | ++++ (1024) +++++ (3648) | ++++ (1–12 nm) +++++ (0.1–10 nm) | 12 bit 16 bit | Ocean Optics STS Ocean Optics USB4000 | |||
| Pushbroom | 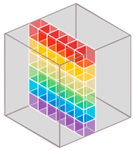 | spatial | VNIR | +++ (1240) | ++++ (200) | +++ (3.2–6.4 nm) | 12 bit | HySpex Mjolnir V Specim AisaKESTREL 10, Headwall micro-hyperspec/nano-hyperspec, Bayspec OCI, Resonon Pika | ||
| SWIR | +++ (620) | ++++ (300) | +++ (~6 nm) | 16 bit | HySpex Mjolnir S (970–2500 nm) Specim AisaKESTREL 16 (600–1640 nm) | |||||
| 2D imager | Multi-camera |  | spatial | +++ (1280 × 960) | + (5) | + (10–40 nm) | 12 bit | Micasense RedEdge-m Parrot Sequoia, Tetracam Mini MCA, macaw | ||
| Sequential (multi-) band |  | spectral | VNIR | +++ (1000 × 1000) | +++ (100) | +++ (5–12 nm) | 12 bit | Rikola FPI VNIR | ||
| SWIR | ++ (320 × 256) | ++ (30) | ++ (20–30 nm) | Prototype FPI SWIR | ||||||
| snapshot | Multi-point |  | none | + (50 × 50) | +++ (125) | +++ (5–25 nm) | 12 bit | Cubert FireFleye | ||
| Filter-on-chip | 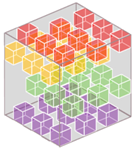 | none | VIS | ++ (512 × 272) | ++ (16) | ++ (5–10 nm) | 10 bit | imec SNm4x4 * | ||
| NIR | ++ (409 × 216) | ++ (25) | ++ (5–10 nm) | 10 bit | imec SNm5x5 * | |||||
| Characterized (modified) RGB |  | none | ++++ 3000 × 4000 | + (3) | + (50–100 nm) | 12 bit | canon s110 (NIR) | |||
| Spatiospectral |  | spatiospectral | ++++ 2000 | ++ (160) | ++ (5–10 nm) | 8 bit | COSI cam Cubert ButterflEYE LS | |||
| Year | Description (Novelties) | Sensor Type | Sensor | Content | Reference |
|---|---|---|---|---|---|
| 2008 | Calibration and application of spectroradiometrically characterized RGB cameras | Multispectral 2D imager | Canon EOS 350D Sony DSC-F828 | C, P | [190] |
| 2009 | Multi-camera multispectral 2D imager on UAV for vegetation monitoring | Multi-camera spectral 2D imager | MiniMCA | C, P | [130] |
| 2012 | Small hyperspectral pushbroom UAVs system for vegetation monitoring | Pushbroom | Micro-Hyperspec VNIR | C, P | [125] |
| 2012 | Characterization and calibration of spectral 2D imager | Multi-camera spectral 2D imager | MiniMCA | C | [50] |
| 2013 | Processing chain for sequential band spectral 2D imager for spectral and 3D data | Sequential band spectral 2D imager | Rikola FPI | P | [44] |
| 2014 | Point spectrometer on UAV Wireless communication to ground spectrometer for irradiance measurements | Point spectrometer | STS-VIS | C, I | [22] |
| 2014 | Self-assembled pushbroom system Orientation of image lines with a combination of GNSS/INS and aerial images | Pushbroom | Self-assembled | C, I, P | [40,126] |
| 2014 | First pushbroom system on multi-rotor UAV for ultra-high resolution imaging spectroscopy Comprehensive description of calibration procedures | Pushbroom | Micro-Hyperspec VNIR | C, I | [38] |
| 2014 | Uncertainty propagation of the hemispherical directional reflectance observations in the radiometric processing chain | Sequential band spectral 2D imager | Rikola FPI | C, P | [162] |
| 2015 | Hyperspectral 3D models Quality assurance information integration | 2D snapshot 2D imager | Cubert Firefleye | C, I, P | [43] |
| 2015 | Multi-angular measurements with UAV | Point spectrometer | OceanOptics STS-VIS | C, I, P | [24] |
| 2016 | Multi-angular measurements with UAV | Pushbroom | Self-build (HYMSY) | P | [187] |
| 2016 | SWIR 2D imaging from UAV | Sequential band 2D imager | Tunable FPI SWIR | P | [65] |
| 2016 | Implementation and calibration of multi-camera system on UAV | Multi-camera spectral 2D imager | Self-assembled | C, I | [58] |
| 2017 | Measuring sun-induced fluorescence in the O2A band Comprehensive description of calibration procedures | Point spectrometer | OceanOptics USB4000 | C, I, P | [25] |
| 2017 | Toolbox for pre-processing drone-borne hyperspectral Data | Sequential spectral 2D imager | Rikola VNIR | C, P | [68] |
| 2017 | BRDF measurements with UAV | Sequential band spectral 2D imager | Rikola FPI | P | [70] |
| 2018 | Theoretical considerations to comprehend imaging spectroscopy with 2D imagers Explanation of differences between imaging and non-imaging data | 2D imagers in general | Cubert Firefleye | C, P | [42] |
| GCPs | on-Board GNSS/IMU | SfM + GCPs and/or GNSS/IMU | Co-Registration | |
|---|---|---|---|---|
| Point spectroradiometer | - | ++ | ++ | - |
| Pushbroom | +/- | ++ | - | + |
| 2D imager | + | + | ++ | + |
| Radiometric Data Calibration Method | Stable Atmosphere | Stable Atmosphere | Unstable Atmosphere | Applicable to |
|---|---|---|---|---|
| Stable Irradiance | Unstable Irradiance | Unstable Irradiance | ||
| empirical line method | + | - | - | (P), PP, 2D |
| radiometric block adjustment | + | + | + | (PP *), 2D |
| stationary radiometric tracking | + | + | - | P, PP, 2D |
| on-board radiometric tracking | + | + | + | P, PP, 2D |
| radiative transfer modeling | + | - | - | P, PP, 2D |
| Pixel | Image | Scene |
|---|---|---|
| signal-to-noise ratio (n, m) radiometric resolution (n, m) viewing geometry (n, m) | capturing position (n, m) illumination (q, m) conditions direct and diffuse (n, a) illumination ratio capturing time (n, m) | sensor description (q, m) (including version) band configuration (n, m) (FWHM, band center) geometric processing (q, m) procedures and accuracies (including software version and parameters) top-of-canopy (q, m) reflectance calculation method reflectance uncertainty (n, a) environmental (q, m) conditions during measurement |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. https://doi.org/10.3390/rs10071091
Aasen H, Honkavaara E, Lucieer A, Zarco-Tejada PJ. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sensing. 2018; 10(7):1091. https://doi.org/10.3390/rs10071091
Chicago/Turabian StyleAasen, Helge, Eija Honkavaara, Arko Lucieer, and Pablo J. Zarco-Tejada. 2018. "Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows" Remote Sensing 10, no. 7: 1091. https://doi.org/10.3390/rs10071091
APA StyleAasen, H., Honkavaara, E., Lucieer, A., & Zarco-Tejada, P. J. (2018). Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sensing, 10(7), 1091. https://doi.org/10.3390/rs10071091





