1. Introduction and Context
The Satellite with ARGOS and AltiKa (SARAL) mission was developed by CNES (Centre National d’Etudes Spatiales) and ISRO (Indian Space Research Organization). Launched in 2013, the SARAL satellite was primarily a gapfiller for the Advanced Research and Global Observation Satellite (ARGOS) localization system and a Ka-band altimeter technology demonstrator (AltiKa). Verron et al. [
1] and Vincent et al. [
2] recall that SARAL/AltiKa was initially designed as a response to the requirements expressed by operational oceanography users to bridge the gap between the ENVIronment SATellite (ENVISAT) and the Sentinel-3 altimeter missions. An important objective of AltiKa was to complement the altimeter constellation and to help resolve large ocean mesoscale variability, i.e., scales ranging from 150 to 500 km and 15 to 50 days [
3]. SARAL/AltiKa was instrumental in providing the ocean mesoscale sampling needed by operational systems such as AVISO [
4] and the Copernicus Marine Environment Monitoring Service (CMEMS) [
5]. Indeed, according to Chelton et al. [
6] and Pascual et al. [
7], two operational altimeters are required to monitor ocean mesoscale variability in delayed time, and up to four are needed in near real time.
Furthermore, Verron et al. [
1,
8] and Bonnefond et al. [
9] recently reported that the Ka-band demonstrator exhibited unprecedented altimeter precision for topography over the ocean, rivers and lakes, and even over sea and land ice, as well as for wind and wave. This precision in turn led to innovative user-products and new scientific findings (e.g., [
10,
11,
12,
13,
14,
15]). Thanks to this demonstrated scientific value, CNES and ISRO decided to extend the SARAL mission beyond the 3-year nominal duration that was successfully completed in Spring 2016.
As reported by Bonnefond and Willis [
16], SARAL exhibited an increasing need to reduce the stress on its momentum wheels in order to extend the lifetime of the mission. This could be achieved by limiting the orbit maintenance maneuvers. The agencies eventually decided that the best strategy was to stop all orbit control maneuvers and to let the altitude decay naturally. This strategy is also known as a drifting phase (DP). It was initiated in July 2016.
The main consequence of a DP was that the SARAL subsatellite track would rapidly drift away from the historical ground track formerly used by the European Remote-sensing Satellite (ERS) and ENVISAT missions. At this point it is important to highlight that the term “drift” refers to the evolution of the nadir track (i.e., position of the altimeter measurement profile): SARAL DP is therefore very different from the ENVISAT mission extension where the orbit was drifting but the nadir ground track was relatively stable and composed of 431 orbits per 30-day cycle.
Sandwell et al. [
17] have shown that using a drifting ground track could be extremely useful for the marine geodesy community: the unprecedented precision of AltiKa could help resolve uncharted sea mounts and sea floor topography. Improving marine geodesy products requires a so-called “geodetic altimeter sampling”, i.e., a sampling pattern where the subsatellite tracks over a long period (e.g., one year) create a very dense grid with a resolution of 8 km or less. In practice, this can be achieved by keeping precisely the satellite on a so-called “geodetic orbit”, i.e., an orbit with a very long exact repeat cycle. This strategy was used for the Jason-1 Geodetic-Mission (GM) phase or the Jason-2 Long Repeat Orbit (LRO) phase. For SARAL DP, there is no longer an exact repeat because the orbit altitude decays continuously, yet the geodetic sampling of SARAL DP is naturally dense, albeit somewhat random (discussed in
Section 3.4 and
Section 4.1).
However, putting SARAL on such a drifting ground track raised the question of the new mesoscale sampling capability (still a high priority for the mission). Dibarboure et al. [
18] have shown that the geodetic orbit used by Cryosat-2 is very poor when it comes to mesoscale monitoring: the orbit has a monthly linear scanning pattern that leaves most of the ocean unobserved over a typical ocean mesoscale decorrelation period of 15 days. On the other hand, Dibarboure et al. [
19] demonstrated that it could be possible to find geodetic orbits that were compatible with mesoscale monitoring: this was achieved by including intermediate sub-cycles (defined in
Section 2.1) that maximize the ocean mesoscale sampling over a period of 15 to 20 days. But these studies were both carried out in the context of a well-maintained altitude, and the mesoscale sampling properties of decaying orbits has not been studied so far.
In this context, the objective of this paper is to demonstrate that it is possible to secure high-quality ocean mesoscale sampling and good marine geodesy sampling for 6 years or more even with an unmaintained decaying altitude.
Section 2 and
Section 3 describe how the continuous evolution of the orbit sub-cycles could be predicted to find mesoscale-friendly altitude bands where a decaying altitude does not alter the altimeter sampling capability. In
Section 4, the anticipated results are confirmed with in-flight data from the first 18 months of SARAL DP. Lastly
Section 5 generalizes the SARAL DP findings to other altimeter missions.
2. Methodology Used to Prepare the Drifting Phase of SARAL
This section gives an overview of the methodology used in 2016 to define the drifting phase of SARAL:
Section 2.1 describes how to infer the quality of mesoscale sampling for a given altitude, and
Section 2.2 shows how we defined conservative scenarios to predict the altitude decay of SARAL DP. These two essential inputs are then used in
Section 3 to predict the evolution of the ocean mesoscale sampling throughout the drifting phase, and to select the best starting point.
2.1. Quality of Mesoscale Sampling and Orbit Sub-Cycles
To measure the quality of the mesoscale sampling for a given altitude, we analyze the distribution of the satellite tracks in the longitude/time plane, following the methodology of Dibarboure et al. [
19] for Jason-1: in essence, the quality of mesoscale sampling is inferred by gauging when altimeter tracks get too close in space or in time. Indeed, a single altimeter cannot resolve all the mesoscale space and time scales [
6], so it is essential to avoid duplications between adjoining tracks: if the satellite tracks are too close, it means that a different region is not properly observed. Here, “too close” is measured in the longitude/time plane because all satellite tracks have the same geometry. Furthermore, the metric is based on mesoscale covariance models used by Ducet et al. [
20] to build a multi-altimeter gridded map of the ocean mesoscale. The covariance models are a statistical approximation of the size of mesoscale features in space and time [
21,
22], i.e., a good description of when altimeter tracks are too close and correlated.
Note that because SARAL is the only satellite of the 2016+ altimeter constellation that is near the historical ERS/ENVISAT orbit, we only optimize its own sampling: we do not try to maximize the combined sampling of the entire altimeter constellation: the ground track geometry and repeat cycles of other altimeters are very different so the constellation-wide gain would be very small.
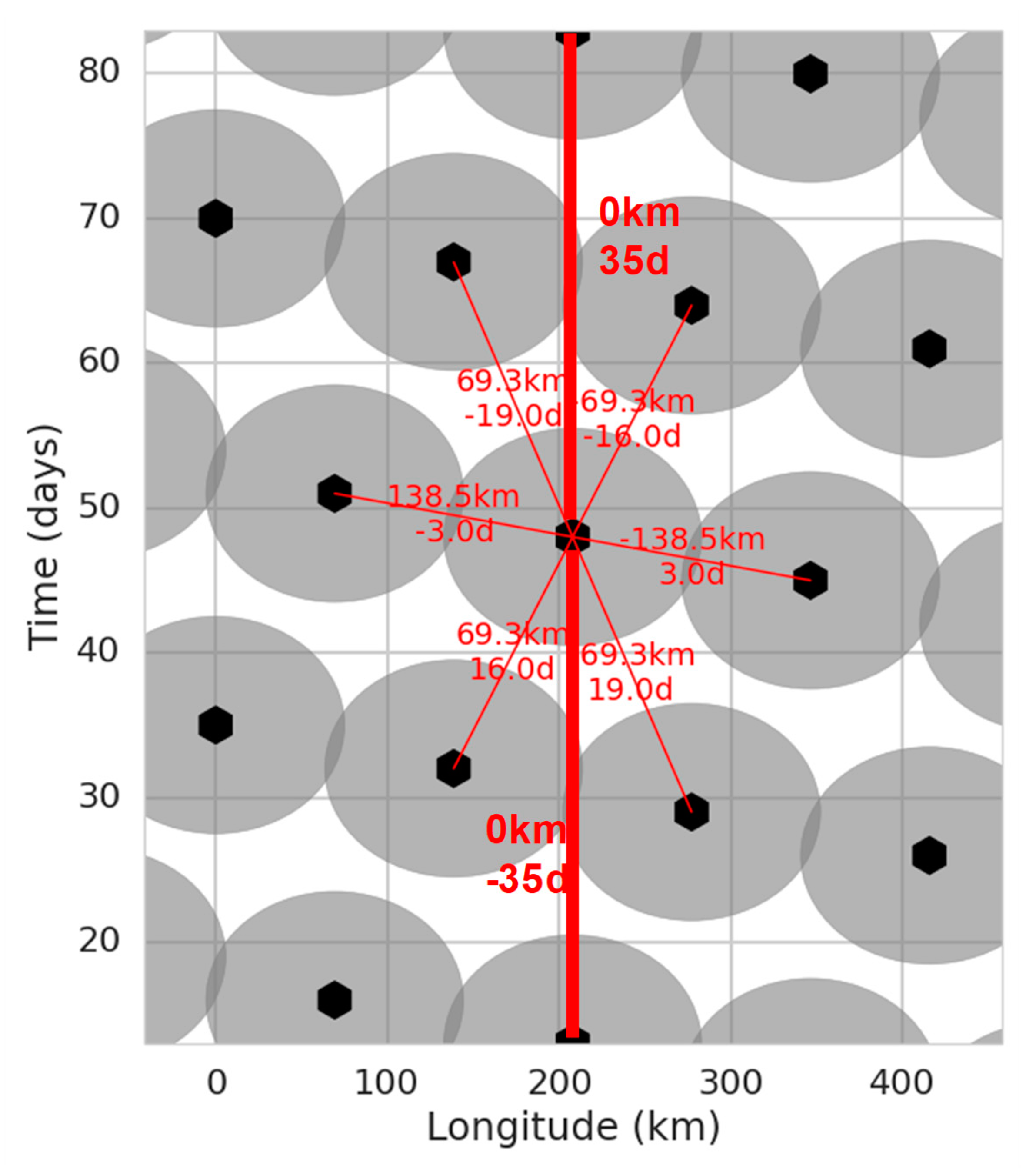
Figure 1 shows the distribution of the satellite tracks for the ERS/ENVISAT altitude originally used by SARAL (approximately 780 km). Each black dot is one satellite track. The vertical alignment of the black dots corresponds to the 35-day exact repeat cycle of this orbit. The grey circles are 150 km by 15 days. This is an approximation of the decorrelation scale of mesoscale eddies at mid-latitudes.
In other words, if two grey circles overlap, then the corresponding satellite tracks are too close in space or in time: their measurements are highly correlated and in turn other regions of the space/time plane are completely unobserved. As expected from Le Traon and Dibarboure [
23], the ERS/ENVISAT orbit is very good for mesoscale observation: the overlap between grey circles is almost non-existent as they are well-scattered in the longitude/time plane.
In addition to the true repeat cycle (highlighted with two thick vertical red lines), the diagonal alignment of grey circles in
Figure 1 (thin red lines) shows the presence of orbital sub-cycles (SC). Orbital sub-cycles are defined by Rees [
24] as a period of near-repeat for Earth remote-sensing satellites. The influence of SC in the context of altimetry missions is explained by Dibarboure et al. [
19].
For the ERS/ENVISAT/SARAL altitude there are two dominant sub-cycles: 3 days and 16 days. In practice, dominant sub-cycles could also be defined by their global coverage: a sub-cycle corresponds to the time needed to collect a coverage that is globally homogeneous (e.g., 1000 km resolution after 3 days, or 180 km after 16 days). The 1002 tracks of the ERS/ENVISAT/SARAL repeat cycle are composed of two interleaved 16-day periods and one 3-day period. A 19-day sub-cycle is also visible in
Figure 1: it is composed of a 16-day and a 3-day sub-cycle.
2.2. Predicting the Altitude Loss
Section 3.1 will show that the quality of the mesoscale sampling changes with the altitude and the associated sub-cycles. To determine how the sampling will evolve throughout the drifting phase, it is necessary to know how the altitude is likely to change in 3 years or more.
Like all low-earth orbit satellites, SARAL experiences an atmospheric drag force in a direction opposite to the direction of its motion. This force slows down the satellite, which in turn decreases its altitude. The drag force is given by Equation (1):
where
ρ is the atmospheric density,
v is the satellite speed, and
Cb the ballistic coefficient. Note that if the orbit is circular, the speed of the satellite is constant and it is a function of the orbit altitude. For the sake of simplicity, we here ignore that the satellite drag actually depends on the speed relative to the atmosphere which in turn creates a modulation of the drag force with latitude: the effect on the ground track geometry is extremely small and an analysis on the longitude of ascending node only requires us to know the mean satellite drag over a long period of time. The ballistic coefficient
Cb is given by Equation (2) where
Cx is the drag coefficient of the satellite,
S is the area of the cross section surface in the direction of flight, and m is the mass of the satellite. In practice the coefficients used for SARAL in this study were estimated through an analysis of all the maneuvers performed by ISRO during the 3-year nominal mission.
To get a projection of the altitude decay, it is necessary to have a prediction of the atmospheric density. The density
as a function of the altitude
h around a reference altitude
h0 can be approximated by a simple exponential with variable scale height
H (Equation (3)). Here, the scale height depends on the solar radio flux which is a proxy of the upper atmosphere density [
25]. In practice, it is more accurate to use more sophisticated atmosphere models (e.g., MSIS2000). These models also use solar activity coefficient to parameterize the atmospheric density at all altitudes.
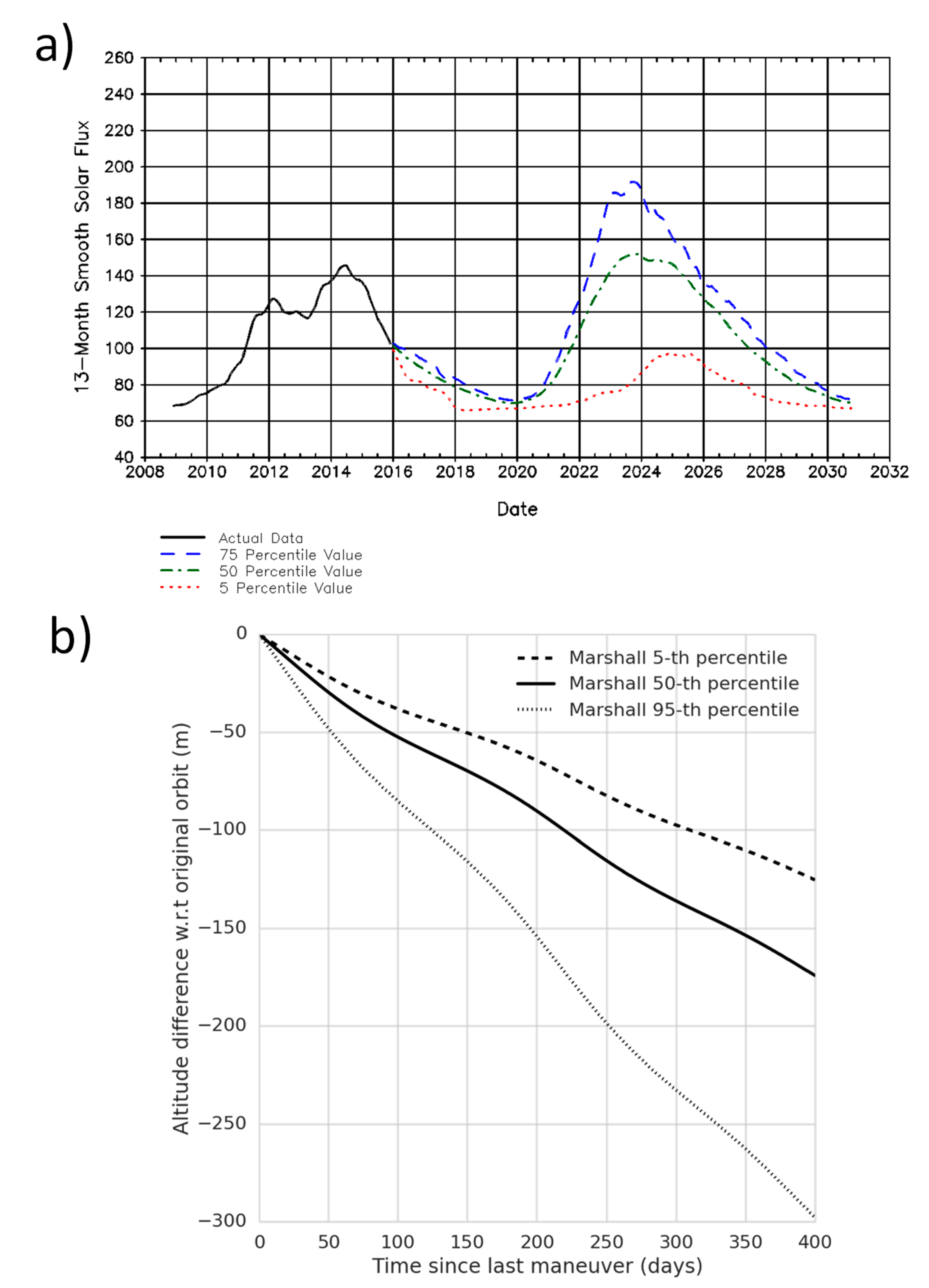
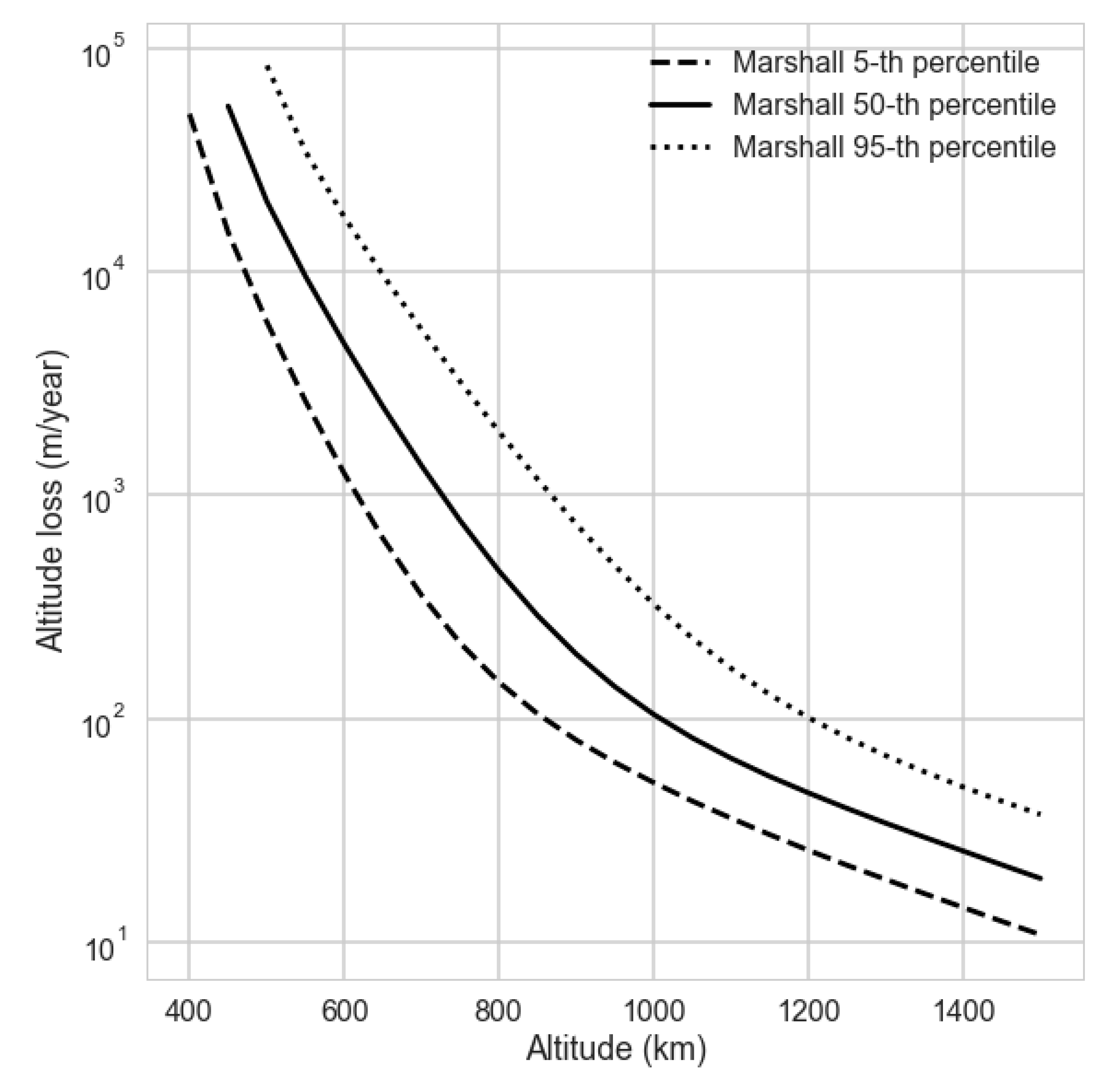
In this study, we used the solar flux predictions from the National Aeronautics and Space Administration (NASA) Marshall Space Flight Center [
26]. The solar flux prediction used to prepare the SARAL DP in 2016 is shown in
Figure 2a. Using the atmosphere model and the measured ballistic coefficient of SARAL, we obtain the altitude prediction in
Figure 2b.
The altitude decay is almost linear over one year, albeit modulated by the solar flux. To that extent, panel (b) shows three predictions: one for the 5-th percentile (weak solar activity, weak altitude decay), one for the 50-th percentile (median solar activity) and one for the 95-th percentile (strong solar activity).
The average altitude decay ranges from 150 m to 300 m per year. To prepare the SARAL drifting phase, we used a conservative value of 300 m/year (95-th percentile solar flux scenario): with this strategy it was very likely that the altitude would decrease more slowly. In other words, the drifting phase SARAL DP could be as long as three times our conservative estimate from
Section 3.3 (the observed solar fluxes where indeed weaker and close to the 5-th percentile value, as discussed in
Section 4.4).
3. Predictions Obtained to Define the Drifting Phase of SARAL
Based on the inputs from
Section 2, the following sections explore the behavior of an unmaintained orbit strategy for SARAL, and the consequence for its mesoscale sampling capability. These predictions helped define the final strategy of the SARAL drifting phase. The observations after 18 months of SARAL DP are discussed in
Section 4.
3.1. Diversity of the Mesoscale Sampling Near the ERS Altitude
The SARAL DP strategy was designed for a baseline of 3 years (i.e., as long as nominal lifespan of SARAL) with a backup scenario as long as 9 years (e.g., scenario where SARAL remains operational as long as the TOPEX/Poseidon mission). Because of the unmaintained decaying altitude and our conservative value of 300 m/year, the entire drifting phase could span over an altitude range of 1 km (baseline) to 3 km (backup).
But the mesoscale sampling properties over such a range of altitude can be very different:
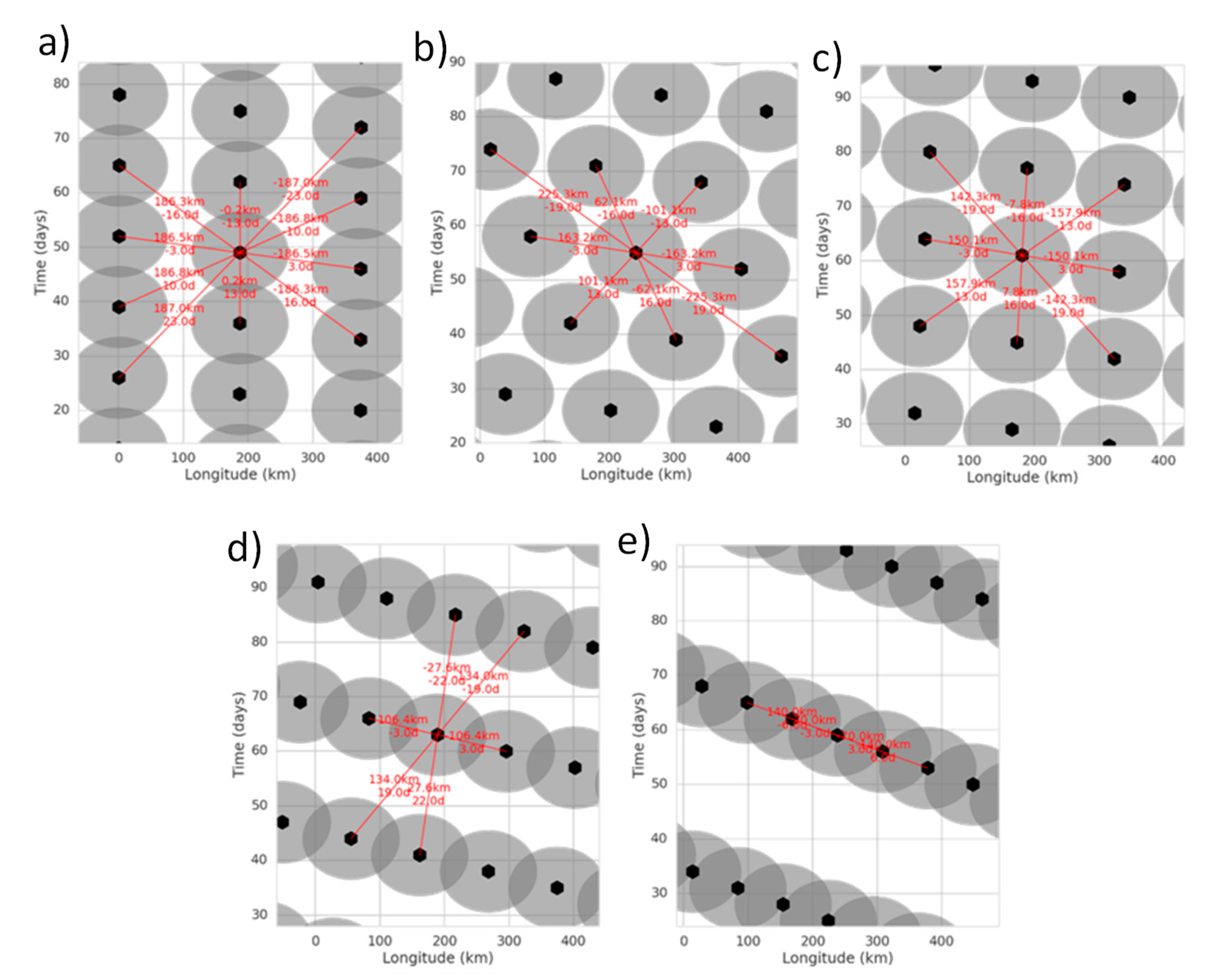
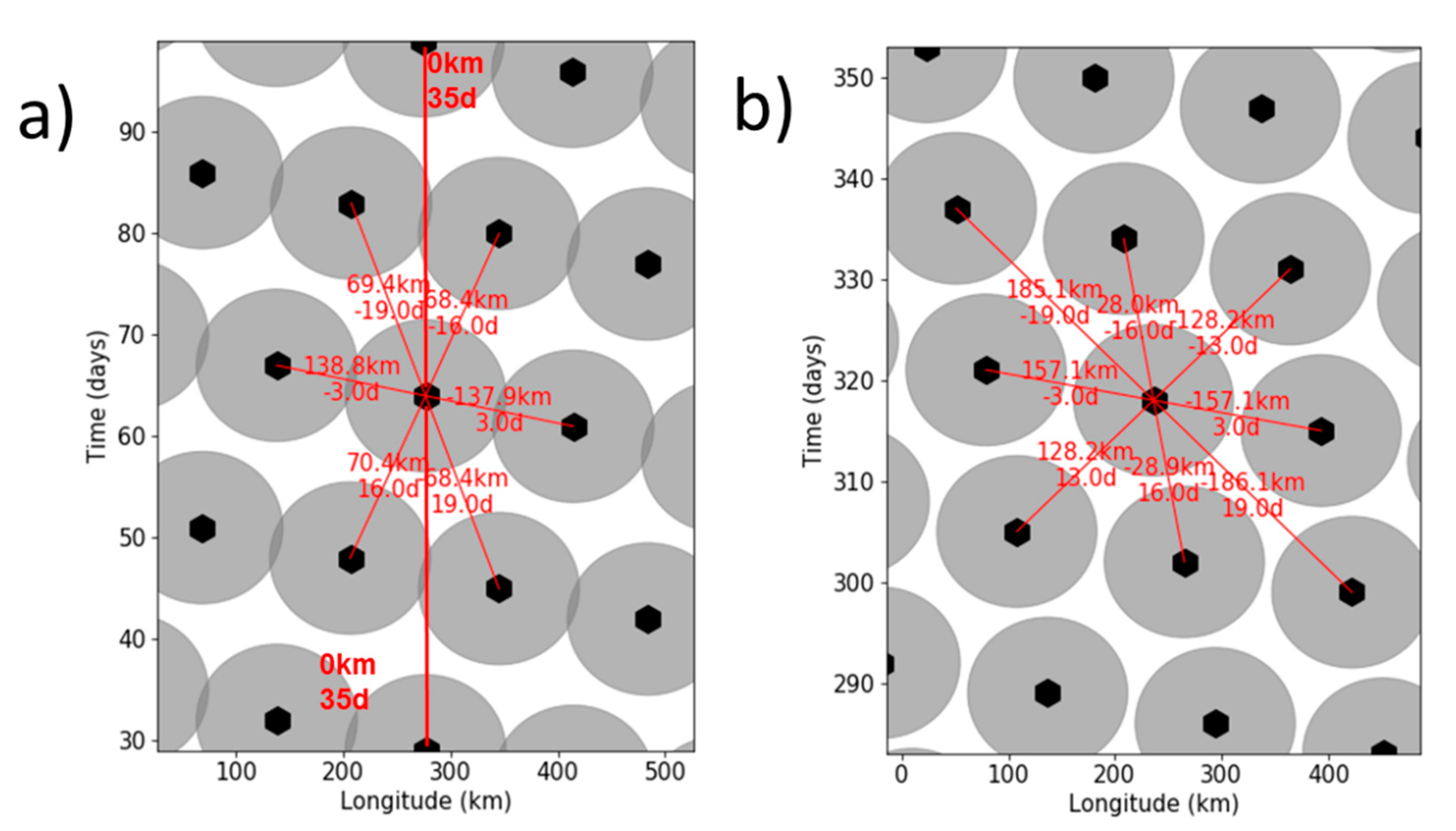
Figure 3 shows the position of SARAL tracks in the longitude/time plane for 5 different altitudes near the ERS orbit. Panel a in
Figure 3 is 2 km above: it exhibits an exact 13-day repeat cycle and the 3-day sub-cycle that exists for all orbits in this altitude range. In panel (a), mesoscale sampling is not as good as for the ERS altitude because the 13-day repeat cycle is slightly too short: the grey circles are overlapping in the vertical direction. This weakness is the same as for the TOPEX orbit [
23].
Panel b in
Figure 3 is 1 km above the ERS orbit. Here, the distribution of altimeter tracks in the longitude/time plane is different: the grey circles are rotated clockwise with respect to panel (a). The 13-day exact repeat of panel (a) has morphed into a 13-day sub-cycle and the 16-day sub-cycle has appeared (the 16-day SC is a composition of the 13-day SC and one 3-day SC). As a result, the mesoscale sampling is excellent at this altitude: the altimeter tracks are as far away from one another as possible, and there is no overlap between them.
Figure 3c is 500 m above the ERS altitude. The grey circles are rotated clockwise with respect to panel b in
Figure 3, but the sampling capability is still excellent. The 16-day sub-cycle is very strong (almost vertical, i.e., a true repeat cycle), and the 19-day sub-cycle starts to appear due to the clockwise rotation (composition of a 16-day SC and a 3-day SC).
Panel d and panel e in
Figure 3 are 1.5 km and 2.5 km below the SARAL altitude, respectively. At these altitudes, the sub-cycles are longer than 20-days, and the grey circles are largely overlapping: they are separated by less than 70 km and 3 days. The overlaps highlight the regions of the space and time plane that are correlated (as defined in
Section 2.1) with two or more altimeter measurements in black. In panel (d) and panel (e), there is a large amount of overlap between adjoining circles; the visible consequence is that there are large bands of the space/time plane which are not observed whatsoever (not covered by grey circles). In essence, the nadir tracks are too close in space or in time and the resulting duplication between altimeter measurements creates large blind regions elsewhere.
The poor mesoscale sampling in panel (d) and (e) is due to the clockwise rotation of the grey circles in the longitude/time plane: they now align diagonally (very strong 3-day SC). This poor sampling pattern is typically observed on CryoSat-2 [
18].
To summarize, the 3 examples above the ERS/ENVISAT orbit are good for mesoscale sampling, and it is preferable to stay between the current altitude and +1 km because the sampling at +2 km is not as good. The other 2 examples below the ERS/ENVISAT orbit are progressively worse and should be avoided because their SC are too long for mesoscale. But these are only a handful of examples, and the satellite altitude will decay continuously and change the sub-cycles.
3.2. The Continuous Evolution of Sub-Cycles (SC)
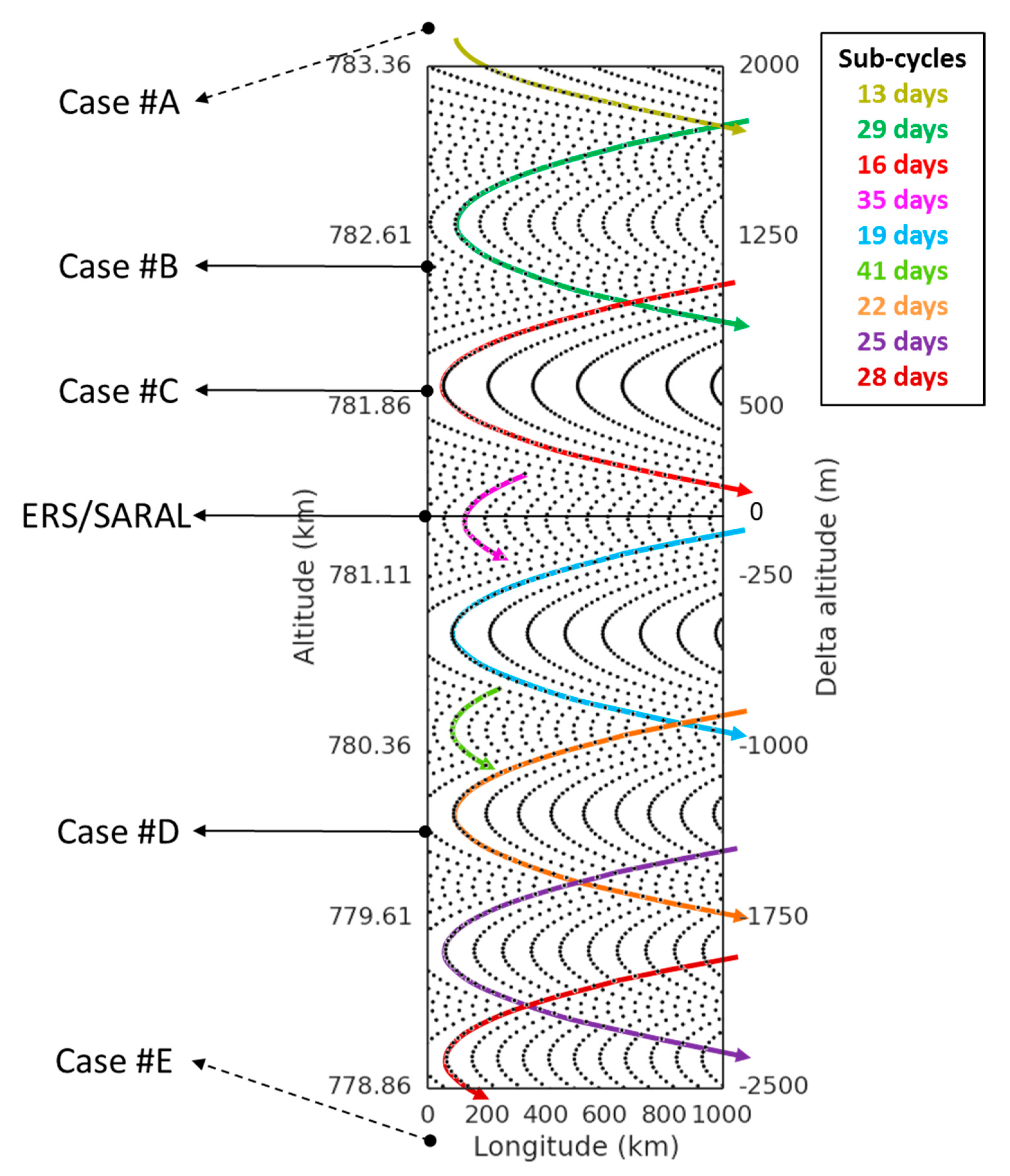
To understand how the orbit sub-cycles would change when there is no station-keeping maneuvers, we performed a long simulation starting 2-km above the ERS altitude and using the 300 m/year altitude decay obtained in
Section 2.2. We chose to keep a constant altitude decay to show how a 15-year SARAL DP (starting in summer 2016) would look like at all altitudes.
Figure 4 shows the longitude of all subsatellite tracks as the altitude decays. We highlighted the altitudes studied in the 5 panels of
Figure 3. The timeline goes from top to bottom (altitude decaying with time, 1 km of altitude is approximately equivalent to 3 years) so here the rotation of the grey circles discussed in
Section 3.1 is counterclockwise: with this broader scale the rotation looks like horizontal parabolas (highlighted as colored arrows).
This continuous parabola-shaped effect is created by the modulo between the duration of a satellite revolution and the Earth rotation as seen by the satellite: a tiny change in the altitude also reduces the revolution period and the new modulo rotates the altimeter tracks in the longitude/time plane.
This result is important for SARAL DP: all sub-cycles appear, strengthen, become a true repeat cycle, weaken, and then disappear. More importantly this phenomenon occurs in a continuous way and the large parabolas are approximately 1-km large in altitude: in other words, if we find one orbit with good sampling properties, then there is also a 3-year time-frame where the sampling will be good because the sub-cycles change only progressively.
Incidentally,
Figure 4 shows that larger sub-cycles are composed of smaller sub-cycles. Most SC can be decomposed as 1-day plus a given multiple of the 3-day sub-cycle (13, 16, 19, 22), but there are also larger sub-cycles composed of shorter sub-cycles (e.g., the 35-day repeat of ERS is 16 + 16 + 3 or 16 + 19). This rather complex composition effect is interesting because if two altitudes are attractive and separated by 1–2 km, then all intermediate altitudes will be good for mesoscale because the grey circle rotation seen in
Figure 3 will ensure that the composition of intermediate sub-cycles is also good.
As a result, the mesoscale-friendly altitudes aggregate in small bands that should be considered for SARAL DP. This aggregation was already observed but not explained by Dibarboure et al. [
19] when they were looking for a good geodetic orbit for Jason-1.
3.3. Finding a Good Starting Point for the SARAL Drifting Phase (DP)
Assuming a baseline duration of 3 years, SARAL DP requires a 1-km altitude range where the sub-cycles are good for mesoscale.
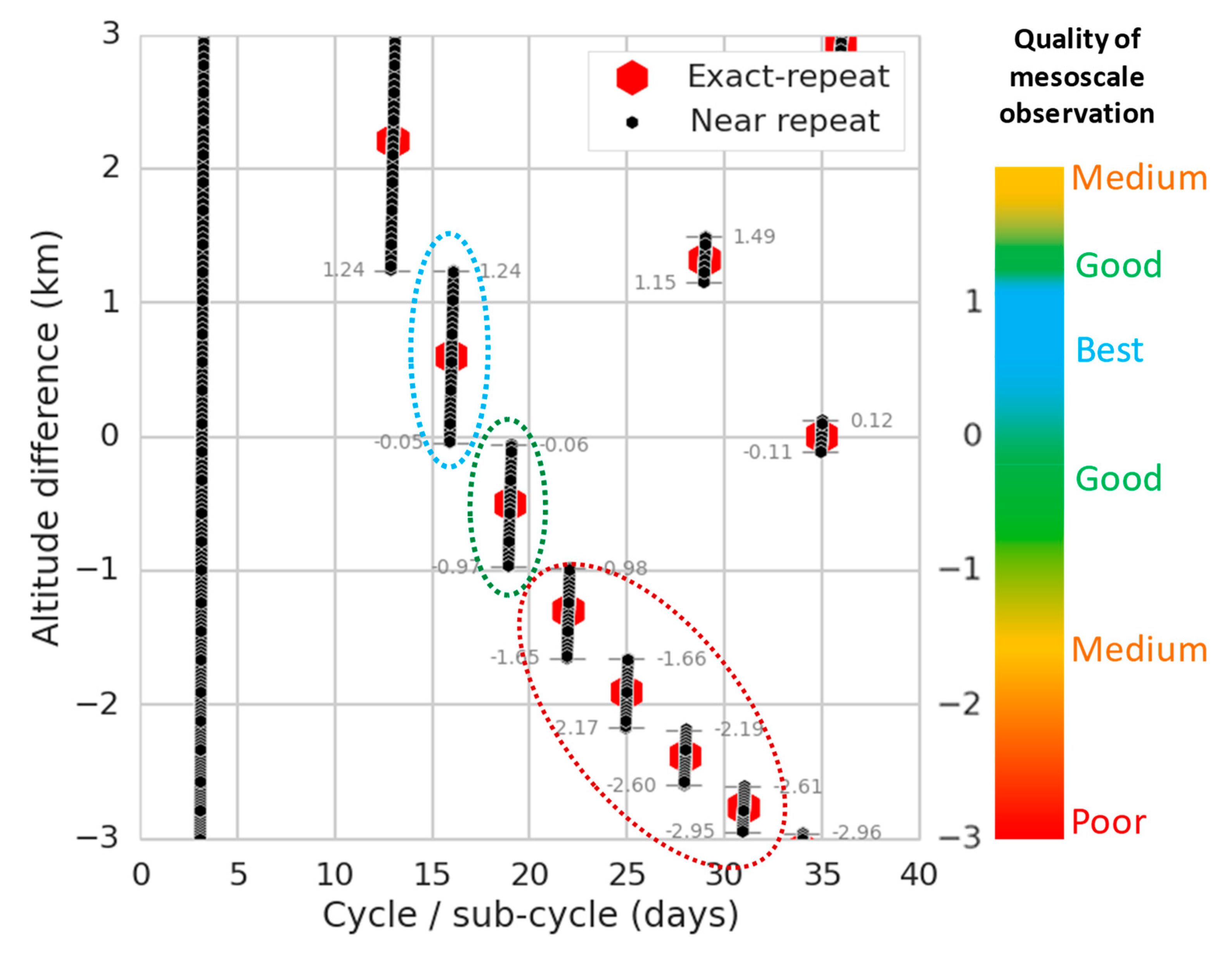
Figure 3 shows that sub-cycles ranging from 13 to 19 days are good although 15 to 17 days is better. Lastly the altitude range should be as close to the ERS/ENVISAT altitude as possible in order to avoid a strong maneuver when the drifting phase starts.
With all these constraints,
Figure 4 shows that the best starting point for SARAL DP is approximately 1 km above the ERS/ENVISAT orbit:
Figure 3b,c showed that the starting and intermediate altitudes yield an excellent sampling for mesoscale. After 3 years, SARAL/AltiKa is back at the ERS/ENVISAT altitude where the sampling capability is still good. From 3 to 6 years of drifting phase, the sampling is decent but sub-optimal due to the long 19-day SC. After 6 years, the sampling degrades because the main SC is too long.
Figure 5 gives an overview of the dominant sub-cycles for all altitude as well as a qualitative index for mesoscale sampling.
3.4. Relaxed Altitude Control or No Control Whatsoever?
Assuming that SARAL/AltiKa is operated at least 3 years on the DP orbit, one might raise the following question: is it better to keep a relaxed altitude control or to have no altitude control whatsoever? E.g., one maneuver every 6–12 months to stay within 150–300 m of the altitude with an optimal sampling pattern for ocean mesoscale. As discussed above, such a yearly maneuver would be good but not essential for mesoscale for at least 3 years. But in this section we show that it would be very detrimental to the geodetic sampling.
Indeed, Zhang and Sandwell [
27] recall that geodesists use altimeter data collected over a very long period (typically one year or more). They use these 1D altimeter datasets (subsatellite track) to compute a series of 2D gridded parameters such as geoid models, mean sea surface models, bathymetries, and gravity anomaly fields. For CryoSat-2 and Jason-1 GM (geodetic mission), the yearly cross-track resolution of altimeter tracks is of the order of 8 km at the equator. Thus, SARAL DP becomes exceedingly useful if it can collect a regular geodetic grid of 8 km after one year and a 4 km grid after two years. Zhang and Sandwell [
27] emphasize the benefit of a drifting phase longer than 1.3 years, i.e., a cross-track resolution better than 6 km, to reveal a large number of uncharted seamounts, and important tectonic features.
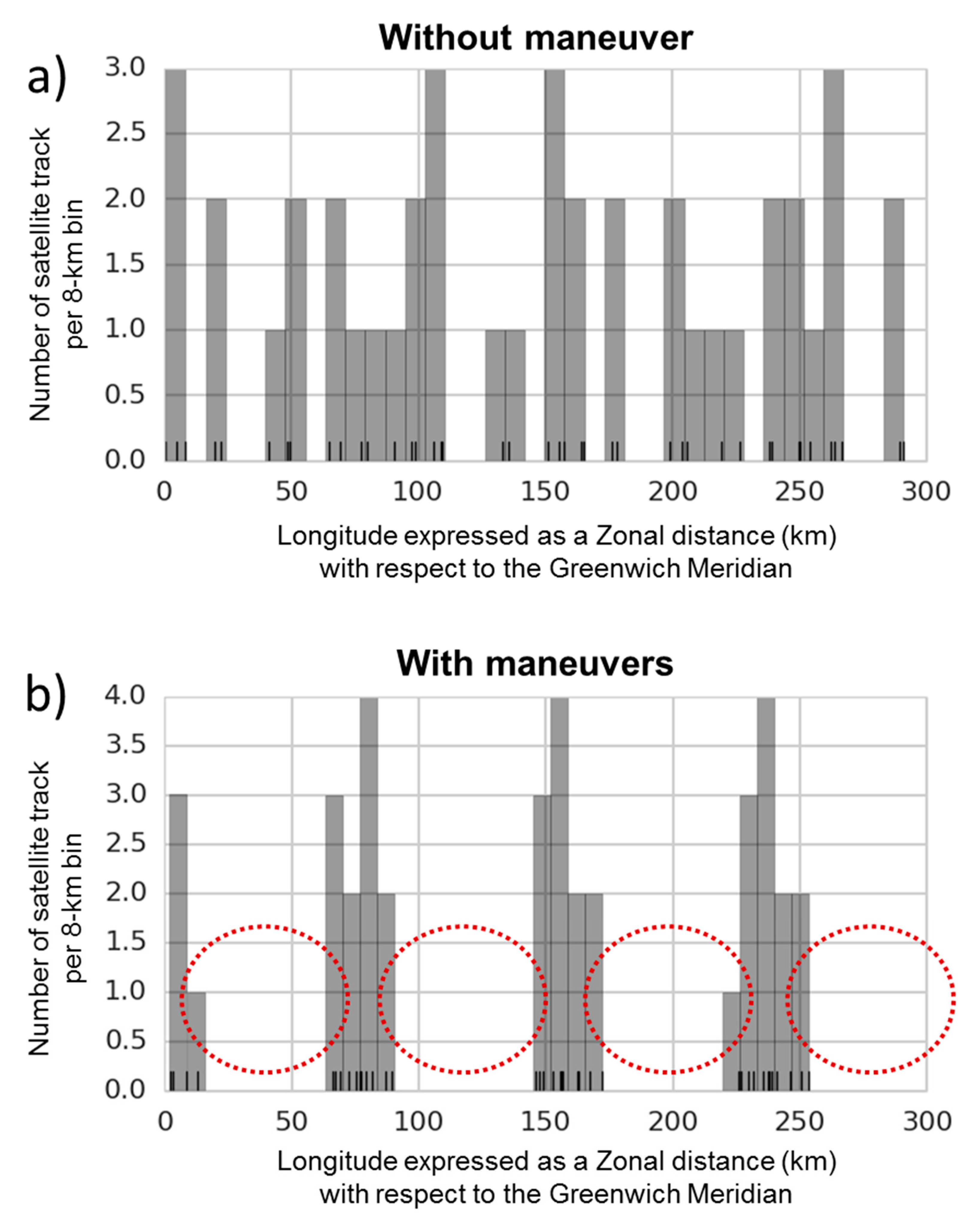
Figure 6a shows a simulation of the zonal distance (in km) of all altimeter tracks (equator crossing, expressed as a distance with respect to the Greenwich meridian) after one year of SARAL DP: each track is a small black tick and the histogram shows how many tracks (i.e., how many black ticks) are located in each 8-km bin. Due to the uncontrolled altitude decay, the distribution is good albeit random with 0 to 3 satellite tracks per 8-km bin.
In other words, this prediction shows that one year of SARAL DP does not yield a perfect 8-km geodetic grid since some grey bins are empty and other bins have up to 3 satellite track samples. But on average, all regions are reasonably well covered, albeit with a somewhat random and irregular pattern. This kind of random distribution was predicted for all regions and all solar flux scenarios.
In contrast, if a relaxed altitude control is performed,
Figure 6b shows a very different picture. In this scenario a single maneuver is performed after 5 months of simulation in order to pull back SARAL to the altitude where the drifting phase was initiated. As a result, all the satellite tracks are put together in small bands of 30-km, leaving 50% of the globe unobserved even after one year. Assuming this pattern is repeated every 6 months, the geodetic dataset collected by AltiKa over the global ocean is less attractive than in Panel (a) of
Figure 6, where the random distribution ensures that observation gaps are neither large nor systematic.
To summarize, as soon as the drifting phase starts, it is better for geodesy users to stop all maneuvers altogether and to let the satellite drift. Assuming that emergency debris avoidance must be performed, it is better to decrease the altitude than to increase it.
4. Observations after 18 Months of SARAL DP
The altitude of SARAL was successfully increased by 1 km in Summer 2016. The satellite has been operated on a slowly decaying altitude for approximately 18 months at the time of writing. This section gives an overview of the results obtained with in-flight data.
Section 4.1 gives an overview of the geodetic sampling collected so far, and
Section 4.2 and
Section 4.3 present some results on ocean mesoscale.
4.1. Geodetic Sampling
As expected from
Section 3.4 and
Figure 6a, the most important change of the drifting phase is the unprecedented cross-track resolution:
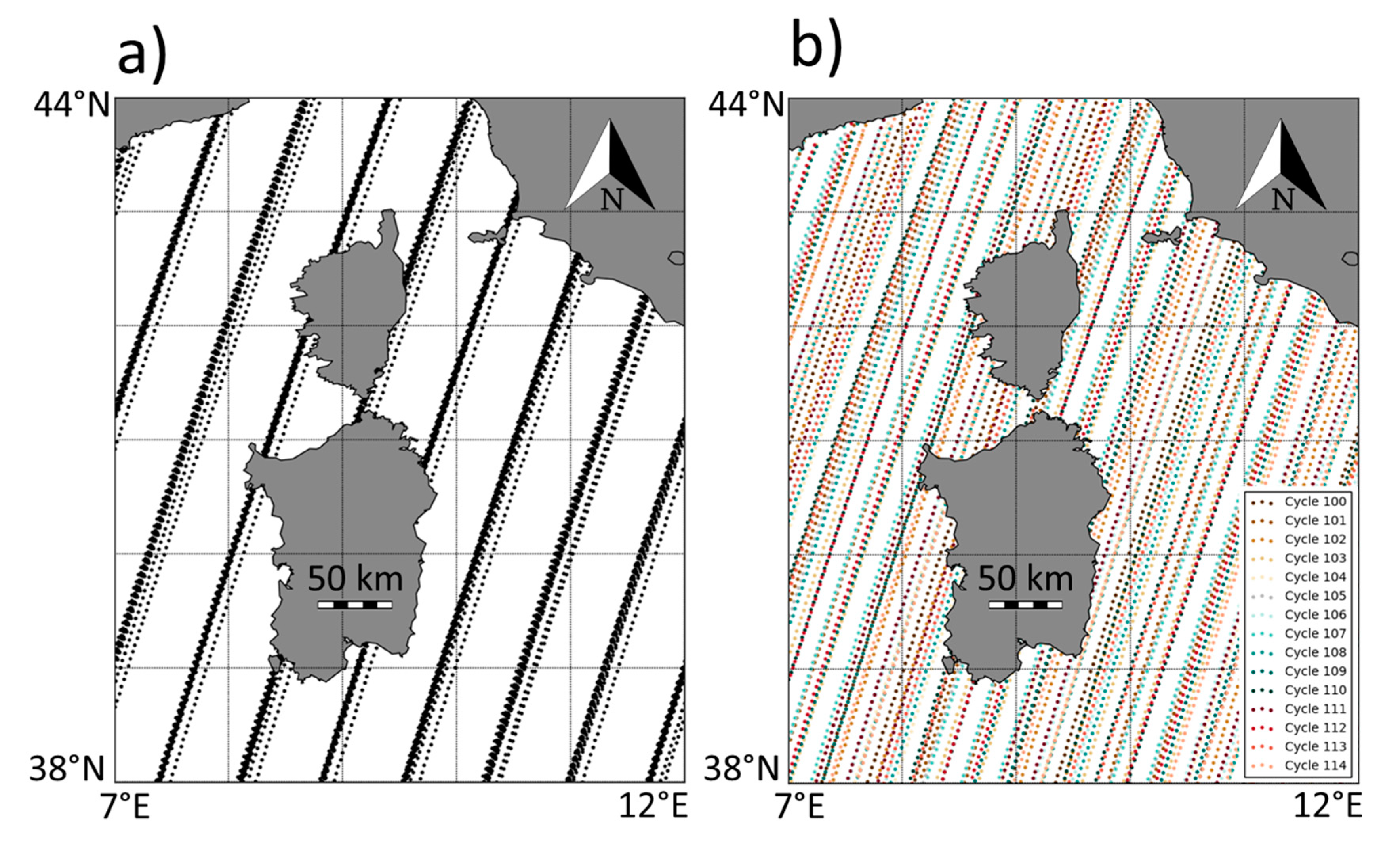
Figure 7 shows the position of descending SARAL subsatellite tracks during the 35-day repeat phase (panel a) and during the first 15 months of SARAL DP (panel b). The longitude resolution of the historical ERS orbit was of the order 50 km at mid-latitudes. The cyclic sampling left very large uncovered regions, even after Spring 2015 when SARAL departed up to 10 km away from its nominal track for a brief period.
In contrast, the SARAL DP coverage is very dense (panel b,
Figure 7): after 15 months, the grid resolution is approximately 4 km on average in this region. As discussed in
Section 3.4, the geodetic grid is also somewhat random and very irregular: it can locally range from 1 km to 15 km.
Sandwell et al. [
28] report that this grid is now used to enhance the smallest scales of geoid models and bathymetry fields in the open ocean. As more AltiKa measurements are collected, the local resolution will keep increasing, albeit still in an irregular way.
4.2. Mesoscale Sampling
Because the altitude of SARAL was increased at the beginning of the drifting phase, its mesoscale sampling has been modified as predicted in
Section 3.3.
Figure 8 shows the distribution of actual SARAL/AltiKa ascending nodes in the longitude/time plane (same metric as the simulations of
Section 2 and
Figure 1, but based on in-flight data). Panel (a) is for the 35-day repeat phase and panel (b) is for December 2017 after 18 months of SARAL DP. Each black dot is one satellite track, and the grey circles are their area of influence (high correlation) for large ocean mesoscale.
Figure 8b shows that the distribution of SARAL DP tracks is consistent with the simulations from
Figure 3, and more specifically with case #B. After 18-months the new phase of SARAL/AltiKa still provides a good sampling capability where each track/measurement minimizes the correlation with adjoining tracks.
More interestingly, the weight of SARAL/AltiKa in the Copernicus Marine Environment Monitoring Service [
5] is routinely monitored in the frame of the operational production of multi-altimeter maps [
22]:
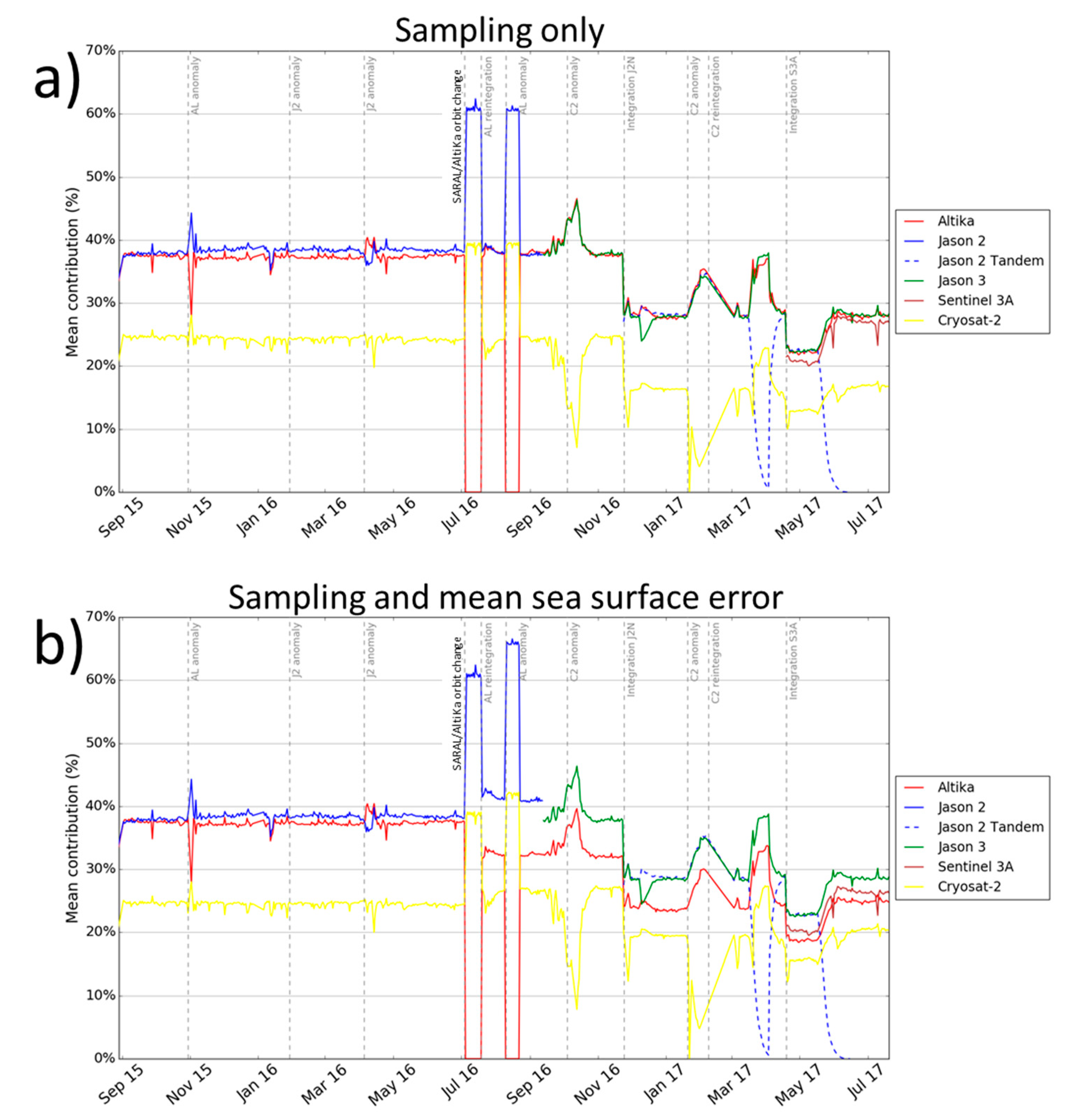
Figure 9 shows the evolution of the mean contribution of each altimeter used by the Optimal Interpolator. The interpolator is derived from Ducet et al. [
20] and Le Traon et al. [
21]. The global contribution of each satellite is measured using Degrees of Freedom of Signal following the methodology of Dibarboure et al. [
29].
Figure 9a shows the contribution of SARAL/AltiKa in an idealized configuration where only the sampling change is taken into account. From September 2015 to June 2016, SARAL is on the historical 35-day orbit and its contribution is of the same order as Jason-2, i.e., substantially more than CryoSat-2. The weaker score of CryoSat-2 is consistent with findings from Dibarboure et al. [
18]. Still, SARAL is slightly below Jason-2 by a couple of points on average. In contrast, after July 2016, SARAL DP is strictly equal to Jason-2: changing the altitude by +1 km slightly improved the sampling capability of AltiKa as predicted in
Section 3.3.
4.3. Impact of the Mean Sea Surface Error
An important component of the accuracy of altimetry products is the reference surface used to transform the Level-2 altimeter sea surface height (SSH) into Level-3 sea-level anomalies (SLA). Dibarboure et al. [
18,
19] have shown the difference between repeat orbits such as the 35-day orbit originally used for SARAL, and geodetic or non-repeat orbits such as SARAL DP.
The former can use a precise mean sea surface height (also known as mean profile) based on more than 2 decades of SSH from ERS-1 to SARAL: it is a very precise local estimate of the mean sea surface (MSS). In contrast, non-repeat missions rely on a global gridded MSS model which is slightly less accurate.
Pujol et al. [
30] have measured the error of recent gridded MSS models using independent measurements from SARAL DP, HY-2A and Sentinel-3A. The error along uncharted tracks was shown to explain up to 30% of the total SLA variance for wavelengths ranging from 30 km to 100 km.
To that extent,
Figure 9a is only an idealized view of the change between the 35-day phase and the drifting phase, because it does not account for the larger SLA error when a gridded MSS reference must be used in place of the precise 20-year mean profile. In contrast,
Figure 9b takes into account both aspects of the orbit change: the slightly increased sampling capability and the additional MSS error.
The overall contribution of AltiKa decreases by approximately 6 points and in turn the relative contributions of other missions increase. Still, SARAL remains a strong contributor of the CMEMS system, including when both Jason-3 and Jason-2 plus Sentinel-3A are active. This is notably visible during the CryoSat-2 or Jason-2 data outages where the contribution of AltiKa exhibits some peaks as high a +5 to 7 points.
4.4. Evolution of the SARAL Altitude
After 18 months of drifting phase, the altitude of SARAL has decreased by less than 150 m. This is approximately the 5th percentile curve of the simulations from
Figure 2, i.e., three times less than our conservative simulations of
Figure 4 which was based on the 95th percentile scenario of the 2016 predictions. Thanks to a particularly weak solar activity, SARAL remains on the upper range of the desirable altitudes of
Figure 5 (blue region, 16-day sub-cycle). In other words, the mesoscale sampling capability of SARAL/AltiKa will remain good for many years, and substantially longer than predicted by the conservative simulations.
5. Discussion: Using an Unmaintained Altitude with Other Altimeters
5.1. Generalizing the SARAL DP Strategy
SARAL/AltiKa is the first altimeter to be operated on an unmaintained decaying altitude. But other altimeters could use the same strategy in the future. There are essentially three reasons to use this kind of orbit in the context of radar altimetry:
Platform ageing: if controlling the satellite’s altitude becomes difficult or risky, it might be better to simply stop maneuvers altogether after the satellite is put on a well-chosen initial altitude.
Simpler operations: keeping the satellite on its nominal orbit requires periodic operations (e.g., every 2 to 4 weeks for ERS and Jason altitudes). Letting the altitude decay naturally in a mesoscale-friendly altitude range might reduce the manpower needed for routine operations. While it is not significant for a single altimeter above 900 km, this strategy could be attractive for lower orbits (e.g., 500 km) or for altimeter constellations (e.g., 5+ satellites) because more manpower is required, and because each maneuver creates a small data gap or temporary degradation (e.g., discontinuity in precise orbit determination). Limiting the maneuvers to debris avoidance could reduce the operation cost of such a low-altitude constellation.
Saving fuel: most of the satellite fuel is used during launch (to reach the nominal orbit) and for de-orbitation. Using a decaying altitude and avoiding station keeping maneuvers would save only a small amount of fuel. But for some satellites that experience major launch events, it is sometimes necessary to consume more fuel than anticipated (e.g., CryoSat-2 was injected relatively far away from its nominal altitude). In this situation, using a decaying altitude might be a backup scenario able to extend the satellite lifespan by saving fuel for the final de-orbitation.
To summarize, the SARAL DP decaying altitude strategy could be used for other altimeters in the future: as a new mission phase when the satellite suffers from ageing anomalies, as a backup orbit after launch anomalies, or for a dedicated mission/constellation put specifically at an altitude where the maintenance effort is limited.
In the following section, we expand the methodology and the results of
Section 3 to determine automatically all the altitude ranges that are compatible with an SARAL DP strategy.
5.2. Methodology Addition
In
Figure 3, we observed very different ocean mesoscale sampling properties. We used the overlap between grey circles as a way to detect poor orbits. This can be automated with the very simple correlation model (Equation (4)) used by Dibarboure et al. [
19] for Jason-1.
Here
rx and
rt are the spatial and temporal decorrelation radiuses of
Section 2.1, and
k is arbitrarily set to yield a correlation of 0.5 on the edge of the
rx/
rt circle. By computing
C(
dx,
dt) where
dx and
dt is the space and time distance between two altimeter tracks, it is possible to approximate the correlation between the datasets. Sensitivity tests show that the type of function and parameter
k do not significantly impact the following results.
For a given altitude, we compute the position of all altimeter tracks in the space/time place over 50 days (i.e., complete mesoscale decorrelation), we pick one arbitrary track and we search for all possible neighbors in a space/time bubble. Then we keep the 5 non-aligned tracks with the highest correlation as they define the sub-cycles for this altitude. Pruning aligned tracks from this list is important: to illustrate, with a 3-day SC, we want to detect only the closest track aligned in this direction because 6, 9 and 12 days are only repeats of this SC (they are not separate sub-cycles because they all follow the same alignment).
This computation gives not only the list of dominant sub-cycles (e.g., 3 and 16 for the ERS/ENVISAT sub-cycles) but also all minor sub-cycles (e.g., 19-day SC visible in
Figure 1) and the true repeat cycle (e.g., 35 days for ERS/ENVISAT). For each sub-cycle, we also have the correlation which indicates if this sub-cycle yields independent or correlated satellite tracks. If the correlation is too high for any SC, then the altitude is not attractive to observe mesoscale. If the correlation is low for all SC, then it is a good orbit candidate: it is worthy of more in-depth analyses not discussed in this paper.
5.3. Finding Good Altitude Ranges
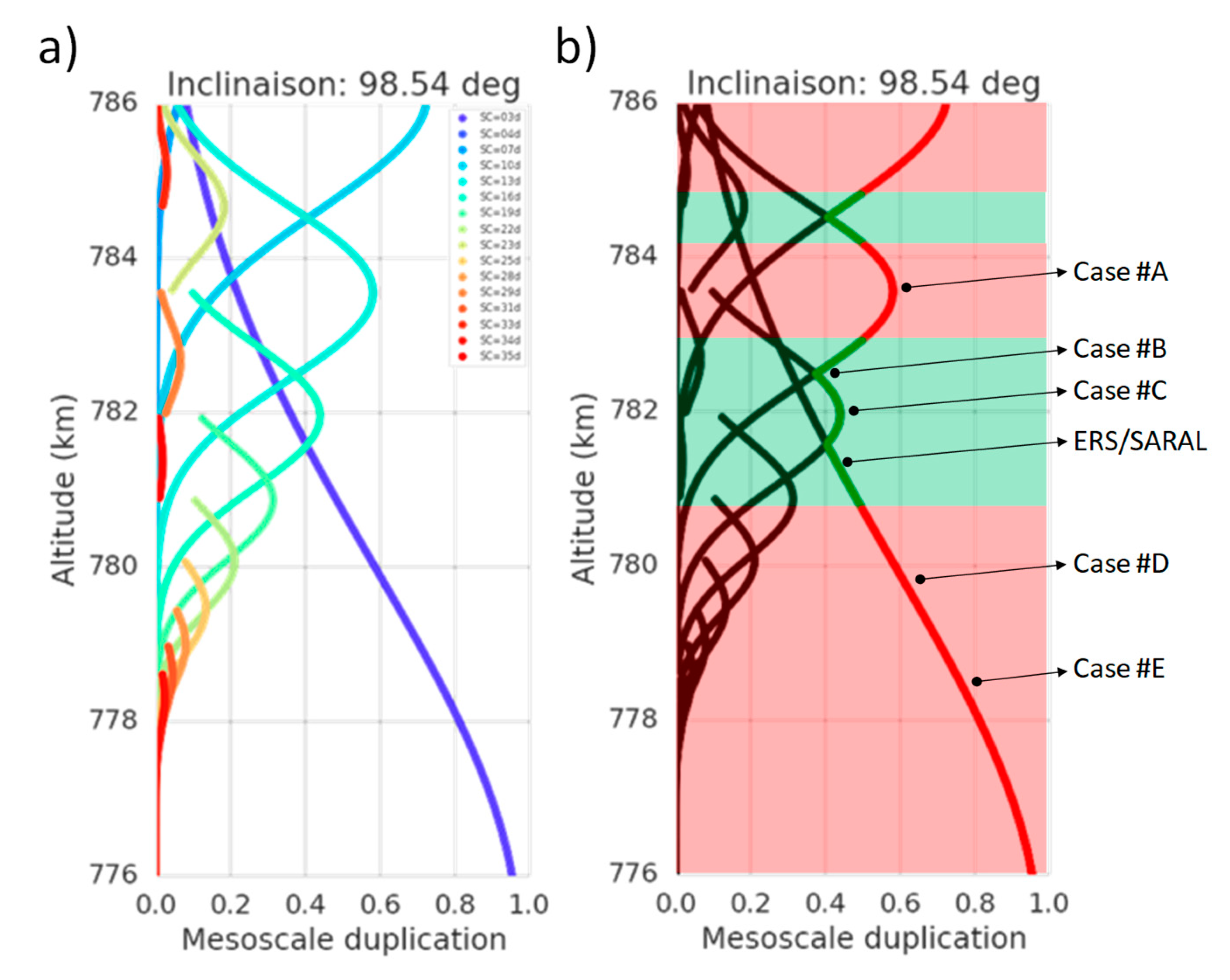
We performed this computation for all altitudes from 300 km to 1500 km with an increment of 30 m. We used a threshold of C = 0.5 to reject mesoscale-unfriendly altitudes. Then we aggregated all valid orbits in altitude bands to determine how large these bands were.
Figure 10 shows the result near the ERS/ENVISAT altitude. Panel (a) of
Figure 10, shows the correlation
C for each altitude (each sub-cycle is displayed with a different color), and panel (b) of
Figure 10, shows the valid (green) and invalid (red) regions based on our threshold (if any sub-cycle has a correlation
C > 0.5 the altitude is in red). Panel (b) also highlights the 5 cases shown in
Figure 3. This representation illustrates how the qualitative overlap discussed in previous sections is now quantified with this metric. The main green region in Panel (b) corresponds to the altitude selected by CNES and ISRO for SARAL DP.
5.4. Mesoscale-Friendly Altitude Bands for Unmaintained Altimeters
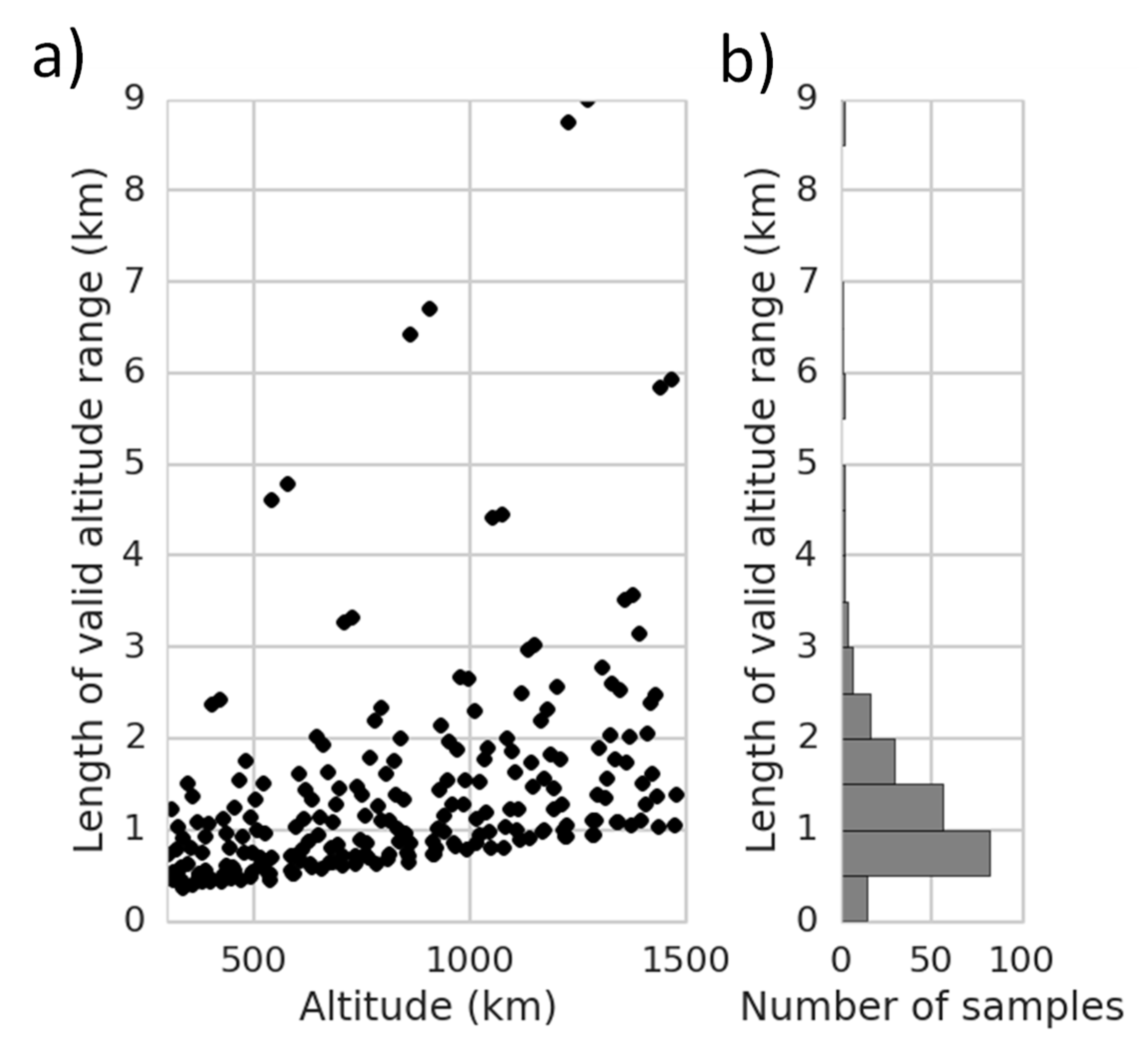
Figure 11 shows all the valid altitude bands found for the ERS/ENVISAT inclination. We performed sensitivity tests with the inclination of various altimetry missions (GEOSAT, Jason, Sentinel-3) that yielded similar results: the good/bad altitude ranges are translated but their properties are essentially the same.
On average, they are rather thin (from 500 m to 1500 m) but a small fraction can be 2 to 3 km large. This finding is consistent with observations from Dibarboure et al. [
19]: their orbit candidates for the so-called Extension-Of-Life phase of Jason-1 were found to be aggregated in thin altitude bands. In the case of SARAL DP there is a 2-km sweet spot just near the historical ERS/ENVISAT orbit: these larger bands are uncommon.
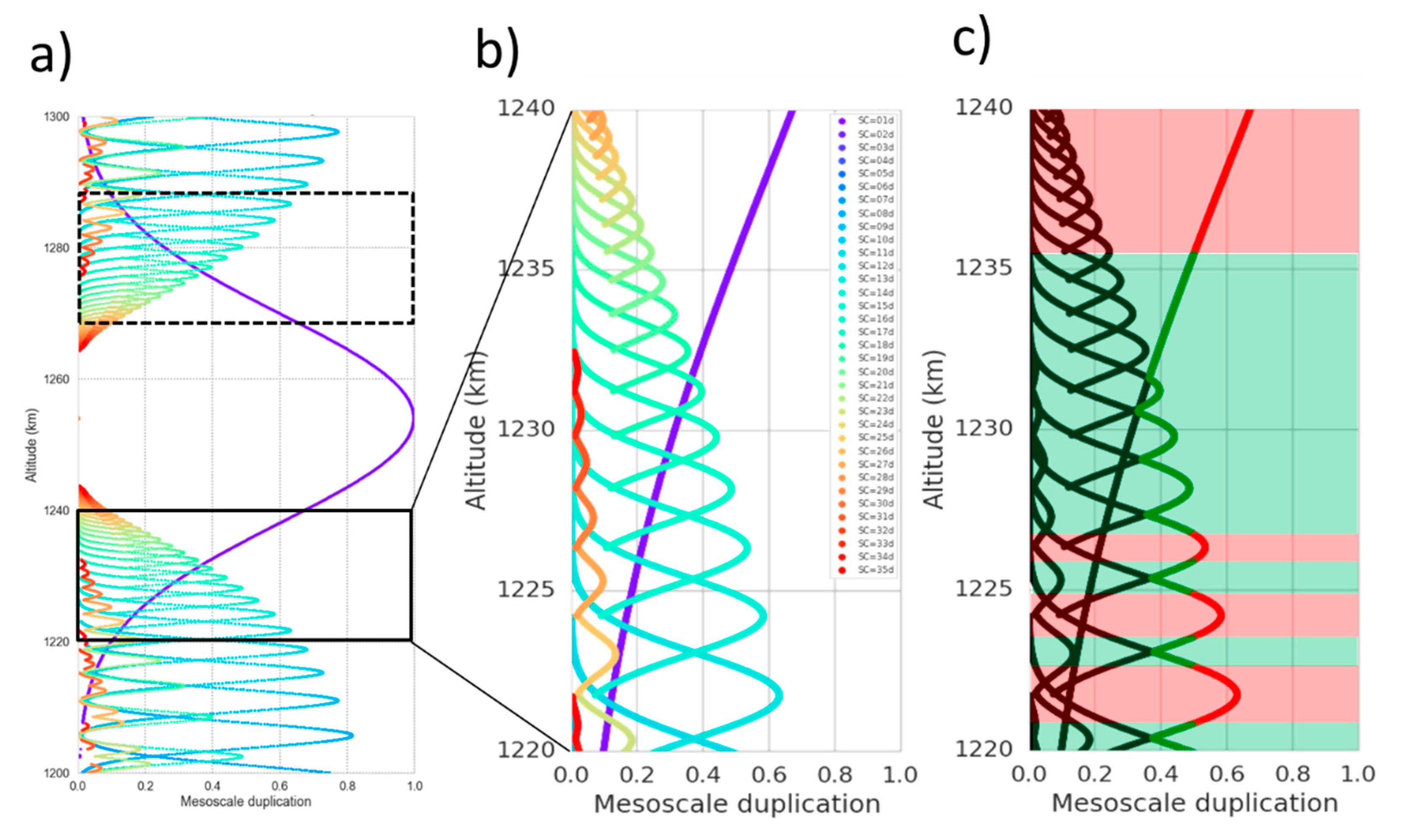
Furthermore
Figure 11 also shows the existence of altitude bands as large as 9 km. These exceptional occurrences always come in pairs. This is explained by
Figure 12: the longest valid altitude ranges are generally located symmetrically near the altitude of a very short repeat cycle. The black rectangles of panel (a) of
Figure 12, on each side of the purple bell-shaped curve highlight are where valid altitude ranges are located. Panel (b) of
Figure 12, is a zoom of the plain black rectangle of panel (a): it shows that the composition of a very short sub-cycle and multiple mesoscale-friendly sub-cycles minimizes ocean mesoscale duplication (i.e., the maximal correlation between adjoining satellite tracks). The validity of the altitude range is shown in green in panel (c) of
Figure 12, the largest valid altitude band range from 1227 to 1236 km. The dashed black rectangle of panel (a) also contains a second valid range (essentially an upside-down mirror of panel (b)). The same dual/mirror pattern can be observed for most of the long valid ranges in
Figure 11a.
The 9-km bands are located above 1200 km where the atmospheric drag is very weak. To that extent, a dedicated altimeter mission parked at this altitude would have a great mesoscale sampling for decades. In practice, 1200 km could be too high for at least three reasons: aggressive radiation environment for the satellite, difficult to de-orbit at the end of the mission, unfavorable signal-to-noise ratio for the altimeter (e.g., possibly incompatible with a very small satellite).
In contrast, one could envision a low-cost, low-maintenance altimeter near 600 km for the following reasons:
The lower altitude would better protect the satellite from radiations.
The satellite de-orbitation would be easier (e.g., good for a small satellite).
Altitudes lower than 700 km are attractive because the space debris density is lower: in turn one could anticipate fewer collision avoidance maneuvers (simpler operations)
Lower altitudes yield a slightly better signal-to-noise ratio for the altimeter (less electrical power needed, i.e., also good for a small satellite).
Nevertheless, at 600 km the atmospheric drag increases exponentially (
Figure 13). Even if there is a 4.5 km valid altimeter band that could host such as dedicated mission, the altitude of a SARAL-looking satellite would decay approximately 10 times faster than the 300 m/year of SARAL. To be viable, the platform should be specifically designed to minimize the atmospheric drag with an aerodynamic profile (e.g., smaller and compact solar arrays like Cryosat-2). The lifespan of the mission could also be extended by a handful of maneuvers (e.g., every couple of years) that would reset the altitude decay and start over a new maneuver-free cycle.
Such a low-cost and low-maintenance altimeter mission would be relevant in the context of low-cost constellations (e.g., 4 to 10 satellites): if all satellites are located at the same altitude in one sun-synchronous orbit plane, the altitude of all altimeters decays in a coherent way. With this scenario, the sampling capability of the entire constellation remains good throughout the entire altitude decay. In essence, this concept is a fire-and-forget constellation of small altimetry satellites whose orbit maintenance is limited to debris avoidance.
6. Conclusions
In this paper we showed that it is possible for altimeter missions to keep a good mesoscale sampling for years even if their altitude is not actively maintained and even if it decays due to the atmospheric drag. This strategy has been successfully applied on SARAL/AltiKa during the so-called drifting phase that was initiated in early July 2016 by ISRO and CNES.
Eighteen months later, SARAL DP has demonstrated the benefits of this strategy: reducing the maneuvers has made it possible to extend the satellite lifetime (less stress on momentum wheels), and the new DP orbit provides an enhanced sampling capability of ocean mesoscale, as well as precious measurements to improve marine geodesy references fields (e.g., bathymetry, geoid or mean sea surface).
For SARAL, the optimal starting point of the drifting phase was approximately 1 km above the historical ERS/ENVISAT orbit. Thanks to a continuously evolving combination of the 13, 16 and 19-day sub-cycles, the mesoscale sampling capability of SARAL DP has been secured for 6 years or more.
More generally, this strategy can be used for any altimeter (e.g., Jason-3 or Sentinel-3), for instance if the satellite maneuvering capability is limited by onboard ageing anomalies. As long as the satellite is put at the top of a favorable altitude range, the decaying altitude will not degrade the mesoscale sampling capability of the altimeter. It is possible to find mesoscale-friendly altitudes at all altitudes from 500 km to 1500 km.
We also identified a small list of larger mesoscale-friendly altitude bands where one could park a full-fledged drifting altimetry mission, or an entire altimeter constellation. In these sweet spots, the quality of mesoscale sampling is guaranteed for a very long time even if the altitude is not maintained. Near 1230 km, there are two very large altitude bands (9 km each) where an unmaintained altimeter would yield a good and stable mesoscale sampling for decades. At 600 km two large altitude ranges (4.5 km each) makes it possible to envision a low-cost/low-maintenance small altimeter satellite (good SNR, easy de-orbitation, orbit control limited to debris avoidance).