Three-Dimensional Structure Inversion of Buildings with Nonparametric Iterative Adaptive Approach Using SAR Tomography
Abstract
1. Introduction
2. Methodology
2.1. Overview of the TomoSAR Imaging Model
2.2. IAA-BIC TomoSAR Method
- (1)
- The parameters x(l) and P are estimated from the IAA algorithm.
- (2)
- Detect all peaks of the reflectivity power and put their indices into . Initializes as an empty set .
- (3)
- The first peak is selected from the set according to the minimum BIC value and put its index into .
- (4)
- The ith peak, from the set , which, together with the selected peaks, gives the minimum BIC, is determined and so on until the BIC value does not decrease anymore. Throughout the loop, keep updating by putting the index of the selected peak.
- (5)
- The selected peak indices and their corresponding reflectivity power are the final estimated results.
3. Numerical Examples
- (1)
- Considering that the classical spectral estimators (Capon and MUSIC) are only suitable for multi-look, a comparison of the reconstruction performance between IAA-BIC and the classical spectral estimators (Capon and MUSIC) is presented for a simulated signal with 25 looks.
- (2)
- In urban areas, CS is generally applied with single-look, maintaining the spatial resolution. Thus, a comparison of the reconstruction performance between IAA-BIC and CS is presented for a simulated signal with single-look.
- (1)
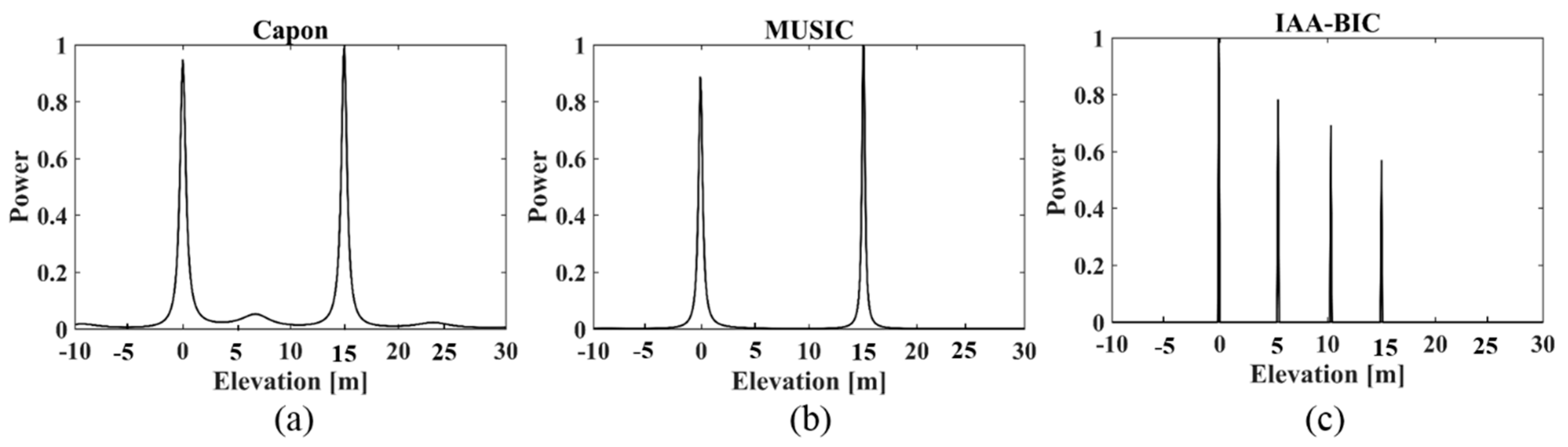
- For the profile reconstruction with multi-look (L = 25), the Capon algorithm clearly detected the two distributed scatterers, but failed to discriminate the two coherent scatterers (see Figure 2a). This situation was also seen in the performance of MUSIC. Although MUSIC obtained a higher elevation resolution and less sidelobe than Capon, it also could not detect the two coherent scatterers (see Figure 2b). However, the IAA-BIC estimator succeeded in recognizing these four scatterers (see Figure 2c). This suggests that IAA-BIC can work well for both distributed and coherent sources, but both Capon and MUSIC showed a degraded performance in the case of coherent sources.
- (2)
- For the sparse profile reconstruction with single-look (see Figure 3), IAA-BIC obtained the height of the four scatterers accurately, without requiring any selection of hyperparameter. This shows that IAA-BIC can obtain a reliable sparse estimation, even with single-look. As for the CS method, its performance depends on the hyperparameter. If this value is not suitable, there will be sidelobes (three red circles in Figure 3b) as well as some elevation estimation bias (two green circles in Figure 3b). When the hyperparameter is appropriate, CS can discriminate the scatterers with a high elevation resolution (as can be seen in Figure 3c). This means that CS requires us to adjust the hyperparameter repeatedly until it obtains a good performance, leading to a high time investment. In this study, the CVX solver [40] was used to solve the L1-norm minimization for the CS estimator, thanks to its ease of implementation and compactness.
- (3)
- According to Figure 2c and Figure 3a, the IAA-BIC estimator can work well for both multi-look and single-look. It is important to maintain the azimuth-range resolution to observe the inherent scale of urban infrastructures, especially for high spatial resolution SAR images. However, in practice, multi-look, which involves averaging pixels in the azimuth and/or range directions, reduces the spatial (azimuth-range) resolution. This is an inappropriate way for the application of TomoSAR over urban areas.
4. Real-Data Experiment and Results
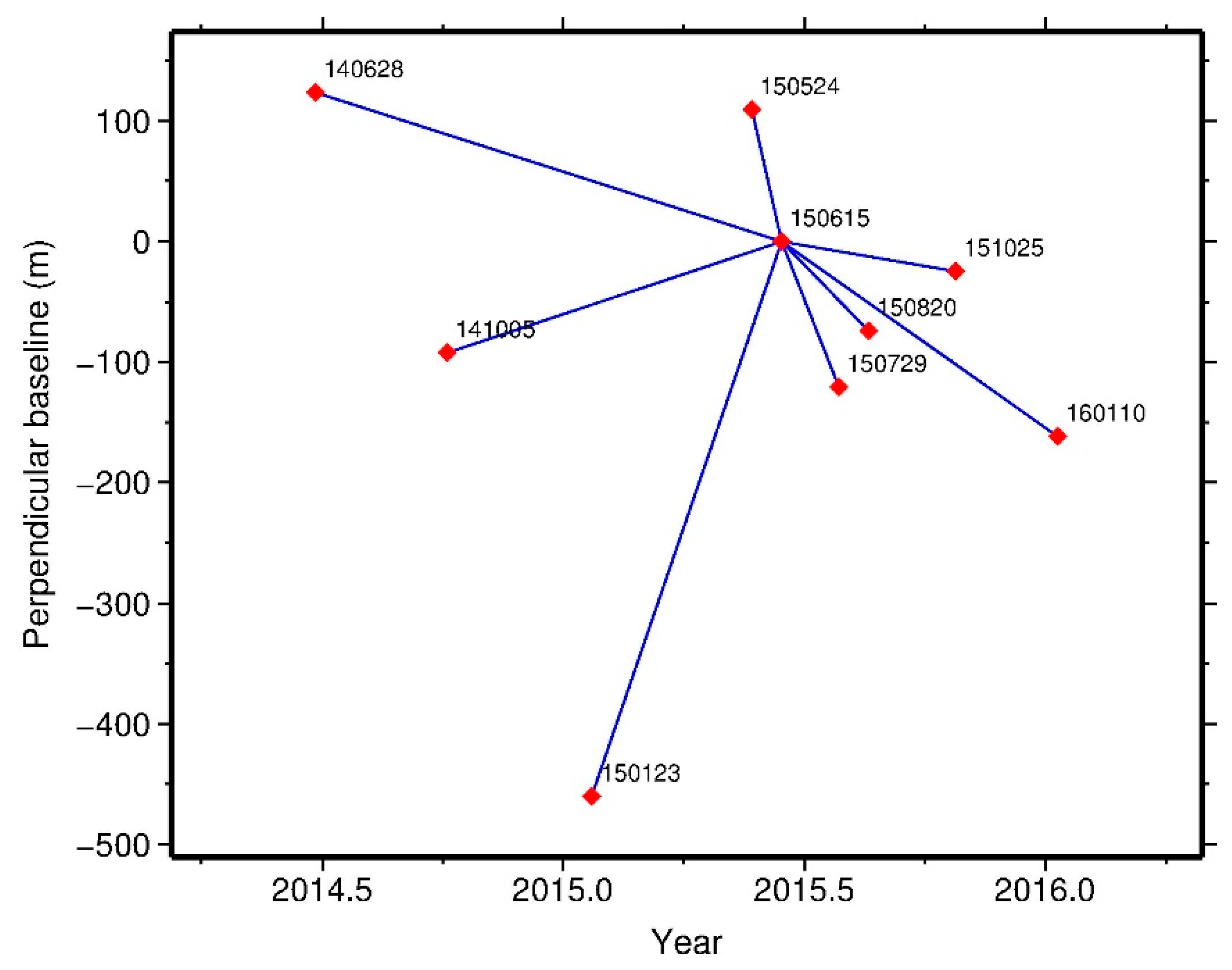
4.1. Study Area and Dataset
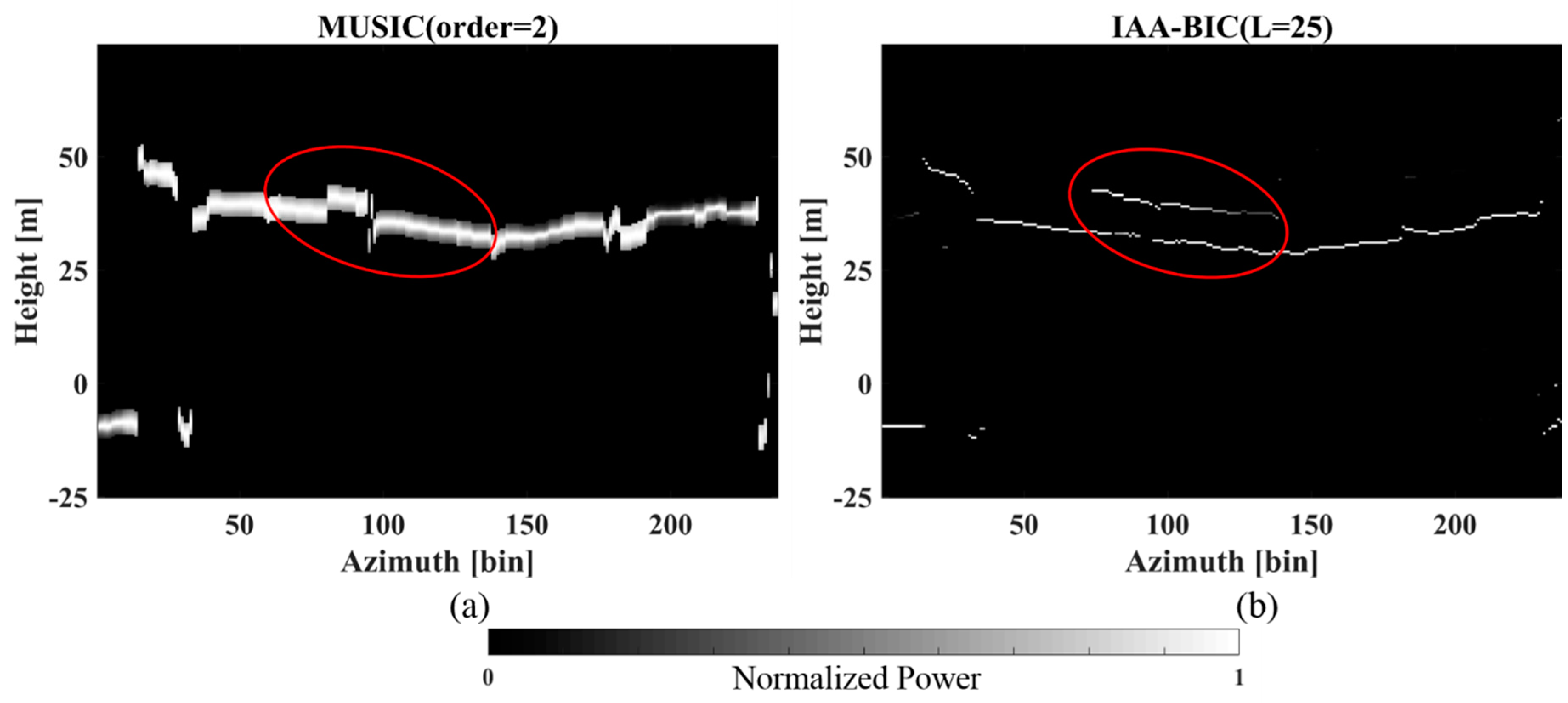
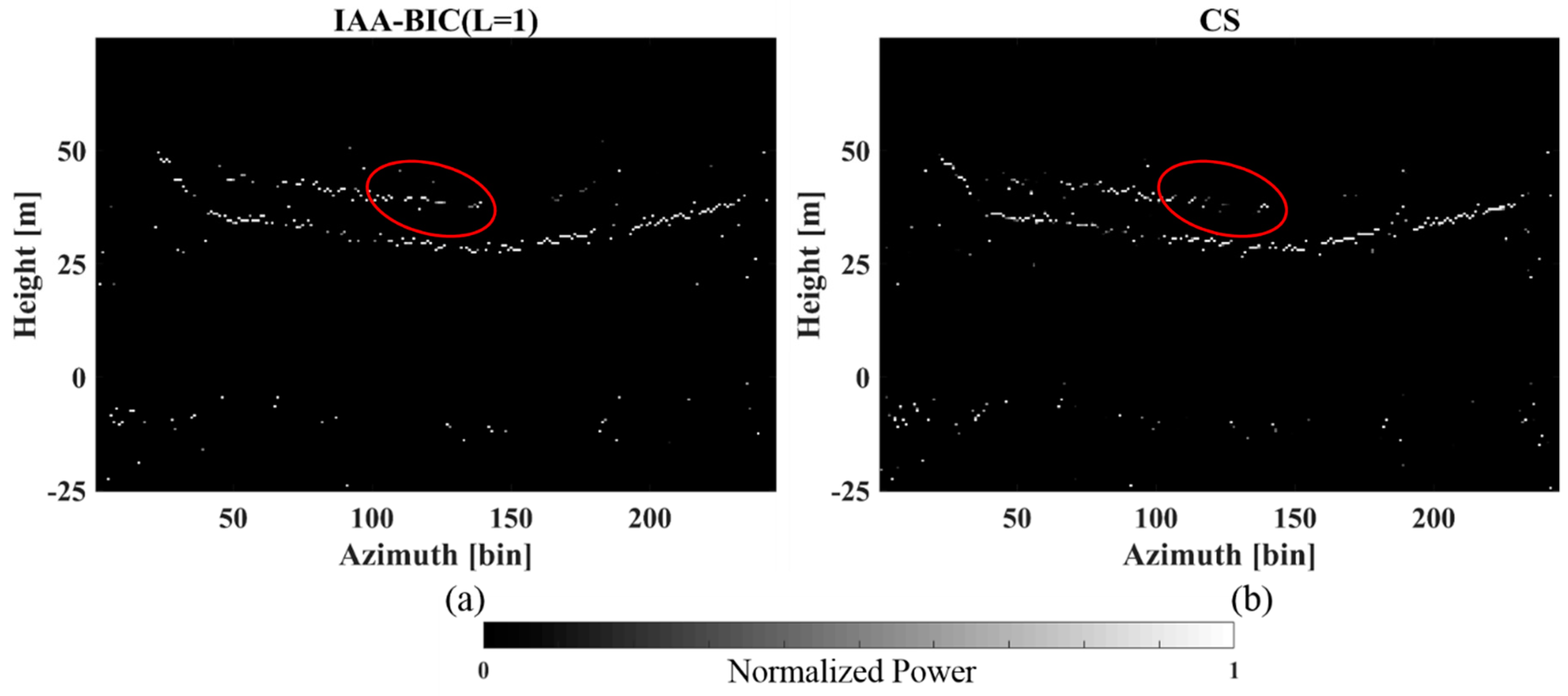
4.2. Results and Analysis
5. Discussion
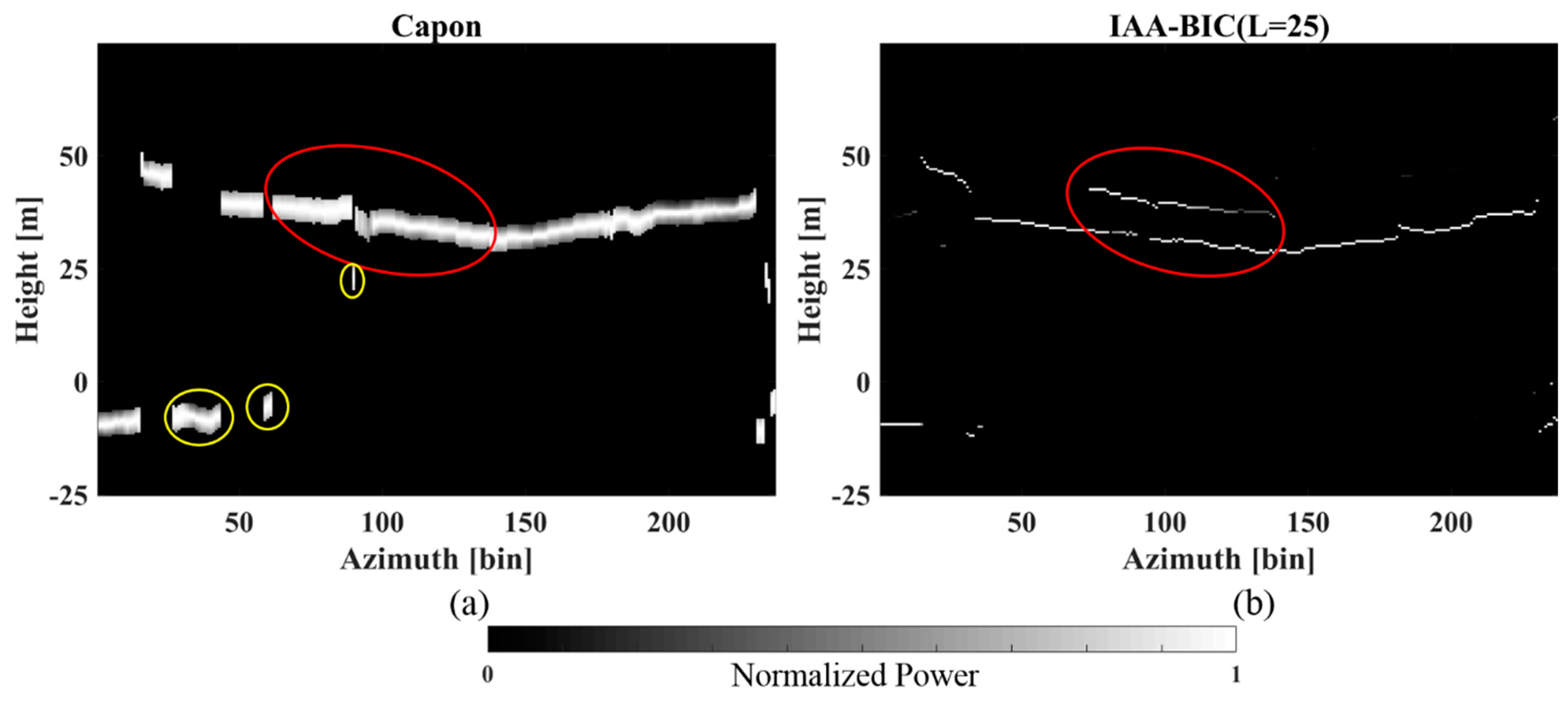
5.1. Comparison between IAA-BIC and Capon
5.1.1. Theoretical Analysis
5.1.2. Experimental Analysis
5.2. Comparison between IAA-BIC and MUSIC
5.2.1. Theoretical Analysis
5.2.2. Experimental Analysis
5.3. Comparison between IAA-BIC and CS
5.3.1. Comparison of Estimation Accuracy
5.3.2. Comparison of Computational Time Consumption
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roth, A. TerraSAR-X: A new perspective for scientific use of high resolution spaceborne SAR data. In Proceedings of the 2nd GRSS/ISPRS Joint Workshop on Remote Sensing and Data Fusion over Urban Areas, Berlin, Germany, 22–23 May 2003. [Google Scholar]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I. TanDEM-X: A satellite formation for high-resolution SAR interferometry. Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Covello, F.; Battazza, F.; Coletta, A.; Lopinto, E.; Fiorentino, C.; Pietranera, L.; Valentini, G.; Zoffoli, S. COSMO-SkyMed an existing opportunity for observing the Earth. J. Geodyn. 2010, 49, 171–180. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Liao, M.; Wang, H. Application of TomoSAR in urban deformation surveillance. Shanghai Land Resour. 2013, 34, 7–11. [Google Scholar]
- Pasquali, P.; Prati, C.; Rocca, F. A 3-D SAR Experiment with EMSL Data. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium (IGARSS’95), Florence, Italy, 10–14 July 1995; pp. 784–786. [Google Scholar]
- Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
- Gini, F.; Lombardini, F.; Montannari, M. Layover solution in multibaseline SAR interferometry. IEEE Trans. Aerosp. Electron. Syst. 2005, 20, 71–93. [Google Scholar] [CrossRef]
- She, Z.; Gray, D.; Bogner, R.; Homer, J. Three-dimensional SAR imaging via multiple pass processing. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium (IGARSS’95), Florance, Italy, 28 June–2 July 1995; Volume 5, pp. 2389–2391. [Google Scholar]
- Lombardini, F.; Reigber, A. Adaptive Spectral Estimation for Multi-baseline SAR Tomography with Airborne L-band Data. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toulouse, France, 21–25 July 2003; Volume 3, pp. 2014–2016. [Google Scholar]
- Fornaro, G.; Serafino, F.; Soldovieri, F. Three-dimensional Focusing with Multipass SAR Data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 507–517. [Google Scholar] [CrossRef]
- Lombardini, F.; Gini, F.; Matteucci, P. Application of array processing techniques to multibaseline InSAR for layover solution. In Proceedings of the 2001 IEEE Radar Conference, Atlanta, GA, USA, 3 May 2001; pp. 210–215. [Google Scholar]
- Kumar, S.; Joshi, S.K.; Govil, H. Spaceborne PolSAR Tomography for Forest Height Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5175–5185. [Google Scholar] [CrossRef]
- Gini, F.; Lombardini, F. Multilook APES for Multi-baseline SAR Interferometry. IEEE Trans. Signal Proc. 2002, 50, 1800–1803. [Google Scholar] [CrossRef]
- Sauer, S.; Ferro-Famil, L.; Reigber, A.; Pottier, E. Three-dimensional imaging and scattering mechanism estimation over urban scenes using dual-baseline polarimetric InSAR observations at L-band. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4616–4629. [Google Scholar] [CrossRef]
- Huang, Y.; Ferro-Famil, L. 3D characterization of buildings in a dense urban environment using L-band PolInSAR data with irregular baselines. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; Volume 3, pp. 29–32. [Google Scholar]
- Huang, Y.; Ferro-Famil, L.; Reigber, A. Under-foliage Object Imaging Using SAR Tomography and Polarimetric Spectral Estimators. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2213–2225. [Google Scholar] [CrossRef]
- Wei, L.; Balz, T.; Liao, M.; Zhang, L. A Novel Fast Approach for SAR Tomography: Two step iterative Shrinkage/Thresholding. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1377–1381. [Google Scholar]
- Tebaldini, S. Algebraic Synthesis of Forest Scenarios from Multi-baseline PolInSAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4132–4142. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Very High Resolution Spaceborne SAR Tomography in Urban Environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [CrossRef]
- Pardini, M.; Papathanassiou, K. On the Estimation of Ground and Volume Polarimetric Covariances in Forest Scenarios with SAR Tomography. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1860–1864. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Tomographic SAR Inversion by L1-Norm Regularization—The Compressive Sensing Approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3839–3846. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Super-Resolution Power and Robustness of Compressive Sensing for Spectral Estimation with Application to Spaceborne Tomographic SAR. IEEE Trans. Geosci. Remote Sens. 2011, 50, 247–258. [Google Scholar] [CrossRef]
- Sun, X.; Yu, A.; Dong, Z.; Liang, D. Three-Dimensional SAR Focusing via Compressive Sensing: The Case Study of Angel Stadium. IEEE Geosci. Remote Sens. Lett. 2012, 9, 759–763. [Google Scholar]
- Zhu, X.X.; Bamler, R. Super Resolution SAR Tomography for Multi-dimensional Imaging of Urban Areas: Compressive Sensing-based TomoSAR Inversion. IEEE Signal Proc. Mag. 2014, 31, 51–58. [Google Scholar] [CrossRef]
- Biondi, F. SAR Tomography Optimization by Interior Point Method via Atomic Decomposition—The Convex Optimization Approach. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGRASS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1879–1882. [Google Scholar]
- Liang, L.; Guo, H.; Li, X. Three-Dimensional Structural Parameter Inversion of Buildings by Distributed Compressive Sensing-Based Polarimetric SAR Tomography Using a Small Number of Baselines. IEEE J. Sel. Top. Appl. Res. Obs. Remote Sens. 2014, 7, 4218–4230. [Google Scholar] [CrossRef]
- Ma, P.F.; Lin, H.; Lan, H.X.; Chen, F.L. On the Performance of Reweighted L1 Minimization for Tomographic SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 895–899. [Google Scholar] [CrossRef]
- Li, X.; Liang, L.; Guo, H. Compressive Sensing for Multibaseline Polarimetric SAR Tomography of Forested Areas. IEEE Trans. Geosci. Remote Sens. 2016, 54, 153–166. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Ferro-Famil, L.; Guo, H.; Zhang, L.; Wu, W. Urban Area Tomography Using a Sparse Representation Based Two-Dimensional Spectral Analysis Technique. Remote Sens. 2018, 10, 109. [Google Scholar] [CrossRef]
- Budillon, A.; Evangelista, A.; Schirinzi, G. Three dimensional SAR focusing from multi-pass signals using compressive sampling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 488–499. [Google Scholar] [CrossRef]
- Budillon, A.; Evangelista, A.; Schirinzi, G. SAR tomography from sparse samples. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. 865–868. [Google Scholar]
- Cazcarra-Bes, V.; Tello-Alonso, M.; Fisher, R.; Heym, M.; Papathanassiou, K. Monitoring of Forest Structure Dynamics by Means of L-Band SAR Tomography. Remote Sens. 2017, 9, 1229. [Google Scholar] [CrossRef]
- Yardibi, T.; Li, J.; Stoica, P.; Xue, M.; Baggeroer, A.B. Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 425–443. [Google Scholar] [CrossRef]
- Du, L.; Yardibi, T.; Li, J.; Stoica, P. Review of user parameter-free robust adaptive beamforming algorithms. Dig. Signal Proc. 2009, 19, 567–582. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Stoica, P.; Selen, Y. Model-order selection: A review of information criterion rules. IEEE Signal Proc. Mag. 2004, 21, 36–47. [Google Scholar] [CrossRef]
- Lombardini, F.; Gini, F. Model order selection in multi-baseline interferometric radar systems. EURASIP J. Appl. Signal Proc. 2005, 20, 3206–3219. [Google Scholar] [CrossRef]
- Wax, M.; Kailath, T. Detection of signals by information theoretic criteria. IEEE Trans. Acoust. Speech Signal Proc. 1985, 33, 387–392. [Google Scholar] [CrossRef]
- Wax, M.; Ziskind, I. Detection and localization of multiple sources via the stochastic signal model. IEEE Trans. Signal Proc. 1991, 39, 2450–2456. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: MATLAB Software for Disciplined Convex Programming, version 2.1; Tech. Rep.; 2014. Available online: http://cvxr.com/cvx (accessed on 10 June 2015).
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Prentice-Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]






| Polarization Mode | Wavelength (cm) | Incidence Angle | Slant Range (m) | Azimuth Spacing (m) | Range Spacing (m) |
|---|---|---|---|---|---|
| HH | 3.10 | 31.003° | 589,061.4613 | 0.17 | 0.45 |
| IAA-BIC | Single-Look | Multi-Look |
|---|---|---|
| Building height (m) | 98.24 | 95.74 |
| Estimation error (m) | 0.76 | 3.26 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Wang, C.; Li, X.; Du, Y.; Fu, H.; Yang, Z.; Xie, Q. Three-Dimensional Structure Inversion of Buildings with Nonparametric Iterative Adaptive Approach Using SAR Tomography. Remote Sens. 2018, 10, 1004. https://doi.org/10.3390/rs10071004
Peng X, Wang C, Li X, Du Y, Fu H, Yang Z, Xie Q. Three-Dimensional Structure Inversion of Buildings with Nonparametric Iterative Adaptive Approach Using SAR Tomography. Remote Sensing. 2018; 10(7):1004. https://doi.org/10.3390/rs10071004
Chicago/Turabian StylePeng, Xing, Changcheng Wang, Xinwu Li, Yanan Du, Haiqiang Fu, Zefa Yang, and Qinghua Xie. 2018. "Three-Dimensional Structure Inversion of Buildings with Nonparametric Iterative Adaptive Approach Using SAR Tomography" Remote Sensing 10, no. 7: 1004. https://doi.org/10.3390/rs10071004
APA StylePeng, X., Wang, C., Li, X., Du, Y., Fu, H., Yang, Z., & Xie, Q. (2018). Three-Dimensional Structure Inversion of Buildings with Nonparametric Iterative Adaptive Approach Using SAR Tomography. Remote Sensing, 10(7), 1004. https://doi.org/10.3390/rs10071004








