Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements
Abstract
1. Introduction
2. Data and Methods
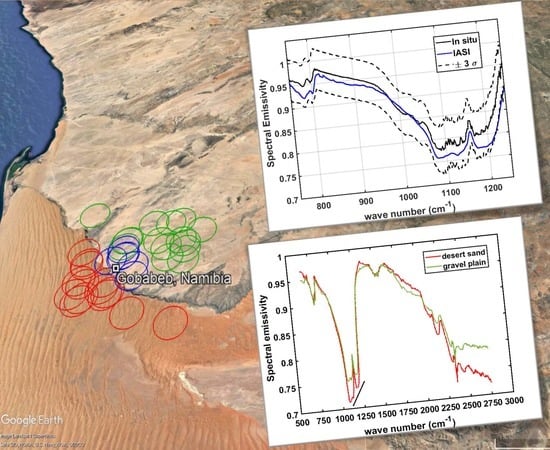
2.1. Validation Site
2.2. Data
2.3. Retrieval Methodology
2.3.1. The Forward Model
2.3.2. The Inverse Approach
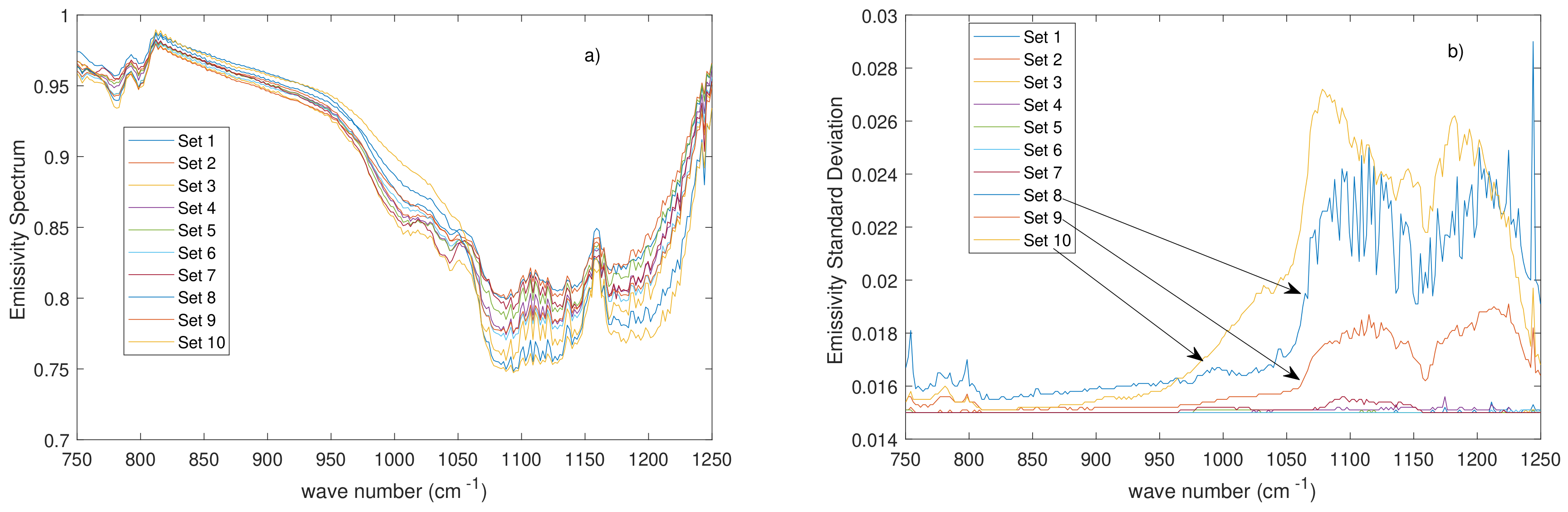
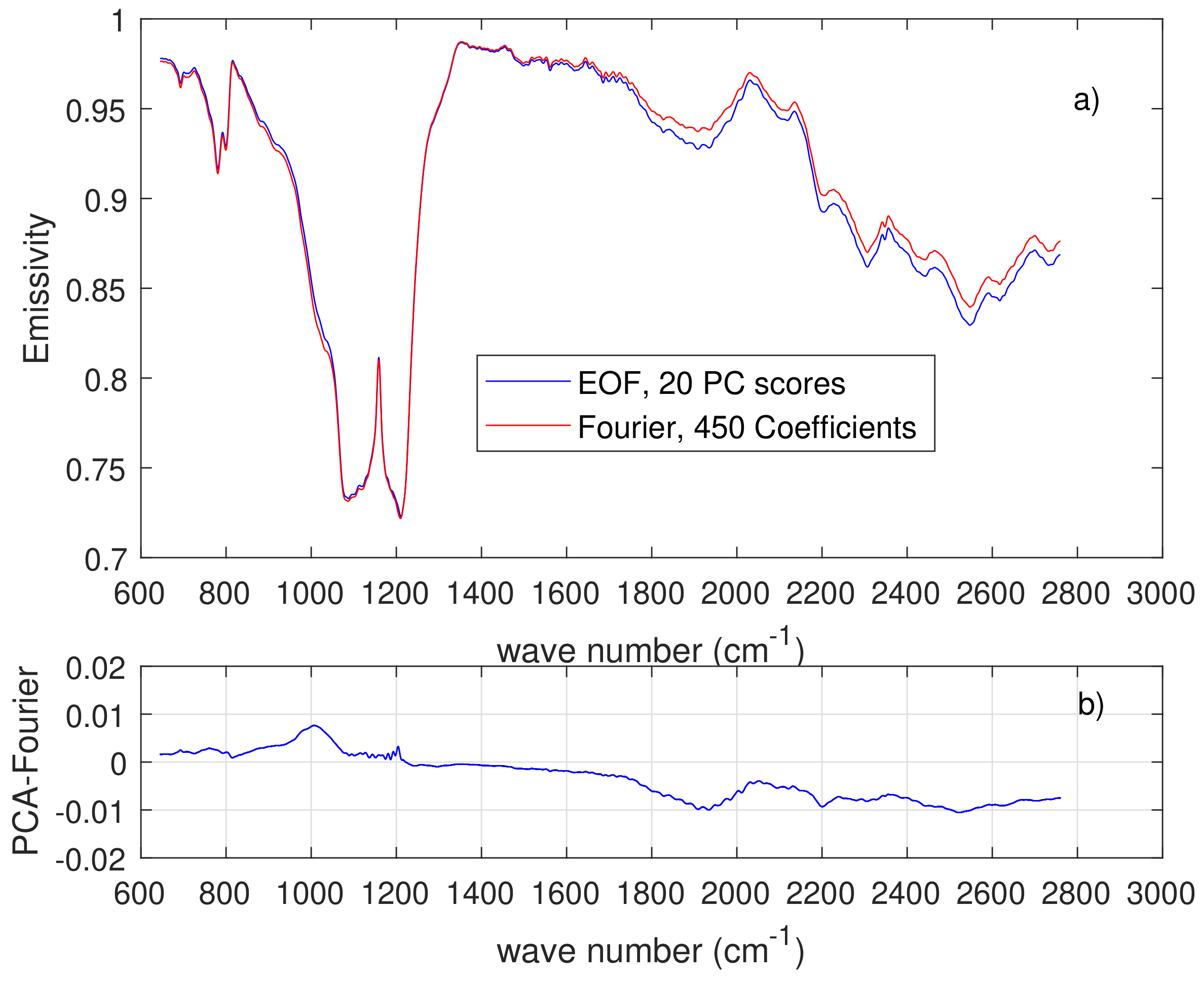
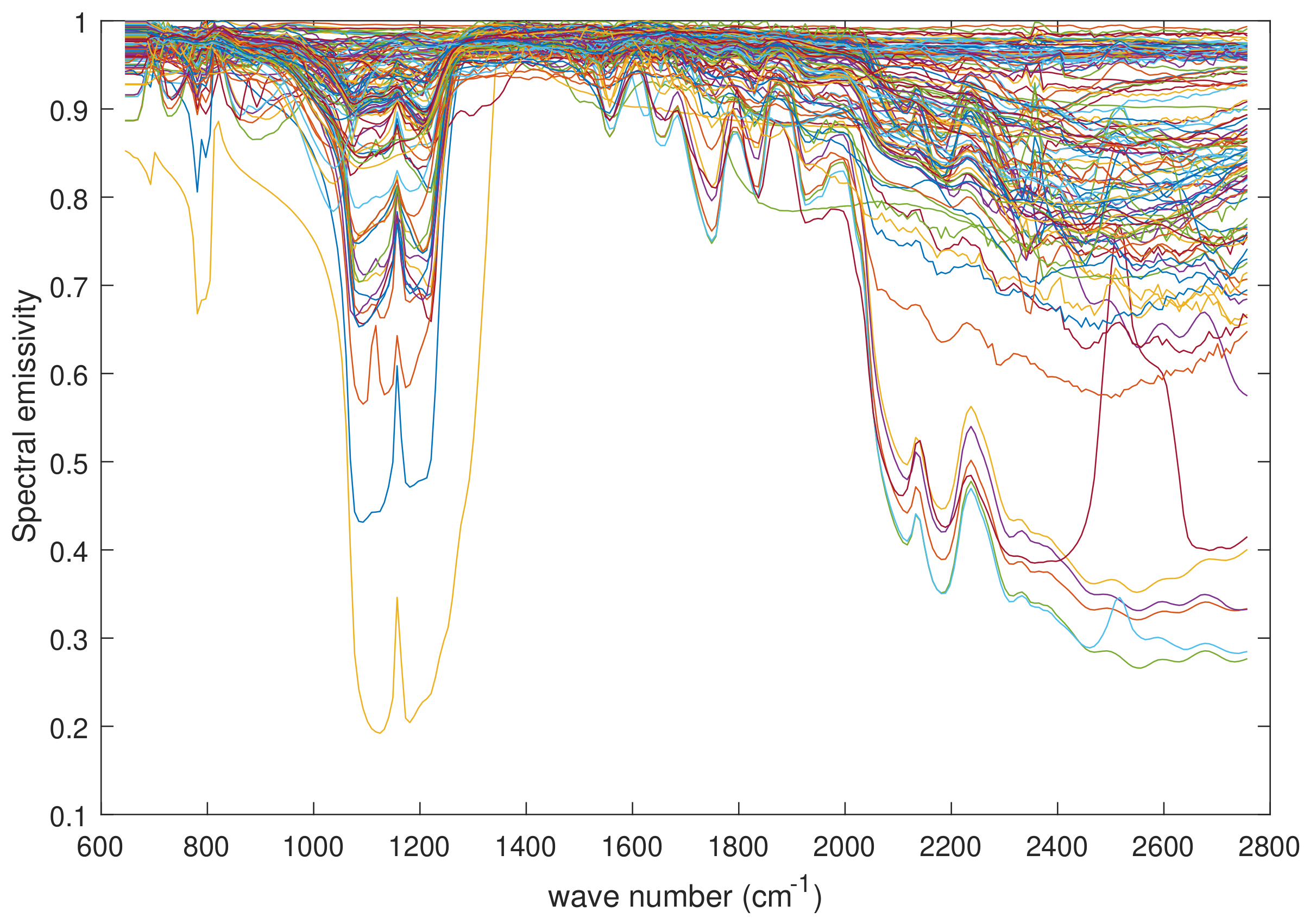
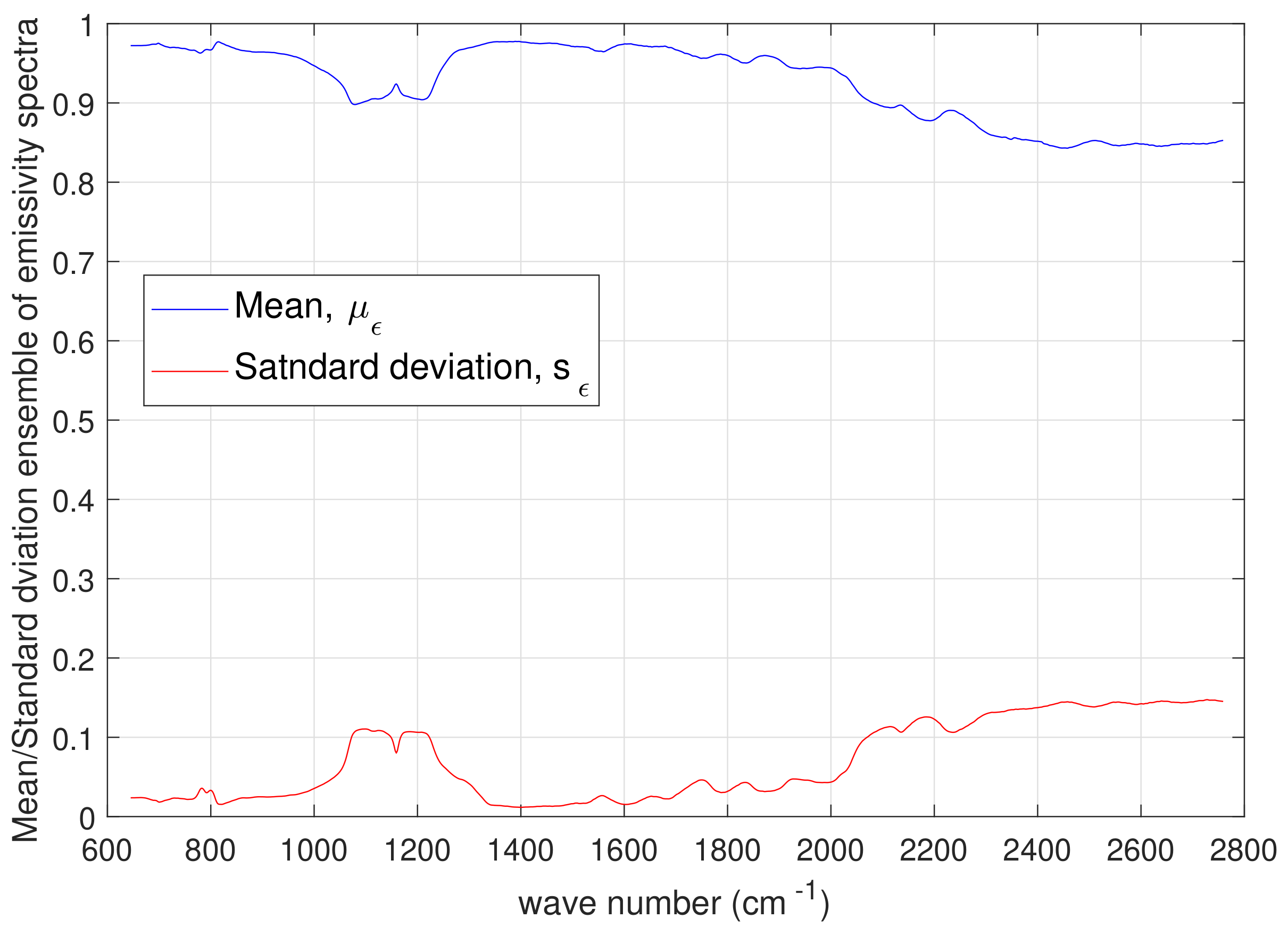
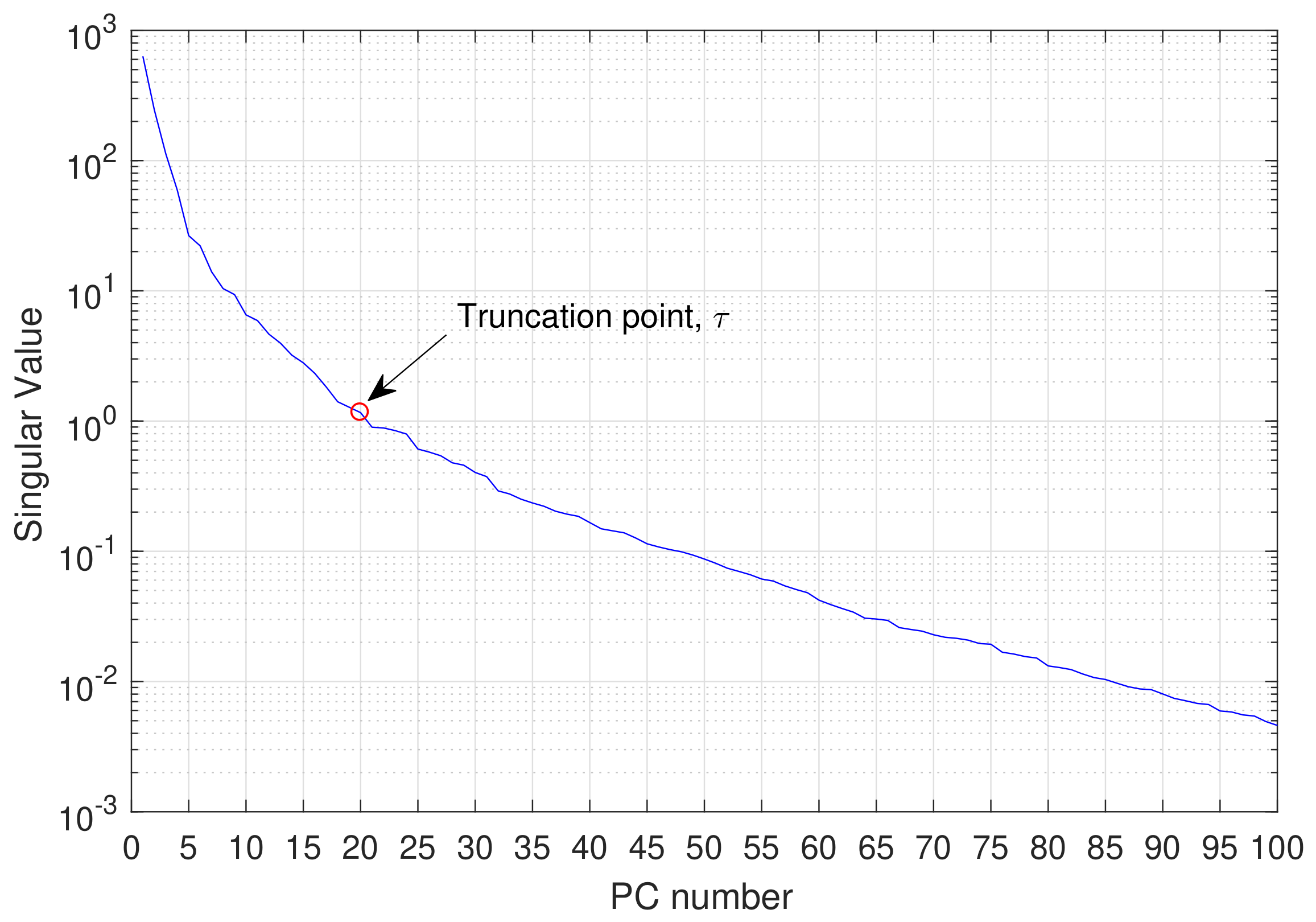
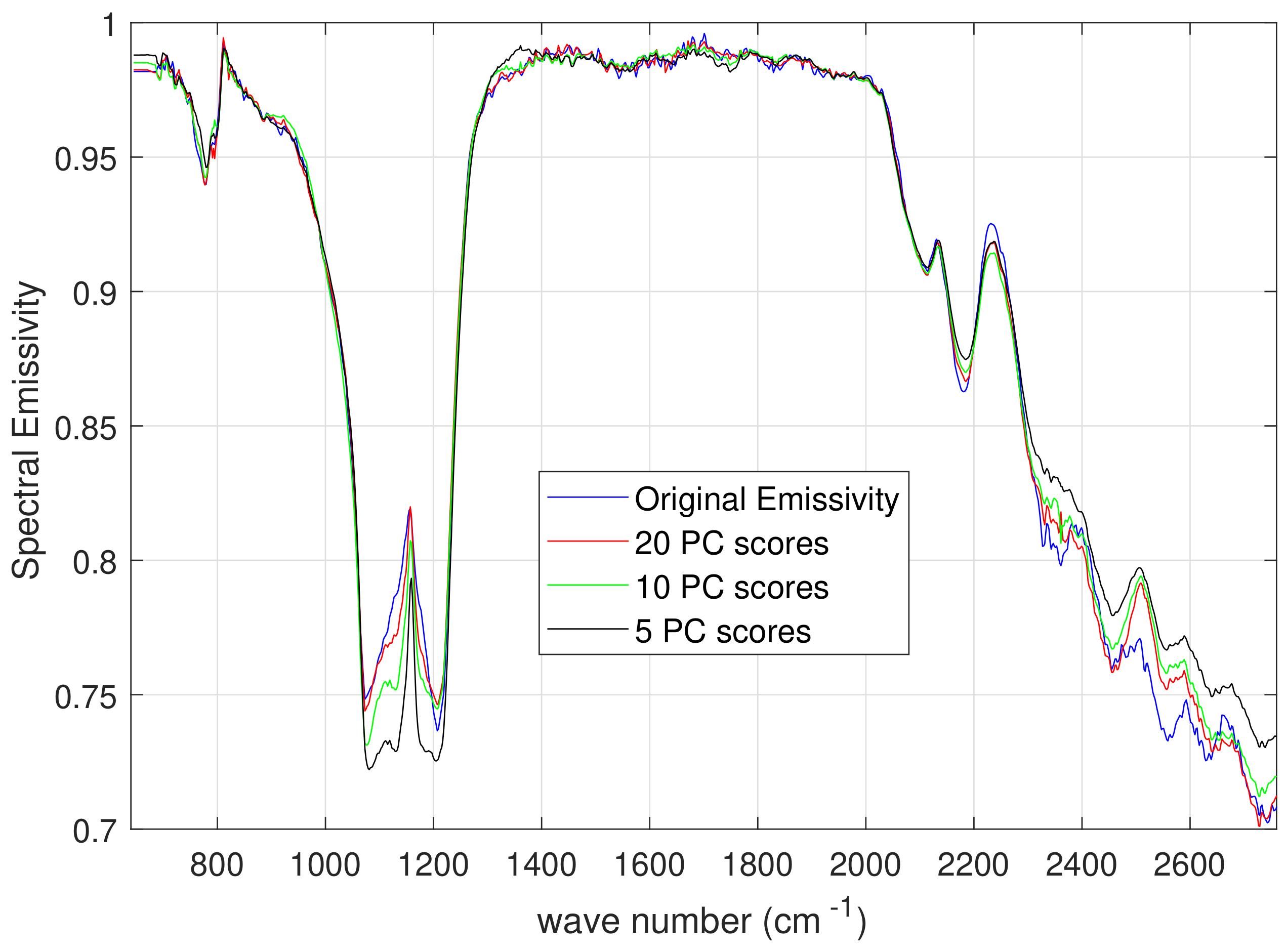
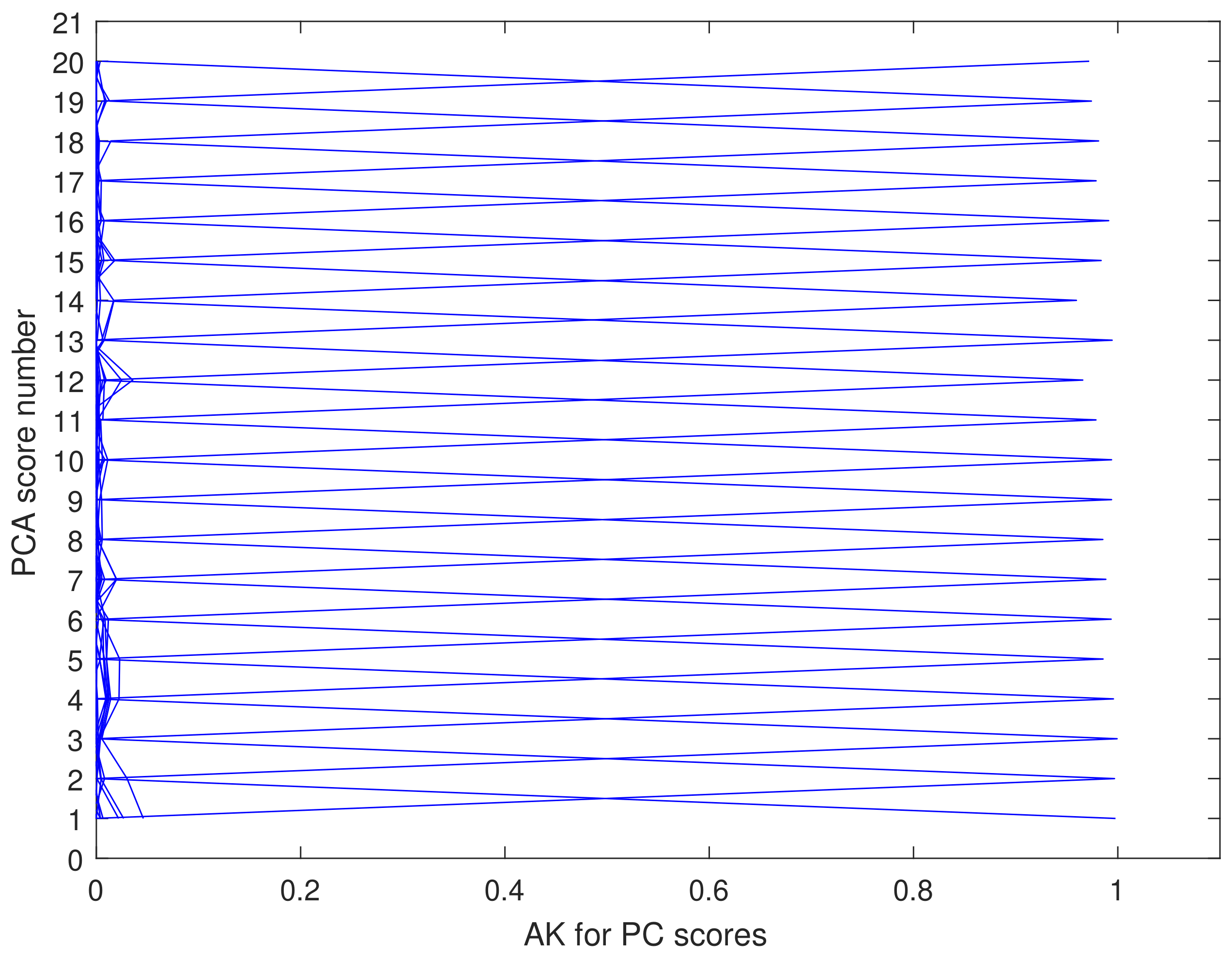
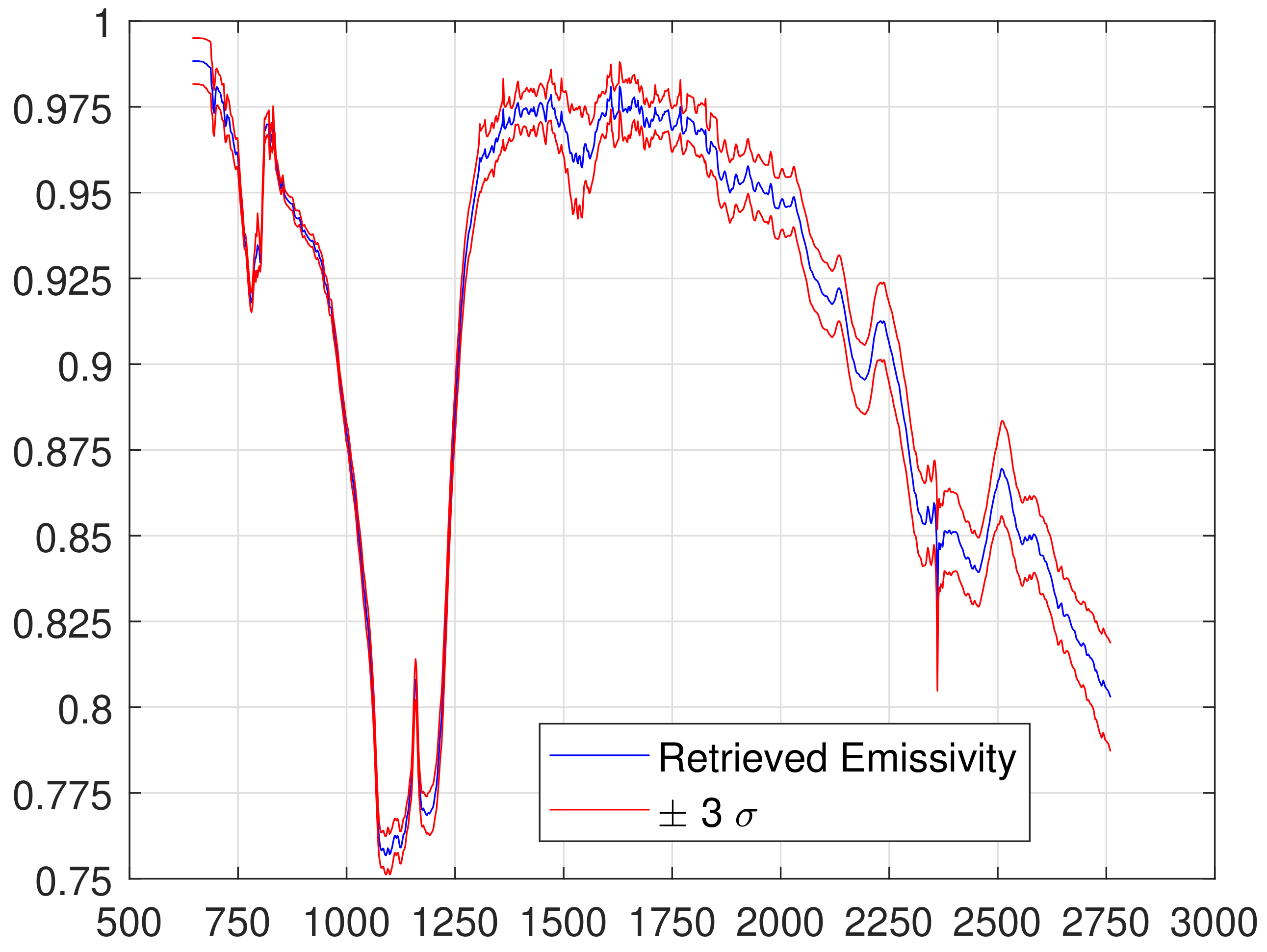
2.3.3. Implementation and Emissivity Error Analysis
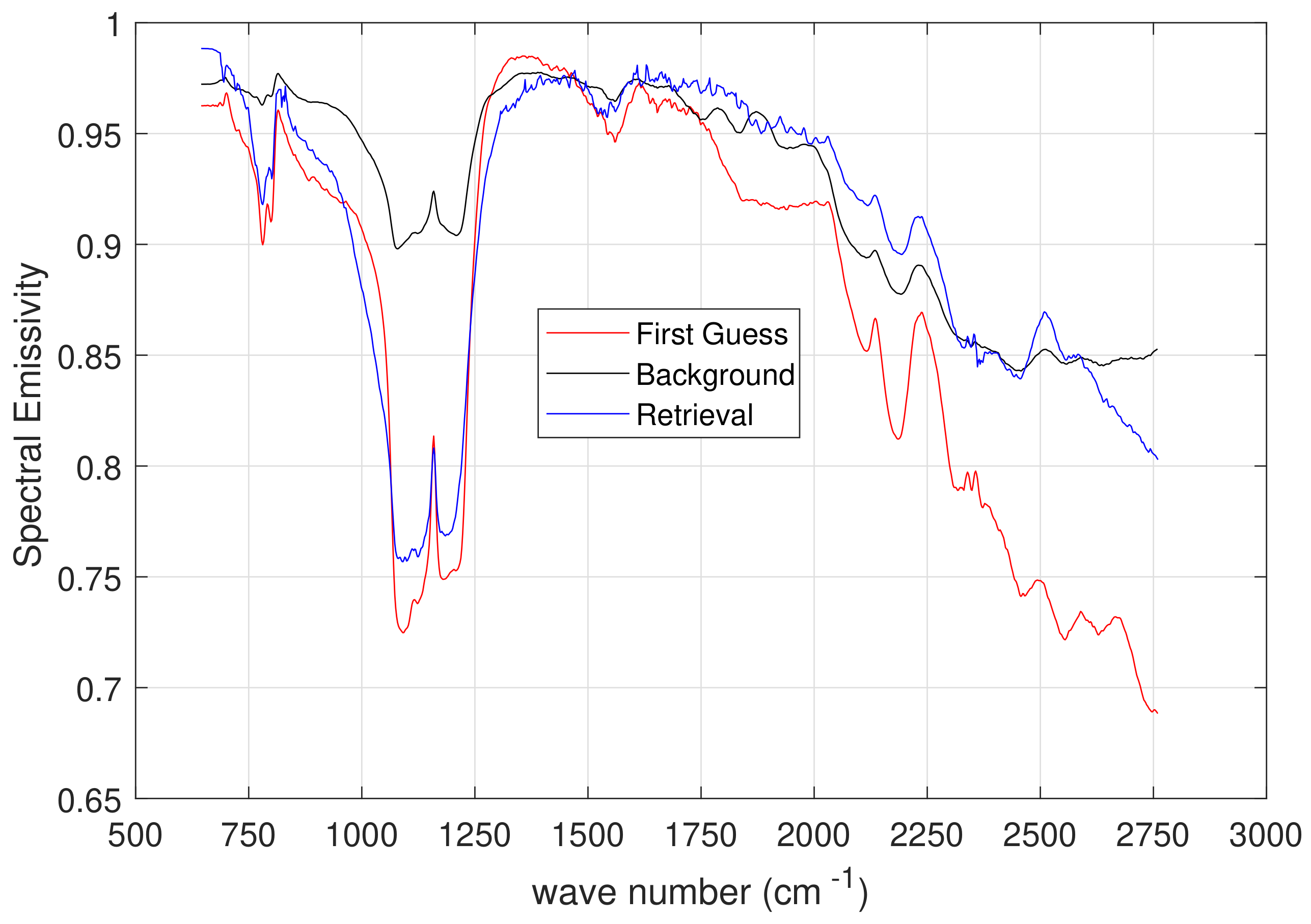
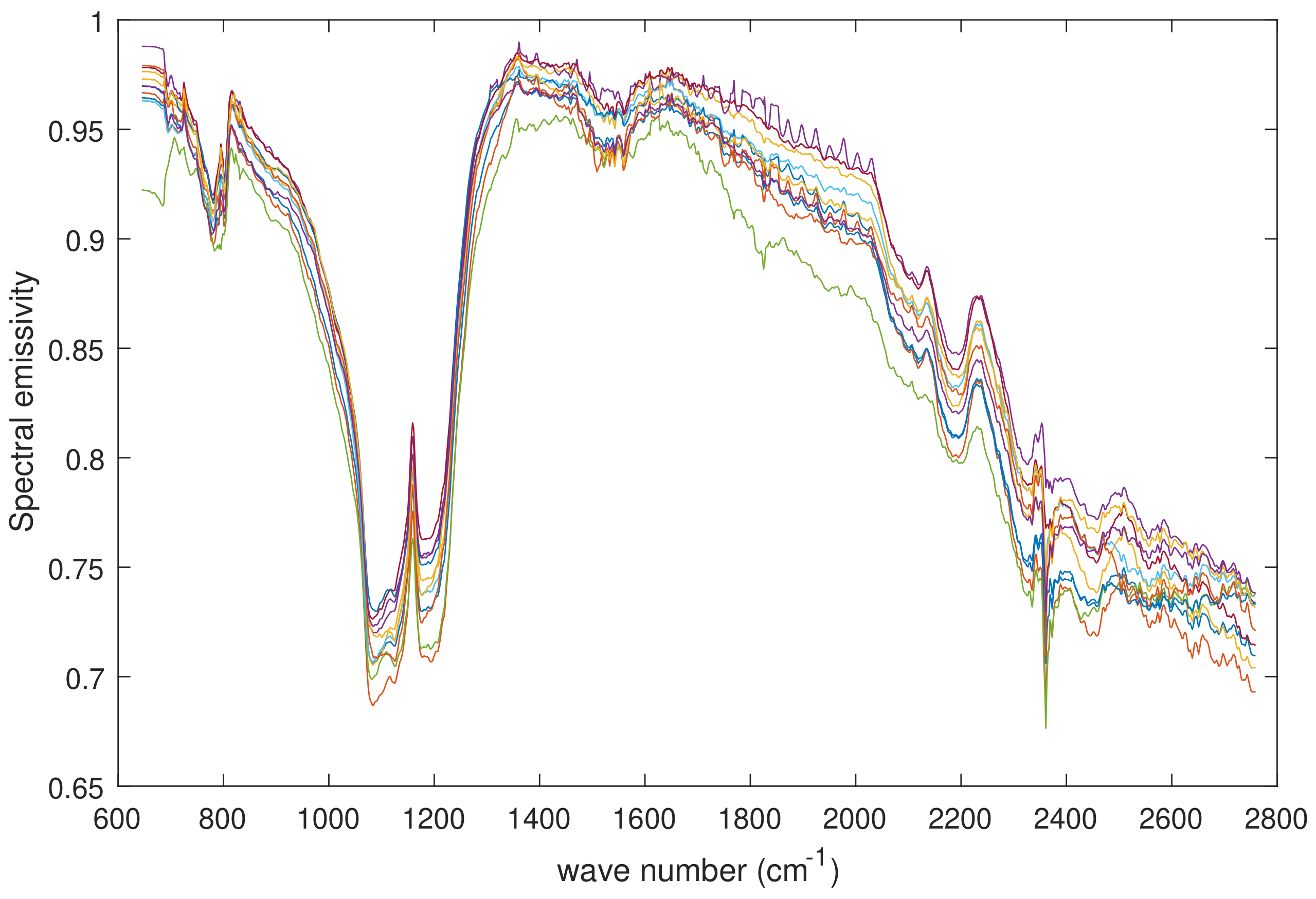
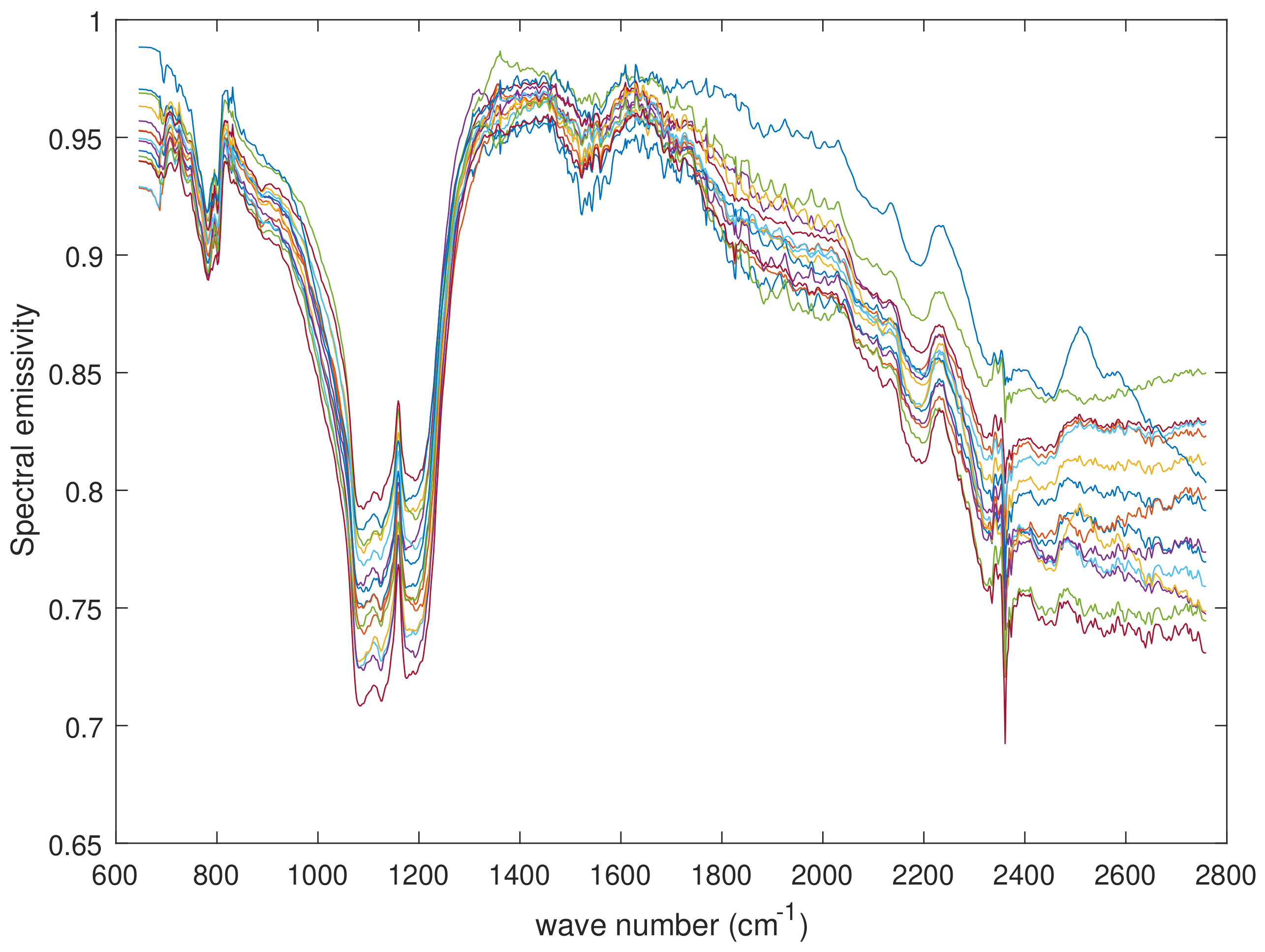
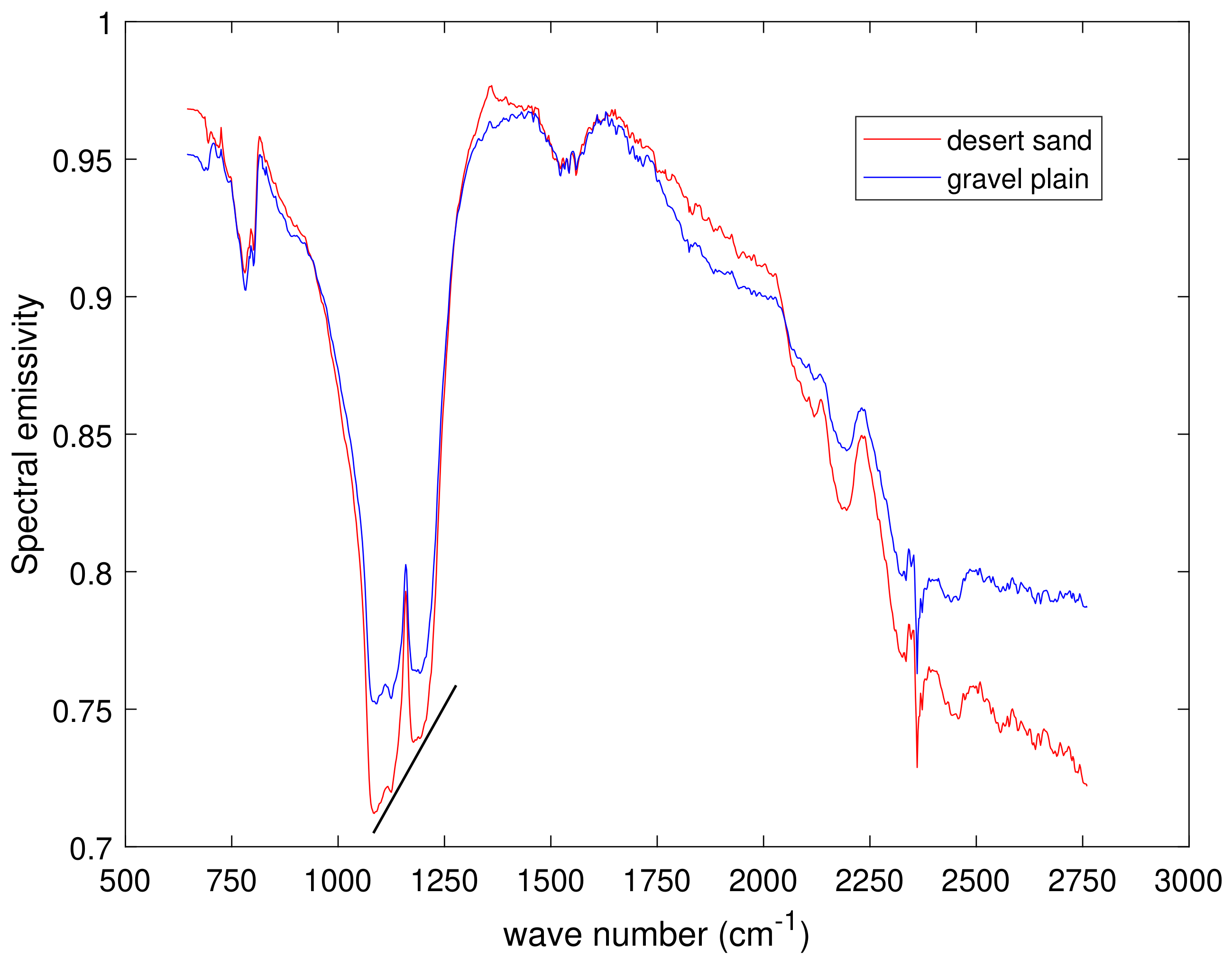
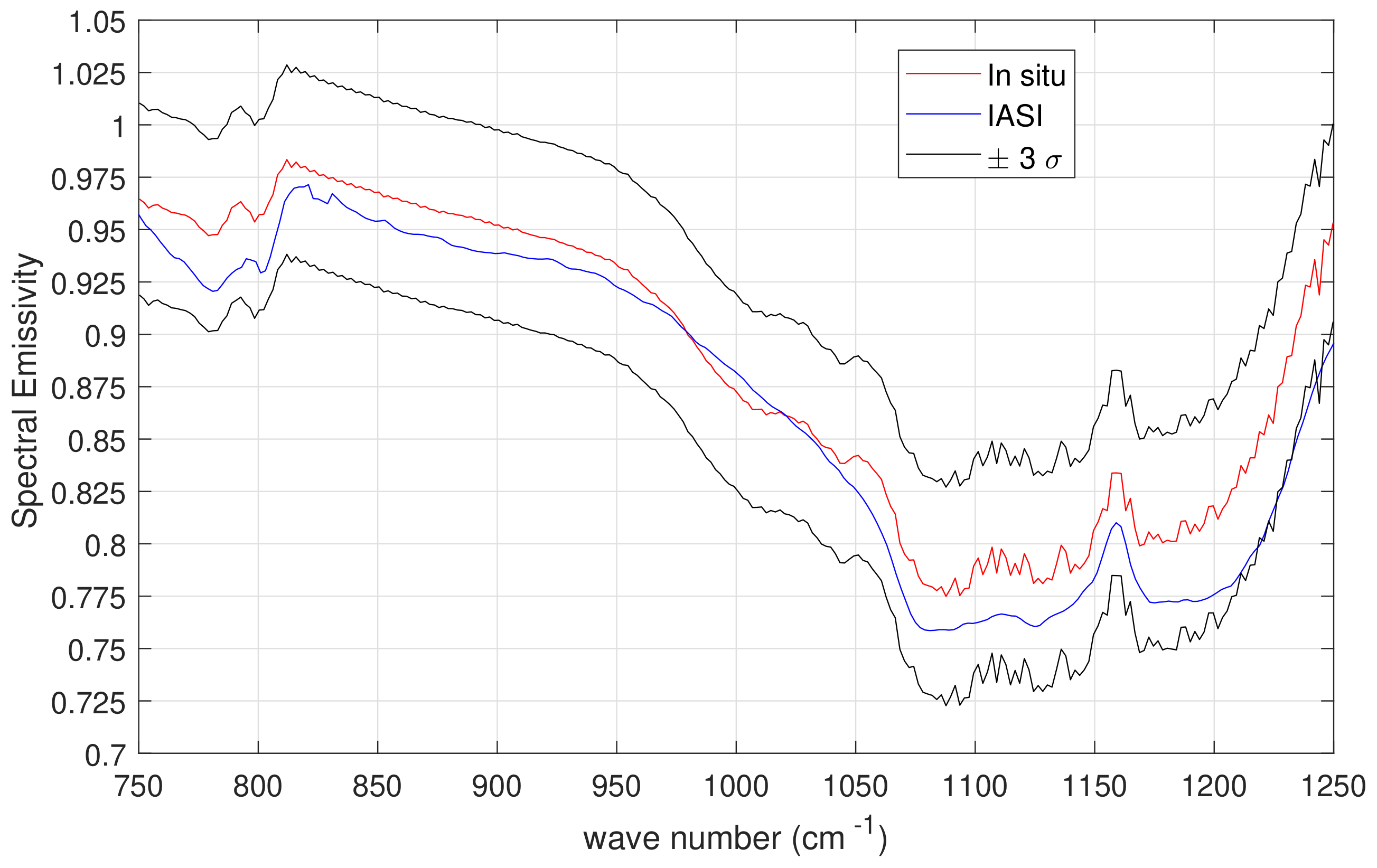
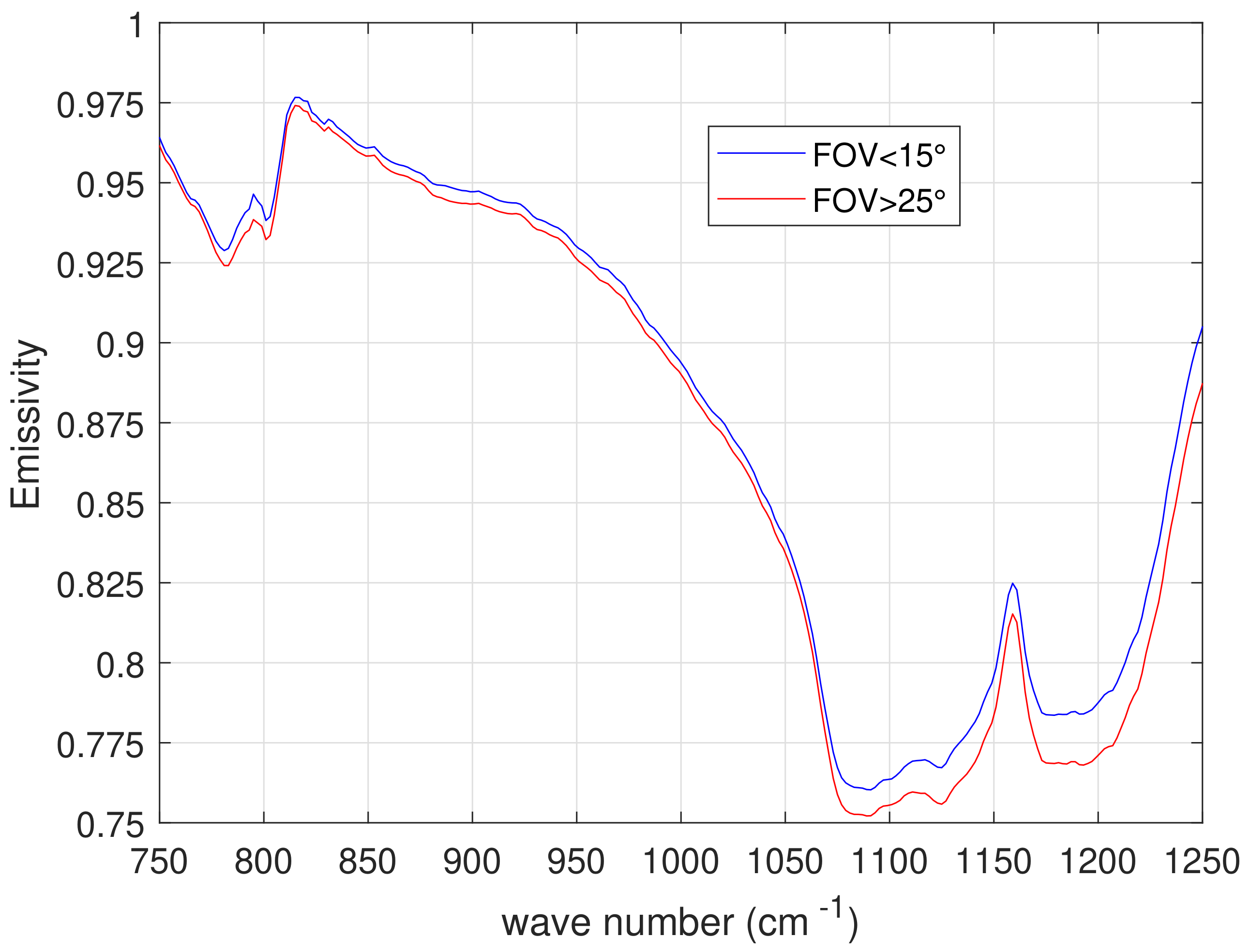
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AVHRR | Advanced Very High Resolution Radiometer |
| ECMWF | European Centre for Medium Range Weather Forecasts |
| EUMETSAT | European Centre for the Exploitation of Meteorological Satellites |
| ESA | European Space Agency |
| FOV | Field of View |
| IASI | Infrared Atmospheric Sounder Interferometer |
| LSA | Land Surface Analysis |
| MIUR | Italian Ministry of Education, University and Research |
| NPL | National Physical Laboratory |
| PCA | Principal Component Analysis |
| SAF | Satellite Applictaion Facility |
References
- Masiello, G.; Serio, C.; De Feis, I.; Amoroso, M.; Venafra, S.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from geostationary infrared radiances. Atmos. Meas. Tech. 2013, 6, 3613–3634. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Göttsche, F.-M.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from SEVIRI infrared channels: A validation and intercomparison study. Atmos. Meas. Tech. 2015, 8, 2981–2997. [Google Scholar] [CrossRef]
- Knuteson, R.O.; Dedecker, R.G.; Feltz, W.F.; Osbourne, B.J.; Revercomb, H.E.; Tobin, D.C. Infrared land surface emissivity in the vicinity of the ARM SGP central facility. In Proceedings of the Thirteenth ARM Science Team Meeting, Broomfield, Colorado, 31 March–4 April 2003; Available online: https://www.arm.gov/publications/proceedings/conf13/extended_abs/knuteson-ro.pdf (accessed on 19 June 2018).
- Knuteson, R.O.; Best, E.A.; DeSlover, D.H.; Osborne, B.J.; Revercomb, H.E.; Smith, W.L. Infrared land surface remote sensing using high spectral resolution aircraft observations. Adv. Space Res. 2004, 33, 1114–1119. [Google Scholar] [CrossRef]
- Smith, W.L.; Knuteson, R.O.; Revercomb, H.E.; Feltz, W.F.; Howell, H.B.; Menzel, W.P.; Brown, O.; Brown, J.; Minnett, P.; McKeown, W. Observations of the infrared radiative properties of the Ocean-Implications for the measurement of sea surface temperature via satellite remote sensing. Bull. Am. Meteorol. Soc. 1996, 77, 41–52. [Google Scholar] [CrossRef]
- Fiedler, L.; Bakan, S. Interferometric measurements of sea surface temperature and emissivity. Deutsch. Hydrogr. Z. 1997, 49, 357–365. [Google Scholar] [CrossRef]
- Minnett, P.J.; Knuteson, R.O.; Best, F.A.; Osborne, B.J.; Hanafin, J.A.; Brown, O.B. The Marine-Atmospheric Emitted Radiance Interferometer: A High-Accuracy, Seagoing Infrared Spectroradiometer. J. Atmos. Ocean. Tech. 2001, 18, 994–1012. [Google Scholar] [CrossRef]
- Newman, S.M.; Smith, J.A.; Glew, M.D.; Rogers, S.M.; Taylor, J.P. Temperature and salinity dependence of sea surface emissivity in the thermal infrared. Q. J. Roy. Meteor. Soc. 2005, 131, 2539–2557. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE T. Geosci. Remote 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Cuomo, V. Exploiting Quartz Spectral Signature for the Detection of Cloud-Affected Satellite Infrared Observations over African Desert Areas. Appl. Opt. 2004, 43, 2305–2315. [Google Scholar] [CrossRef] [PubMed]
- Clough, S.A.; Shephard, M.W.; Worden, J.; Brown, P.D.; Worden, H.M.; Mingzhao, L.; Rodgers, C.D.; Rinsland, C.P.; Goldman, A.; Brown, L.; et al. Forward model and Jacobians for Tropospheric Emission Spectrometer retrievals. IEEE Trans. Geosci. Remote 2006, 44, 1308–1323. [Google Scholar] [CrossRef]
- Seemann, S.W.; Borbas, E.F.; Knuteson, R.O.; Stephenson, G.R.; Huang, H.L. Development of a Global Infrared Land Surface Emissivity Database for Application to Clear Sky Sounding Retrievals from Multispectral Satellite Radiance Measurements. J. Appl. Meteor. Clim. 2007, 47, 108–123. [Google Scholar] [CrossRef]
- Wan, Z.M. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Baldridge, A.M. ASTER land surface emissivity database of California and Nevada. Geophys. Res. Lett. 2008, 35, L13401. [Google Scholar] [CrossRef]
- Péquignot, E.; Chédin, A.; Scott, N.A. Infrared continental surface emissivity spectra retrieved from AIRS hyperspectral sensor. J. Appl. Meteor. Clim. 2008, 47, 1619–1633. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Manning, E.; Lee, S.-Y.; Fetzer, E. Validation of the Atmospheric Infrared Sounder (AIRS) version 5 land surface emissivity product over the Namib and Kalahari deserts. J. Geophys. Res. 2009, 114, D19104. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. Intercomparison of versions 4, 4.1 and 5 of the MODIS land surface temperature and emissivity products and validation with laboratory measurements of sand samples from the Namib Desert, Namibia. Remote Sens. Environ. 2009, 113, 1313–1318. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. The North American ASTER Land Surface Emissivity Database (NAALSED) version 2.0. Remote Sens. Environ. 2009, 113, 1967–1975. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Weisz, E.; Zhou, D. Physical retrieval of surface emissivity spectrum from hyperspectral infrared radiances. Geophys. Res. Lett. 2007, 34, L16812. [Google Scholar] [CrossRef]
- Zhou, D.K.; Goldberg, M.; Barnet, C.; Cheng, Z.; Sun, F.; Wolf, W.; King, T.; Liu, X.; Sun, H.; Divakarla, M. Regression of surface spectral emissivity from hyperspectral instruments. IEEE T. Geosci. Remote 2008, 46, 328–333. [Google Scholar] [CrossRef]
- Zhou, D.K.; Larar, A.M.; Liu, X.; Smith, W.L.; Strow, L.L.; Yang, P.; Schlüssel, P.; Calbet, X. Global Land Surface Emissivity Retrieved From Satellite Ultraspectral IR Measurements. IEEE Trans. Geosci. Remote 2011, 49, 1277–1290. [Google Scholar] [CrossRef]
- Ma, X.; Wan, Z.; Moeller, C.; Menzel, W.; Gumley, L. Simultaneous Retrieval of Atmospheric Profiles, Land-Surface Temperature, and Surface Emissivity from Moderate-Resolution Imaging Spectroradiometer Thermal Infrared Data: Extension of a Two-Step Physical Algorithm. Appl. Opt. 2002, 41, 909–924. [Google Scholar] [CrossRef] [PubMed]
- Masiello, G.; Serio, C. Simultaneous physical retrieval of surface emissivity spectrum and atmospheric parameters from infrared atmospheric sounder interferometer spectral radiances. Appl. Opt. 2013, 52, 2428–2446. [Google Scholar] [CrossRef] [PubMed]
- Hilton, F.; Armante, R.; August, T.; Barnet, C.; Bouchard, A.; Camy-Peyret, C.; Capelle, V.; Clarisse, L.; Clerbaux, C.; Coheur, P.; et al. Hyperspectral Earth Observation from IASI: Five Years of Accomplishments. Bull. Am. Meteorol. Soc. 2012, 93, 347–370. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Trigo, I.F.; Bork-Unkelbach, A.; Martin, M.A. Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa. Remote Sens. 2016, 8, 410. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.; Poutier, L.; Langlois, S.; Wimmer, W.; Garcia Santos, V.; Coll, C.; Niclos, R.; Arbelo, M.; Monchau, J.P. Fiducial Reference Measurements for Validation of Surface Temperature from Satellites (FRM4STS), Report from the Field Inter-Comparison Experiment (FICE) for Land Surface Temperature (OFE-D130-LST-FICE-Report-V1-Iss-1-Ver-1); ESA: Noordwijk, The Netherlands, accepted by ESA on 5 June 2018.
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Lancaster, J.; Lancaster, N.; Seely, M.K. Climate of the central Namib desert. Madoqua 1984, 14, 5–61. Available online: https://journals.co.za/content/madoqua/14/1/AJA10115498_484 (accessed on 19 June 2018).
- Eckardt, F.D.; Soderberg, K.; Coop, L.J.; Muller, A.A.; Vickery, K.J.; Grandin, R.D.; Jack, C.; Kapalanga, T.S.; Henschel, J. The nature of moisture at Gobabeb, in the central Namib Desert. J. Arid Environ. 2013, 93, 7–19. [Google Scholar] [CrossRef]
- Seely, M.K. Standing crop as an index of precipitation in the central Namib grassland. Madoqua 1978, 9, 5–13. Available online: https://journals.co.za/content/madoqua/11/1/AJA10115498_168 (accessed on 19 June 2018).
- Kanani, K.; Poutier, L.; Nerry, F.; Stoll, M.-P. Directional effects consideration to improve out-doors emissivity retrieval in the 3–13 μm domain. Opt. Express 2007, 15, 12464–12482. [Google Scholar] [CrossRef] [PubMed]
- Borel, C.C. Surface emissivity and temperature retrieval for a hyperspectral sensor. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing Symposium, Seattle, WA, USA, 6–10 July 1998; pp. 546–549. [Google Scholar] [CrossRef]
- Theocharous, E.; Barker Snook, I.; Fox, N.P. Results from the 4th CEOS TIR FRM Field Radiometer Laboratory Inter-Comparison Exercise Part 1 of 4: Blackbody laboratory Comparison, ESA Technical Report OFE-D100 (Part1); ESA: Noordwijk, The Netherlands, 2017.
- Theocharous, E.; Barker Snook, I.; Fox, N.P. Results from the 4th CEOS TIR FRM Field Radiometer Laboratory Inter-Comparison Exercise Part 2 of 4: Laboratory Comparison of Cadiation thermometers, ESA Technical Report OFE-D100 (Part2); ESA: Noordwijk, The Netherlands, 2017.
- Masiello, G.; Serio, C.; Shimoda, H. Qualifying IMG Tropical Spectra for Clear Sky. J. Quant. Spectrosc. Radiat. 2003, 77, 131–148. [Google Scholar] [CrossRef]
- Amato, U.; Lavanant, L.; Liuzzi, G.; Masiello, G.; Serio, C.; Stuhlmann, R.; Tjemkes, S.A. Cloud mask via cumulative discriminant analysis applied to satellite infrared observations: scientific basis and initial evaluation. Atmos. Meas. Tech. 2014, 7, 3355–3372. [Google Scholar] [CrossRef]
- Amato, U.; Masiello, G.; Serio, C.; Viggiano, M. The σ-IASI code for the calculation of infrared atmospheric radiance and its derivatives. Environ. Modell. Softw. 2002, 17, 651–667. [Google Scholar] [CrossRef]
- Rizzi, R.; Palchetti, L.; Carli, B.; Bonsignori, R.; Harries, J.E.; Leotin, J.; Peskett, S.C.; Serio, C.; Sutera, A. Feasibility of the spaceborne radiation explorer in the far infrared (REFIR). In Optical Spectroscopic Techniques, Remote Sensing, and Instrumentation for Atmospheric and Space Research IV; SPIE-The International Society for Optical Engineering: Bellingham, WA, USA, 2002. [Google Scholar] [CrossRef]
- Esposito, F.; Grieco, G.; Masiello, G.; Pavese, G.; Restieri, R.; Serio, C.; Cuomo, V. Intercomparison of line-parameter spectroscopic databases using downwelling spectral radiance. Q. J. R. Meteorol. Soc. 2007, 133, 191–202. [Google Scholar] [CrossRef]
- Serio, C.; Esposito, F.; Masiello, G.; Pavese, G.; Calvello, M.R.; Grieco, G.; Cuomo, V.; Buijs, H.L.; Roy, C.B. Interferometer for ground-based observations of emitted spectral radiance from the troposphere: Evaluation and retrieval performance. Appl. Opt. 2008, 47, 3909–3919. [Google Scholar]
- Bhawar, R.; Bianchini, G.; Bozzo, A.; Cacciani, M.; Calvello, M.R.; Carlotti, M.; Castagnoli, F.; Cuomo, V.; Di Girolamo, P.; Di Iorio, T.; et al. Spectrally resolved observations of atmospheric emitted radiance in the H2O rotation band. Geophys. Res. Lett. 2008, 35, L04812. [Google Scholar] [CrossRef]
- Carissimo, A.; De Feis, I.; Serio, C. The physical retrieval methodology for IASI: the δ-IASI code. Environ. Modell. Softw. 2005, 20, 1111–1126. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmopsheric Sounding: Theory abd Practice; World Scientific: Singapore, 2000; ISBN 981-02-2740-X. [Google Scholar]
- Masiello, G.; Serio, C.; Antonelli, P. Inversion for atmospheric thermodynamical parameters of IASI data in the principal components space. Q. J. Roy. Meteor. Soc. 2012, 138, 103–117. [Google Scholar] [CrossRef]
- Amato, U.; Antoniadis, A.; De Feis, I.; Masiello, G.; Matricardi, M.; Serio, C. Technical Note: Functional sliced inverse regression to infer temperature, water vapour and ozone from IASI data. Atmos. Chem. Phys. 2009, 9, 5321–5330. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Carissimo, A.; Grieco, G.; Matricardi, M. Application of φ-IASI to IASI: Retrieval products evaluation and radiative transfer consistency. Atmos. Chem. Phys. 2009, 9, 8771–8783. [Google Scholar] [CrossRef]
- Grieco, G.; Masiello, G.; Serio, C. Interferometric vs. Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters. Remote Sens. 2010, 2, 2323–2346. [Google Scholar] [CrossRef]
- Masiello, G.; Matricardi, M.; Serio, C. The use of IASI data to identify systematic errors in the ECMWF forecasts of temperature in the upper stratosphere. Atmos. Chem. Phys. 2011, 11, 1009–1021. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Venafra, S.; De Feis, I.; Borbas, E.E. Diurnal variation in Sahara desert sand emissivity during the dry season from IASI observations. J. Geophys. Res. 2014, 119, 1626–1638. [Google Scholar] [CrossRef]
- Rozenstein, O.; Agam, N.; Serio, C.; Masiello, G.; Venafra, S.; Achal, S.; Puckrin, E.; Karnieli, A. Diurnal emissivity dynamics in bare versus biocrusted sand dunes. Sci. Total Environ. 2015, 506–507, 422–429. [Google Scholar] [CrossRef] [PubMed]
- Serio, C.; Masiello, G.; Liuzzi, G. Demonstration of random projections applied to the retrieval problem of geophysical parameters from hyper-spectral infrared observations. Appl. Opt. 2016, 55, 6576–6587. [Google Scholar] [CrossRef] [PubMed]
- Liuzzi, G.; Masiello, G.; Serio, C.; Venafra, S.; Camy-Peyret, C. Physical inversion of the full IASI spectra: Assessment of atmospheric parameters retrievals, consistency of spectroscopy and forward modelling. J. Quant. Spectrosc. Radiat. 2016, 182, 128–157. [Google Scholar] [CrossRef]
- Camy-Peyret, C.; Liuzzi, G.; Masiello, G.; Serio, C.; Venafra, S.; Montzka, S.A. Assessment of IASI capability for retrieving carbonyl sulphide (OCS). J. Quant. Spectrosc. Radiat. 2017, 201, 197–208. [Google Scholar] [CrossRef]
- Liuzzi, G.; Masiello, G.; Serio, C.; Meloni, D.; Di Biagio, C.; Formenti, P. Consistency of dimensional distributions and refractive indices of desert dust measured over Lampedusa with IASI radiances. Atmos. Meas. Tech. 2017, 10, 599–615. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER Spectral Library Version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Eckardt, F.D.; Livingstone, I.; Seely, M.; Von Holdt, J. An introduction to the surface geology and geomorphology around Gobabeb, Namib Desert, Namibia. Geogr. Ann. A 2013, 95, 271–284. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- García-Santos, V.; Valor, E.; Caselles, V.; Ángeles Burgos, M.; Coll, C. On the angular variation of thermal infrared emissivity of inorganic soils. J. Geophys. Res. 2012, 117, D19116. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Poutier, L.; Göttsche, F.-M. Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements. Remote Sens. 2018, 10, 976. https://doi.org/10.3390/rs10060976
Masiello G, Serio C, Venafra S, Liuzzi G, Poutier L, Göttsche F-M. Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements. Remote Sensing. 2018; 10(6):976. https://doi.org/10.3390/rs10060976
Chicago/Turabian StyleMasiello, Guido, Carmine Serio, Sara Venafra, Giuliano Liuzzi, Laurent Poutier, and Frank-M. Göttsche. 2018. "Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements" Remote Sensing 10, no. 6: 976. https://doi.org/10.3390/rs10060976
APA StyleMasiello, G., Serio, C., Venafra, S., Liuzzi, G., Poutier, L., & Göttsche, F.-M. (2018). Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements. Remote Sensing, 10(6), 976. https://doi.org/10.3390/rs10060976