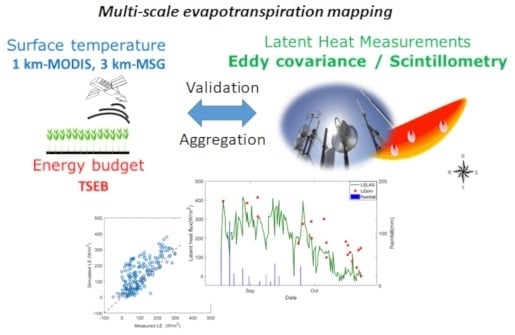
Combining a Two Source Energy Balance Model Driven by MODIS and MSG-SEVIRI Products with an Aggregation Approach to Estimate Turbulent Fluxes over Sparse and Heterogeneous Vegetation in Sahel Region (Niger)
Abstract
1. Introduction
2. Data and Methods
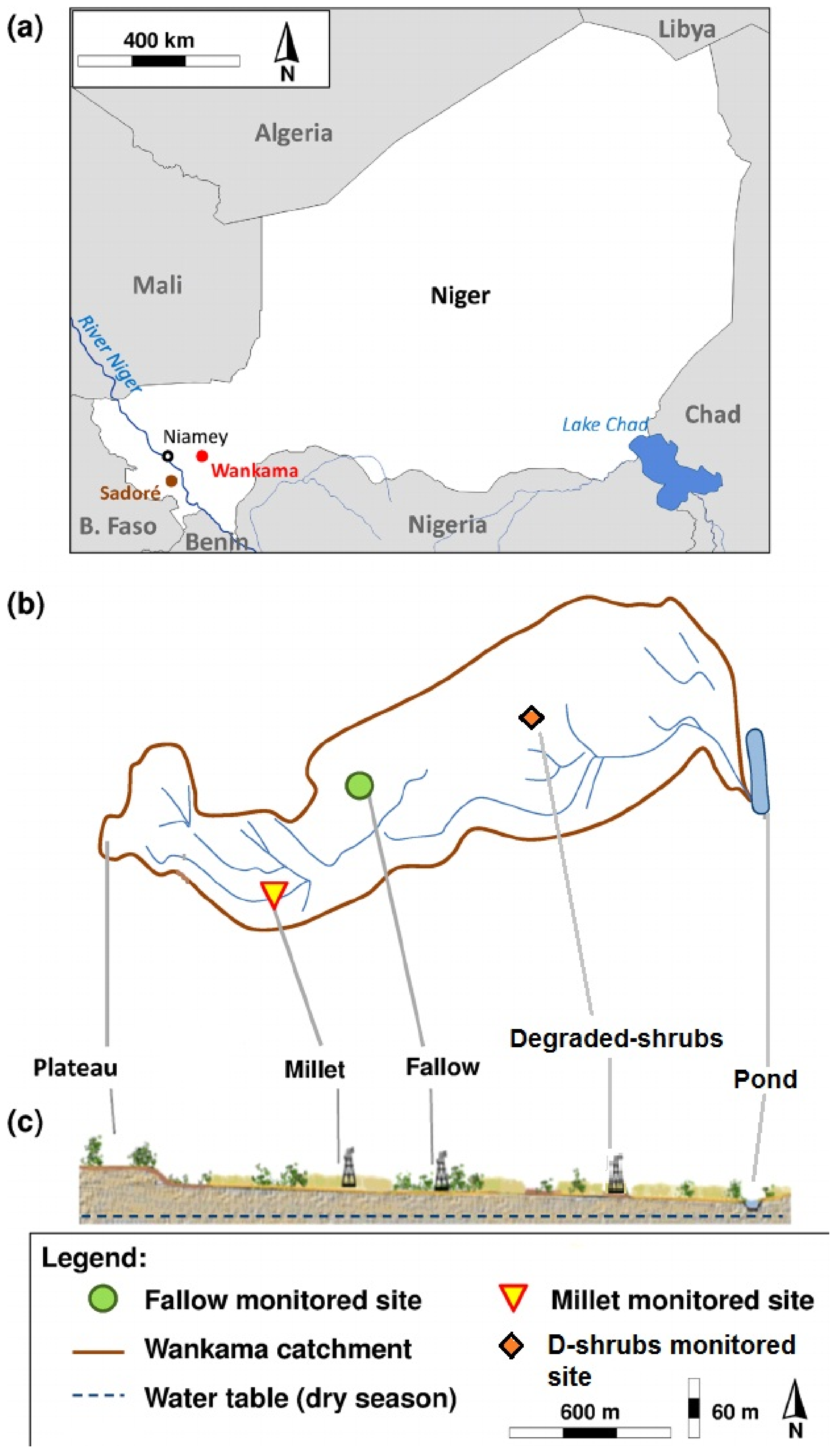
2.1. Experimental Site and Measurements
2.1.1. Site Description
2.1.2. Experimental Setup
Patch Scale
Grid Scale
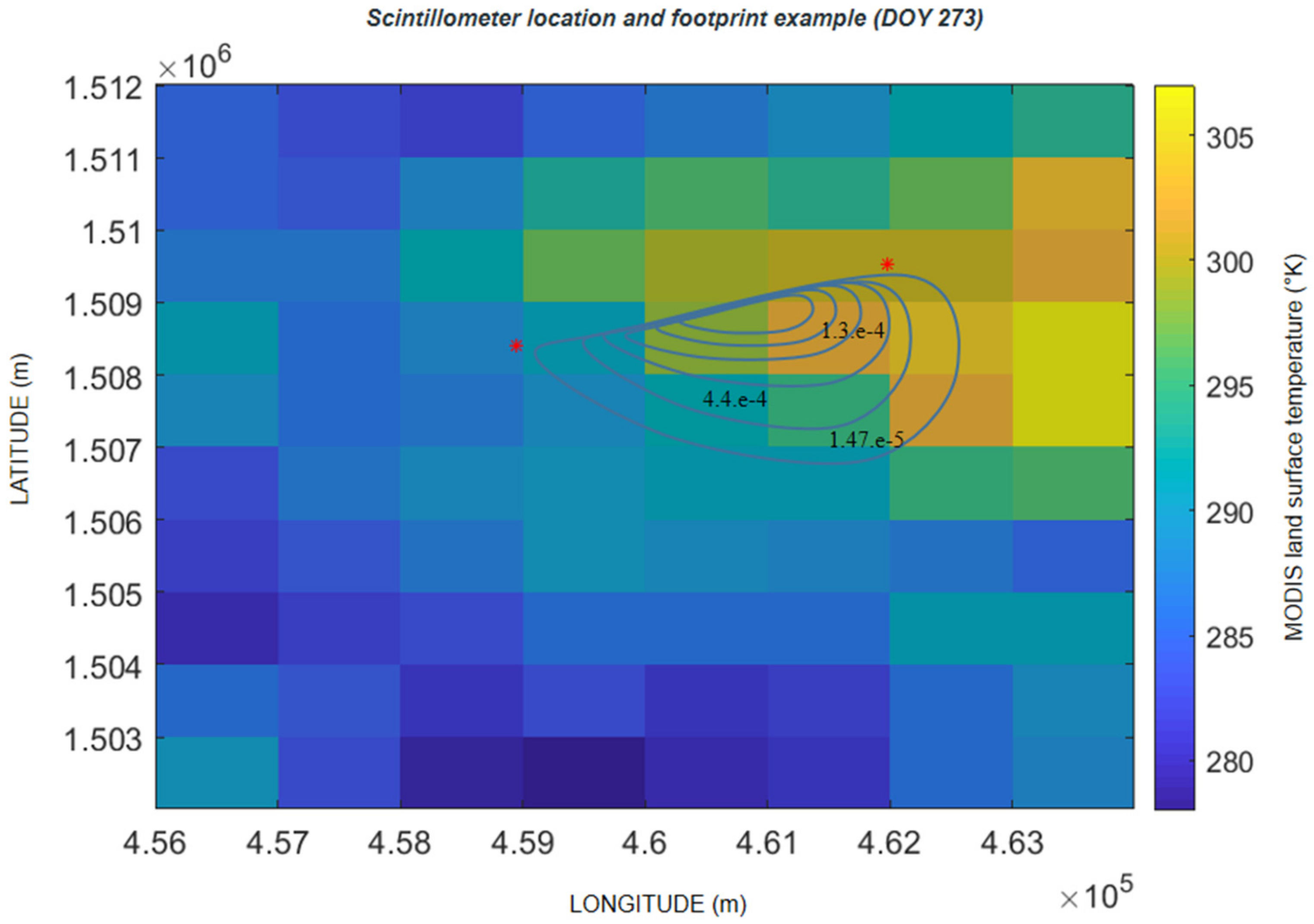
2.2. Scintillometer Measurements
2.2.1. Scintillometry Theory
2.2.2. Footprint Model
2.3. Remote Sensing Data
2.3.1. MODIS Products
2.3.2. SEVIRI Land Surface Temperature
2.4. TSEB Model Description and Implementation
2.5. Aggregation Scheme
3. Results and Discussion
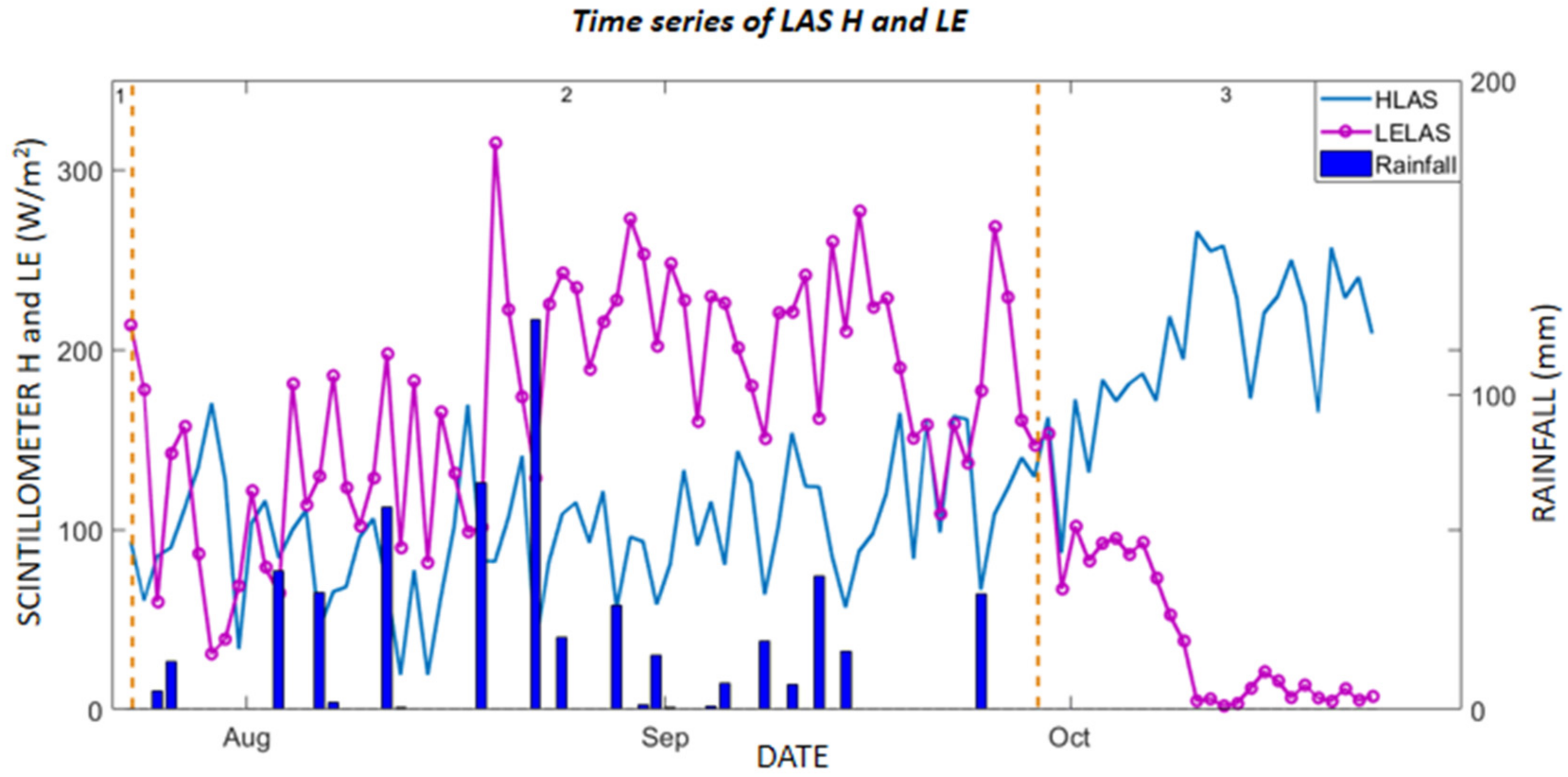
3.1. Experimental Data Analysis
3.1.1. In-Situ Surface Fluxes
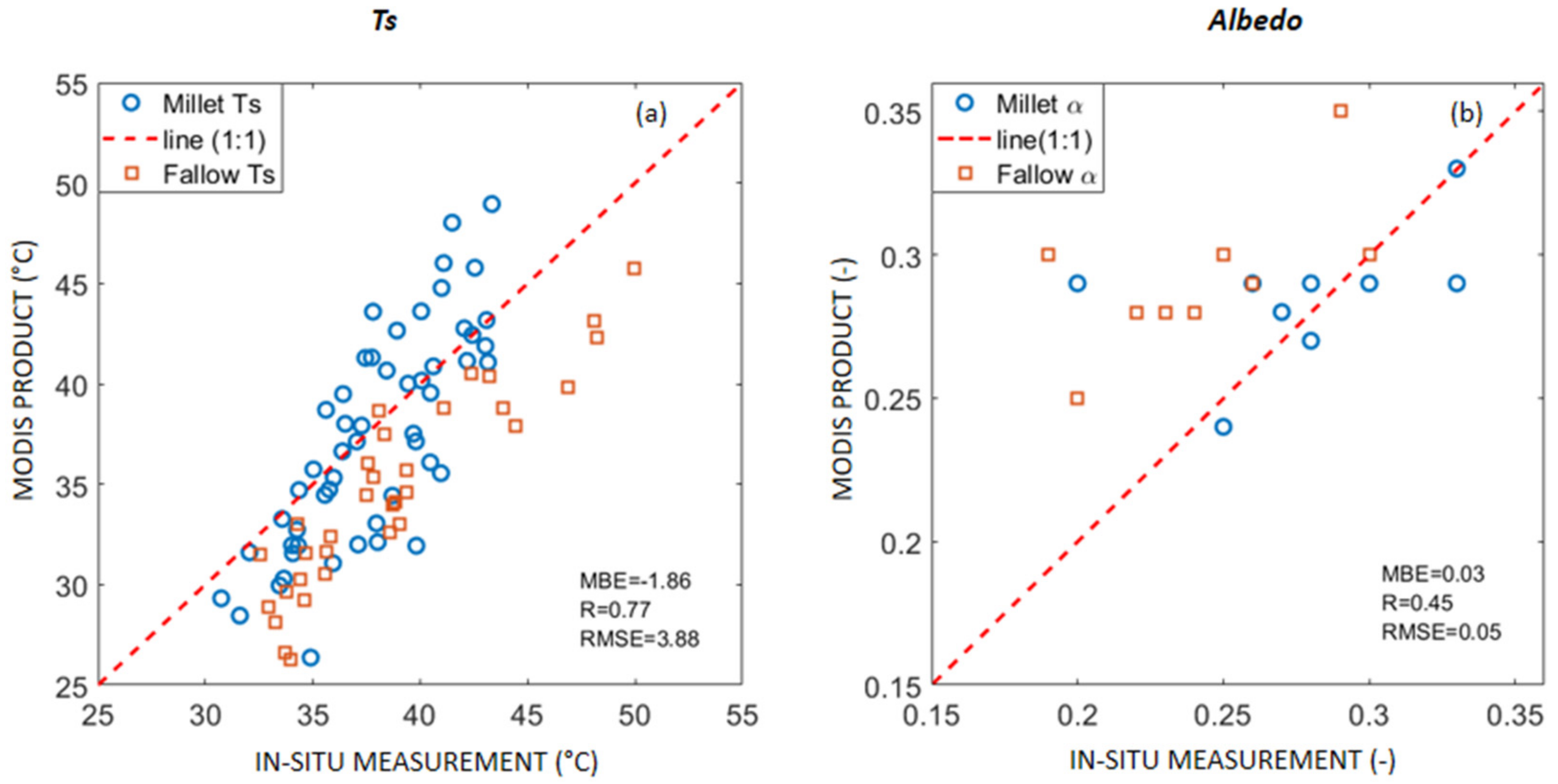
3.1.2. Remote Sensing Products
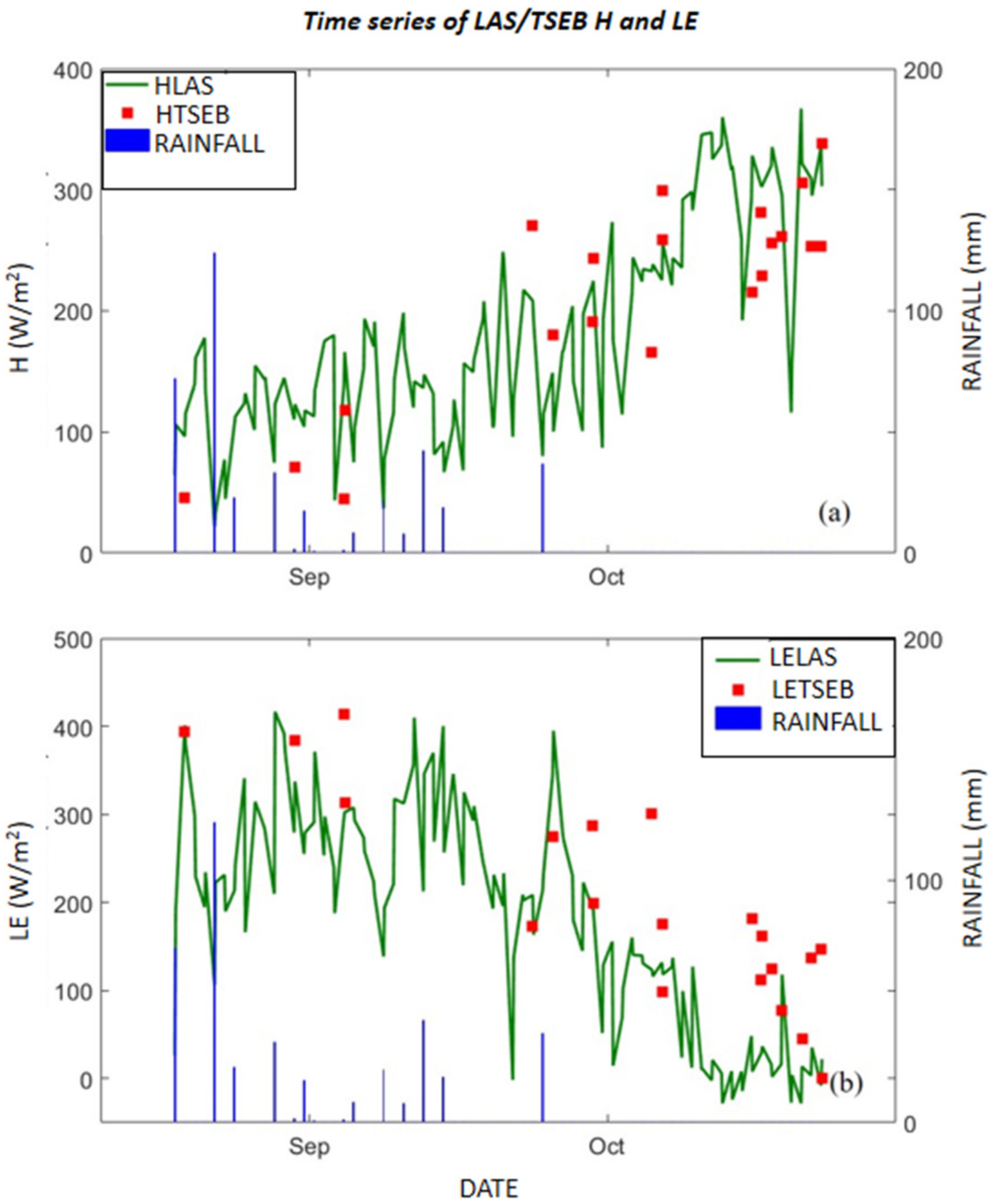
3.2. Multi-Scale Convective and Evaporative Fluxes Predictions
3.2.1. Station Scale
Using In Situ Data
Using MODIS Data
3.2.2. Three-Kilometer Grid Scale
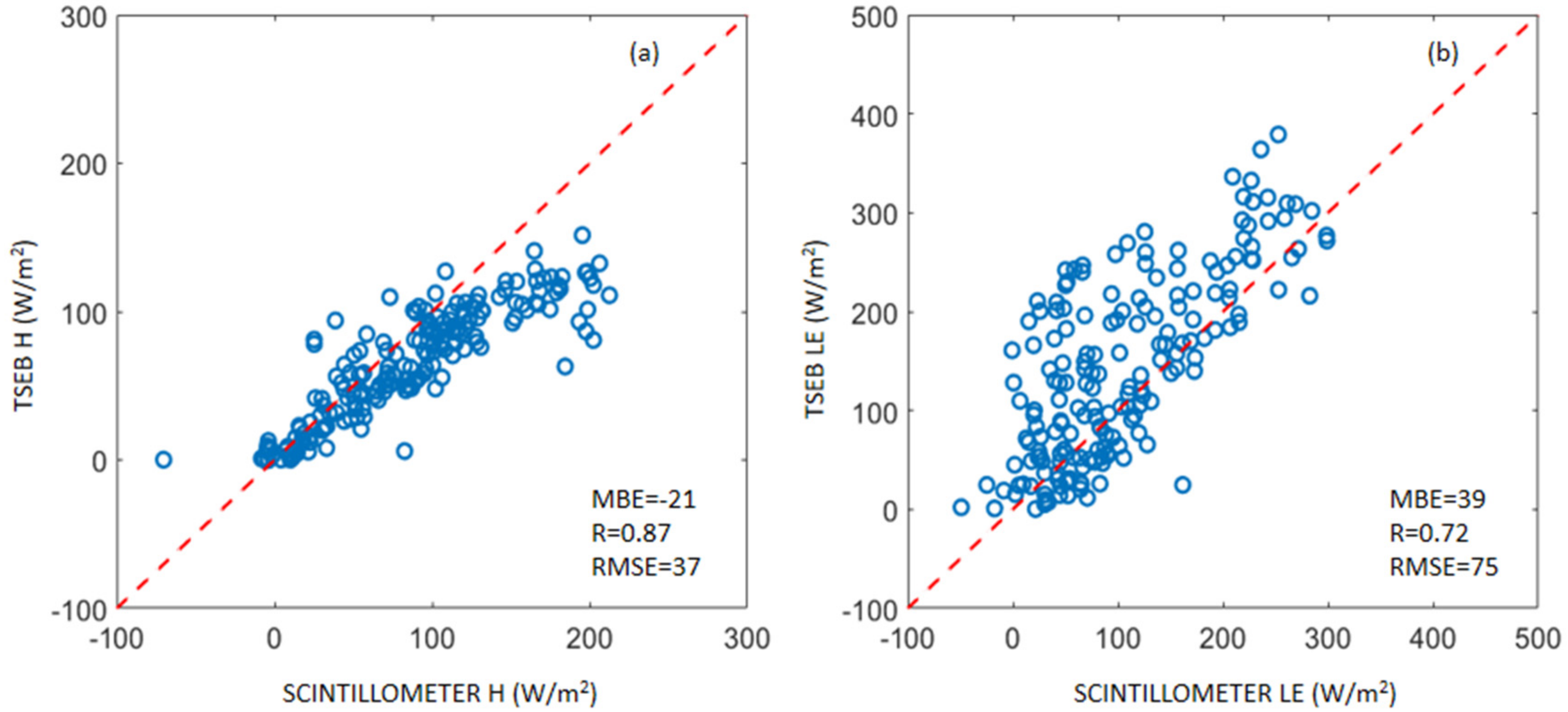
Using In-Situ Data
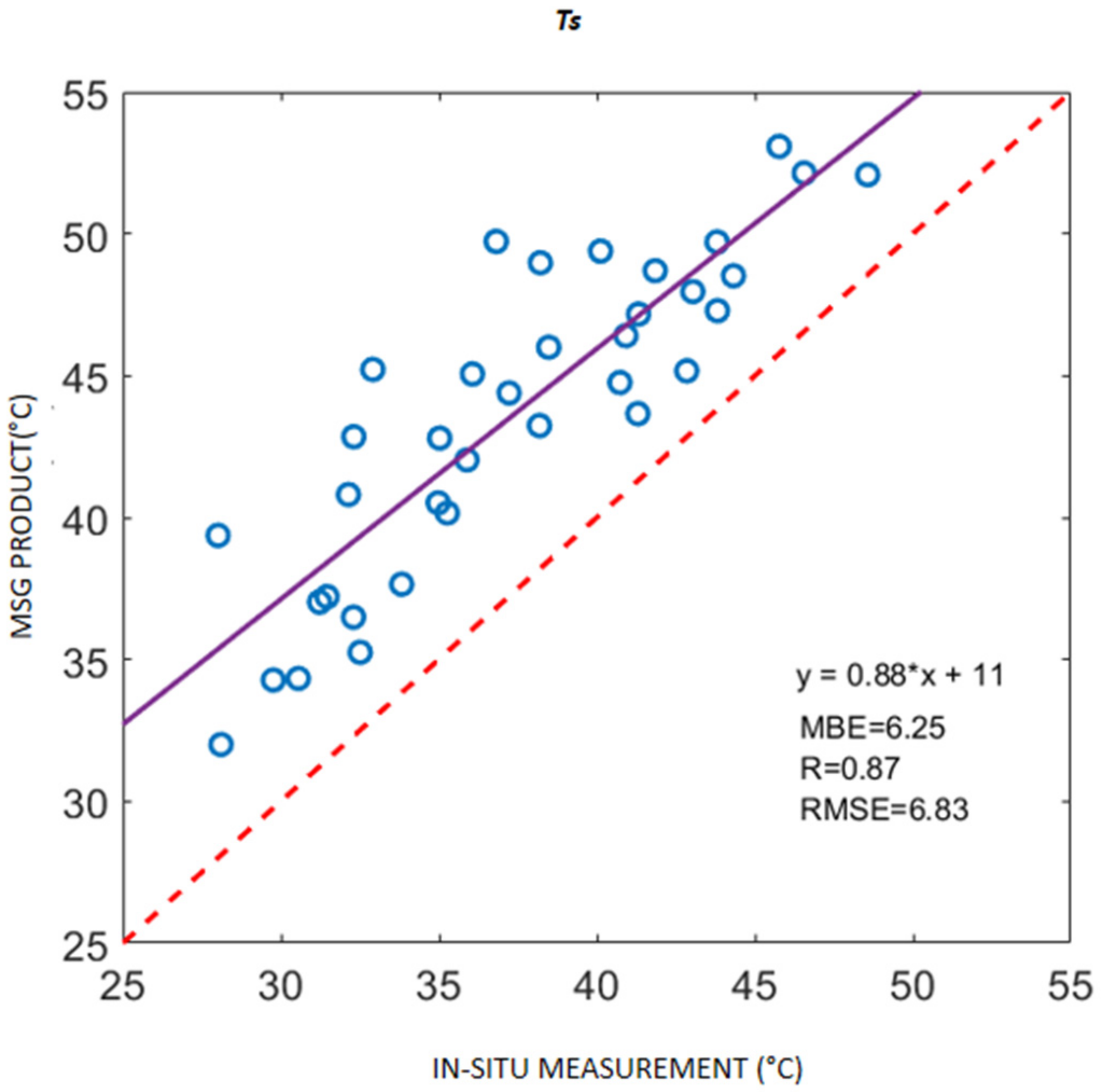
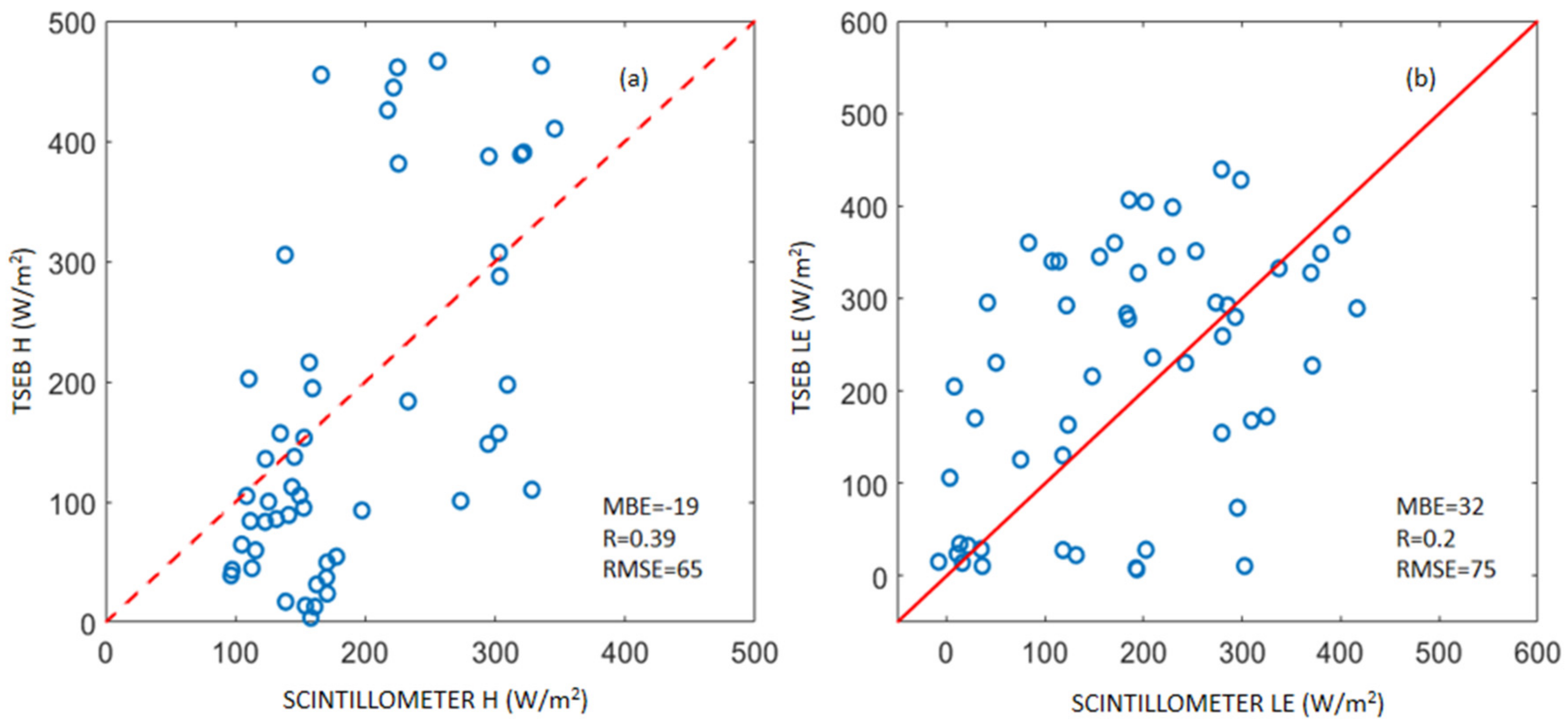
Using 3-km MSG SEVIRI Ts
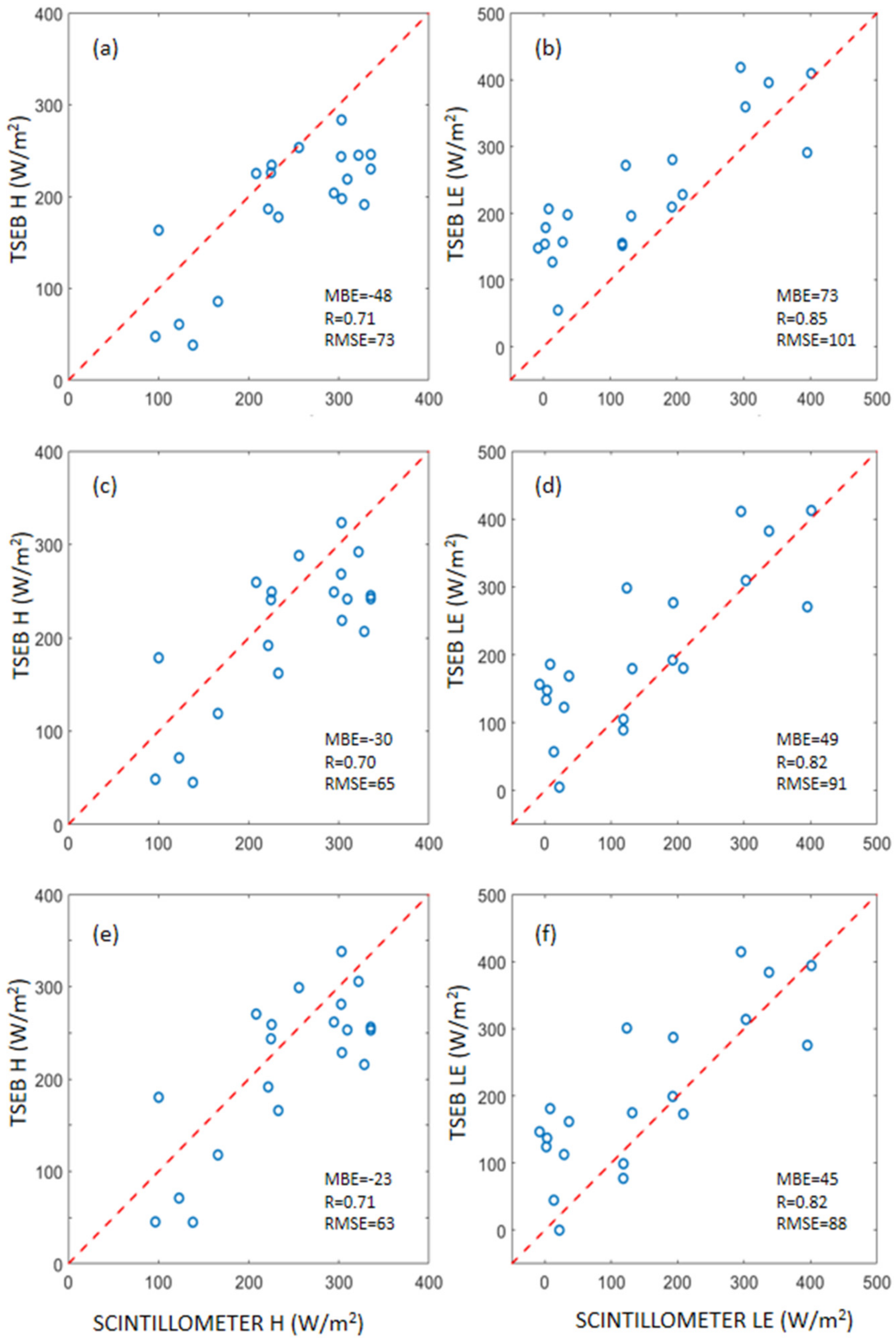
Using MODIS Products
4. Summary and Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Goutorbe, J.P.; Lebel, T.; Tinga, A.; Bessemoulin, P.; Brouwer, J.; Dolman, A.J.; Engman, E.T.; Gash, J.H.C.; Hoepffner, M.; Kabat, P.; et al. HAPEX-Sahel: A large scale study of land-atmosphere interactions in the semi-arid tropics. Ann. Geophys. 1994, 12, 53–64. [Google Scholar] [CrossRef]
- Lebel, T.; Parker, D.J.; Flamant, C.; Holler, H.; Polcher, J.; Redelsperger, J.L.; Thorncroft, C.; Bock, O.; Bourles, B.; Galle, S.; et al. The AMMA field campaigns: Accomplishments and lessons learned. Atmos. Sci. Lett. 2011, 12, 123–128. [Google Scholar] [CrossRef]
- Beljaars, A.C.; Viterbo, P.; Miller, M.J.; Betts, A.K. The anomalous rainfall over the United States during July 1993: Sensitivity to land surface parameterization and soil moisture anomalies. Mon. Weather Rev. 1993, 124, 362–383. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Shukla, J.; Mintz, Y. Influence of Land-Surface Evapotranspiration on the Earth’s Climate. Science 1982, 215, 1498–1501. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage No 56: Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Coudert, B.; Ottlé, C.; Boudevillain, B.; Guillevic, P.C.; Demarty, J. Contribution of thermal infrared remote sensing data in multiobjective calibration of a dual source SVAT model. J. Hydrometeorol. 2006, 7, 404–420. [Google Scholar] [CrossRef]
- Noilhan, J.; Mahfouf, J.F. The ISBA Land surface parametrisation scheme. Glob. Planet. Charg. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Braud, I.; Dantas-Antonino, A.C.; Vauclin, M.; Thony, J.-L.; Ruelle, P. A Simple Soil-Plant-Atmosphere Transfer model (SiSPAT): Development and field verification. J. Hydrol. 1995, 166, 213–250. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating land surface evaporation: Areview of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Li, X.; Li, X.W.; Li, Z.Y.; Ma, M.G.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.X.; Yan, G.J.; et al. Watershed allied telemetry experimental research. J. Geophys. Res. Atmos. 2009, 114, D22103. [Google Scholar] [CrossRef]
- Sandholt, P.E.; Dyrland, M.; Farrugia, C.J. Dayside aurorae and polar arcs under south east IMF orientation. Ann. Geophys. 2006, 24, 3421–3432. [Google Scholar] [CrossRef]
- Fensholt, R.; Nielsen, T.T.; Stisen, S. Evaluation of AVHRR PAL and GIMMS 10-day composite NDVI time series products using SPOT-4 vegetation data for the African continent. Int. J. Remote Sens. 2006, 27, 2719–2733. [Google Scholar] [CrossRef]
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I.F. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Trigo, I.F.; Jitan, M.A.; Temesgen Enku, N.; Van Der Tol, C.; Gieske, A.S.M. Reference crop evapotranspiration derived from geo-stationary satellite imagery: A case study for the Fogera flood plain, NW-Ethiopia and the Jordan Valley, Jordan. Hydrol. Earth Syst. Sci. 2010, 14, 2219–2228. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Gellens-Meulenberghs, F. Evapotranspiration modelling at large scale using near-real time MSG SEVIRI derived data. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 7079–7120. [Google Scholar] [CrossRef]
- Sun, Z.; Gebremichael, M.; Ardö, J.; De Bruin, H.A.R. Mapping daily evapotranspiration and dryness index in the East African highlands using MODIS and SEVIRI data. Hydrol. Earth Syst. Sci. 2011, 15, 163–170. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Proud, S.R.; Stisen, S.; Rasmussen, M.O. Assessment of MODIS sun-sensor geometry variations effect on observed NDVI using MSG SEVIRI geostationary data. Int. J. Remote Sens. 2010, 31, 6163–6187. [Google Scholar] [CrossRef]
- Rulinda, C.M.; Bijker, W.; Stein, A. Image mining for drought monitoring in eastern Africa using Meteosat SEVIRI data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 63–68. [Google Scholar] [CrossRef]
- Boulain, N.; Cappelaere, B.; Ramier, D.; Issoufou, H.B.A.; Halilou, O.; Seghieri, J.; Guillemin, F.; Oi, M.; Gignoux, J.; Timouk, F. Towards an understanding of coupled physical and biological processes in the cultivated Sahel–2. Vegetation and carbon dynamics. J. Hydrol. 2009, 375, 190–203. [Google Scholar] [CrossRef]
- Boulain, N.; Cappelaere, B.; Seguis, L.; Favreau, G.; Gignoux, J. Water balance and vegetation change in the Sahel: A case study at the watershed scale with an eco-hydrological model. J. Arid Environ. 2009, 73, 1125–1135. [Google Scholar] [CrossRef]
- Ramier, D.; Boulain, N.; Cappelaere, B.; Timouk, F.; Rabanit, M.; Lloyd, C.R.; Boukraoui, S.; Métayer, F.; Descroix, L.; Wawrzyniak, V. Towards an understanding of coupled physical and biological processes in the cultivated Sahel–1. Energy and water. J. Hydrol. 2009, 375, 204–216. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.; Ramier, D.; Boulain, N.; Boubkraoui, S.; Cappelaere, B.; Descroix, L.; Mougenot, B.; Timouk, F. Combining scintillometer measurements and an aggregation scheme to estimatearea-averaged latent heat flux during the AMMA experiment. J. Hydrol. 2009, 375, 217–226. [Google Scholar] [CrossRef]
- Velluet, C.; Demarty, J.; Cappelaere, B.; Braud, I.; Issoufou, H.B.A.; Boulain, N.; Ramier, D. Building a field- and model-based climatology of local water and energy cycles in the cultivated Sahel–Annual budgets and seasonality. Hydrol. Earth Syst. Sci. 2014, 18, 5001–5024. [Google Scholar] [CrossRef]
- Allies, A.; Demarty, J.; Olioso, A.; Bouzou Moussa, I.; Issoufou, H.B.-A.; Velluet, C.; Bahir, M.; Mainassara, I.; Oï, M.; Chazarin, J.P.; et al. Adapting EVASPA/S-SEBI to evapotranspiration mapping in the Sahel with uncertainty characterization: The E3S method. Remote Sens. Environ. 2018, in press. [Google Scholar]
- Ezzahar, J.; Chehbouni, A.; Er-Raki, S.; Hanich, L. Combining a large aperture scintillometer and estimates of available energy to derive evapotranspiration over several agricultural fields in a semi-arid region. Plant Biosyst. 2009, 143, 209–221. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Su, Z.; Olioso, A. Footprint issues in scintillometry overheterogeneous landscapes. Hydrol. Earth Syst. Sci. 2009, 13, 2179–2190. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, L.Z. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor? J. Geophys. Res. 2011, 116, D21107. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Walker, J.P. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to thesatellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Saadi, S.; Boulet, G.; Bahir, M.; Brut, A.; Mougenot, B.; Fanise, P.; Simonneaux, V.; Chabaane, Z.L. Assessment of actual evapotranspiration over a semi-arid heterogeneous land surface by means of coupled low resolution remote sensing data with energy balance model: Comparaison to extra Large Aperture Scintillometer measurements. Hydrol. Earth Syst. Sci. 2017. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Baldocchi, D. Measuring fluxes of trace gases and energy between ecosystems and atmosphere the state and future of the eddy covariance method. Glob. Chang. Biol. 2014, 20, 3600–3609. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.; Ryu, Y.; Keenan, T. Terrestrial Carbon Cycle Variability [version 1; referees: 2 approved]. F1000Research 2016, 5, 2371. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.; Chu, H.; Reichsteinb, M. Inter-annual variability of net and gross ecosystem carbon fluxes: A review. Agric. For. Meteorol. 2017, 249, 520–533. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Ham, J.M.; Arnold, K.A. Validating remotely sensed land surface fluxes in heterogeneous terrain with large aperture scintillometry. Int. J. Remote Sens. 2011, 32, 6295–6314. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.M.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1991, 94, 13–29. [Google Scholar] [CrossRef]
- Diarra, A.; Jarlan, L.; Er-Raki, S.; Le Page, M.; Aouade, G.; Tavernier, A.; Boulet, G.; Ezzahar, J.; Merlin, O.; Khabba, S. Performance of the Two-Source Energy Budget (TSEB) Model for the Monitoring of Evapotranspiration Over Irrigated Annual Crops in North Africa. Agric. Water Manag. 2017, 193, 71–88. [Google Scholar] [CrossRef]
- Aït Hssaine, B.; Merlin, O.; Rafi, Z.; Ezzahar, J.; Jarlan, L.; Khabba, S.; Er-Raki, S. Calibrating an evapotranspiration model using radiometric surface temperature, vegetation cover fraction and near-surface soil moisture data. Agric. For. Meteorol. 2018, 256, 104–115. [Google Scholar] [CrossRef]
- Boulain, N.; Cappelaere, B.; Seguis, L.; Gignoux, J.; Peugeot, C. Hydrologic and land use impacts on vegetation growth and NPP at the watershed scale in a semi-arid environment. Reg. Environ. Chang. 2006, 6, 147–156. [Google Scholar] [CrossRef]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boulain, N.; Ramier, D.; Laurent, J.-P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Moussa, I.B.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of South-West Niger. Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- Lebel, T.; Cappelaere, B.; Galle, S.; Hanan, N.; Kergoat, L.; Levis, S.; Vieux, B.; Descroix, L.; Gosset, M.; Mougin, E.; et al. AMMA-CATCH studies in the Sahelian region of West-Africa: An overview. J. Hydrol. 2009, 375, 3–13. [Google Scholar] [CrossRef]
- Massuel, S.; Cappelaere, B.; Favreau, G.; Leduc, C.; Lebel, T.; Vischel, T. Integrated surface water-groundwater modelling in the context of increasing water reserves of a Sahelian aquifer. Hydrol. Sci. J. 2011, 56, 1242–1264. [Google Scholar] [CrossRef]
- Rockström, J.; Valentin, C. Hillslope dynamics of on-farm generation of surface water flows: The case of rainfed cultivation of pearl millet on sandy soil in the Sahel. Agric. Water Manag. 1997, 33, 183–210. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy Covariance Software Package TK2. Report No. 26, U. Bayreuth–Abt. Mikrometeorologie. 2004. Available online: http://www.geo.uni-bayreuth.de/mikrometeorologie/ARBERG/ARBERG26.pdf (accessed on 19 December 2004).
- Wilczak, J.; Oncley, S.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Schotanus, P.; Nieuwstadt, F.; De Bruin, H.A.R. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound. Layer Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Moore, C.J. Frequency response corrections for eddy correlation systems. Bound. Layer Meteorol. 1986, 37, 17–35. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Van Dijk, A.; Kohsiek, W.; De Bruin, H.A.R. Oxygen sensitivity of krypton and lymann—A hygrometers. J. Atmos. Ocean. Technol. 2003, 20, 143–151. [Google Scholar] [CrossRef]
- Ochs, G.R.; Wilson, J.J. A Second-Generation Large-Aperture Scintillometer; NOAA Tech. Memo, ERL WPL-232; NOAA Environmental Research Laboratories Publ.: Boulder, CO, USA, 1993; Volume 177, pp. 117–132. [Google Scholar]
- Meijninger, W.M.L.; Moene, A.; Hartogensis, O.; De Bruin, H.A.R. User Manual and Technical Information to the Large Aperture Scintillometer; Wageningen University: Wageningen, The Netherlands, 2000. [Google Scholar]
- Wesely, M.L. The combined effect of temperature and humidity fluctuations on refractive index. J. Appl. Meteorol. 1976, 15, 43–49. [Google Scholar] [CrossRef]
- Moene, A.F. Effects of water vapour on the structure parameter of the refractive index for near-infrared radiation. Bound. Layer Meteorol. 2003, 107, 635–653. [Google Scholar] [CrossRef]
- Hartogensis, O.K.; Watts, C.J.; Rodriguez, J.C.; De Bruin, H.A.R. Derivation of an Effective Height for Scintillometers: La Poza Experiment in Northwest Mexico. J. Hydrometeorol. 2003, 4, 915–928. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Dutton, J.A. Atmospheric Turbulence; John Wiley: New York, NY, USA, 1984. [Google Scholar]
- Andreas Edgar, L. Estimating Cn2 over snow and sea ice from meteorological quantities. In Proceedings of the SPIE 0926, Optical, Infrared, Millimeter Wave Propagation Engineering, Orlando, FL, USA, 10 August 1988. [Google Scholar]
- Thiermann, V.; Grassl, H. The measurement of turbulent surface layer fluxes by use of bichromatic scintillation. Bound. Layer Meteorol. 1992, 58, 367–384. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; van den Hurk, B.J.J.M.; Kohsiek, W. The scintillation method tested over a dry vineyard area. Bound. Layer Meteorol. 1995, 76, 25–40. [Google Scholar] [CrossRef]
- Wyngaard, J.C. On surface-layer turbulence. In Workshop on Micrometeorology; Haugen, D.A., Ed.; AMS: Boston, MA, USA, 1973; pp. 101–149. [Google Scholar]
- Chehbouni, A.; Watts, C.; Kerr, Y.H.; Dedieu, G.; Rodríguez, J.C.; Santiago, F.; Cayrol, P.; Boulet, G.; Goodrich, D.C. Methods to aggregate turbulent fluxes over heterogeneous surfaces: Application to SALSA data set in Mexico. Agric. For. Meteorol. 2000, 105, 133–144. [Google Scholar] [CrossRef]
- Chehbouni, A.; Escadafal, R.; Duchemin, B.; Boulet, G.; Simonneaux, V.; Dedieu, G.; Mougenot, B.; Khabba, S.; Kharrou, H.; Maisongrande, P.; et al. An Integrated Modeling and Remote Sensing Approach for Hydrological Study in Arid and Semi-arid Regions: The SUDMED Programme. Int. J. Remote Sens. 2008, 29, 5161–5181. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.C.B.; Chehbouni, A. On the application of scintillometry over heterogeneous grids. J. Hydrol. 2007, 334, 493–501. [Google Scholar] [CrossRef]
- Hemakumara, H.M.; Chandrapala, L.; Moene, A.F. Evapotranspiration fluxes over mixed vegetation areas measured from large scintillometer. Agric. Water Manag. 2003, 58, 109–122. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Zuurbier, R.M.; Watts, C.J. Large aperture scintillometer used over a homogeneous irrigated area, partly affected by regional advection. Bound. Layer Meteorol. 2002, 105, 99–117. [Google Scholar] [CrossRef]
- Solignac, P.A.; Brut, A.; Selves, J.L.; Beteille, J.P.; Gastellu-Etchegorry, J.P.; Keravec, P.; Beziat, P.; Ceschia, E. Uncertainty analysis of computational methods for deriving sensible heat flux values from scintillometer measurements. Atmos. Meas. Tech. 2009, 2, 741–753. [Google Scholar] [CrossRef]
- Horst, T.W.; Weil, J.C. How far is far enough? The fetch requirements for micrometeorological measurement of surface fluxes. J. Atmos. Ocean. Technol. 1994, 11, 1018–1025. [Google Scholar] [CrossRef]
- Leclerc, M.Y.; Thurtell, G.W. Footprint prediction of scalar fluxes using a Markovian analysis. Bound. Layer Meteorol. 1990, 52, 247–258. [Google Scholar] [CrossRef]
- Lewis, P.; Barnsley, M.J. Influence of the Sky Radiance Distribution on Various Formulations of the Earth Surface Albedo. Available online: http://www2.geog.ucl.ac.uk/~plewis/LewisBarnsley1994.pdf (accessed on 18 June 2018).
- Wan, Z.; Dozier, J. A generalised split-window algorithm for retrieving land surface temperature from space, IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Madeira, C. Generalised Split-Window Algorithm for Retrieving Land-Surface Temperature from MSG/SEVIRI Data. In Proceedings of the SAF on Land Surface Analysis Training Workshop, Lisbon, Portugal, 8–10 July 2002. [Google Scholar]
- Kustas, W.P.; Norman, J.M. A two-source approach for estimating turbulent fluxes using multiple angle thermal infrared observations. Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere; D. Reidel: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Sauer, T.J.; Norman, J.M.; Tanner, C.B.; Wilson, T.B. Measurement of heat and vapor transfer at the soil surface beneath a maize canopy using source plates. Agric. For. Meteorol. 1995, 75, 161–189. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Choudhury, B.J.; Idso, S.; Reginato, R. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evaporation by an infrared-temperature based energy balance equation. Agric. For. Meteorol. 1987, 39, 283–297. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Monteny, B.; Amadou, M. Estimating sensible heat flux from radiometric temperature over sparse millet. Agric. For. Meteorol. 1994, 68, 77–91. [Google Scholar] [CrossRef]
- Chehbouni, A.; Njoku, E.G.; Lhomme, J.P.; Kerr, Y.H. An approach for averaging surface temperature and surface fluxes over heterogeneous surfaces. J. Clim. 1995, 5, 1386–1393. [Google Scholar] [CrossRef]
- Foken, T.; Wimmer, F.; Mauder, M.; Thomas, C.; Liebethal, C. Some aspects of the energy balance closure problem. Atmos. Chem. Phys. 2006, 6, 4395–4402. [Google Scholar] [CrossRef]
- Heusinkveld, B.G.; Jacobs, A.F.G.; Holtslag, A.A.M.; Berkowicz, S.M. Surface energy balance closure in an arid region: Role of soil heat flux. Agric. For. Meteorol. 2004, 122, 21–37. [Google Scholar] [CrossRef]
- Guyot, A.; Cohard, J.-M.; Anquetin, S.; Galle, S.; Lloyd, R. Combined analysis of energy and water balances to estimate latent heat flux of a Sudanian small catchment. J. Hydrol. 2009, 375, 227–240. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Impact of post-field data processing on eddy covariance flux estimates and energy balance closure. Meteorol. Z. 2006, 15, 597–609. [Google Scholar] [CrossRef]
- Yu, W.; Ma, M.; Wang, X.; Geng, L.; Tan, J.; Shi, J. Evaluation of MODIS LST Products Using Longwave Radiation Ground Measurements in the Northern Arid Region of China. Remote Sens. 2014, 6, 11494–11517. [Google Scholar] [CrossRef]
- Aksakal, S.K. Geometric Accuracy Investigations of SEVIRI High Resolution Visible (HRV) Level 1.5 Imagery. Remote Sens. 2013, 5, 2475–2491. [Google Scholar] [CrossRef]
- Verhoef, A.; Ottlé, C.; Cappelaere, B.; Murray, T.; Saux Picart, S.; Zribi, A.; Maignan, F.; Boulain, N.; Demarty, J.; Ramier, D. Spatio-temporal surface soil heat flux estimates from satellite data; results for the AMMA experiment, Fakara supersite. Agric. For. Meteorol. 2012, 154–155, 55–66. [Google Scholar] [CrossRef]
- Brutsaert, W. On a derivable formula for long-wave radiation from clear skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]
- Thom, A.S. Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 1971, 97, 414–428. [Google Scholar] [CrossRef]
- Shaw, R.H.; Pereira, A.R. Aerodynamic roughness of a plant canopy: A numerical experiment. Agric. Meteorol. 1982, 26, 51–65. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Chehbouni, A.; Ezzahar, J.; Escadafal, R.; De Bruin, H.A.R. Comparison of large aperture scintillometer and Eddy covariance measurements: Can thermal infrared data be used to capture footprint induced differences? J. Hydrometeorol. 2007, 8, 144–159. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Irvine, M.; Bonnefond, J.M.; Grimmond, C.S.B.; Long, N.; Oke, T.R.; Salmond, J.A.; Offerele, B. Monitoring the sensible heat flux over urban areas using large aperture scintillometry: Case study of marseille city during the escompte experiment. Bound. Layer Meteorol. 2005, 118, 449–476. [Google Scholar] [CrossRef]
- Bindlish, R.; Kustas, W.P.; French, A.N.; Diak, G.R.; Mecikalski, J.R. Influence of near-surface soil moisture on regional scale heat fluxes: Model results using microwave remote sensing data from SGP97. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1719–1728. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; Anderson, M.C. Two source energy balance model to calculate E.; T.; and ET: Comparison of Priestley-Taylor and Penman-Monteith formulations and two time scaling methods. Trans. ASABE 2014, 57, 479–498. [Google Scholar]
- Eichinger, W.E.; Parlange, M.B.; Stricker, H. On the concept of equilibrium evaporation and the value of the priestley-taylor coefficient. Water Resour. Res. 1996, 32, 161–164. [Google Scholar] [CrossRef]
- Song, L.; Kustas, W.P.; Liu, S.; Colaizzi, P.D.; Nieto, H.; Xu, Z.; Ma, Y.; Li, M.; Xu, T.; Agam, N.; et al. Applications of a thermal-based two-source energy balance model using Priestley-Taylor approach for surface temperature partitioning under advective conditions. J. Hydrol. 2016, 540, 574–587. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]

| Symbol | Description | Unit | Value |
|---|---|---|---|
| The refractive index of air | m−2/3 | ||
| The structure parameters of temperature | K2 m−2/3 | ||
| The structure parameters of Humidity | kg2 m−6 m−2/3 | ||
| The structure parameters of the covariant term | K kg m−3 m−2/3 | ||
| The specific heat of air at constant pressure | J kg−1 K−1 | 1006 | |
| d | The displacement of reference plan | m | |
| The vegetation cover fraction | (-) | ||
| fg | The fraction of leaf area index (LAI) that is green | (-) | 1 |
| The soil sensible heat flux | W m−2 | ||
| The vegetation sensible heat flux | W m−2 | ||
| hc | The canopy height | m | |
| G | The surface soil heat flux | W m−2 | |
| k | The von Karman constant | (-) | 0.4 |
| L | The Obukhov length | m | |
| LAI | The leaf area index | (-) | |
| The soil latent heat flux | W m−2 | ||
| The vegetation latent heat flux | W m−2 | ||
| g | The gravitational acceleration | m s−2 | 9.8 |
| The soil net radiation | W m−2 | ||
| The vegetation net radiation | W m−2 | ||
| rah | The aerodynamic resistance | s m−1 | |
| rs | The resistance to heat flux in the boundary layer immediately above the soil surface | s m−1 | |
| s | The leaf size | m | 0.01 |
| Ts | The surface temperature | K | |
| Tair | The air temperature | K | |
| The friction velocity | s m−1 | ||
| Us | The wind speed at a height above the ground | s m−1 | |
| The roughness length for momentum | m | ||
| The height of temperature measurement | m | ||
| The roughness length | m | ||
| The height of wind speed measurement | m | ||
| ZLAS | The effective height of the LAS above the surface | m | 9 |
| γ | The psychometric constant | Pa K−1 | 67 |
| Δ | The slope of the saturation vapor pressure versus temperature curve | Pa K−1 | |
| The view zenith angle | (°) | ||
| Albedo | (-) | ||
| Air density | Kg m−3 | 1.18 | |
| The adiabatic correction factors for momentum | (-) | ||
| The adiabatic correction factors for heat | (-) | ||
| The Bowen ratio | (-) | ||
| The integrated stability function | (-) | ||
| The temperature scale | K | ||
| The standard deviation of the lateral spread | (m) | ||
| The lateral wind fluctuations | (m s−1) | ||
| αPT | The Priestley–Taylor coefficient | (-) | 1.26 |
| MODIS Product | Scientific Data Sets (SDSs) | Spacial Resolution | Number of Clear Images during the Study Period |
|---|---|---|---|
| MCD43B3 | _BSA_Band_shortwave (Black Sky ) | 1 km | 8 |
| _WSA_Band_shortwave (White Sky ) | 1 km | 8 | |
| MOD15A2 | Lai_1km | 1 km | 8 |
| MYd11A1 | Daytime land surface temperature | 1 km | 11 |
| Daytime LST view zenith angle | 1 km | 11 | |
| MOD11A1 | Daytime land surface temperature | 1 km | 9 |
| Daytime LST view zenith angle | 1 km | 9 |
| Fluxes | n | R | MBE | RMSE | ||
|---|---|---|---|---|---|---|
| (-) | (-) | (W/m2) | (W/m2) | |||
| Millet | H | 1442 | 0.81 | 26 | 43 | |
| LE | 1442 | 0.69 | −17 | 66 | ||
| -G | 1442 | 0.92 | −23 | 52 | ||
| Fallow | H | 1905 | 0.89 | −21 | 40 | |
| LE | 1905 | 0.88 | 0.38 | 65 | ||
| -G | 1905 | 0.98 | −37 | 49 | ||
| Degraded-shrubs | H | 486 | 0.82 | 0.92 | 24 | |
| LE | 486 | 0.71 | 11 | 65 | ||
| -G | 486 | 0.95 | −42 | 57 | ||
| Patch-scale (using MODIS data) | Millet | H | 52 | 0.45 | 13 | 31 |
| LE | 52 | 0.58 | 58 | 94 | ||
| -G | 52 | 0.67 | 4 | 50 | ||
| Fallow | H | 52 | 0.73 | 25 | 54 | |
| LE | 52 | 0.71 | 32 | 93 | ||
| -G | 52 | 0.79 | 23 | 69 | ||
| Degraded-shrubs | H | - | - | - | - | |
| LE | - | - | - | - | ||
| -G | - | - | - | |||
| Grid-scale (using in-situ data) | H | 370 | 0.87 | −21 | 37 | |
| LE | 186 | 0.72 | 39 | 75 | ||
| Grid-scale using MSG SEVIRI data | H | 51 | 0.39 | −19 | 65 | |
| LE | 51 | 0.2 | 32 | 75 | ||
| Grid-scale (using MODIS data) | Scheme 1 | H | 20 | 0.71 | −48 | 73 |
| LE | 0.85 | 73 | 102 | |||
| Scheme 2 | H | 20 | 0.7 | −30 | 65 | |
| LE | 0.82 | 49 | 91 | |||
| Scheme 3 | H | 20 | 0.71 | −23 | 63 | |
| LE | 0.82 | 45 | 88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hssaine, B.A.; Ezzahar, J.; Jarlan, L.; Merlin, O.; Khabba, S.; Brut, A.; Er-Raki, S.; Elfarkh, J.; Cappelaere, B.; Chehbouni, G. Combining a Two Source Energy Balance Model Driven by MODIS and MSG-SEVIRI Products with an Aggregation Approach to Estimate Turbulent Fluxes over Sparse and Heterogeneous Vegetation in Sahel Region (Niger). Remote Sens. 2018, 10, 974. https://doi.org/10.3390/rs10060974
Hssaine BA, Ezzahar J, Jarlan L, Merlin O, Khabba S, Brut A, Er-Raki S, Elfarkh J, Cappelaere B, Chehbouni G. Combining a Two Source Energy Balance Model Driven by MODIS and MSG-SEVIRI Products with an Aggregation Approach to Estimate Turbulent Fluxes over Sparse and Heterogeneous Vegetation in Sahel Region (Niger). Remote Sensing. 2018; 10(6):974. https://doi.org/10.3390/rs10060974
Chicago/Turabian StyleHssaine, Bouchra Ait, Jamal Ezzahar, Lionel Jarlan, Olivier Merlin, Said Khabba, Aurore Brut, Salah Er-Raki, Jamal Elfarkh, Bernard Cappelaere, and Ghani Chehbouni. 2018. "Combining a Two Source Energy Balance Model Driven by MODIS and MSG-SEVIRI Products with an Aggregation Approach to Estimate Turbulent Fluxes over Sparse and Heterogeneous Vegetation in Sahel Region (Niger)" Remote Sensing 10, no. 6: 974. https://doi.org/10.3390/rs10060974
APA StyleHssaine, B. A., Ezzahar, J., Jarlan, L., Merlin, O., Khabba, S., Brut, A., Er-Raki, S., Elfarkh, J., Cappelaere, B., & Chehbouni, G. (2018). Combining a Two Source Energy Balance Model Driven by MODIS and MSG-SEVIRI Products with an Aggregation Approach to Estimate Turbulent Fluxes over Sparse and Heterogeneous Vegetation in Sahel Region (Niger). Remote Sensing, 10(6), 974. https://doi.org/10.3390/rs10060974