Relation between Convective Rainfall Properties and Antecedent Soil Moisture Heterogeneity Conditions in North Africa
Abstract
1. Introduction
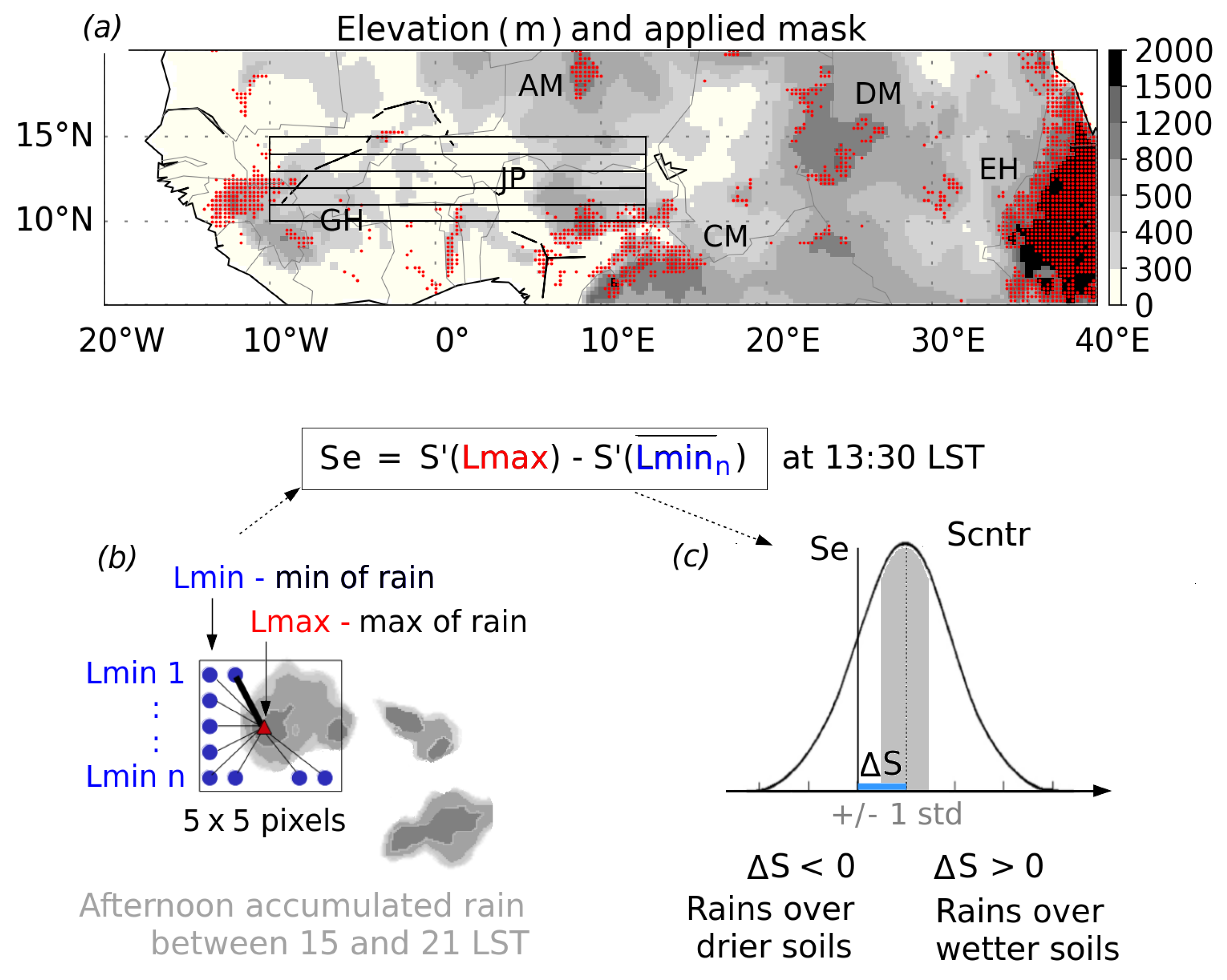
2. Study Domain
3. Data
3.1. Satellite-Based Soil Moisture and Precipitation Datasets
3.2. Atmospheric Profile Data from ERA-Interim
4. Methods
4.1. Definition of Afternoon Convective Rainfall Event
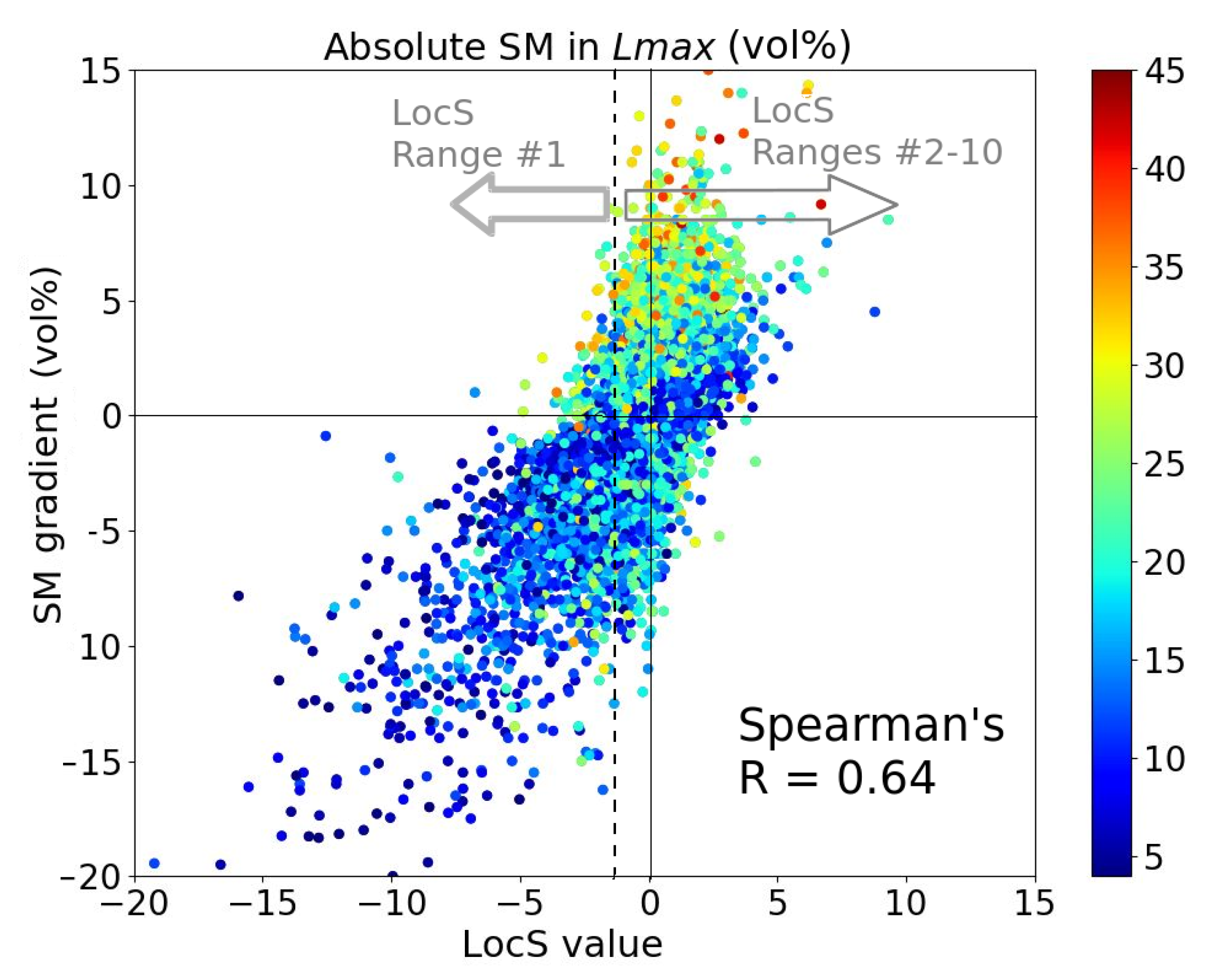
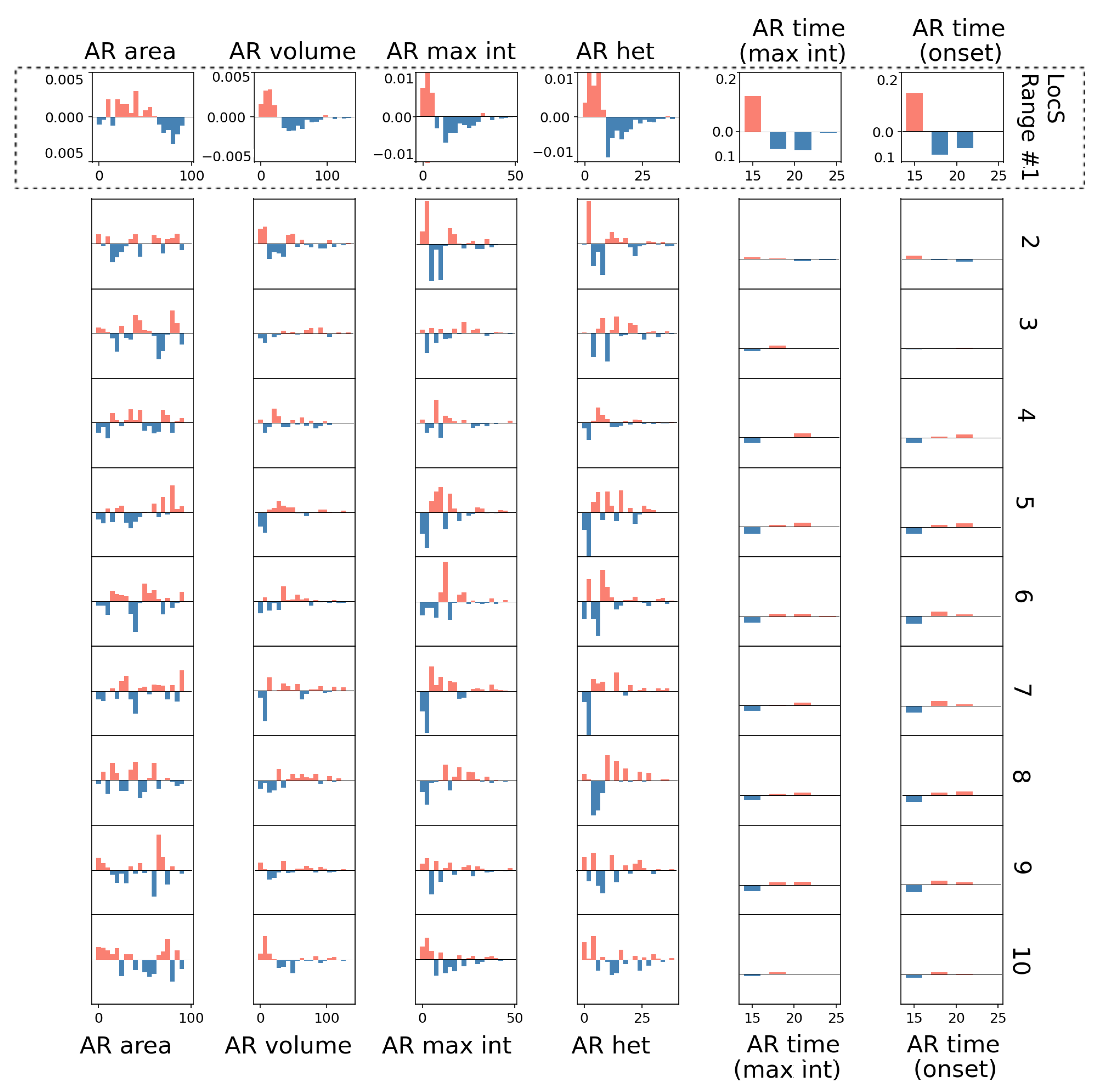
4.2. Measure of Local Soil Moisture Heterogeneity
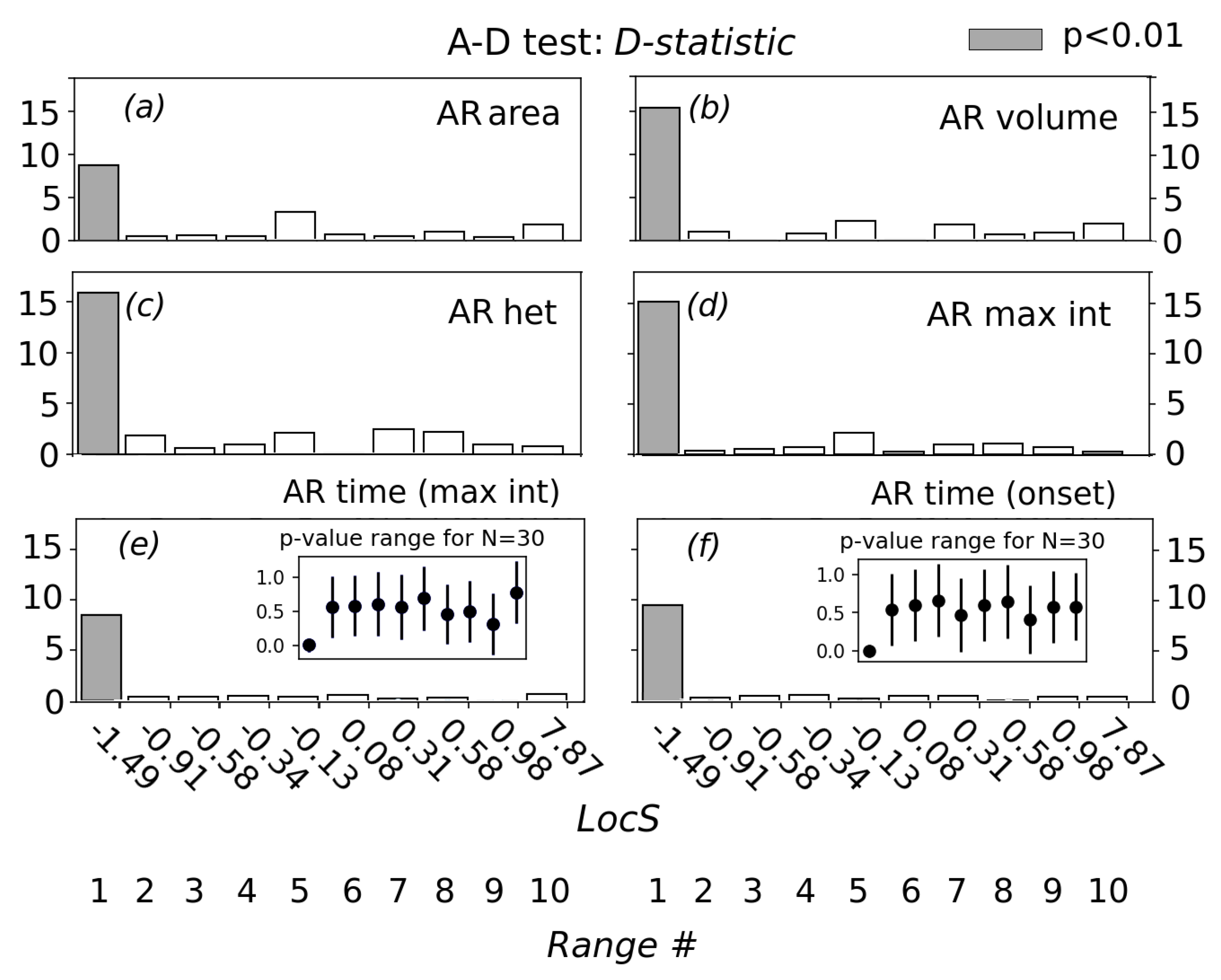
4.3. Statistical Test for Differences in Rain Characteristics
5. Results and Discussion
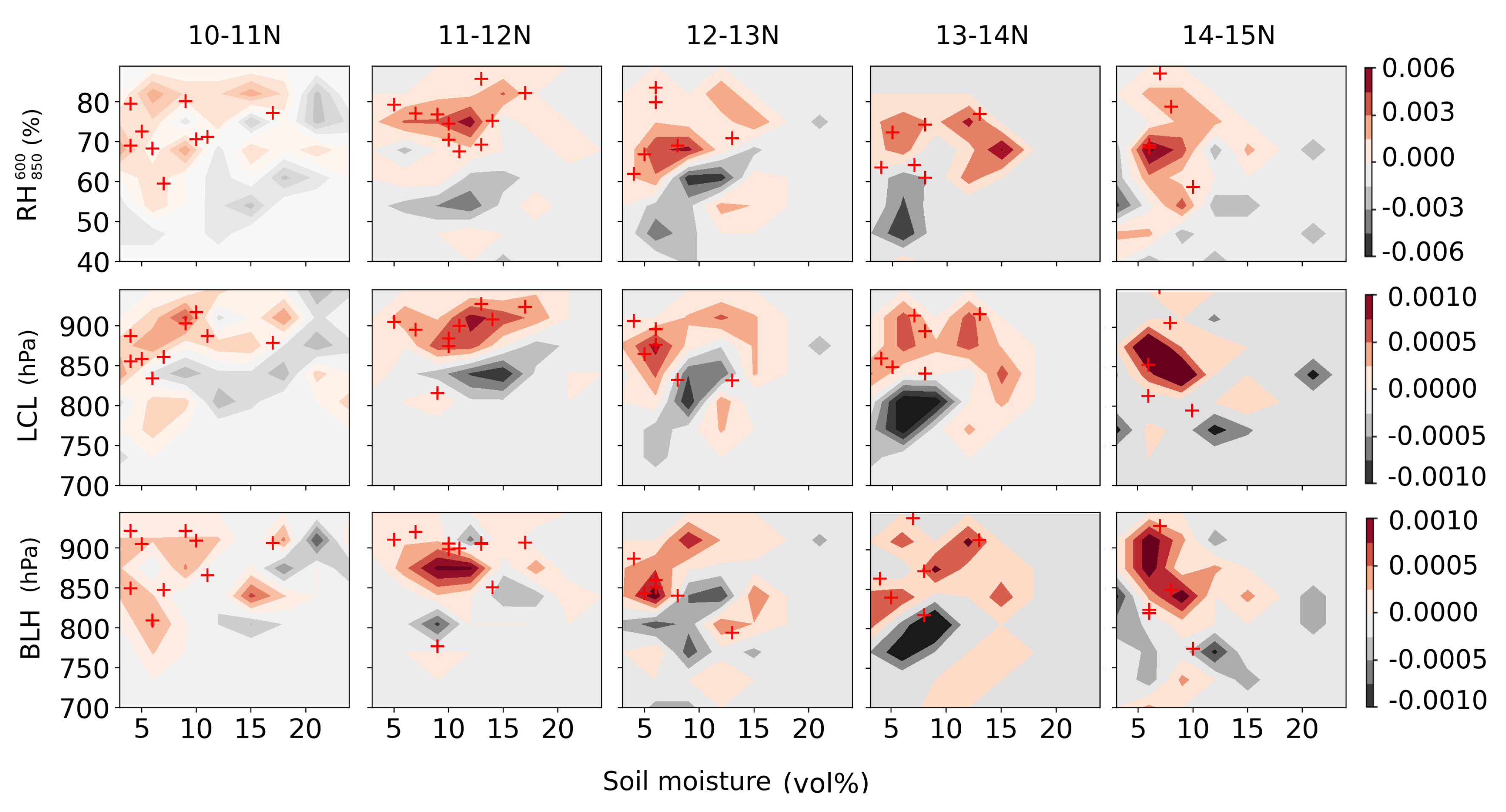
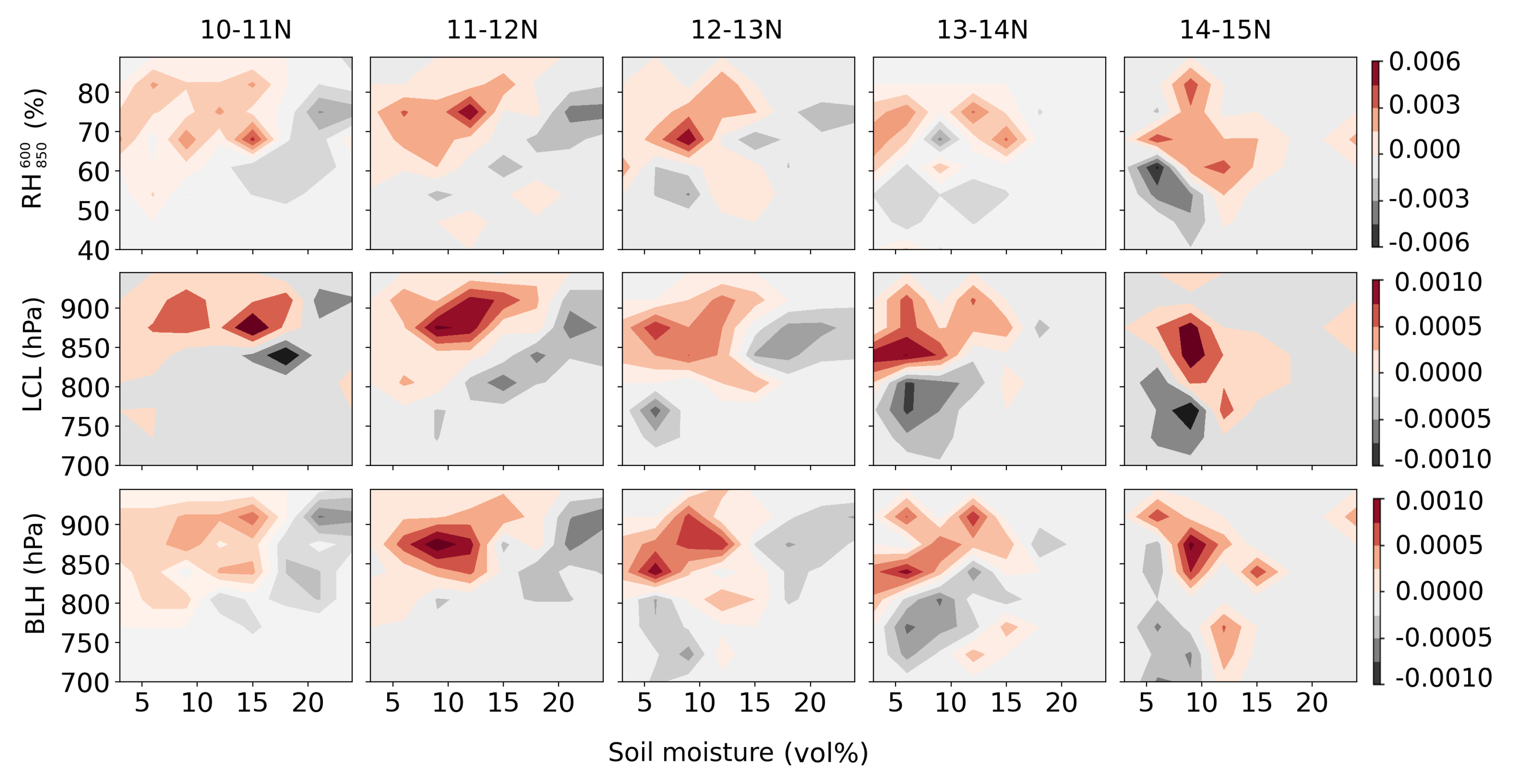
5.1. Sensitivity of Afternoon Rain Properties to Preceding Soil Moisture Heterogeneity State
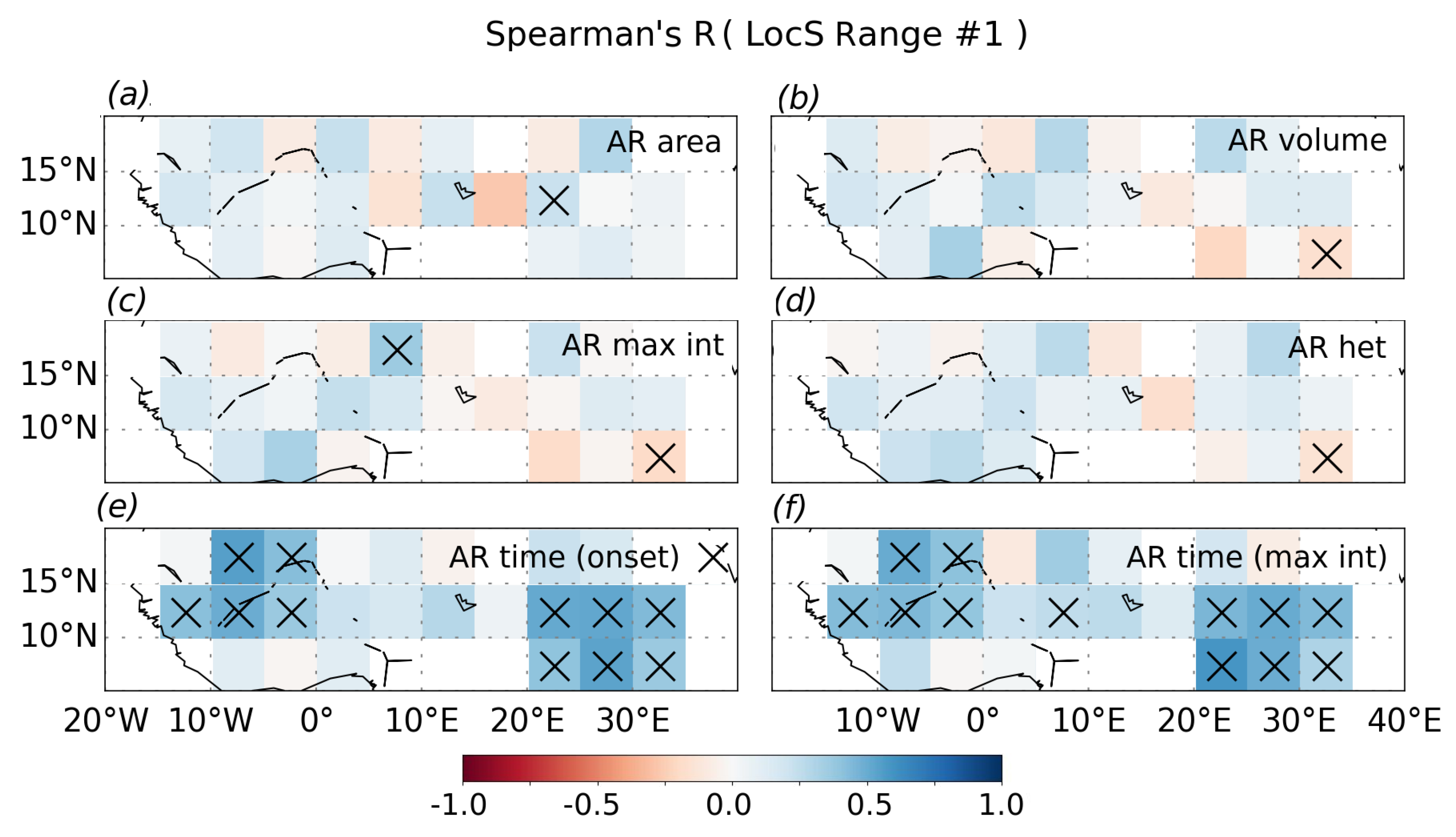
5.2. Relationship between Rainfall Properties and Strong Negative Soil Moisture Gradients
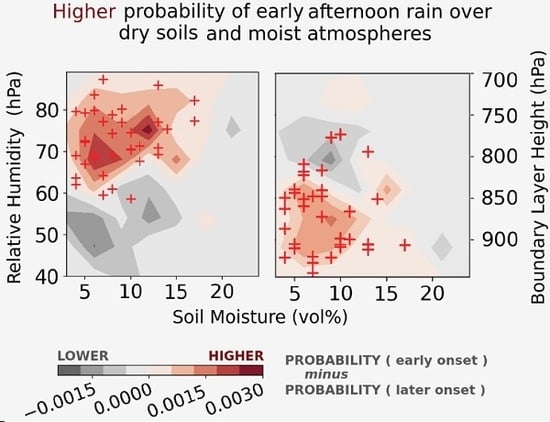
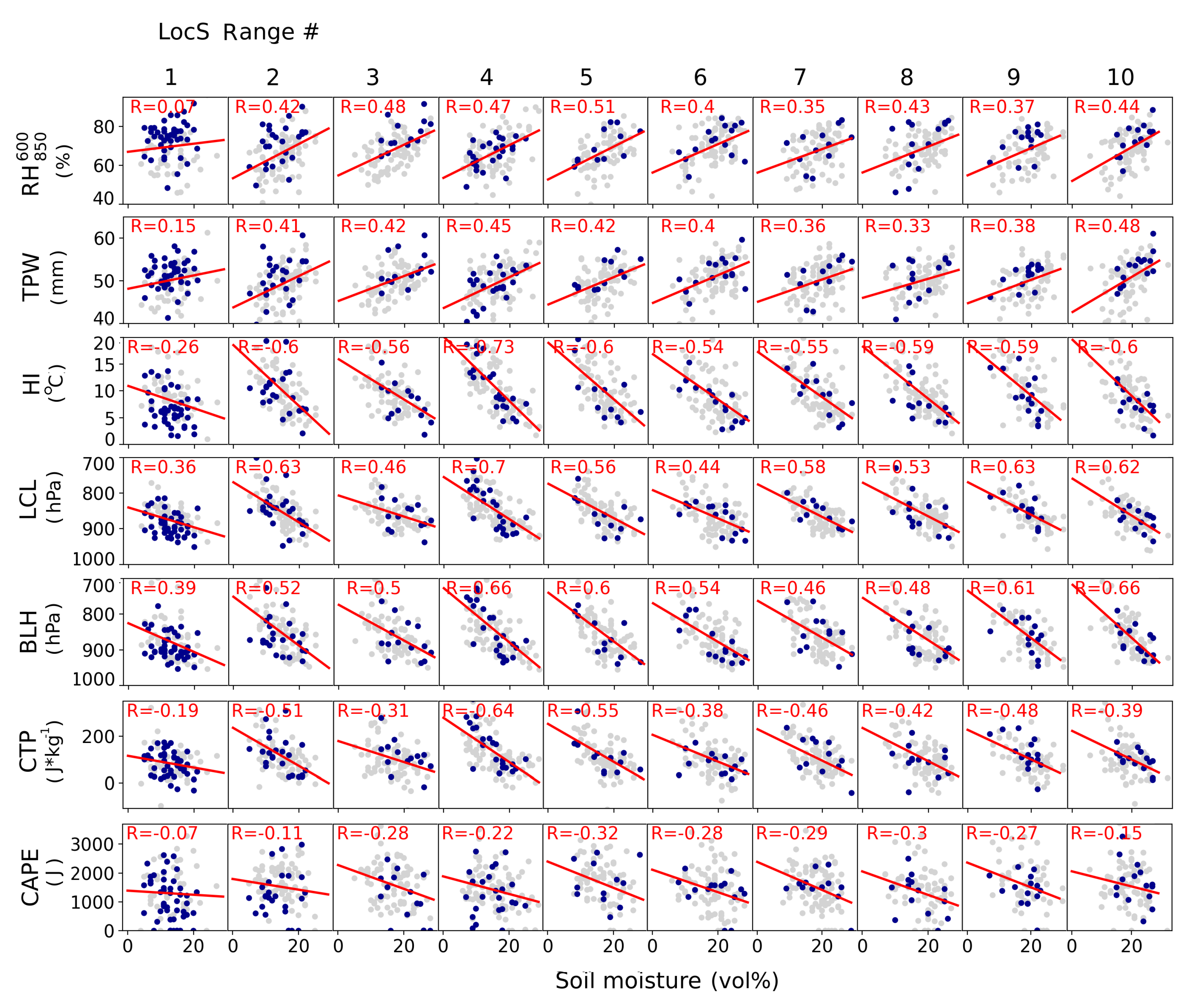
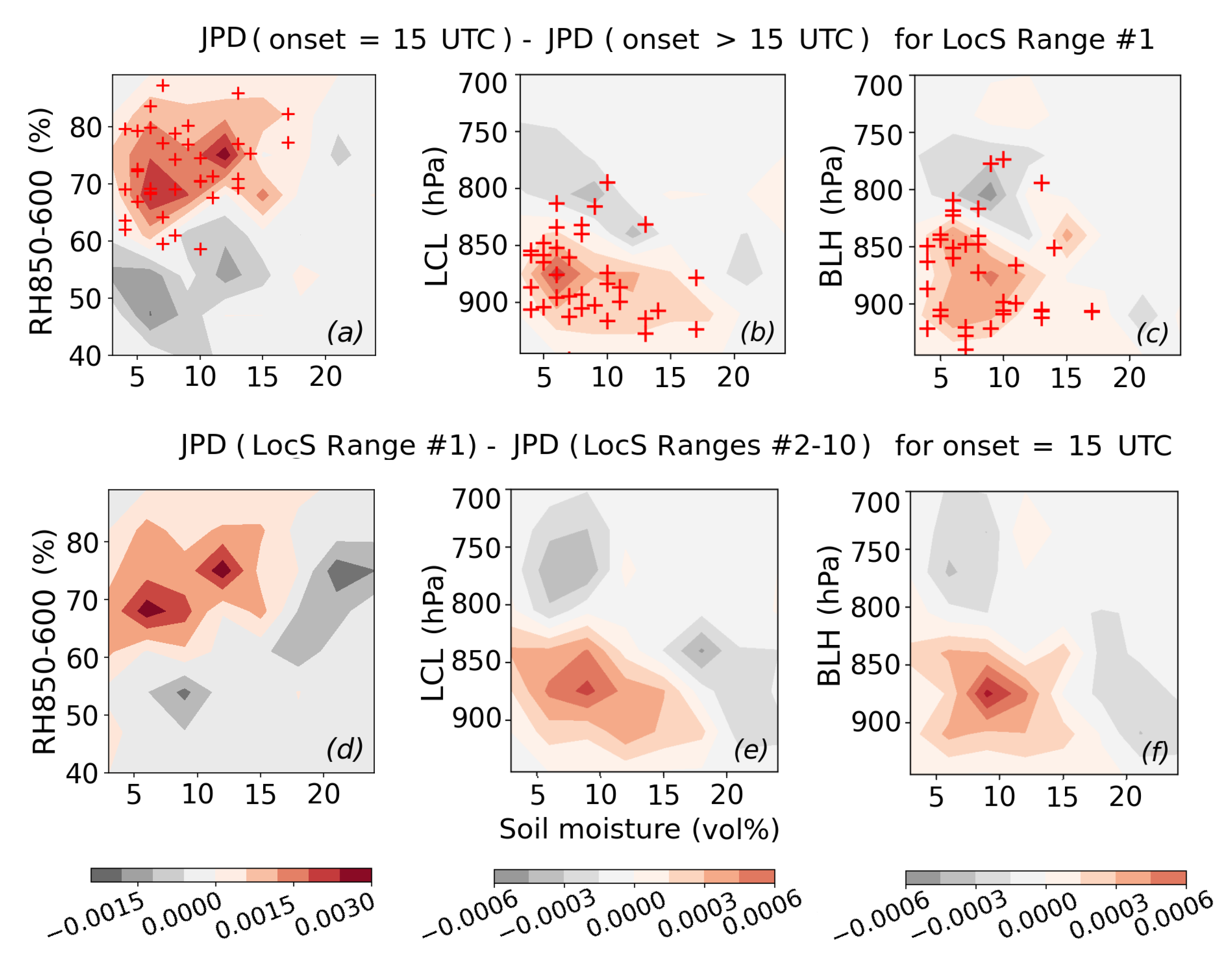
5.3. Atmospheric Moisture on Days with Early AR Onset
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LPRM | Land Surface Parameter Model |
| AMSR-E | Advanced Microwave Scanning Radiometer for Earth Observing System |
| TRMM | Tropical Rainfall Measuring Mission |
| TMPA | TRMM Multi-satellite Precipitation Analysis |
| CMORPH | Climate Prediction Center Morphing Method |
| PERSIANN | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| LST | Local Solar Time |
| UTC | Coordinated Universal Time |
| AR | Afternoon Rain |
| A–D test | Anderson–Darling test |
| TPW | Total Precipitable Water |
| HI | Humidity Index |
| RH | Relative Humidity |
| LCL | Lifting Condensation Level |
| BLH | Boundary Layer Height |
| CTP | Convective Triggering Potential |
| CAPE | Convective Available Potential Energy |
| JPD | Joint Probability Distribution |
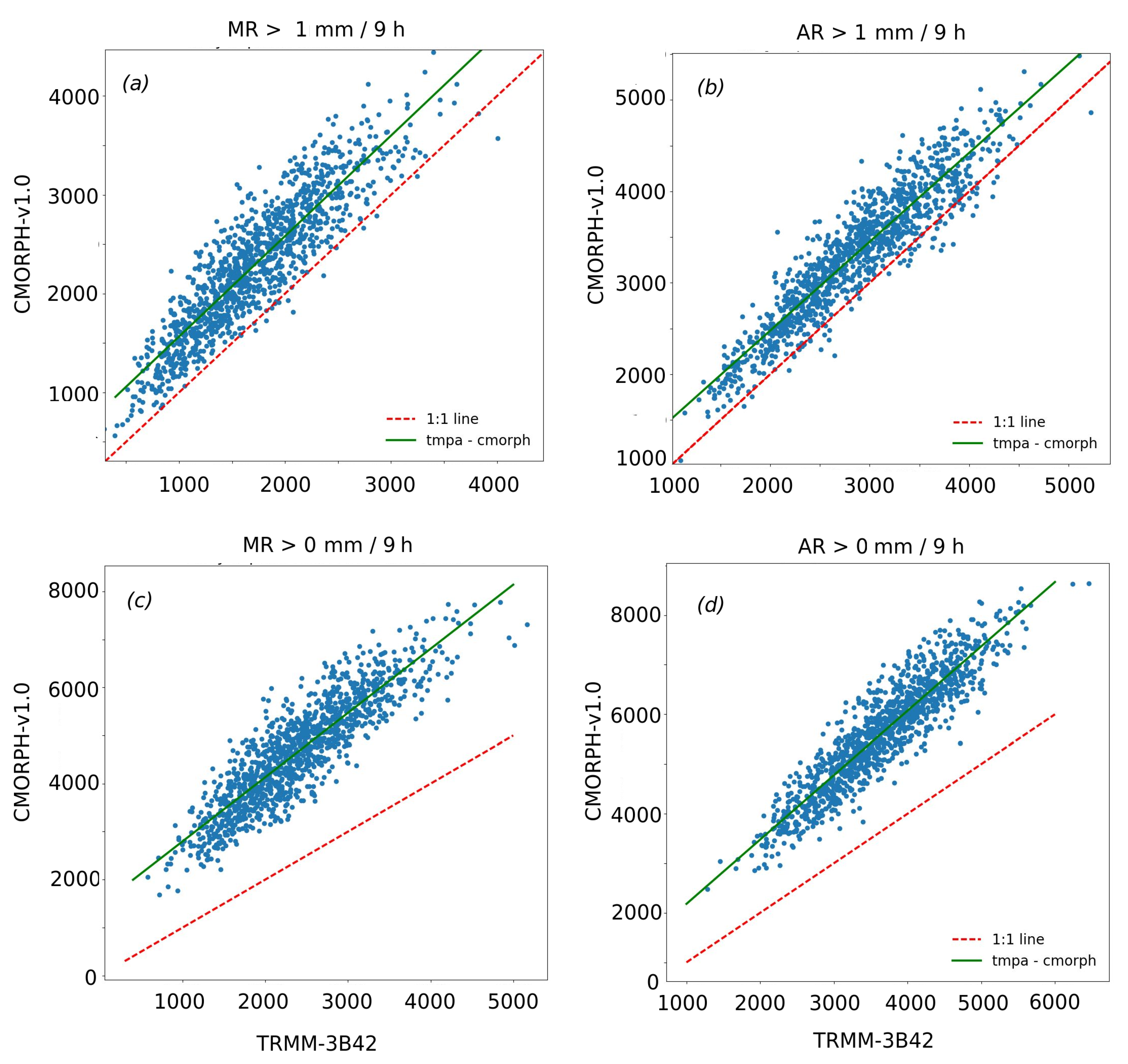
Appendix A. Comparison of Rainfall Event Properties Obtained Using TRMM-3B42 and CMORPH-v0.1 Datasets
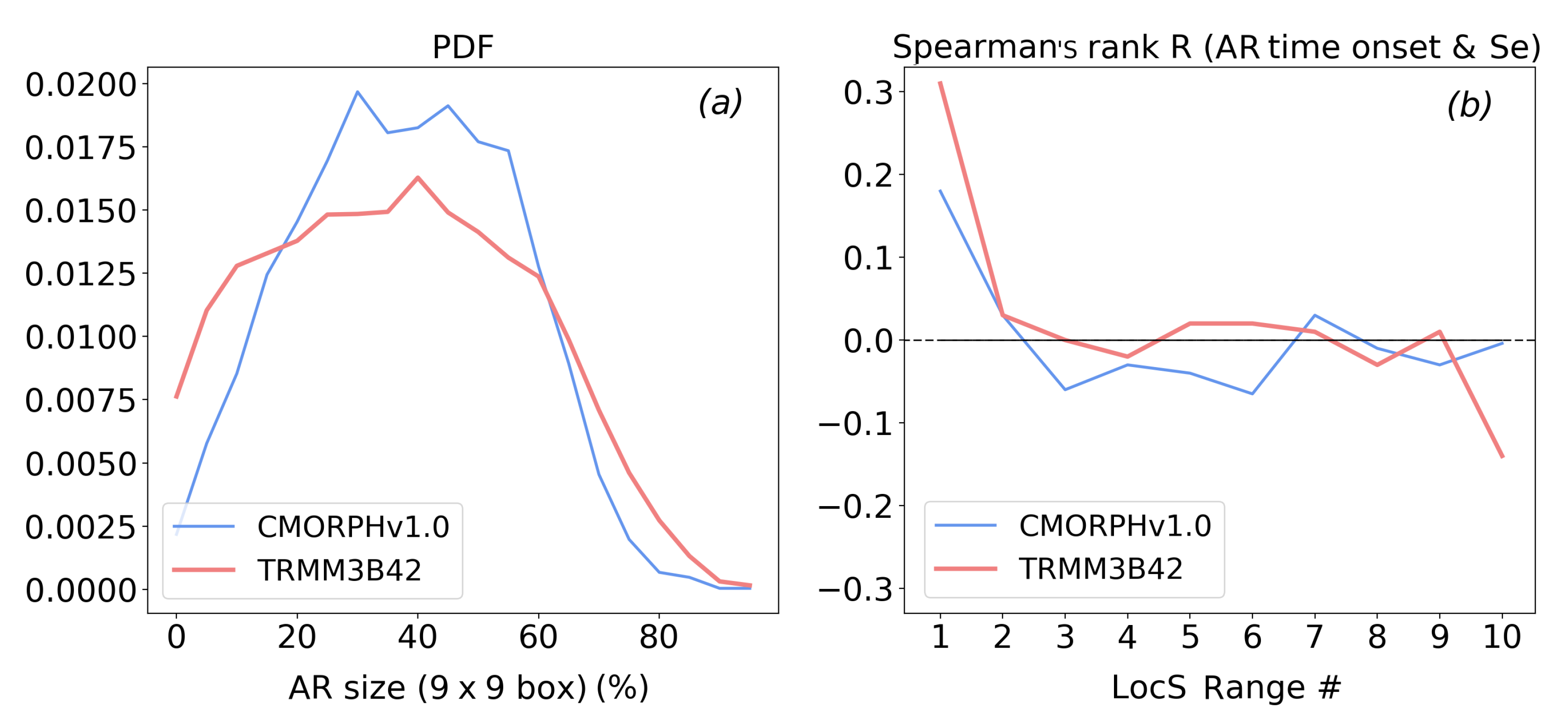
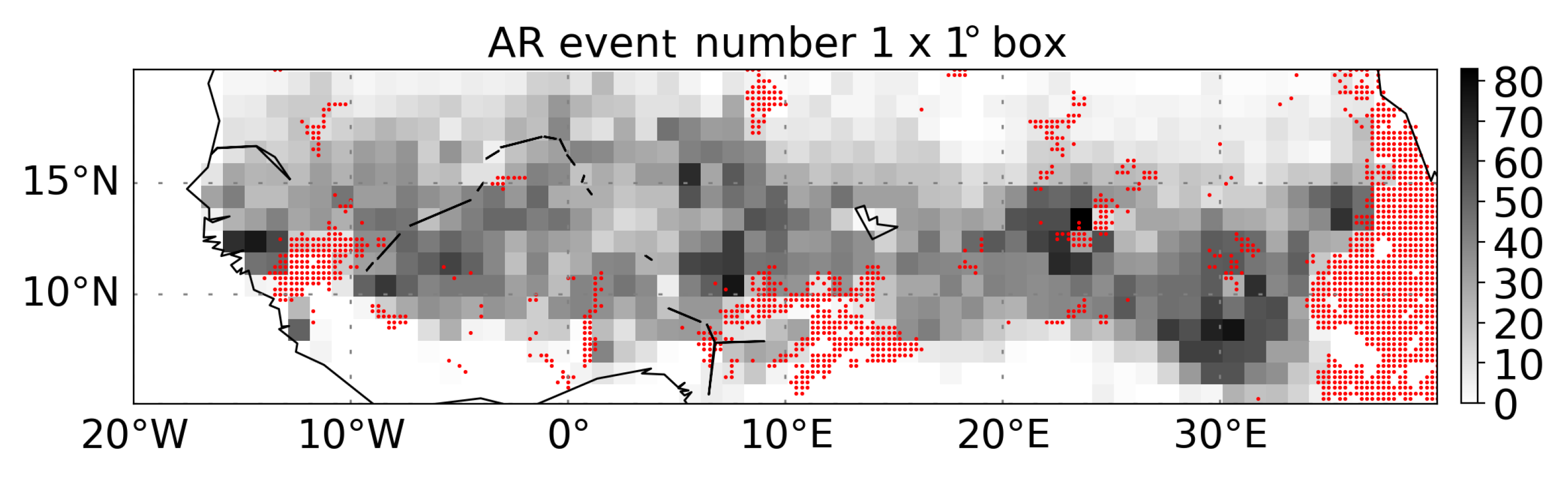
Appendix B. Supplementary Plots
References
- Entekhabi, D.; Rodriguez-Iturbe, I.; Bras, R.L. Variability in large-scale water balance with land surface-atmosphere interaction. J. Clim. 1992, 5, 798–813. [Google Scholar] [CrossRef]
- Savenije, H.H. New definitions for moisture recycling and the relationship with land-use changes in the Sahel. J. Hydrol. 1995, 167, 57–78. [Google Scholar] [CrossRef]
- Taylor, C.M.; Parker, D.J.; Lloyd, C.R.; Thorncroft, C.D. Observations of synoptic-scale land surface variability and its coupling with the atmosphere. Q. J. R. Meteorol. Soc. 2005, 131, 913–937. [Google Scholar] [CrossRef]
- Cook, B.I.; Bonan, G.B.; Levis, S. Soil moisture feedbacks to precipitation in Southern Africa. J. Clim. 2006, 19, 4198–4206. [Google Scholar] [CrossRef]
- Eltahir, E.A.B. A soil moisture rainfall feedback mechanism 1. Theory and observations. Water Resour. Res. 1998, 34, 765–776. [Google Scholar] [CrossRef]
- Pielke, S. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus convective rainfall. Rev. Geophys. 2001, 39, 151–177. [Google Scholar] [CrossRef]
- Kohler, M.; Kalthoff, N.; Kottmeier, C. The impact of soil moisture modifications on CBL characteristics in West Africa: A case-study from the AMMA campaign. Q. J. R. Meteorol. Soc. 2010, 136, 442–455. [Google Scholar] [CrossRef]
- Rowell, D.P.; Blondin, C. The influence of soil wetness distribution on short-range rainfall forecasting in the West African Sahel. Q. J. R. Meteorol. Soc. 1990, 116, 1471–1485. [Google Scholar] [CrossRef]
- Sutton, C.; Hamill, T.M.; Warner, T.T. Will Perturbing Soil Moisture Improve Warm-Season Ensemble Forecasts? A Proof of Concept. Mon. Weather Rev. 2006, 134, 3174–3189. [Google Scholar] [CrossRef]
- Van den Hurk, B.; Doblas-Reyes, F.; Balsamo, G.; Koster, R.D.; Seneviratne, S.I.; Camargo, H. Soil moisture effects on seasonal temperature and precipitation forecast scores in Europe. Clim. Dyn. 2012, 38, 349–362. [Google Scholar] [CrossRef]
- Collow, T.W.; Robock, A.; Wu, W. Influences of soil moisture and vegetation on convective precipitation foerecasts over the United States Great Plains. J. Geophys. Res. Atmos. 2014, 119, 9338–9358. [Google Scholar] [CrossRef]
- Hirschi, M.; Seneviratne, S.I.; Alexandrov, V.; Boberg, F.; Boroneant, C.; Christensen, O.B.; Formayer, H.; Orlowsky, B.; Stepanek, P. Observational evidence for soil-moisture impact on hot extremes in southeastern Europe. Nat. Geosci. 2011, 4, 17–21. [Google Scholar] [CrossRef]
- Thiery, W.; Davin, E.L.; Seneviratne, S.I.; Bedka, K.; Lhermitte, S.; Van Lipzig, N.P. Hazardous thunderstorm intensification over Lake Victoria. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.M.; Harris, P.P.; Parker, D.J. Impact of soil moisture on the development of a sahelian mesoscale convective system: A case-study from the AMMA special observing period. Q. J. R. Meteorol. Soc. 2010, 136, 456–470. [Google Scholar] [CrossRef]
- Birch, C.E.; Parker, D.J.; O’Leary, A.; Marsham, J.H.; Taylor, C.M.; Harris, P.P.; Lister, G.M.S. Impact of soil moisture and convectively generated waves on the initiation of a West African mesoscale convective system. Q. J. R. Meteorol. Soc. 2013, 139, 1712–1730. [Google Scholar] [CrossRef]
- Nicholson, S.E. Evolution and current state of our understanding of the role played in the climate system by land surface processes in semi-arid regions. Glob. Planet. Chang. 2015, 133, 201–222. [Google Scholar] [CrossRef]
- Van Heerwaarden, C.C.; Guerau de Arellano, J.V. Relative Humidity as an Indicator for Cloud Formation over Heterogeneous Land Surfaces. J. Atmos. Sci. 2008, 65, 3263–3277. [Google Scholar] [CrossRef]
- Santanello, J.A.; Peters-Lidard, C.D.; Kumar, S.V.; Alonge, C.; Tao, W.K. A Modeling and Observational Framework for Diagnosing Local Land–Atmosphere Coupling on Diurnal Time Scales. J. Hydrometeorol. 2009, 10, 577–599. [Google Scholar] [CrossRef]
- Santanello, J.A.; Peters-Lidard, C.D.; Kumar, S.V. Diagnosing the Sensitivity of Local Land–Atmosphere Coupling via the Soil Moisture–Boundary Layer Interaction. J. Hydrometeorol. 2011, 12, 766–786. [Google Scholar] [CrossRef]
- Tawfik, A.B.; Dirmeyer, P.A.; Santanello, J.A. The Heated Condensation Framework. Part I: Description and Southern Great Plains Case Study. J. Hydrometeorol. 2015, 16, 1929–1945. [Google Scholar] [CrossRef]
- Tawfik, A.B.; Dirmeyer, P.A.; Santanello, J.A. The Heated Condensation Framework. Part II: Climatological Behavior of Convective Initiation and Land–Atmosphere Coupling over the Conterminous United States. J. Hydrometeorol. 2015, 16, 1946–1961. [Google Scholar] [CrossRef]
- Findell, K.L.; Eltahir, E.A.B. Atmospheric Controls on Soil Moisture–Boundary Layer Interactions. Part I: Framework Development. J. Hydrometeorol. 2003, 4, 552–569. [Google Scholar] [CrossRef]
- Chen, F.; Avissar, R. Impact of Land-Surface Moisture Variability on Local Shallow Convective Cumulus and Precipitation in Large-Scale Models. J. Appl. Meteorol. 1994, 33, 1382–1401. [Google Scholar] [CrossRef]
- Avissar, R.; Schmidt, T. An Evaluation of the Scale at which Ground-Surface Heat Flux Patchiness Affects the Convective Boundary Layer Using Large-Eddy Simulations. J. Atmos. Sci. 1998, 55, 2666–2689. [Google Scholar] [CrossRef]
- Huang, H.Y.; Margulis, S.A. Impact of soil moisture heterogeneity length scale and gradients on daytime coupled land-cloudy boundary layer interactions. Hydrol. Process. 2013, 27, 1988–2003. [Google Scholar] [CrossRef]
- Rochetin, N.; Couvreux, F.; Guichard, F. Morphology of breeze circulations induced by surface flux heterogeneities and their impact on convection initiation. Q. J. R. Meteorol. Soc. 2017, 143, 463–478. [Google Scholar] [CrossRef]
- Taylor, C.M.; Parker, D.J.; Harris, P.P. An observational case study of mesoscale atmospheric circulations induced by soil moisture. Geophys. Res. Lett. 2007, 34, 2–7. [Google Scholar] [CrossRef]
- Taylor, C.M.; Gounou, A.; Guichard, F.; Harris, P.P.; Ellis, R.J.; Couvreux, F.; De Kauwe, M. Frequency of sahelian storm initiation enhanced over mesoscale soil-moisture patterns. Nat. Geosci. 2011, 4, 430–433. [Google Scholar] [CrossRef]
- Dione, C.; Lothon, M.; Badiane, D.; Campistron, B.; Couvreux, F.; Guichard, F.; Sall, S.M. Phenomenology of Sahelian convection observed in Niamey during the early monsoon. Q. J. R. Meteorol. Soc. 2013, 140, 500–516. [Google Scholar] [CrossRef]
- Taylor, C.M. Detecting soil moisture impacts on convective initiation in Europe. Geophys. Res. Lett. 2015, 42, 4631–4638. [Google Scholar] [CrossRef]
- Clark, D.B.; Taylor, C.M.; Thorpe, A.J. Feedback between the Land Surface and Rainfall at Convective Length Scales. J. Hydrometeorol. 2004, 5, 625–639. [Google Scholar] [CrossRef]
- Froidevaux, P.; Schlemmer, L.; Schmidli, J.; Langhans, W.; Schär, C. Influence of the Background Wind on the Local Soil Moisture–Precipitation Feedback. J. Atmos. Sci. 2014, 71, 782–799. [Google Scholar] [CrossRef]
- Ford, T.W.; Rapp, A.D.; Quiring, S.M.; Blake, J. Soil moisture-precipitation coupling: Observations from the Oklahoma Mesonet and underlying physical mechanisms. Hydrol. Earth Syst. Sci. 2015, 19, 3617–3631. [Google Scholar] [CrossRef]
- Ford, T.W.; Rapp, A.D.; Quiring, S.M. Does Afternoon Precipitation Occur Preferentially over Dry or Wet Soils in Oklahoma? J. Hydrometeorol. 2015, 16, 874–888. [Google Scholar] [CrossRef]
- Gantner, L.; Kalthoff, N. Sensitivity of a modelled life cycle of a mesoscale convective system to soil conditions over West Africa. Q. J. R. Meteorol. Soc. 2010, 136, 471–482. [Google Scholar] [CrossRef]
- Taylor, C.M.; Lebel, T. Observational Evidence of Persistent Convective-Scale Rainfall Patterns. Mon. Weather Rev. 1998, 126, 1597–1607. [Google Scholar] [CrossRef]
- Clark, D.B.; Taylor, C.M.; Thorpe, A.J.; Harding, R.J.; Nicholls, M.E. The influence of spatial variability of boundary-layer moisture on tropical continental squall lines. Q. J. R. Meteorol. Soc. 2003, 129, 1101–1121. [Google Scholar] [CrossRef]
- Taylor, C.M.; De Jeu, R.A.M.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Guillod, B.P.; Orlowsky, B.; Miralles, D.G.; Teuling, A.J.; Seneviratne, S.I. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.M.; Ellis, R.J. Satellite detection of soil moisture impacts on convection at the mesoscale. Geophys. Res. Lett. 2006, 33, 11–14. [Google Scholar] [CrossRef]
- Petrova, I.Y.; Heerwaarden, C.C.V.; Hohenegger, C.; Guichard, F. Regional co-variability of spatial and temporal soil moisture—precipitation coupling in North Africa: an observational perspective. Hydrol. Earth Syst. Sci. 2018, 22, 3275–3294. [Google Scholar] [CrossRef]
- Clark, C.A.; Arritt, P.W. Numerical Simulations of the Effect of Soil Moisture and Vegetation Cover on the Development of Deep Convection. J. Appl. Meteorol. 1995, 34, 2029–2045. [Google Scholar] [CrossRef]
- Alonge, C.J.; Mohr, K.I.; Tao, W.K. Numerical Studies of Wet versus Dry Soil Regimes in the West African Sahel. J. Hydrometeorol. 2007, 8, 102–116. [Google Scholar] [CrossRef]
- Cioni, G.; Hohenegger, C. Effect of Soil Moisture on Diurnal Convection and Precipitation in Large-Eddy Simulations. J. Hydrometeorol. 2017, 18, 1885–1903. [Google Scholar] [CrossRef]
- Wetzel, P.J.; Argentini, S.; Boone, A. Role of land surface in controlling daytime cloud amount: Two case studies in the GCIP-SW area. J. Geophys. Res. Atmos. 1996, 101, 7359–7370. [Google Scholar] [CrossRef]
- Cioni, G.; Hohenegger, C. A simplified model of precipitation enhancement over a heterogeneous surface. Hydrol. Earth Syst. Sci. Discuss. 2018, 2, 1–26. [Google Scholar] [CrossRef]
- Dirmeyer, P. The terrestrial segment of soil moisture-climate coupling. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Miralles, D.G.; van den Berg, M.J.; Teuling, A.J.; de Jeu, R.A.M. Soil moisture-temperature coupling: A multiscale observational analysis. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Gallego-Elvira, B.; Taylor, C. Global observational diagnosis of soil moisture control on the land surface energy balance. Geophys. Res. Lett. 2016, 43, 2623–2631. [Google Scholar] [CrossRef]
- Nicholson, S.E. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. ISRN Meteorol. 2013, 2013, 1–32. [Google Scholar] [CrossRef]
- Duvel, J. Convection over tropical Africa and the Atlantic Ocean during northern summer. Part II: Modulation by easterly waves. Mon. Weather Rev. 1990, 118, 1855–1868. [Google Scholar] [CrossRef]
- Mohr, K.; Thorncroft, C. Intense convective systems in West Africa and their relationship to the African easterly jet. Q. J. R. Meteorol. Soc. 2006, 132, 163–176. [Google Scholar] [CrossRef]
- Schwendike, J.; Kalthoff, N.; Kohler, M. The impact of mesoscale convective systems on the surface and boundary-layer structure in West Africa: Case-studies from the AMMA campaign 2006. Q. J. R. Meteorol. Soc. 2010, 136, 566–582. [Google Scholar] [CrossRef]
- Lohou, F.; Kergoat, L.; Guichard, F.; Boone, A.; Cappelaere, B.; Cohard, J.M.; Demarty, J.; Galle, S.; Grippa, M.; Peugeot, C.; et al. Surface response to rain events throughout the West African monsoon. Atmos. Chem. Phys. 2014, 14, 3883–3898. [Google Scholar] [CrossRef]
- Taylor, C.; Ellis, R. Linking boundary-layer variability with convection: A case-study from JET2000. Q. J. R. Meteorol. Soc. 2003, 129, 2233–2253. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–228. [Google Scholar] [CrossRef]
- Gruhier, C.; de Rosnay, P.; Kerr, Y.; Mougin, E.; Ceschia, E.; Calvet, J.C.; Richaume, P. Evaluation of AMSR-E soil moisture product based on ground measurements over temperate and semi-arid regions. Geophys. Res. Lett. 2008, 35, 2–7. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; De Jeu, R.A.; Naeimi, V. Error characterisation of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation; Tech. Rep; Mesoscale Atmospheric Processes Laboratory, NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2014. Available online: https://pmm.nasa.gov/sites/default/files/document_files/3B42_3B43_doc_V7.pdf (accessed on 15 September 2017).
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite–Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Roca, R.; Chambon, P.; Jobard, I.; Kirstetter, P.E.; Gosset, M.; Bergés, J.C. Comparing satellite and surface rainfall products over West Africa at meteorologically relevant scales during the AMMA campaign using error estimates. J. Appl. Meteorol. Climatol. 2010, 49, 715–731. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of several rainfall products used for hydrological applications over West Africa using two high-resolution gauge networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Trentmann, J.; Fink, A.H.; Ahrens, B. Evaluating satellite-based diurnal cycles of precipitation in the African tropics. J. Appl. Meteorol. Climatol. 2016, 55, 23–39. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Lebel, T. Seasonal cycle and interannual variability of the Sahelian rainfall at hydrological scales. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. In NOAA Technical Memorandum NESDIS NGDC-24; NOAA: Silver Spring, ML, USA, 2009; p. 19. [Google Scholar]
- Mathon, V.; Laurent, H. Life cycle of Sahelian mesoscale convective cloud systems. Q. J. R. Meteorol. Soc. 2001, 127, 377–406. [Google Scholar] [CrossRef]
- Pan, Z.T.; Takle, E.; Segal, M.; Turner, R. Influences of model parameterization schemes on the response of rainfall to soil moisture in the central United States. Mon. Weather Rev. 1996, 124, 1786–1802. [Google Scholar] [CrossRef]
- Goyens, C.; Lauwaet, D.; Schröder, M.; Demuzere, M.; Van Lipzig, N.P.M. Tracking mesoscale convective systems in the Sahel: relation between cloud parameters and precipitation. Int. J. Climatol. 2011, 32, 1921–1934. [Google Scholar] [CrossRef]
- Mathon, V.; Laurent, H.; Lebel, T. Mesoscale Convective System Rainfall in the Sahel. J. Appl. Meteorol. 2002, 41, 1081–1092. [Google Scholar] [CrossRef]
- Weckwerth, T.M. The Effect of Small-Scale Moisture Variability on Thunderstorm Initiation. Mon. Weather Rev. 2000, 128, 4017–4030. [Google Scholar] [CrossRef]
- Klüpfel, V.; Kalthoff, N.; Gantner, L.; Taylor, C.M. Convergence zones and their impact on the initiation of a mesoscale convective system in West Africa. Q. J. R. Meteorol. Soc. 2012, 138, 950–963. [Google Scholar] [CrossRef]
- Cuesta, J.; Lavaysse, C.; Flamant, C.; Mimouni, M.; Knippertz, P. Northward bursts of the West African monsoon leading to rainfall over the Hoggar Massif, Algeria. Q. J. R. Meteorol. Soc. 2010, 136, 174–189. [Google Scholar] [CrossRef]
- Barthe, C.; Asencio, N.; Lafore, J.P.; Chong, M.; Campistron, B.; Cazenave, F. Multi-scale analysis of the 25–27 July 2006 convective period over Niamey: Comparison between doppler radar observations and simulations. Q. J. R. Meteorol. Soc. 2010, 136, 190–208. [Google Scholar] [CrossRef]
- Gounou, A.; Guichard, F.; Couvreux, F. Observations of Diurnal Cycles Over a West African Meridional Transect: Pre-Monsoon and Full-Monsoon Seasons. Bound. Lay. Meteorol. 2012, 144, 329–357. [Google Scholar] [CrossRef]
- Wolters, D.; Van Heerwaarden, C.C.; De Arellano, J.V.G.; Cappelaere, B.; Ramier, D. Effects of soil moisture gradients on the path and the intensity of a West African squall line. Q. J. R. Meteorol. Soc. 2010, 136, 2162–2175. [Google Scholar] [CrossRef]
- Adler, B.; Kalthoff, N.; Gantner, L. The impact of soil moisture inhomogeneities on the modification of a mesoscale convective system: An idealised model study. Atmos. Res. 2011, 101, 354–372. [Google Scholar] [CrossRef]
- Findell, K.L.; Gentine, P.; Lintner, B.R.; Kerr, C. Probability of afternoon precipitation in eastern United States and Mexico enhanced by high evaporation. Nat. Geosci. 2011, 4, 434–439. [Google Scholar] [CrossRef]
- Berg, A.; Findell, K.; Lintner, B.R.; Gentine, P.; Kerr, C. Precipitation Sensitivity to Surface Heat Fluxes over North America in Reanalysis and Model Data. J. Hydrometeorol. 2013, 14, 722–743. [Google Scholar] [CrossRef]
- Aires, F.; Gentine, P.; Findell, K.L.; Lintner, B.R.; Kerr, C. Neural network-based sensitivity analysis of summertime convection over the continental united states. J. Clim. 2014, 27, 1958–1979. [Google Scholar] [CrossRef]
- Duerinck, H.M.; van der Ent, R.J.; van de Giesen, N.C.; Schoups, G.; Babovic, V.; Yeh, P.J.F. Observed Soil Moisture–Precipitation Feedback in Illinois: A Systematic Analysis over Different Scales. J. Hydrometeorol. 2016, 17, 1645–1660. [Google Scholar] [CrossRef]
- Klüpfel, V.; Kalthoff, N.; Gantner, L.; Kottmeier, C. Evaluation of soil moisture ensemble runs to estimate precipitation variability in convection-permitting model simulations for West Africa. Atmos. Res. 2011, 101, 178–193. [Google Scholar] [CrossRef]
- Hohenegger, C.; Brockhaus, P.; Bretherton, C.S.; Schär, C. The soil moisture-precipitation feedback in simulations with explicit and parameterized convection. J. Clim. 2009, 22, 5003–5020. [Google Scholar] [CrossRef]
- Taylor, C.M.; Birch, C.E.; Parker, D.J.; Dixon, N.; Guichard, F.; Nikulin, G.; Lister, G.M.S. Modeling soil moisture-precipitation feedback in the Sahel: Importance of spatial scale versus convective parameterization. Geophys. Res. Lett. 2013, 40, 6213–6218. [Google Scholar] [CrossRef]
| Variable | Dataset | Period | Horizontal Resolution | Time Frequency | Dimensions |
|---|---|---|---|---|---|
| Soil moisture | LPRM AMSR-E | 2002–2011 | 0.25 × 0.25 | Twice a day at 1:30 and 13:30 LST | Volumetric SM, vol% |
| Precipitation | TRMM 3B42 v7 | 1998–2015 | 0.25 × 0.25 | 3-hourly | mm/h |
| Precipitation | CMORPHv1.0 | 2002–present | 0.25 × 0.25 | 3-hourly | mm/3 h |
| Temperature, | ERA-Interim | 1979–present | 0.75 × 0.75 | 00 and 12 analyses | K |
| Specific humidity, | time steps; 3-hourly | kg ∗ kg | |||
| Surface pressure, | forecast time steps, 37 | Pa | |||
| Geopotential, | pressure levels | m ∗ s | |||
| Boundary Layer | m | ||||
| Height (BLH) |
| Afternoon Rain (AR) Property | Definition | Min-Max Range |
|---|---|---|
| AR area | Percentage of pixels within the 5 × 5 pixel box with AR >1 mm/9 h | 4–92% |
| AR volume | Afternoon rain accumulations from 15–21 LST in location | 6–190 mm/9 h |
| AR max intensity | Maximum rain rate between 15 and 24 LST in location | 0.8–63 mm/h |
| AR heterogeneity | St. dev. of AR volume in 5 × 5 pixel box | 1–47 mm/9 h |
| AR time of max intensity | Time of AR max intensity in | 15, 18, 21, 24 LST |
| AR time of first rain (onset) | Time of first rain > 0 mm/ h in | 15, 18, 21, 24 LST |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrova, I.Y.; Miralles, D.G.; Van Heerwaarden, C.C.; Wouters, H. Relation between Convective Rainfall Properties and Antecedent Soil Moisture Heterogeneity Conditions in North Africa. Remote Sens. 2018, 10, 969. https://doi.org/10.3390/rs10060969
Petrova IY, Miralles DG, Van Heerwaarden CC, Wouters H. Relation between Convective Rainfall Properties and Antecedent Soil Moisture Heterogeneity Conditions in North Africa. Remote Sensing. 2018; 10(6):969. https://doi.org/10.3390/rs10060969
Chicago/Turabian StylePetrova, Irina Y., Diego G. Miralles, Chiel C. Van Heerwaarden, and Hendrik Wouters. 2018. "Relation between Convective Rainfall Properties and Antecedent Soil Moisture Heterogeneity Conditions in North Africa" Remote Sensing 10, no. 6: 969. https://doi.org/10.3390/rs10060969
APA StylePetrova, I. Y., Miralles, D. G., Van Heerwaarden, C. C., & Wouters, H. (2018). Relation between Convective Rainfall Properties and Antecedent Soil Moisture Heterogeneity Conditions in North Africa. Remote Sensing, 10(6), 969. https://doi.org/10.3390/rs10060969