1. Introduction
Atmospheric water vapor plays an important role in hydrological processes, atmospheric circulation, and weather systems. Precipitable water vapor (PWV) is defined as a vertically integrated water vapor column within a layer, and it is the most active component in the global hydrological cycle, which makes water vapor an important factor affecting regional climate change, water balance and energy balance [
1,
2,
3]. Research on temporal and spatial distributions of atmospheric water vapor and precipitable water vapor not only aid in studies of global and regional climate change, cloud formation and precipitation process, but also provide a theoretical basis for atmospheric water resources.
In recent years, researchers at home and abroad have realized the retrieval and estimation of PWV by ground-based observations or space-based remote sensing methods employing radiosondes, GPS, solar photometers, meteorological station data and lidars. Radiosondes can potentially be used to estimate PWV, and are also used to provide reference data for comparisons with PWV retrieved from Aeronet sun photometers, GPS, and MODIS products [
4,
5]. Ground-based GPS observations have high temporal resolution, long-term stability, and are independent of all weather conditions. The accuracy of estimated PWV obtained from ground-based GPS observations has been investigated in many studies [
6,
7,
8]. Sun photometers are an important tool for atmospheric research and meteorological observations and have advantages in studying the optical and physical properties of aerosol particles. By employing direct radiation analyses of solar forcing, aerosol size distributions, PWV, optical thicknesses and ozone contents can also be obtained and used to calibrate satellite remote sensing results [
9,
10].
With the development of laser technology and Raman spectroscopy, Raman lidars have been successfully used to measure atmospheric temperature, water vapor, and aerosols [
11,
12,
13]. Vibrational Raman scattering signals from water vapor molecules (H
2O) and nitrogen molecules (N
2) have been widely used in the detection of water vapor profiles [
14,
15]. Many ground-based Raman lidar systems currently exist around the world, and significant achievements have been made in the measurement of atmospheric water vapor and aerosol profiles [
16,
17,
18]. At present, atmospheric water vapor mixing ratio profiles can be obtained up to the top of the troposphere by employing Raman lidars; they can also be used to estimate PWV content.
Xi’an city (34.233°N, 108.911°E), which is located in the northwest inland area of China, is characterized by an arid to semi-arid monsoon climate, and is also an important watershed that affects the climate of northern and southern China. It is of value to study the temporal and spatial distributions of water vapor and PWV in Xi’an and to determine the response of the semi-arid area to climate change. Thus, we have focused on the distribution and variations in the characteristics of lidar PWV and a correlation analysis with meteorological parameters to further evaluate the potential of Raman lidar observations for measuring PWV. The Raman lidar system involved was developed at the Xi’an University of Technology in 2013, and the system configuration and retrieval method will be briefly introduced in
Section 2. The lidar PWV from the water vapor mixing ratio profiles is first compared with radiosonde PWV, and the correlation analyses used to verify the ability and accuracy are described. More than 2000 sets of Raman lidar data from 2013 to 2016 were employed in a statistical analysis to obtain the diurnal and monthly mean PWV, and the seasonal variation and proportion of PWV in different layers are investigated in
Section 3. The lidar PWV and meteorological station data are also compared in
Section 4, and the correlations of PWV with vapor pressure, surface temperature and humidity are presented. In
Section 5, a comprehensive analysis of lidar PWV with meteorological parameters during a rainfall process is undertaken, and the vertical change of atmospheric water vapor before and after rainfall is discussed. Further correlation analyses were also conducted to study the prediction of rainfall.
2. Lidar Data and Its Evaluation
2.1. Raman Lidar System
The high temporal resolution PWV data used in this study were obtained using the established ultraviolet Raman lidar system at the Xi’an University of Technology. The Raman lidar system has become a routine tool for simultaneously measuring the atmospheric temperature, water vapor, relative humidity and aerosol profile over Xi’an, China, since 2013 [
12]. A schematic diagram of the Raman lidar system is presented in
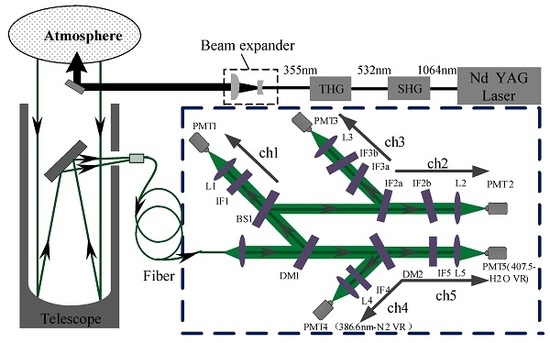
Figure 1. The system employs a pulsed Nd:YAG laser as a light source. The laser operates at a frequency-tripled wavelength of 354.7 nm and has a 20 Hz repetition rate, energy output of 150 mJ, and 9 ns full width at half maximum (FWHM) pulse duration. Returned signals are collected using a 600 mm Newtonian telescope and then coupled into a multimode optical fiber and guided into a spectroscopic box; all signals are detected using photomultiplier tubes (PMTs).
A set of dichroic mirrors (DMs) and narrow-band interference filters (IFs) is used to construct a high-efficiency polychromator, which divides the return signals into five channels. Channel 1 is used for the detection of elastic Mie-Rayleigh signals, and channels 2 and 3 are used for the extraction of two pure rotational Raman signals for retrieving atmospheric temperature profiles. Channels 4 and 5 are used to detect the vibrational Raman signals of nitrogen and water vapor molecules in order to retrieve atmospheric water vapor mixing ratio profiles.
The DMs require an incident angle of 15° and have dichroic characteristics. They transmit the spectra in a certain wavelength range with a peak transmittance of >98%, and almost completely reflect other wavelengths; IFs are used to select the wavelengths of interest and to reduce the background radiation and block the strong elastic signals.
The reflection of DM1 is used to reflect the lidar returns with spectral wavelengths shorter than 365 nm to build the channels of the elastic scattering signal and the rotational Raman signals. A beam splitter (BS) is used to divide this portion of the lidar returns into two parts, of which one part, with 30% of the energy, is used to build the elastic channel, and the other, with 70% of the energy, is used to build the channels of the pure rotational Raman signals. Double-interference filters are utilized, where IF2a and IF2b are at incident angles of 5°, with the central wavelength of 353.9 nm, bandwidths of 0.6 nm, and peak transmissions of 0.5, to extract the low-quantum-number pure rotational Raman signals. IF3a and IF3b are at incident angles of 7°, with the central wavelength of 352.5 nm, bandwidths of 1.1 nm and peak transmissions of 0.5 to extract the high-quantum-number pure rotational Raman signals.
The transmission of DM1 serves to build the channels which detect the vibrational Raman signals. The vibrational Raman signals of nitrogen and water vapor are separated by DM2, which transmits the spectral wavelengths greater than 400 nm. Fine extraction of these two spectra is executed by IF4 and IF5, with the central wavelength of 386.7 nm and 407.5 nm, and bandwidth of 1 nm and 5 nm, respectively. The combination of DMs and IFs achieves fine extraction of the required central-wavelength return signals in channels 1–5 and a sufficient rejection rate of the elastic scattering light in the Raman channels.
2.2. Rereieval Method for Lidar Data
According to its definition, atmospheric water vapor mixing ratio
w(
z) can be retrieved using the ratio of the Raman signals of water vapor and nitrogen molecules, and given as [
14]:
where the subscripts
H and
N denote
H2O and
N2 molecules respectively,
P is the output power of the channel,
σ the Raman scattering cross section,
αλ is the extinction coefficient at wavelength λ, and
k the system efficiency factor, including the optical efficiency and electrical efficiency of the system.
kN/kH is the system constant, which can be calibrated by comparison with radiosonde data at the same height.
The mixing ratio
q (units: g/kg) is a function of water vapor mixing ratio, and given as:
PWV is defined as the vertically integrated water vapor column (units: mm) within a layer and can be calculated as [
6]:
where p
0 and p are the atmospheric pressures (units: Pascals) at the layer’s upper and lower boundaries, respectively,
g is the acceleration due to gravity (9.806 ms
−2), and ρ is vapor density. Consequently, lidar PWV can be obtained from the atmospheric mixing ratio profiles.
2.3. PWV Evaluation by Lidar and Radiosonde
To validate lidar PWV observations, the water vapor profiles obtained using the lidar are first calibrated using radiosonde data from the local Meteorological Bureau of Xi’an. In addition, the obtained lidar PWV are compared with those obtained by radiosonde in this section. Radiosonde PWV estimates can be obtained from the mixing ratio q, which is calculated by [
8]:
q is related to the vapor pressure e, which is a function of dew-piont temperature t
d (°C) [
8]:
and therefore, the profile of geopotential height and dew-piont temperature at pressure levels can be used to assess the radiosonde PWV.
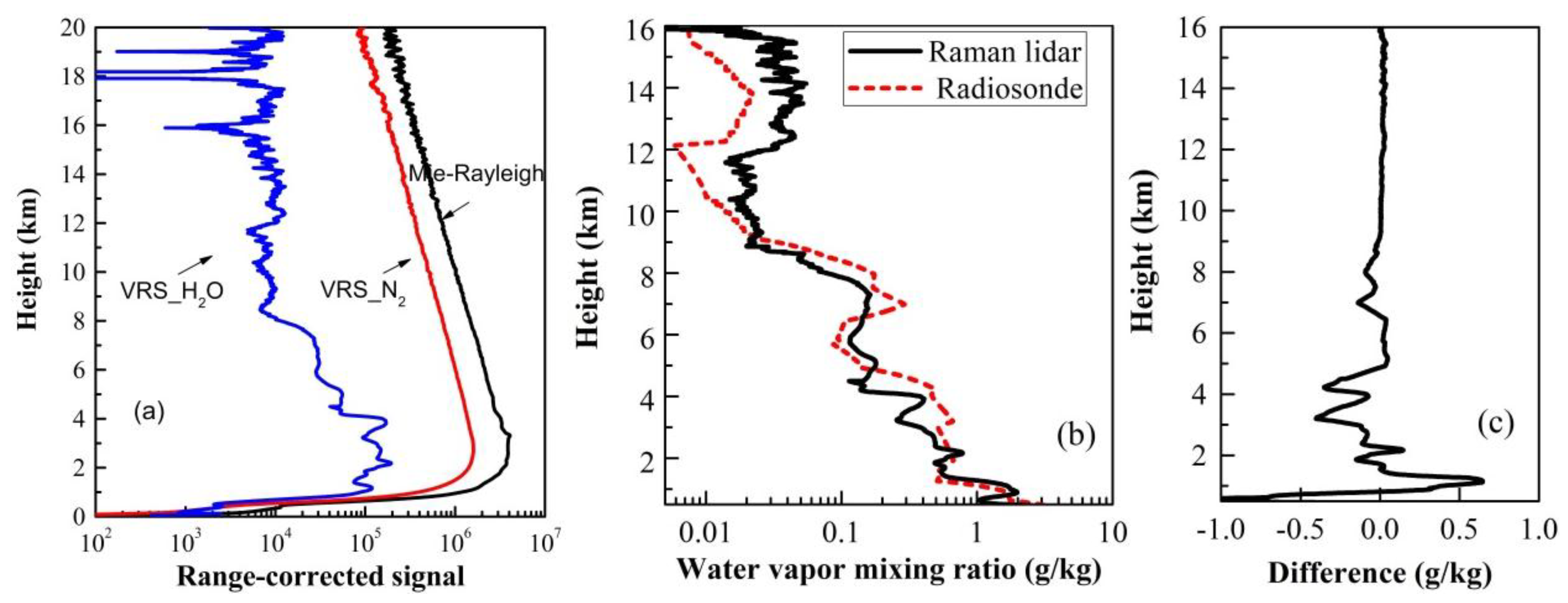
Figure 2 shows a measurement example for atmospheric water vapor performed under clear weather conditions at 20:00 CST (Chinese standard time) on 16 November 2013, and comparisons with radiosonde data are also shown.
Figure 2a shows the range-corrected power signals of lidar returns, including Mie-Rayleigh scattering, nitrogen, and water vapor Raman scattering signals. The pulsed energy was 150 mJ, and the integration time of water vapor measurements was 15 min. All the raw data were collected with an altitude resolution of 3.75 m and were smoothed with a sliding window length of 75–150 m. All the heights in this study are relative to the ground level. By comparing the shapes, Mie-Rayleigh scattering and nitrogen Raman scattering signal are more smooth and attenuated with increasing height, and the water vapor Raman scattering signal are decreased with drastic change. The retrieved water vapor mixing ratio profile is shown in
Figure 2b as a solid line. It should be explained that the complete overlap region of the system starts from approximately 0.5 km, and the lidar return signal was simply discarded in the first few hundred meters. Obvious increases in water vapor density can be found at 6–8 km and 12–16 km, indicating the occurrence of water vapor layers that are not associated with the cloud layer because no enhancement is observed from the range-corrected signals of the elastic Mie-Rayleigh scattering signals. Also, radiosonde data at 20:00 CST obtained from the local Meteorological Bureau of Xi’an (∼8 km from the lidar) are plotted for comparison, as the dashed line. It can be seen that the retrieved water vapor density profiles are in very good agreement with the radiosonde data below the height of 16 km, especially in the regions of water vapor layers. The bias is less than 0.5 g/kg and is close to 0 at high levels, as shown in
Figure 1c.
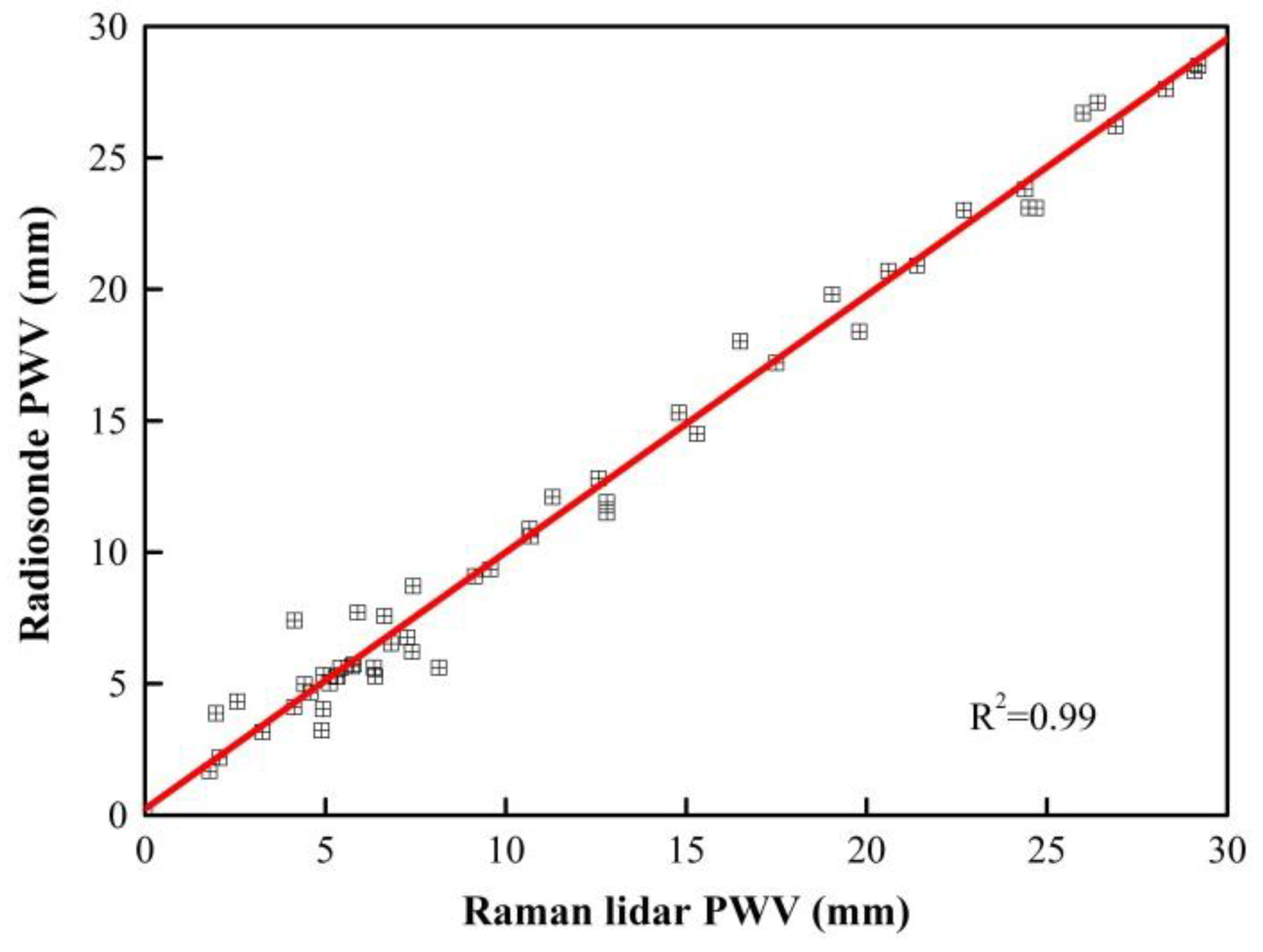
To further evaluate the lidar PWV, 60 sets of water vapor profiles under clear weather condition were compared with those obtained via radiosonde. The altitude interval is mainly within the height range of 0.5–5 km, also including several sets of those within 0.5–10 km. The integration time for water vapor measurement is 15 min; thus, water vapor data by Raman lidar taken from 19:45 to 20:15 CST is involved in the comparisons. The scatter plot in
Figure 3 displays the correlation between the lidar and radiosonde PWV. The abbreviation mm means the unit of millimeter. After undertaking a least squares fit to the points, good agreement was found among the Raman lidar and radiosonde water vapor measurements. The correlation coefficient for the comparison results was approximately 0.99, which suggests that Raman lidar are highly comparable with radiosonde PWV, and could be useful for measuring PWV with high precision.
4. Investigation of PWV and Meteorological Data
The ground meteorological data have important significance for the prediction and assessment of precipitable water vapor, and the amount and variation of precipitable water vapor also influence precipitation to a certain extent. In this section, we focus on the correlations between the lidar PWV and meteorological data from meteorological stations such as surface temperature, water vapor pressure, and relative humidity for PWV and the precipitation parameters.
4.1. Investigation of PWV and Surface Meteorological Data
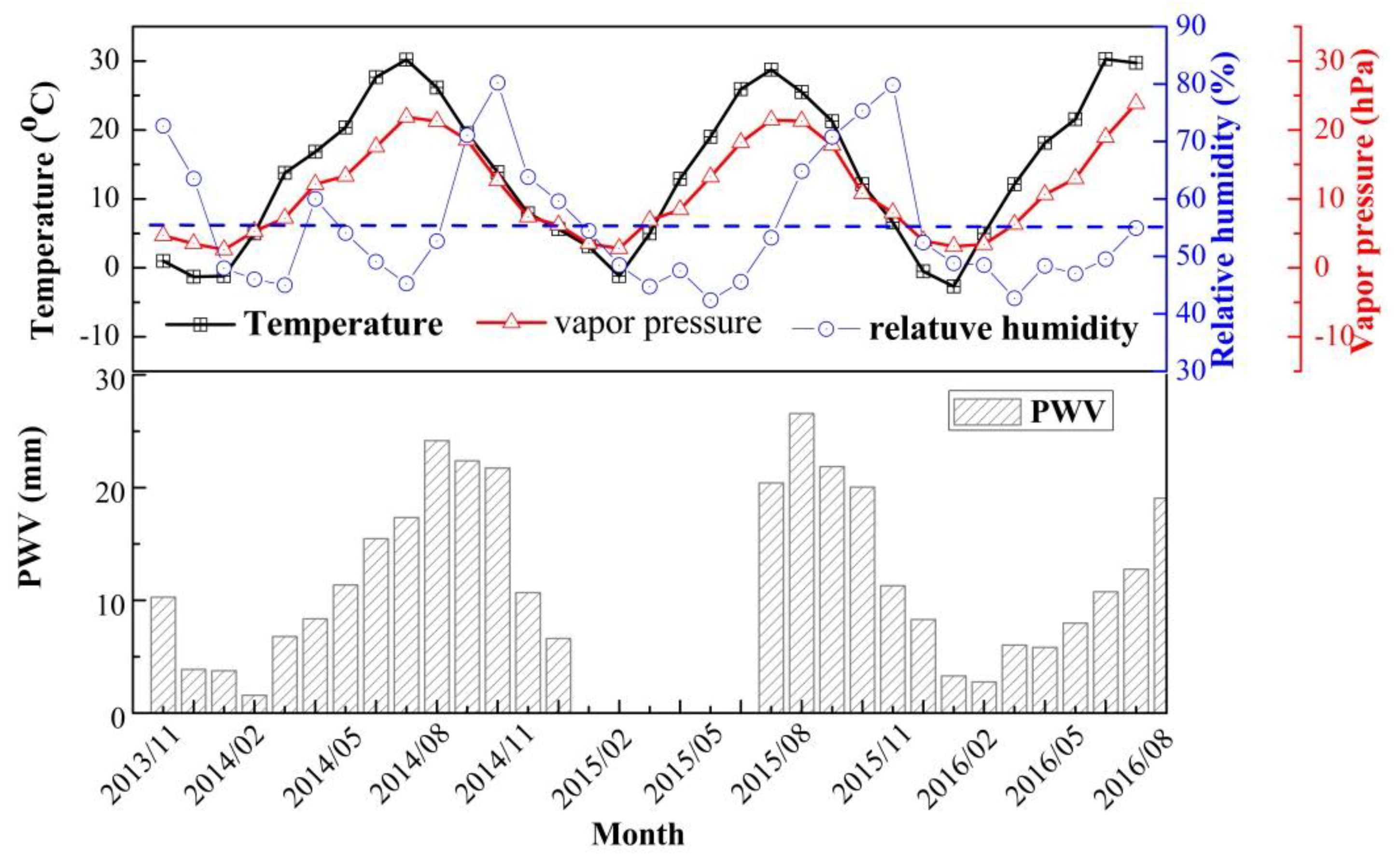
To investigate the correlation between PWV and the surface meteorological data, more than 1000 sets of water vapor profiles from the Raman lidar and the meteorological data from the ground weather stations were simultaneously employed in the statistical analysis. The daily PWV was averaged from the water vapor data at height ranges from the near ground to 700 hPa at 19:30–20:30 using the Raman lidar. The same statistical means were also used for the meteorological data, including those of surface temperature, water vapor pressure and relative humidity.
Figure 8 displays the variations in lidar PWV, surface temperature, water vapor pressure, and relative humidity for 1000 days. The red curves correspond to the lidar PWV (mm), and the blue curves correspond to surface temperature, water vapor pressure, and relative humidity in
Figure 8a–c, respectively.
Figure 8a presents the comparisons of PWV and surface temperature, which show a consistent variation trend between them. The PWV increased due to the increasing temperature, and declined due to decreasing temperature. By comparisons of PWV and water vapor pressure, we can also see from
Figure 8b that the lidar PWV and water vapor pressure were more consistent in their general trends. However, there was no certain trend in relative humidity. It varied greatly ranging from 20% to 90%, and there was no obvious variation trend. Therefore, no consistent variation trend was observed between the PWV and relative humidity, as shown in
Figure 8c. We also further examined the regression analysis between PWV and the above meteorological data, as shown in
Figure 9. A positive linear regression was observed between PWV, surface temperature, and water vapor pressure, with correlation coefficients of 0.894 and 0.866, respectively; they were both significant at the 0.01 level, indicating that there are strong positive correlations between PWV and surface temperature and water vapor pressure. However, the correlation of PWV with the relative humidity is relatively low. The main reasons can be considered as follows: (1) as a function of water vapor and temperature, relative humidity does not depend entirely on water vapor; (2) PWV reflects the effect of vertical water vapor and surface temperature, not just horizontal advection of humidity.
To undertake a better analysis of the seasonal correlations between them, we performed a statistical analysis of lidar PWV and the above ground meteorological parameters. The monthly mean PWV values were obtained from the daily averages, which was also the case for the statistical mean values of the meteorological data.
Figure 10 displays the monthly and seasonal variation trends in PWV and ground meteorological data. The PWV in Xi’an presented an obvious seasonal variation trend; it was higher during summer and lower in winter. The temperature and PWV showed consistent seasonal variation trends; the PWV increased due to the increasing monthly mean temperature in summer and declined due to the decreasing monthly mean temperature in winter. In addition, the monthly mean variation in water vapor pressure was similar to that of PWV, and clearly showed the same inter-seasonal transition change. There was higher water vapor pressure and PWV in spring and summer and lower water vapor pressure and PWV in autumn and winter, and the PWV increased and reached its maximum in summer when the vapor pressure had risen. However, a not completely consistent seasonal trend was observed in relative humidity. The monthly mean humidity varied from 40% to 80% in Xi’an, and the annual averaged humidity was approximately 56%. Higher humidity occurred in the late summer and beginning of autumn of each year, and the humidity reached its minimum value in spring and winter. The accumulation of water vapor in summer might have contributed to the increase in humidity in autumn.
4.2. Investigation of PWV and Precipitation
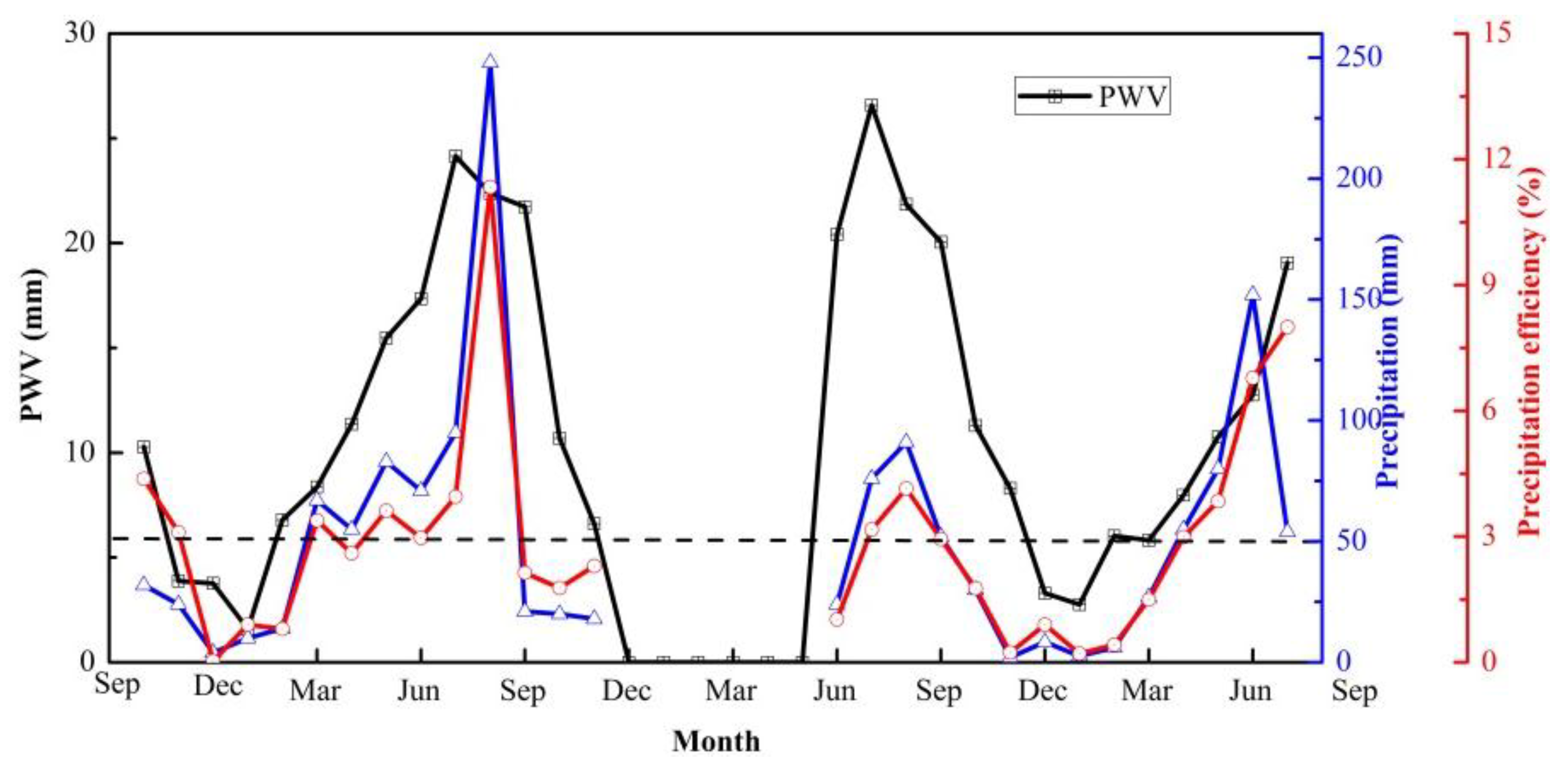
The amount and variation of PWV influence precipitation to a certain extent. The monthly mean values of lidar PWV and the precipitation parameters are considered in this section. The scatter plot and histogram in
Figure 11 display the variations in precipitation and precipitation efficiency over Xi’an, and the lidar PWV are also shown. We can clearly see that they show the same inter-seasonal transition change with PWV. Regarding precipitation, the monthly mean precipitation was larger in summer and autumn and lower in winter and spring; a maximum value of 247 mm occurred in September 2014, and the average annual precipitation was 50 mm in Xi’an. The precipitation efficiency was also found to be high in spring and summer and low in winter and autumn, similar to precipitation. The monthly mean precipitation efficiency was relatively low (less than 5%), except that the maximum efficiency of 12% occurred in September 2014 and July 2016. Therefore, it was found that the precipitation in Xi’an was mainly concentrated in summer and autumn (June–September), accounting for more than half of the total annual precipitation, and the precipitation efficiency was lower than 2% in December to February, indicating extremely small rainfall, which caused the dry climate in winter in Xi’an.
The comparison results also revealed inconsistent phenomena between lidar PWV and precipitation. For example, the monthly PWV reached a maximum value of 23.42 mm in July 2015, but the average precipitation in that month was only 24 mm. This inconsistency exists because the PWV does not directly determine whether precipitation occurs but just represents the potential for atmospheric precipitation. Although there is a certain correlation between precipitation and PWV in the area, total PWV is only one of the necessary conditions for precipitation. In general, large precipitation requires the transportation and supplementation of water vapor and does not merely depend on local precipitable water vapor.
5. Case Study
Horizontal and vertical distributions of humidity and related parameters such as relative humidity, vapor pressure, and PWV are important factors during rainfall. In this section, time series of lidar PWV, vapor pressure, humidity, and dew-point temperature difference (DTD) are compared in detail to investigate the evolution trends and the correlation among them during a rainfall case of 1–10 October 2015 that passed over Xi’an.
Taking advantage of lidar detection, water vapor density profiles are compared and analyzed before and after rainfall.
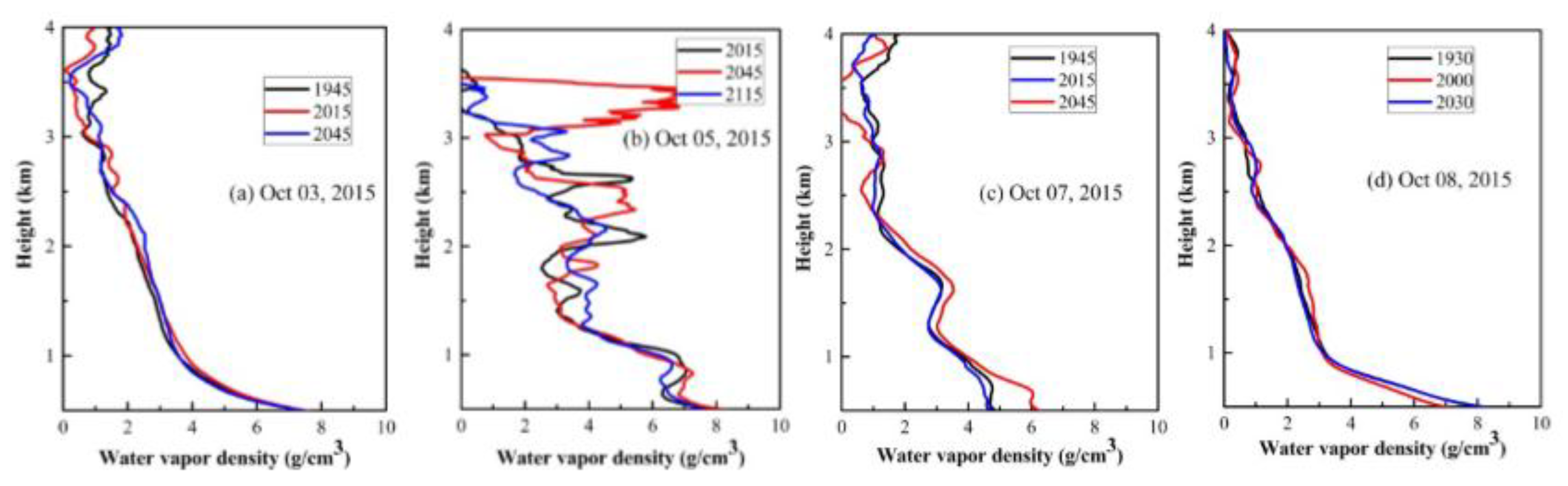
Figure 12 showed the atmospheric water vapor density profiles on 3, 5, 7, and 8 October, of which the front 2 days correspond to those before rainfall, and the latter 2 days correspond to those after rainfall. The atmospheric water vapor profile at 19:30–21:15 CST at nighttime is used to investigate the spatial and temporal distribution of water vapor below 4 km. It can be clearly seen that obvious difference was found in the vertical change in water vapor profiles before and after rainfall.
The left
Figure 12a presents the profiles of 19:45, 20:15, and 20:45 CST on 3 October; water vapor density decreases sharply with height, and there are small fluctuations in the height range of 3–4 km. Different profiles and variation characteristics can be observed on 5 October, as shown in
Figure 12b. Regarding vertical variation, water vapor changes rapidly with height, and there also exist several water vapor layers with fast change in the height range of 1.5–3.5 km at different times. That is to say, vertical change in water vapor is intensified and water vapor layers are also changed rapidly during onsets of rainfall. Furthermore, it is shown that water vapor density below 1 km is obviously enhanced and aggregated, reflecting the accumulation of water vapor and precipitation for the forthcoming rainfall on October 6.
Figure 12c showed the profiles of 19:45, 20:15, and 20:45 CST on 7 October, the first day after rainfall, and the water vapor profiles presented a relatively steady decline trend with water vapor layers, indicating the slowing down change with time. As the weather clears up, water vapor also presents a rapidly decreasing trend of with height.
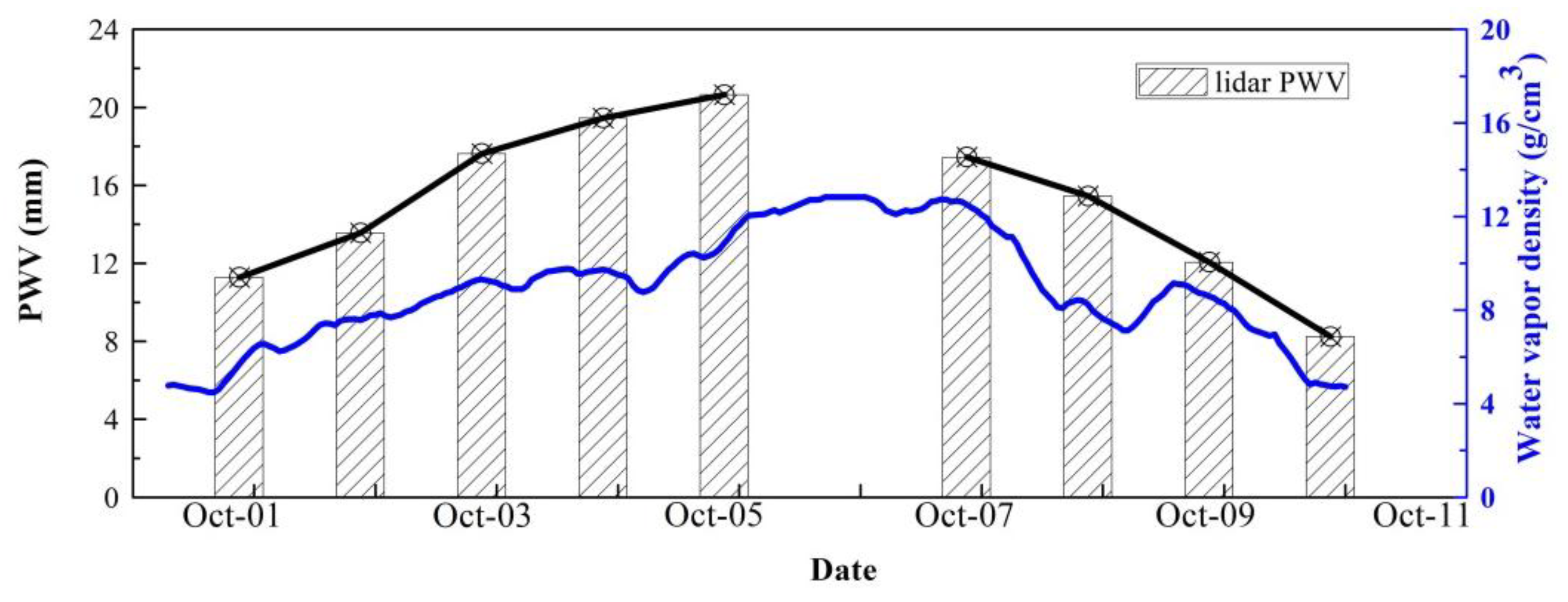
Figure 13 presents the time series of the lidar PWV during the process. Obvious changes can be observed in lidar PWV as the weather changed from clear to rainy and again to clear during the process. The PWV was valued at 10 mm on 1 October under clear weather conditions, and gradually increased to ~20 mm until 5 October under overcast weather. The lidar PWV was absent on 6 October because of moderate rainy weather throughout the day, and the corresponding average precipitation was 8 mm. It reached a value of 17 mm on 7 October after light rain in the daytime and then slowed to less than 10 mm during a change from overcast to clear weather during 8–10 October.
For purposes of comparison, the surface water vapor density was obtained by using temperature and relative humidity from the ground meteorological station, and the results are also shown in
Figure 13. It can be seen that the surface water vapor density also showed a gradual increase trend, and it reached the maximum with a value of about 12 g/cm
3 on 5 October, and then remained stable with a value of 12–14 g/cm
3 during the whole day of 6 October. After the rain, the surface water vapor density gradually decreased during 7 and 8 October, and a slight increase appeared on 9 October, before beginning to drop again to a value of 6 g/cm
3. It is thus clear that lidar PWV has a good consistency with the surface water vapor density during the whole rainfall process. Therefore, lidar PWV underwent a long preparatory period before the rainfall, and decreased gradually after the rainfall.
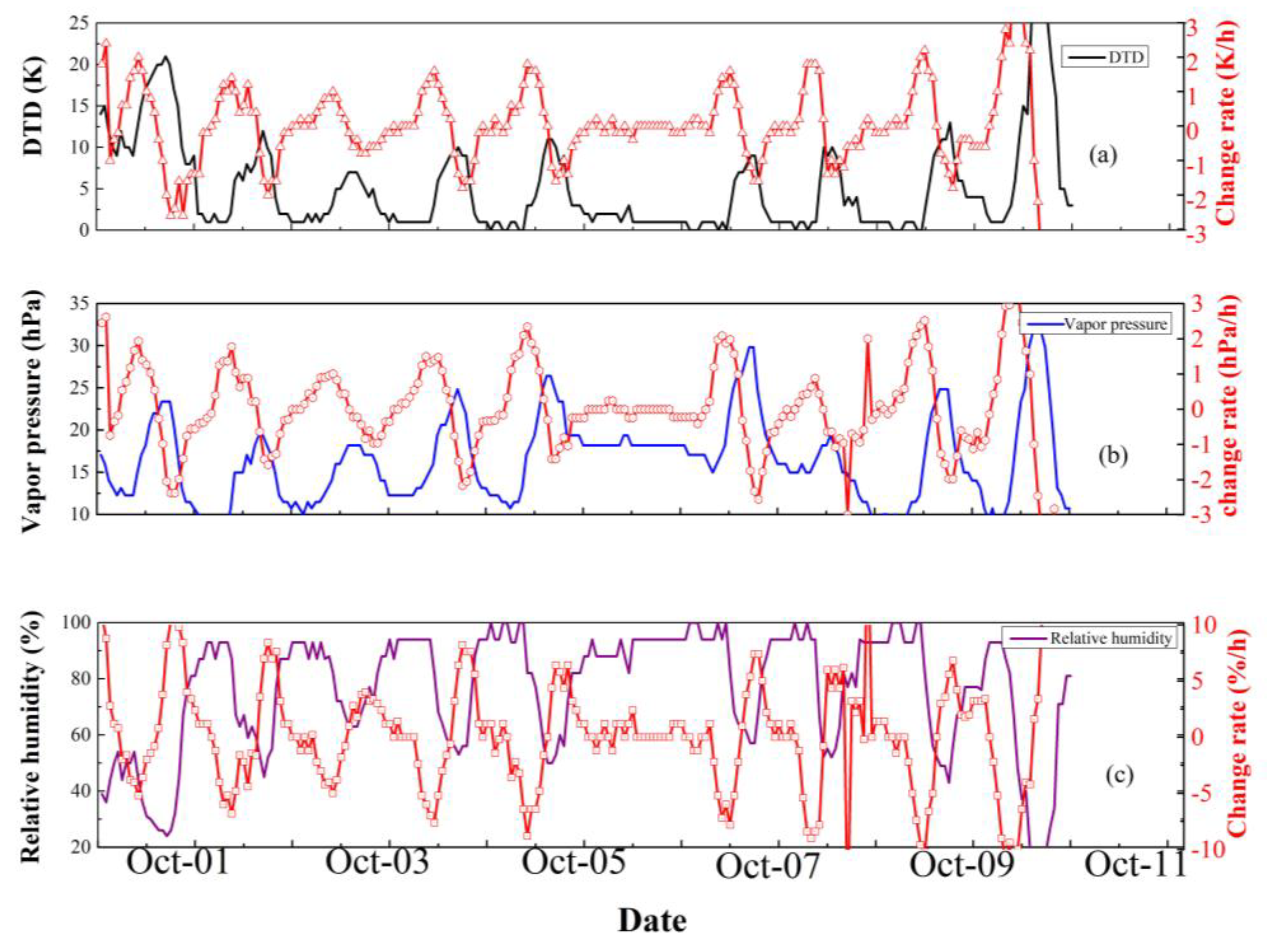
The synchronous time series of metrological parameters, including relative humidity, vapor pressure and DTD, are shown in
Figure 14 a–c, and the corresponding change rates are also given. Before and after rainfall, it is clearly seen that both vapor pressure and DTD showed trends of obvious diurnal changes, with maxima at midday and minima at night. Meanwhile, the opposite diurnal trend was observed in relative humidity, with highs at night and lows at midday. However, obviously different change trends were found in these metrological parameters during the rainfall. They all showed a stable trend and less change. The relative humidity was stable and remained within a range of 80–100%. The vapor pressure and DTD were both steady and less variable. The vapor pressure was approximately 20 hPa, and DTD was less than 2 K. The corresponding change rates can also reflect the variation trend of these metrological parameters. An obvious trend in change rate can be seen for individual parameters before and after rainfall. The change rate is within the range of −3 K to +3 K per hour for DTD, in the scope of −3 hPa to +3 hPa per hour for vapor pressure, and −10 to 10% per hour for relative humidity before and after rainfall. However, these meteorological parameters are accompanied with stable trends with change rate of close to 0 in the rainfall processes. Therefore, higher and stable humidity, lower and stable vapor pressure and dew-point temperature differences were found to accompany the rainfall processes.
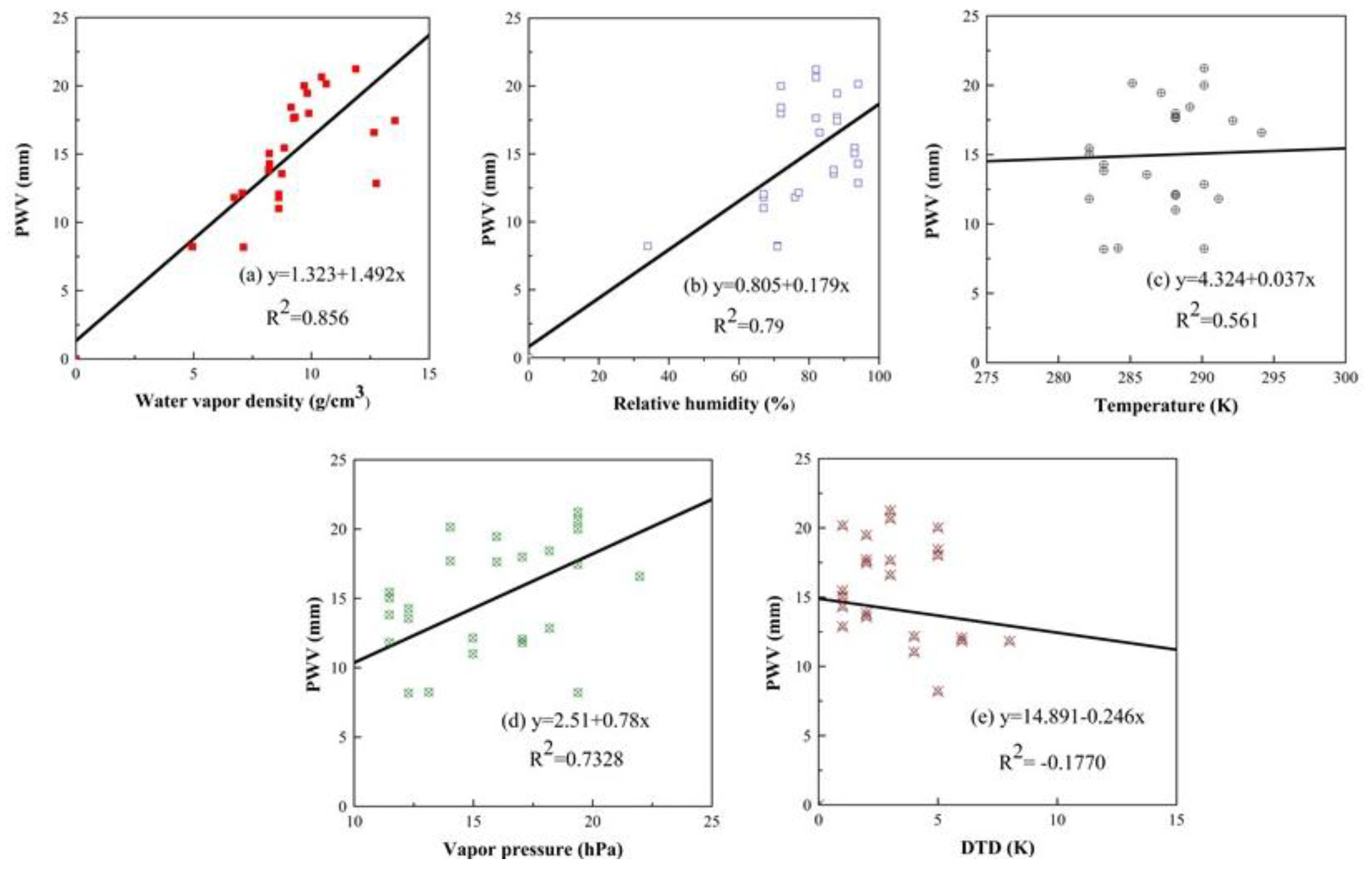
Furthermore, correlation analysis between lidar PWV and the above metrological parameters are also investigated. Positive correlation can be obtained between lidar PWV and the surface water vapor density with a high correlation coefficient of 0.856, as shown in
Figure 15a.
Figure 15b–d presented the positive correlation between lidar PWV with relative humidity, temperature and vapor pressure, with correlation coefficients of 0.79, 0.561 and 0.7382, respectively. It should to be noted that PWV and relative humidity are positively related due to the small range of temperature at different nights. As for DTD, negative correlation can be found between lidar PWV and DTD with a coefficient of −0.1770, which is mainly because of the small range of temperature and DTD on different nights.
Therefore, lidar detection can capture the intensifying vertical change characteristics of water vapor, and thus, make the accumulation of perceptible water vapor in the lower troposphere before rainfall. Synchronized meteorological parameters are accompanied with stable trends, with change rates of close to 0 in the rainfall processes. They also show a high correlation with lidar PWV. Thus, with the advantage of lidar detection, investigation of water vapor profiles and PWV by Raman lidar and the comprehensive correlation analyses with synchronic meteorological parameters can prove to be good indications of rainfall.
6. Summary and Discussion
Retrieved water vapor mixing ratio profiles by Raman lidar were used to calculate the PWV in different layers. The obtained lidar and radiosonde PWV were compared, and it was verified that the Raman lidar can be used to measure PWV with high precision. We discussed the variation and distribution characteristics of PWV in Xi’an and found that different proportions of PWV existed in different layers, and the PWV in each layer presented consistent seasonal variations, being relatively rich in summer, less so in spring and autumn, and relatively deficient in winter.
Furthermore, after studying the monthly mean values of meteorological parameters and lidar PWV data, comparisons of lidar PWV and meteorological parameters were studied in detail, and the correlations between them were also explored. The results show that water vapor pressure and surface temperature showed the same inter-seasonal oscillations as PWV, with a monthly mean correlation coefficient of ~0.90. However, incomplete synchronizations of the seasonal trends in PWV and humidity were revealed such that humidity reached its minimum values in spring and winter, and higher humidity appeared in the late summer and beginning of autumn of each year.
Taking the advantage of lidar detection, atmospheric water vapor density profiles and the obtained PWV by Raman lidar are discussed employing a rainfall case. The intensifying characteristics of vertical change in water vapor and the accumulation of PWV in the lower troposphere can be captured before the onset of rainfall. In addition, time series of lidar PWV and meteorological parameters are also investigated in detail. It can be clearly found that meteorological parameters such as water vapor pressure, relative humidity, and dew-point temperature difference showed obvious diurnal change trends before the onset of rainfall. However, in rainfall processes, stable and higher humidity, and stable and lower variations in water vapor pressure and dew-point temperature difference were instead accompanied with change rates of close to 0. Also, obvious correlations were also found between lidar PWV and these meteorological parameters during the entire process. Therefore, the intensifying characteristics of vertical change in water vapor, the gradual growth in PWV by Raman lidar, and the high correlated variations in synchronized surface meteorological parameters can prove to be good indications of rainfall.