Integration of Single-Frequency GNSS and Strong-Motion Observations for Real-Time Earthquake Monitoring
Abstract
1. Introduction
2. Methodology
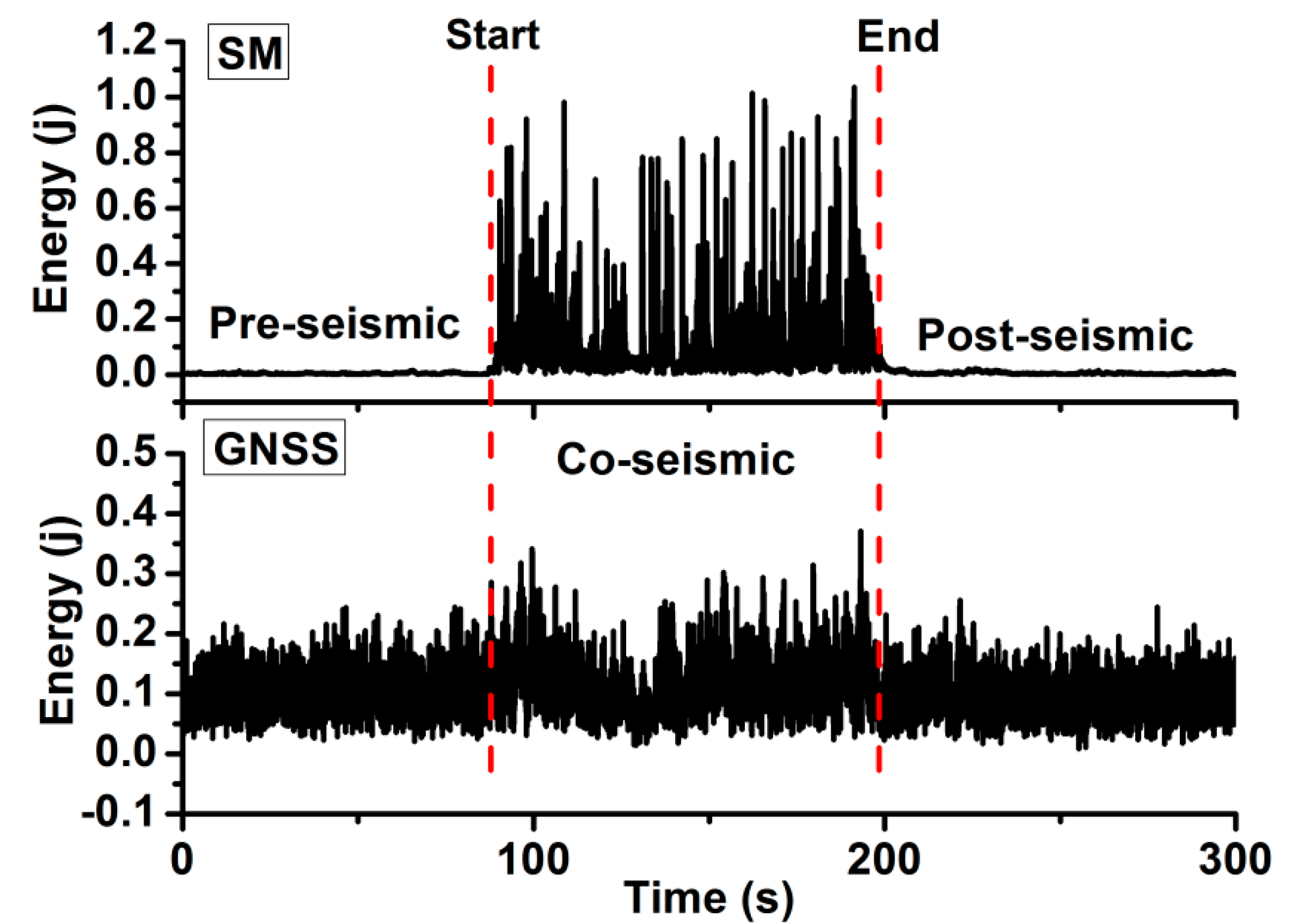
2.1. Determination of the Signal Window
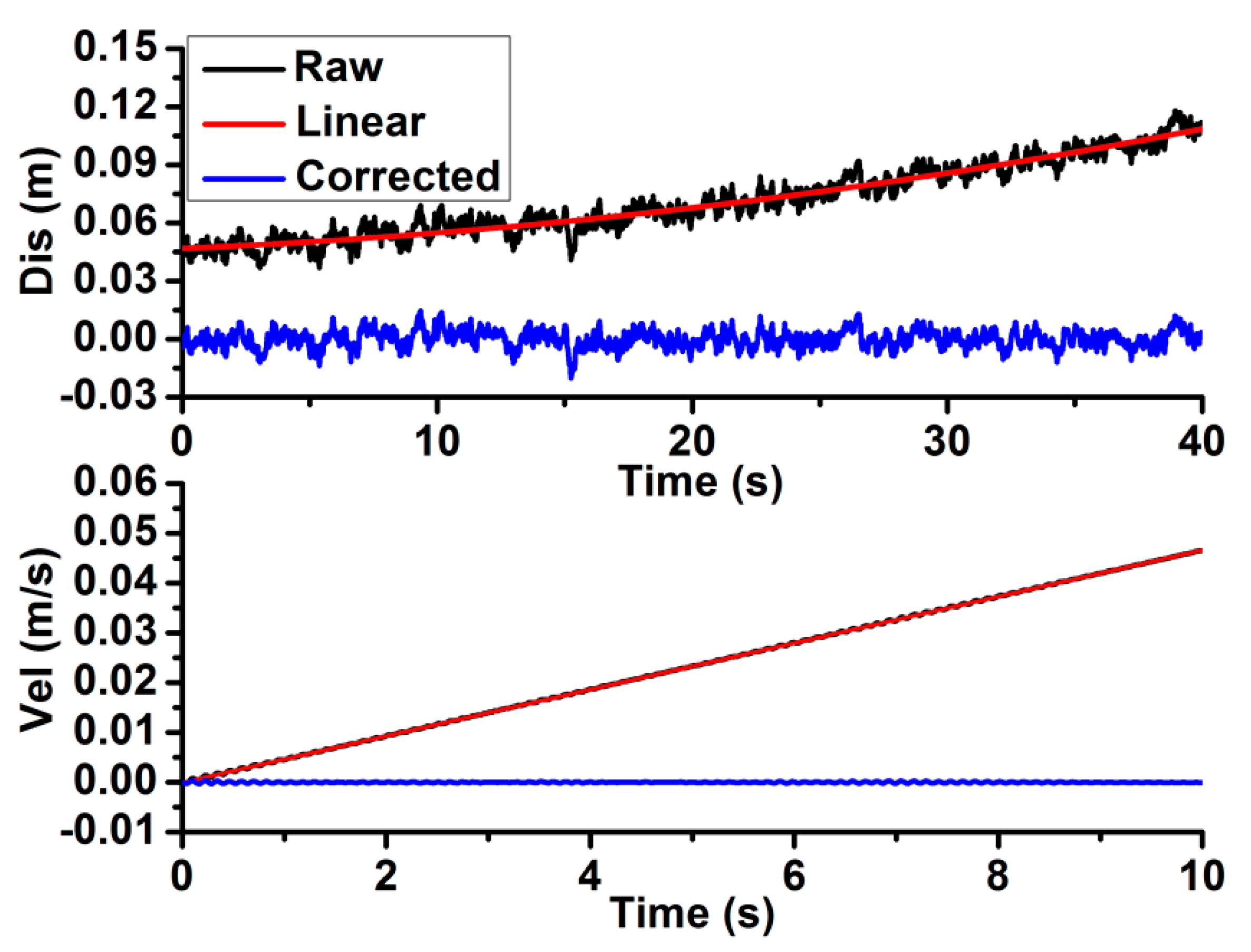
2.2. Initial Baseline Shift Correction of the Integrated System before an Earthquake
2.3. Integration during an Earthquake
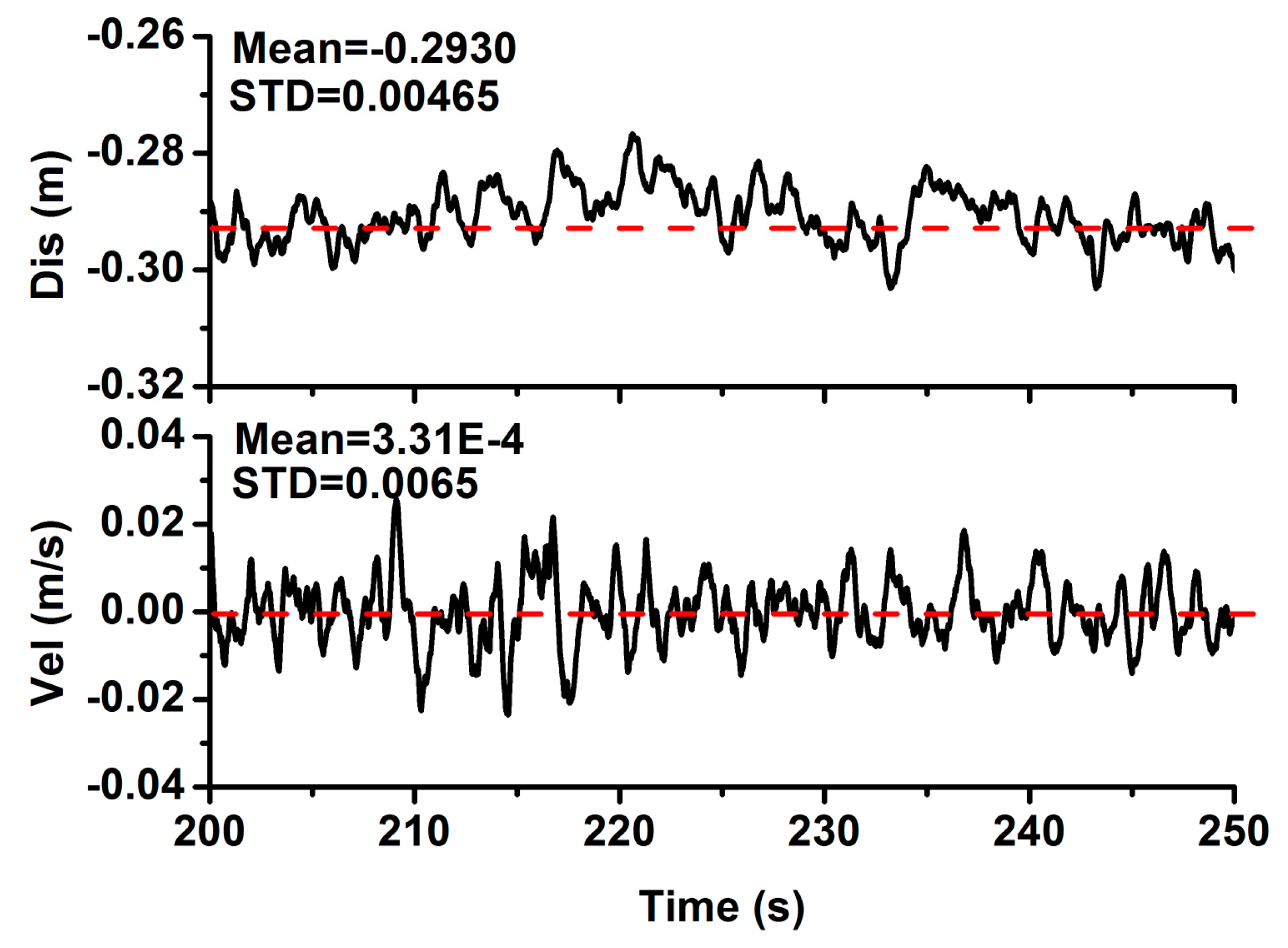
2.4. Quality Assessment of the Integrated System
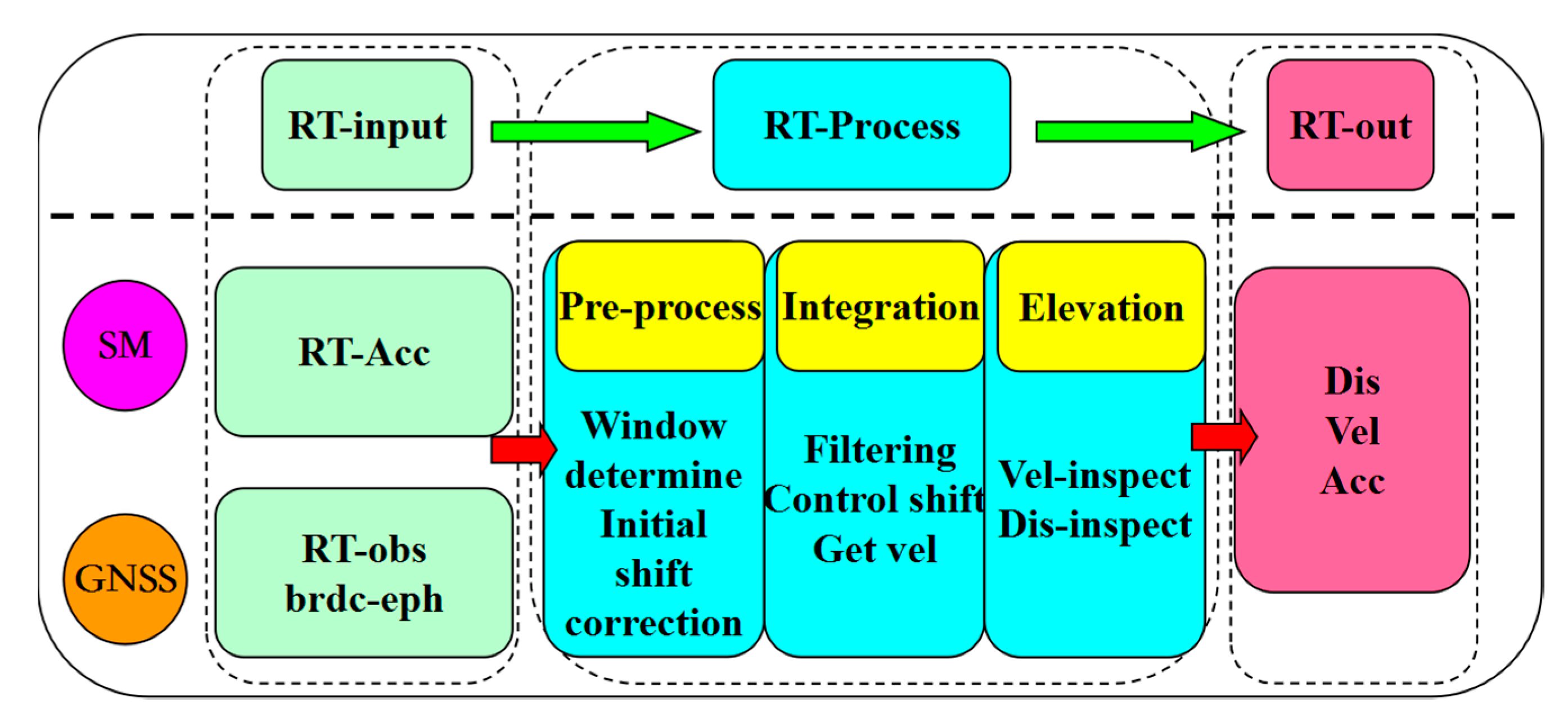
2.5. Implementation of the Real-Time Integrated System
- (1)
- The real-time data stream input module collects SM acceleration data, GNSS observation data, satellite broadcast ephemeris products, and associated parameters.
- (2)
- The real-time data processing module include pre-processing, integration, and quality control. During the pre-process period, after the SM determines the signal start, each subsystem carries out an initial shift correction. Then, the GNSS system provides accurate displacement information and the SM system provides accurate acceleration information. In the integration process period, the GNSS displacement and SM acceleration are the system inputs to the Kalman filter process; the accurate and low-frequency displacement can effectively constrain the SM’s baseline shift and retrieve high-precision velocity information. In the quality control module, the integrated system’s velocity and displacement are inspected; the accuracy and reliability are also verified.
- (3)
- The real-time output module controls the output of the displacement, velocity, acceleration, and accuracy information.
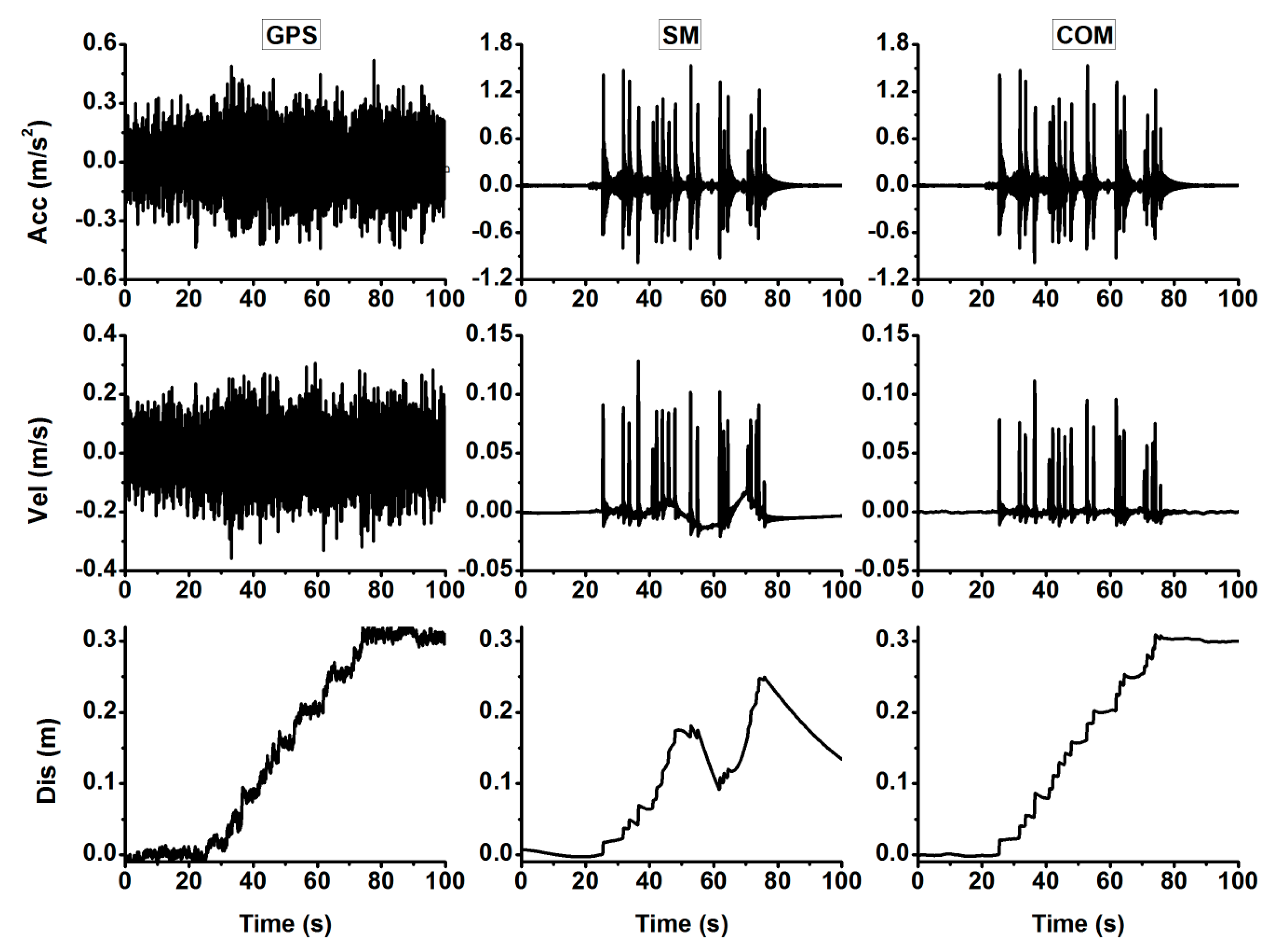
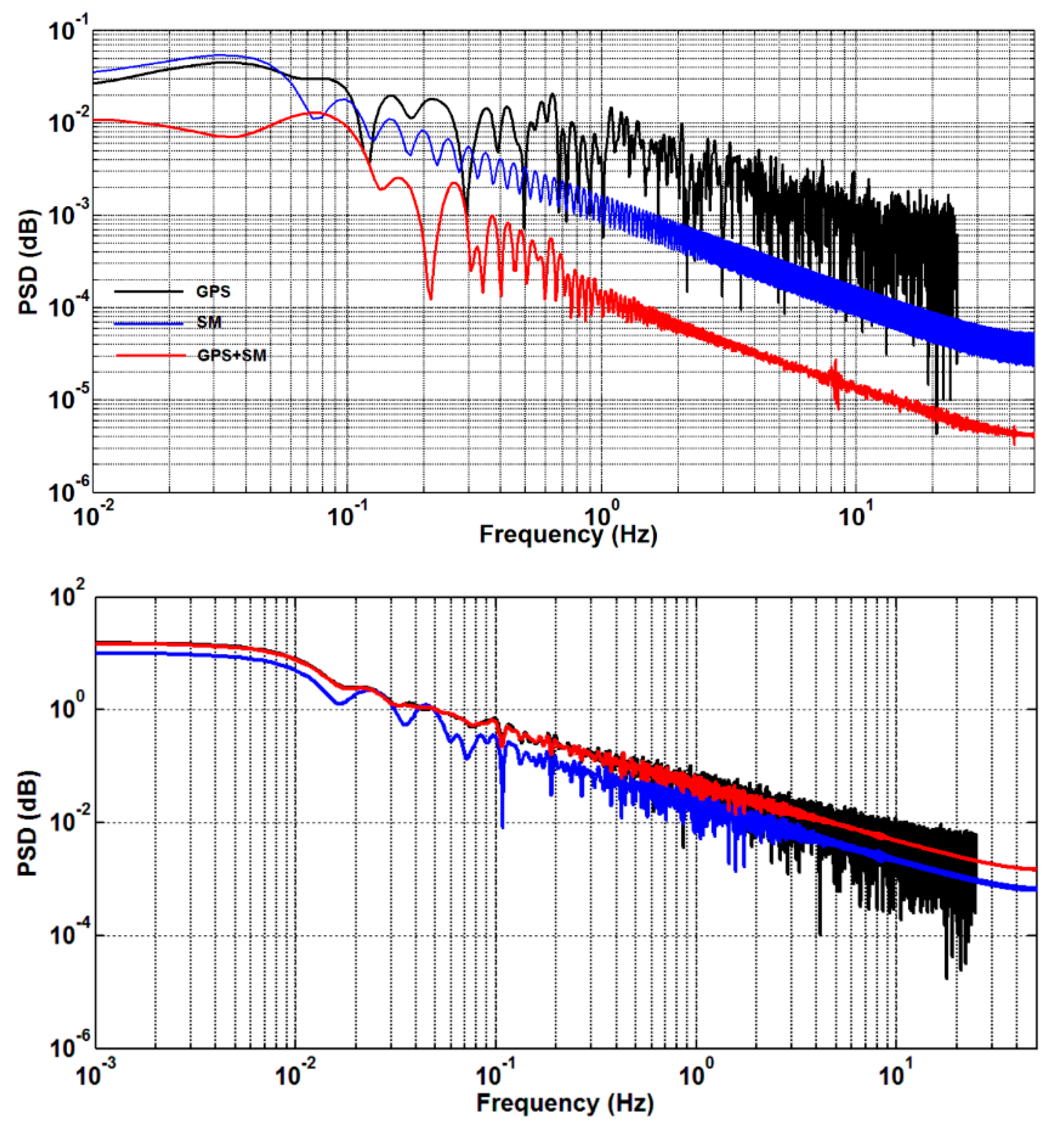
3. Validation Results and Analysis
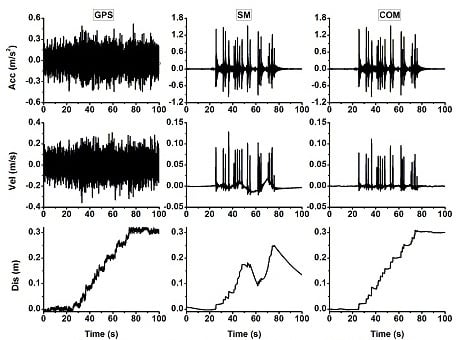
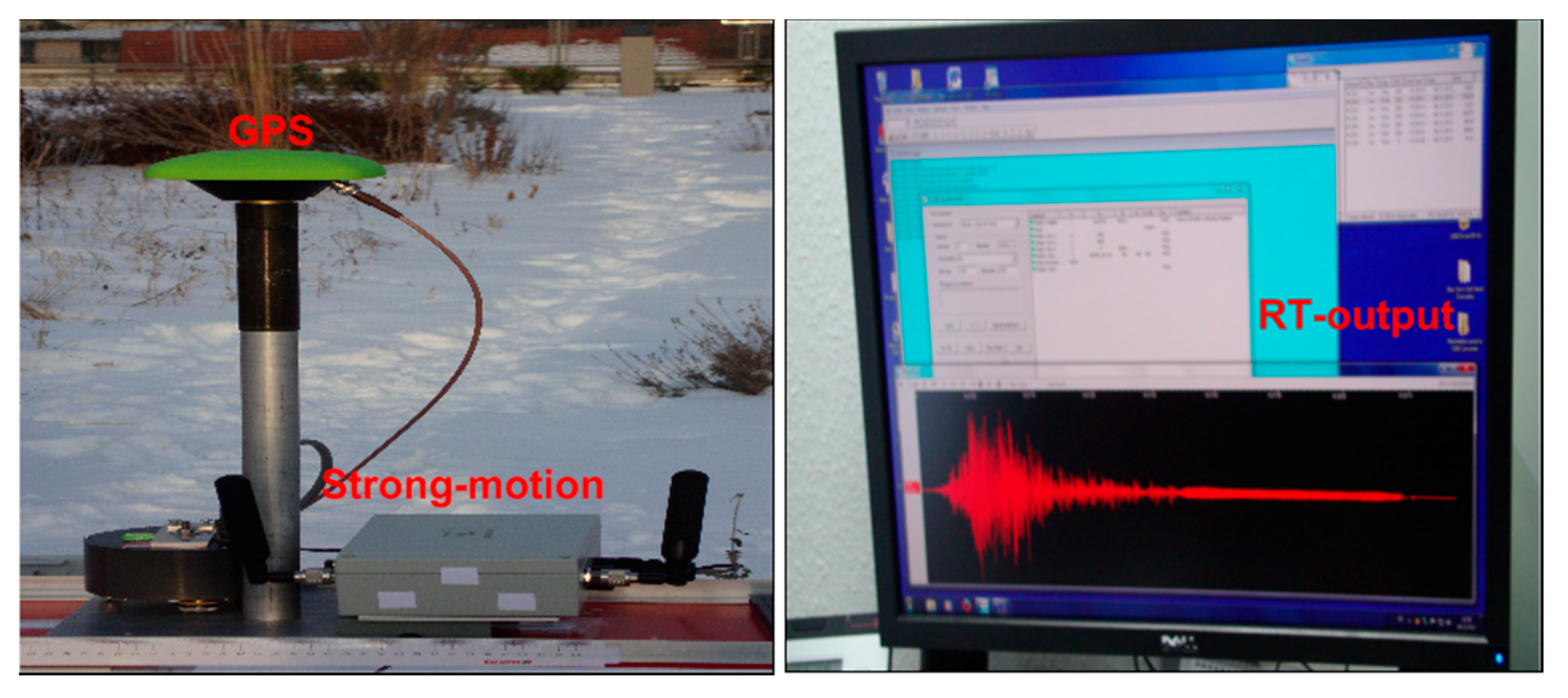
3.1. GPS and SM Data Test
3.2. BDS and SM Data Test
3.3. Baja Earthquake Data Test
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Colosimo, G.; Crespi, M.; Mazzoni, A. Real-time GPS seismology with a stand-alone receiver: A preliminary feasibility demonstration. J. Geophys. Res. 2011, 116, B11302. [Google Scholar] [CrossRef]
- Meng, X. From Structural Health Monitoring to Geo-Hazard Early Warning: An Integrated Approach Using GNSS Positioning Technology. In Earth Observation of Global Changes (EOGC); Springer: Berlin/Heidelberg, Germany, 2013; pp. 285–293. [Google Scholar]
- Bellone, T.; Dabove, P.; Manzino, A.M.; Taglioretti, C. Real-time monitoring for fast deformations using GNSS low-cost receivers. Geomat. Nat. Hazards Risk 2016, 7, 458–470. [Google Scholar] [CrossRef]
- Dabove, P.; Manzino, A. Kalman Filter as Tool for the Real-time Detection of Fast Displacements by the Use of Low-cost GPS Receivers. In Proceedings of the 2nd International Conference on Geographical Information Systems Theory, Applications and Management, Rome, Italy, 26–27 April 2016; pp. 15–23, ISBN 978-989-758-188-5. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Fang, R.; Shi, C.; Zhao, Q. Real-time high-precision earthquake monitoring using single-frequency GPS receivers. GPS Solut. 2015, 19, 27–35. [Google Scholar] [CrossRef]
- Elo’segui, P.; Davis, J.L.; Oberlander, D.; Baena, R.; Ekström, G. Accuracy of high-rate GPS for seismology. Geophys. Res. Lett. 2006, 33, L11308. [Google Scholar] [CrossRef]
- Genrich, J.F.; Bock, Y. Instantaneous geodetic positioning with 10–50 Hz GPS measurements: Noise characteristics and implications for monitoring networks. J. Geophys. Res. 2006, 111, B03403. [Google Scholar] [CrossRef]
- Larson, K.M.; Bilich, A.; Axelrad, P. Improving the precision of high-rate GPS. J. Geophys. Res. 2007, 112, B05422. [Google Scholar] [CrossRef]
- Iwan, W.; Moser, M.; Peng, C. Some observations on strong-motion earthquake measurement using a digital acceleration. Bull. Seismol. Soc. Am. 1985, 75, 1225–1246. [Google Scholar]
- Boore, D.M. Effect of baseline corrections on displacement and response spectra for several recordings of the 1999 Chi-Chi, Taiwan, earthquake. Bull. Seismol. Soc. Am. 2001, 91, 1199–1211. [Google Scholar] [CrossRef]
- Zhu, L. Recovering permanent displacements from seismic records of the June 9, 1994 Bolivia deep earthquake. Geophys. Res. Lett. 2003, 30, 1740. [Google Scholar] [CrossRef]
- Graizer, V. Tilts in strong ground motion. Bull. Seismol. Soc. Am. 2006, 96, 2090–2106. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, C. Approximate recovery of coseismic deformation from Taiwan strong-motion records. J. Seismol. 2007, 11, 159–170. [Google Scholar] [CrossRef]
- Wang, R.; Schurr, B.; Milkereit, C.; Shao, Z.; Jin, M. An improved automatic scheme for empirical baseline correction of digital strong-motion records. Bull. Seismol. Soc. Am. 2011, 101, 2029–2044. [Google Scholar] [CrossRef]
- Bock, Y.; Melgar, D.; Crowell, B.W. Real-time strong-motion broadband displacements from collocated GPS and accelerometers. Bull. Seismol. Soc. Am. 2011, 101, 2904–2925. [Google Scholar] [CrossRef]
- Tu, R.; Wang, R.; Ge, M.; Walter, T.R.; Ramatschi, M.; Milkereit, C.; Bindi, D.; Dahm, T. Cost effective monitoring of ground motion related to earthquakes, landslides or volcanic activities by joint use of a single-frequency GPS and a MEMS accelerometer. Geophys. Res. Lett. 2013, 40, 3825–3829. [Google Scholar] [CrossRef]
- Tu, R.; Ge, M.; Wang, R.; Walter, T.R. A new algorithm for tight integration of real-time GPS and strong-motion records, demonstrated on simulated, experimental, and real seismic data. J. Seismol. 2014, 18, 151–161. [Google Scholar] [CrossRef]
- Tu, R.; Wang, R.; Walter, T.R.; Diao, F.Q. Adaptive recognition and correction of baseline shifts from collocated GPS and accelerometer using two phases Kalman filter. Adv. Space Res. 2014, 54, 1924–1932. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, Q.; Wang, L.; Liu, Z.K.; Huang, G.W. An improved method for tight integration of GPS and strong-motion records: Complementary advantages. Adv. Space Res. 2015, 56, 2335–2344. [Google Scholar] [CrossRef]
- Tu, R.; Liu, J.H.; Lu, C.X.; Zhang, R.; Zhang, P.F.; Lu, X.C. Cooperating the BDS, GPS, GLONASS and strong-motion observations for real-time deformation monitoring. Geophys. J. Int. 2017, 209, 1408–1417. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y.; Melgar, D.; Crowell, B.W.; Haase, S. A new seismogeodetic approach applied to GPS and accelerometer observations of the 2012 Brawley seismic swarm: Implications for earthquake early warning. Geochem. Geophys. Geosyst. 2013, 14, 2124–2142. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, Y.; Wang, R.; Klotz, J.; Wicket, J. High-rate coseismic displacements from tightly-integrated processing of raw GPS and accelerometer data. Geophys. J. Int. 2013, 195, 612–624. [Google Scholar] [CrossRef]
- Wang, R.; Parolai, S.; Ge, M.; Jin, M.; Walter, T.R.; Zschau, J. The 2011 Mw 9.0 Tohoku-Oki earthquake: Comparison of GPS and Strong-motion. Bull. Seismol. Soc. Am. 2012. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y.; Melgar, D.; Crowell, B.; Haase, J. A new seismogeodetic approach applied to GPS and accelerometer observations of the 2012 Brawley seismic swarm: Implications for earthquake early warning. Geochem. Geophys. Geosyst. 2013, 14, 2124–2142. [Google Scholar] [CrossRef]
- Geng, J.; Melgar, D.; Bock, Y.; Pantoli, E.; Restrepo, J. Recovering coseismic point ground tilts from collocated high-rate GPS and accelerometers. Geophys. Res. Lett. 2013, 40, 5095–5100. [Google Scholar] [CrossRef]
- Saunders, J.; Goldberg, E.; Haase, J.; Bock, Y.; Offield, D.; Melgar, D.; Restrepo, J.; Fleischman, R.; Nema, A.; Geng, J.; et al. Seismogeodesy Using GPS and Low-Cost MEMS Accelerometers:Perspectives for Earthquake Early Warning and Rapid Response. Bull. Seismol. Soc. Am. 2016, 106, 2469–2489. [Google Scholar] [CrossRef]
- Fleming, K.; Picozzi, M.; Milkereit, C.; Kuehnlenz, F.; Lichtblau, B.; Fischer, J.; Zulfikar, C.; Ozel, O. The SAFER and EDIM Working Groups. The Self-Organising Seismic Early Warning Information System (SOSEWIN). Seismol. Res. Lett. 2009, 80, 755–771. [Google Scholar] [CrossRef]
- Msaewe, H.; Hancock, C.; Psimoulis, P.; Roberts, G.; Bonenberg, L. Monitoring Dynamic Deflections at Towers of Severn Suspension Bridge in the UK Using GNSS Technique. In Proceedings of the ISGNSS, Hong Kong, China, 10–13 December 2017. [Google Scholar]
- Roberts, G.; Tang, X.; He, X. Accuracy analysis of GPS/BDS relative positioning using zero-baseline measurements. J. Glob. Position. Syst. 2018, 16, 7. [Google Scholar] [CrossRef]
- Psimoulis, P.; Pytharouli, S.; Karambalis, D.; Stiros, S. Potential of GPS to measure frequencies of oscillation of engineering structures. J. Sound Vib. 2008, 318, 606–623. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic Deflections of a Stiff Footbridge Using 100-Hz GNSS and Accelerometer Data. J. Surv. Eng. 2015, 141, 04015003. [Google Scholar] [CrossRef]
- Häberling, S.; Rothacher, M.; Zhang, Y.; Clinton, J.; Geiger, A. Assessment of high-rate GPS using a single-axis shake table. J. Geod. 2015, 89, 697–709. [Google Scholar] [CrossRef]
- Michel, C.; Kelevitz, K.; Houlié, N.; Edwards, B.; Psimoulis, P.; Su, Z.; Clinton, J.; Giardini, D. The Potential of High-Rate GPS for Strong Ground Motion Assessment. Bull. Seismol. Soc. Am. 2017, 107, 1849–1859. [Google Scholar] [CrossRef]
- Psimoulis, P.; Houlié, N.; Meindl, M.; Rothacher, M. Consistency of GPS and strong-motion records: Case study of Mw9.0 Tohoku-Oki 2011 earthquake. Smart Struct. Syst. 2015. [Google Scholar] [CrossRef]

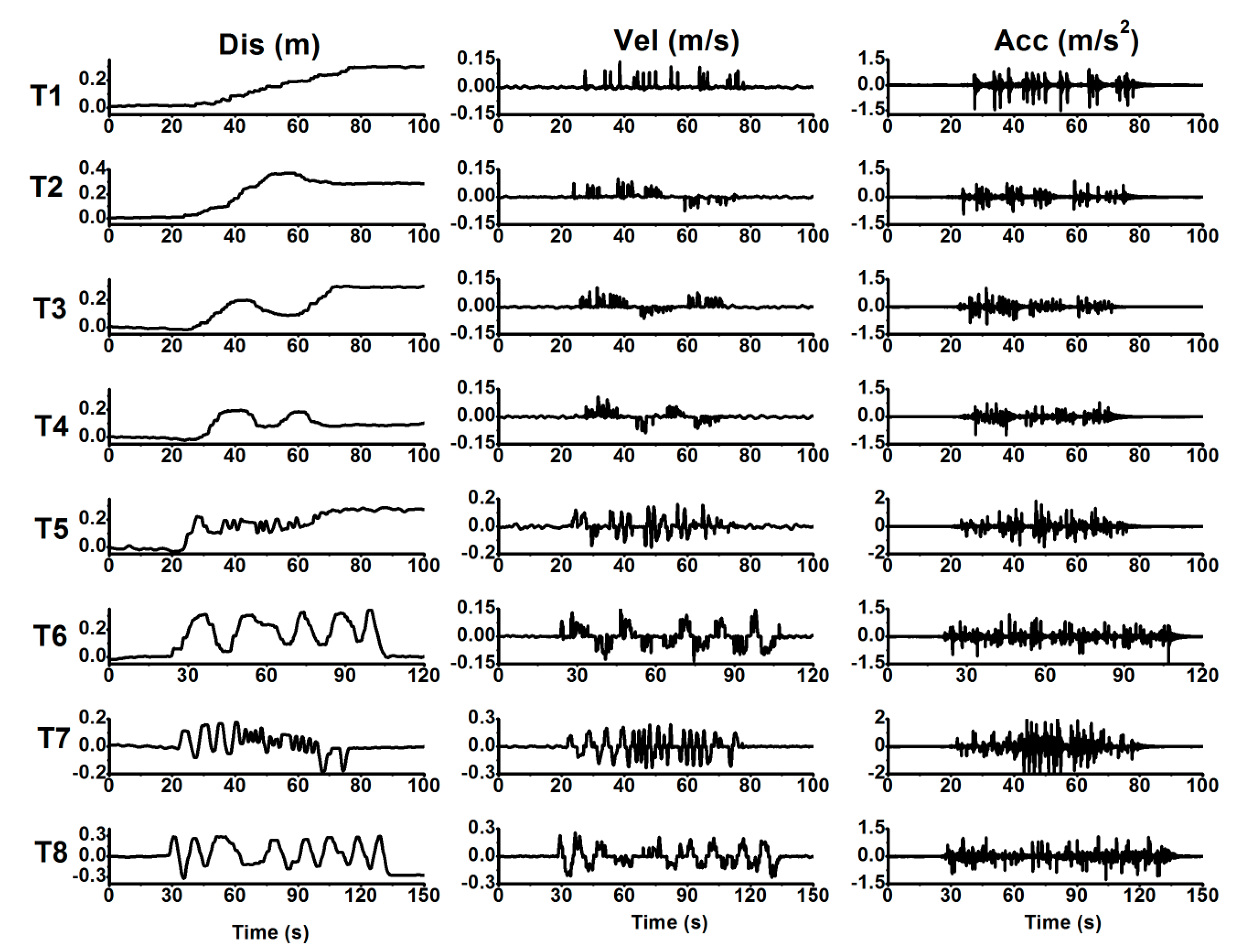

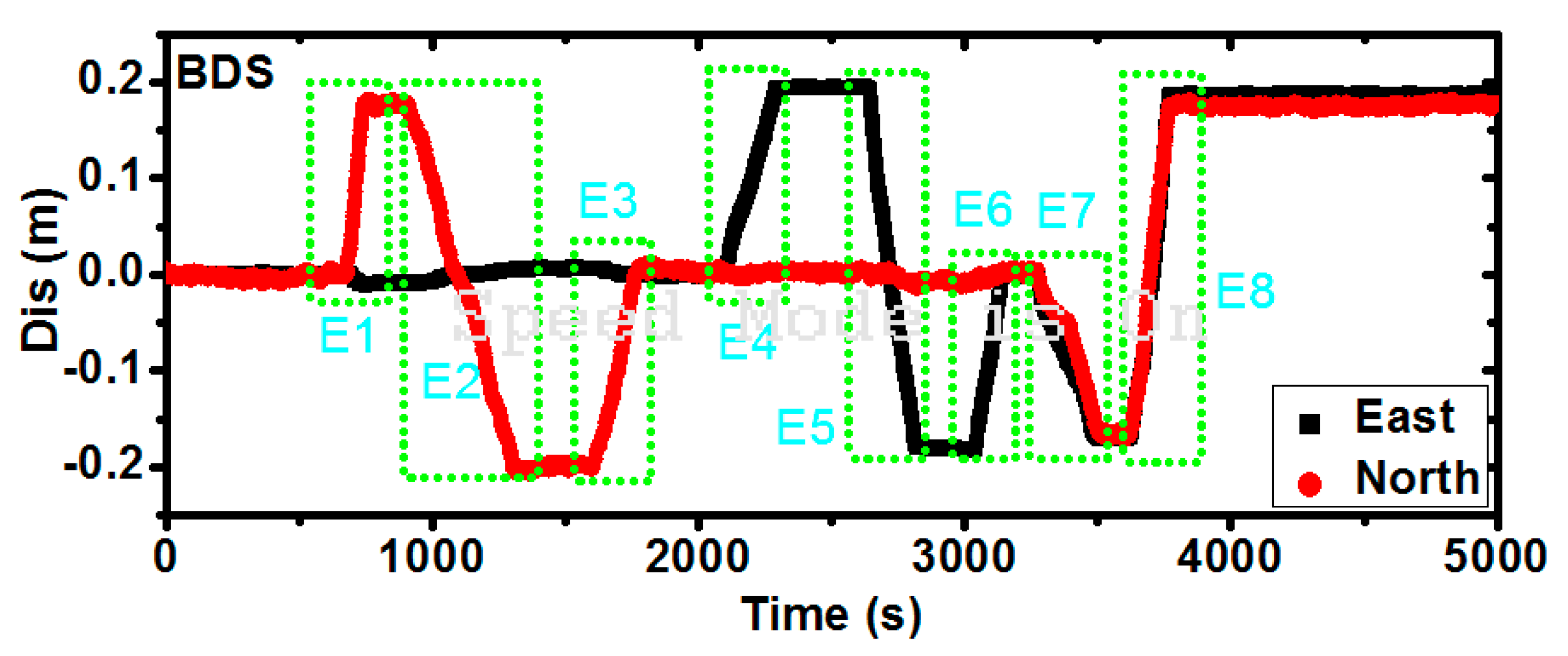
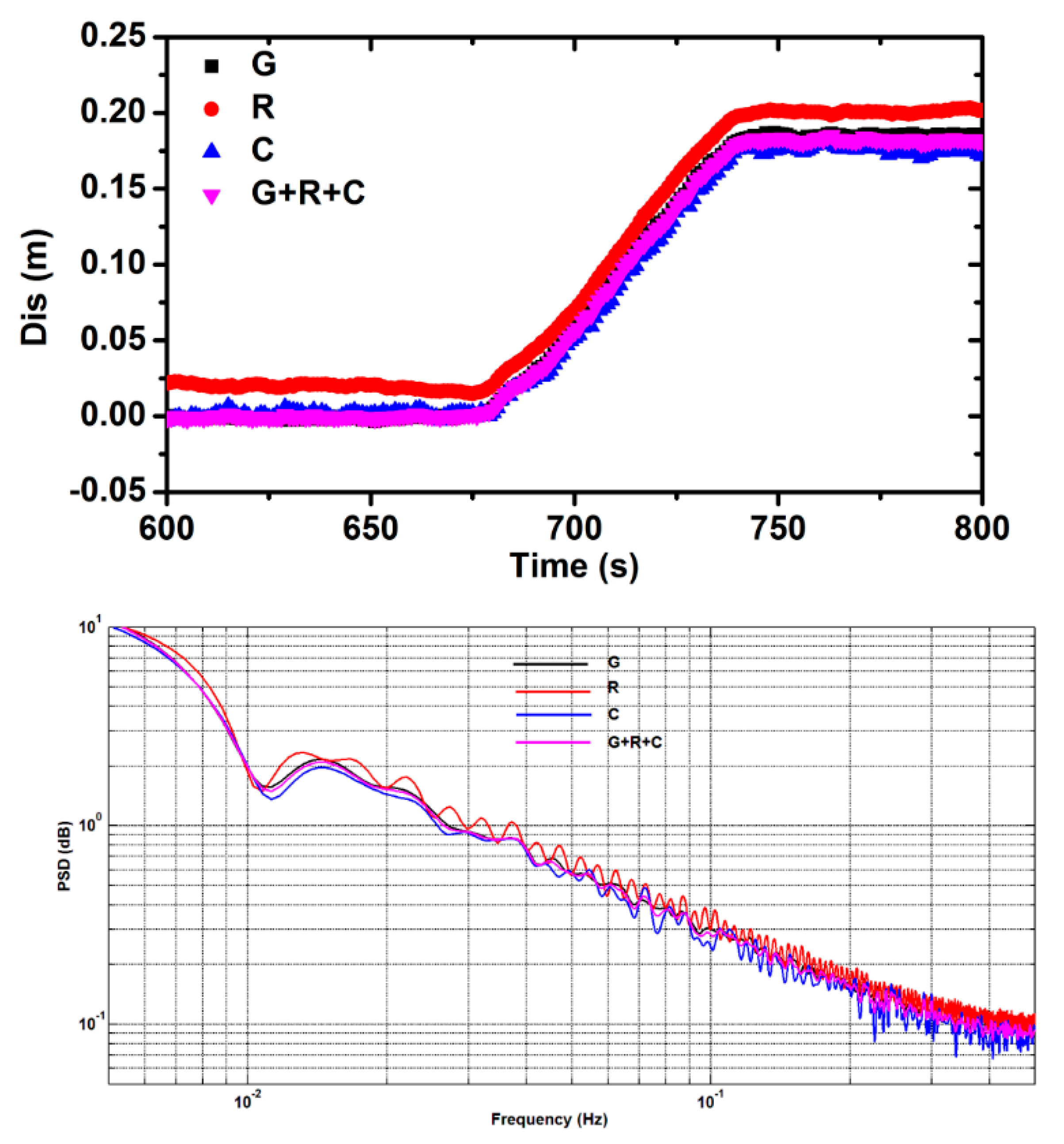
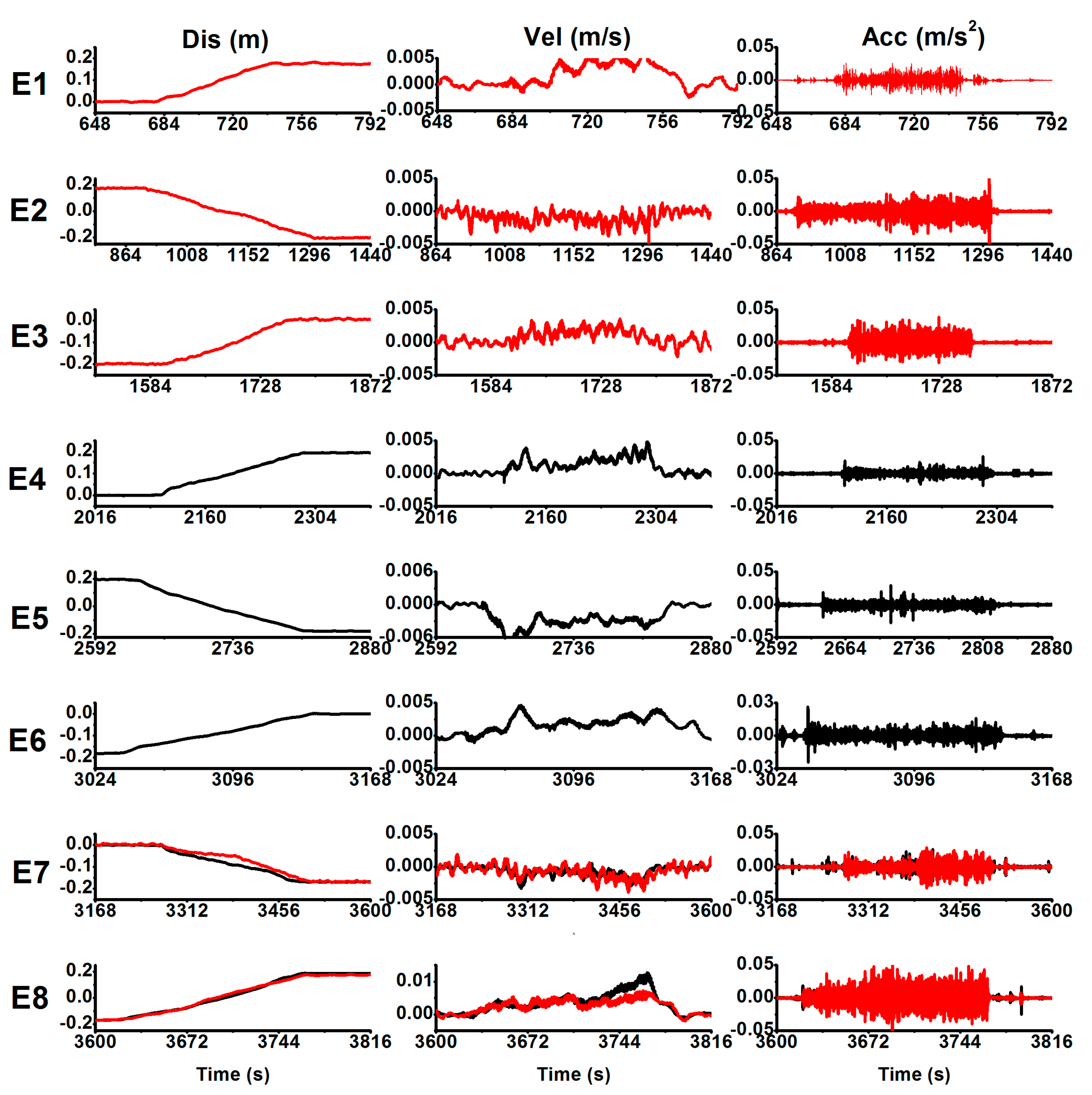
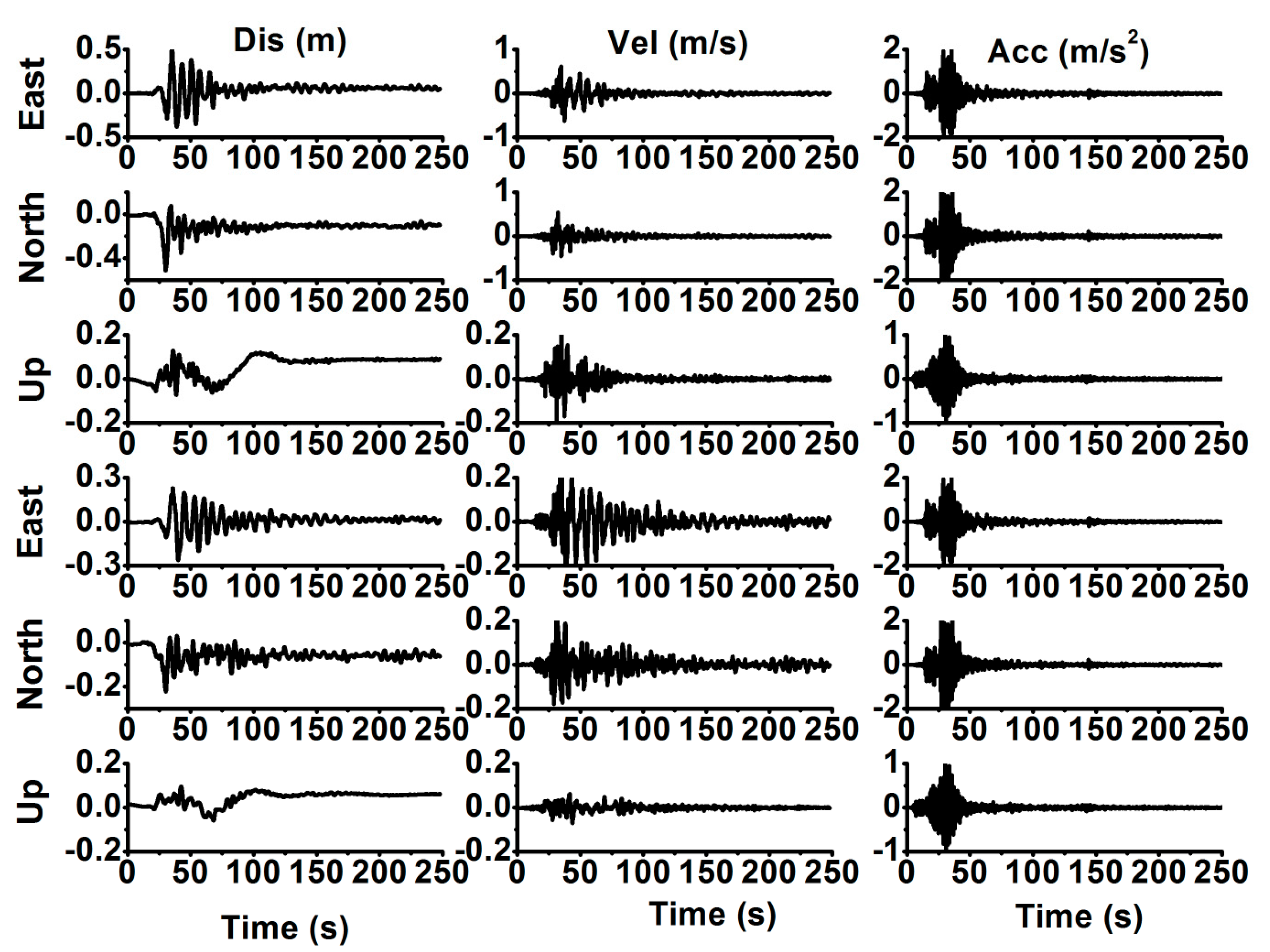
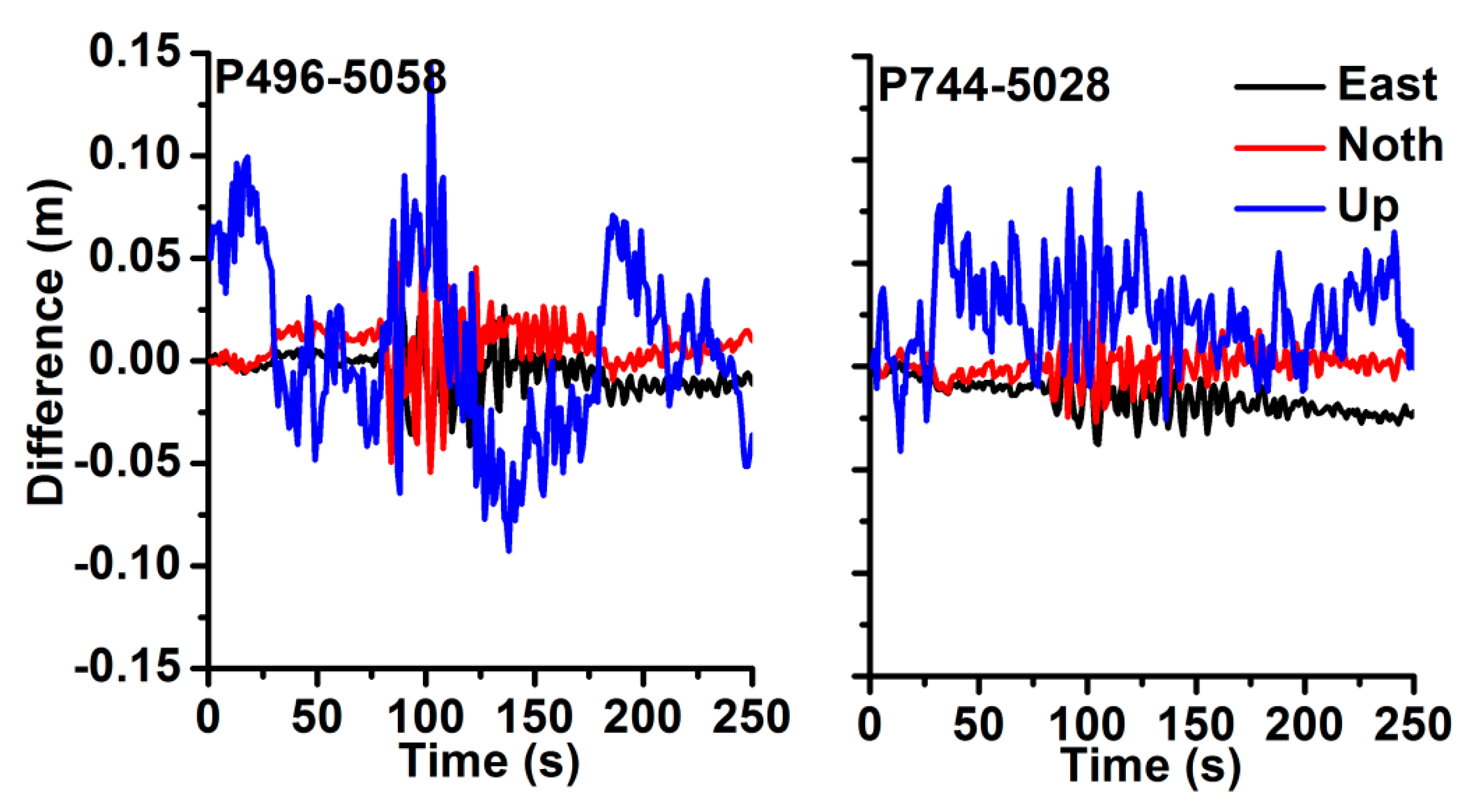
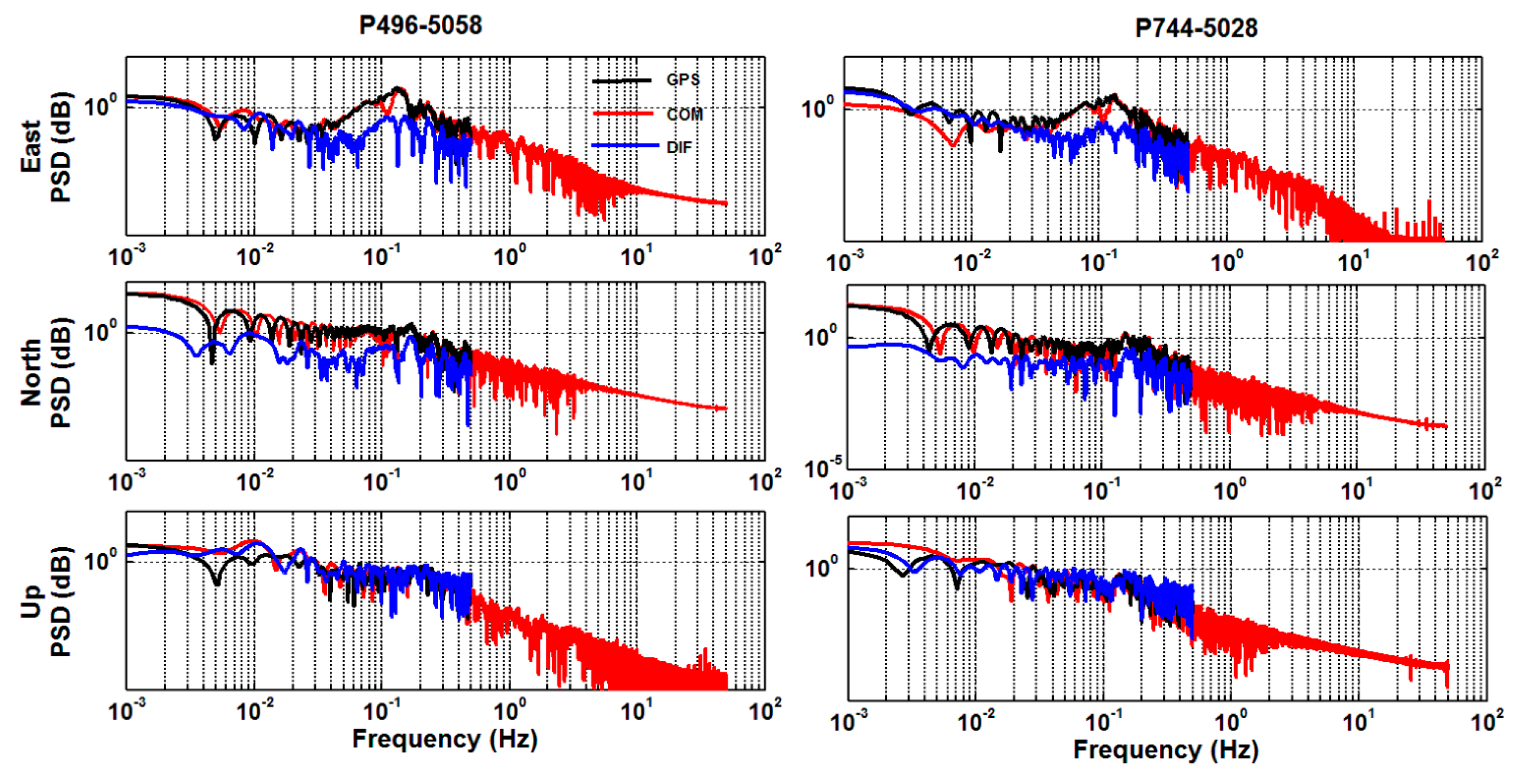
| Test | D-Bias | D-STD | V-Bias | V-STD | Test | D-Bias | D-STD | V-Bias | V-STD |
|---|---|---|---|---|---|---|---|---|---|
| T1 | −0.006 | 0.002 | 1.3 × 10−4 | 0.001 | T5 | 0.012 | 0.003 | 1.2 × 10−4 | 0.001 |
| T2 | 0.011 | 0.003 | 1.1 × 10−4 | 0.001 | T6 | 0.008 | 0.002 | −1.0 × 10−4 | 0.001 |
| T3 | 0.013 | 0.003 | −1.1 × 10−4 | 0.001 | T7 | 0.016 | 0.003 | 1.4 × 10−4 | 0.001 |
| T4 | −0.014 | 0.002 | 1.2 × 10−4 | 0.001 | T8 | −0.013 | 0.003 | 1.1 × 10−4 | 0.001 |
| Test | D-Bias | D-STD | V-Bias | V-STD | Test | D-Bias | D-STD | V-Bias | V-STD |
|---|---|---|---|---|---|---|---|---|---|
| E1(N) | −0.013 | 0.002 | 1.3 × 10−4 | 0.001 | E4(E) | −0.014 | 0.002 | 0.6 × 10−4 | 0.001 |
| E2(N) | 0.014 | 0.002 | 1.0 × 10−4 | 0.001 | E5(E) | 0.012 | 0.003 | 1.1 × 10−4 | 0.001 |
| E3(N) | 0.013 | 0.002 | 0.9 × 10−4 | 0.001 | E6(E) | 0.013 | 0.002 | 2.0 × 10−4 | 0.001 |
| E7(E) | 0.016 | 0.003 | 1.0 × 10−4 | 0.001 | E7(N) | 0.015 | 0.002 | 1.1 × 10−4 | 0.001 |
| E8(E) | 0.013 | 0.003 | −0.9 × 10−4 | 0.001 | E8(N) | 0.017 | 0.003 | −1.4 × 10−4 | 0.001 |
| Pairs | Component | D-Bias | D-STD | V-Bias | V-STD |
|---|---|---|---|---|---|
| P496-5058 | East | 0.026 | 0.003 | 1.4 × 10−4 | 0.002 |
| North | 0.011 | 0.003 | −1.2 × 10−4 | 0.002 | |
| Up | 0.044 | 0.005 | 1.0 × 10−4 | 0.001 | |
| P744-5028 | East | 0.021 | 0.002 | 1.3 × 10−4 | 0.002 |
| North | 0.018 | 0.003 | 1.0 × 10−4 | 0.002 | |
| Up | 0.036 | 0.004 | −0.9 × 10−4 | 0.001 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, R.; Zhang, R.; Zhang, P.; Liu, J.; Lu, X. Integration of Single-Frequency GNSS and Strong-Motion Observations for Real-Time Earthquake Monitoring. Remote Sens. 2018, 10, 886. https://doi.org/10.3390/rs10060886
Tu R, Zhang R, Zhang P, Liu J, Lu X. Integration of Single-Frequency GNSS and Strong-Motion Observations for Real-Time Earthquake Monitoring. Remote Sensing. 2018; 10(6):886. https://doi.org/10.3390/rs10060886
Chicago/Turabian StyleTu, Rui, Rui Zhang, Pengfei Zhang, Jinhai Liu, and Xiaochun Lu. 2018. "Integration of Single-Frequency GNSS and Strong-Motion Observations for Real-Time Earthquake Monitoring" Remote Sensing 10, no. 6: 886. https://doi.org/10.3390/rs10060886
APA StyleTu, R., Zhang, R., Zhang, P., Liu, J., & Lu, X. (2018). Integration of Single-Frequency GNSS and Strong-Motion Observations for Real-Time Earthquake Monitoring. Remote Sensing, 10(6), 886. https://doi.org/10.3390/rs10060886