Optimal Seamline Detection for Orthoimage Mosaicking Based on DSM and Improved JPS Algorithm
Abstract
:1. Introduction
2. Methods
2.1. Generation of Obstacle Areas
2.1.1. Selection of the Search Map
2.1.2. Threshold Segmentation Operation
2.1.3. Morphological Opening Operation
2.2. Seamline Detection Based on an Improved JPS Algorithm
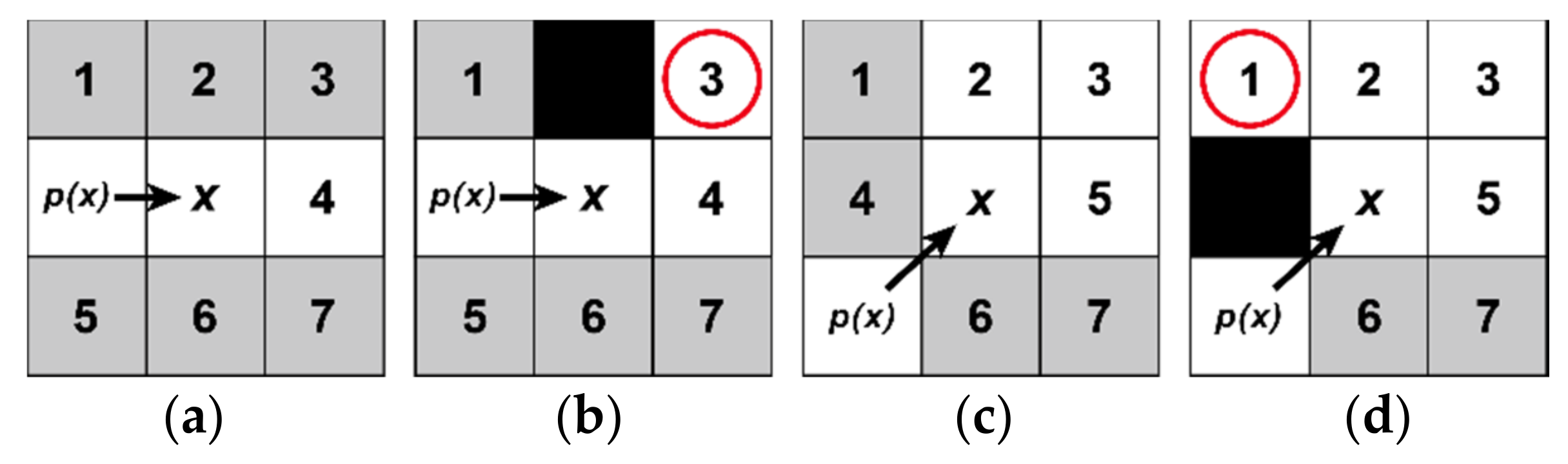
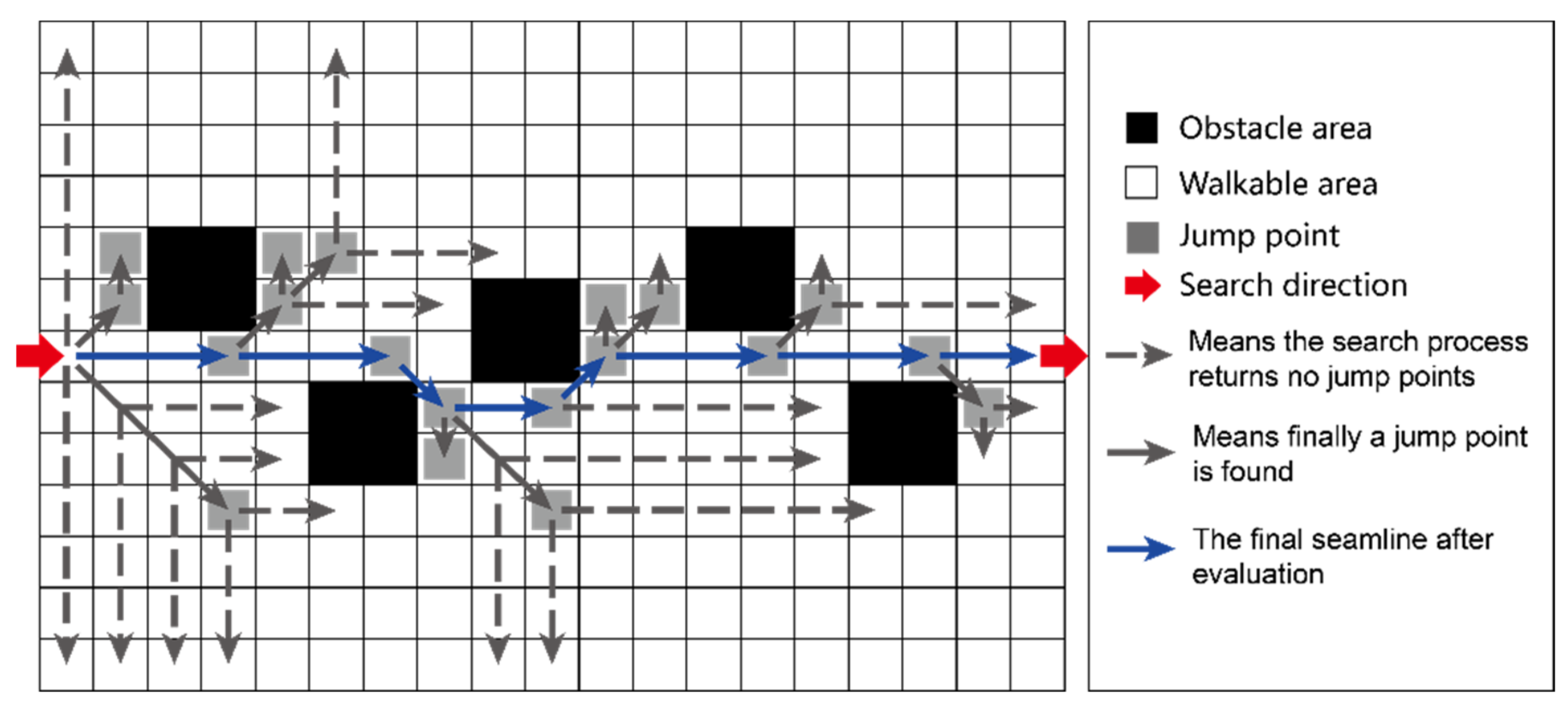
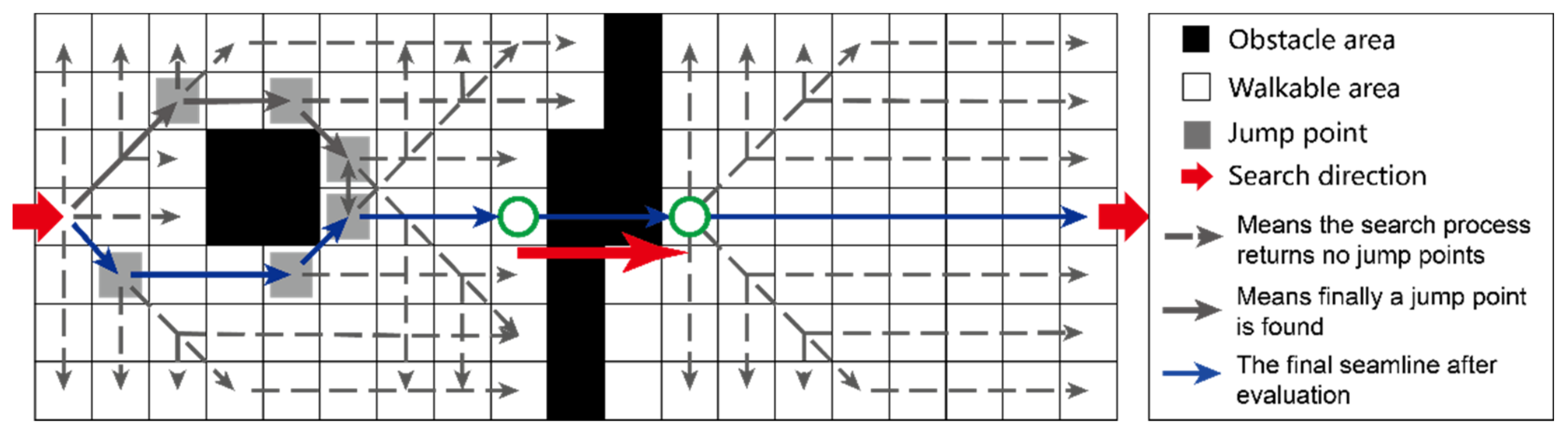
2.2.1. The Principle of JPS Algorithm
- (1)
- There is a path from node to node n, that is strictly shorter than the path from node to node n via node x.
- (2)
- There is a path from node to node n via node y, that is strictly shorter than the path from node to node n via node x.
- (3)
- There is a path from node to node n via node y, with the same length as the path from node to node n via node x, but path moves earlier than path with a diagonal type.
- (1)
- Straight moves: from the start node x, respectively move to different neighbor nodes according to the straight natural successor directions, the node :
- (a)
- If node has forced neighbors, return node as a jump point successor of the node x;
- (b)
- If node is an obstacle or out of the map, just ignore this direction;
- (c)
- If nothing happens, repeat the above search process from the node .
- (2)
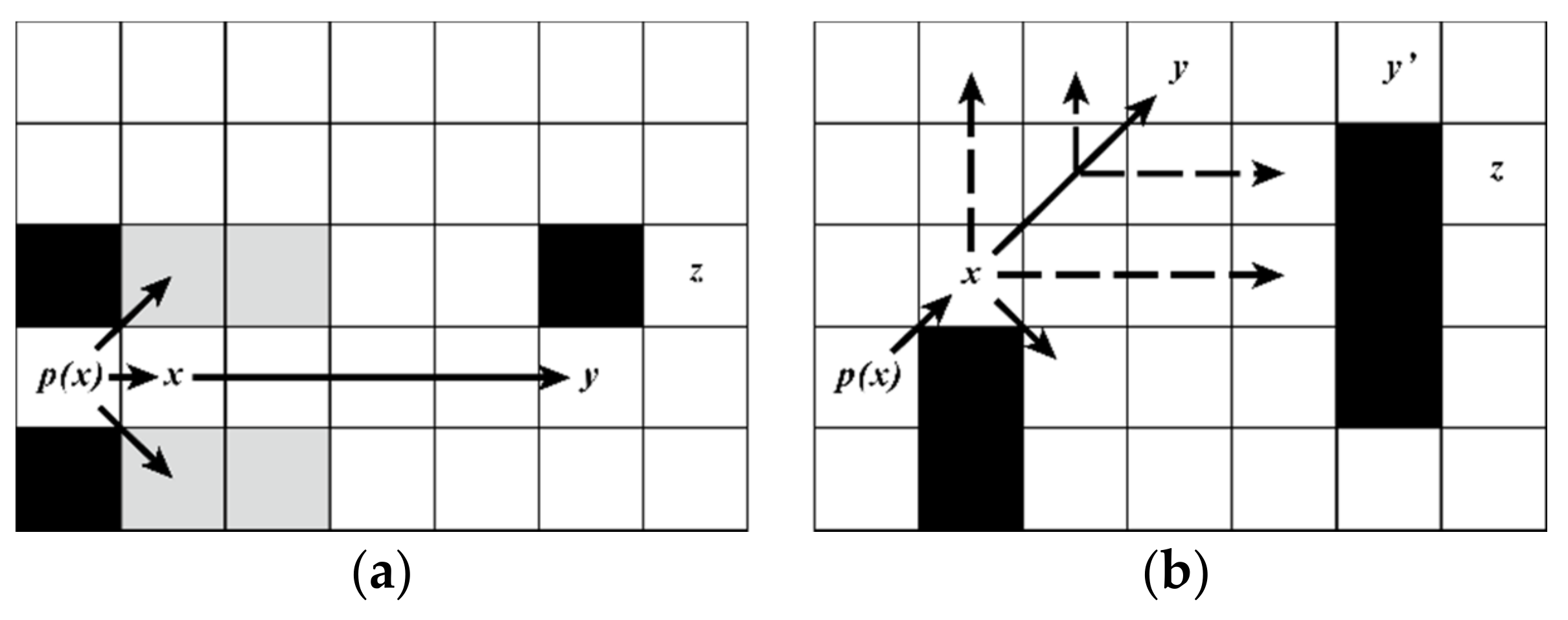
- Diagonal moves: from the start node x, respectively move to different neighbor nodes according to the diagonal natural successor directions, the node :
- (a)
- If node has forced neighbors, return node as a jump point successor of the node x;
- (b)
- If node is an obstacle or out of the map, just ignore this direction;
- (c)
- Implementing straight moves from the node , if there is a jump point successor of the node n, then return the node n as a jump point successor of the node x;
- (d)
- If nothing happens, repeat the above search process from the node .
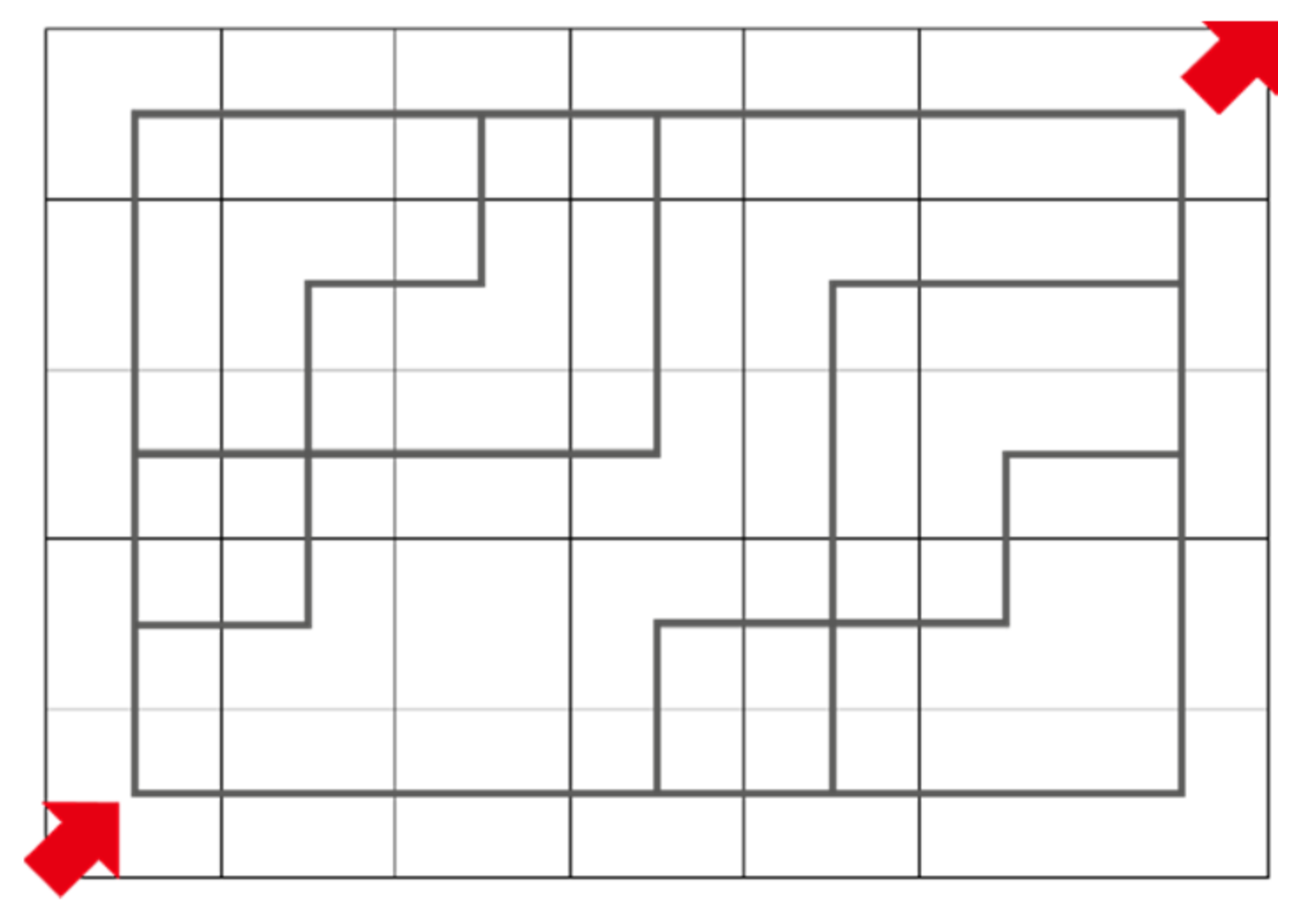
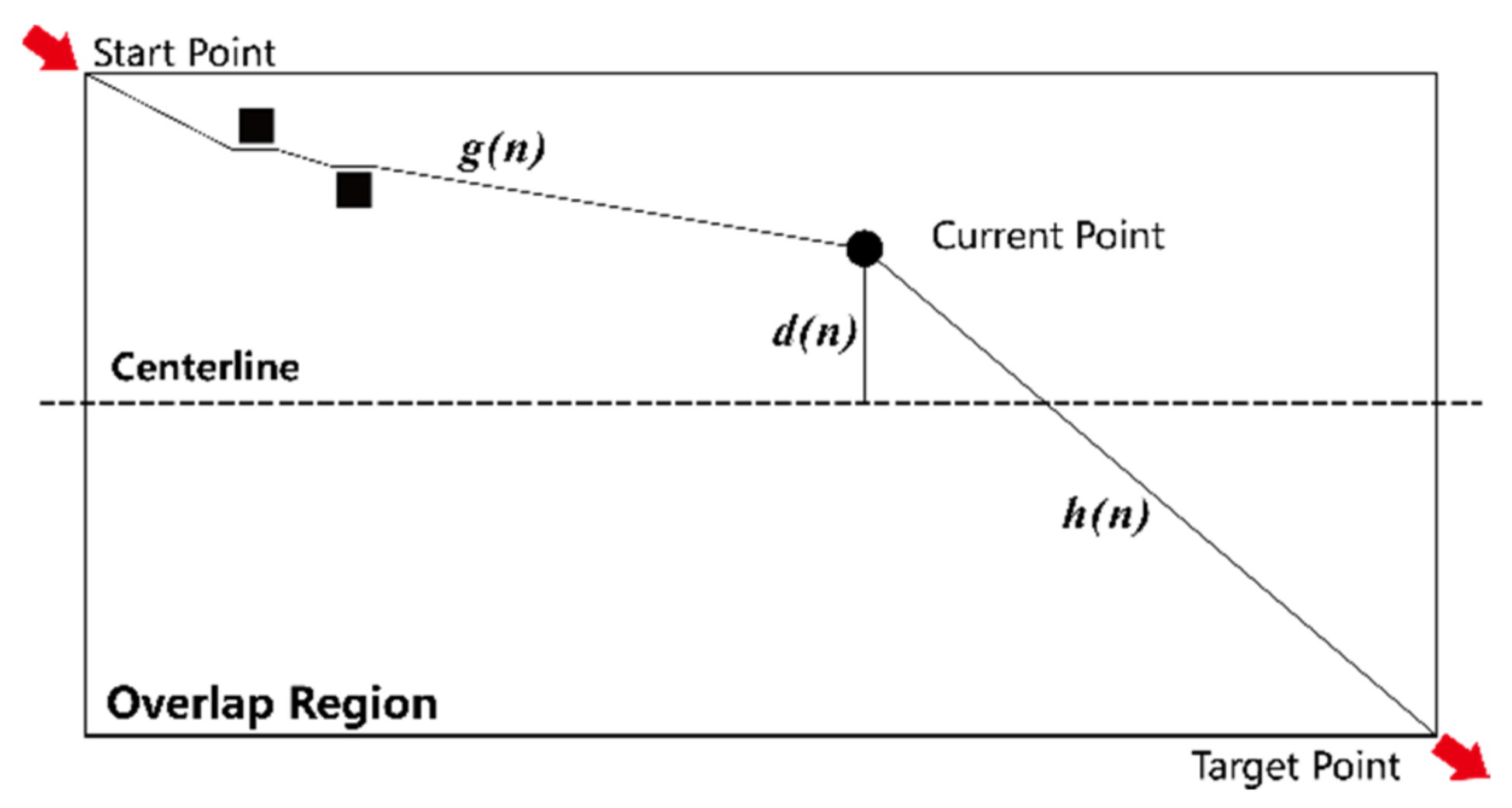
2.2.2. Optimal Seamline Detection
- (1)
- Add the start node to the open list, set the close list to empty, and start search from start node to all neighbor nodes separately.
- (2)
- If there were nodes in the open list, select the node n with the lowest cost value . If node n was the target node, then the path search was completed, otherwise it would be removed from the open list and added to the close list, and no longer needed to be evaluated.
- (3)
- From the node n, search for the jump point t (node t) in the direction of its natural successors:
- (a)
- If there was no returned node or the returned node t was in the close list, just ignore it;
- (b)
- If the returned node t was not in the open list, add the node t to the open list and calculate its , and values. Regard the node n as the parent node of the node t and record the parent direction of the node t;
- (c)
- If node t was in the open list, calculate the new value to see whether it was lower than the previous . If so, change its parent to the node n and calculate its value.
- (4)
- Repeat the step (2) to step (3) until the target node was found, the optimal path was then generated according to the recorded parent direction. Figure 8 is an illustration of the path search process.
3. Experiment and Results
3.1. Design of Experiments
3.2. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Soille, P. Morphological image compositing. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 673–683. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Holden, E.J.; Dentith, M.C.; Zhang, H. Towards the automatic selection of optimal seam line locations when merging optical remote-sensing images. Int. J. Remote Sens. 2012, 33, 1000–1014. [Google Scholar] [CrossRef]
- Chen, Q.; Sun, M.; Hu, X.; Zhang, Z. Automatic seamline network generation for urban orthophoto mosaicking with the use of a digital surface model. Remote Sens. 2014, 6, 12334–12359. [Google Scholar] [CrossRef]
- Pang, S.; Sun, M.; Hu, X.; Zhang, Z. SGM-based seamline determination for urban orthophoto mosaicking. ISPRS J. Photogramm. Remote Sens. 2016, 112, 1–12. [Google Scholar] [CrossRef]
- Kerschner, M. Seamline detection in colour orthoimage mosaicking by use of twin snakes. ISPRS J. Photogramm. Remote Sens. 2001, 56, 53–64. [Google Scholar] [CrossRef]
- Pan, J.; Wang, M.; Li, D.; Li, J. Automatic generation of seamline network using area Voronoi diagrams with overlap. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1737–1744. [Google Scholar] [CrossRef]
- Pan, J.; Zhou, Q.; Wang, M. Seamline determination based on segmentation for urban image mosaicking. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1335–1339. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Lu, X.; Tu, J.; Shan, J. Optimal seamline detection for multiple image mosaicking via graph cuts. ISPRS J. Photogramm. Remote Sens. 2016, 113, 1–16. [Google Scholar] [CrossRef]
- Davis, J. Mosaics of scenes with moving objects. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 23–25 June 1998. [Google Scholar]
- Zhang, J.; Sun, M.; Zhang, Z. Automated seamline detection for orthophoto mosaicking based on ant colony algorithm. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 675–678. (In Chinese) [Google Scholar]
- Chon, J.; Kim, H.; Lin, C.S. Seam-line determination for image mosaicking: A technique minimizing the maximum local mismatch and the global cost. ISPRS J. Photogramm. Remote Sens. 2010, 65, 86–92. [Google Scholar] [CrossRef]
- Pan, J.; Wang, M. A seam-line optimized method based on difference image and gradient image. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011. [Google Scholar]
- Lin, C.H.; Chen, B.H.; Lin, B.Y.; Chou, H.S. Blending zone determination for aerial orthimage mosaicking. ISPRS J. Photogramm. Remote Sens. 2016, 119, 426–436. [Google Scholar] [CrossRef]
- Fernandez, E.; Garfinkel, R.; Arbiol, R. Mosaicking of aerial photographic maps via seams defined by bottleneck shortest paths. Oper. Res. 1998, 46, 293–304. [Google Scholar] [CrossRef]
- Pyka, K. Detection of orthoimage mosaicking seamlines by means of wavelet transform. ISPRS Arch. 2016, XLI-B4, 45–50. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 2007, 4, 100–107. [Google Scholar] [CrossRef]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 377–384. [Google Scholar]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Yuan, X.; Duan, M.; Cao, J. A seam line detection algorithm for orthophoto mosaicking based on disparity image. Acta Geod. Cartogr. Sin. 2015, 44, 877–883. (In Chinese) [Google Scholar]
- Zuo, Z.; Zhang, Z.; Zhang, J. Seamlines intelligent detection in large-scale urban orthoimage mosaicking. Acta Geod. Cartogr. Sin. 2011, 40, 84–89. (In Chinese) [Google Scholar]
- Li, L.; Yao, J.; Liu, Y.; Yuan, W.; Shi, S.; Yuan, S. Optimal seamline detection for orthoimage mosaicking by combining deep convolutional neural network and graph cuts. Remote Sens. 2017, 9, 701. [Google Scholar] [CrossRef]
- Dong, Q.; Liu, J. Seamline determination based on PKGC segmentation for remote sensing image mosaicking. Sensors 2017, 17, 1721. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Zhou, S.; Xiong, X.; Zhu, J. A novel orthoimage mosaic method using the weighted A* algorithm for UAV imagery. Comput. Geosci. 2017, 109, 238–246. [Google Scholar] [CrossRef]
- Zheng, M.; Xiong, X.; Zhu, J. Automatic seam-line determination for orthoimage mosaics using edge–tracking based on a DSM. Remote Sens. Lett. 2017, 8, 977–986. [Google Scholar] [CrossRef]
- Ma, H.; Sun, J. Intelligent optimization of seam-line finding for orthophoto mosaicking with LiDAR point clouds. J. Zhejiang Univ. Sci. C 2011, 12, 417–429. [Google Scholar] [CrossRef]
- Wang, D.; Cao, W.; Xin, X.; Shao, Q.; Brolly, M.; Xiao, J.; Wan, Y.; Zhang, Y. Using vector building maps to aid in generating seams for low-attitude aerial orthoimage mosaicking: Advantages in avoiding the crossing of buildings. ISPRS J. Photogramm. Remote Sens. 2017, 125, 207–224. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, D.; Xiao, J.; Lai, X.; Xu, J. Automatic determination of seamlines for aerial image mosaicking based on vector roads alone. ISPRS J. Photogramm. Remote Sens. 2013, 76, 1–10. [Google Scholar] [CrossRef]
- Wang, D.; Wan, Y.; Xiao, J.; Lai, X.; Huang, W.; Xu, J. Aerial image mosaicking with the aid of vector roads. Photogramm. Eng. Remote Sens. 2015, 78, 1141–1150. [Google Scholar] [CrossRef]
- Harabor, D.D.; Grastien, A. Online graph pruning for pathfinding on grid maps. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 9–11 August 2011. [Google Scholar]
- Harabor, D.; Grastien, A. Improving jump point search. In Proceedings of the Twenty–Fourth International Conference on Automated Planning and Scheduling, Portsmouth, NH, USA, 21–26 June 2014; pp. 128–135. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Publishing House of Electronics Industry: Beijing, China, 2010. [Google Scholar]
- Zhou, K.; Yu, L.; Long, Z.; Mo, S. Local path planning of driverless car navigation based on jump point search method under urban environment. Future Internet 2017, 9, 51. [Google Scholar] [CrossRef]
- Pan, J.; Wang, M.; Ma, D.; Zhou, Q.; Li, J. Seamline network refinement based on area Voronoi diagrams with overlap. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1658–1666. [Google Scholar] [CrossRef]
- Chen, J.; Biao, X.; Li, Z.; Haibin, A.I.; Quanye, D.U. Fast and intelligent seamline detection for orthoimage mosaicking based on minimum spanning tree. Acta Geod. Cartogr. Sin. 2015, 44, 1125–1131. (In Chinese) [Google Scholar]






| Area | Image Size | Spectral Bands | Ground Resolution | DSM Grid Width | Overlap Size for Processing 1 | Area Description |
|---|---|---|---|---|---|---|
| 1 | 7500 × 11,500 pixels | R-G-B | 15 cm | 25 cm | 1700 × 4000 pixels | City area with flat ground and neat medium-sized buildings. |
| 2 | 7680 × 13,824 pixels | IR-R-G | 8 cm | 14 cm | 1500 × 4000 pixels | Area with small-sized and detached buildings surrounded by many trees |
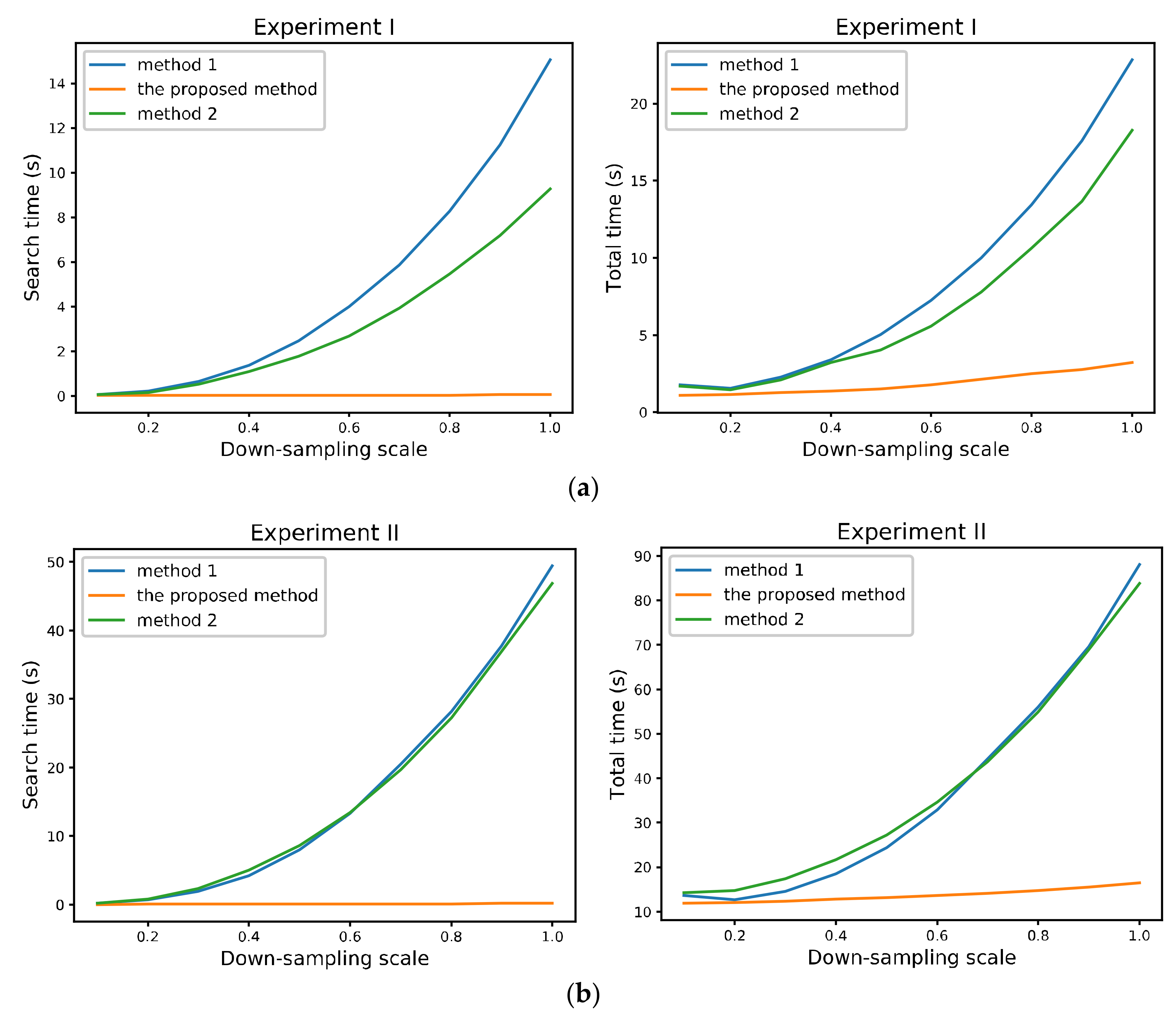
| Exp. | Method | Memory Usage/MB | Search Time/s | Total Time/s | Effect of the Seamline | |
|---|---|---|---|---|---|---|
| G Value 2 | Number of Object Crossing | |||||
| I | Method 1 1 | 1964.7 | 15.064 | 22.845 | 8.93 | 5 buildings, 11 cars |
| Proposed algorithm | 138.6 | 0.06 | 3.234 | 11.24 | 1 building, 14 cars | |
| Method 2 1 | 1968.4 | 9.276 | 18.285 | 12.86 | 2 buildings, 20 cars | |
| II | Method 1 | 2688.5 | 49.46 | 88.03 | 9.06 | 19 buildings, 15 cars |
| Proposed algorithm | 1063.2 | 0.168 | 16.472 | 12.36 | 2 buildings, 16 cars | |
| Method 2 | 2688.7 | 46.84 | 83.78 | 13.84 | 4 buildings, 22 cars | |
| Exp. | Method | Number of Seamline Nodes | Percentage of Evaluated Nodes 2 | Average Length 3 | Standard Deviation 3 |
|---|---|---|---|---|---|
| I | Method 1 1 | 4807 | 99.62 | --- | --- |
| Proposed algorithm | 620 | 0.18 | 5.57 | 11.89 | |
| Method 2 1 | 4265 | 60.13 | --- | --- | |
| II | Method 1 | 18,982 | 88.14 | --- | --- |
| Proposed algorithm | 5030 | 0.60 | 3.21 | 6.12 | |
| Method 2 | 17,300 | 73.78 | --- | --- |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Chen, S.; Li, X.; Zhou, P.; Zhou, Z. Optimal Seamline Detection for Orthoimage Mosaicking Based on DSM and Improved JPS Algorithm. Remote Sens. 2018, 10, 821. https://doi.org/10.3390/rs10060821
Chen G, Chen S, Li X, Zhou P, Zhou Z. Optimal Seamline Detection for Orthoimage Mosaicking Based on DSM and Improved JPS Algorithm. Remote Sensing. 2018; 10(6):821. https://doi.org/10.3390/rs10060821
Chicago/Turabian StyleChen, Gang, Song Chen, Xianju Li, Ping Zhou, and Zhou Zhou. 2018. "Optimal Seamline Detection for Orthoimage Mosaicking Based on DSM and Improved JPS Algorithm" Remote Sensing 10, no. 6: 821. https://doi.org/10.3390/rs10060821
APA StyleChen, G., Chen, S., Li, X., Zhou, P., & Zhou, Z. (2018). Optimal Seamline Detection for Orthoimage Mosaicking Based on DSM and Improved JPS Algorithm. Remote Sensing, 10(6), 821. https://doi.org/10.3390/rs10060821






