Online Hashing for Scalable Remote Sensing Image Retrieval
Abstract
:1. Introduction
- (1)
- A novel online hashing method is developed for scalable RS image retrieval problem. To the best of our knowledge, our work is the first attempt to exploit online hash function learning in the large-scale remote sensing image retrieval literature.
- (2)
- By learning the hash functions in an online manner, the parameters of our hash model can be updated continuously according to the new obtained RS images by time, which in contrast is one main drawback of the existing batch hashing methods.
- (3)
- The proposed online hashing approach reduces the computing complexity and memory cost in the learning process compared with batch hashing methods. Experimental results show the superiority of our online hashing for scalable RS image retrieval tasks.
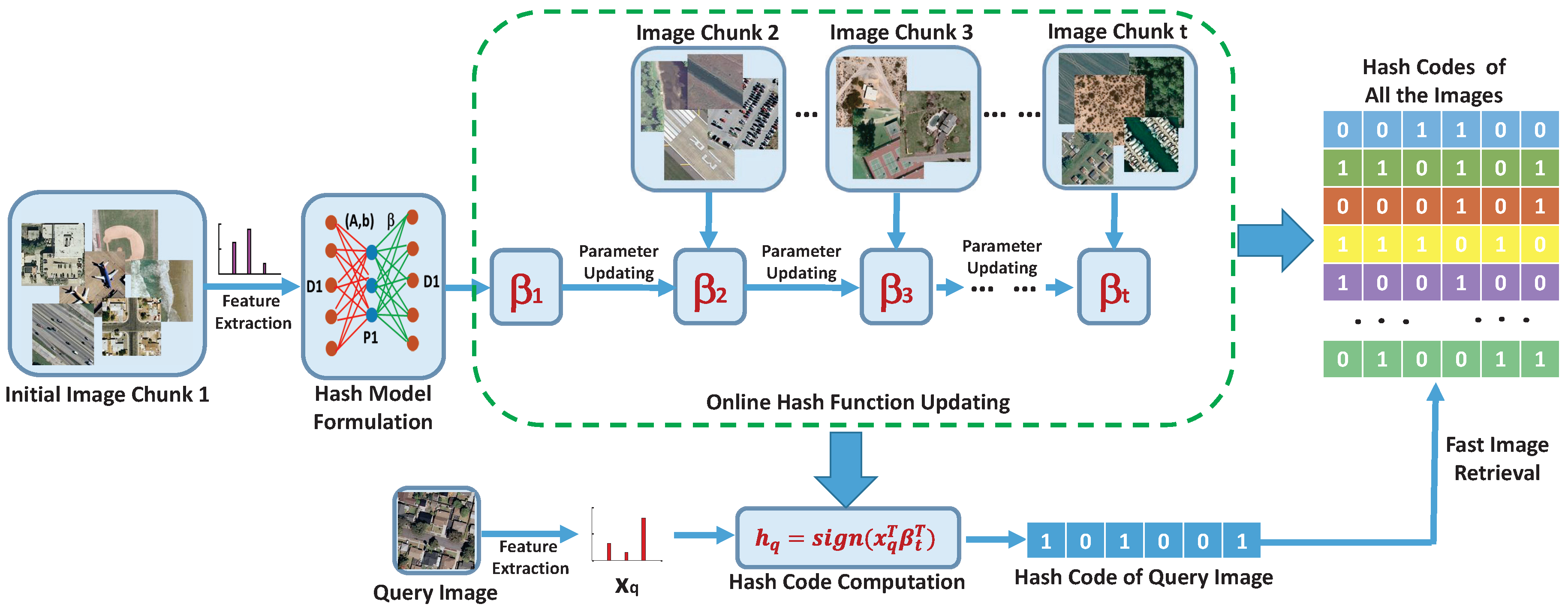
2. The Proposed Approach
2.1. Hash Model Formulation
2.2. Online Hash Function Learning
| Algorithm 1 Online Binary Code Learning with OPRH | |
| 1: | Input: Streaming image data chunk , code length r |
| 2: | Output: Hash codes for all the images |
| 3: | Randomly generate a projection matrix and a bias row vector |
| 4: | Compute by |
| 5: | Compute and |
| 6: | for do |
| 7: | Compute by |
| 8: | Update with Equation (8) |
| 9: | Update with Equation (9) |
| 10: | end for |
| 11: | Compute the hash codes for the whole database by |
2.3. Complexity Analysis
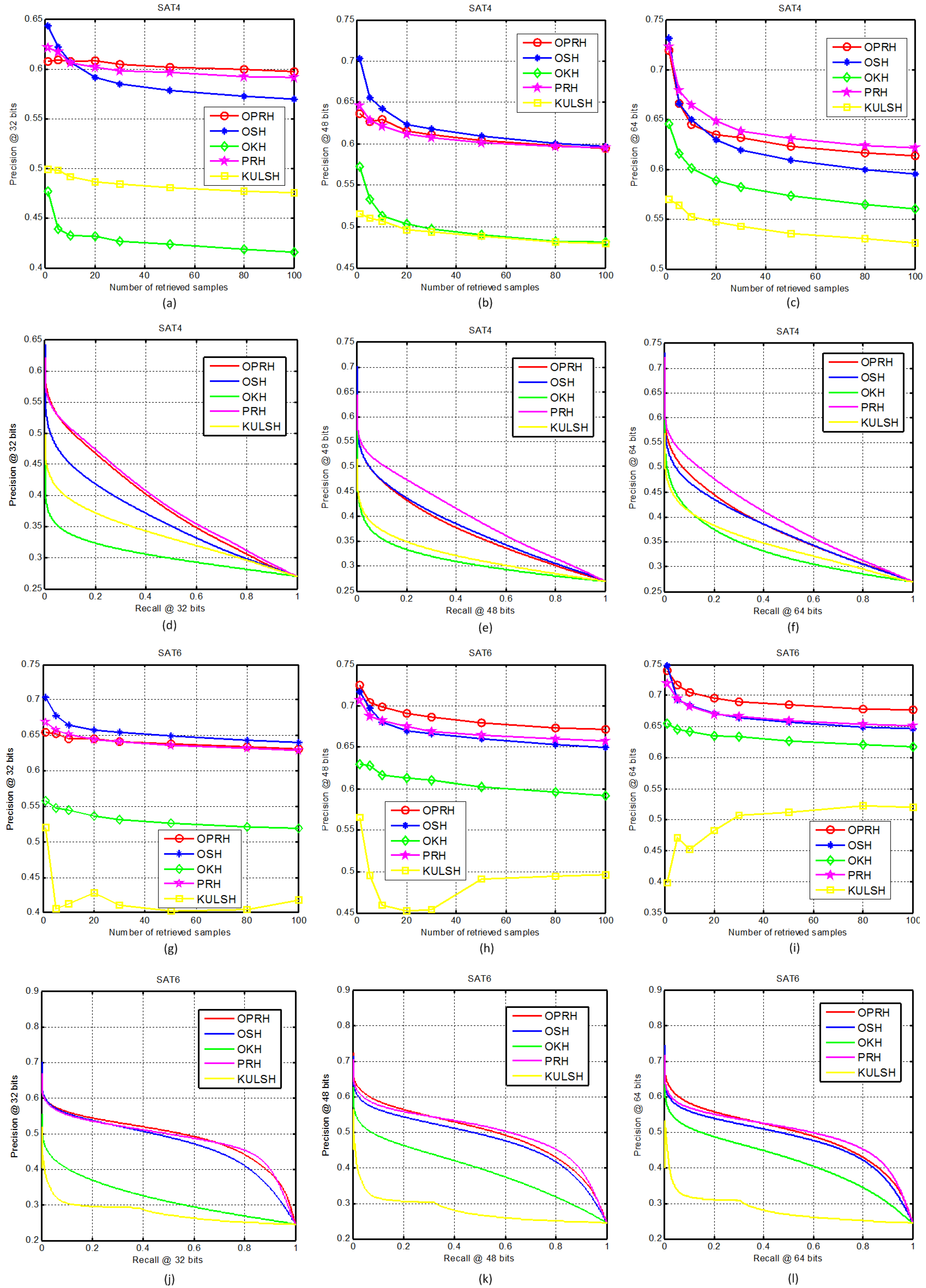
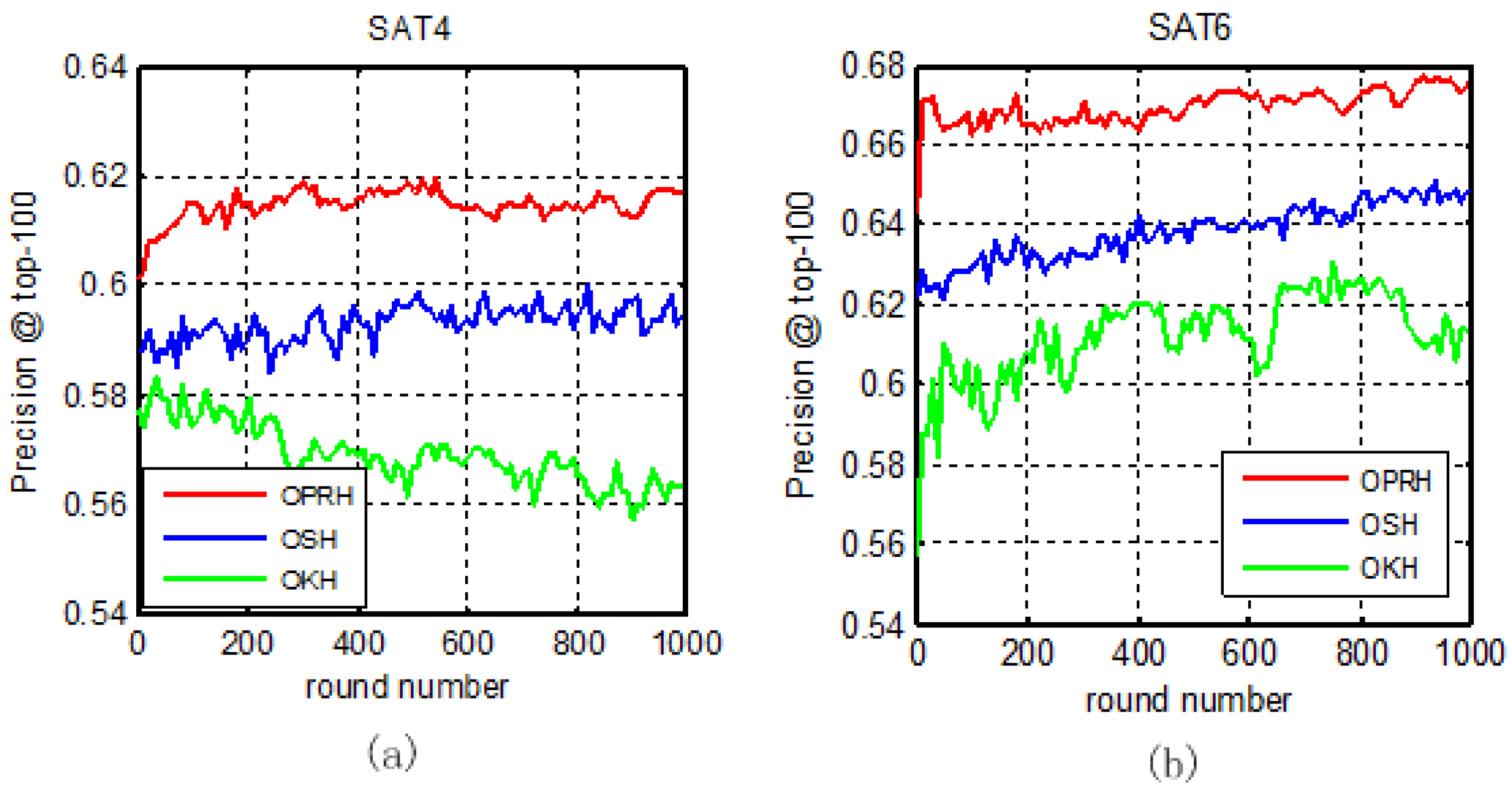
3. Experiments
3.1. Datasets and Settings
3.2. Results and Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Du, R.; Chen, Y.; Tang, H.; Fang, T. Study on content-based remote sensing image retrieval. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, South Korea, 25–29 July 2005; pp. 707–710. [Google Scholar]
- Wang, Q.; Zhu, G.; Yuan, Y. Statistical quantization for similarity search. Comput. Vis. Image Underst. 2014, 124, 22–30. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Dai, Q. An improved Bag-of-Words framework for remote sensing image retrieval in large-scale image databases. Int. J. Digit. Earth 2015, 8, 273–292. [Google Scholar] [CrossRef]
- Sevilla, J.; Bernabe, S.; Plaza, A. Unmixing-based content retrieval system for remotely sensed hyperspectral imagery on GPUs. J. Supercomput. 2014, 70, 588–599. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Geographic image retrieval using local invariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 818–832. [Google Scholar] [CrossRef]
- Aptoula, E. Remote sensing image retrieval with global morphological texture descriptors. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3023–3034. [Google Scholar] [CrossRef]
- Newsam, S.; Wang, L.; Bhagavathy, S.; Manjunath, B.S. Using texture to analyze and manage large collections of remote sensed image and video data. Appl. Opt. 2004, 43, 210–217. [Google Scholar] [CrossRef] [PubMed]
- Luo, B.; Aujol, J.F.; Gousseau, Y.; Ladjal, S. Indexing of satellite images with different resolutions by wavelet features. IEEE Trans. Image Process. 2008, 17, 1465–1472. [Google Scholar] [PubMed]
- Rosu, R.; Donias, M.; Bombrun, L.; Said, S.; Regniers, O.; Da Costa, J.-P. Structure tensor Riemannian statistical models for CBIR and classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 248–260. [Google Scholar] [CrossRef]
- Zhou, W.; Shao, Z.; Diao, C.; Cheng, Q. High-resolution remotesensing imagery retrieval using sparse features by auto-encoder. Remote Sens. Lett. 2015, 6, 775–783. [Google Scholar] [CrossRef]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. Learning low dimensional convolutional neural networks for high-resolution remote sensing image retrieval. Remote Sens. 2017, 9, 489. [Google Scholar] [CrossRef]
- Du, Z.; Li, X.; Lu, X. Local structure learning in high resolution remote sensing image retrieval. Neurocomputing 2016, 207, 813–822. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, J.; Yuan, Y. Deep metric learning for crowdedness regression. IEEE Trans. Trans. Circuits Syst. 2017. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Tao, C.; Zhu, H. Content-based high-resolution remote sensing image retrieval via unsupervised feature learning and collaborative affinity metric fusion. Remote Sens. 2016, 8, 709. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Tong, X.; Zhang, L.; Zhang, Z.; Liu, H.; Xing, X.; Takis Mathiopoulos, P. A three-layered graph-based learning approach for remote sensing image retrieval. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6020–6034. [Google Scholar] [CrossRef]
- Andoni, A.; Indyk, P. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. In Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS), Berkeley, CA, USA, 21–24 October 2006; pp. 459–468. [Google Scholar]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the 20th Annual Symposium on Computational Geometry (SCG), Brooklyn, NY, USA, 8–11 June 2004; pp. 253–262. [Google Scholar]
- Kulis, B.; Grauman, K. Kernelized locality-sensitive hashing for scalable image search. In Proceedings of the IEEE 12th International Conference on Computer Vision (ICCV), Kyoto, Japan, 27 September–4 October 2009; pp. 2130–2137. [Google Scholar]
- Weiss, Y.; Torralba, A.B.; Fergus, R. Spectral hashing. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–11 December 2008; pp. 1753–1760. [Google Scholar]
- Gong, Y.; Lazebnik, S. Iterative quantization: A procrustean approach to learning binary codes for large-scale image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2916–2929. [Google Scholar] [CrossRef] [PubMed]
- Heo, J.; Lee, Y.; He, J.; Chang, S.; Yoon, S. Spherical hashing: binary code embedding with hyperspheres. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2304–2316. [Google Scholar] [CrossRef] [PubMed]
- Kong, W.; Li, W. Isotropic hashing. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1655–1663. [Google Scholar]
- Shen, F.; Shen, C.; Shi, Q.; Hengel, A.; Tang, Z. Inductive hashing on manifolds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 1562–1569. [Google Scholar]
- Norouzi, M.; Fleet, D.J. Minimal loss hashing for compact binary codes. In Proceedings of the 28th International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011; pp. 353–360. [Google Scholar]
- Liu, W.; Wang, J.; Ji, R.; Jiang, Y.; Chang, S. Supervised hashing with kernels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16-21 June 2012; pp. 2074–2081. [Google Scholar]
- Lin, G.; Shen, C.; Shi, Q.; Hengel, A.; Suter, D. Fast supervised hashing with decision trees for high-dimensional data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1971–1978. [Google Scholar]
- Shen, F.; Shen, C.; Liu, W.; Shen, H. Supervised discrete hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 37–45. [Google Scholar]
- Xia, R.; Pan, Y.; Lai, H.; Liu, C.; Yan, S. Supervised hashing via image representation learning. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence (AAAI), Quebec City, QC, Canada, 27–31 July 2014; pp. 2156–2162. [Google Scholar]
- Zhao, F.; Huang, Y.; Wang, L.; Tan, T. Deep semantic ranking based hashing for multi-label image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1556–1564. [Google Scholar]
- Li, W.; Wang, S.; Kang, W. Feature learning based deep supervised hashing with pairwise labels. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI), New York, NY, USA, 7–15 July 2016; pp. 1711–1717. [Google Scholar]
- Demir, B.; Bruzzone, L. Hashing-based scalable remote sensing image search and retrieval in large archives. IEEE Trans. Geosci. Remote Sens. 2016, 54, 892–904. [Google Scholar] [CrossRef]
- Li, P.; Ren, P. Partial randomness hashing for large-scale remote sensing image retrieval. IEEE Geosci. Remote Sens. Lett. 2017, 14, 464–468. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Zhu, H.; Ma, J. Large-scale remote sensing image retrieval by deep hashing neural networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 950–965. [Google Scholar] [CrossRef]
- Ye, D.; Li, Y.; Tao, C.; Xie, X.; Wang, X. Multiple feature hashing learning for large-scale remote sensing image retrieval. ISPRS Int. J. Geo-Inform. 2017, 6, 364. [Google Scholar] [CrossRef]
- Huang, L.; Yang, Q.; Zheng, W. Online hashing. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 3–9 August 2013; pp. 1422–1428. [Google Scholar]
- Leng, C.; Wu, J.; Cheng, J.; Bai, X.; Lu, H. Online sketching hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2503–2511. [Google Scholar]
- Liang, N.; Huang, G.; Saratchandran, P.; Sundararajan, N. A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Zhu, Q.; Siew, C. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; Dibiano, R.; Karki, M.; Nemani, R. DeepSat: A learning framework for satellite imagery. In Proceedings of the SIGSPATIAL International Conference on Advances in Geographic Information Systems (SIGSPATIAL/GIS), Bellevue, WA, USA, 3–6 November 2015; pp. 37:1–37:10. [Google Scholar]
- Oliva, A.; Torralba, A. Modeling the shape of the sence: A holistic representation of spatial envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]


| Methods | Top-10 | Top-100 | ||||
|---|---|---|---|---|---|---|
| 32-bits | 48-bits | 64-bits | 32-bits | 48-bits | 64-bits | |
| IMH | 0.560 | 0.538 | 0.548 | 0.550 | 0.524 | 0.541 |
| IsoHash | 0.606 | 0.640 | 0.655 | 0.576 | 0.594 | 0.597 |
| ITQ | 0.636 | 0.653 | 0.662 | 0.609 | 0.607 | 0.610 |
| SpH | 0.596 | 0.623 | 0.658 | 0.563 | 0.588 | 0.607 |
| KULSH | 0.492 | 0.507 | 0.553 | 0.476 | 0.479 | 0.526 |
| PRH | 0.607 | 0.621 | 0.665 | 0.592 | 0.595 | 0.622 |
| OKH | 0.439 | 0.516 | 0.600 | 0.418 | 0.480 | 0.561 |
| OSH | 0.603 | 0.637 | 0.647 | 0.568 | 0.596 | 0.596 |
| OPRH | 0.608 | 0.630 | 0.656 | 0.598 | 0.594 | 0.616 |
| Methods | Top-10 | Top-100 | ||||
|---|---|---|---|---|---|---|
| 32-bits | 48-bits | 64-bits | 32-bits | 48-bits | 64-bits | |
| IMH | 0.583 | 0.626 | 0.604 | 0.575 | 0.614 | 0.582 |
| IsoHash | 0.667 | 0.680 | 0.673 | 0.635 | 0.645 | 0.642 |
| ITQ | 0.672 | 0.691 | 0.681 | 0.649 | 0.660 | 0.653 |
| SpH | 0.642 | 0.664 | 0.694 | 0.616 | 0.631 | 0.657 |
| KULSH | 0.413 | 0.459 | 0.452 | 0.418 | 0.496 | 0.520 |
| PRH | 0.651 | 0.682 | 0.683 | 0.629 | 0.658 | 0.652 |
| OKH | 0.541 | 0.619 | 0.638 | 0.521 | 0.592 | 0.617 |
| OSH | 0.669 | 0.684 | 0.680 | 0.639 | 0.650 | 0.647 |
| OPRH | 0.645 | 0.699 | 0.705 | 0.631 | 0.672 | 0.677 |
| Methods | SAT-4 Dataset | SAT-6 Dataset | ||||
|---|---|---|---|---|---|---|
| Round Time | Total Time | Memory Cost | Round Time | Total Time | Memory Cost | |
| IMH | - | 67.6 | 3696 | - | 67.7 | 2990 |
| IsoHash | - | 5.5 | 4915 | - | 5.8 | 3942 |
| ITQ | - | 47.9 | 5857 | - | 61.1 | 5529 |
| SpH | - | 196.3 | 5109 | - | 200 | 4177 |
| KULSH | - | 10.3 | 3901 | - | 8.2 | 3143 |
| PRH | - | 4.6 | 1556 | - | 5.0 | 1198 |
| OKH | 0.32 | 315.8 | 10.4 | 0.27 | 267 | 8 |
| OSH | 0.11 | 113.5 | 4.4 | 0.11 | 105.4 | 3.5 |
| OPRH | 0.01 | 12 | 2.3 | 0.009 | 8.7 | 1.8 |
| GIST Scan | CNN Scan | OPRH+GIST | OPRH+CNN | |||||
|---|---|---|---|---|---|---|---|---|
| Time | Precision@100 | Time | Precision@100 | Time | Precision@100 | Time | Precision@100 | |
| SAT-4 | 1.93 | 0.60 | 4.01 | 1 | 0.06 | 0.61 | 0.06 | 0.98 |
| SAT-6 | 1.67 | 0.69 | 3.15 | 0.98 | 0.05 | 0.67 | 0.05 | 0.97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhang, X.; Zhu, X.; Ren, P. Online Hashing for Scalable Remote Sensing Image Retrieval. Remote Sens. 2018, 10, 709. https://doi.org/10.3390/rs10050709
Li P, Zhang X, Zhu X, Ren P. Online Hashing for Scalable Remote Sensing Image Retrieval. Remote Sensing. 2018; 10(5):709. https://doi.org/10.3390/rs10050709
Chicago/Turabian StyleLi, Peng, Xiaoyu Zhang, Xiaobin Zhu, and Peng Ren. 2018. "Online Hashing for Scalable Remote Sensing Image Retrieval" Remote Sensing 10, no. 5: 709. https://doi.org/10.3390/rs10050709
APA StyleLi, P., Zhang, X., Zhu, X., & Ren, P. (2018). Online Hashing for Scalable Remote Sensing Image Retrieval. Remote Sensing, 10(5), 709. https://doi.org/10.3390/rs10050709






