Coastal Improvements for Tide Models: The Impact of ALES Retracker
Abstract
1. Introduction
2. Dataset Description
2.1. Altimeter Dataset
- Application of a pre-existing tide model to correct the SLA
- Estimation of residual periodic components associated with tides in the corrected SLA
- Estimation of a new tide correction to adjust and improve the original FES2014 solution
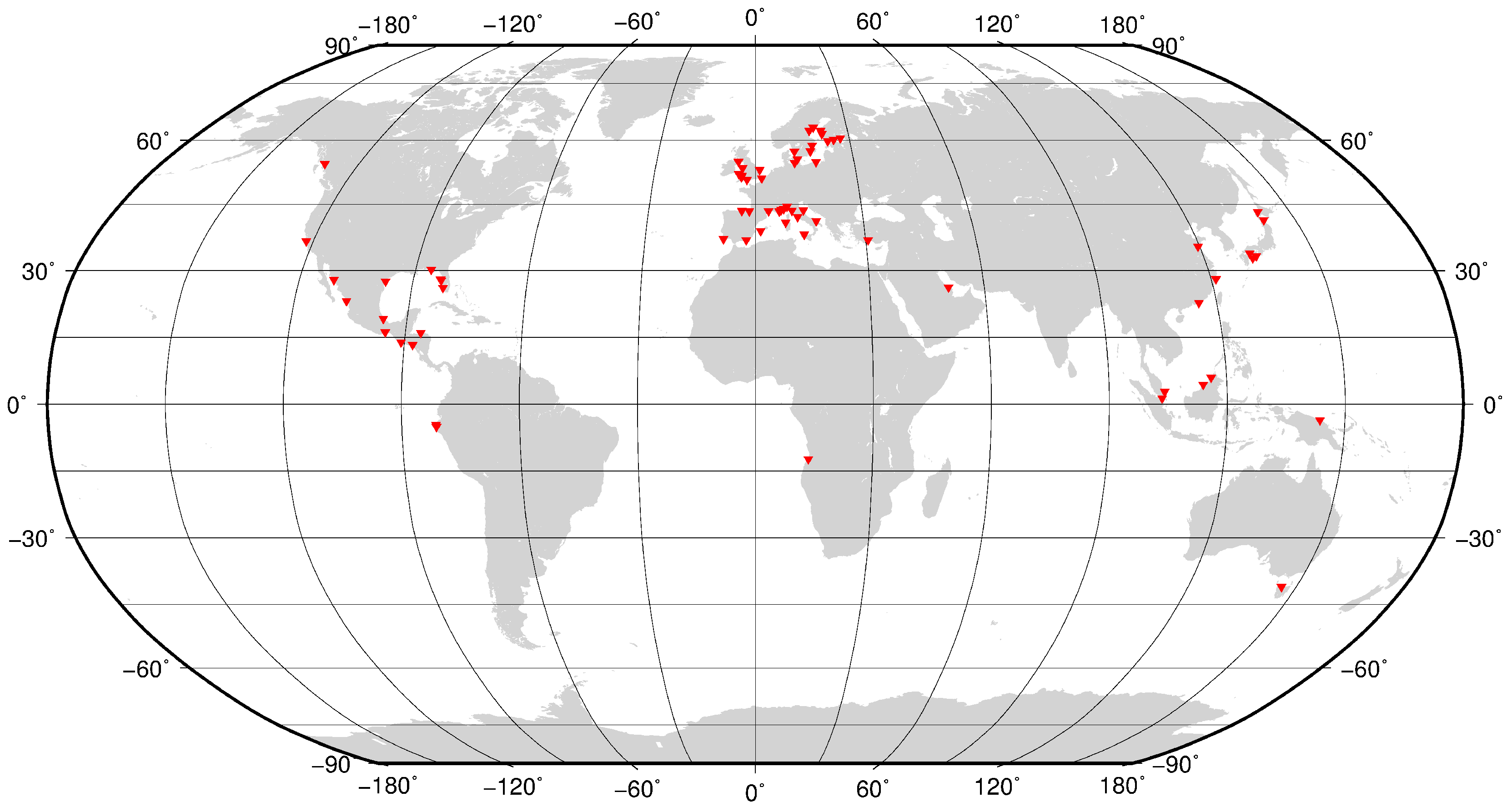
2.2. Tide Gauge Dataset
- Maximum distance to satellite track: 50 km.
- GESLA data already assimilated in FES2014 model (Cancet, personal communication) are discarded.
- Stations near estuaries are discarded. Exceptions for fjords (e.g., Finnish and Canadian coasts).
- Final manual screening on the selected stations: tide gauges with timeseries shorter than one year are discarded while part of the timeseries containing doubtful offsets are not considered.
3. Tide Model Approach
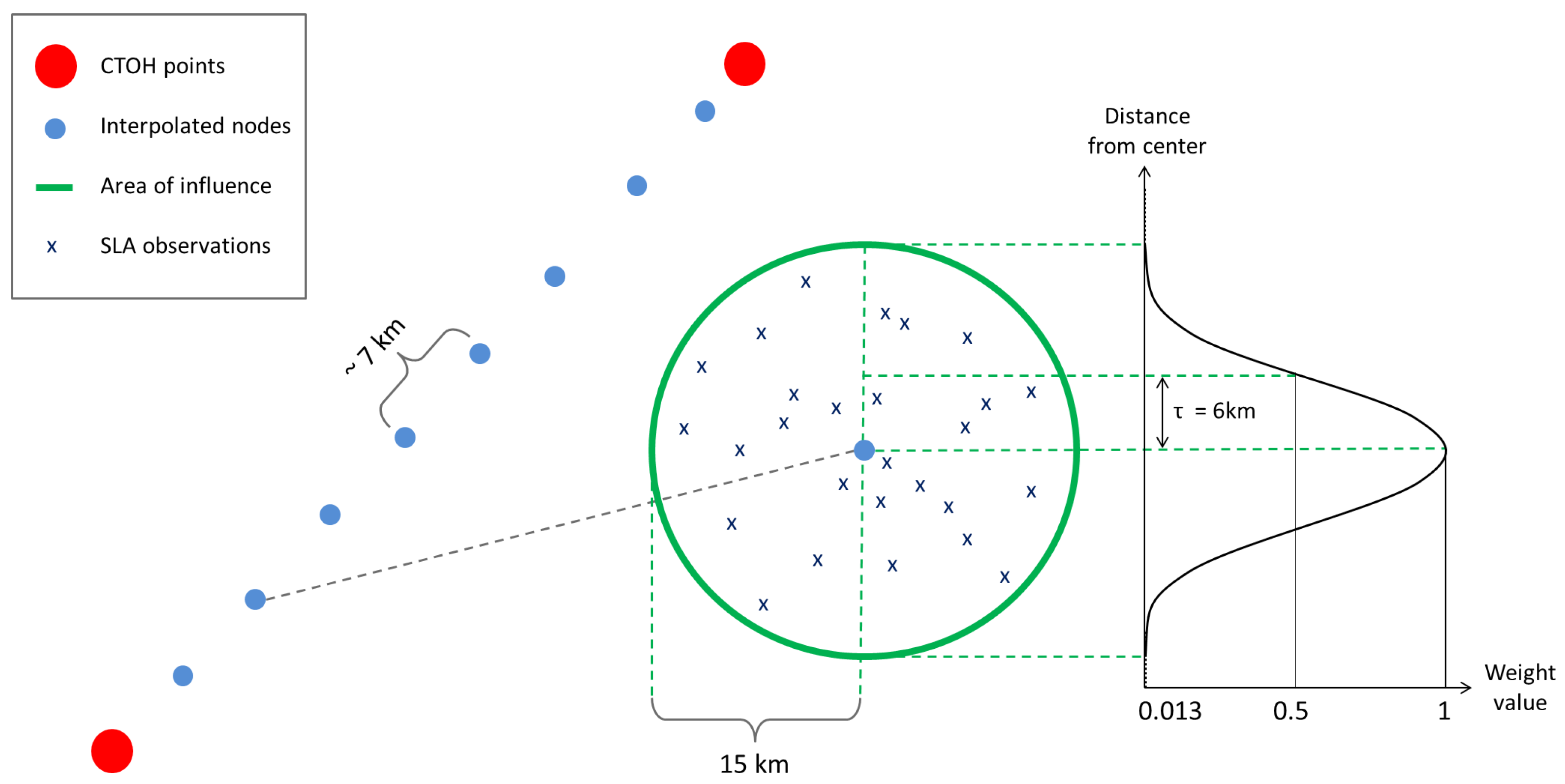
3.1. Selection of the Nodes
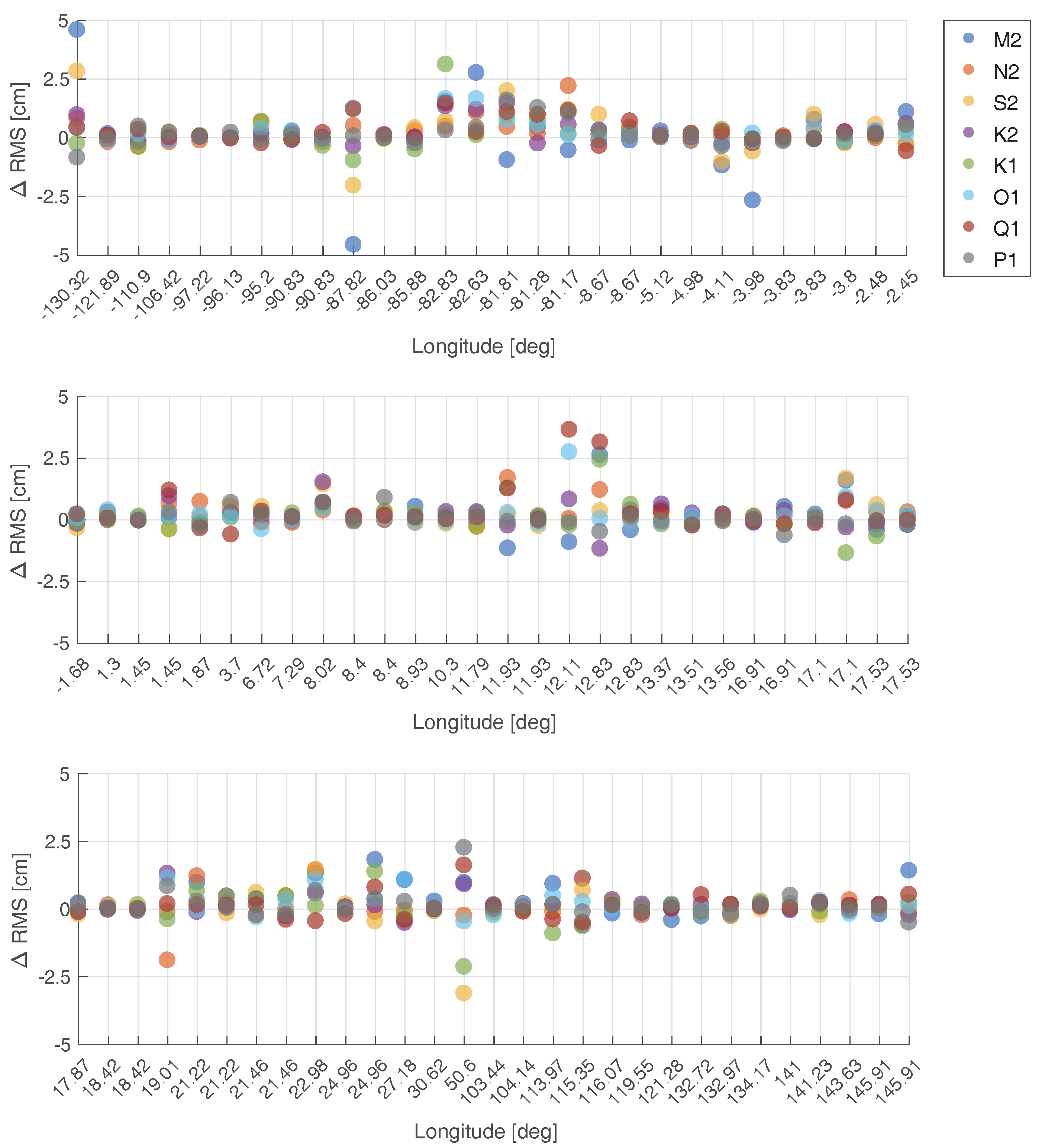
3.2. Computation of Tidal Constituents
4. Evaluation Methods
5. Results and Discussion
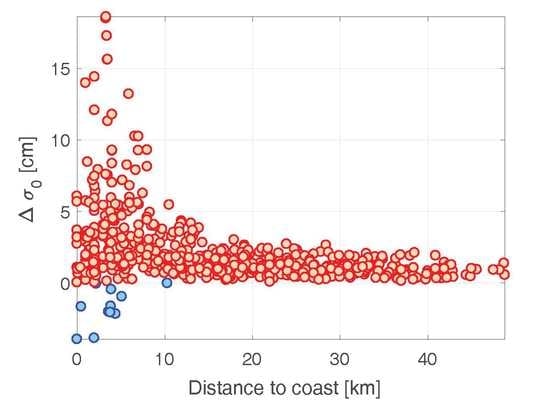
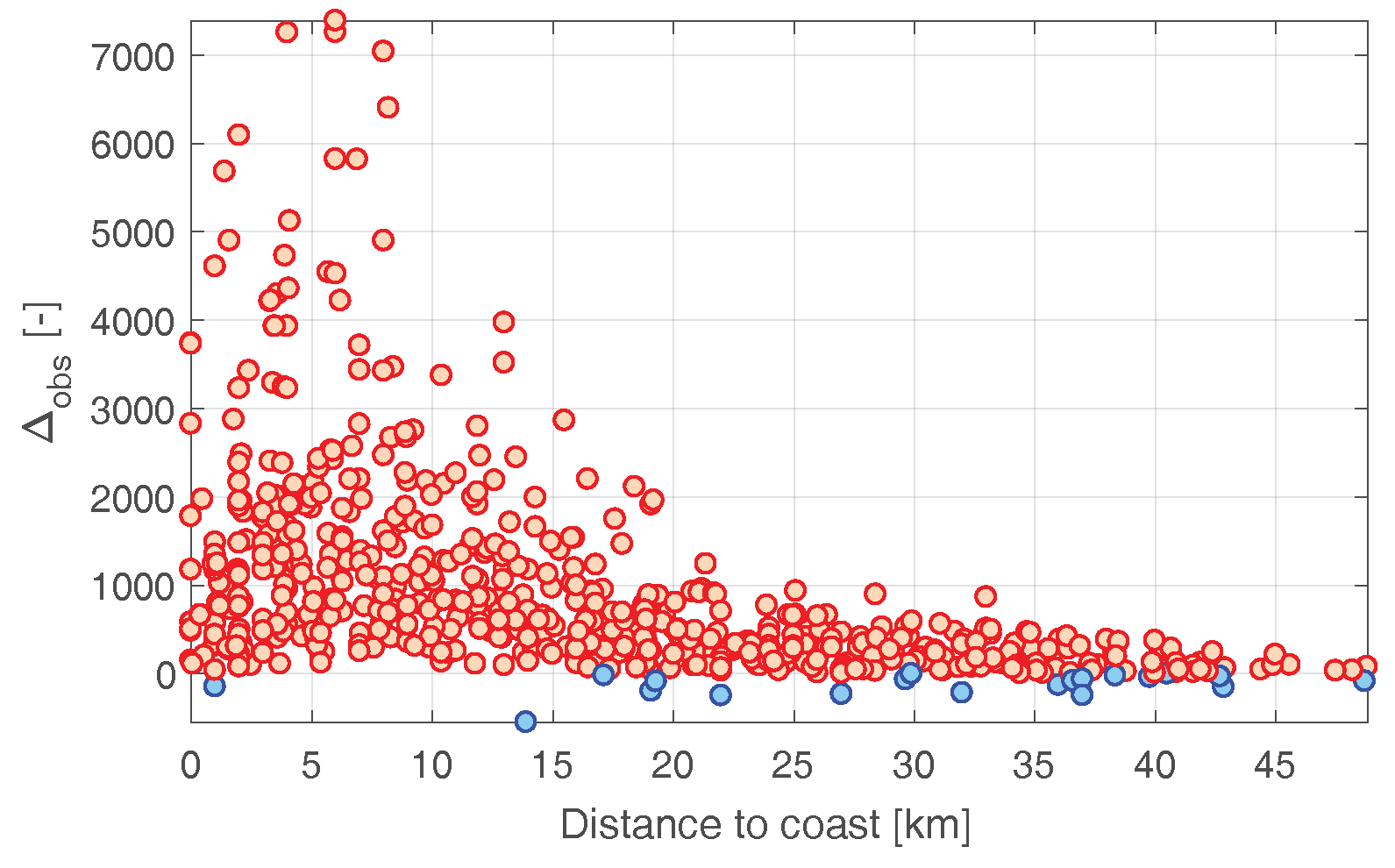
5.1. Number of Observations
5.2. Fitting Uncertainty
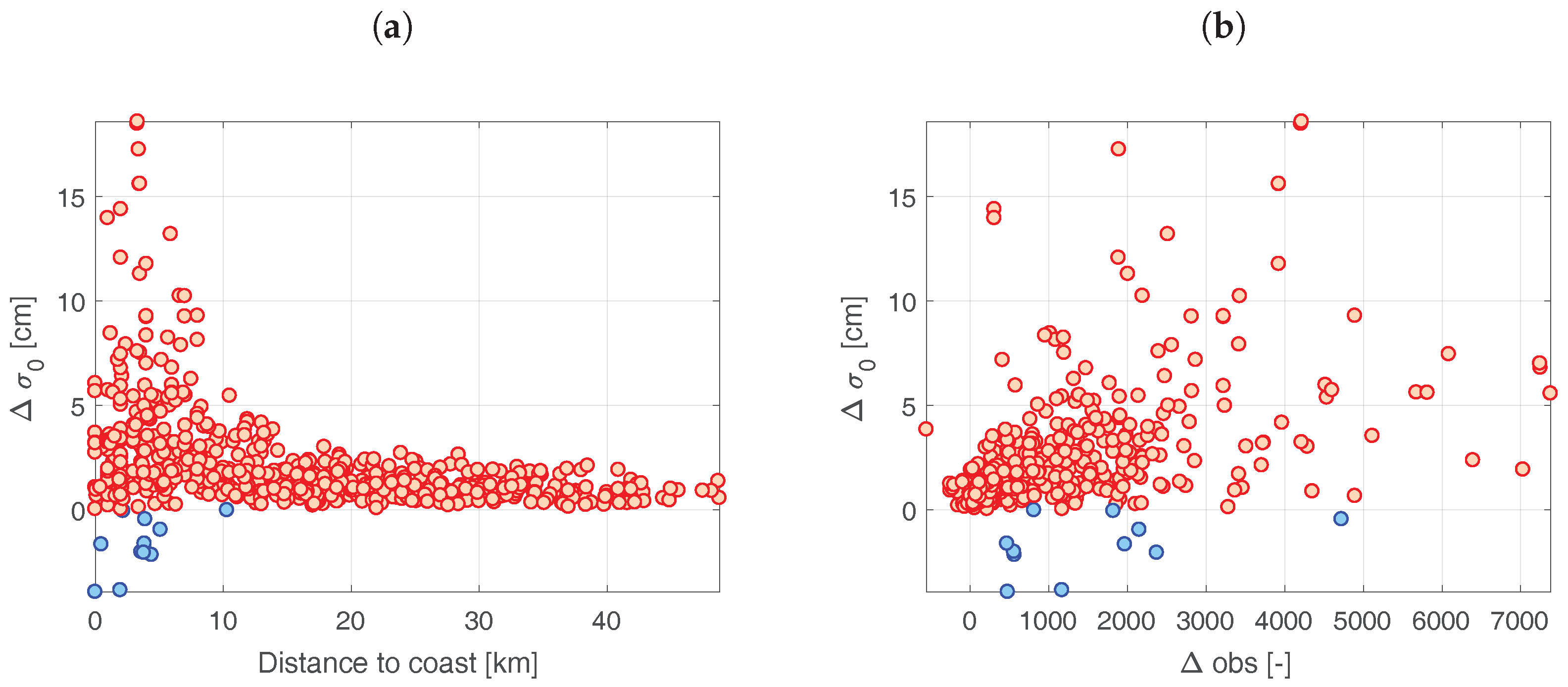
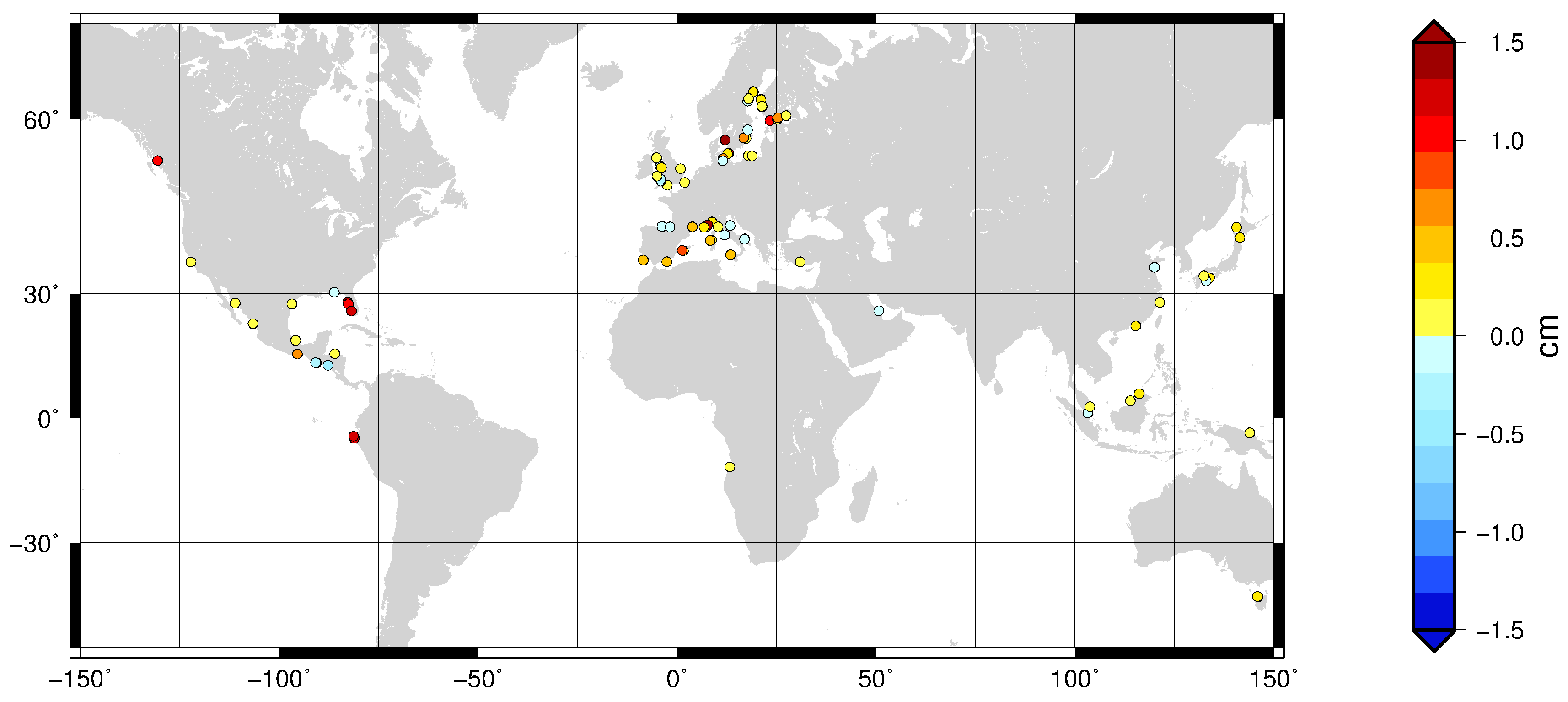
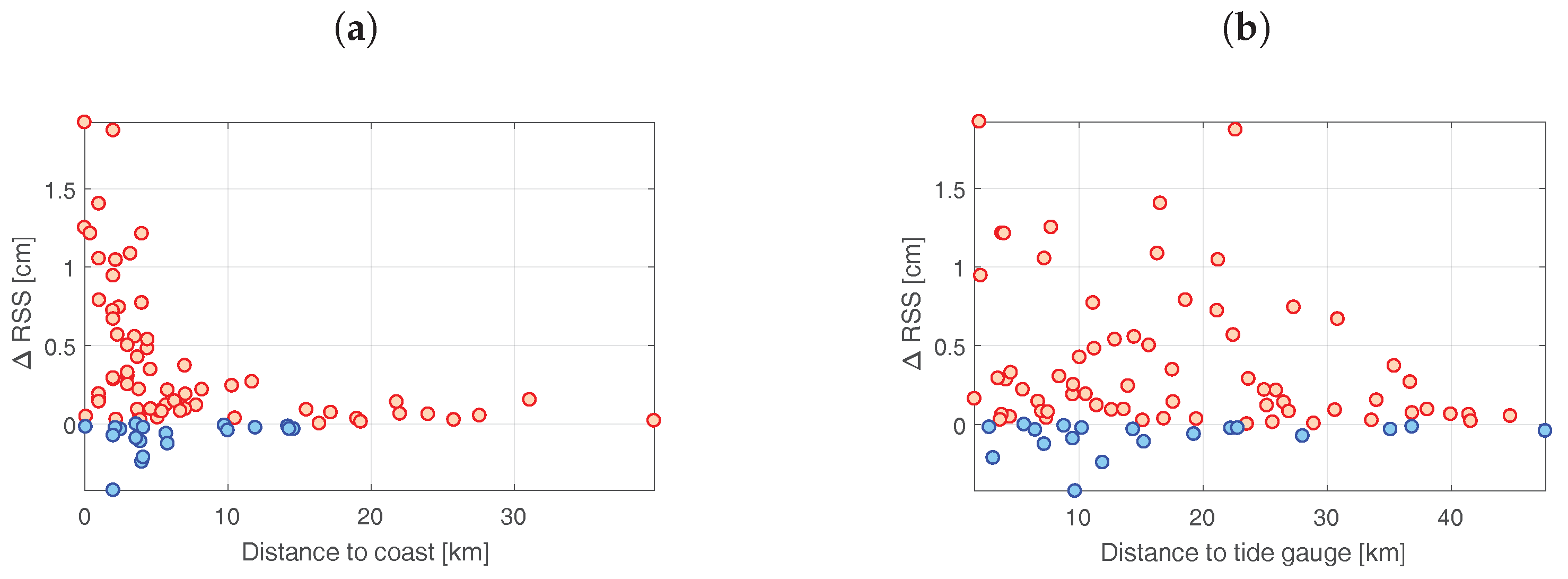
5.3. Comparison Against In Situ Data
5.3.1. General Results
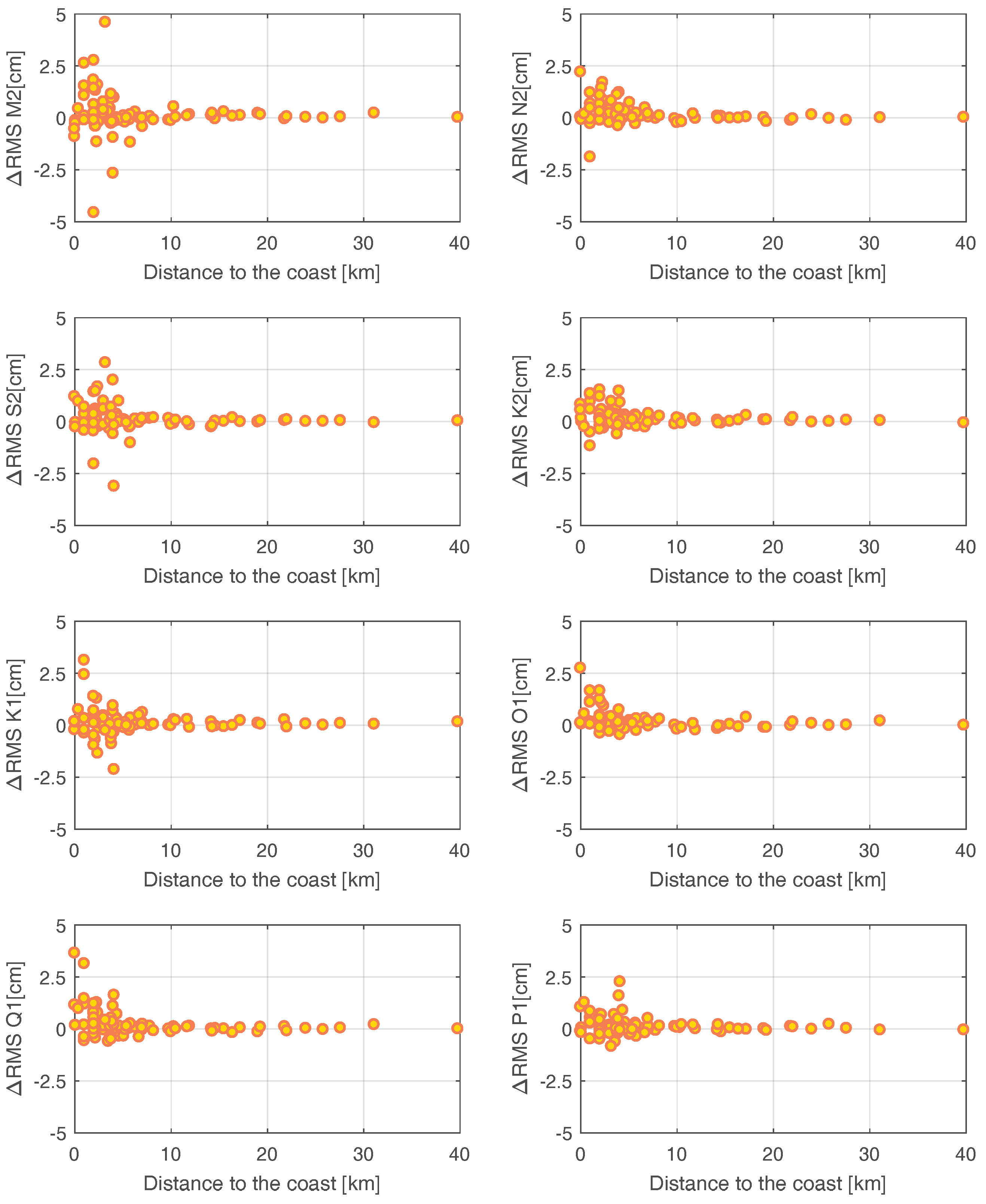
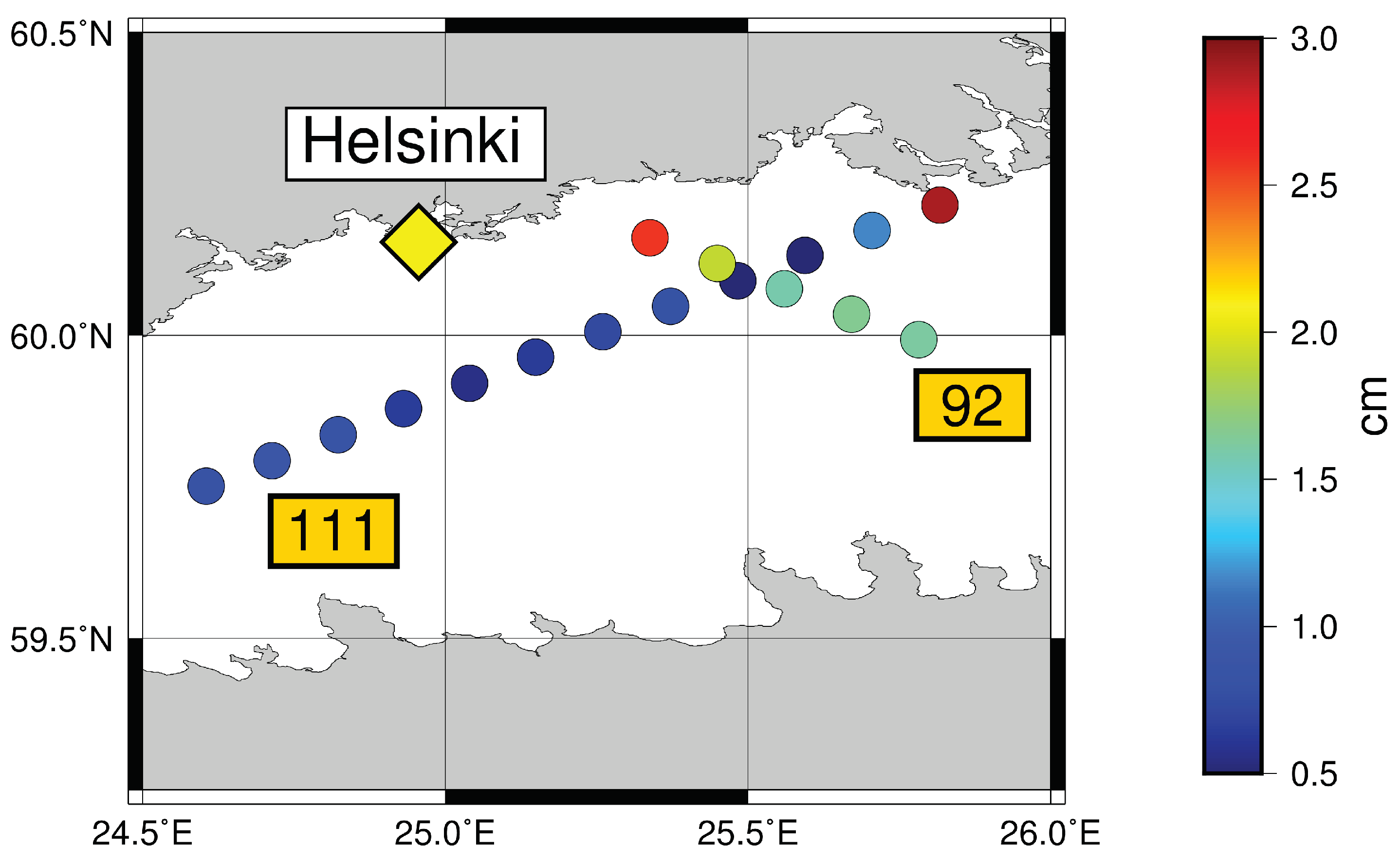
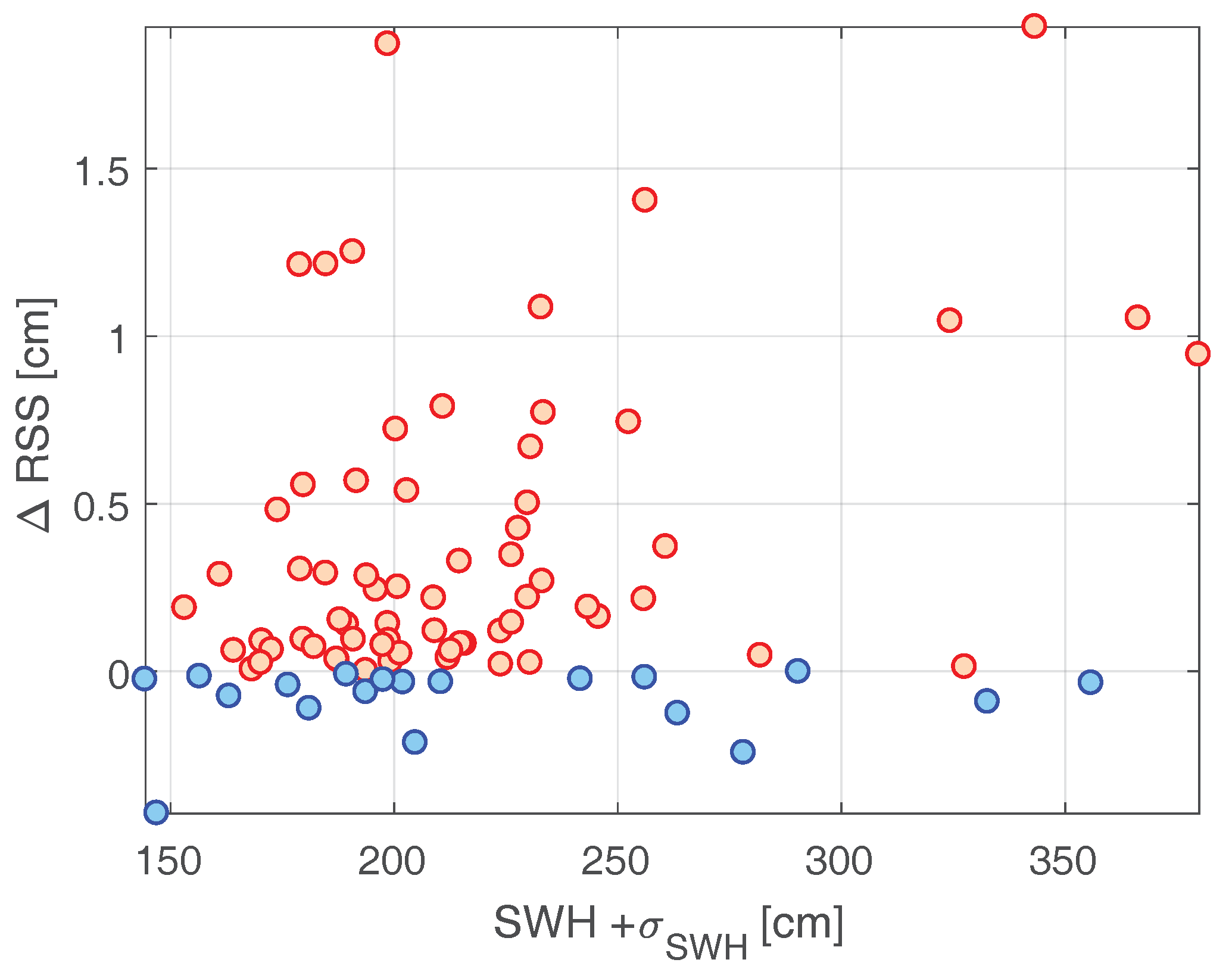
5.3.2. Study of the Dependencies
6. Conclusions and Outlook
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bonnefond, P.; Haines, B.J.; Watson, C. In situ absolute calibration and validation. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 259–296. ISBN 978-3-642-12795-3. [Google Scholar]
- Shum, C.K.; Woodworth, P.L.; Andersen, O.B.; Egbert, G.D.; Francis, O.; King, C.; Klosko, S.M.; Provost, C.L.; Li, X.; Molines, J.-M.; et al. Accuracy assessment of recent ocean tide models. J. Geophys. Res. 1997, 102, 25173–25194. [Google Scholar] [CrossRef]
- Savcenko, R.; Bosch, W. EOT11a—Empirical Ocean Tide Model From Multi-Mission Satellite Altimetry; DGFI Report No. 89; Deutsches Geodätisches Forschungsinstitut: Munich, Germany, 2012. [Google Scholar] [CrossRef]
- Andersen, O.B. Shallow water tides in the Northwest European shelf region from TOPEX/POSEIDON altimetry. J. Geophys. Res. 1999, 104, 7729–7741. [Google Scholar] [CrossRef]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Gommenginger, C.; Thibaut, P.; Fenoglio-Marc, L.; Quartly, G.; Deng, X.; Gómez-Enri, J.; Challenor, P.; Gao, Y. Retracking altimeter waveforms near the coasts. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–101. ISBN 978-3-642-12795-3. [Google Scholar]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- Andersen, O.B.; Piccioni, G. Recent Arctic sea level variations from satellites. Front. Mar. Sci. 2016, 3, 76. [Google Scholar] [CrossRef]
- Cipollini, P.; Benveniste, J.; Birol, F.; Fernandes, M.J.; Passaro, M.; Vignudelli, S. Satellite altimetry in coastal regions. In Satellite Altimetry over Oceans and Land Surfaces; Stammer, D., Cazenave, A., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 343–380. [Google Scholar]
- Liu, Y.; Weisberg, R.H.; Vignudelli, S.; Roblou, L.; Merz, C.R. Comparison of the X-TRACK altimetry estimated currents with moored ADCP and HF radar observations on the West Florida Shelf. Adv. Space Res. 2012, 50, 1085–1098. [Google Scholar] [CrossRef]
- Passaro, M.; Fenoglio-Marc, L.; Cipollini, P. Validation of Significant Wave Height from improved satellite altimetry in the German Bight. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4. [Google Scholar] [CrossRef]
- Passaro, M.; Dinardo, S.; Quartly, G.D.; Snaith, H.M.; Benveniste, J.; Cipollini, P.; Lucas, B. Cross-calibrating ALES Envisat and CryoSat-2 Delay-Doppler: A coastal altimetry study in the Indonesian Seas. Adv. Space Res. 2016, 58, 289–303. [Google Scholar] [CrossRef]
- Lago, L.S.; Saraceno, M.; Ruiz-Etcheverry, L.A.; Passaro, M.; Oreiro, F.A.; D’Onofrio, E.E.; González, R. Improved sea surface height from satellite altimetry in coastal zones: A case study in Southern Patagonia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3493–3503. [Google Scholar] [CrossRef]
- Andersen, O.B.; Scharroo, R. Range and geophysical corrections in coastal regions—And implications for mean sea surface determination. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 103–145. ISBN 978-3-642-12795-3. [Google Scholar]
- Picot, N.; Case, K.; Desai, S.; Vincent, P.; Bronner, E. AVISO and PODAAC User Handbook. IGDR and GDR Jason Products; SALP-MU-M5-OP-13184-CN (AVISO), JPL D-21352 (PODAAC); Physical Oceanography Distributed Active Archive Center: Pasadena, CA, USA, 2012. [Google Scholar]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Hayne, G.S. Radar altimeter mean return waveforms from near-normal- incidence ocean surface scattering. IEEE Trans. Antennas Propag. 1980, 28, 687–692. [Google Scholar] [CrossRef]
- Tran, N.; Thibaut, P.; Poisson, J.-C.; Philipps, S.; Bronner, E.; Picot, N. Impact of Jason-2 wind speed calibration on the sea state bias correction. Mar. Geod. 2011, 34, 3–4. [Google Scholar] [CrossRef]
- Gómez-Enri, J.; Cipollini, P.; Passaro, M.; Vignudelli, S.; Tejedor, B.; Coca, J. Coastal altimetry products in the strait of Gibraltar. IEEE Trans. Geosci. Remote Sens. 2016, 54, 99. [Google Scholar] [CrossRef]
- Andersen, O.B.; Stenseng, L.; Piccioni, G.; Knudsen, P. The DTU15 MSS (Mean Sea Surface) and DTU15LAT (Lowest Astronomical Tide) reference surface. In Proceedings of the ESA Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Carrère, L.; Faugère, Y.; Bronner, E.; Benveniste, J. Improving the dynamic atmospheric correction for mean sea level and operational applications of atimetry. In Proceedings of the Ocean Surface Topography Science Team (OSTST) Meeting, San Diego, CA, USA, 19–21 October 2011. [Google Scholar]
- Persson, A. User Guide to ECMWF Forecast Products; ECMWF: Reading, UK, 2015. [Google Scholar]
- Scharroo, R.; Smith, W.H.F. A global positioning system-based climatology for the total electron content in the ionosphere. J. Geophys. Res. 2010, 115, 16. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F.; Cancet, M.; Guillot, A.; Picot, N. FES 2014, a new tidal model—Validation results and perspectives for improvements. In Proceedings of the ESA Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- McCarthy, D.D.; Petit, G. (Eds.) IERS Conventions (2003); IERS Technical Note 32; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2004. [Google Scholar]
- Passaro, M.; Kildegaard Rose, S.; Andersen, O.B.; Boergens, E.; Calafat, F.M.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters. Remote Sens. Environ. 2018, in press. [Google Scholar] [CrossRef]
- Woodworth, P.L.; Hunter, J.R.; Marcos, M.; Caldwell, P.; Menendez, M.; Haigh, I. Towards a global higher-frequency sea level data set. Geosci. Data J. 2017, 3, 50–59. [Google Scholar] [CrossRef]
- Savcenko, R.; Bosch, W. Residual tide analysis in shallow water-contribution of ENVISAT and ERS altimetry. In ESA-SP636 (CD-ROM), Proceedings of the Envisat Symposium 2007, Montreux, Switzerland, 23–27 April 2007; Lacoste, H., Ouwehand, L., Eds.; ESA: Noordwijk, The Netherlands, 2007. [Google Scholar]
- Bosch, W.; Savcenko, R.; Flechtner, F.; Dahle, C.; Mayer-Gürr, T.; Stammer, D.; Taguchi, E.; Ilk, K.H. Residual ocean tide signals from satellite altimetry, GRACE gravity fields, and hydrodynamic modelling. Geophys. J. Int. 2009, 178, 1185–1192. [Google Scholar] [CrossRef]
- Doodson, A.T.; Warburg, H.D. Admiralty Manual of Tides; H. M. Stationery Off.: London, UK, 1941. [Google Scholar]
- Teunissen, P.; Amiri-Simkooei, A. Variance component estimation by the method of least-squares. In VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy, Proceedings of the IAG Symposium, Wuhan, China, 29 May–2 June 2006; Xu, P., Liu, J., Dermanis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-74583-9. [Google Scholar]
- Koch, K.-R. Parameter Estimation and Hypothesis Testing in Linear Models, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1999; ISBN 978-3-540-65257-1. [Google Scholar]
- Passaro, M.; Cipollini, P.; Benveniste, J. Annual sea level variability of the coastal ocean: The Baltic Sea-North Sea transition zone. J. Geophys. Res. Oceans 2015, 120, 3061–3078. [Google Scholar] [CrossRef]
| Correction | Model | Reference |
|---|---|---|
| Mean Sea Surface | DTU15MSS | Andersen et al. [20] |
| Inverse barometer | Dynamic Atmospheric Correction (DAC) | Carrère et al. [21] |
| Wet and Dry troposphere | ECMWF | ECMWF [22] |
| Ionosphere | NOAA Ionosphere Climatology 2009 (NIC09) | Scharroo and Smith [23] |
| Ocean and Load tide | FES2014 | Carrère et al. [24] |
| Solid Earth and Pole Tide | IERS Conventions 2003 | McCarthy and Petit [25] |
| ALES Sea State Bias | ALES | Passaro et al. [19,26] |
| SGDR Sea State Bias | SGDR | AVISO/PODAAC [15] |
| Constituents | (cm) | (cm) | (%) |
|---|---|---|---|
| M2 | 8.0 | 8.2 | 2.4 |
| N2 | 2.1 | 2.3 | 8.7 |
| S2 | 3.5 | 3.7 | 5.4 |
| K2 | 1.4 | 1.6 | 12.5 |
| K1 | 2.1 | 2.2 | 4.5 |
| O1 | 1.4 | 1.6 | 12.5 |
| Q1 | 0.8 | 1.1 | 27.3 |
| P1 | 1.2 | 1.4 | 14.3 |
| Constituents | Land to Ocean: 30 | Ocean to Land: 34 | Land-Ocean-Land: 15 | Parallel to Land: 6 | ||||
|---|---|---|---|---|---|---|---|---|
| M2 | 6.6 | 6.9 | 4.8 | 5.0 | 19.3 | 19.2 | 4.6 | 4.7 |
| N2 | 1.7 | 1.8 | 1.3 | 1.6 | 4.8 | 5.2 | 1.4 | 1.4 |
| S2 | 3.1 | 3.2 | 2.1 | 2.4 | 7.7 | 7.8 | 2.6 | 2.5 |
| K2 | 1.2 | 1.3 | 1.0 | 1.3 | 2.8 | 2.9 | 1.7 | 1.7 |
| K1 | 1.9 | 1.9 | 1.4 | 1.5 | 3.8 | 4.2 | 2.2 | 2.2 |
| O1 | 1.2 | 1.3 | 1.0 | 1.3 | 2.5 | 2.7 | 1.6 | 1.6 |
| Q1 | 0.8 | 0.9 | 0.7 | 1.0 | 1.3 | 1.8 | 0.9 | 1.0 |
| P1 | 1.5 | 1.7 | 0.7 | 0.9 | 1.9 | 1.9 | 1.1 | 1.2 |
| RSS | 8.4 | 8.5 | 5.8 | 6.4 | 22.1 | 22.8 | 6.5 | 6.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piccioni, G.; Dettmering, D.; Passaro, M.; Schwatke, C.; Bosch, W.; Seitz, F. Coastal Improvements for Tide Models: The Impact of ALES Retracker. Remote Sens. 2018, 10, 700. https://doi.org/10.3390/rs10050700
Piccioni G, Dettmering D, Passaro M, Schwatke C, Bosch W, Seitz F. Coastal Improvements for Tide Models: The Impact of ALES Retracker. Remote Sensing. 2018; 10(5):700. https://doi.org/10.3390/rs10050700
Chicago/Turabian StylePiccioni, Gaia, Denise Dettmering, Marcello Passaro, Christian Schwatke, Wolfgang Bosch, and Florian Seitz. 2018. "Coastal Improvements for Tide Models: The Impact of ALES Retracker" Remote Sensing 10, no. 5: 700. https://doi.org/10.3390/rs10050700
APA StylePiccioni, G., Dettmering, D., Passaro, M., Schwatke, C., Bosch, W., & Seitz, F. (2018). Coastal Improvements for Tide Models: The Impact of ALES Retracker. Remote Sensing, 10(5), 700. https://doi.org/10.3390/rs10050700