Rainfall Variability, Wetland Persistence, and Water–Carbon Cycle Coupling in the Upper Zambezi River Basin in Southern Africa
Abstract
1. Introduction
2. Data and Methods
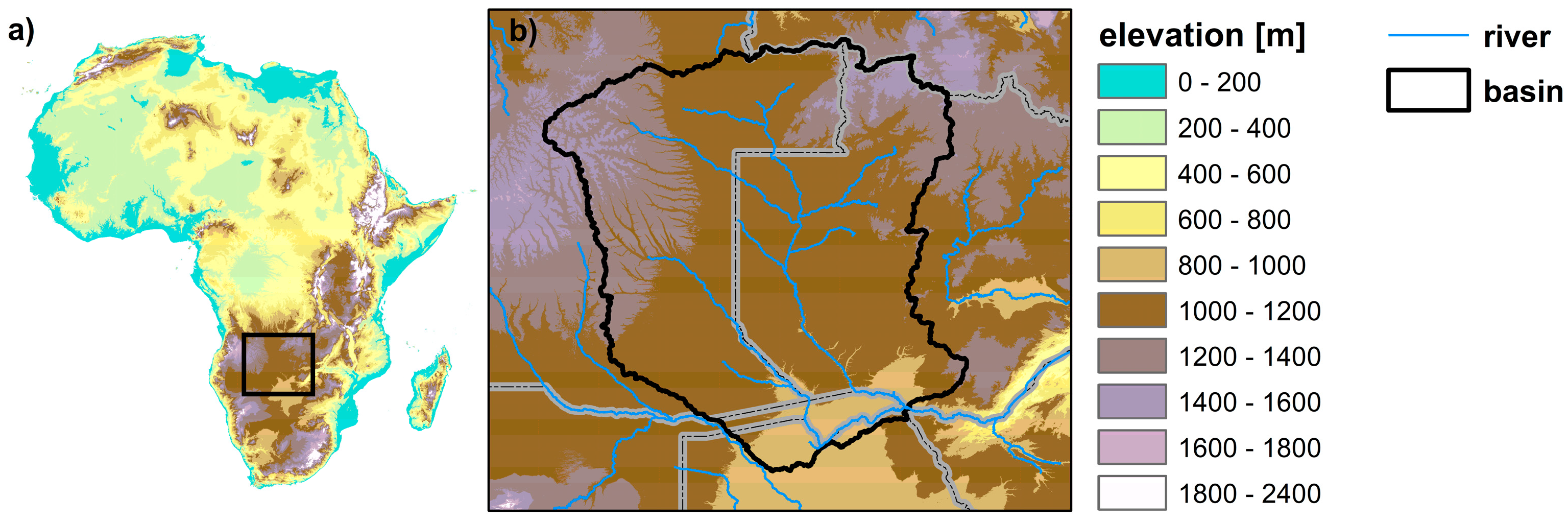
2.1. Study Area
2.2. Data
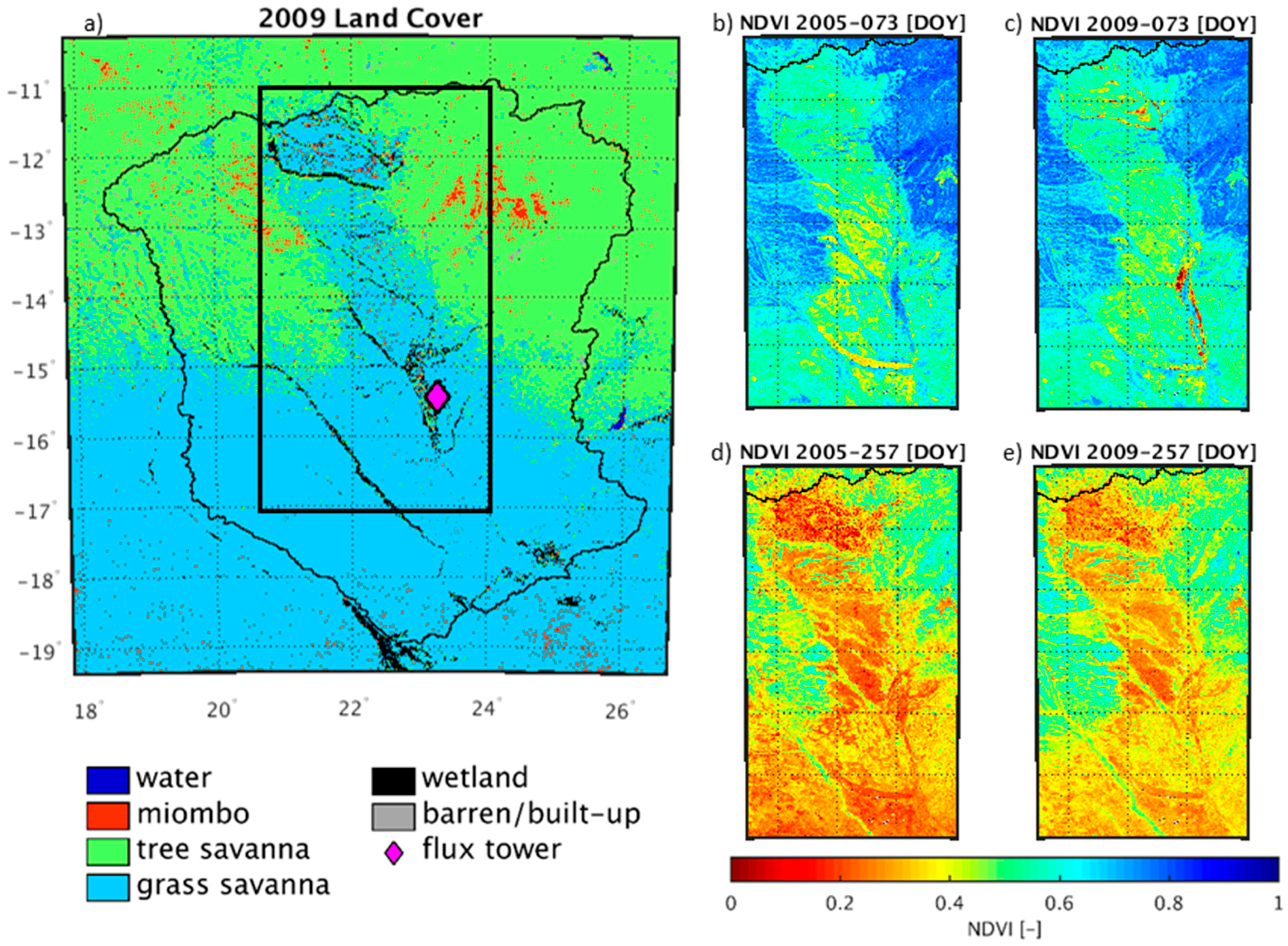
2.2.1. Land Surface Properties
2.2.2. Meteorological Forcing and Ancillary Data
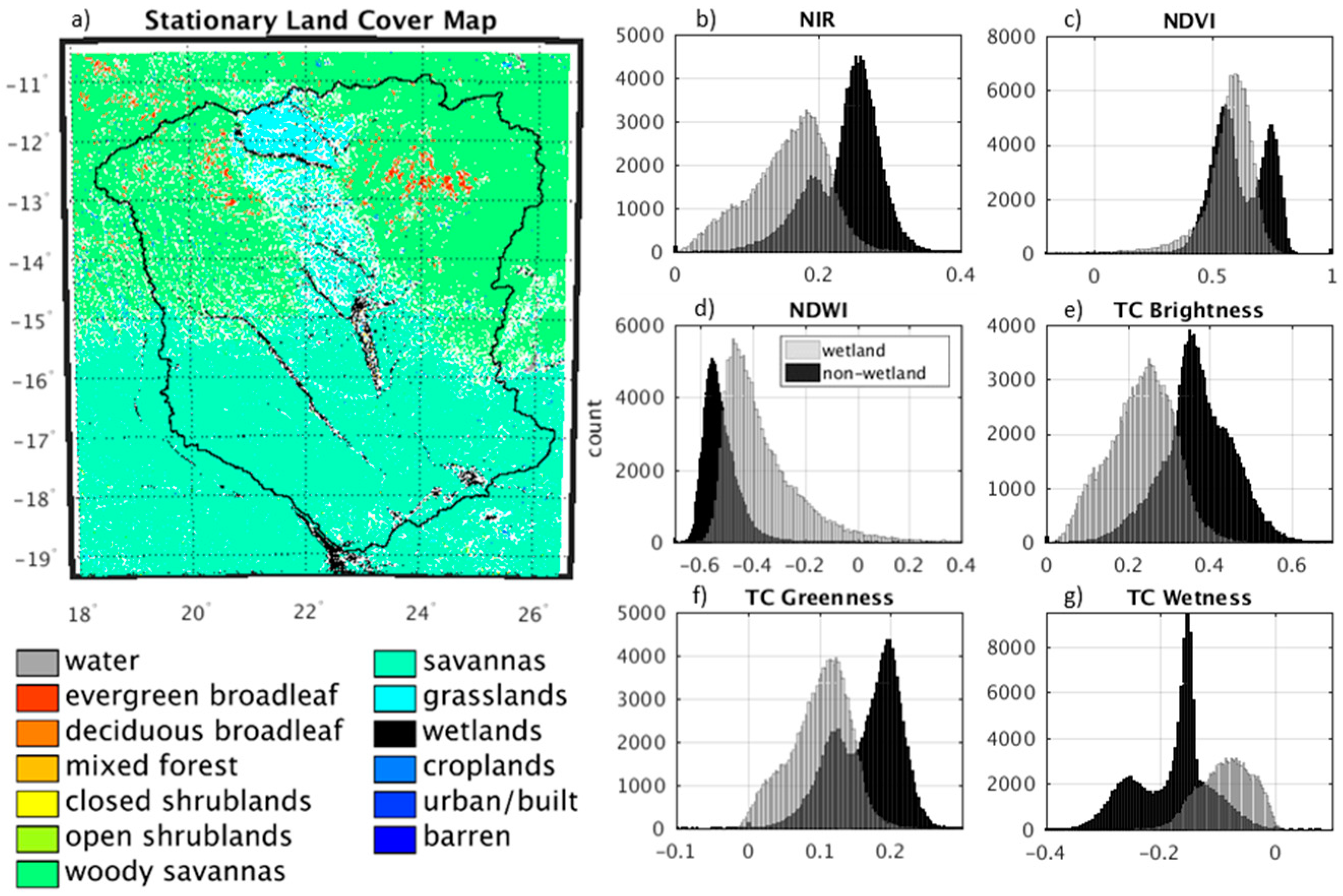
2.3. Wetland Probability Mapping Algorithm
2.3.1. NIR and NDVI
2.3.2. NDWI
2.3.3. Tasseled Cap Transformation
2.3.4. Logistic Regression Model for Probability Mapping
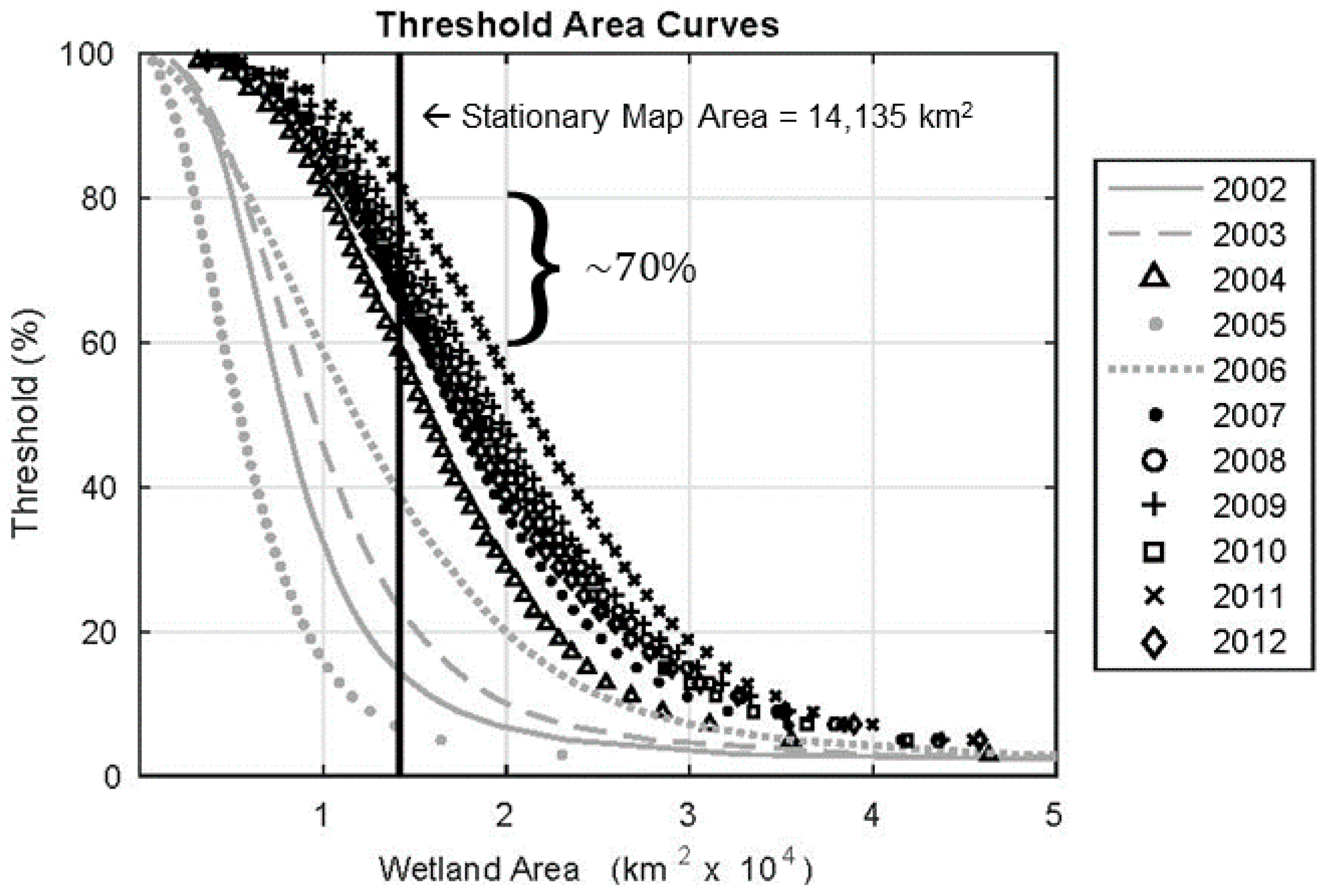
2.3.5. Calculating Wetland Fractions
2.4. Land-Surface Eco-Hydrology Modeling
2.5. Simulating Contributions of Wetlands to Water and Carbon Budgets
3. Results
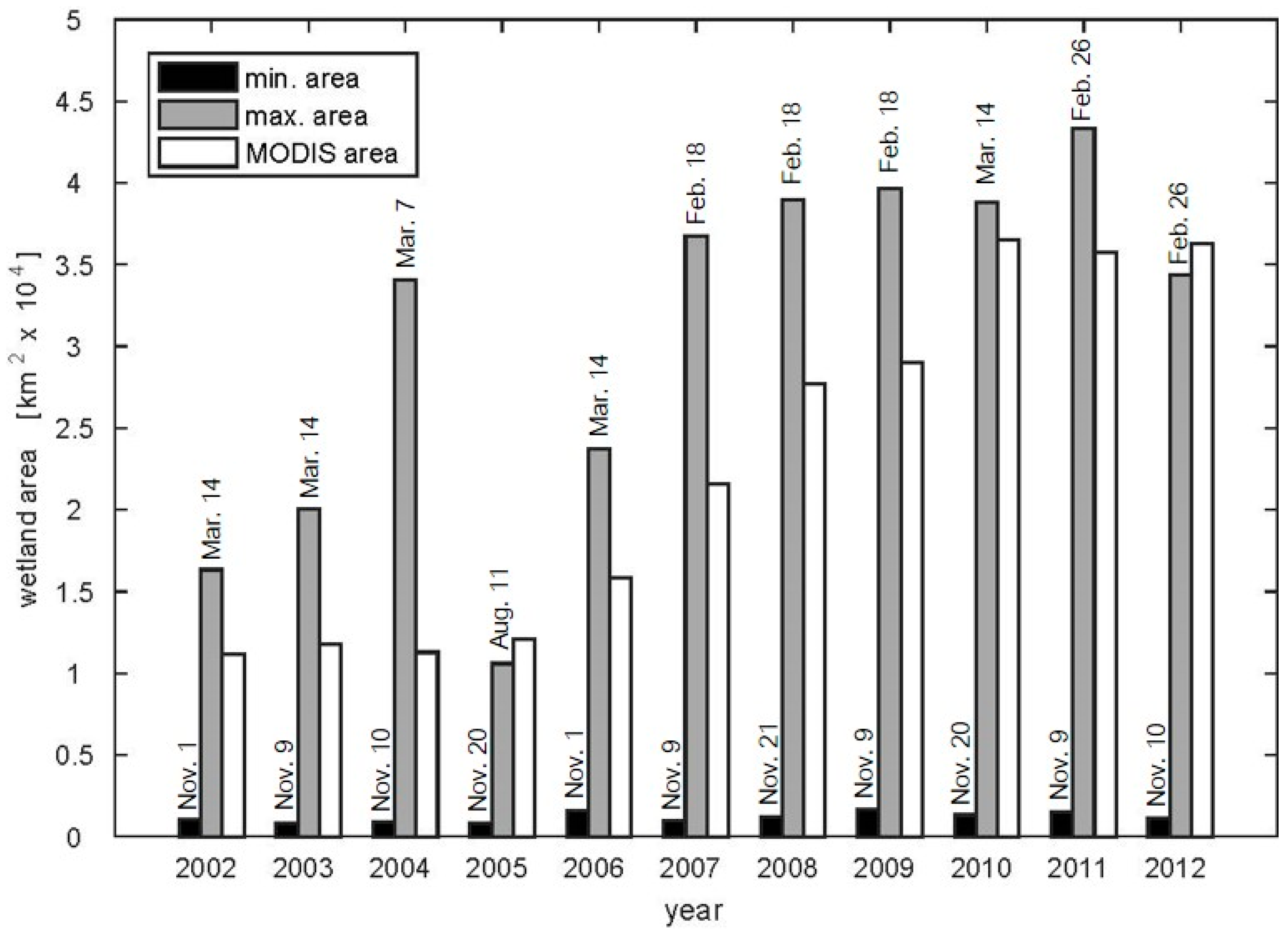
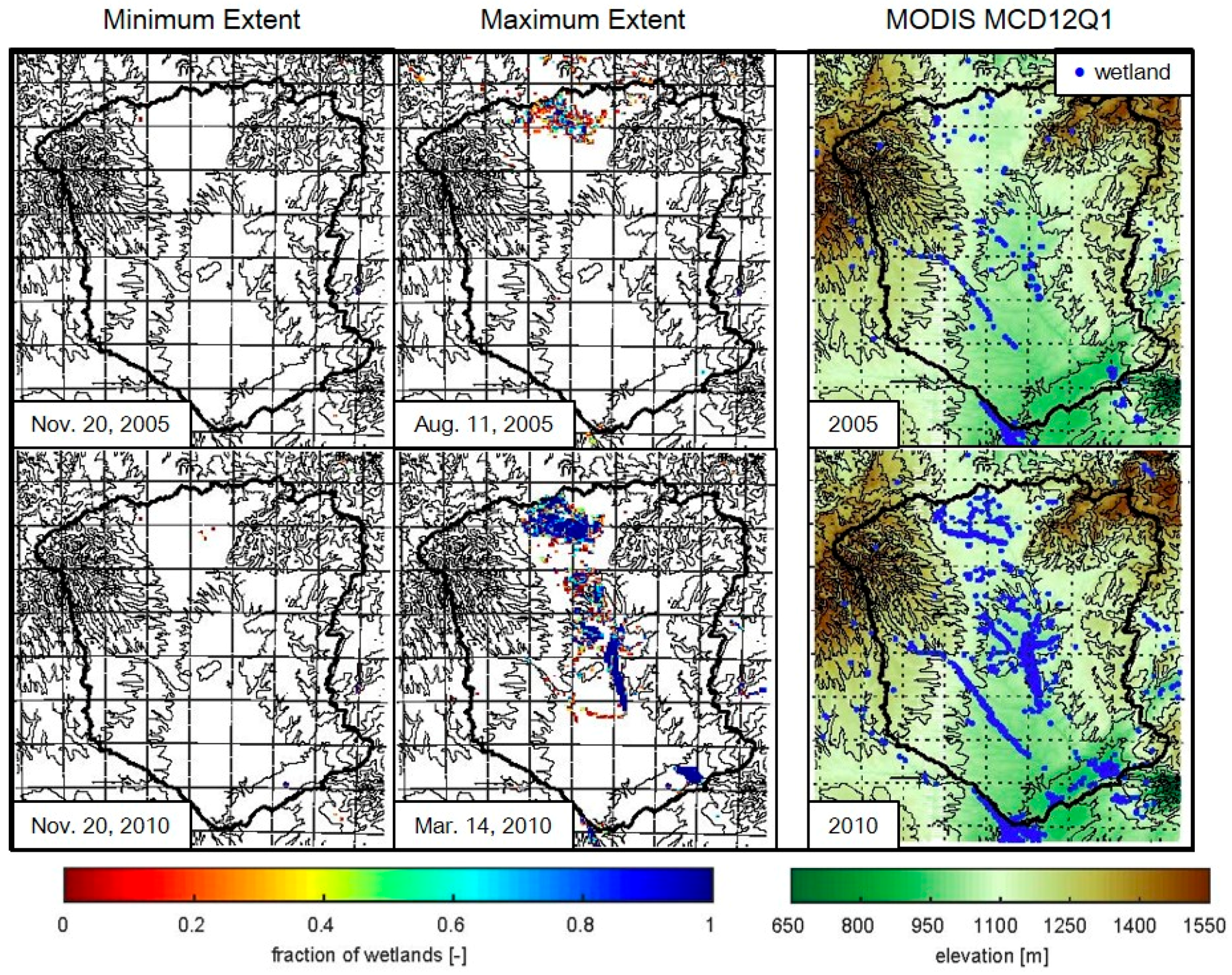
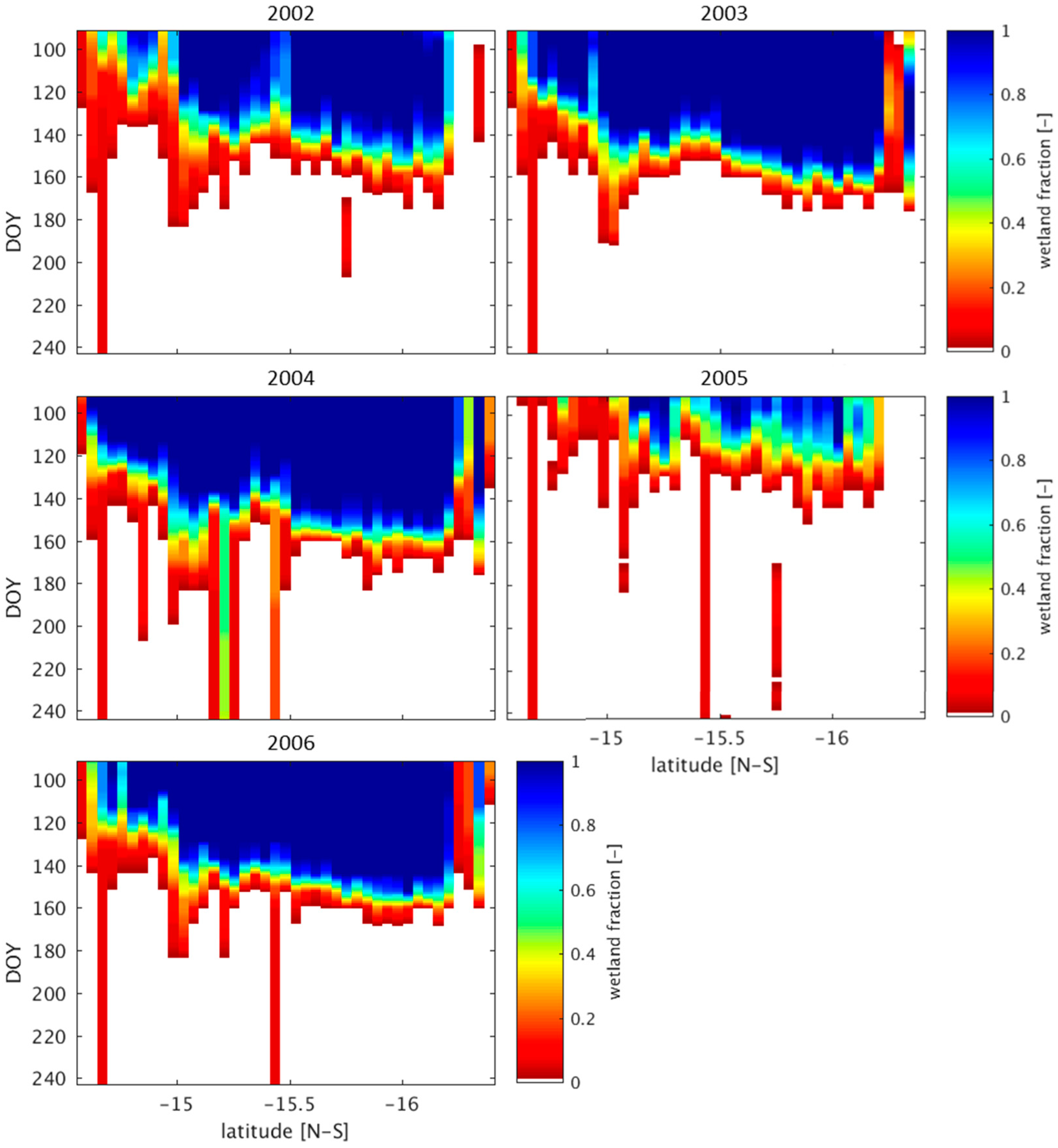
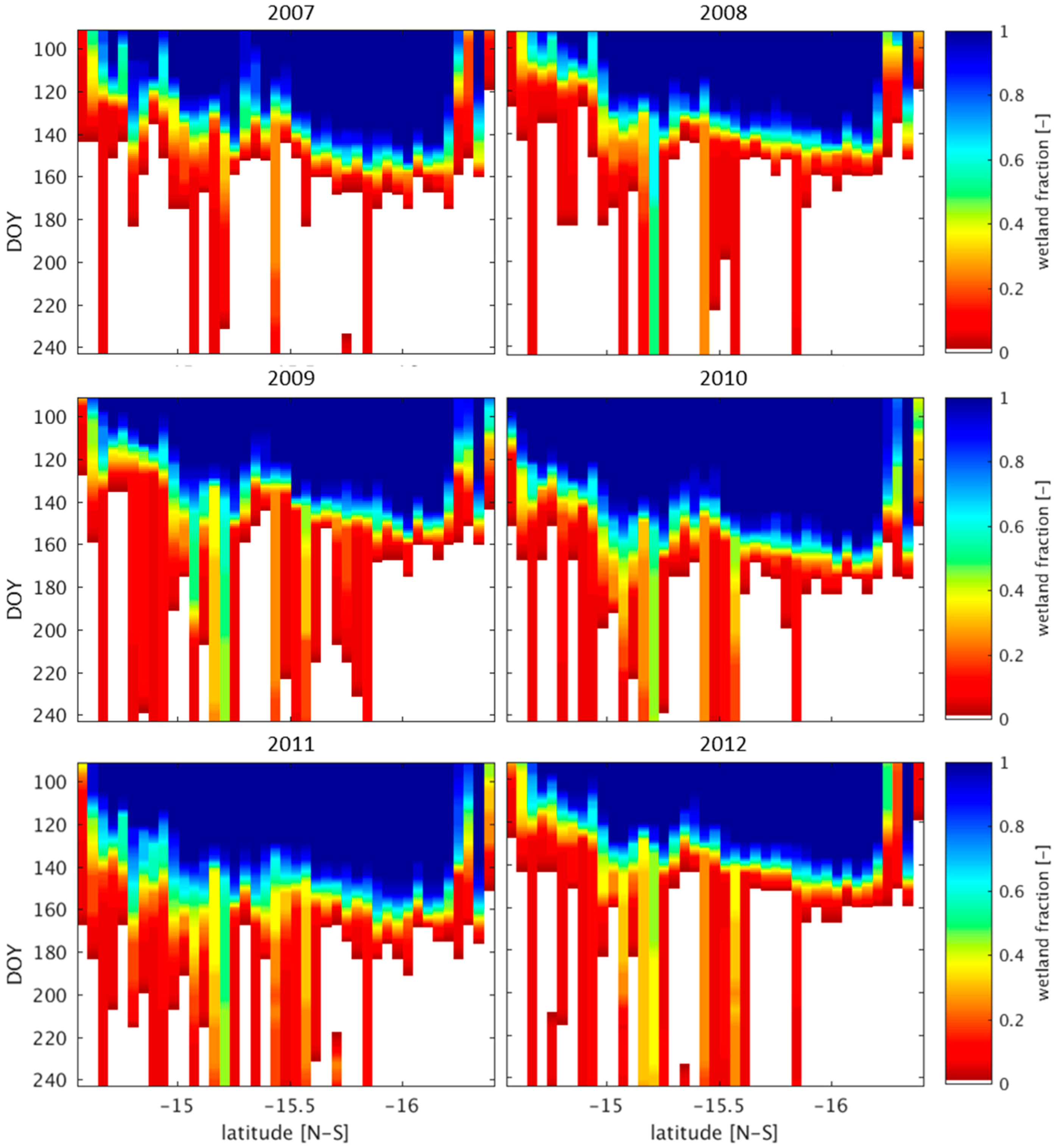
3.1. Wetland Mapping
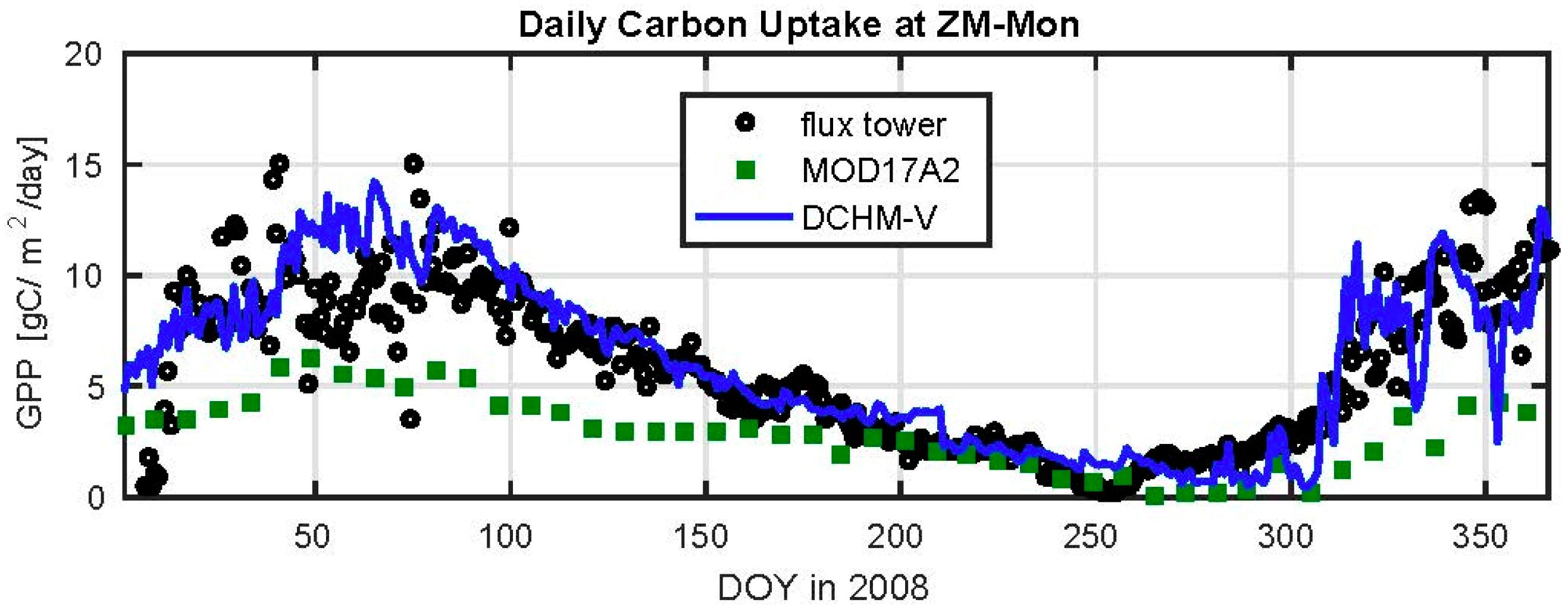
3.2. Evaluation of C4 Photosynthesis Routine at Mongu, Zambia
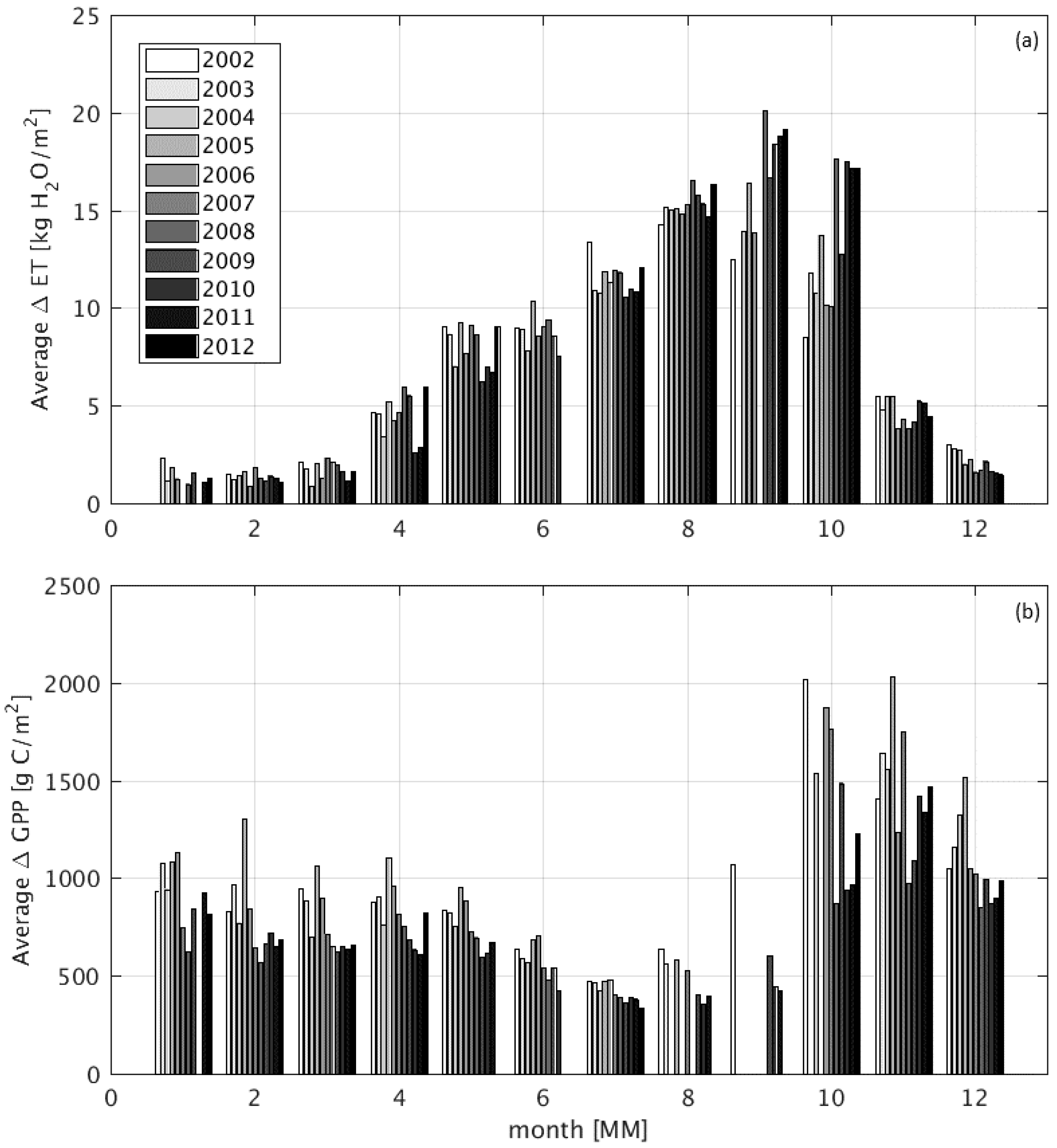
3.3. Modeled Surface Fluxes
4. Discussion
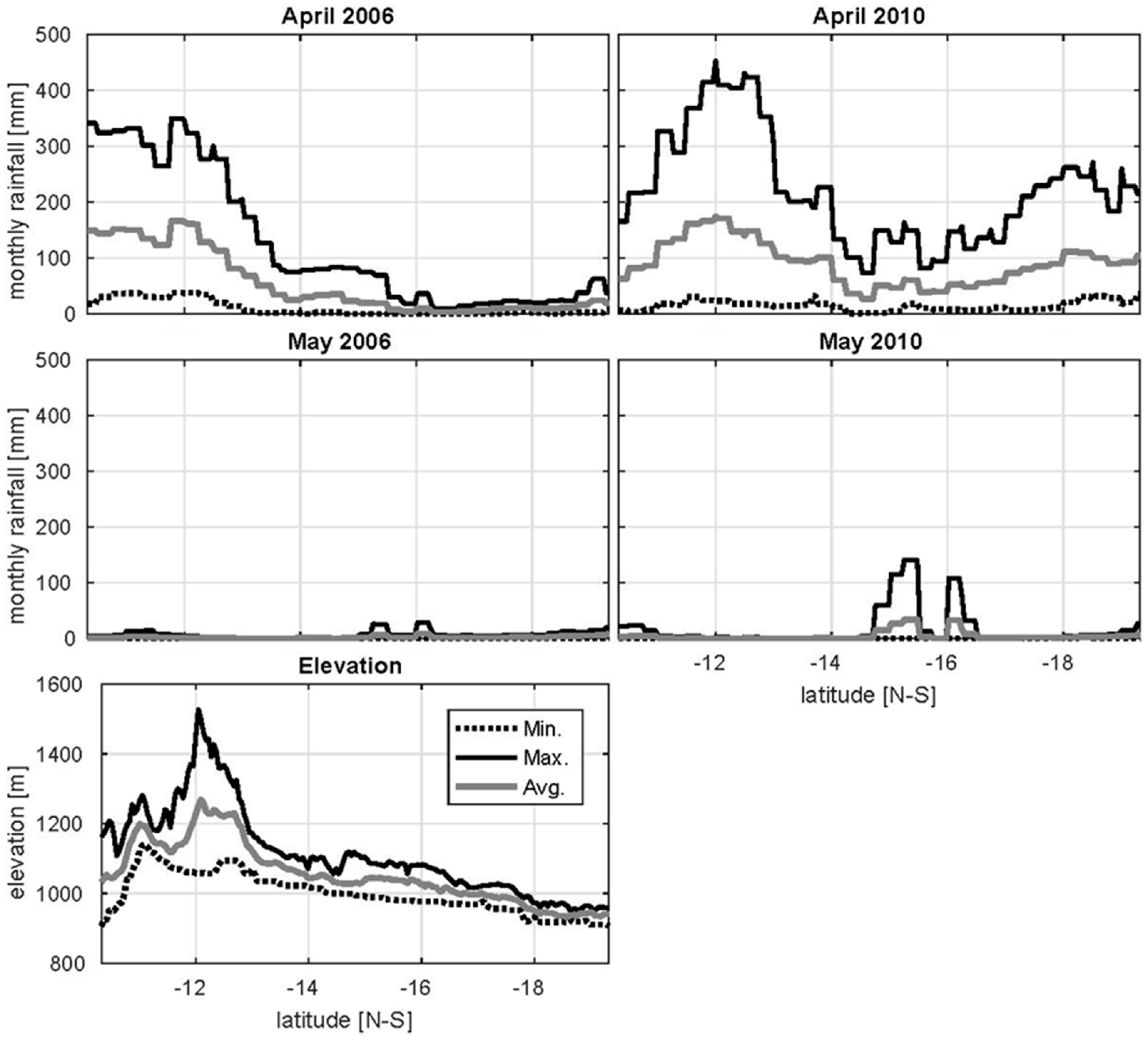
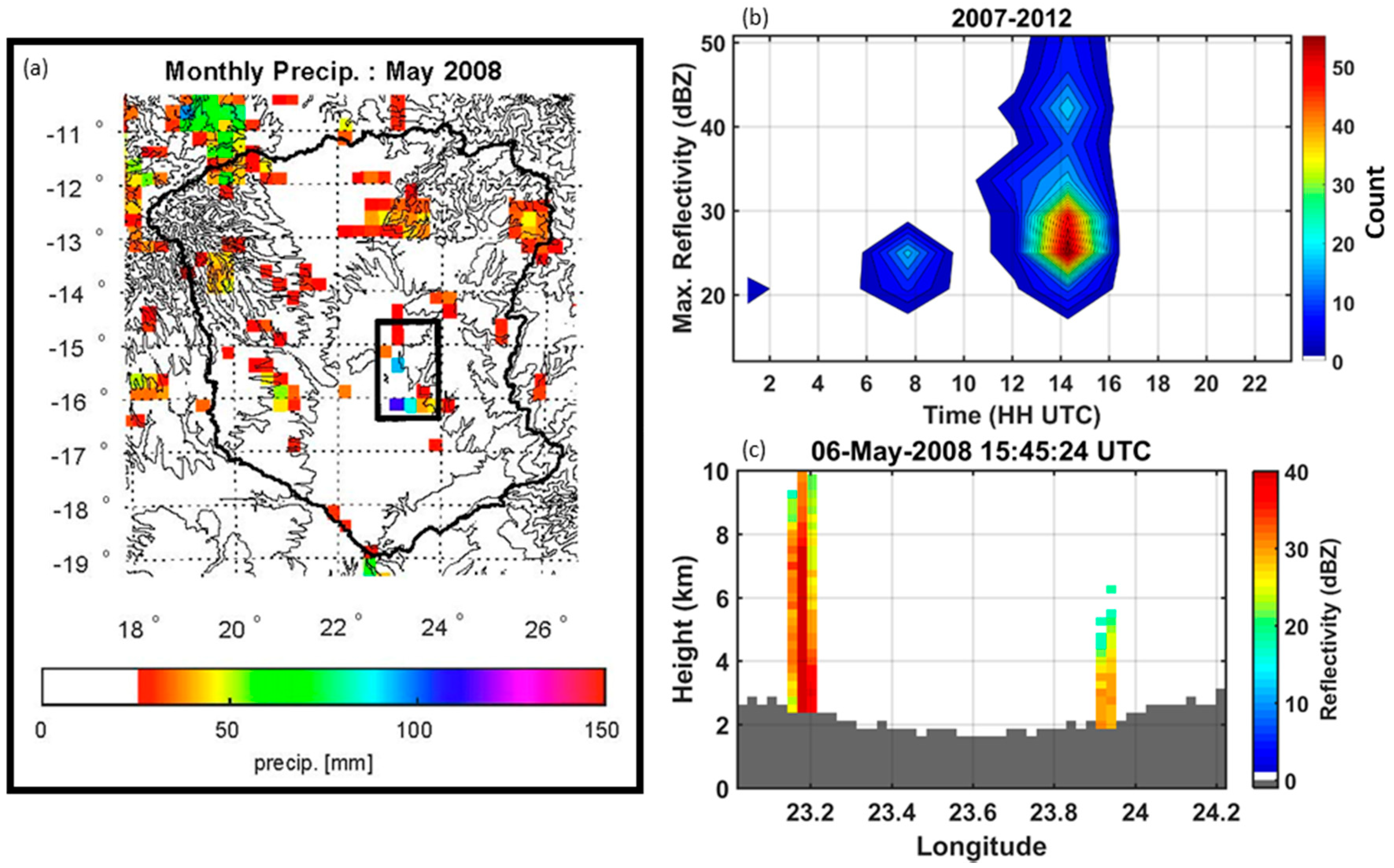
4.1. Precipitation Gradients in the UZRB
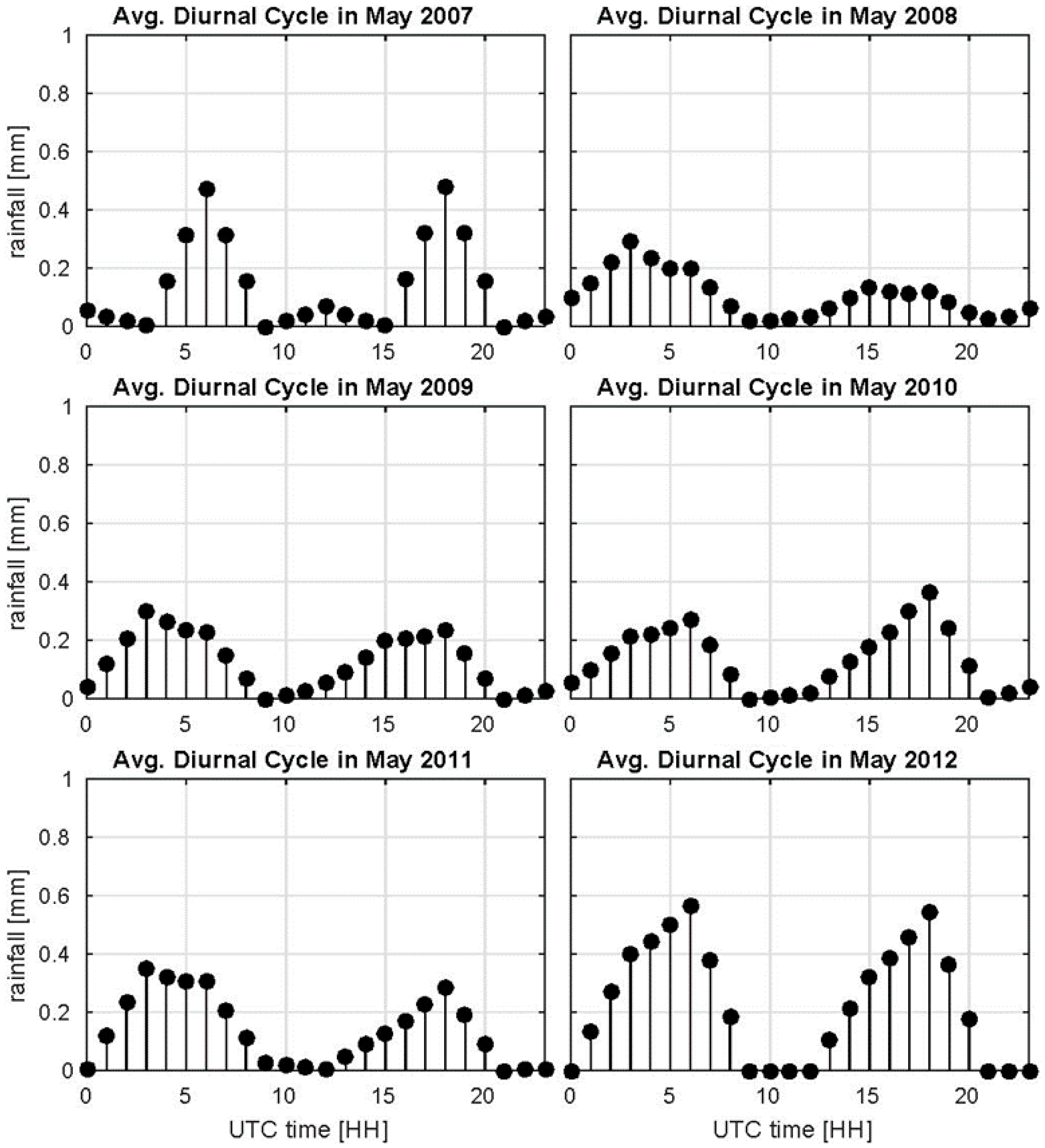
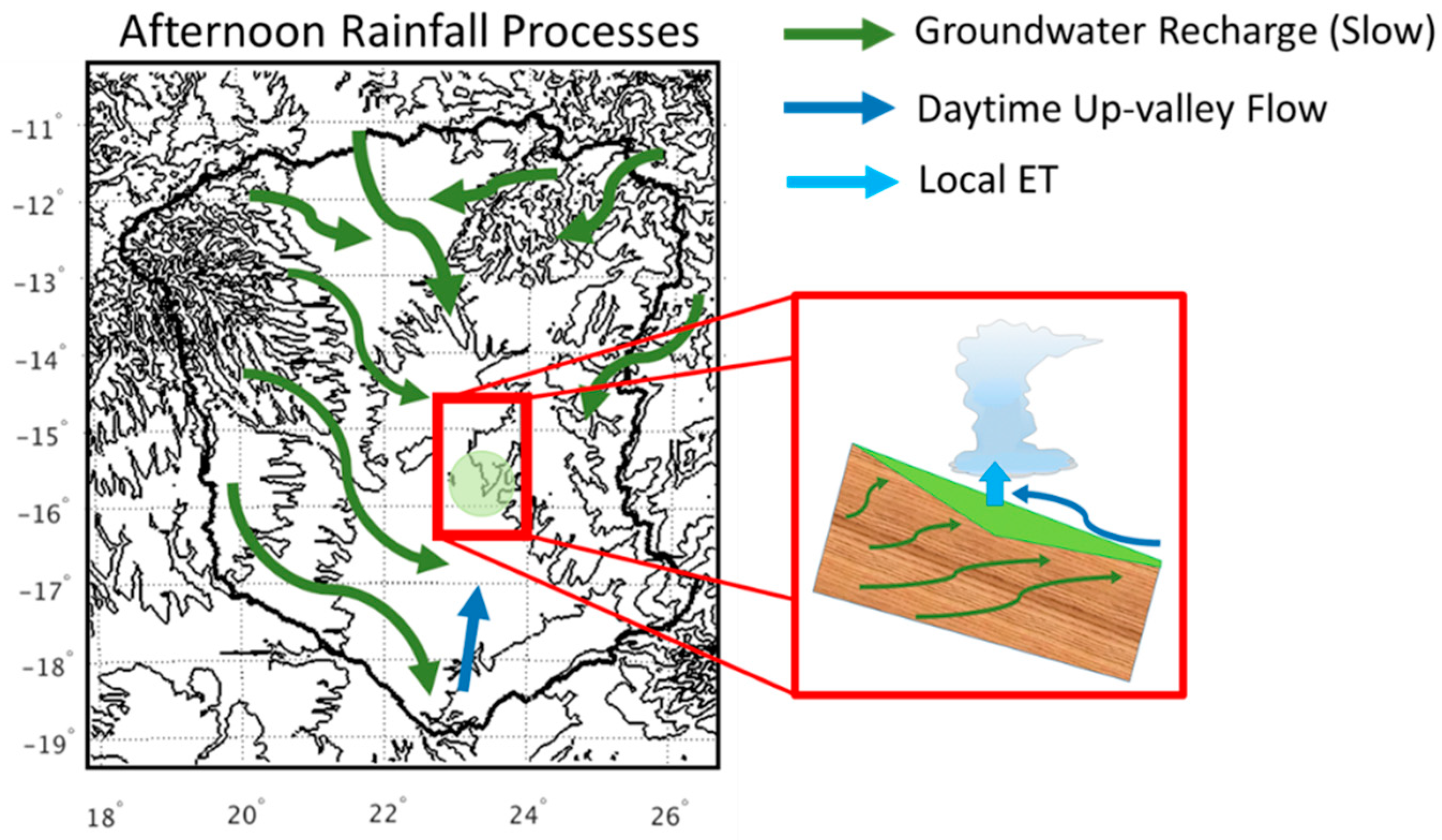
4.2. Wetland Persistence and Dry Season Rainfall
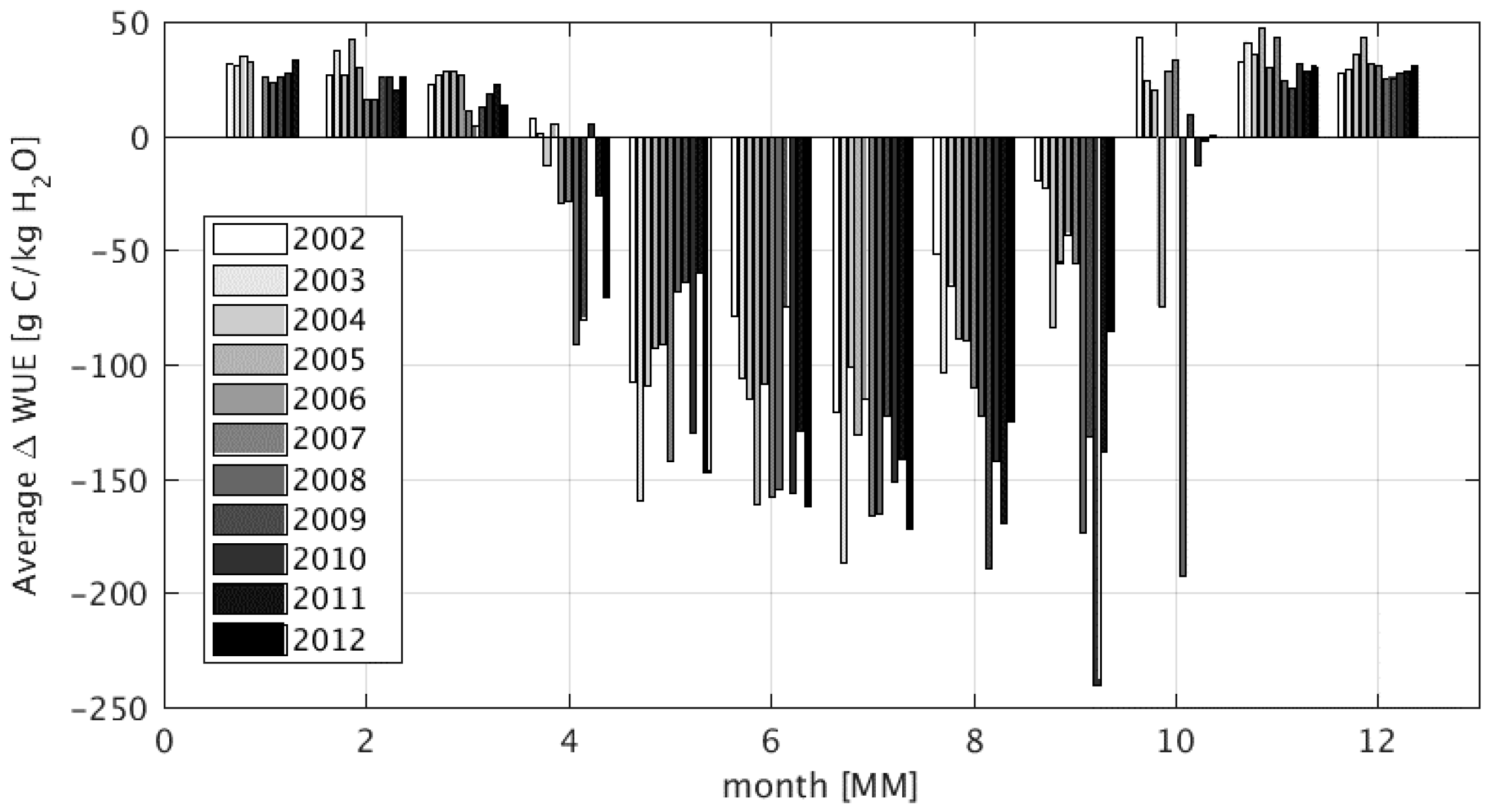
4.3. Impact of Wetlands on Productivity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. C4 Photosynthesis Equations for DCHM-V
Appendix A.1. Overview
Appendix A.2. C4 Photosynthesis Model Equations
Appendix A.2.1. Carboxylation Equations
Appendix A.2.2. RuBP Regeneration/Election Transport Rate Equations
Appendix A.2.3. Temperature Dependencies for Maximum Enzymatic Rates
| Model Variable | Description | Units |
|---|---|---|
| Net carbon assimilation rate | mol C m−2 s−1 | |
| RuBP regeneration rate | mol C m−2 s−1 | |
| Carboxylation rate | mol C m−2 s−1 | |
| Rate of PEP carboxylation | mol C m−2 s−1 | |
| Rate of Rubisco carboxylation at high irradiance | mol C m−2 s−1 | |
| Maximum rate of carboxylation by Rubisco | mol C m−2 s−1 | |
| Michaelis–Menten constant for PEP carboxylase of CO2 | ubar | |
| Maximum rate of carboxylation by PEP | mol C m−2 s−1 | |
| Maximum rate of electron transport | mol C m−2 s−1 | |
| CO2 compensation point in bundle sheath cells | mol mol−1 | |
| Bundle-sheath CO2 partial pressure | unity | |
| Bundle-sheath O2 partial pressure | unity | |
| Rate of electron transport in mesophyll cells | mol C m−2 s−1 | |
| Rate of electron transport in bundle sheath cells | mol C m−2 s−1 | |
| Total rate of electron transport | mol C m−2 s−1 |
| Model Parameter | Description | Value | Units | Reference |
|---|---|---|---|---|
| Bundle sheath conductance | 3 | mmol m−2 s−1 | [96] | |
| CO2 concentration in mesophyll cell | mol m−3 | [67] | ||
| CO2 concentration outside the leaf boundary layer | 0.0145 | mol m−3 | [67] | |
| Mesophyll mitochondrial respiration | umol C m−2 s−1 | [94] | ||
| Leaf mitochondrial respiration | umol C m−2 s−1 | [94] | ||
| PEP regeneration rate | 80 | umol C m−2 s−1 | [94] | |
| Intercellular O2 concentration | 210 | mmol mol−1 | [97] | |
| Partitioning factor of electron transport rate | 0.4 | unity | [94] | |
| Half of reciprocal of Rubisco specificity | 0.000193 | unity | [94] |
| Parameter | Units | Measured at 25 °C | [umol m−2 s−1] | [kJ mol−1] | [kJ mol−1 K−1] | [kJ mol−1] | Reference |
|---|---|---|---|---|---|---|---|
| Kp | Pa CO2 | 16.0 ± 1.3 | 13.9 ± 1.0 | 36.3 ± 2.4 | - | - | [95] |
| μM HCO3 | 62.8 ± 5.0 | 60.5 ± 2.4 | 27.2 ± 2.8 | - | - | [95] | |
| Kc | Pa CO2 | 94.7 ± 15.1 | 121 ± 7 | 64.2 ± 4.5 | - | - | [95] |
| Ko | kPa of oxygen | 28.9 ± 5.4 | 29.2 ± 1.9 | 10.5 ± 4.8 | - | - | [95] |
| Sc/o | Pa/Pa | 1610 ± 66 | 1310 ± 52 | −31.1 ± 2.9 | - | - | [95] |
| Vpmax | μmol HCO3/m2/s | 450 ± 16 | - | - | [95] | ||
| Normalized to 1 at 25 °C | 1 | 1.01 ± 0.07 | 94.8 ± 40.8 | 0.25 ± 0.12 | 73.3 ± 39.6 | [95] | |
| μmol/m2/s | - | 125 | 70,373 | 376 | 177,910 | [96] | |
| μmol/m2/s | - | 159.9 ± 6.8 | 175.2 ± 3.8 171.6 ± 1.0 2 | - | - | [98] | |
| Vcmax | Normalized to 1 at 25° | 0.96 ± 0.04 | 0.89 ± 0.05 | 78.0 ± 4.1 | - | - | [95] |
| μmol/m2/s | - | 32 | 67,294 | 472 | 144,568 | [96] | |
| mol/m2/s | - | 3.9 ± 0.3 | 100.6 ± 2.0 156.1 ± 1.4 2 | [98] | |||
| Jmax | μmol/m2/s | - | 191 | 77,900 | 627 | 191,929 | [96] |
References
- Zedler, J.B.; Kercher, S. WETLAND RESOURCES: Status, Trends, Ecosystem Services, and Restorability. Annu. Rev. Environ. Resour. 2005, 30, 39–74. [Google Scholar] [CrossRef]
- Winter, T.C. The vulnerability of wetlands to climate change: A hydrologic landscape perspective1. JAWRA J. Am. Water Resour. Assoc. 2007, 36, 305–311. [Google Scholar] [CrossRef]
- Zhuang, Q.; Melillo, J.M.; Kicklighter, D.W.; Prinn, R.G.; McGuire, A.D.; Steudler, P.A.; Felzer, B.S.; Hu, S. Methane fluxes between terrestrial ecosystems and the atmosphere at northern high latitudes during the past century: A retrospective analysis with a process-based biogeochemistry model. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Matthews, E.; Fung, I. Methane emission from natural wetlands: Global distribution, area, and environmental characteristics of sources. Glob. Biogeochem. Cycles 1987, 1, 61–86. [Google Scholar] [CrossRef]
- Djebou, D.C.S. Integrated approach to assessing streamflow and precipitation alterations under environmental change: Application in the Niger River Basin. J. Hydrol. Reg. Stud. 2015, 4, 571–582. [Google Scholar] [CrossRef]
- Hunt, R.J.; Walker, J.F.; Krabbenhoft, D.P. Characterizing hydrology and the importance of ground-water discharge in natural and constructed wetlands. Wetlands 1999, 19, 458–472. [Google Scholar] [CrossRef]
- Taylor, A.R.D.; Howard, G.W.; Begg, G.W. Developing wetland inventories in southern Africa: A review. Vegetatio 1995, 118, 57–79. [Google Scholar] [CrossRef]
- Rebelo, L.-M.; McCartney, M.P.; Finlayson, C.M. Wetlands of Sub-Saharan Africa: Distribution and contribution of agriculture to livelihoods. Wetl. Ecol. Manag. 2010, 18, 557–572. [Google Scholar] [CrossRef]
- Merbold, L.; Ardö, J.; Arneth, A.; Scholes, R.J.; Nouvellon, Y.; de Grandcourt, A.; Archibald, S.; Bonnefond, J.M.; Boulain, N.; Brueggemann, N.; et al. Precipitation as driver of carbon fluxes in 11 African ecosystems. Biogeosciences 2009, 6, 1027–1041. [Google Scholar] [CrossRef]
- Gondwe, B.R.N.; Hong, S.-H.; Wdowinski, S.; Bauer-Gottwein, P. Hydrologic Dynamics of the Ground-Water-Dependent Sian Ka’an Wetlands, Mexico, Derived from InSAR and SAR Data. Wetlands 2010, 30, 1–13. [Google Scholar] [CrossRef]
- Lang, M.W.; Kasischke, E.S. Using C-Band Synthetic Aperture Radar Data to Monitor Forested Wetland Hydrology in Maryland’s Coastal Plain, USA. IEEE Trans. Geosci. Remote Sens. 2008, 46, 535–546. [Google Scholar] [CrossRef]
- Lee, H.; Beighley, R.E.; Alsdorf, D.; Jung, H.C.; Shum, C.K.; Duan, J.; Guo, J.; Yamazaki, D.; Andreadis, K. Characterization of terrestrial water dynamics in the Congo Basin using GRACE and satellite radar altimetry. Remote Sens. Environ. 2011, 115, 3530–3538. [Google Scholar] [CrossRef]
- Marechal, C.; Pottier, E.; Allain-Bailhache, S.; Meric, S.; Hubert-Moy, L.; Corgne, S. Mapping dynamic wetland processes with a one year RADARSAT-2 quad pol time-series. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 126–129. [Google Scholar]
- Milzow, C.; Krogh, P.E.; Bauer-Gottwein, P. Combining satellite radar altimetry, SAR surface soil moisture and GRACE total storage changes for hydrological model calibration in a large poorly gauged catchment. Hydrol. Earth Syst. Sci. 2011, 15, 1729–1743. [Google Scholar] [CrossRef]
- O’Grady, D.; Leblanc, M.; Bass, A. The use of radar satellite data from multiple incidence angles improves surface water mapping. Remote Sens. Environ. 2014, 140, 652–664. [Google Scholar] [CrossRef]
- Papa, F.; Prigent, C.; Rossow, W.B.; Legresy, B.; Remy, F. Inundated wetland dynamics over boreal regions from remote sensing: The use of Topex-Poseidon dual-frequency radar altimeter observations. Int. J. Remote Sens. 2006, 27, 4847–4866. [Google Scholar] [CrossRef]
- Sass, G.Z.; Creed, I.F. Characterizing hydrodynamics on boreal landscapes using archived synthetic aperture radar imagery. Hydrol. Process. 2008, 22, 1687–1699. [Google Scholar] [CrossRef]
- Landmann, T.; Schramm, M.; Colditz, R.R.; Dietz, A.; Dech, S. Wide Area Wetland Mapping in Semi-Arid Africa Using 250-Meter MODIS Metrics and Topographic Variables. Remote Sens. 2010, 2, 1751–1766. [Google Scholar] [CrossRef]
- Schroeder, R.; Rawlins, M.A.; McDonald, K.C.; Podest, E.; Zimmermann, R.; Kueppers, M. Satellite microwave remote sensing of North Eurasian inundation dynamics: Development of coarse-resolution products and comparison with high-resolution synthetic aperture radar data. Environ. Res. Lett. 2010, 5, 015003. [Google Scholar] [CrossRef]
- Baker, C.; Lawrence, R.L.; Montagne, C.; Patten, D. Change detection of wetland ecosystems using landsat imagery and change vector analysis. Wetlands 2007, 27, 610–619. [Google Scholar] [CrossRef]
- Baker, C.; Lawrence, R.; Montagne, C.; Patten, D. Mapping wetlands and riparian areas using landsat etm+ imagery and decision-tree-based models. Wetlands 2006, 26, 465–474. [Google Scholar] [CrossRef]
- Johnston, R.M.; Barson, M.M. Remote sensing of Australian wetlands: An evaluation of Landsat TM data for inventory and classification. Mar. Freshw. Res. 1993, 44, 235–252. [Google Scholar] [CrossRef]
- Davranche, A.; Lefebvre, G.; Poulin, B. Wetland monitoring using classification trees and SPOT-5 seasonal time series. Remote Sens. Environ. 2010, 114, 552–562. [Google Scholar] [CrossRef]
- Harvey, K.R.; Hill, G.J.E. Vegetation mapping of a tropical freshwater swamp in the Northern Territory, Australia: A comparison of aerial photography, Landsat TM and SPOT satellite imagery. Int. J. Remote Sens. 2001, 22, 2911–2925. [Google Scholar] [CrossRef]
- Akumu, C.E.; Pathirana, S.; Baban, S.; Bucher, D. Monitoring coastal wetland communities in north-eastern NSW using ASTER and Landsat satellite data. Wetl. Ecol. Manag. 2010, 18, 357–365. [Google Scholar] [CrossRef]
- Pantaleoni, E.; Wynne, R.H.; Galbraith, J.M.; Campbell, J.B. A logit model for predicting wetland location using ASTER and GIS. Int. J. Remote Sens. 2009, 30, 2215–2236. [Google Scholar] [CrossRef]
- Pantaleoni, E.; Wynne, R.H.; Galbraith, J.M.; Campbell, J.B. Mapping wetlands using ASTER data: A comparison between classification trees and logistic regression. Int. J. Remote Sens. 2009, 30, 3423–3440. [Google Scholar] [CrossRef]
- Campos, J.C.; Sillero, N.; Brito, J.C. Normalized difference water indexes have dissimilar performances in detecting seasonal and permanent water in the Sahara–Sahel transition zone. J. Hydrol. 2012, 464–465, 438–446. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, R.D.; Jain, M.K.; Lohani, A.K. Delineation of Flood-Prone Areas Using Remote Sensing Techniques. Water Resour. Manag. 2005, 19, 333–347. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Ozesmi, S.L.; Bauer, M.E. Satellite remote sensing of wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Tao, J. Understanding the Coupled Surface-Groundwater System from Event to Decadal Scale Using an Un-Calibrated Hydrologic Model and Data Assimilation. Ph.D. Thesis, Duke University, Durham, NC, USA, 2015. [Google Scholar]
- Desanker, P.V.; Prentice, I.C. MIOMBO—A vegetation dynamics model for the miombo woodlands on Zambezian Africa. For. Ecol. Manag. 1994, 69, 87–95. [Google Scholar] [CrossRef]
- Lawton, R.M. A Study of the Dynamic Ecology of Zambian Vegetation. J. Ecol. 1978, 66, 175–198. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Dezfuli, A.K.; Klotter, D. A Two-Century Precipitation Dataset for the Continent of Africa. Bull. Am. Meteorol. Soc. 2012, 93, 1219–1231. [Google Scholar] [CrossRef]
- Tazalika, L.; Jury, M.R. Intra-seasonal rainfall oscillations over central Africa: Space-time character and evolution. Theor. Appl. Climatol. 2008, 94, 67–80. [Google Scholar] [CrossRef]
- Schefuß, E.; Kuhlmann, H.; Mollenhauer, G.; Prange, M.; Pätzold, J. Forcing of wet phases in southeast Africa over the past 17,000 years. Nature 2011, 480, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Dupont, L.M.; Behling, H.; Kim, J.-H. Thirty thousand years of vegetation development and climate change in Angola (Ocean Drilling Program Site 1078). Clim. Past 2008, 4, 107–124. [Google Scholar] [CrossRef]
- NASA LP DAAC. MODIS MCD43B4 Nadir BRDF-Adjusted Reflectance; Version 5; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd43b4 (accessed on 12 July 2017).
- NASA LP DAAC. MODIS MCD43B2 BRDF-Albedo Quality; Version 5; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1 (accessed on 12 July 2017).
- NASA LP DAAC. MODIS MCD12Q1 Land Cover Type; Version 51; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1 (accessed on 12 July 2017).
- NASA LP DAAC. MODIS MOD15A2 Leaf Area Index—Fraction of Photosynthetically Active Radiation; Version 5; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod15a2 (accessed on 12 July 2017).
- NASA LP DAAC. MODIS MOD17A2 Gross Primary Productivity; Version 55; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod17a2 (accessed on 12 July 2017).
- Lobser, S.E.; Cohen, W.B. MODIS tasselled cap: Land cover characteristics expressed through transformed MODIS data. Int. J. Remote Sens. 2007, 28, 5079–5101. [Google Scholar] [CrossRef]
- Dwyer, J.L.; Schmidt, G.L. The MODIS reprojection tool. In Earth Science Satellite Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 162–177. [Google Scholar]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- ERA-Interim Project. Available online: https://doi.org/10.5065/D6CR5RD9 (accessed on 1 July 2015).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Fischer, G.; Nachtergaele, F.O.; Prieler, S.; van Velthuizen, H.T.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment of Agriculture in the 21st Century; International Instituefor Applied Systems Analysis: Laxenburg, Austria; FAO: Rome, Italy, 2008. [Google Scholar]
- Rawles, W.J.; Brakensiek, D.L. Estimating Soil Water Retention from Soil Properties. J. Irrig. Drain. Div. 1982, 108, 166–171. [Google Scholar]
- Rawls, W.J.; Gish, T.J.; Brakensiek, D.L. Estimating Soil Water Retention from Soil Physical Properties and Characteristics. In Advances in Soil Science; Advances in Soil Science; Springer: New York, NY, USA, 1991; pp. 213–234. ISBN 978-1-4612-7812-2. [Google Scholar]
- Rawls, W.J.; Ahuja, L.R.; Brakensiek, D.L.; Shirmohammadi, A. Infiltration and soil water movement. In Handbook of Hydrology; Maidment, R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Di Vittorio, C.A.; Georgakakos, A.P. Land cover classification and wetland inundation mapping using MODIS. Remote Sens. Environ. 2018, 204, 1–17. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Gao, B.C. Remote sensing of water vapor in the near IR from EOS/MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 871–884. [Google Scholar] [CrossRef]
- Vermote, E.F.; El Saleous, N.Z.; Justice, C.O. Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
- Chen, D.; Huang, J.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near- and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M.; Shuey, C.J.; Walthall, C.; Daughtry, C.; Morisette, J.; Schaaf, C.; Strahler, A. Validating MODIS land surface reflectance and albedo products: Methods and preliminary results. Remote Sens. Environ. 2002, 83, 149–162. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; van Leeuwen, W.; Miura, T.; Glenn, E. MODIS Vegetation Indices. In Land Remote Sensing and Global Environmental Change: NASA’s Earth Observing System and the Science of ASTER and MODIS, Remote Sensing and Digital Image Processing; Springer: New York, NY, USA, 2011; p. 579. [Google Scholar]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Li, Z.-L.; Becker, F. Properties and comparison of temperature-independent thermal infrared spectral indices with NDVI for HAPEX data. Remote Sens. Environ. 1990, 33, 165–182. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- McFeeters, S.K. Using the Normalized Difference Water Index (NDWI) within a Geographic Information System to Detect Swimming Pools for Mosquito Abatement: A Practical Approach. Remote Sens. 2013, 5, 3544–3561. [Google Scholar] [CrossRef]
- Zhang, X.; Schaaf, C.B.; Friedl, M.A.; Strahler, A.H.; Gao, F.; Hodges, J.C.F. MODIS tasseled cap transformation and its utility. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium; Toronto, ON, Canada, 24–28 June 2002; Volume 2, pp. 1063–1065. [Google Scholar]
- Crist, E.P.; Cicone, R.C. A Physically-Based Transformation of Thematic Mapper Data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 256–263. [Google Scholar] [CrossRef]
- Barros, A.P. Adaptive Multilevel Modeling of Land-Atmosphere Interactions. J. Clim. 1995, 8, 2144–2160. [Google Scholar] [CrossRef]
- Devonec, E.; Barros, A.P. Exploring the transferability of a land-surface hydrology model. J. Hydrol. 2002, 265, 258–282. [Google Scholar] [CrossRef]
- Garcia-Quijano, J.F.; Barros, A.P. Incorporating canopy physiology into a hydrological model: Photosynthesis, dynamic respiration, and stomatal sensitivity. Ecol. Model. 2005, 185, 29–49. [Google Scholar] [CrossRef]
- Gebremichael, M.; Barros, A. Evaluation of MODIS Gross Primary Productivity (GPP) in tropical monsoon regions. Remote Sens. Environ. 2006, 100, 150–166. [Google Scholar] [CrossRef]
- Yildiz, O.; Barros, A.P. Climate Variability, Water Resources, and Hydrologic Extremes—Modeling the Water and Energy Budgets. Clim. Hydrol. Mt. Areas 2006. [Google Scholar] [CrossRef]
- Yildiz, O.; Barros, A.P. Elucidating vegetation controls on the hydroclimatology of a mid-latitude basin. J. Hydrol. 2007, 333, 431–448. [Google Scholar] [CrossRef]
- Yıldız, O.; Barros, A.P. Evaluating spatial variability and scale effects on hydrologic processes in a midsize river basin. Sci. Res. Essays 2009, 4, 217–225. [Google Scholar]
- Tao, J.; Barros, A.P. The Integrated Precipitation and Hydrology Experiment—Hydrologic Applications for the Southeast US (IPHEx-H4SE) Part II: Atmospheric Forcing and Topographic Corrections; Duke University: Durham, NC, USA, 2014. [Google Scholar]
- Tao, J.; Barros, A.P. Coupled prediction of flood response and debris flow initiation during warm- and cold-season events in the Southern Appalachians, USA. Hydrol. Earth Syst. Sci. 2014, 18, 367–388. [Google Scholar] [CrossRef]
- Lowman, L.E.L.; Barros, A.P. Interplay of drought and tropical cyclone activity in SE U.S. gross primary productivity. J. Geophys. Res. Biogeosci. 2016, 121, 1540–1567. [Google Scholar] [CrossRef]
- Lowman, L.E.L.; Barros, A.P. Predicting canopy biophysical properties and sensitivity of plant carbon uptake to water limitations with a coupled eco-hydrological framework. Ecol. Model. 2018, 372, 33–52. [Google Scholar] [CrossRef]
- Skarpe, C. Plant functional types and climate in a southern African savanna. J. Veg. Sci. 1996, 7, 397–404. [Google Scholar] [CrossRef]
- Caylor, K.K.; Shugart, H.H. Simulated productivity of heterogeneous patches in Southern African savanna landscapes using a canopy productivity model. Landsc. Ecol. 2004, 19, 401–415. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Jury, M.R. A return to wet conditions over Africa: 1995–2010. Theor. Appl. Climatol. 2013, 111, 471–481. [Google Scholar] [CrossRef]
- Sjöström, M.; Zhao, M.; Archibald, S.; Arneth, A.; Cappelaere, B.; Falk, U.; de Grandcourt, A.; Hanan, N.; Kergoat, L.; Kutsch, W.; et al. Evaluation of MODIS gross primary productivity for Africa using eddy covariance data. Remote Sens. Environ. 2013, 131, 275–286. [Google Scholar] [CrossRef]
- Sjöström, M.; Ardö, J.; Arneth, A.; Boulain, N.; Cappelaere, B.; Eklundh, L.; de Grandcourt, A.; Kutsch, W.L.; Merbold, L.; Nouvellon, Y.; et al. Exploring the potential of MODIS EVI for modeling gross primary production across African ecosystems. Remote Sens. Environ. 2011, 115, 1081–1089. [Google Scholar] [CrossRef]
- Jin, C.; Xiao, X.; Merbold, L.; Arneth, A.; Veenendaal, E.; Kutsch, W.L. Phenology and gross primary production of two dominant savanna woodland ecosystems in Southern Africa. Remote Sens. Environ. 2013, 135, 189–201. [Google Scholar] [CrossRef]
- Cohen, L.T.; Matos, J.P.; Boillat, J.-L.; Schleiss, A.J. Comparison and evaluation of satellite derived precipitation products for hydrological modeling of the Zambezi River Basin. Hydrol. Earth Syst. Sci. 2012, 16, 489–500. [Google Scholar] [CrossRef]
- Barros, A.P.; Hwu, W. A study of land-atmosphere interactions during summertime rainfall using a mesoscale model. J. Geophys. Res. Atmos. 2002, 107, ACL 17-1–ACL 17-18. [Google Scholar] [CrossRef]
- Sun, X.; Barros, A.P. Isolating the Role of Surface Evapotranspiration on Moist Convection along the Eastern Flanks of the Tropical Andes Using a Quasi-Idealized Approach. J. Atmos. Sci. 2014, 72, 243–261. [Google Scholar] [CrossRef]
- Sun, X.; Barros, A.P. Impact of Amazonian evapotranspiration on moisture transport and convection along the eastern flanks of the tropical Andes. Q. J. R. Meteorol. Soc. 2015, 141, 3325–3343. [Google Scholar] [CrossRef]
- Gong, C.; Eltahir, E. Sources of moisture for rainfall in West Africa. Water Resour. Res. 1996, 32, 3115–3121. [Google Scholar] [CrossRef]
- Zhu, L.; Southworth, J. Disentangling the Relationships between Net Primary Production and Precipitation in Southern Africa Savannas Using Satellite Observations from 1982 to 2010. Remote Sens. 2013, 5, 3803–3825. [Google Scholar] [CrossRef]
- Sankaran, M.; Hanan, N.P.; Scholes, R.J.; Ratnam, J.; Augustine, D.J.; Cade, B.S.; Gignoux, J.; Higgins, S.I.; Le Roux, X.; Ludwig, F.; et al. Determinants of woody cover in African savannas. Nature 2005, 438, 846–849. [Google Scholar] [CrossRef] [PubMed]
- Campo-Bescós, M.A.; Muñoz-Carpena, R.; Southworth, J.; Zhu, L.; Waylen, P.R.; Bunting, E. Combined Spatial and Temporal Effects of Environmental Controls on Long-Term Monthly NDVI in the Southern Africa Savanna. Remote Sens. 2013, 5, 6513–6538. [Google Scholar] [CrossRef]
- Melton, J.R.; Wania, R.; Hodson, E.L.; Poulter, B.; Ringeval, B.; Spahni, R.; Bohn, T.; Avis, C.A.; Beerling, D.J.; Chen, G.; et al. Present state of global wetland extent and wetland methane modelling: Conclusions from a model inter-comparison project (WETCHIMP). Biogeosciences 2013, 10, 753–788. [Google Scholar] [CrossRef]
- Gowik, U.; Westhoff, P. The Path from C3 to C4 Photosynthesis. Plant Physiol. 2011, 155, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Lara, M.V.; Andreo, C.S. C4 Plants Adaptation to High Levels of CO2 and to Drought Environments. In Abiotic Stress in Plants-Mechanisms and Adaptations; IntechOpen: Hampshire, UK, 2011. [Google Scholar] [CrossRef]
- Von Caemmerer, S. Biochemical Models of Leaf Photosynthesis; CSIRO Publishing: Clayton, Australia, 2000. [Google Scholar]
- Boyd, R.A.; Gandin, A.; Cousins, A.B. Temperature Responses of C4 Photosynthesis: Biochemical Analysis of Rubisco, Phosphoenolpyruvate Carboxylase, and Carbonic Anhydrase in Setaria viridis. Plant Physiol. 2015, 169, 1850–1861. [Google Scholar] [CrossRef] [PubMed]
- Massad, R.-S.; Tuzet, A.; Bethenod, O. The effect of temperature on C4-type leaf photosynthesis parameters. Plant Cell Environ. 2007, 30, 1191–1204. [Google Scholar] [CrossRef] [PubMed]
- Medlyn, B.E.; Dreyer, E.; Ellsworth, D.; Forstreuter, M.; Harley, P.C.; Kirschbaum, M.U.F.; Le Roux, X.; Montpied, P.; Strassemeyer, J.; Walcroft, A.; et al. Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant Cell Environ. 2002, 25, 1167–1179. [Google Scholar] [CrossRef]
- Kubien, D.S.; von Caemmerer, S.; Furbank, R.T.; Sage, R.F. C4 Photosynthesis at Low Temperature. A Study Using Transgenic Plants with Reduced Amounts of Rubisco. Plant Physiol. 2003, 132, 1577–1585. [Google Scholar] [CrossRef] [PubMed]
| Band | Light | Wavelength (nm) | Brightness (wb) | Greenness (wg) | Wetness (ww) |
|---|---|---|---|---|---|
| 1 | Red | 620–670 | 0.4395 | −0.4064 | 0.1147 |
| 2 | Near-infrared (NIR1) | 841–876 | 0.5945 | 0.5129 | 0.2489 |
| 3 | Blue | 459–479 | 0.2460 | −0.2744 | 0.2408 |
| 4 | Green | 545–565 | 0.3918 | −0.2893 | 0.3132 |
| 5 | Near-infrared (NIR2) | 1230–1250 | 0.3506 | 0.4882 | −0.3122 |
| 6 | Mid-infrared (MIR1) | 1628–1652 | 0.2136 | −0.0036 | −0.6416 |
| 7 | Mid-infrared (MIR2) | 2105–2155 | 0.2678 | −0.4169 | −0.5087 |
| Land Cover | MODIS Code (IGBP) | Number of Pixels in Stationary Map 1 | Number of Training Pixels |
|---|---|---|---|
| Water | 0 | 480 | 0 |
| Evergreen needle-leaf forest | 1 | 0 | 0 |
| Evergreen broadleaf forest | 2 | 6732 | 2000 |
| Deciduous needle-leaf forest | 3 | 0 | 0 |
| Deciduous broadleaf forest | 4 | 77 | 0 |
| Mixed forest | 5 | 173 | 0 |
| Closed shrublands | 6 | 251 | 0 |
| Open shrublands | 7 | 1067 | 0 |
| Woody savannas | 8 | 355,893 | 4000 |
| Savannas | 9 | 432,824 | 4000 |
| Grasslands | 10 | 17,067 | 4000 |
| Permanent wetlands | 11 | 14,135 | 14,000 |
| Croplands | 12 | 879 | 0 |
| Urban and built-up | 13 | 251 | 0 |
| Cropland/Natural vegetation mosaic | 14 | 1343 | 0 |
| Snow and ice | 15 | 0 | 0 |
| Barren or sparsely vegetated | 16 | 3 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lowman, L.E.L.; Wei, T.M.; Barros, A.P. Rainfall Variability, Wetland Persistence, and Water–Carbon Cycle Coupling in the Upper Zambezi River Basin in Southern Africa. Remote Sens. 2018, 10, 692. https://doi.org/10.3390/rs10050692
Lowman LEL, Wei TM, Barros AP. Rainfall Variability, Wetland Persistence, and Water–Carbon Cycle Coupling in the Upper Zambezi River Basin in Southern Africa. Remote Sensing. 2018; 10(5):692. https://doi.org/10.3390/rs10050692
Chicago/Turabian StyleLowman, Lauren E. L., Tiffany M. Wei, and Ana P. Barros. 2018. "Rainfall Variability, Wetland Persistence, and Water–Carbon Cycle Coupling in the Upper Zambezi River Basin in Southern Africa" Remote Sensing 10, no. 5: 692. https://doi.org/10.3390/rs10050692
APA StyleLowman, L. E. L., Wei, T. M., & Barros, A. P. (2018). Rainfall Variability, Wetland Persistence, and Water–Carbon Cycle Coupling in the Upper Zambezi River Basin in Southern Africa. Remote Sensing, 10(5), 692. https://doi.org/10.3390/rs10050692





