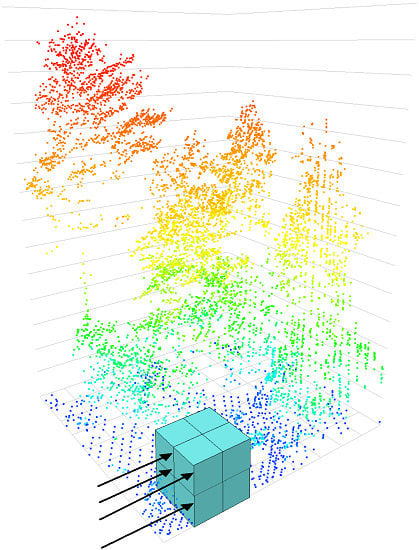
The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Data
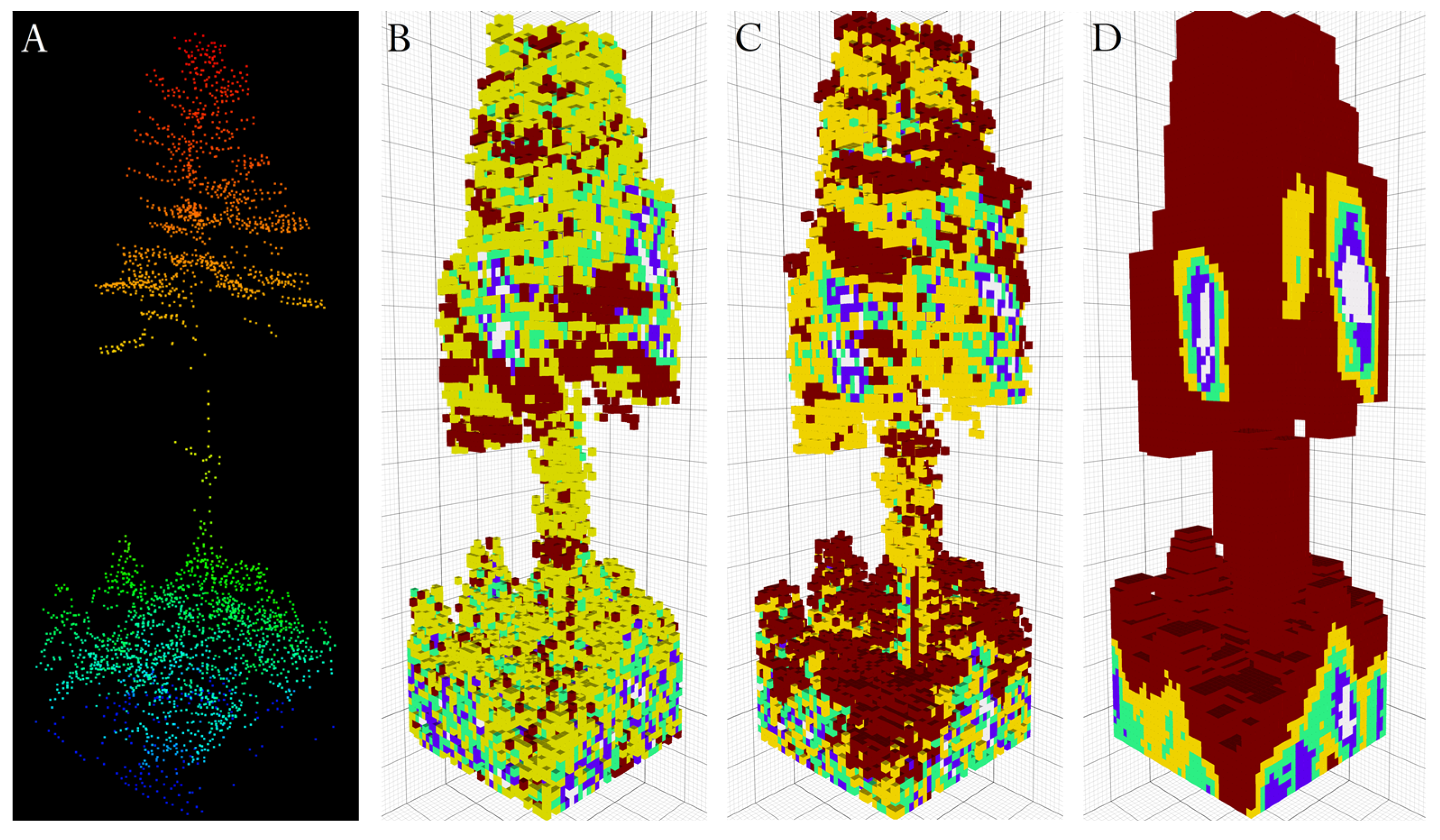
2.2. LiDAR Data
2.3. Network Architecture
- Convolutional layers are a series of moving windows passed over data with spatial or temporal relationships. The values of these windows are used as multipliers and are initially randomized, but are defined over time as the network trains. Often these are used to identify features such as edges.
- Dropout layers are commonly applied following a convolution. These consist of randomized removals of data. This can prevent overfitting of the network by altering architecture during the training process, preventing specific pathways from becoming relied upon [53].
- Batch normalization is another layer frequently applied after a convolution, and is used to standardize input data. This can speed up model training by ensuring data fall upon the same scale from which weights are initially randomly derived. These shift subtly with each training step, and so are another way of preventing model overfitting [54].
- Activation layers are an essential component to any neural network. They act as thresholds for data passage onto the next layer, similar to the action potential in a living neuron. The most common type of activation function is the rectified linear unit (ReLU), which is a linear gateway allowing only data with a value greater than zero to pass.
- Pooling layers are spatial aggregations of data. These are used primarily to reduce dimensionality and condense important information. Maximum pooling is the most common type of pooling, which takes the largest data value inside a moving window [55].
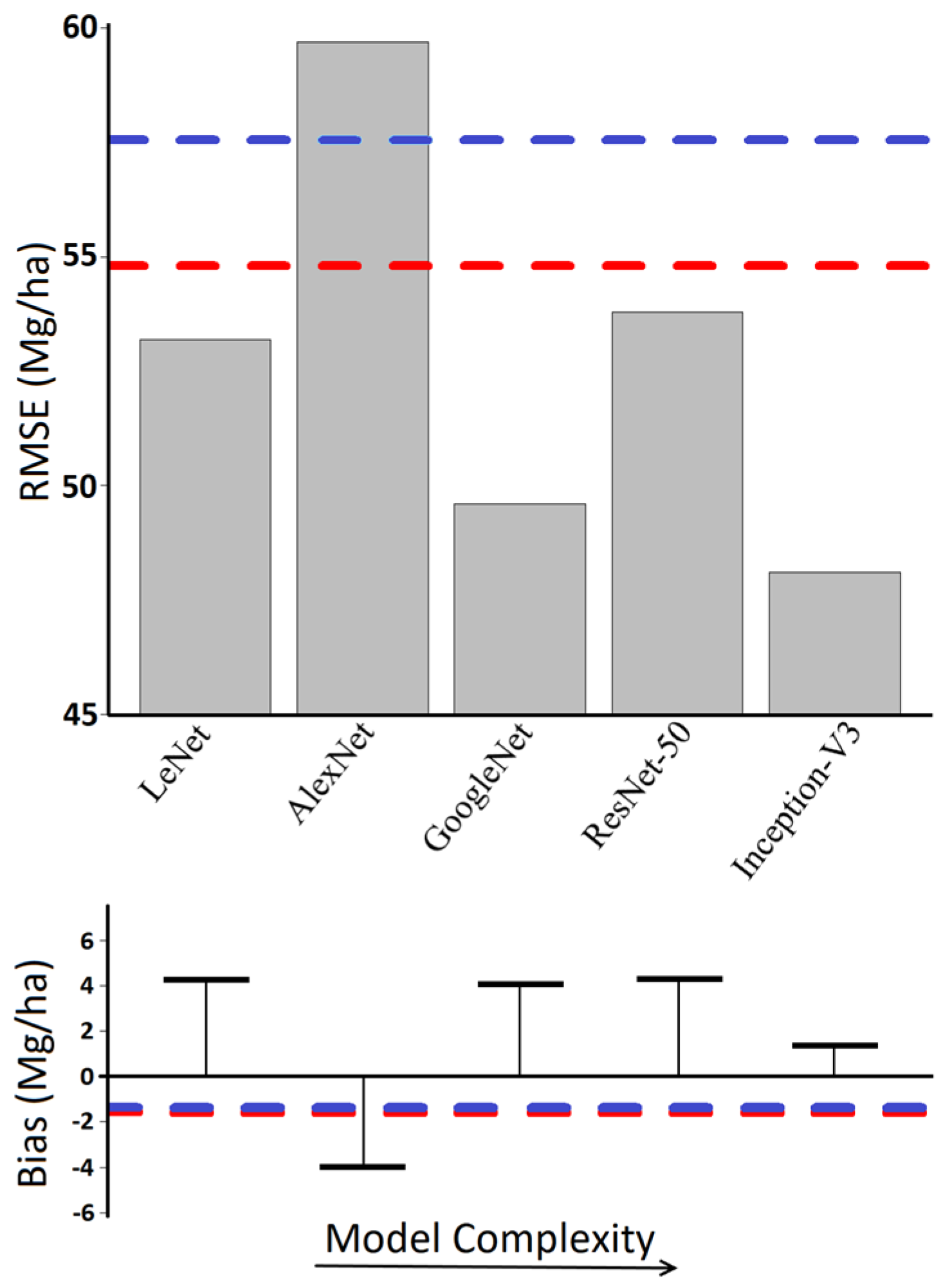
- The first network architecture we tested was LeNet, the earliest CNN [27]. LeNet consists of two layers of convolutions each followed by maximum pooling and dropout. These feed into a further two fully connected layers (consisting of a ReLU activator and dropout) before producing a prediction.
- The second network we tested was AlexNet [28], which was first introduced in 2012. This network is largely credited as the first ‘deep’ CNN, and it resulted in a dramatic increase in image classification accuracy. AlexNet consists of five layers of convolutions, each with an activator, with pooling following the first, second, and fifth convolutions. These lead into a further three fully connected layers and a final prediction.
- Next, we implemented GoogLenet, introduced in 2014 [29]. GoogLeNet improved upon image classification performance by introducing groups of convolutional layers called inception layers. Inception layers are bundles of convolutions of varying sizes and strides, useful for identifying different types of features. These are followed by batch normalization and activation, with the outputs concatenated. GoogLenet begins with three convolutional layers and pooling, and is followed by nine inception layers, with pooling after the second and seventh inception layer. The data are then funneled into a single fully connected output to achieve a prediction.
- A series of networks succeeded GoogLenet, including Inception-V3 [45]. This expanded upon GoogLenet’s inception layers, adding additional convolutions with four pathways by which the incoming data is analyzed before being concatenated. Inception-V3 begins with five convolution layers and two pooling layers, followed by eleven inception layers of varying compositions, and pooling layers interspersed along the way to continuously reduce dimensionality.
- The final network architecture we tested was ResNet-50 [31]. Rather than use inception layers, ResNet-50 uses residual layers. Data entering a residual layer is subject to several convolutions, batch normalization, and activation, the results of which are added to the original input. By retaining the input values, useful information from the previous residual layers is preserved and improved upon, reducing the potential for values running through the network to drift. Our implementation of ResNet-50 contained an initial convolution, ReLU, and pooling layer, followed by sixteen residual layers (each containing three convolutions) with three pooling layers interspersed to gradually reduce dimensionality.
2.4. Traditional Height Metrics Modelling
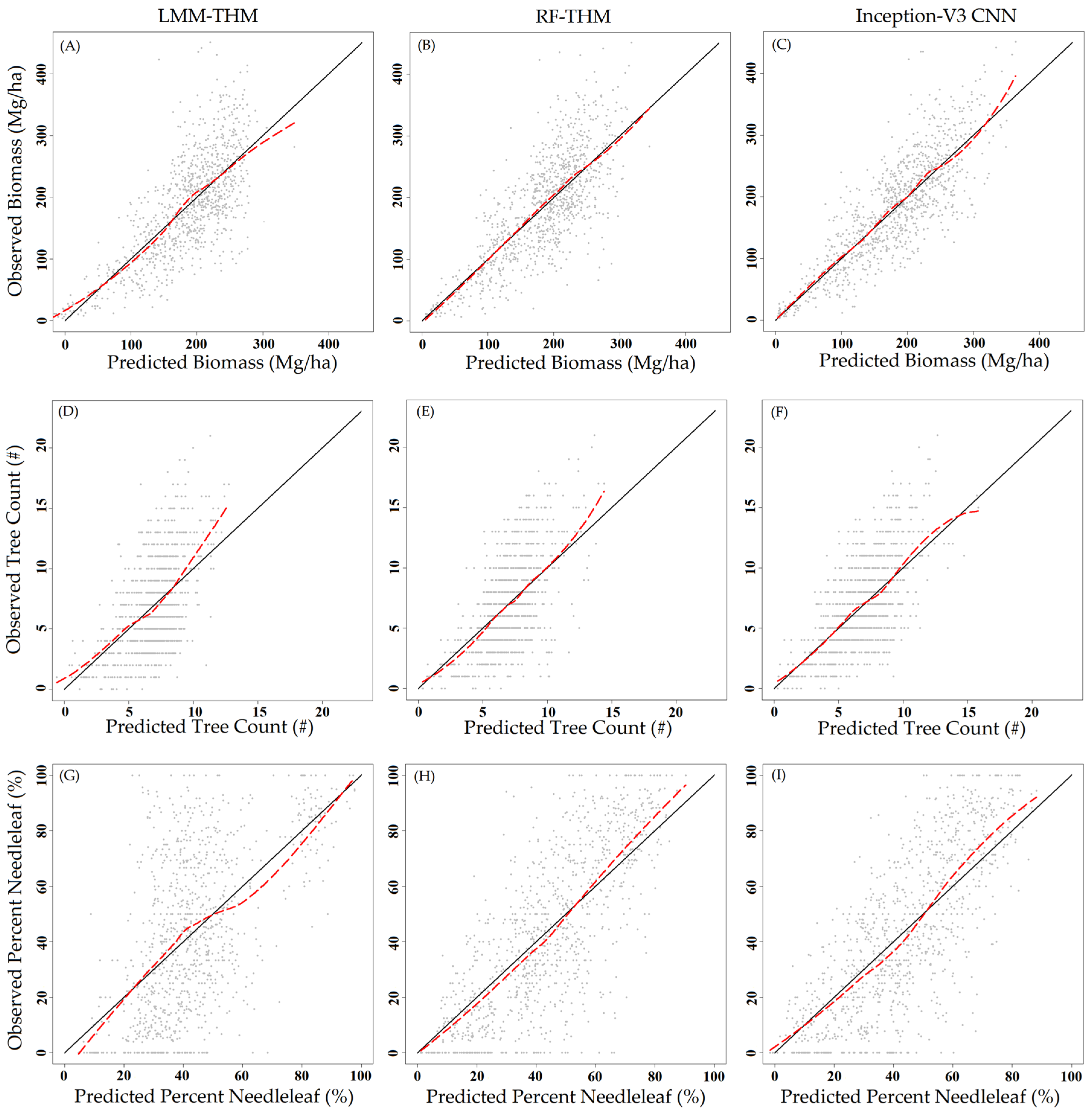
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lim, K.S.; Treitz, P.M. Estimation of above ground forest biomass from airborne discrete return laser scanner data using canopy-based quantile estimators. Scand. J. For. Res. 2004, 19, 558–570. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.; Martinuzzi, S.; Falkowski, M.J. Quantifying aboveground forest carbon pools and fluxes from repeat LiDAR surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Graf, R.F.; Mathys, L.; Bollmann, K. Habitat assessment for forest dwelling species using LiDAR remote sensing: Capercaillie in the Alps. For. Ecol. Manag. 2009, 257, 160–167. [Google Scholar] [CrossRef]
- Woods, M.; Pitt, D.; Penner, M.; Lim, K.; Nesbitt, D.; Etheridge, D.; Treitz, P. Operational implementation of a LiDAR inventory in Boreal Ontario. For. Chron. 2011, 87, 512–528. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Penner, M.; Pitt, D.G.; Woods, M.E. Parametric vs. nonparametric LiDAR models for operational forest inventory in boreal Ontario. Can. J. Remote Sens. 2013, 39, 426–443. [Google Scholar]
- Latifi, H.; Nothdurft, A.; Koch, B. Non-parametric prediction and mapping of standing timber volume and biomass in a temperate forest: Application of multiple optical/LiDAR-derived predictors. Forestry 2010, 83, 395–407. [Google Scholar] [CrossRef]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1372. [Google Scholar]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J. A nationwide forest attribute map of Sweden predicted using airborne laser scanning data and field data from the National Forest Inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Goodbody, T.R.; Coops, N.C.; Tompalski, P.; Crawford, P.; Day, K.J. Updating residual stem volume estimates using ALS-and UAV-acquired stereo-photogrammetric point clouds. Int. J. Remote Sens. 2017, 38, 2938–2953. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2009; Volume 123.
- Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A. rLiDAR: An R Package for Reading, Processing and Visualizing LiDAR (Light Detection and Ranging) Data, Version 0.1. 2015. Available online: https://cran.r-project.org/package=rLiDAR (accessed on 12 December 2017).
- Junttila, V.; Kauranne, T.; Finley, A.O.; Bradford, J.B. Linear models for airborne-laser-scanning-based operational forest inventory with small field sample size and highly correlated LiDAR data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5600–5612. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Coops, N.C.; Culvenor, D.S. Assessment of forest structure with airborne LiDAR and the effects of platform altitude. Remote Sens. Environ. 2006, 103, 140–152. [Google Scholar] [CrossRef]
- Roussel, J.R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Holmgren, J.; Nilsson, M.; Olsson, H. Simulating the effects of lidar scanning angle for estimation of mean tree height and canopy closure. Can. J. Remote Sens. 2003, 29, 623–632. [Google Scholar] [CrossRef]
- Treitz, P.; Lim, K.; Woods, M.; Pitt, D.; Nesbitt, D.; Etheridge, D. LiDAR sampling density for forest resource inventories in Ontario, Canada. Remote Sens. 2012, 4, 830–848. [Google Scholar] [CrossRef]
- Hayashi, R.; Weiskittel, A.; Sader, S. Assessing the feasibility of low-density LiDAR for stand inventory attribute predictions in complex and managed forests of northern Maine, USA. Forests 2014, 5, 363–383. [Google Scholar] [CrossRef]
- Shang, C.; Treitz, P.; Caspersen, J.; Jones, T. Estimating stem diameter distributions in a management context for a tolerant hardwood forest using ALS height and intensity data. Can. J. Remote Sens. 2017, 43, 79–94. [Google Scholar] [CrossRef]
- Antani, S.; Kasturi, R.; Jain, R. A survey on the use of pattern recognition methods for abstraction, indexing and retrieval of images and video. Pattern Recognit. 2002, 35, 945–965. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.Q.; Liu, C. Biomass retrieval from high-dimensional active/passive remote sensing data by using artificial neural networks. Int. J Remote Sens. 1997, 18, 971–979. [Google Scholar] [CrossRef]
- Joibary, S.S. Forest attributes estimation using aerial laser scanner and TM data. For. Syst. 2013, 22, 484–496. [Google Scholar]
- Niska, H.; Skon, J.P.; Packalen, P.; Tokola, T.; Maltamo, M.; Kolehmainen, M. Neural networks for the prediction of species-specific plot volumes using airborne laser scanning and aerial photographs. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1076–1085. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 255–258. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press Ltd.: Cambridge, MA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015. [Google Scholar]
- Taigman, Y.; Yang, M.; Ranzato, M.; Wolf, L. Deepface: Closing the gap to human-level performance in face verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1701–1708. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI-17: Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 4, p. 12. [Google Scholar]
- Smith, L.N.; Topin, N. Deep convolutional neural network design patterns. arXiv, 2016; arXiv:1611.00847. [Google Scholar]
- Guan, H.; Yu, Y.; Ji, Z.; Li, J.; Zhang, Q. Deep learning-based tree classification using mobile LiDAR data. Remote Sens. Lett. 2015, 6, 864–873. [Google Scholar] [CrossRef]
- Ghamisi, P.; Höfle, B.; Zhu, X.X. Hyperspectral and LiDAR data fusion using extinction profiles and deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3011–3024. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. 3D convolutional neural networks for landing zone detection from lidar. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3471–3478. [Google Scholar]
- Li, B. 3D fully convolutional network for vehicle detection in point cloud. arXiv, 2016; arXiv:1611.08069. [Google Scholar]
- Matti, D.; Ekenel, H.K.; Thiran, J. Combining LiDAR space clustering and convolutional neural networks for pedestrian detection. arXiv, 2017; arXiv:1710.06160. [Google Scholar]
- Prasoon, A.; Petersen, K.; Igel, C.; Lauze, F.; Dam, E.; Nielsen, M. Deep feature learning for knee cartilage segmentation using a triplanar convolutional neural network. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2013; pp. 246–253. [Google Scholar]
- Kamnitsas, K.; Ledig, C.; Newcombe, V.F.; Simpson, J.P.; Kane, A.D.; Menon, D.K.; Rueckert, D.; Glocker, B. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Med. Image Anal. 2017, 36, 61–78. [Google Scholar] [CrossRef] [PubMed]
- Yi, D.; Zhou, M.; Chen, Z.; Gevaert, O. 3-D Convolutional Neural Networks for Glioblastoma Segmentation. arXiv, 2016; arXiv:1611.04534. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and multi-view CNNS for object classification on 3d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 5648–5656. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. In Advances in Neural Information Processing Systems; MIT Press Ltd.: Cambridge, MA, USA, 2016; pp. 82–90. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Weiskittel, A.; Russell, M.; Wagner, R.; Seymour, R. Refinement of the Forest Vegetation Simulator Northeast Variant Growth and Yield Model: Phase III; Cooperative Forestry Research Unit—University of Maine: Orono, ME, USA, 2012; pp. 96–104. [Google Scholar]
- Woodall, C.W.; Heath, L.S.; Domke, G.M.; Nichols, M.C. Methods and Equations for Estimating Aboveground Volume, Biomass, and Carbon for Trees in the US Forest Inventory, 2010; United States Department of Agriculture: Washington, DC, USA, 2011.
- Russell, M.B.; Weiskittel, A.R. Maximum and largest crown width equations for 15 tree species in Maine. North J. Appl. For. 2011, 28, 84–91. [Google Scholar]
- Amaral, T.; Silva, L.M.; Alexandre, L.A.; Kandaswamy, C.; de Sá, J.M.; Santos, J.M. Transfer learning using rotated image data to improve deep neural network performance. In International Conference Image Analysis and Recognition; Springer: Berlin/Heidelberg, Germany, 2014; pp. 290–300. [Google Scholar]
- Paulin, M.; Revaud, J.; Harchaoui, Z.; Perronnin, F.; Schmid, C. Transformation pursuit for image classification. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 3646–3653. [Google Scholar]
- Cook, B.D.; Nelson, R.F.; Middleton, E.M.; Morton, D.C.; McCorkel, J.T.; Masek, J.G.; Ranson, K.J.; Ly, V.; Montesano, P.M. NASA Goddard’s LiDAR, hyperspectral and thermal (G-LiHT) airborne imager. Remote Sens. 2013, 5, 4045–4066. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv, 2012; arXiv:1207.0580. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv, 2016; arXiv:1603.04467. [Google Scholar]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. Package ‘lmerTest’. R Package Version 2.0. 2015. Available online: https://cran.r-project.org/package=lmerTest (accessed on 12 December 2017).
- Diaz-Uriarte, R.; de Andrés, S.A. Variable selection from random forests: Application to gene expression data. arXiv, 2005; arXiv:q-bio/0503025. [Google Scholar]
- Hayashi, R.; Weiskittel, A.; Kershaw, J.A., Jr. Influence of prediction cell size on LiDAR-derived area-based estimates of total volume in mixed-species and multicohort forests in northeastern North America. Can. J. Remote Sens. 2016, 42, 473–488. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Tuominen, S.; Haapanen, R. Estimation of forest biomass by means of genetic algorithm-based optimization of airborne laser scanning and digital aerial photograph features. Silva Fenn. 2013, 47. [Google Scholar] [CrossRef]
- Véga, C.; Renaud, J.P.; Durrieu, S.; Bouvier, M. On the interest of penetration depth, canopy area and volume metrics to improve Lidar-based models of forest parameters. Remote Sens. Environ. 2016, 175, 32–42. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Pinto, N.; Cox, D.D.; DiCarlo, J.J. Why is real-world visual object recognition hard? PLoS Comput. Biol. 2008, 4, e27. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L.; Nitschke, G. Improving Deep Learning using Generic Data Augmentation. arXiv, 2017; arXiv:1708.06020. [Google Scholar]
- Simonyan, K.; Zisserman, A. Two-stream convolutional networks for action recognition in videos. In Advances in Neural Information Processing Systems; MIT Press Ltd.: Cambridge, MA, USA, 2014; pp. 568–576. [Google Scholar]
- Peng, X.; Sun, B.; Ali, K.; Saenko, K. Learning deep object detectors from 3D models. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1278–1286. [Google Scholar]
- Ros, G.; Sellart, L.; Materzynska, J.; Vazquez, D.; Lopez, A.M. The synthia dataset: A large collection of synthetic images for semantic segmentation of urban scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3234–3243. [Google Scholar]
- Fischer, R.; Bohn, F.; de Paula, M.D.; Dislich, C.; Groeneveld, J.; Gutiérrez, A.G.; Kazmierczak, M.; Knapp, N.; Lehmann, S.; Paulick, S. Lessons learned from applying a forest gap model to understand ecosystem and carbon dynamics of complex tropical forests. Ecol. Model. 2016, 326, 124–133. [Google Scholar] [CrossRef]
- Shin, H.-C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef] [PubMed]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 818–833. [Google Scholar]
- Yosinski, J.; Clune, J.; Nguyen, A.; Fuchs, T.; Lipson, H. Understanding neural networks through deep visualization. arXiv, 2015; arXiv:1506.06579. [Google Scholar]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A., Jr.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer Stacking: A Novel Algorithm for Individual Forest Tree Segmentation from LiDAR Point Clouds. Can. J. Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Szegedy, C.; Toshev, A.; Erhan, D. Deep neural networks for object detection. In Advances in Neural Information Processing Systems; MIT Press Ltd.: Cambridge, MA, USA, 2013; pp. 2553–2561. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Kulkarni, T.D.; Whitney, W.F.; Kohli, P.; Tenenbaum, J. Deep convolutional inverse graphics network. In Advances in Neural Information Processing Systems; MIT Press Ltd.: Cambridge, MA, USA, 2015; pp. 2539–2547. [Google Scholar]
- Yan, X.; Yang, J.; Sohn, K.; Lee, H. Attribute2image: Conditional image generation from visual attributes. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 776–791. [Google Scholar]
| Site Name | Location | Number of Plots | LiDAR Acquisition | Species * |
|---|---|---|---|---|
| Acadia National Park | 44°20′N, 68°16′W | 9 | G-LIHT | 69% Piru, 8% Thoc, 6% Acru, 5% Pist, 5% Abba |
| Bartlett Experimental Forest | 44°2′N, 71°17′W | 46 | NEON | 46% Fagr, 18% Tsca, 14% Acru, 9% Acsa, 5% Beal |
| University of Maine’s Cooperative Forest Research Unit | 45°11′N, 69°42′W | 90 | G-LIHT | 50% Piru, 42% Abba |
| University of Maine’s Dwight B. Demeritt Forest | 44°55′N, 68°40′W | 344 | G-LIHT | 28% Acru, 23% Abba, 10% Thoc, 8% Tsca, 7% Piru |
| Harvard Forest | 42°31′N, 72°11′W | 13,470 | G-LIHT and NEON | 32% Tsca, 25% Acru, 14% Quru, 6% Pist, 5% Beal |
| Holt Research Forest | 43°52′N, 69°46′W | 2002 | G-LIHT | 25% Pist, 24% Acru, 21% Quru, 7% Piru, 7% Abba |
| Howland Research Forest | 45°12′N, 68°45′W | 1014 | G-LIHT | 40% Piru, 31% Tsca, 11% Thoc, 10% Acru |
| Penobscot Experimental Forest | 44°52′N, 68°37′W | 301 | G-LIHT | 27% Abba, 23% Tsca, 13% Pist, 13% Piru, 12% Acru |
| Min | Mean | Max | SD | |
|---|---|---|---|---|
| Aboveground Biomass (Mg/ha) | 0 | 185.7 | 715.7 | 88.5 |
| Tree Count (#) | 0 | 6.93 | 25 | 3.65 |
| Percent Needleleaf (%) | 0 | 42.9 | 100 | 28.9 |
| Aboveground Biomass (Mg/ha) | Tree Count (#) | Percent Needleleaf (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Pseudo R2 | RMSE (%) | Bias (%) | Pseudo R2 | RMSE (%) | Bias (%) | Pseudo R2 | RMSE | Bias | |
| THM with LMM | 0.55 | 57.6 (31.3) | −1.3 (0.7) | 0.31 | 3.10 (44.9) | 0.03 (0.5) | 0.31 | 24.1 | −0.4 |
| THM with Random Forest | 0.61 | 54.1 (29.5) | −1.6 (0.9) | 0.36 | 2.96 (43.0) | 0.1 (1.4) | 0.57 | 19.1 | 0.5 |
| Inception-V3 CNN | 0.69 | 48.1 (26.1) | 1.3 (0.7) | 0.43 | 2.78 (40.3) | 0.2 (2.8) | 0.58 | 18.7 | 0.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayrey, E.; Hayes, D.J. The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory. Remote Sens. 2018, 10, 649. https://doi.org/10.3390/rs10040649
Ayrey E, Hayes DJ. The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory. Remote Sensing. 2018; 10(4):649. https://doi.org/10.3390/rs10040649
Chicago/Turabian StyleAyrey, Elias, and Daniel J. Hayes. 2018. "The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory" Remote Sensing 10, no. 4: 649. https://doi.org/10.3390/rs10040649
APA StyleAyrey, E., & Hayes, D. J. (2018). The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory. Remote Sensing, 10(4), 649. https://doi.org/10.3390/rs10040649