Evaluation of Heavy Precipitation Simulated by the WRF Model Using 4D-Var Data Assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China
Abstract
:1. Introduction
2. Data
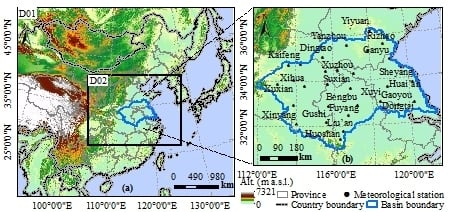
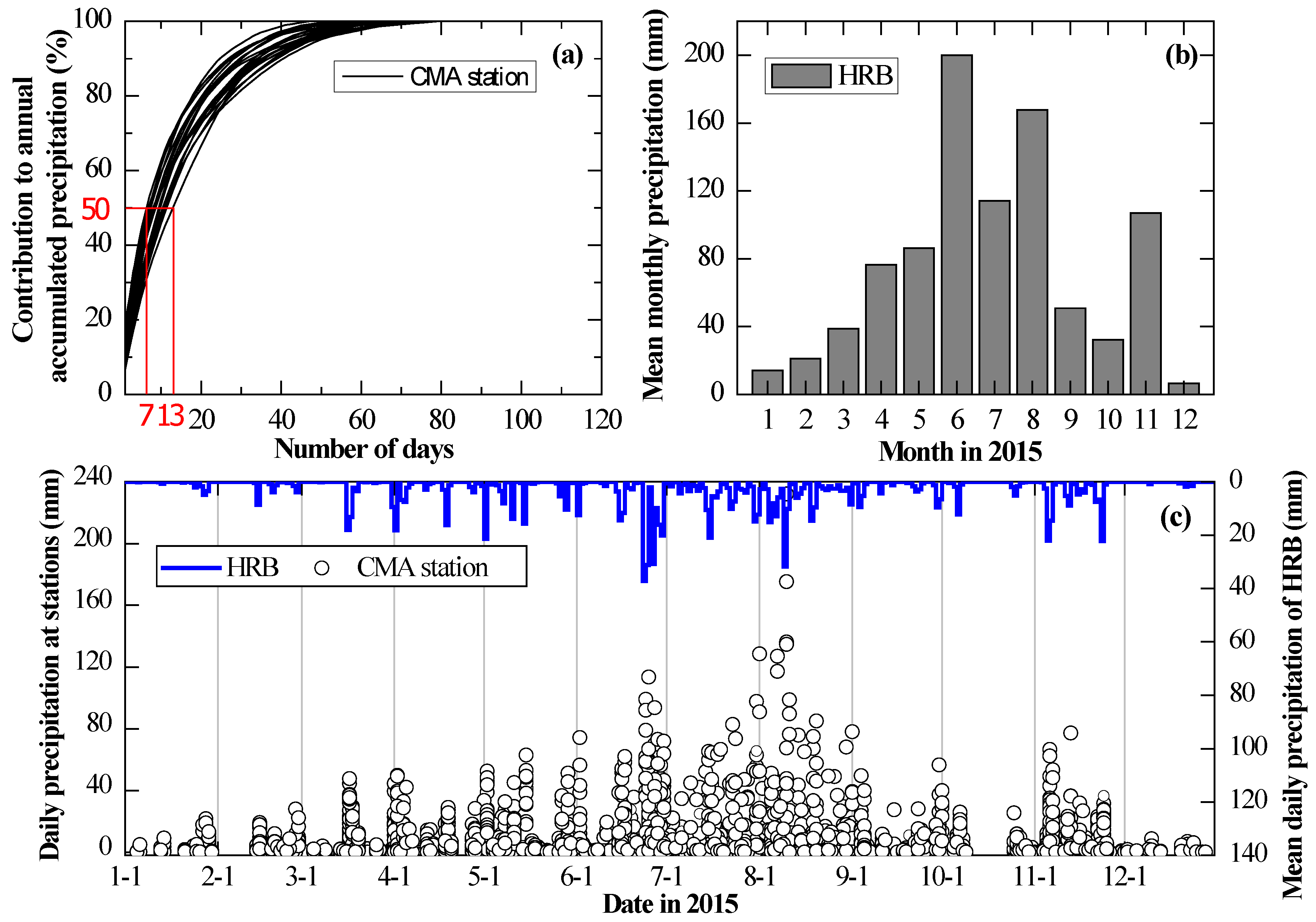
2.1. Study Area and Events
2.2. Study Data
2.2.1. Satellite Precipitation Products for Assimilation
2.2.2. Forcing Data for the WRF Model
2.2.3. In Situ and Gauge-Corrected Data for Evaluation
3. Methods
3.1. WRF Configuration, 4D-Var Methodology, and Experimental Design
3.1.1. WRF Configuration
3.1.2. WRF Configuration
3.1.3. Experimental Design
3.2. Evaluation Metrics
4. Results
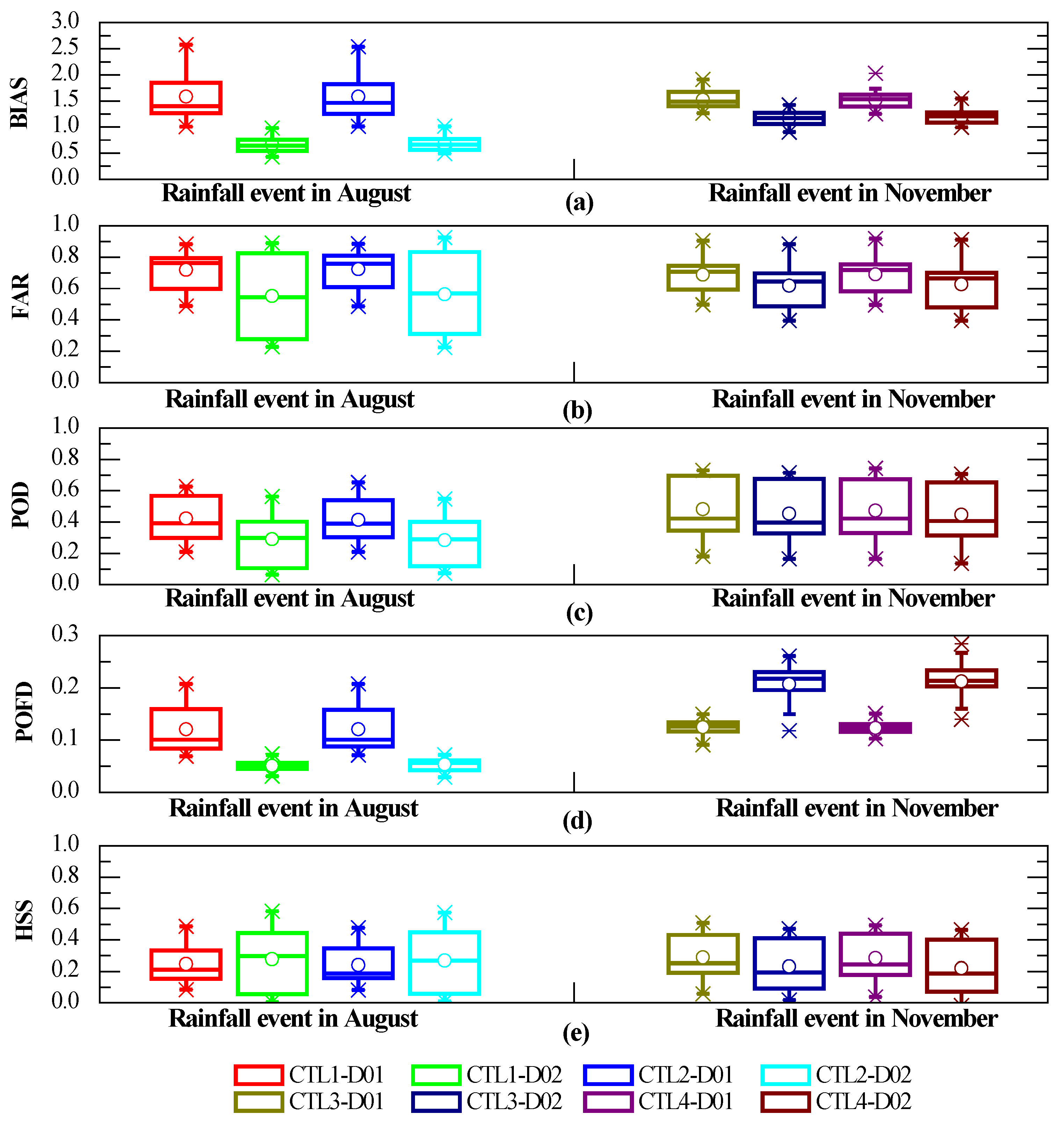
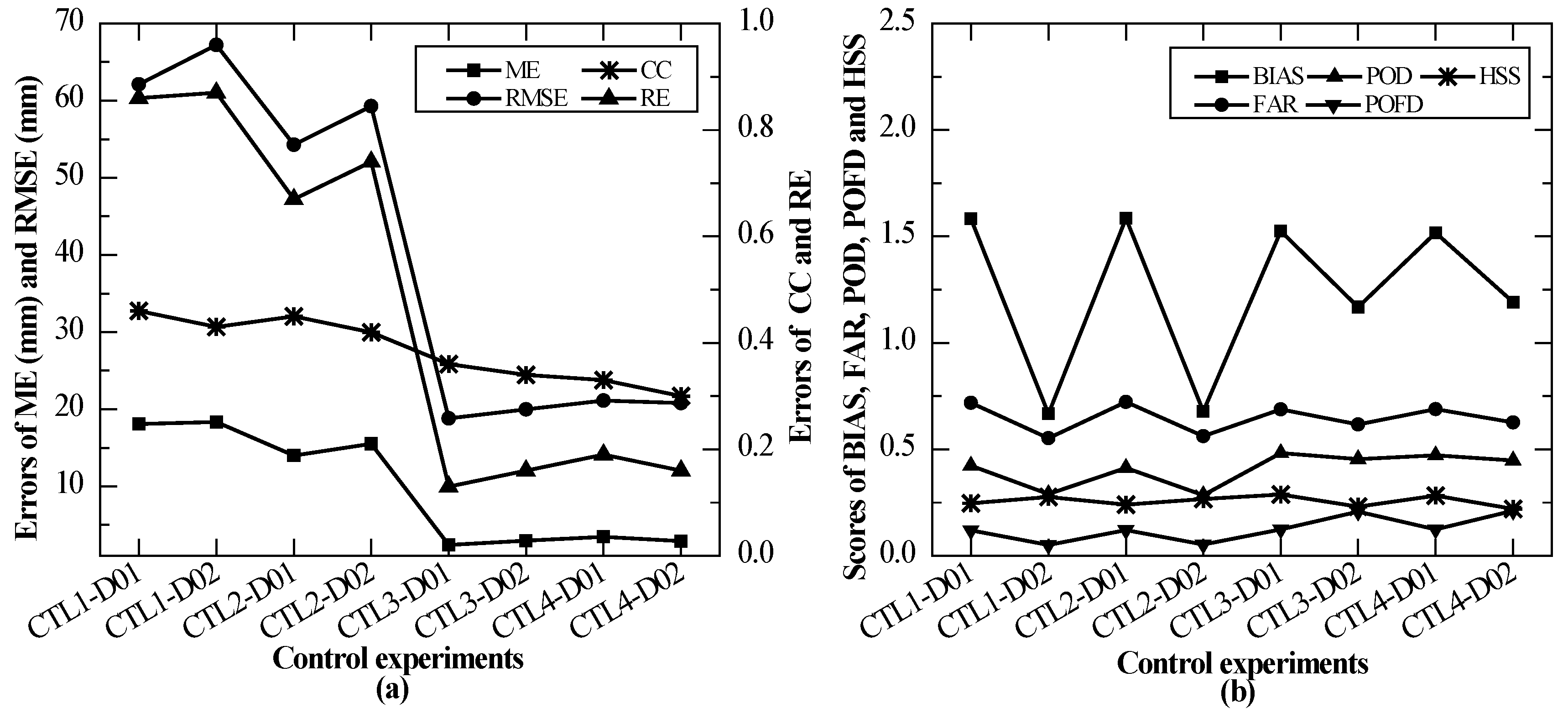
4.1. Evaluation of Simulated Precipitation in the CTL Experiments
4.1.1. Evaluation of Simulated Precipitation in the CTL Experiments at the Point Scale
4.1.2. Evaluation of the Simulated Precipitation in the CTL experiments at the Grid Scale
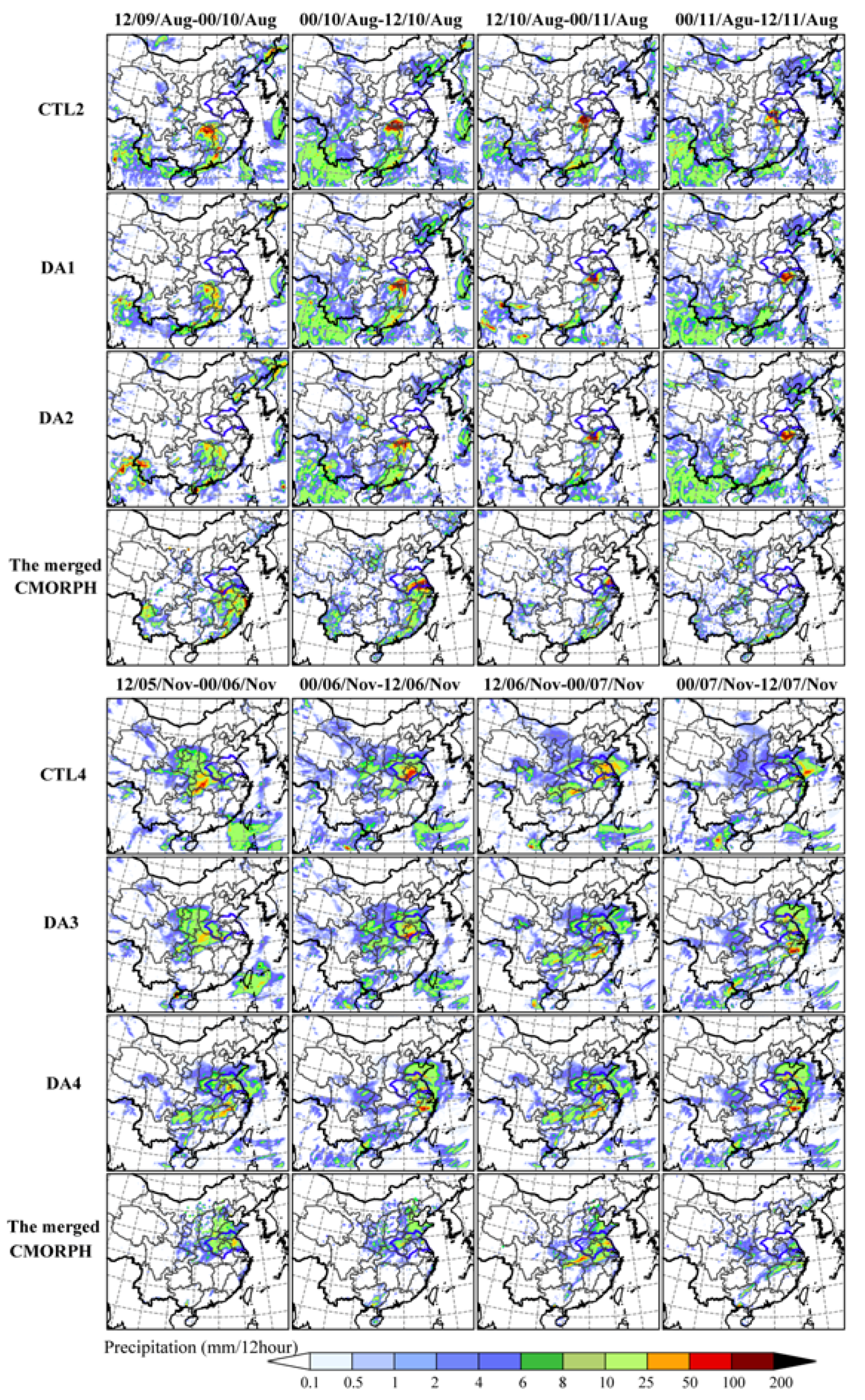
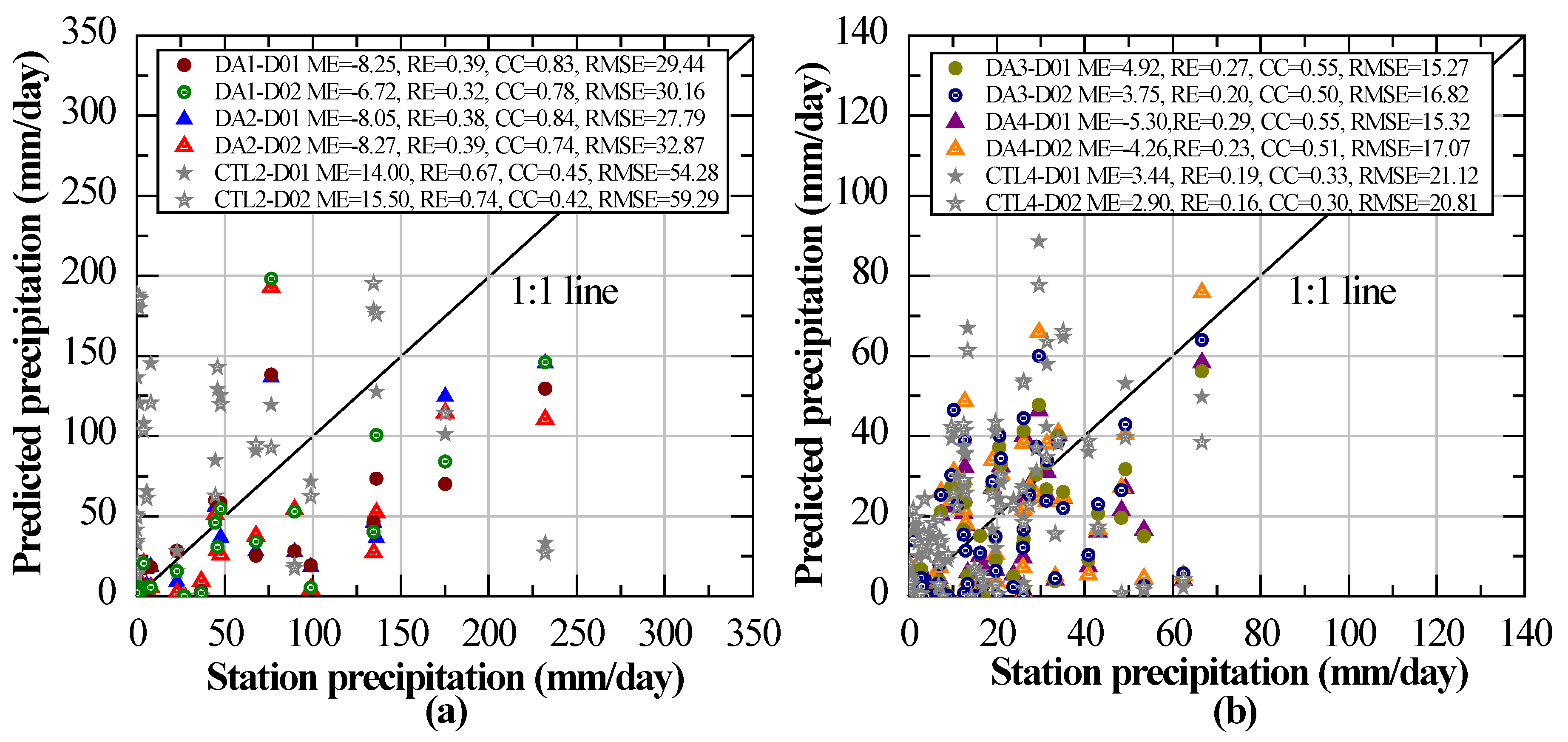
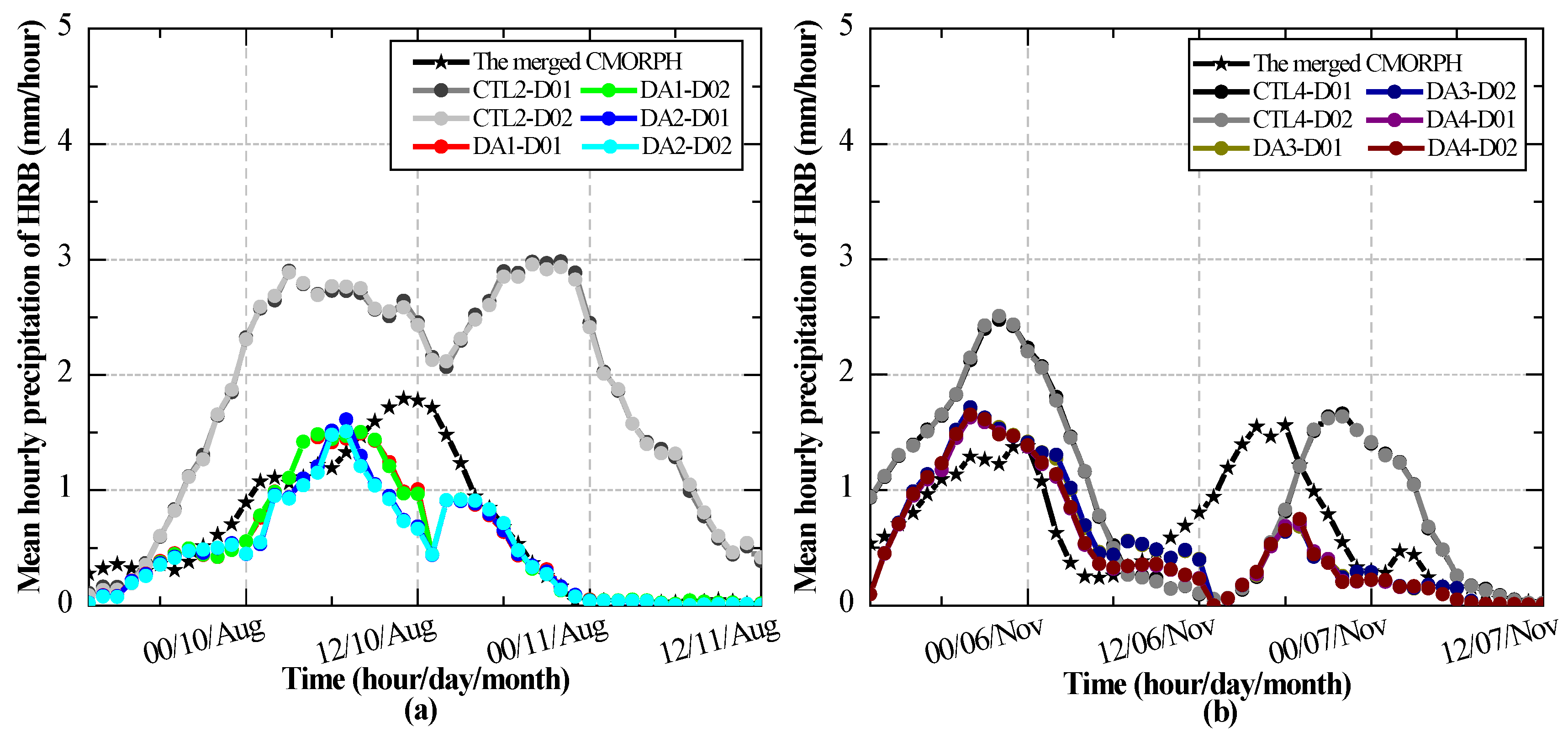
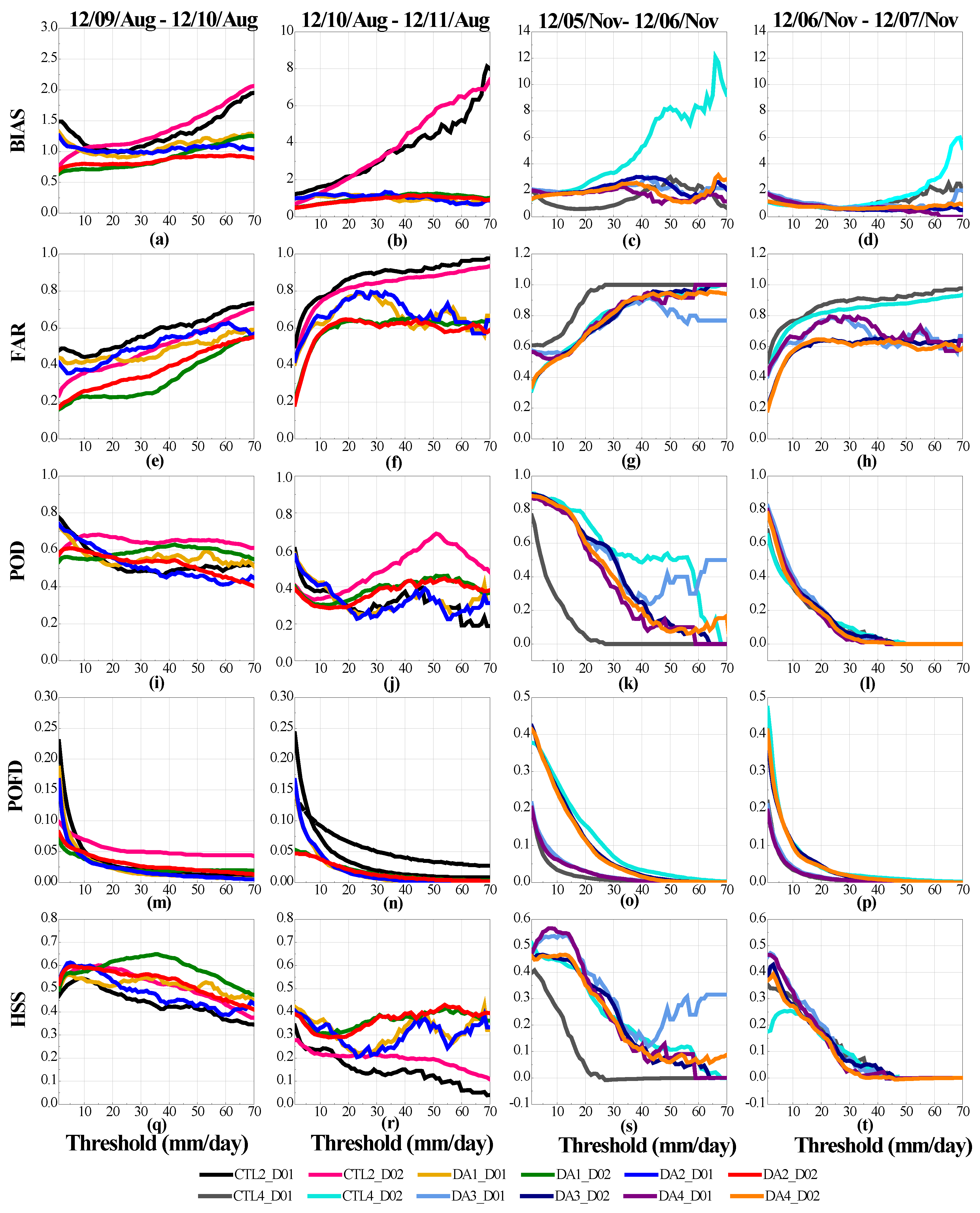
4.2. Evaluation of the Simulated Precipitation in the DA Experiments
4.2.1. Evaluation of Simulated Precipitation in the DA Experiments at the Point Scale
4.2.2. Evaluation of Simulated Precipitation in the DA experiments at the Grid Scale
5. Discussions
5.1. WRF Sensitivity to Different Rainfall Events, Forcing Data, and Spatial Resolutions
5.2. The Effectiveness of WRF 4D-Var at Different Thresholds and Time
5.3. Comparison of the 4D-Var Performance Assimilated with TRMM 3B42 and GPM IMERG
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Palmer, T.N.; Ralsanen, J. Quantifying the risk of extreme seasonal precipitation events in a changing climate. Nature 2002, 415, 512–514. [Google Scholar] [CrossRef] [PubMed]
- Groisman, P.Y.; Karl, T.R.; Easterling, D.R.; Knight, R.W.; Jamason, P.F.; Hennessy, K.J.; Suppiah, R.; Page, C.M.; Wibig, J.; Fortuniak, K.; et al. Changes in the probability of heavy precipitation: Important indicators of climatic change. Clim. Chang. 1999, 42, 243–283. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R. Heavy precipitation and high streamflow in the contiguous United States: Trends in the twentieth century. Bull. Am. Meteorol. Soc. 2001, 82, 219–246. [Google Scholar] [CrossRef]
- Zhang, W.; Villarini, G. Heavy precipitation is highly sensitive to the magnitude of future warming. Clim. Chang. 2017, 145, 249–257. [Google Scholar] [CrossRef]
- Zeng, J.Y.; Li, Z.; Chen, Q.; Bi, H.Y.; Qiu, J.X.; Zou, P.F. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Zeng, J.Y.; Chen, K.S.; Bi, H.Y.; Chen, Q. A Preliminary Evaluation of the SMAP Radiometer Soil Moisture Product over United States and Europe Using Ground-Based Measurements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4929–4940. [Google Scholar] [CrossRef]
- Pan, X.D.; Li, X.; Cheng, G.D.; Hong, Y. Effects of 4D-Var data assimilation using remote sensing precipitation products in a WRF Model over the complex terrain of an arid region river basin. Remote Sens. 2017, 9, 693. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; McLaughlin, D.B.; Entekhabi, D. Quantifying precipitation uncertainty for land data assimilation applications. Mon. Weather Rev. 2015, 143, 3276–3299. [Google Scholar] [CrossRef]
- Ward, E.; Buytaert, W.; Peaver, L.; Wheater, H. Evaluation of precipitation products over complex mountainous terrain: A water resources perspective. Adv. Water Resour. 2011, 34, 1222–1231. [Google Scholar] [CrossRef]
- Chen, Y.J.; Ebert, E.; Walsh, K.E.; Davidson, N. Evaluation of TRMM 3B42 precipitation estimates of tropical cyclone rainfall using PACRAIN data. J. Geophys. Res. Atmos. 2013, 118, 2184–2196. [Google Scholar] [CrossRef]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E.; et al. The future of earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef]
- Steiner, M.; Smith, J.A.; Burges, S.J.; Alonso, C.V.; Darden, R.W. Effect of bias adjustment and rain gauge data quality control on radar rainfall estimation. Water Resour. Res. 1999, 35, 2487–2503. [Google Scholar] [CrossRef]
- Lorenz, C.; Kunstmann, H. The hydrological cycle in three state-of-the-art reanalyses: Intercomparison and performance analysis. J. Hydrometeorol. 2012, 13, 1397–1420. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The Global Precipitation Climatology Project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Garstang, M.; Kummerow, C.D. The joanne simpson special issue on the Tropical Rainfall Measuring Mission (TRMM). J. Appl. Meteorol. 2000, 39, 1961. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701. [Google Scholar] [CrossRef]
- Gaona, M.F.R.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. First-year evaluation of GPM rainfall over the Netherlands: IMERG Day 1 final run (VO3D). J. Hydrometeorol. 2016, 17, 2799–2814. [Google Scholar] [CrossRef]
- Schmidli, J.; Goodess, C.M.; Frei, C.; Haylock, M.R.; Hundecha, Y.; Ribalaygua, J.; Schmith, T. Statistical and dynamical downscaling of precipitation: An evaluation and comparison of scenarios for the European Alps. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Zhang, X.X.; Anagnostou, E.; Frediani, M.; Solomos, S.; Kallos, G. Using NWP simulations in satellite rainfall estimation of heavy precipitation events over mountainous areas. J. Hydrometeorol. 2013, 14, 1844–1858. [Google Scholar] [CrossRef]
- Koizumi, K.; Ishikawa, Y.; Tsuyuki, T. Assimilation of precipitation data to the JMA mesoscale model with a four-dimensional variational method and its impact on precipitation forecasts. Sola 2005, 1, 45–48. [Google Scholar] [CrossRef]
- Mazrooei, A.; Sinha, T.; Sankarasubramanian, A.; Kumar, S.; Peters-Lidard, C.D. Decomposition of sources of errors in seasonal streamflow forecasting over the US Sunbelt. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef]
- Case, J.L.; Crosson, W.L.; Kumar, S.V.; Lapenta, W.M.; Peters-Lidard, C.D. Impacts of high-resolution land surface initialization on regional sensible weather forecasts from the WRF Model. J. Hydrometeorol. 2008, 9, 1249–1266. [Google Scholar] [CrossRef]
- Flesch, T.K.; Reuter, G.W. WRF model simulation of two Alberta flooding events and the impact of topography. J. Hydrometeorol. 2012, 13, 695–708. [Google Scholar] [CrossRef]
- Janjic, Z.I. The step-mountain coordinate -physical package. Mon. Weather Rev. 1990, 118, 1429–1443. [Google Scholar] [CrossRef]
- Black, T.L. The new NMC mesoscale ETA model—Description and forecast examples. Weather Forecast. 1994, 9, 265–278. [Google Scholar] [CrossRef]
- Mesinger, F.; Janjic, Z.I.; Nickovic, S.; Gavrilov, D.; Deaven, D.G. The step-mountain coordinate - model description and performance for cases of description and performance for cases of Alpine Lee Cyclongensis and for a case of an Appalachian redevelopment. Mon. Weather Rev. 1988, 116, 1493–1518. [Google Scholar] [CrossRef]
- Dudhia, J.; Klemp, J.; Skamarock, W.; Dempsey, D.; Janjic, Z.; Benjamin, S.; Brown, J.; Ams, A.M.S. A collaborative effort towards a future community mesoscale model (WRF). In Proceedings of the 12th Conference on Numerical Weather Prediction, Phoenix, AZ, USA, 11–16 January 1998; pp. 242–243. [Google Scholar]
- Saito, K.; Fujita, T.; Yamada, Y.; Ishida, J.I.; Kumagai, Y.; Aranami, K.; Ohmori, S.; Nagasawa, R.; Kumagai, S.; Muroi, C.; et al. The operational JMA nonhydrostatic mesoscale model. Mon. Weather Rev. 2006, 134, 1266–1298. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Quart. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Yang, B.; Qian, Y.; Lin, G.; Leung, R.; Zhang, Y. Some issues in uncertainty quantification and parameter tuning: A case study of convective parameterization scheme in the WRF regional climate model. Atmos. Chem. Phys. 2012, 12, 2409–2427. [Google Scholar] [CrossRef]
- Angevine, W.M.; Brioude, J.; McKeen, S.; Holloway, J.S. Uncertainty in Lagrangian pollutant transport simulations due to meteorological uncertainty from a mesoscale WRF ensemble. Geosci. Model Dev. 2014, 7, 2817–2829. [Google Scholar] [CrossRef]
- Panofsky, H.A. Objective Weather-manp analysis. J. Meteorol. 1949, 6, 386–392. [Google Scholar] [CrossRef]
- Leneman, O.A.Z. Random sampling of random processes—Optimum linear interpolation. J. Frankl. Inst. Eng. Appl. Math. 1966, 281, 302. [Google Scholar] [CrossRef]
- Sasaki, Y. An objective analysis based on the variational method. J. Meteorol. Soc. Jpn. 1958, 36, 77–88. [Google Scholar] [CrossRef]
- Sasaki, Y. Some basic formalisms in numerical variational analysis. Mon. Weather Rev. 1970, 98, 875. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using monte-carlo methods to forecast error statistics. J. Geophys. Res. Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G. Advanced data assimilation for strongly nonlinear dynamics. Mon. Weather Rev. 1997, 125, 1342–1354. [Google Scholar] [CrossRef]
- Tsuyuki, T. Variational data assimilation in the tropics using precipitation data part I: Column model. Meteorol. Atmos. Phys. 1996, 60, 87–104. [Google Scholar] [CrossRef]
- Zupanski, D.; Mesinger, F. 4-dimensional variational assimilation of precipitation data. Mon. Weather Rev. 1995, 123, 1112–1127. [Google Scholar] [CrossRef]
- Lopez, P. Direct 4D-Var assimilation of NCEP stage IV radar and gauge precipitation data at ECMWF. Mon. Weather Rev. 2011, 139, 2098–2116. [Google Scholar] [CrossRef]
- Lin, L.F.; Ebtehaj, A.M.; Bras, R.L.; Flores, A.N.; Wang, J.F. Dynamical precipitation downscaling for hydrologic applications using WRF 4D-Var data assimilation: Implications for GPM era. J. Hydrometeorol. 2015, 16, 811–829. [Google Scholar] [CrossRef]
- Chambon, P.; Zhang, S.Q.; Hou, A.Y.; Zupanski, M.; Cheung, S. Assessing the impact of pre-GPM microwave precipitation observations in the Goddard WRF ensemble data assimilation system. Quart. J. R. Meteorol. Soc. 2014, 140, 1219–1235. [Google Scholar] [CrossRef]
- Ballard, S.P.; Li, Z.H.; Simonin, D.; Caron, J.F. Performance of 4D-Var NWP-based nowcasting of precipitation at the Met Office for summer 2012. Quart. J. R. Meteorol. Soc. 2016, 142, 472–487. [Google Scholar] [CrossRef]
- Verlinde, J.; Cotton, W.R. Fitting microphysical observations of nonsteady convective clouds to a numerical model: An application of the adjoint technique of data assimilation to a kinematic model. Mon. Weather Rev. 1993, 121, 2776–2793. [Google Scholar] [CrossRef]
- Xia, J.; She, D.X.; Zhang, Y.Y.; Du, H. Spatio-temporal trend and statistical distribution of extreme precipitation events in Huaihe River Basin during 1960–2009. J. Geogr. Sci. 2012, 22, 195–208. [Google Scholar] [CrossRef]
- Cao, Q.; Qi, Y.C. The variability of vertical structure of precipitation in Huaihe River Basin of China: Implications from long-term spaceborne observations with TRMM precipitation radar. Water Resour. Res. 2014, 50, 3690–3705. [Google Scholar] [CrossRef]
- Zhou, Y.K.; Ma, Z.Y.; Wang, L.C. Chaotic dynamics of the flood series in the Huaihe River Basin for the last 500 years. J. Hydrol. 2002, 258, 100–110. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.J.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Tang, G.Q.; Ma, Y.Z.; Long, D.; Zhong, L.Z.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Huffman, G.; Stocker, E.; Petersen, W. Successes with the Global Precipitation Measurment (GPM) mission in 2016 Ieee International Geoscience and Remote Sensing Symposium. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3910–3912. [Google Scholar]
- 52. Xuan, Z.; Yali, L.; Xueliang, G. Application of a CMORPH-a WS merged hourly gridded precipitation product in analyzing charateristics of short-duration heavy rainfall over southern China. J. Trop. Meteorol. 2015, 31, 333–344. [Google Scholar]
- Maussion, F.; Scherer, D.; Finkelnburg, R.; Richters, J.; Yang, W.; Yao, T. WRF simulation of a precipitation event over the Tibetan Plateau, China—An assessment using remote sensing and ground observations. Hydrol. Earth Syst. Sci. 2011, 15, 1795–1817. [Google Scholar] [CrossRef]
- Lim, K.S.S.; Hong, S.Y. Development of an effective double-moment cloud microphysics scheme with prognostic Cloud Condensation Nuclei (CCN) for weather and climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Grell, G.A.; Devenyi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Courtier, P.; Thepaut, J.N.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Quart. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Veerse, F.; Thepaut, J.N. Multiple-truncation incremental approach for four-dimensional variational data assimilation. Quart. J. R. Meteorol. Soc. 1998, 124, 1889–1908. [Google Scholar] [CrossRef]
- Lorenc, A.C. Modelling of error covariances by 4D-Var data assimilation. Quart. J. R. Meteorol. Soc. 2003, 129, 3167–3182. [Google Scholar] [CrossRef]
- Barker, D.; Huang, X.Y.; Liu, Z.Q.; Auligne, T.; Zhang, X.; Rugg, S.; Ajjaji, R.; Bourgeois, A.; Bray, J.; Chen, Y.S.; et al. The weather research and forecasting model’s community variational/ensemble data assimilation system WRFDA. Bull. Am. Meteorol. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef]
- Huang, X.Y.; Xiao, Q.N.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.S.; Ma, Z.Z.; et al. Four-dimensional variational data assimilation for WRF: Formulation and preliminary results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef]
- Lynch, P.; Huang, X.Y. Initialization of the hirlam model using a digital-filter. Mon. Weather Rev. 1992, 120, 1019–1034. [Google Scholar] [CrossRef]
- Gauthier, P.; Thepaut, J.N. Impact of the digital filter as a weak constraint in the preoperational 4DVAR assimilation system of Meteo-France. Mon. Weather Rev. 2001, 129, 2089–2102. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The national-meteorological-centers spectral statistical-interpolation analysis system Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Kleczek, M.A.; Steeneveld, G.J.; Holtslag, A.A.M. Evaluation of the Weather Research and Forecasting mesoscale model for GABLS3: Impact of boundary-layer schemes, boundary conditions and spin-up. Bound.-Layer Meteorol. 2014, 152, 213–243. [Google Scholar] [CrossRef]
- Srinivas, D.; Rao, D.V.B. Implications of vortex initialization and model spin-up in tropical cyclone prediction using Advanced Research Weather Research and Forecasting Model. Nat. Hazards 2014, 73, 1043–1062. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2006; Volume 91, p. 627. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]




| Map and Grids | |
|---|---|
| Map projection | Lambert conformal |
| Center point of the domain | 35.8 °N, 114 °E |
| Number of vertical layers | 27 |
| Horizontal grid resolution | 27 km (D01), 9 km (D02) |
| Domain grid | 180 * 155, 226 * 175 |
| Static geographical fields time step | Standard dataset at a 30” resolution 150 s, 50 s from the United States Geological Survey (USGS) |
| Physical Parameterization Schemes | |
| Cloud microphysics | WRF double-moment six scheme [54] |
| Long-wave radiation | Rapid Radiative Transfer Model (RRTM) [55] |
| Short-wave radiation | Dudhia scheme [56] |
| Land surface model | Noah land surface model (LSM) [57] |
| Planetary boundary layer | Yonsei University scheme [58] |
| Cumulus parameterization | New Grell–Devenyi 3 scheme [59] (except for the 9-km domain: no cumulus) |
| No. | Studied Event | Forcing Data | No. | Studied Event | Assimilated Data |
|---|---|---|---|---|---|
| CTL1 | Event A | FNL ds083.2 | DA1 | Event A | TRMM 3B42 |
| CTL2 | FNL ds083.3 | DA2 | GPM IMERG | ||
| CTL3 | Event N | FNL ds083.2 | DA3 | Event N | TRMM 3B42 |
| CTL4 | FNL ds083.3 | DA4 | GPM IMERG |
| Statistical Metrics | Equation | Perfect Value |
|---|---|---|
| Mean Error (ME; unit: mm) | 0 | |
| Relative Error (RE) | 0 | |
| Root Mean Square Error (RMSE; unit: mm) | 0 | |
| Correlation Coefficient (CC) | 1 | |
| Bias Score (BIAS) | 1 | |
| False Alarm Ratio (FAR) | 0 | |
| Probability of Detection (POD) | 1 | |
| Probability of False Detection (POFD) | 0 | |
| Heidke Skill Score (HSS) | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, L.; Zhang, W.; Wang, K. Evaluation of Heavy Precipitation Simulated by the WRF Model Using 4D-Var Data Assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China. Remote Sens. 2018, 10, 646. https://doi.org/10.3390/rs10040646
Yi L, Zhang W, Wang K. Evaluation of Heavy Precipitation Simulated by the WRF Model Using 4D-Var Data Assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China. Remote Sensing. 2018; 10(4):646. https://doi.org/10.3390/rs10040646
Chicago/Turabian StyleYi, Lu, Wanchang Zhang, and Kai Wang. 2018. "Evaluation of Heavy Precipitation Simulated by the WRF Model Using 4D-Var Data Assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China" Remote Sensing 10, no. 4: 646. https://doi.org/10.3390/rs10040646
APA StyleYi, L., Zhang, W., & Wang, K. (2018). Evaluation of Heavy Precipitation Simulated by the WRF Model Using 4D-Var Data Assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China. Remote Sensing, 10(4), 646. https://doi.org/10.3390/rs10040646