NWP-Based Adjustment of IMERG Precipitation for Flood-Inducing Complex Terrain Storms: Evaluation over CONUS
Abstract
1. Introduction
2. Study Regions and Datasets
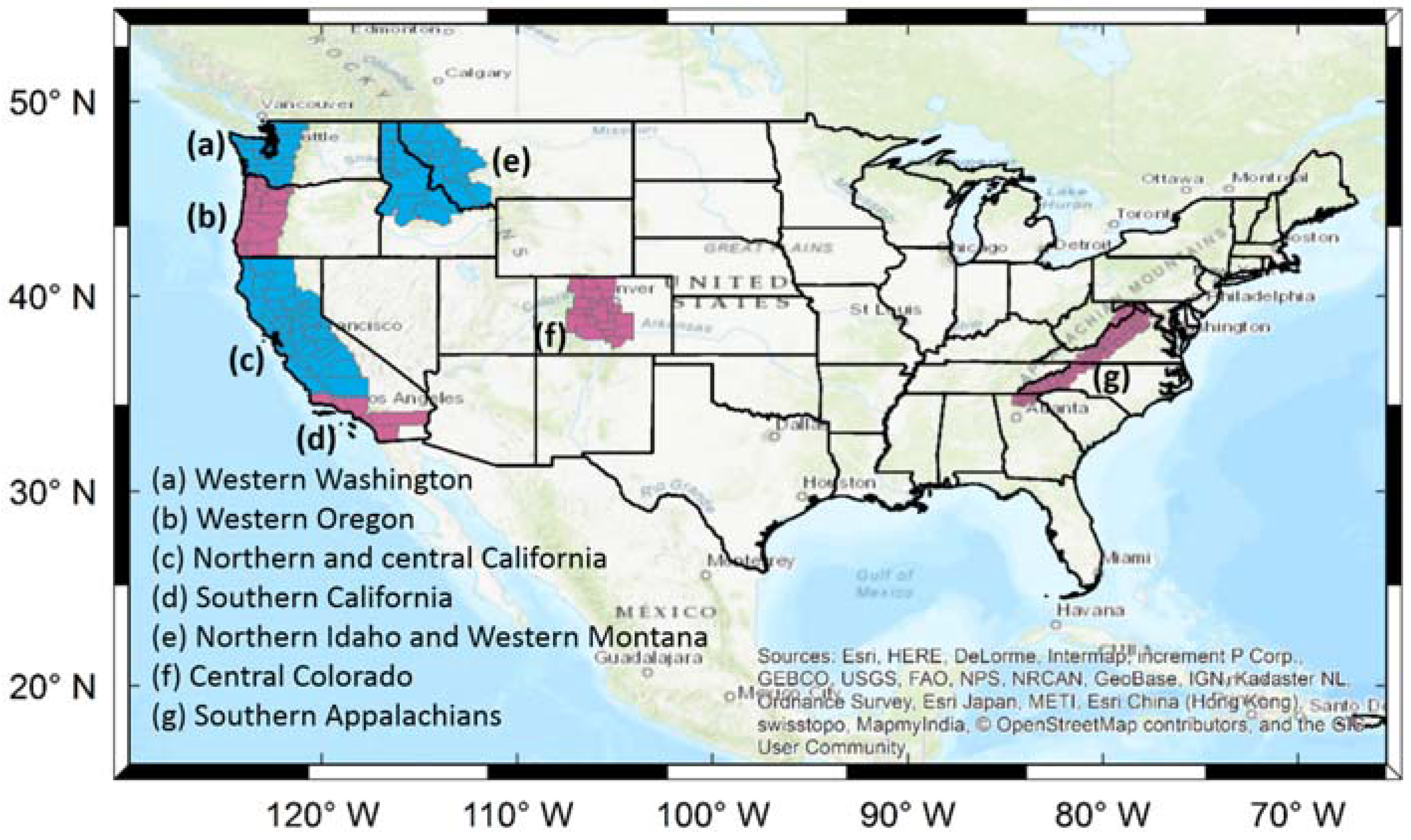
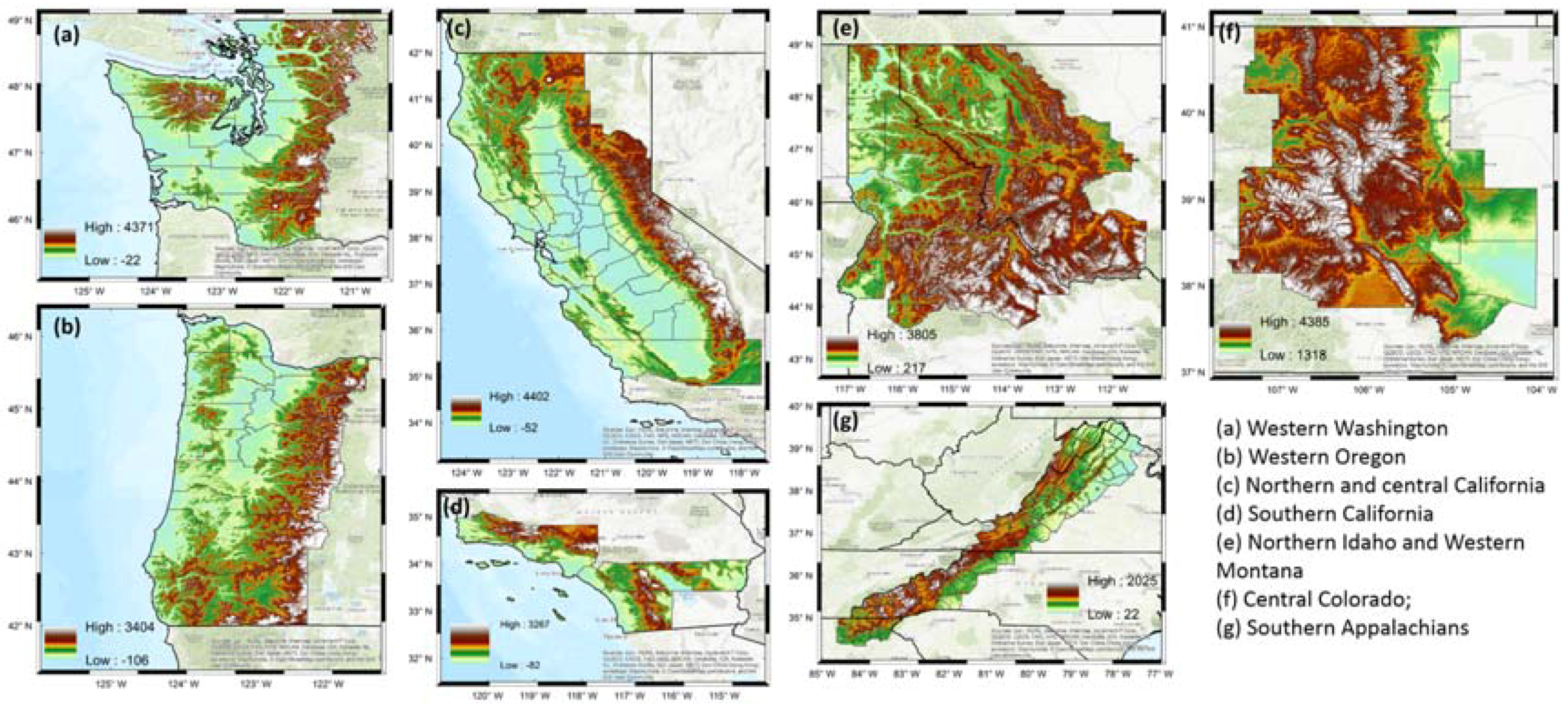
2.1. Study Regions
2.2. Precipitation Datasets
2.2.1. Satellite-Retrieved Product
2.2.2. Numerical Weather Prediction
2.2.3. NCEP Stage IV Product
3. Methodology
3.1. Event Selection
3.2. IMERG Adjustment
3.3. Data Evaluation
- A is counted when estimator ≥ threshold and Stage IV ≥ threshold (hits);
- B is counted when estimator ≥ threshold and Stage IV < threshold (false alarms);
- C is counted when estimator < threshold and Stage IV ≥ threshold (misses);
- D is counted when estimator < threshold and Stage IV < threshold (correct rejections).
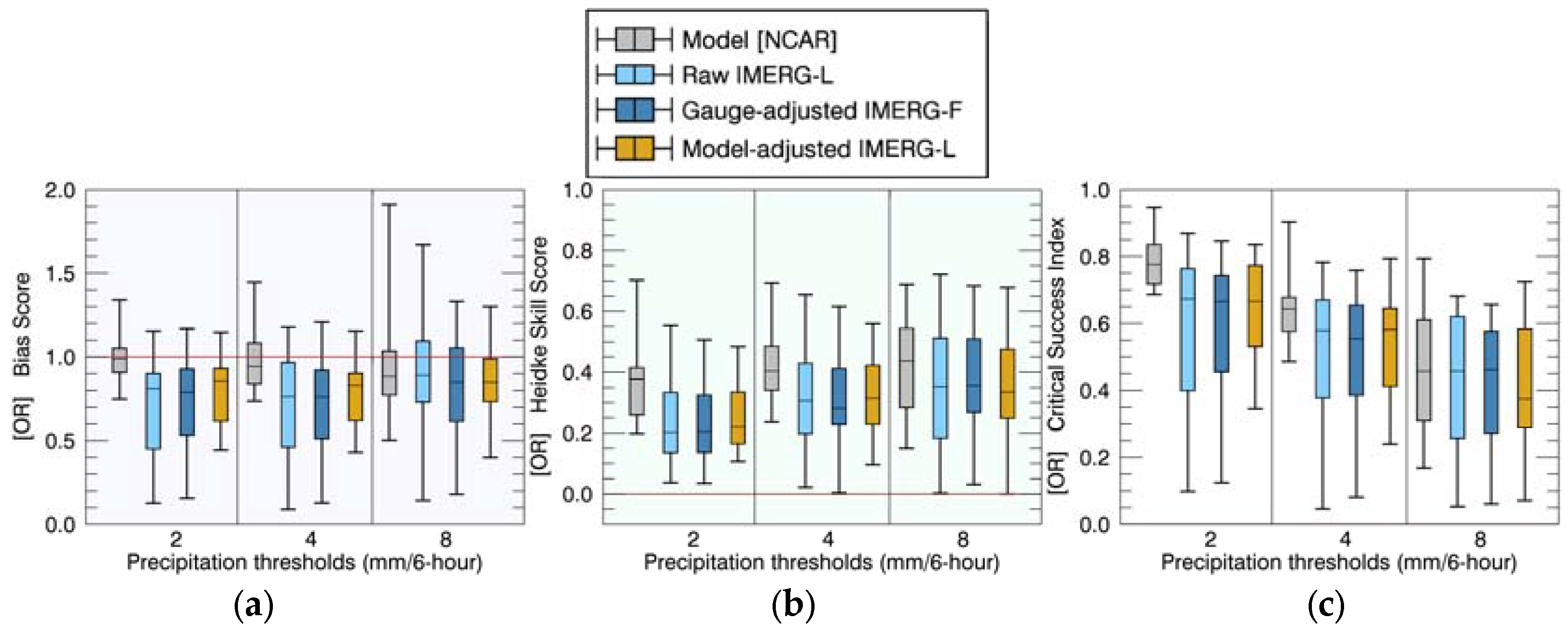
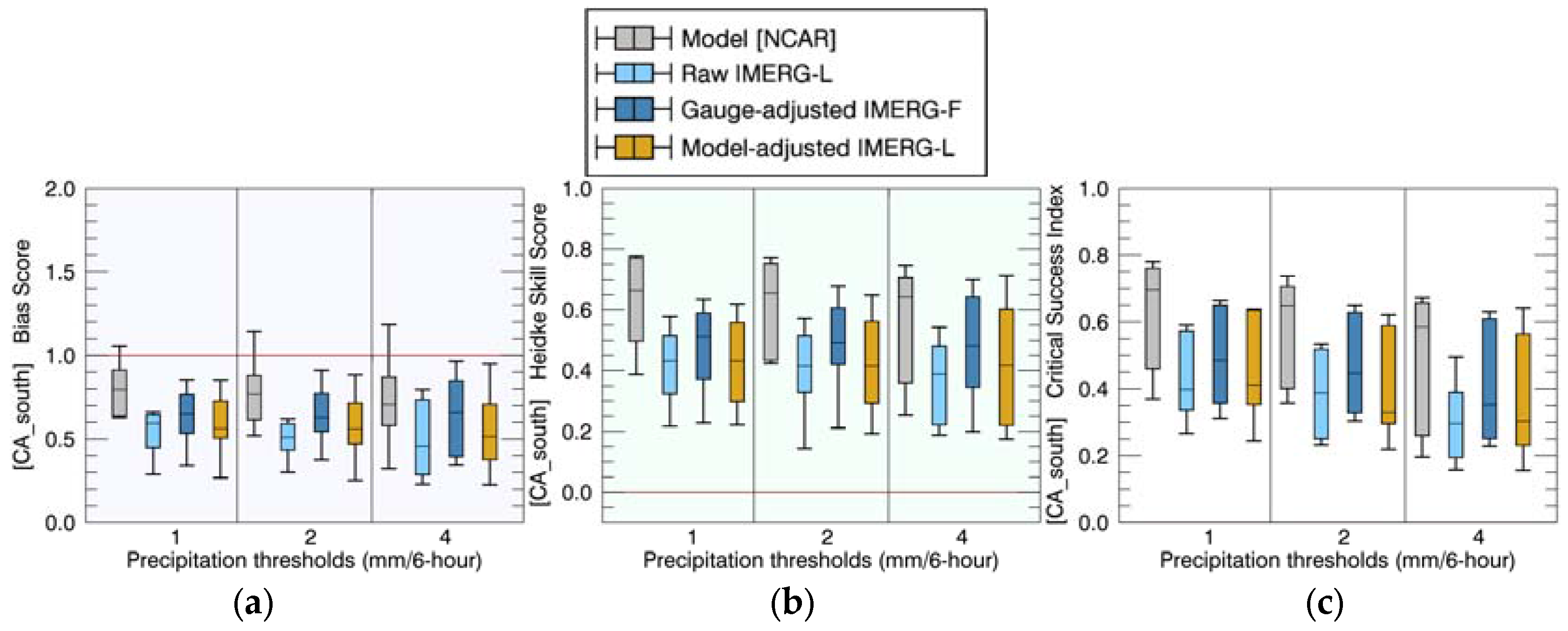
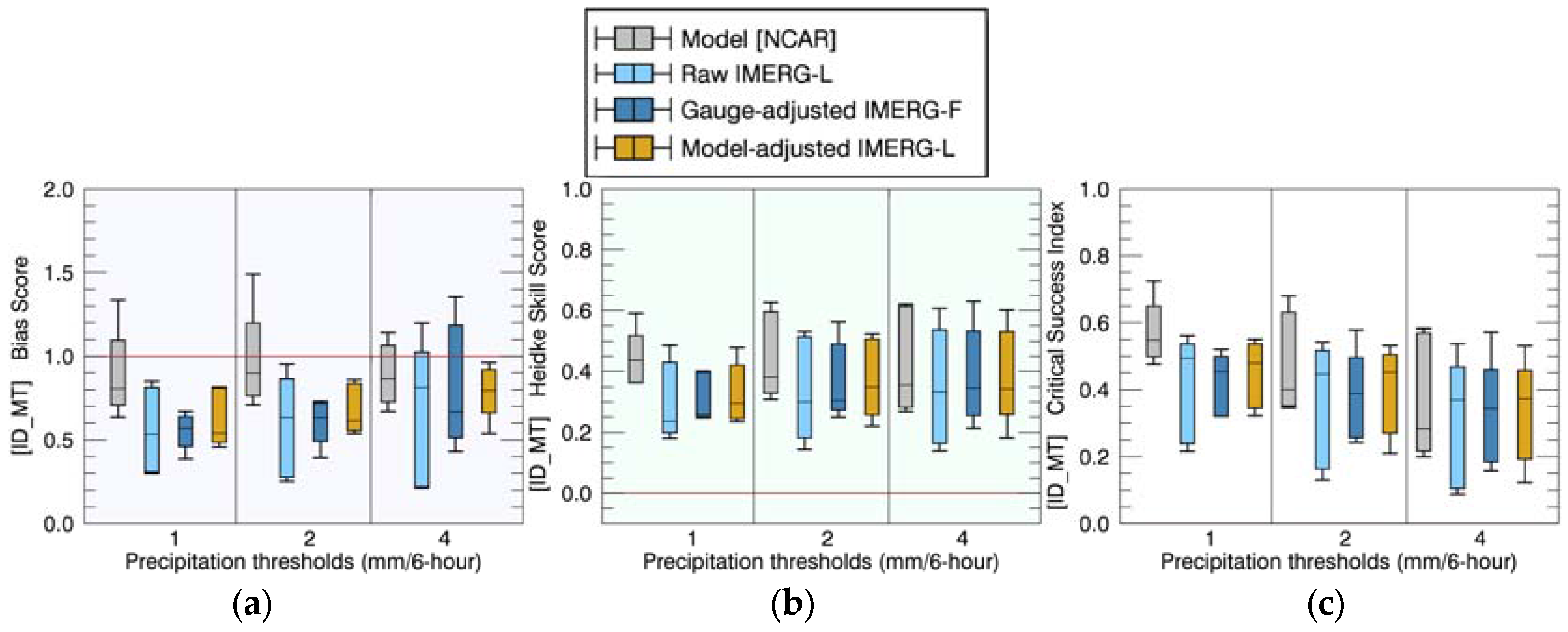
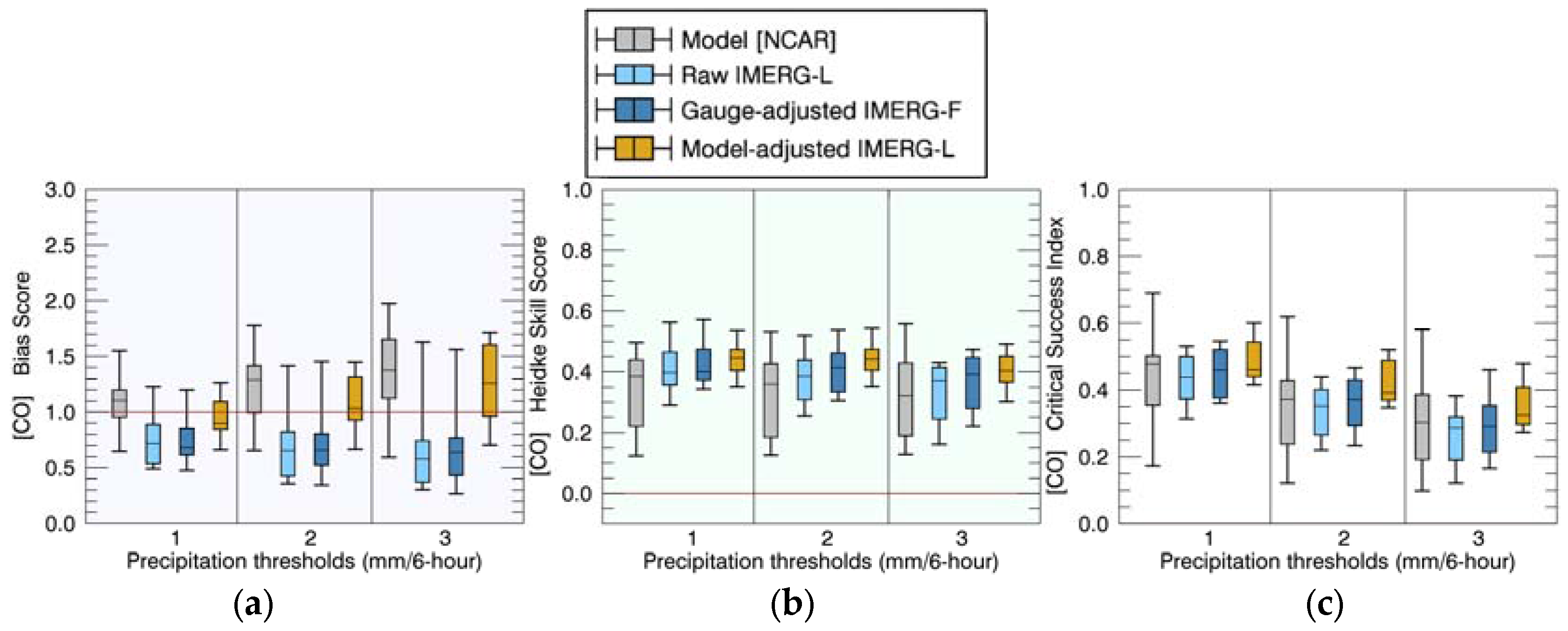
4. Results and Discussion
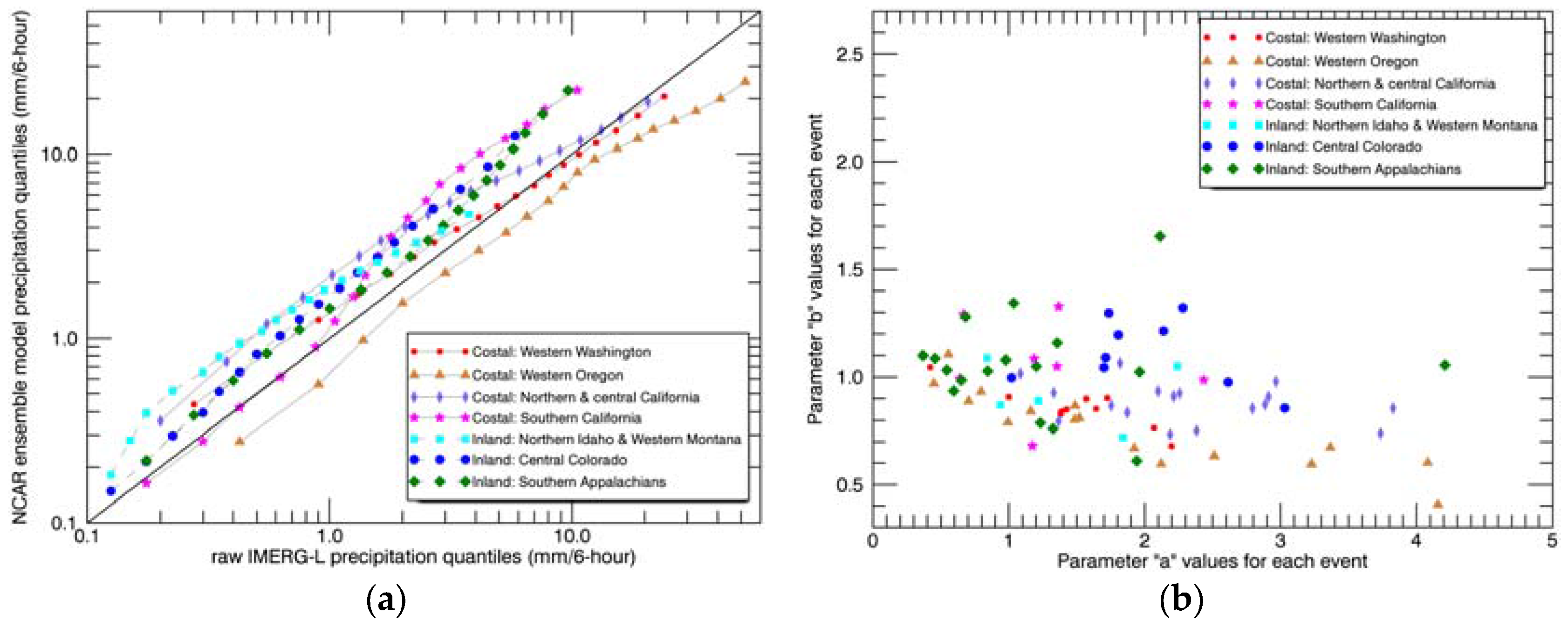
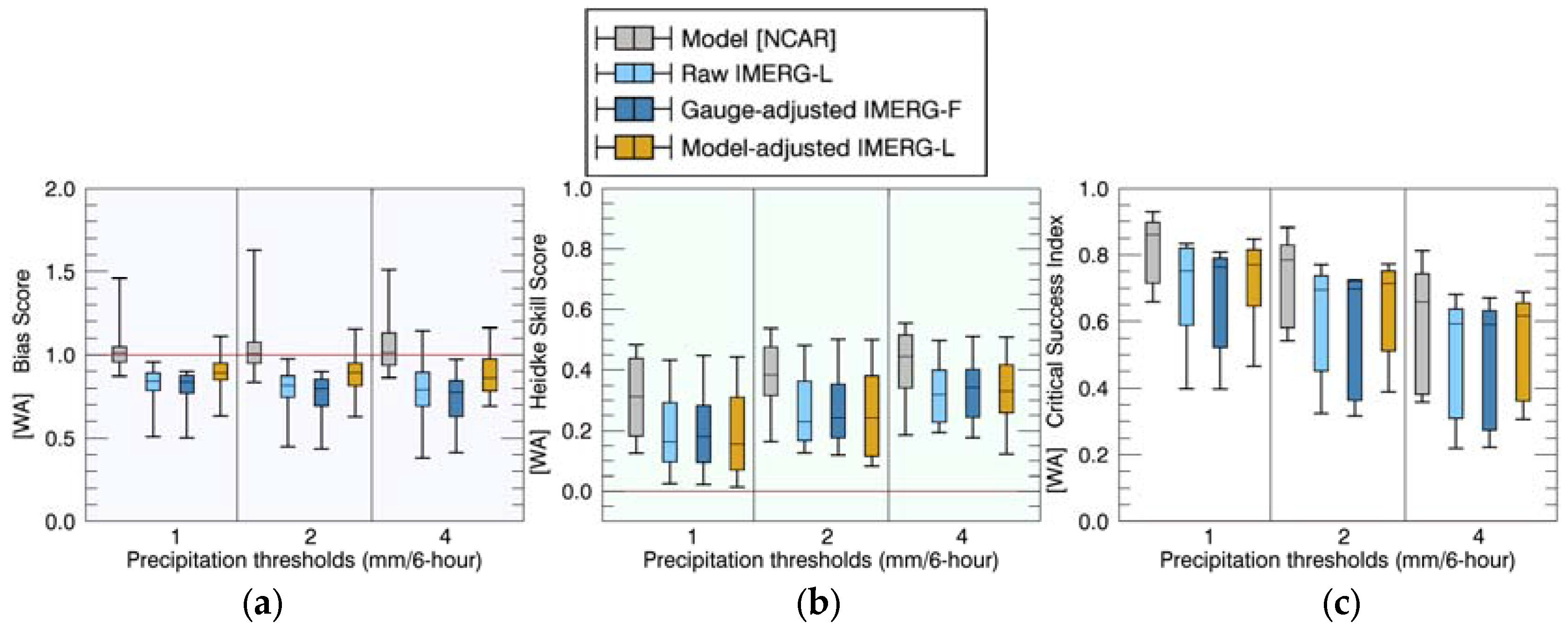
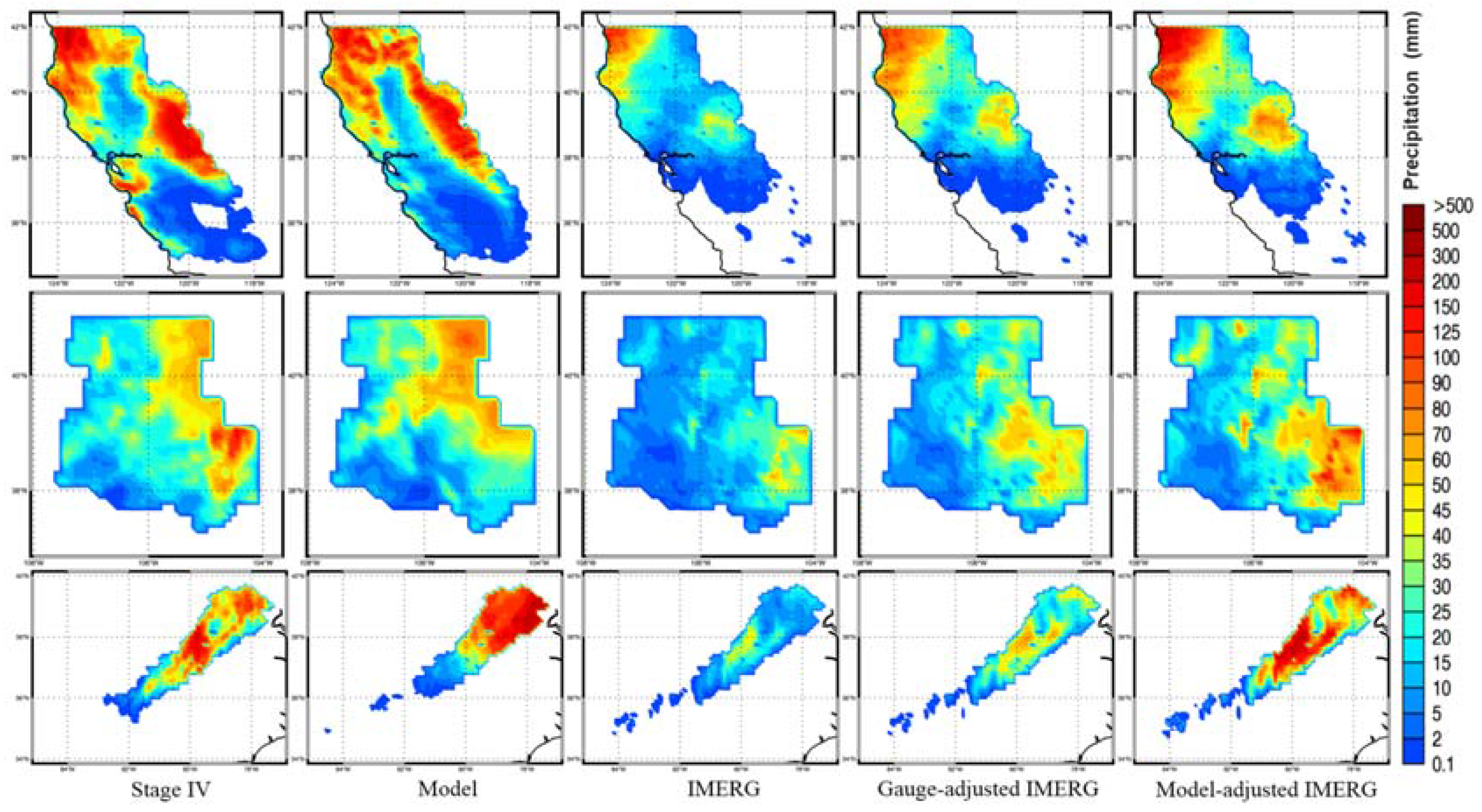
4.1. Comparisons of Precipitation Rates
4.2. Comparisons of Event Total Precipitation
4.3. Discussion: Comparison to Previous Studies
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Roe, G.H. Orographic precipitation. Annu. Rev. Earth Planet. Sci. 2005, 33, 645–671. [Google Scholar] [CrossRef]
- Houze, R.A. Orographic effects on precipitating clouds. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U.; Schröder, M.; Stender, P. Global gridded precipitation over land: A description of the new GPCC First Guess Daily product. Earth Syst. Sci. Data 2014, 6, 49–60. [Google Scholar] [CrossRef]
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Yatagai, A.; Arakawa, O.; Kamiguchi, K.; Kawamoto, H.; Nodzu, M.I.; Hamada, A. A 44-year daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Sola 2009, 5, 137–140. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Smith, J.A. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Q. J. R. Meteorol. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the different sources of uncertainty in single polarization radar-based estimates of rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite–based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; Iwanami, K. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M. A Kalman filter approach to the Global Satellite Mapping of Precipitation (GSMaP) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Jpn. Ser. II 2009, 87, 137–151. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). In Algorithm Theoretical Basis Document, version 5.1; National Aeronautics and Space Administration: Washington, DC, USA, 2017. [Google Scholar]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N.; Nikolopoulos, E.I. Assessment of high-resolution satellite-based rainfall estimates over the Mediterranean during heavy precipitation events. J. Hydrometeorol. 2013, 14, 1500–1514. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.-H.; Delrieu, G.; Hong, Y.; Hsu, Y.C. Multiregional satellite precipitation products evaluation over complex terrain. J. Hydrometeorol. 2016, 17, 1817–1836. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A review of merged high-resolution satellite precipitation product accuracy during the Tropical Rainfall Measuring Mission (TRMM) era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201. [Google Scholar] [CrossRef]
- Lin, Y.; Mitchell, K.E. The NCEP stage II/IV hourly precipitation analyses: Development and applications. In Proceedings of the 19th Conf. Hydrology, San Diego, CA, USA, 9–13 January 2005. [Google Scholar]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Mega, T.; Ushio, T.; Kubota, T.; Kachi, M.; Aonashi, K.; Shige, S. Gauge adjusted global satellite mapping of precipitation (GSMaP_Gauge). In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Xie, P.; Yoo, S.-H.; Joyce, R.; Yarosh, Y. Bias-corrected CMORPH: A 13-year analysis of high-resolution global precipitation. Geophys. Res. Abstr. 2011, 13. Abstract EGU2011-1809. [Google Scholar]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, bias-corrected CMORPH global high-resolution precipitation estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Zhang, X.; Anagnostou, E.N.; Frediani, M.; Solomos, S.; Kallos, G. Using NWP simulations in satellite rainfall estimation of heavy precipitation events over mountainous areas. J. Hydrometeorol. 2013, 14, 1844–1858. [Google Scholar] [CrossRef]
- Scofield, R.A.; Kuligowski, R.J. Status and outlook of operational satellite precipitation algorithms for extreme-precipitation events. Weather Forecast. 2003, 18, 1037–1051. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Bartsotas, N.S.; Anagnostou, E.N.; Kallos, G. Using high-resolution numerical weather forecasts to improve remotely sensed rainfall estimates: The case of the 2013 Colorado flash flood. J. Hydrometeorol. 2015, 16, 1742–1751. [Google Scholar] [CrossRef]
- Zhang, X.; Anagnostou, E.N.; Vergara, H. Hydrologic Evaluation of NWP-Adjusted CMORPH Estimates of Hurricane-Induced Precipitation in the Southern Appalachians. J. Hydrometeorol. 2016, 17, 1087–1099. [Google Scholar] [CrossRef]
- Zhang, X.; Anagnostou, E.N. Evaluation of Numerical Weather Model-based Satellite Precipitation Adjustment in Tropical Mountainous Regions. J. Hydrometeorol. 2018. under review. [Google Scholar]
- Schwartz, C.S.; Romine, G.S.; Sobash, R.A.; Fossell, K.R.; Weisman, M.L. NCAR’s experimental real-time convection-allowing ensemble prediction system. Weather Forecast. 2015, 30, 1645–1654. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF, version 3; NCAR Technical Note; NCAR/TN-475+ STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Gowan, T.M.; Steenburgh, W.J.; Schwartz, C.S. Validation of mountain precipitation forecasts from the convection-permitting NCAR Ensemble and operational forecast systems over the Western United States. Weather Forecast. 2018, in press. [Google Scholar] [CrossRef]
- Nelson, B.R.; Prat, O.P.; Seo, D.-J.; Habib, E. Assessment and implications of NCEP stage IV quantitative precipitation estimates for product intercomparisons. Weather Forecast. 2016, 31, 371–394. [Google Scholar] [CrossRef]
- Maddox, R.A.; Zhang, J.; Gourley, J.J.; Howard, K.W. Weather radar coverage over the contiguous United States. Weather Forecast. 2002, 17, 927–934. [Google Scholar] [CrossRef]
- Hou, D.; Charles, M.; Luo, Y.; Toth, Z.; Zhu, Y.; Krzysztofowicz, R.; Lin, Y.; Xie, P.; Seo, D.-J.; Pena, M. Climatology-calibrated precipitation analysis at fine scales: Statistical adjustment of stage IV toward CPC gauge-based analysis. J. Hydrometeorol. 2014, 15, 2542–2557. [Google Scholar] [CrossRef]
- NOAA Storm Events Database. Available online: https://www.ncdc.noaa.gov/stormevents/ (accessed on 20 February 2018).
- Heidke, P. Berechnung des Erfolges und der Güte der Windstärkevorhersagen im Sturmwarnungsdienst. Geogr. Ann. 1926, 8, 301–349. [Google Scholar] [CrossRef]

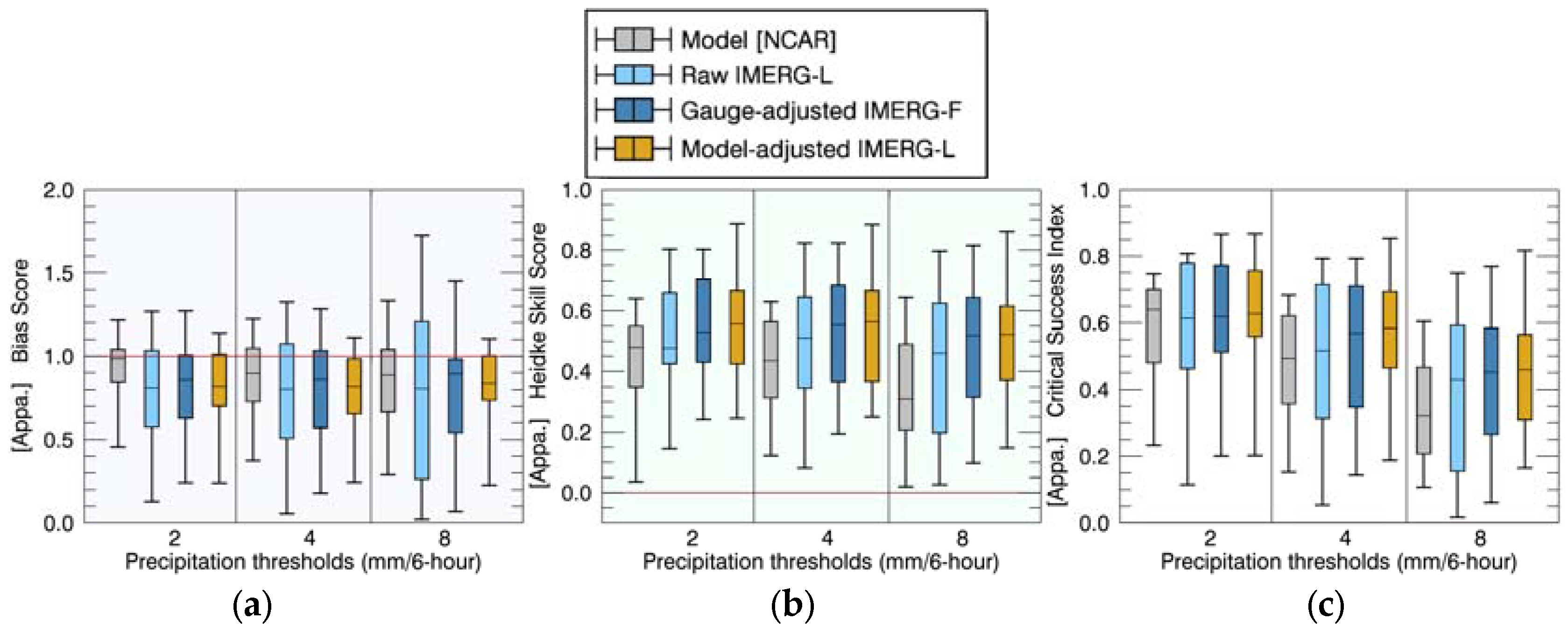
| Coastal Regions (50 Events) | Model-Based Adjustment | Gauge-Based Adjustment | ||||
|---|---|---|---|---|---|---|
| Percentage of Event (%) | BS | HSS | CSI | BS | HSS | CSI |
| Improved | 64 | 52 | 60 | 62 | 58 | 50 |
| Neutral | 8 | 28 | 26 | 4 | 30 | 32 |
| Worsened | 28 | 20 | 14 | 34 | 12 | 18 |
| Inland Regions (31 Events) | Model-Based Adjustment | Gauge-Based Adjustment | ||||
|---|---|---|---|---|---|---|
| Percentage of Event (%) | BS | HSS | CSI | BS | HSS | CSI |
| Improved | 74 | 58 | 58 | 61 | 52 | 52 |
| Neutral | 3 | 35 | 32 | 10 | 32 | 29 |
| Worsened | 23 | 6 | 10 | 29 | 16 | 19 |
| Coastal Regions (50 Events) | Inland Regions (31 Events) | |||
|---|---|---|---|---|
| CORR | NRMSE | CORR | NRMSE | |
| Model | 0.981 | 0.19 | 0.844 | 0.323 |
| Raw IMERG-L | 0.916 | 0.444 | 0.609 | 0.629 |
| Gauge-adjusted IMERG-F | 0.961 | 0.277 | 0.754 | 0.377 |
| Model-adjusted IMERG-L | 0.961 | 0.255 | 0.863 | 0.28 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Anagnostou, E.N.; Schwartz, C.S. NWP-Based Adjustment of IMERG Precipitation for Flood-Inducing Complex Terrain Storms: Evaluation over CONUS. Remote Sens. 2018, 10, 642. https://doi.org/10.3390/rs10040642
Zhang X, Anagnostou EN, Schwartz CS. NWP-Based Adjustment of IMERG Precipitation for Flood-Inducing Complex Terrain Storms: Evaluation over CONUS. Remote Sensing. 2018; 10(4):642. https://doi.org/10.3390/rs10040642
Chicago/Turabian StyleZhang, Xinxuan, Emmanouil N. Anagnostou, and Craig S. Schwartz. 2018. "NWP-Based Adjustment of IMERG Precipitation for Flood-Inducing Complex Terrain Storms: Evaluation over CONUS" Remote Sensing 10, no. 4: 642. https://doi.org/10.3390/rs10040642
APA StyleZhang, X., Anagnostou, E. N., & Schwartz, C. S. (2018). NWP-Based Adjustment of IMERG Precipitation for Flood-Inducing Complex Terrain Storms: Evaluation over CONUS. Remote Sensing, 10(4), 642. https://doi.org/10.3390/rs10040642





