SWOT Spatial Scales in the Western Mediterranean Sea Derived from Pseudo-Observations and an Ad Hoc Filtering
Abstract
1. Introduction
2. Data and Methods
2.1. The SWOT Simulator
2.2. Input Data: The Western Mediterranean OPerational (WMOP) Model
2.3. Analysis and Processing of SWOT-Derived SSH Data
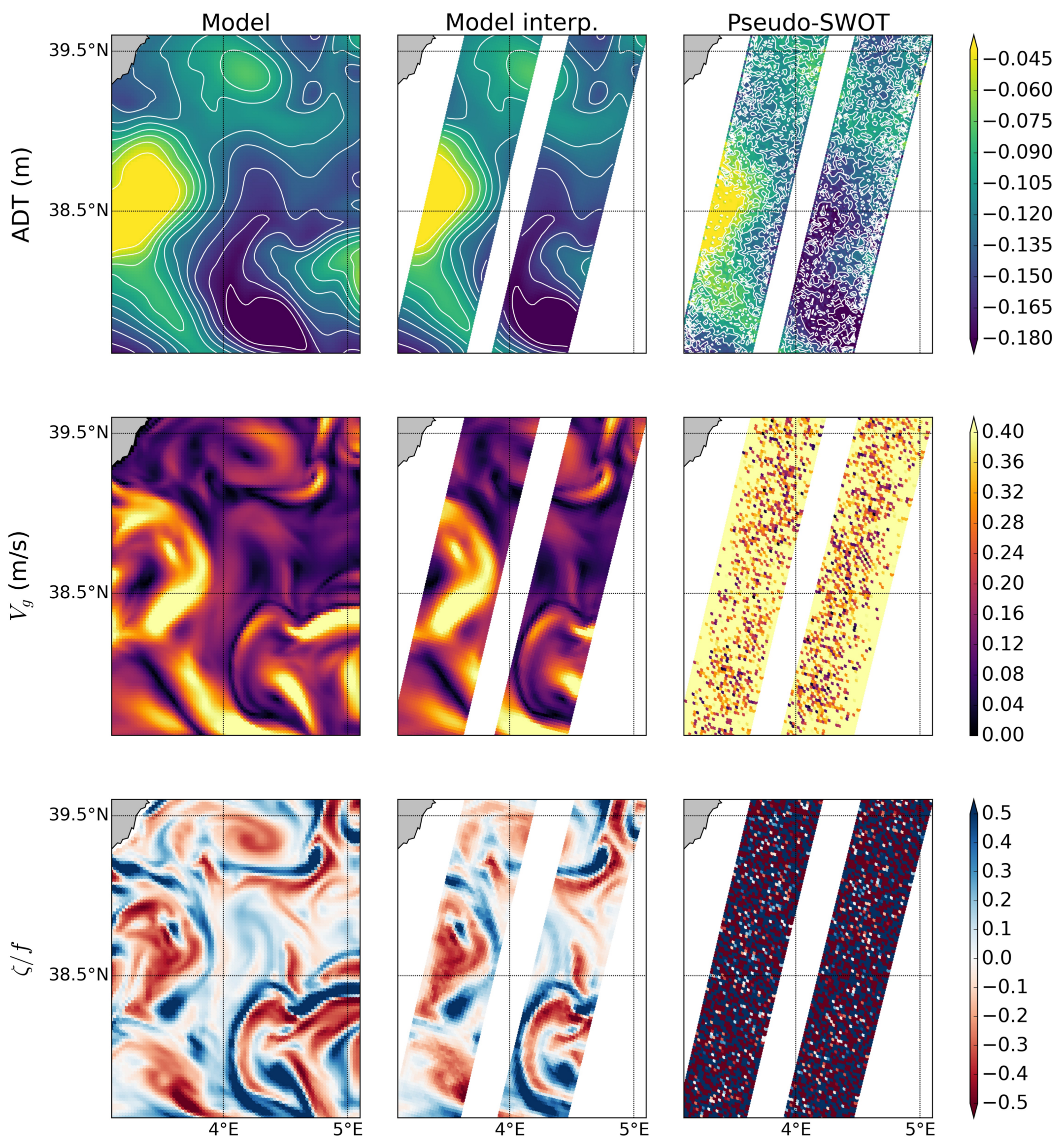
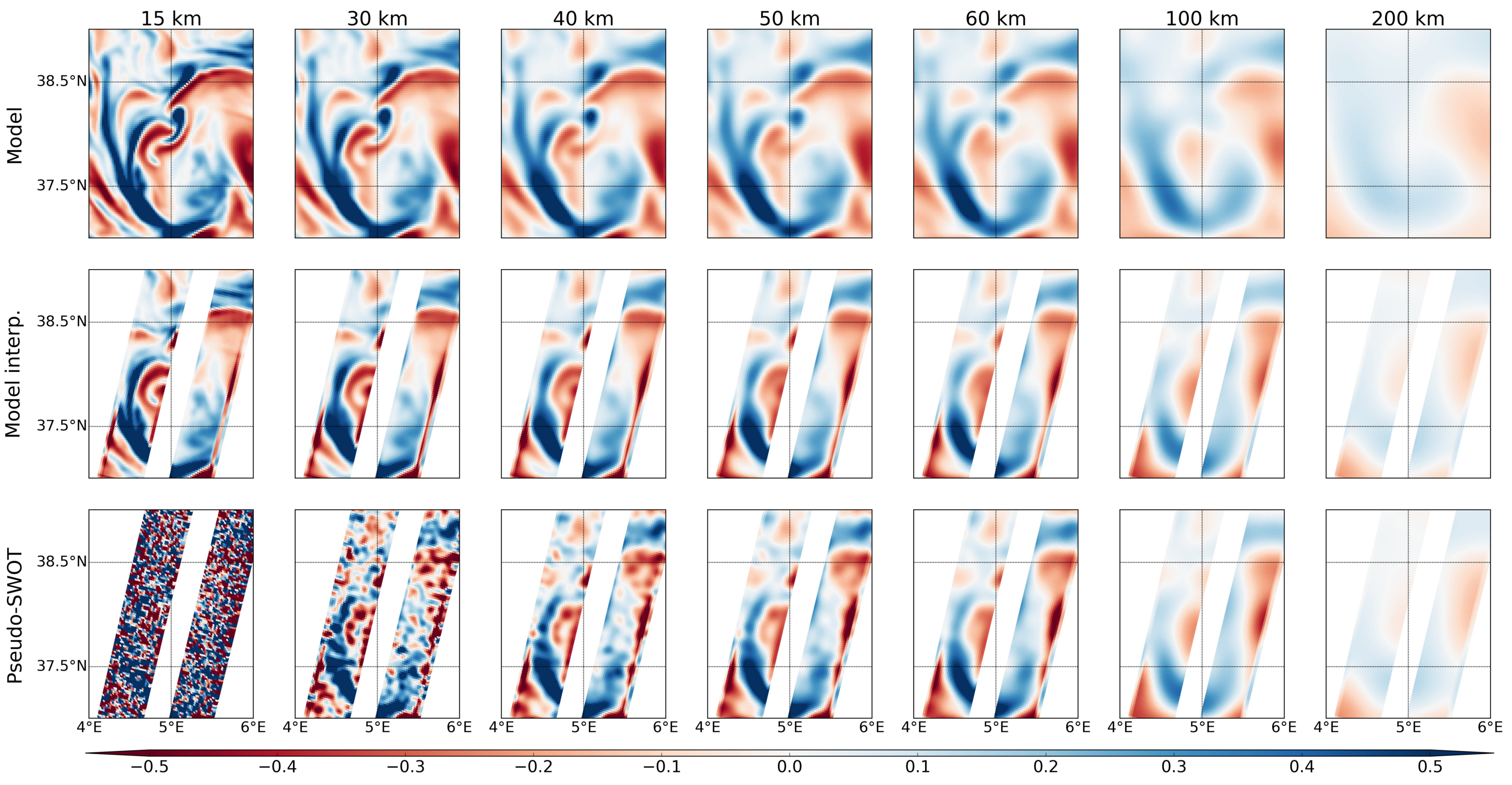
2.3.1. Geostrophic Velocity and Vorticity
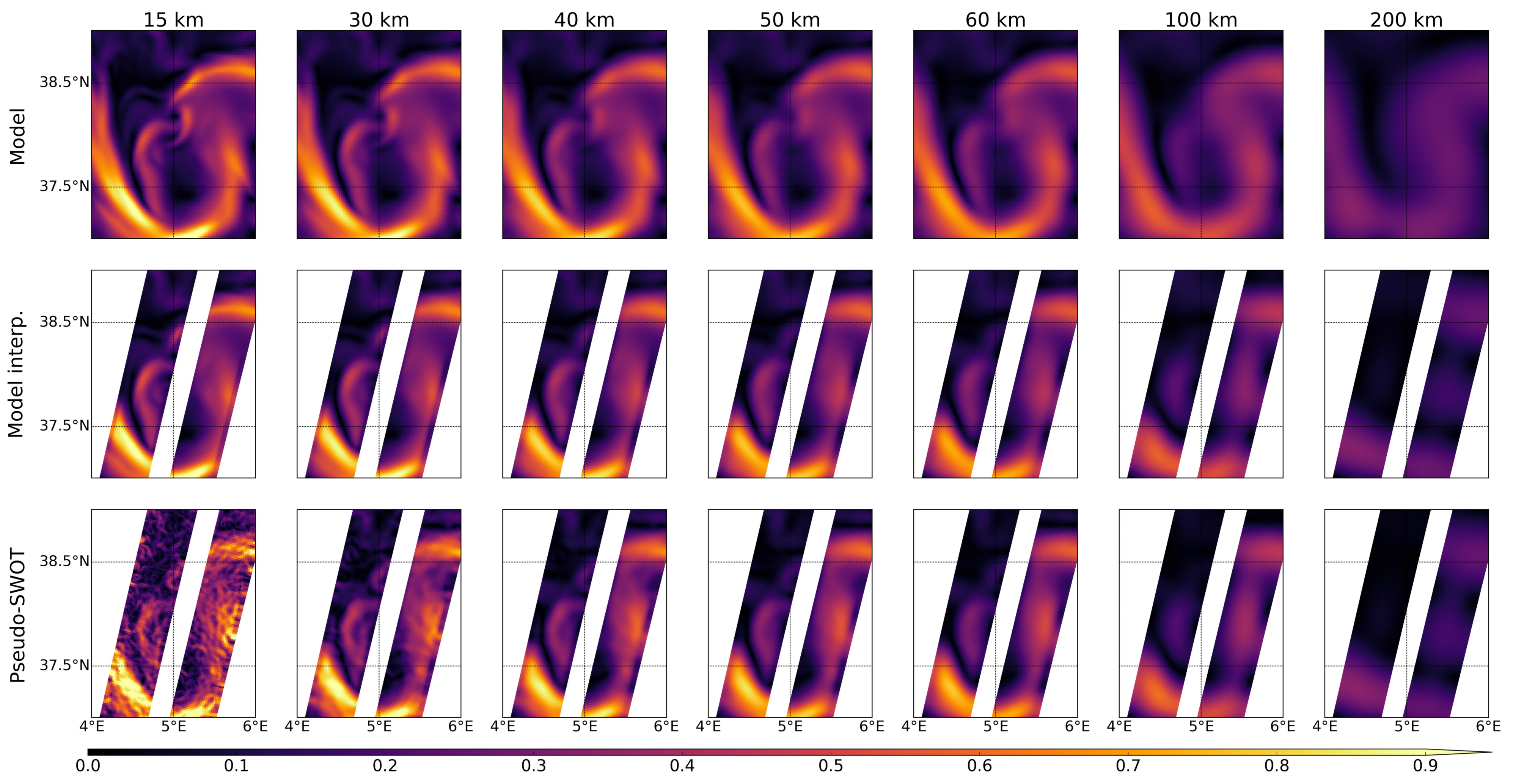
2.3.2. Noise Filtering
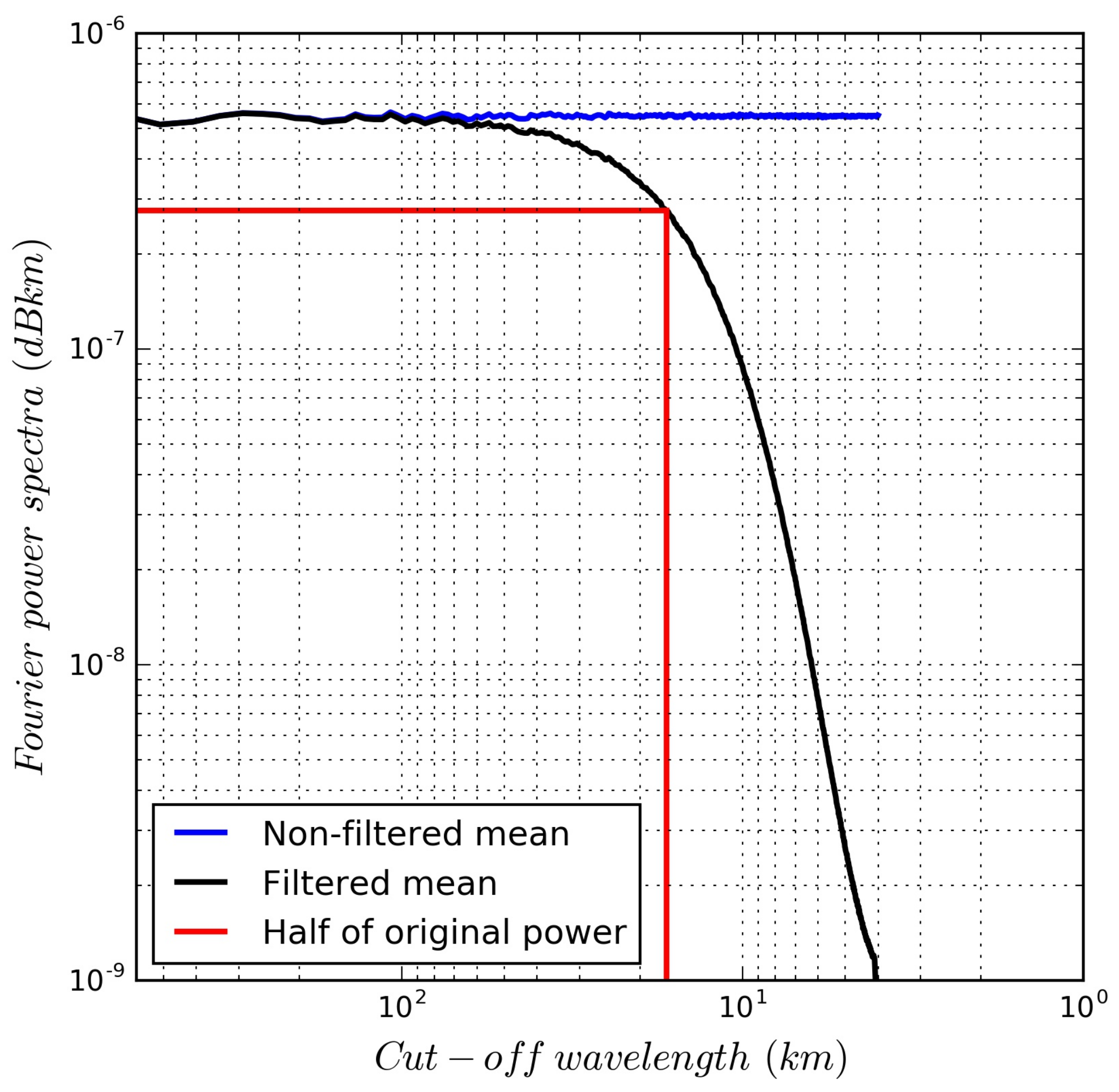
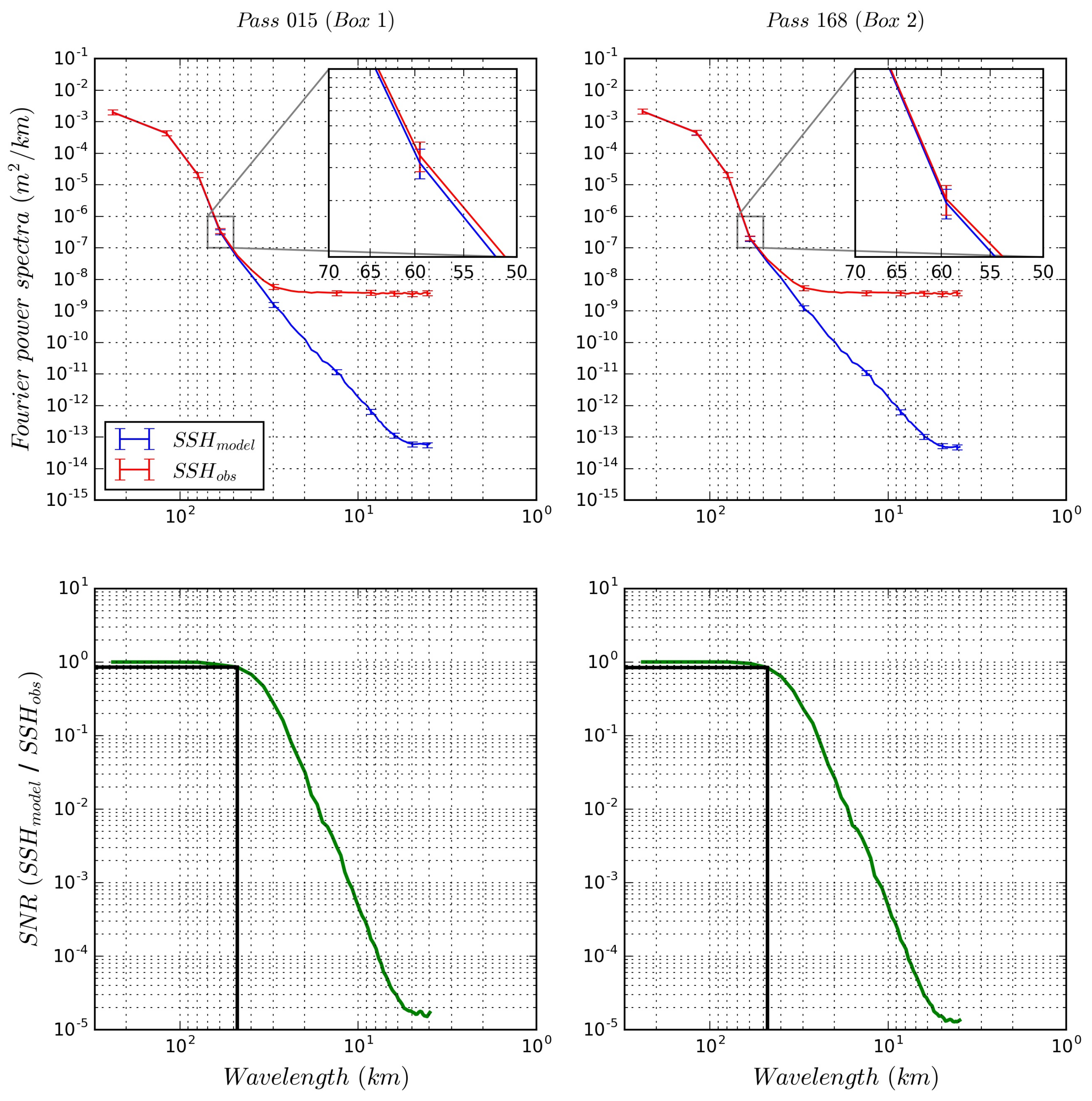
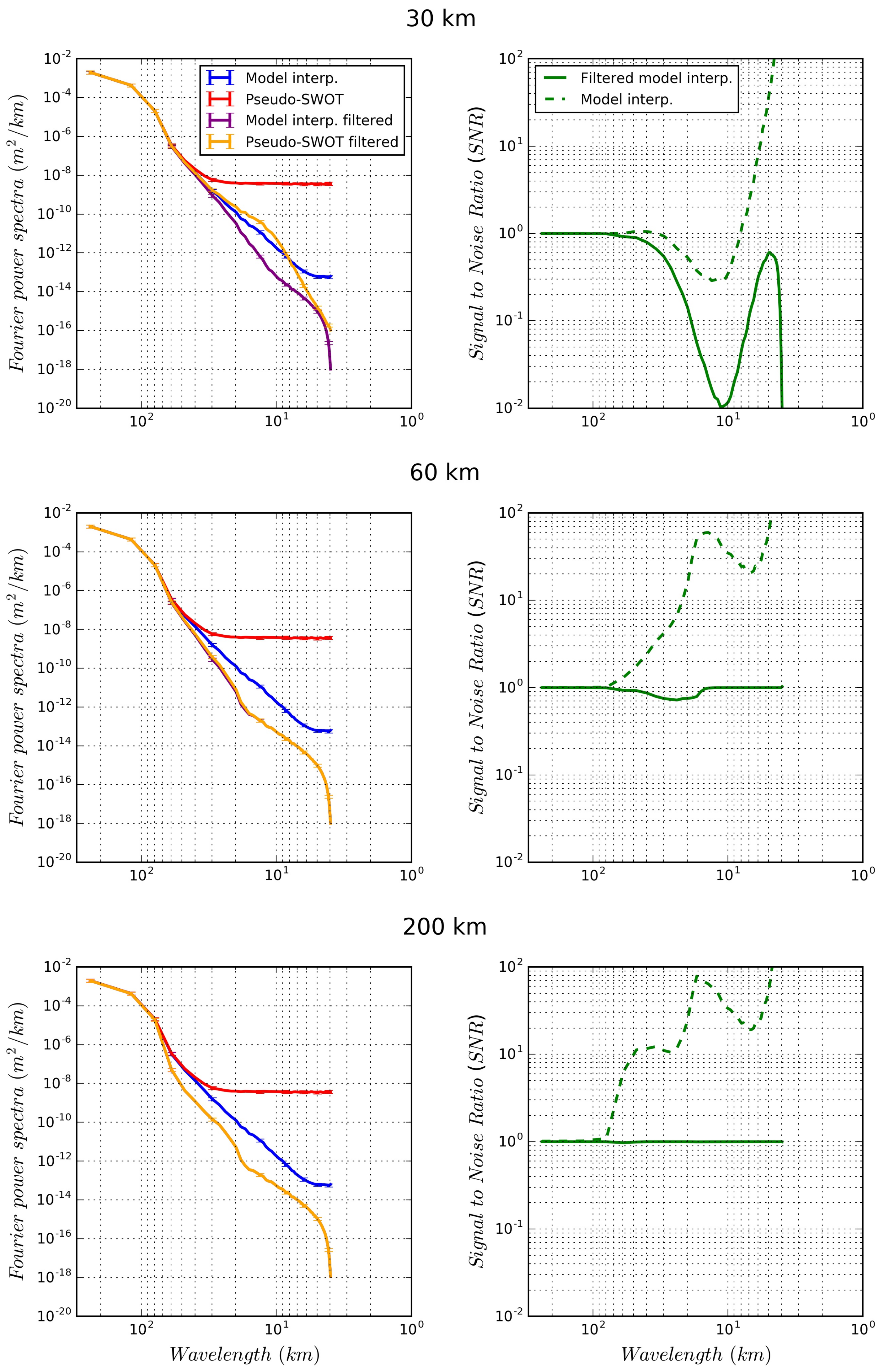
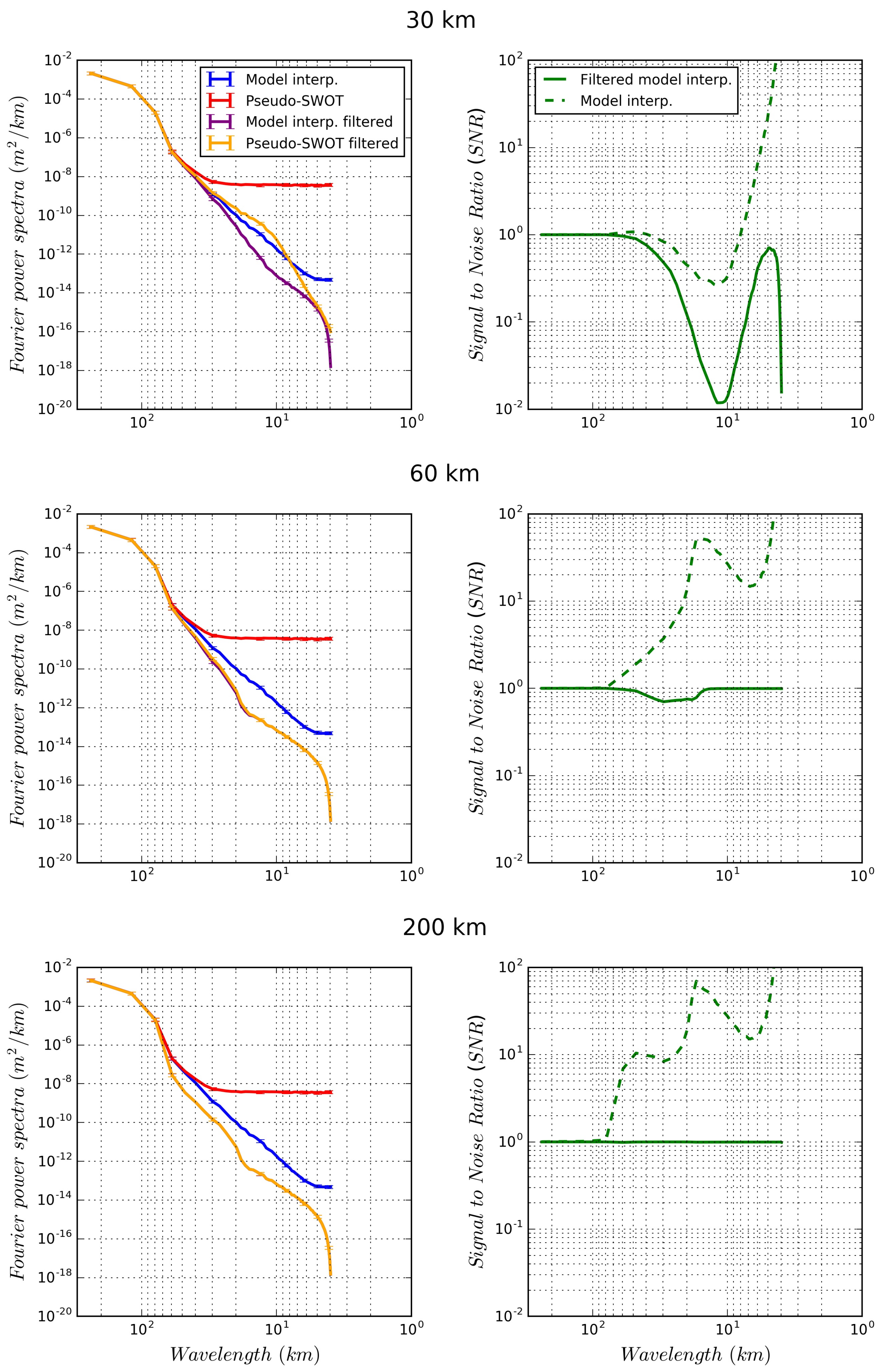
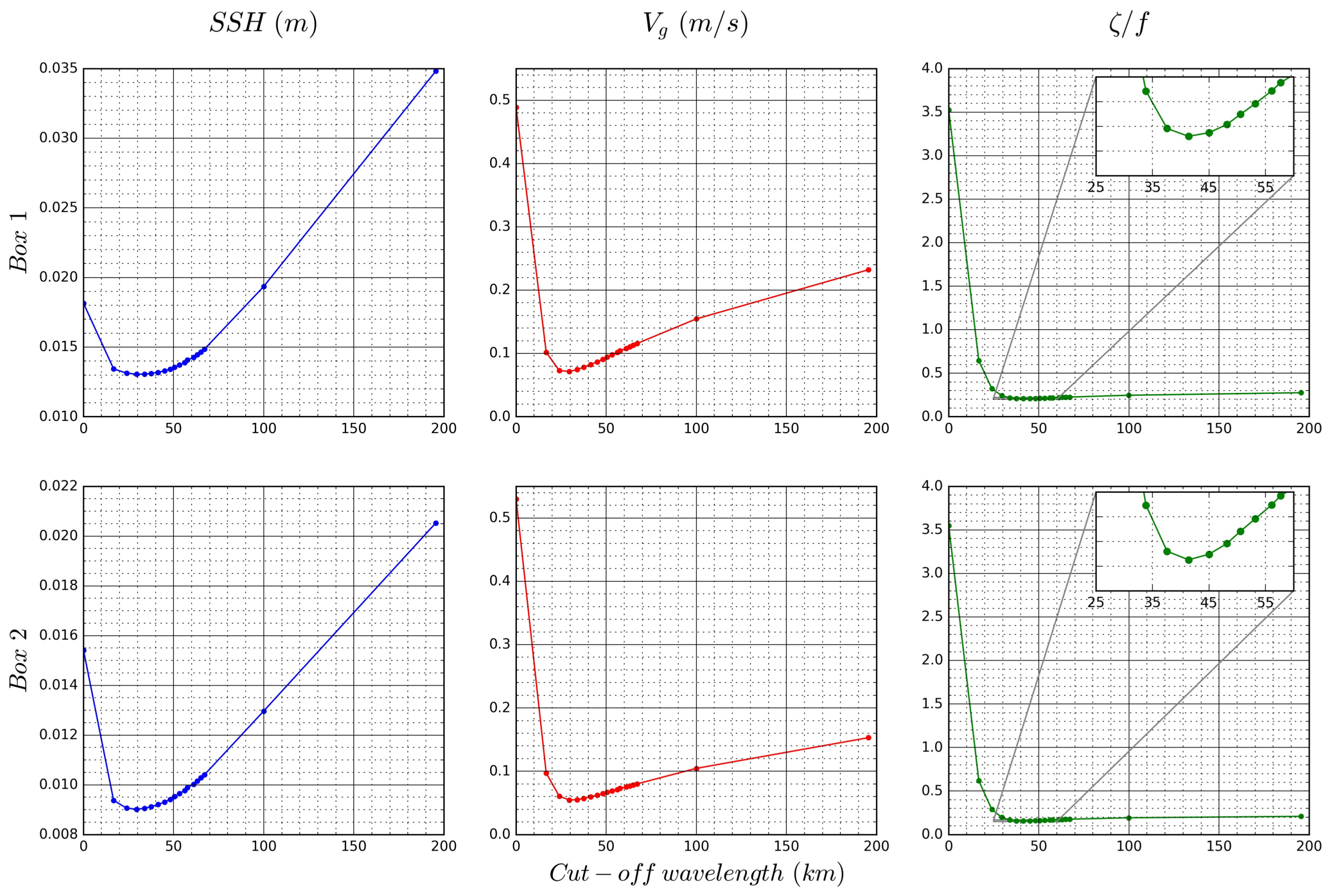
2.3.3. Filter Evaluation
- The radial power spectral density: This variable was calculated to obtain the SWOT spatial spectra. The radially averaged power spectral density (power spectrum) of an image (in our case, the SWOT swath data) is computed.
- The Root Mean Squared Error (RMSE): The RMSE was calculated for the SSH, velocity and vorticity variables as follows:where N is the number of points. Data is taken to be SSH (or its derived variables, i.e., velocity and vorticity) without filtering. An estimate is taken to be the simulated noisy SSH fields (or its derived variables) without filtering, and filtered with different . RMSE values are therefore calculated for different estimates.
3. Results
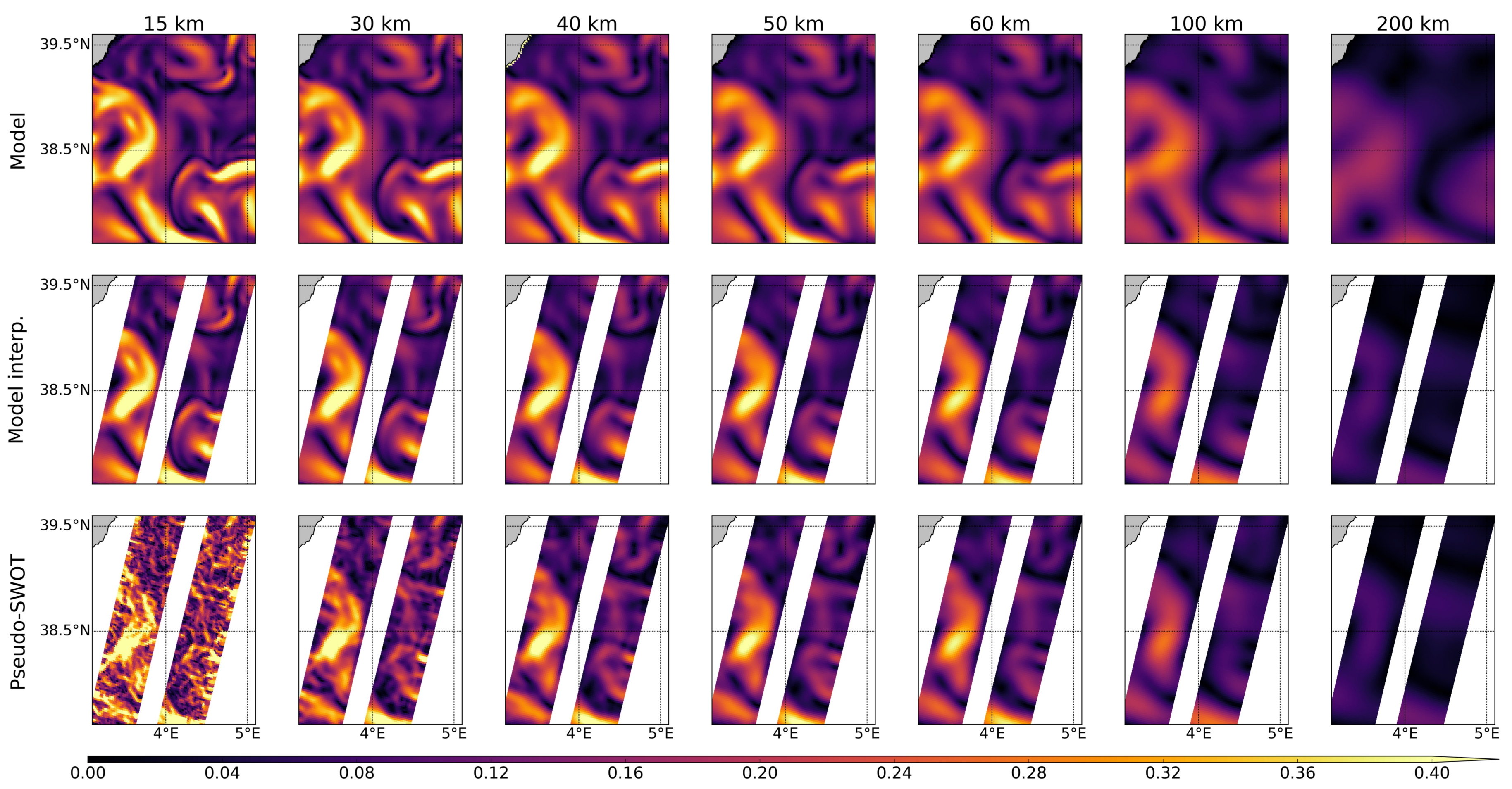
3.1. Spatial and Temporal Sampling
3.2. Pre-Filtering Analysis of Simulator Outputs
3.3. SWOT Data Filtering
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ADT | Absolute Dynamic Topography |
| AEMET | Spanish Meteorological Agency |
| CNES | Centre National d’Études Spatiales |
| HIRLAM | HIgh Resolution Limited Area Model |
| KaRIn | Ka-band Radar Interferometer |
| NASA | National Aeronautics and Space Administration |
| OGCM | Oceanic General Circulation Model |
| PDE | Partial Derivative Equation |
| RMSE | Root Mean Square Error |
| ROMS | Regional Oceanic Modeling System |
| SOCIB | the Balearic Islands Islands Coastal Observing and Forecasting System |
| SSH | Sea Surface Height |
| SNR | Signal to Noise Ratio |
| SWOT | Surface Water Ocean Topography |
| WMOP | Western Mediterranean OPerational forecasting system |
Appendix A
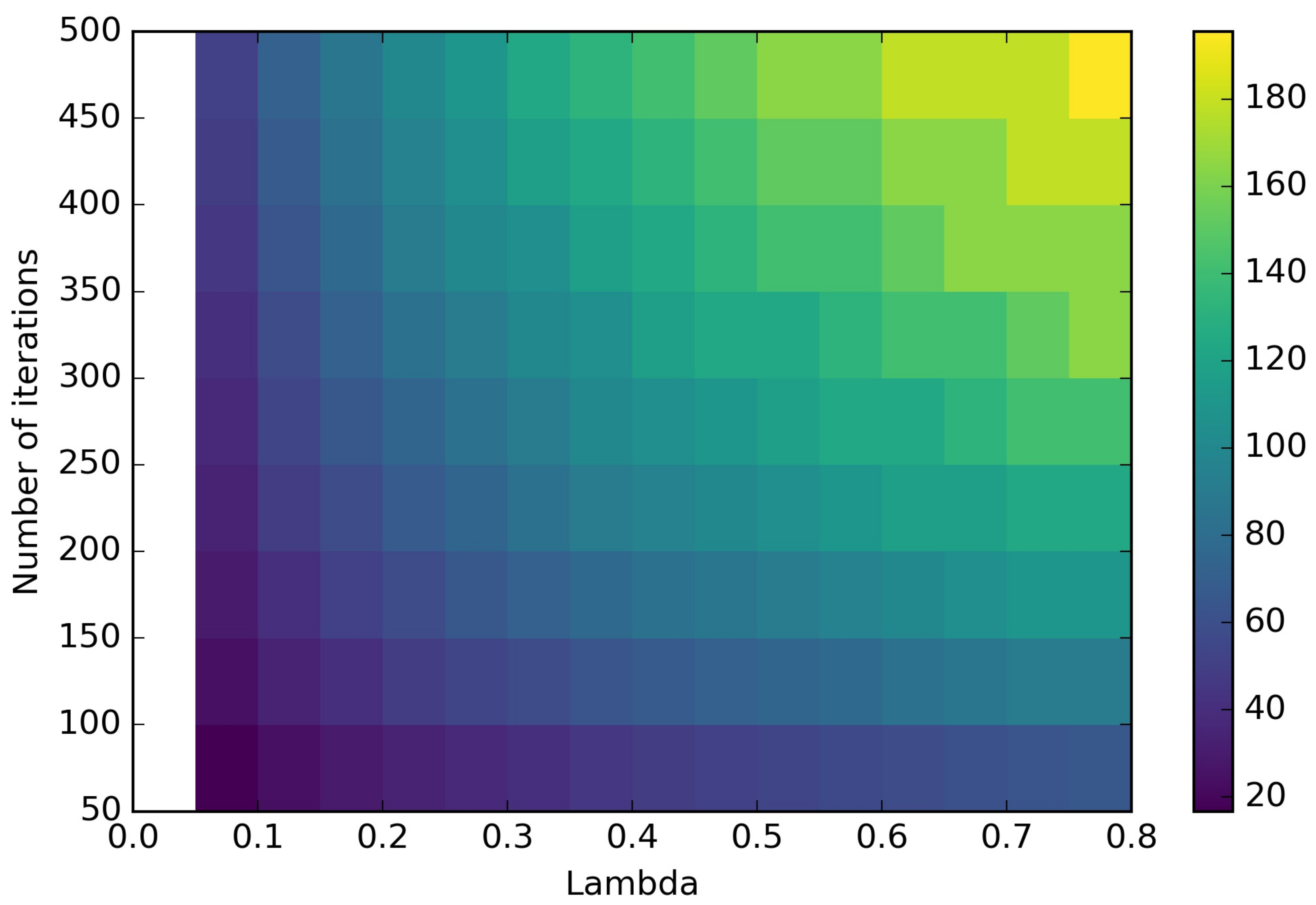
| Cut-off | Lambda | Iter | Cut-off | Lambda | Iter | Cut-off | Lambda | Iter | Cut-off | Lambda | Iter |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 16.72 | 0.05 | 50 | 71.88 | 0.10 | 450 | 105.09 | 0.20 | 500 | 141.41 | 0.35 | 500 |
| 23.95 | 0.05 | 100 | 0.15 | 300 | 0.25 | 400 | 0.40 | 450 | |||
| 0.10 | 50 | 0.30 | 150 | 0.30 | 350 | 0.45 | 400 | ||||
| 29.47 | 0.05 | 150 | 0.45 | 100 | 0.35 | 300 | 0.50 | 350 | |||
| 0.15 | 50 | 74.5 | 0.10 | 500 | 0.40 | 250 | 0.55 | 350 | |||
| 33.85 | 0.05 | 200 | 0.20 | 250 | 0.50 | 200 | 0.60 | 300 | |||
| 0.10 | 100 | 0.25 | 200 | 0.65 | 150 | 0.65 | 300 | ||||
| 0.20 | 50 | 0.50 | 100 | 110.78 | 0.25 | 450 | 0.70 | 250 | |||
| 37.58 | 0.05 | 250 | 77.31 | 0.15 | 350 | 0.45 | 250 | 0.75 | 250 | ||
| 0.25 | 50 | 0.35 | 150 | 0.55 | 200 | 151.91 | 0.40 | 500 | |||
| 41.38 | 0.05 | 300 | 0.55 | 100 | 0.70 | 150 | 0.45 | 450 | |||
| 0.10 | 150 | 83.63 | 0.15 | 400 | 0.75 | 150 | 0.50 | 400 | |||
| 0.15 | 100 | 0.20 | 300 | 117.12 | 0.25 | 500 | 0.55 | 400 | |||
| 0.30 | 50 | 0.25 | 250 | 0.30 | 400 | 0.60 | 350 | ||||
| 45.02 | 0.05 | 350 | 0.30 | 200 | 0.35 | 350 | 0.70 | 300 | |||
| 0.35 | 50 | 0.40 | 150 | 0.40 | 300 | 0.80 | 250 | ||||
| 48.19 | 0.05 | 400 | 0.60 | 100 | 0.50 | 250 | 164.1 | 0.45 | 500 | ||
| 0.10 | 200 | 87.19 | 0.15 | 450 | 0.60 | 200 | 0.50 | 450 | |||
| 0.20 | 100 | 0.45 | 150 | 0.65 | 200 | 0.50 | 500 | ||||
| 0.40 | 50 | 0.65 | 100 | 0.80 | 150 | 0.55 | 450 | ||||
| 50.58 | 0.05 | 450 | 91.07 | 0.15 | 500 | 124.24 | 0.30 | 450 | 0.60 | 400 | |
| 0.15 | 150 | 0.20 | 350 | 0.30 | 500 | 0.65 | 350 | ||||
| 0.45 | 50 | 0.25 | 300 | 0.35 | 400 | 0.65 | 400 | ||||
| 53.2 | 0.05 | 500 | 0.30 | 250 | 0.40 | 350 | 0.70 | 350 | |||
| 0.10 | 250 | 0.35 | 200 | 0.45 | 300 | 0.75 | 300 | ||||
| 0.25 | 100 | 0.50 | 150 | 0.50 | 300 | 0.75 | 350 | ||||
| 0.50 | 50 | 0.70 | 100 | 0.55 | 250 | 0.80 | 300 | ||||
| 56.12 | 0.55 | 50 | 0.75 | 100 | 0.60 | 250 | 178.42 | 0.55 | 500 | ||
| 57.7 | 0.10 | 300 | 95.31 | 0.20 | 400 | 0.70 | 200 | 0.60 | 450 | ||
| 0.15 | 200 | 0.40 | 200 | 0.75 | 200 | 0.60 | 500 | ||||
| 0.20 | 150 | 0.55 | 150 | 132.27 | 0.35 | 450 | 0.65 | 450 | |||
| 0.30 | 100 | 0.80 | 100 | 0.40 | 400 | 0.70 | 400 | ||||
| 0.60 | 50 | 99.96 | 0.20 | 450 | 0.45 | 350 | 0.70 | 450 | |||
| 61.15 | 0.65 | 50 | 0.25 | 350 | 0.55 | 300 | 0.75 | 400 | |||
| 63.03 | 0.1 | 350 | 0.3 | 300 | 0.65 | 250 | 0.8 | 350 | |||
| 0.35 | 100 | 0.35 | 250 | 0.80 | 200 | 0.80 | 400 | ||||
| 0.70 | 50 | 0.45 | 200 | 195.49 | 0.65 | 500 | |||||
| 65.03 | 0.15 | 250 | 0.60 | 150 | 0.70 | 500 | |||||
| 0.25 | 150 | 0.75 | 450 | ||||||||
| 0.75 | 50 | 0.75 | 500 | ||||||||
| 67.17 | 0.1 | 400 | 0.8 | 450 | |||||||
| 0.20 | 200 | 0.8 | 500 | ||||||||
| 0.40 | 100 | ||||||||||
| 0.80 | 50 |
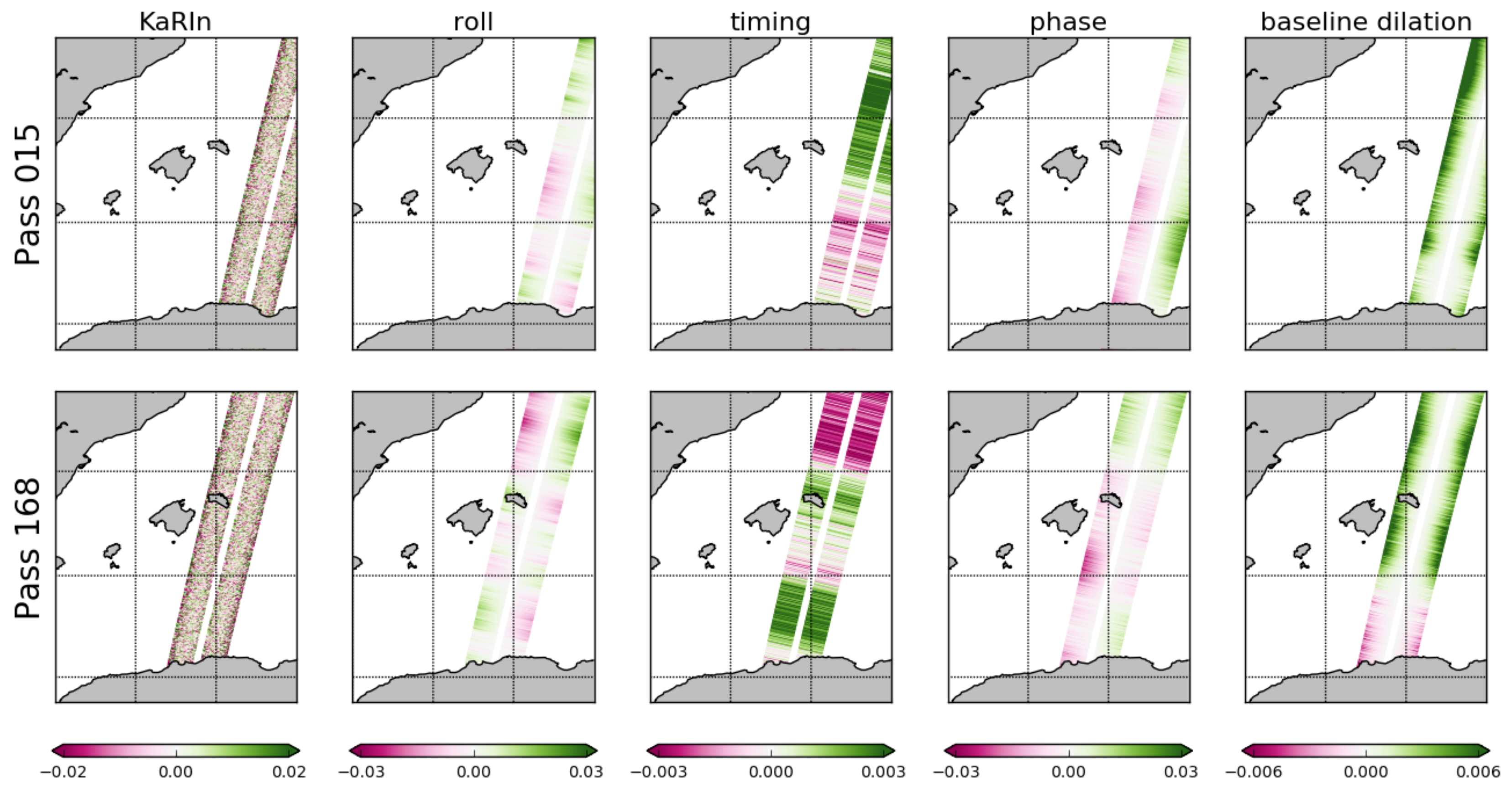
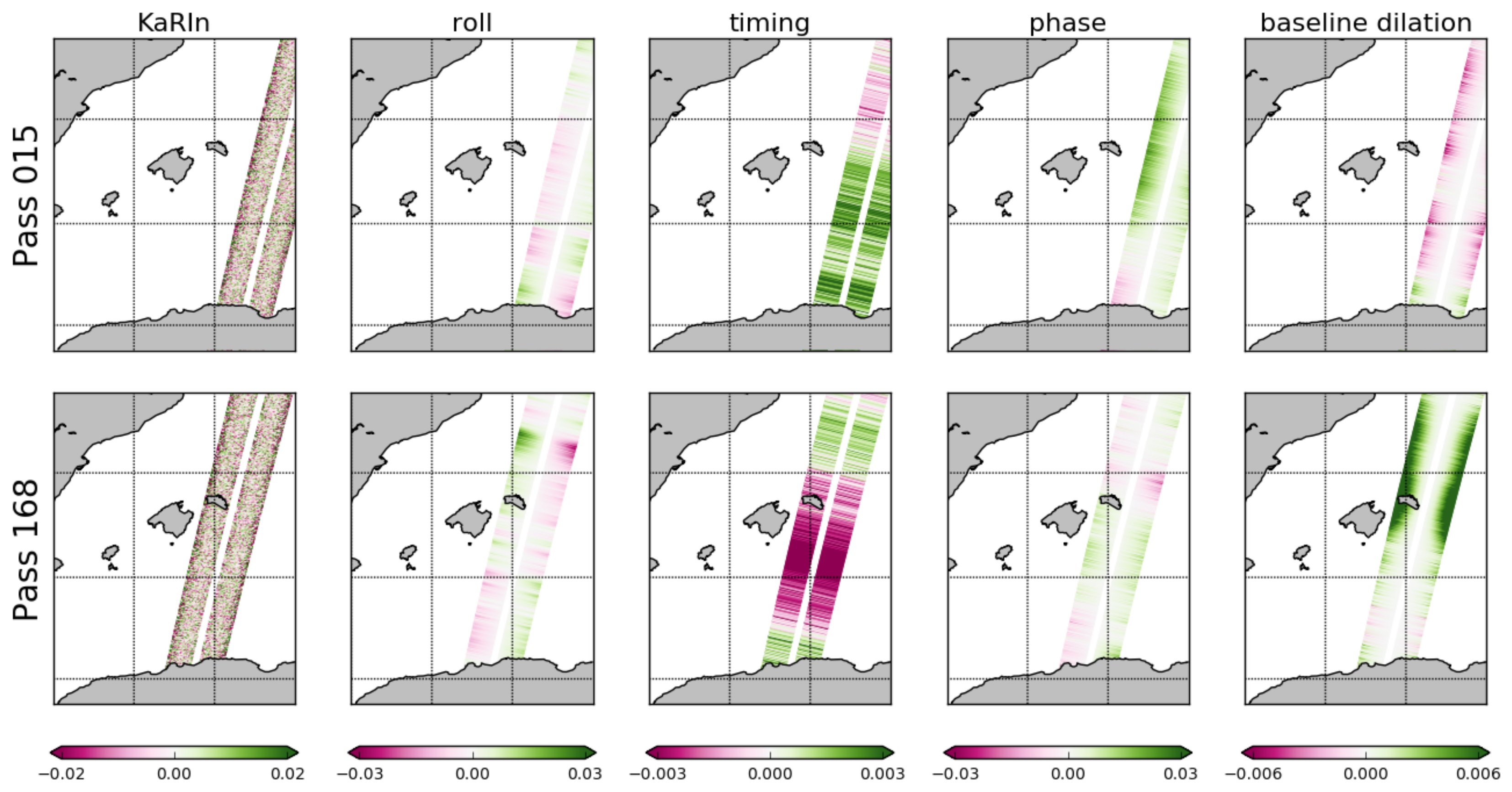
Appendix B
- Instrument errors: There are the different types of noise that can affect the signal due to the satellite itself:
- –
- Ka-Band Radar Interferometer (KaRIn)
- –
- Roll
- –
- Timing
- –
- Phase
- –
- Baseline dilation
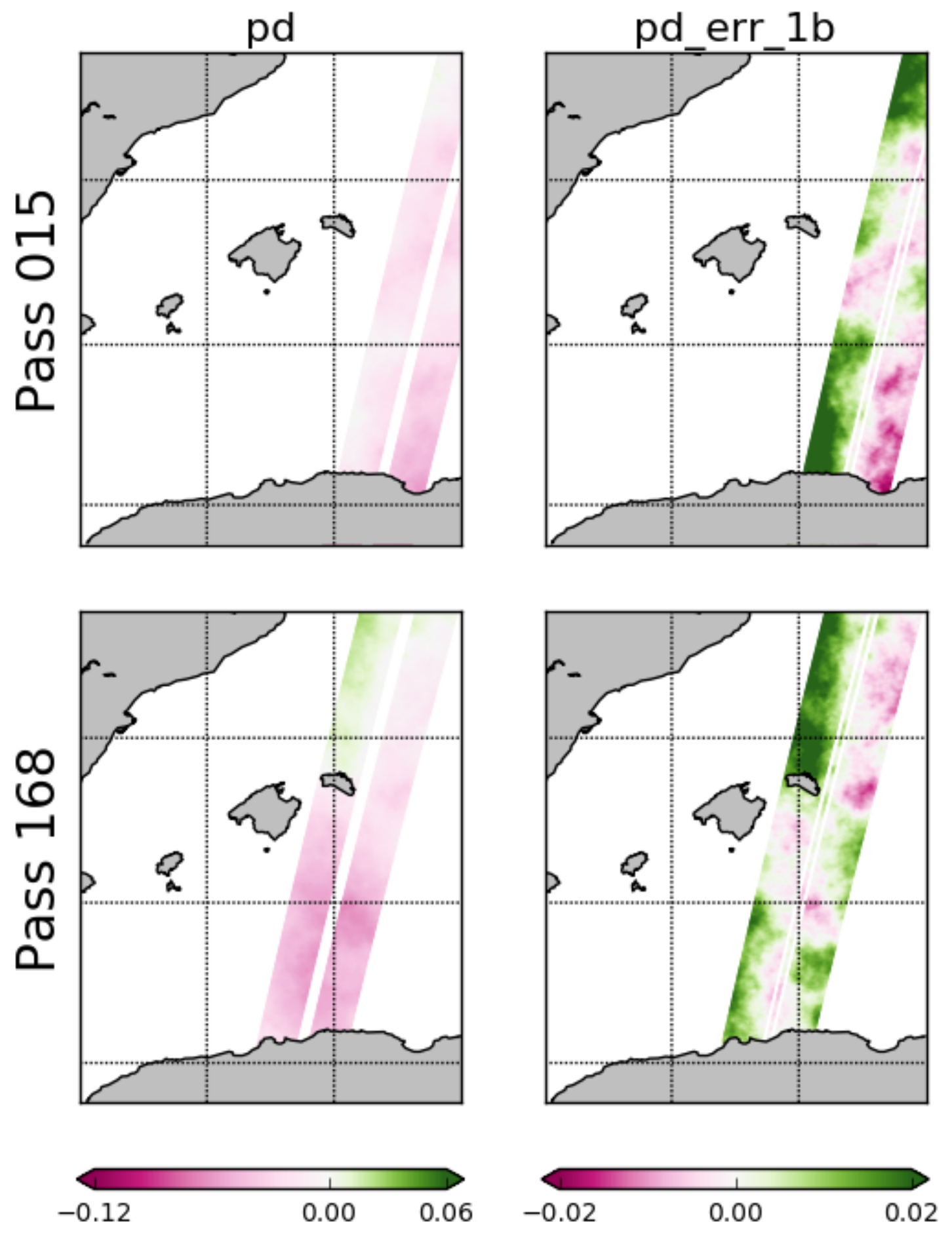
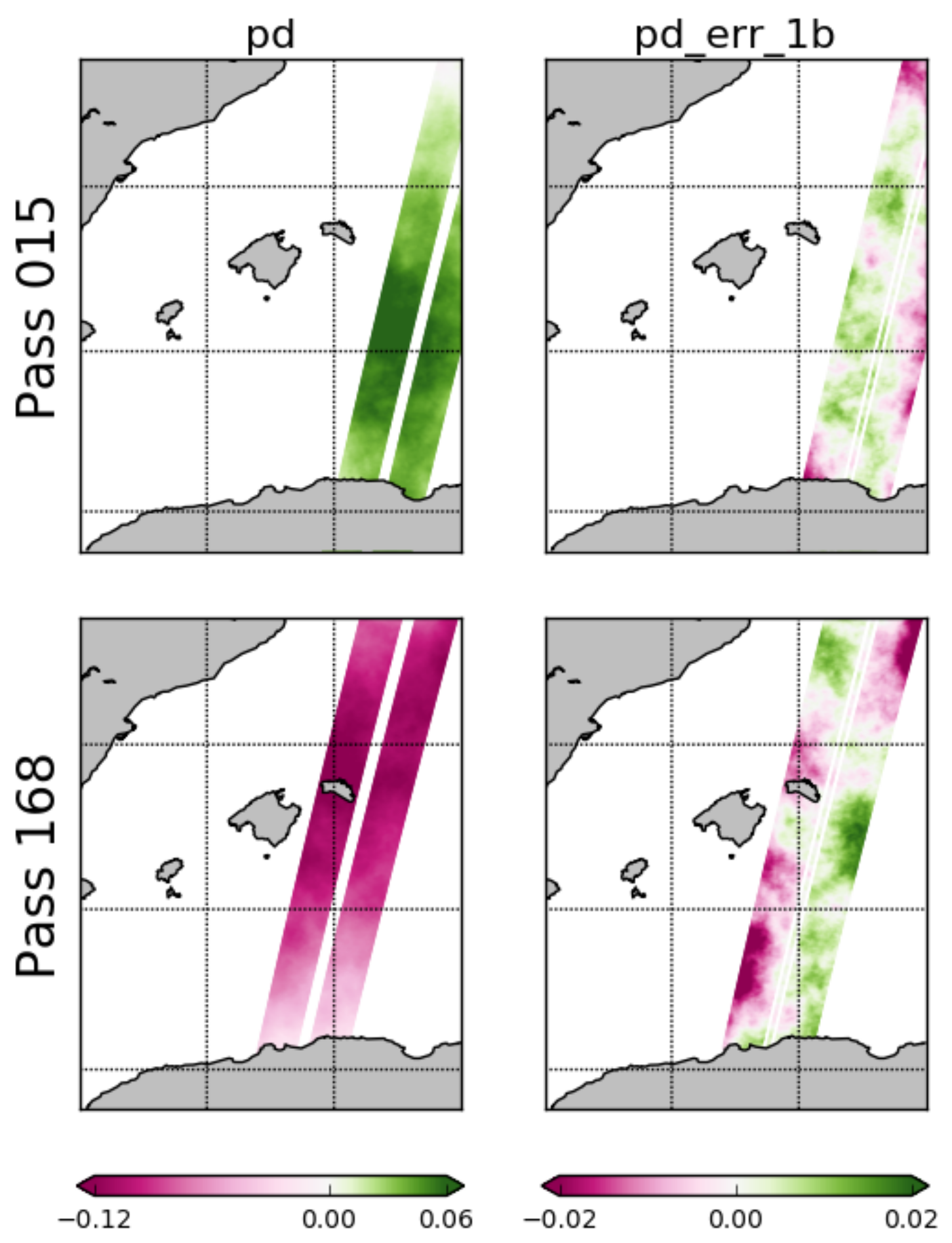
- Geophysical errors: In version 1 of the simulator, only the geophysical error due to the wet troposphere is implemented. Other geophysical errors include those due to the dry troposphere, the ionosphere and the sea state bias (electromagnetic bias). However, the wet troposphere is a major source of geophysical errors and it is implemented via these following two variables:
- –
- Path delay (pd),
- –
- Residual path delay (pd_err_1b).
References
- Alsdorf, D.; Mognard, N.; Lettenmaier, D. Remote Sensing of Surface Water and Recent Developments in the SWOT Mission. In Proceedings of the Session H21J-06, AGU Fall Meeting, San Francisco, CA, USA, 5–9 December 2011. [Google Scholar]
- Fu, L.L.; Morrow, R. A next generation altimeter for mapping the sea surface variability: Opportunities and challenges. In Proceedings of the 48th Liege Colloquium on Ocean Dynamics, Liège, Belgium, 23–27 May 2016. [Google Scholar]
- Lee, H.; Biancamaria, S.; Alsdorf, D.; Andreadis, K.; Clark, E.; Durand, M.; Jung, H.C.; Lettenmaier, D.; Mognard, N.; Rodríguez, E.; et al. Capability of SWOT to Measure Surface Water Storage Change. In Proceedings of the Towards high-resolution of oceans dynamics and terrestrial water from space meeting, Lisbon, Portugal, 21–22 October 2010. [Google Scholar]
- Rodríguez, E. The Surface Water and Ocean Topography (SWOT) Mission. In Proceedings of the OSTST (Ocean Surface Topography Science Team) meeting, Lisbon, Portugal, 18–20 October 2010. [Google Scholar]
- Pujol, M.I.; Dibarboure, G.; Le Traon, P.Y.; Klein, P. Using high-resolution altimetry to observe mesoscale signals. J. Atmos. Ocean. Technol. 2012, 29, 1409–1416. [Google Scholar] [CrossRef]
- Rodríguez, E. Surface Water and Ocean Topography Mission Project Science Requirements Document. Jet Propulsion Laboratory, California Institute of Technology, JPL D-61923; March 2016; 28p. Available online: https://swot.jpl.nasa.gov/documents.htm (accessed on 12 April 2018).
- Rogé, M.; Morrow, R.; Ubelmann, C.; Dibarboure, G. Using a dynamical advection to reconstruct a part of the SSH evolution in the context of SWOT, application to the Mediterranean Sea. Ocean Dyn. 2017, 67, 1047–1066. [Google Scholar] [CrossRef]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring Sea Level in the Coastal Zone with Satellite Altimetry and Tide Gauges. Surv. Geophys. 2017, 38, 33–57. [Google Scholar] [CrossRef]
- Fu, L.L.; Ferrari, R. Observing Oceanic Submesoscale Processes From Space. Eos Trans. Am. Geophys. Union 2008, 89, 488. [Google Scholar] [CrossRef]
- Dufau, C.; Orsztynowicz, M.; Dibarboure, G.; Morrow, R.; Le Traon, P.Y. Mesoscale resolution capability of altimetry: Present and future. J. Geophys. Res. Ocean. 2016. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Fu, L.L.; Ubelmann, C. On the transition from profile altimeter to swath altimeter for observing global ocean surface topography. J. Atmos. Ocean. Technol. 2014, 31, 560–568. [Google Scholar] [CrossRef]
- Mémery, L.; Olivier, F. Primary production and export fluxes at the Almeria-Oran front: A numerical study. In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003. [Google Scholar]
- Lévy, M.; Klein, P.; Treguier, A.M. Impact of sub-mesoscale physics on production and subduction of phytoplankton in an oligotrophic regime. J. Mar. Res. 2001, 59, 535–565. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P. Impact of the small-scale elongated filaments on the oceanic vertical pump. J. Mar. Res. 2006, 64, 835–851. [Google Scholar] [CrossRef]
- Omand, M.M.; D’Asaro, E.A.; Lee, C.M.; Perry, M.J.; Briggs, N.; Cetinić, I.; Mahadevan, A. Eddy-driven subduction exports particulate organic carbon from the spring bloom. Science 2015, 348, 222–225. [Google Scholar] [CrossRef] [PubMed]
- McGillicuddy, D.J.; Anderson, L.A.; Bates, N.R.; Bibby, T.; Buesseler, K.O.; Carlson, C.A.; Davis, C.S.; Ewart, C.; Falkowski, P.G.; Goldthwait, S.A.; et al. Eddy/wind interactions stimulate extraordinary mid-ocean plankton blooms. Science 2007, 316, 1021–1026. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.; Smeed, D.; Tintoré, J.; Ruiz, S. Mesoscale subduction at the almeria–oran front: Part 1: Ageostrophic flow. J. Mar. Syst. 2001, 30, 263–285. [Google Scholar] [CrossRef][Green Version]
- Ruiz, S.; Pascual, A.; Garau, B.; Faugère, Y.; Alvarez, A.; Tintoré, J. Mesoscale dynamics of the Balearic Front, integrating glider, ship and satellite data. J. Mar. Syst. 2009, 78, S3–S16. [Google Scholar] [CrossRef]
- Pascual, A.; Ruiz, S.; Olita, A.; Troupin, C.; Claret, M.; Casas, B.; Mourre, B.; Poulain, P.M.; Tovar-Sanchez, A.; Capet, A.; et al. A multiplatform experiment to unravel meso-and submesoscale processes in an intense front (alborex). Front. Mar. Sci. 2017, 4, 39. [Google Scholar] [CrossRef]
- Bethoux, J.; Gentili, B.; Morin, P.; Nicolas, E.; Pierre, C.; Ruiz-Pino, D. The Mediterranean Sea: A miniature ocean for climatic and environmental studies and a key for the climatic functioning of the North Atlantic. Progress Oceanogr. 1999, 44, 131–146. [Google Scholar] [CrossRef]
- Malanotte-Rizzoli, P.; Artale, V.; Borzelli-Eusebi, G.L.; Brenner, S.; Crise, A.; Gacic, M.; Kress, N.; Marullo, S.; d’Alcalà, M.R.; Sofianos, S.; et al. Physical forcing and physical/biochemical variability of the Mediterranean Sea: A review of unresolved issues and directions for future research. Ocean Sci. 2014, 10, 281. [Google Scholar] [CrossRef]
- Robinson, A.R.; Leslie, W.G.; Theocharis, A.; Lascaratos, A. Mediterranean sea circulation. In Ocean Currents: A Derivative of the Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1689–1705. [Google Scholar]
- Hallberg, R. Using a resolution function to regulate parameterizations of oceanic mesoscale eddy effects. Ocean Model. 2013, 72, 92–103. [Google Scholar] [CrossRef]
- Escudier, R.; Renault, L.; Pascual, A.; Brasseur, P.; Chelton, D.; Beuvier, J. Eddy properties in the Western Mediterranean Sea from satellite altimetry and a numerical simulation. J. Geophys. Res. 2016, 121, 3990–4006. [Google Scholar] [CrossRef]
- Chelton, D.B.; Deszoeke, R.A.; Schlax, M.G.; El, K.; And, N.; Siwertz, N. Geographical Variability of the First Baroclinic Rossby Radius of Deformation. J. Phys. Oceanogr. 1998, 28, 433–460. [Google Scholar] [CrossRef]
- Nurser, A.J.G.; Bacon, S. Arctic Ocean Rossby radius Eddy length scales and the Rossby radius in the Arctic Ocean Arctic Ocean Rossby radius. Ocean Sci. Discuss. 2013, 10, 1807–1831. [Google Scholar] [CrossRef]
- Wang, J.; Fu, L.L.; Qiu, B.; Menemenlis, D.; Farrar, J.T.; Chao, Y.; Thompson, A.F.; Flexas, M.M. An Observing System Simulation Experiment for the Calibration and Validation of the Surface Water Ocean Topography Sea Surface Height Measurement Using In Situ Platforms. J. Atmos. Ocean. Technol. 2018, 35, 281–297. [Google Scholar] [CrossRef]
- Gaultier, L.; Ubelmann, C.; Fu, L.L. SWOT Simulator Documentation; Tech. Rep. 1.0.0; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2015.
- Gaultier, L.; Ubelmann, C.; Fu, L.L. The challenge of using future SWOT data for oceanic field reconstruction. J. Atmos. Ocean. Technol. 2016, 33, 119–126. [Google Scholar] [CrossRef]
- Juza, M.; Mourre, B.; Renault, L.; Gómara, S.; Sebastián, K.; Lora, S.; Beltran, J.; Frontera, B.; Garau, B.; Troupin, C.; et al. SOCIB operational ocean forecasting system and multi-platform validation in the Western Mediterranean Sea. J. Oper. Oceanogr. 2016, 9, s155–s166. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis, and Machine Vision; Cengage Learning: Boston, MA, USA, 2014. [Google Scholar]
- Aubert, G.; Kornprobst, P. Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations; Springer Science & Business Media: Berlin, Germany, 2006; Volume 147. [Google Scholar]
- Escudier, R.; Mourre, B.; Juza, M.; Tintoré, J. Subsurface circulation and mesoscale variability in the Algerian subbasin from altimeter-derived eddy trajectories. J. Geophys. Res. Ocean. 2016, 121, 6310–6322. [Google Scholar] [CrossRef]
- Gunturk, B.K.; Li, X. Image Restoration: Fundamentals and Advances; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Klein, P.; Morrow, R.; Samelson, R.; Chelton, D.; Lapeyre, G.; Fu, L.; Qiu, B.; Ubelmann, C.; Le Traon, P.Y.; Capet, X.; et al. Mesoscale/Sub-Mesoscale Dynamics in the Upper Ocean. 2015. NASA Surface Water and Ocean Topography (SWOT). Available online: https://www.aviso.altimetry.fr/fileadmin/documents/missions/Swot/WhitePaperSWOTSubmesoscale.pdf (accessed on 12 April 2018).
- Ruggiero, G.; Cosme, E.; Brankart, J.; Sommer, J.L.; Ubelmann, C. An efficient way to account for observation error correlations in the assimilation of data from the future SWOT High-Resolution altimeter mission. J. Atmos. Ocean. Technol. 2016, 33, 2755–2768. [Google Scholar] [CrossRef]
- Pujol, M.I.; Faugere, Y.; Taburet, G.; Dupuy, S.; Pelloquin, C.; Ablain, M.; Picot, N. DUACS DT2014: The new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 2016, 12, 1067–1090. [Google Scholar] [CrossRef]
- Ubelmann, C.; Klein, P.; Fu, L.L. Dynamic interpolation of sea surface height and potential applications for future high-resolution altimetry mapping. J. Atmos. Ocean. Technol. 2015, 32, 177–184. [Google Scholar] [CrossRef]
- Fablet, R.; Verron, J.; Mourre, B.; Chapron, B.; Pascual, A. Improving mesoscale altimetric data from a multitracer convolutional processing of standard satellite-derived products. IEEE Trans. Geosci. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Lguensat, R.; Viet, P.H.; Sun, M.; Chen, G.; Fenglin, T.; Chapron, B.; Fablet, R. Data-driven Interpolation of Sea Level Anomalies Using Analog Data Assimilation. 2017. Available online: https://hal.archives-ouvertes.fr/hal-01609851 (accessed on 12 April 2018).
- Moro, M.D.; Brankart, J.M.; Brasseur, P.; Verron, J. Exploring image data assimilation in the prospect of high-resolution satellite oceanic observations. Ocean Dyn. 2017, 67, 875–895. [Google Scholar] [CrossRef]
- Mason, E.; Pascual, A.; McWilliams, J.C. A new sea surface height-based code for oceanic mesoscale eddy tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
- Conti, D.; Orfila, A.; Mason, E.; Sayol, J.M.; Simarro, G.; Balle, S. An eddy tracking algorithm based on dynamical systems theory. Ocean Dyn. 2016, 66, 1415–1427. [Google Scholar] [CrossRef]
- D’Ortenzio, F.; Iudicone, D.; de Boyer Montegut, C.; Testor, P.; Antoine, D.; Marullo, S.; Santoleri, R.; Madec, G. Seasonal variability of the mixed layer depth in the Mediterranean Sea as derived from in situ profiles. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Houpert, L.; Testor, P.; de Madron, X.D.; Somot, S.; D’ortenzio, F.; Estournel, C.; Lavigne, H. Seasonal cycle of the mixed layer, the seasonal thermocline and the upper-ocean heat storage rate in the Mediterranean Sea derived from observations. Progress Oceanogr. 2015, 132, 333–352. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Ubelmann, C.; Fu, L.; Sasaki, H. Reconstructability of 3-Dimensional upper ocean circulation from SWOT Sea Surface Height measurements (early online release). J. Phys. Oceanogr. J. Phys. Ocean. 2016, 46, 947–963. [Google Scholar] [CrossRef]
- Lindstrom, E.; Cherchal, S.; Fu, L.L.; Morrow, R.; Pavelsky, T.; Cretaux, J.F.; Vaze, P.; Lafon, T.; Coutin-Faye, S.; Amen, L.; et al. Summary Report of the 2nd SWOT Science Team Meeting 2017; Techreport; Meteo-France Conference Centre: Touloue, France, 2017. [Google Scholar]
- Esteban-Fernandez, D. SWOT Project: Mission Performance and Error Budget Document. Jet Propulsion Laboratory, California Institute of Technology, JPL D-79084; April 2017; 117p. Available online: https://swot.jpl.nasa.gov/documents.htm (accessed on 12 April 2018).



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Navarro, L.; Fablet, R.; Mason, E.; Pascual, A.; Mourre, B.; Cosme, E.; Le Sommer, J. SWOT Spatial Scales in the Western Mediterranean Sea Derived from Pseudo-Observations and an Ad Hoc Filtering. Remote Sens. 2018, 10, 599. https://doi.org/10.3390/rs10040599
Gómez-Navarro L, Fablet R, Mason E, Pascual A, Mourre B, Cosme E, Le Sommer J. SWOT Spatial Scales in the Western Mediterranean Sea Derived from Pseudo-Observations and an Ad Hoc Filtering. Remote Sensing. 2018; 10(4):599. https://doi.org/10.3390/rs10040599
Chicago/Turabian StyleGómez-Navarro, Laura, Ronan Fablet, Evan Mason, Ananda Pascual, Baptiste Mourre, Emmanuel Cosme, and Julien Le Sommer. 2018. "SWOT Spatial Scales in the Western Mediterranean Sea Derived from Pseudo-Observations and an Ad Hoc Filtering" Remote Sensing 10, no. 4: 599. https://doi.org/10.3390/rs10040599
APA StyleGómez-Navarro, L., Fablet, R., Mason, E., Pascual, A., Mourre, B., Cosme, E., & Le Sommer, J. (2018). SWOT Spatial Scales in the Western Mediterranean Sea Derived from Pseudo-Observations and an Ad Hoc Filtering. Remote Sensing, 10(4), 599. https://doi.org/10.3390/rs10040599






