Impact of Surface Soil Moisture Variations on Radar Altimetry Echoes at Ku and Ka Bands in Semi-Arid Areas
Abstract
1. Introduction
2. Radar Altimetry Backscattering Modeling
2.1. Simulation of the Surface Backscattering Using the Kirchoff Model
2.1.1. Kirchoff Model of the Stationary Phase
2.1.2. Soil Dielectric Permittivity Estimates at Ku and Ka Bands
2.2. Altimeter Waveform Generation
2.2.1. Vectorial Polarimetric Backscattering
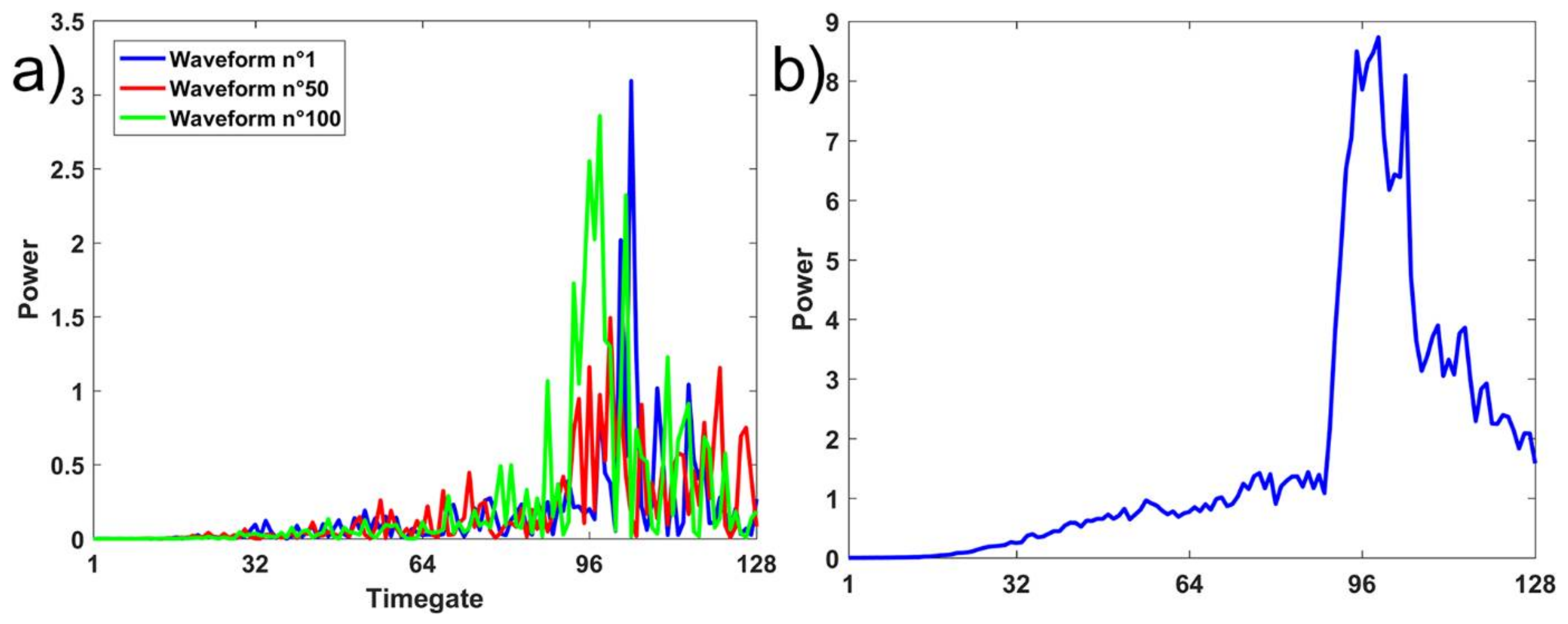
2.2.2. Monopulse Waveform
2.2.3. Averaged Waveform
3. Datasets
3.1. Radar Altimetry Data
3.2. ASTER DEM
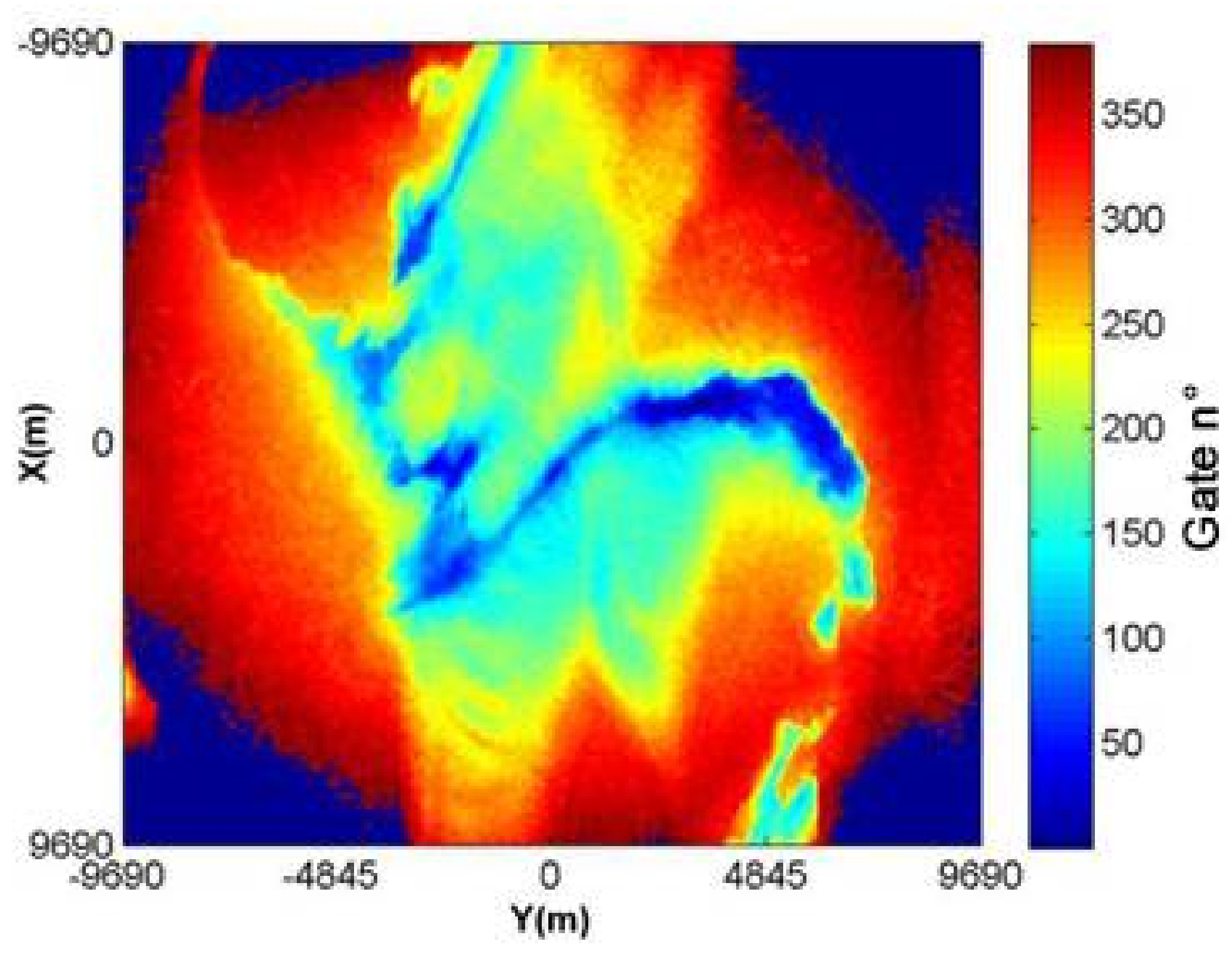
4. Study Area
5. Results
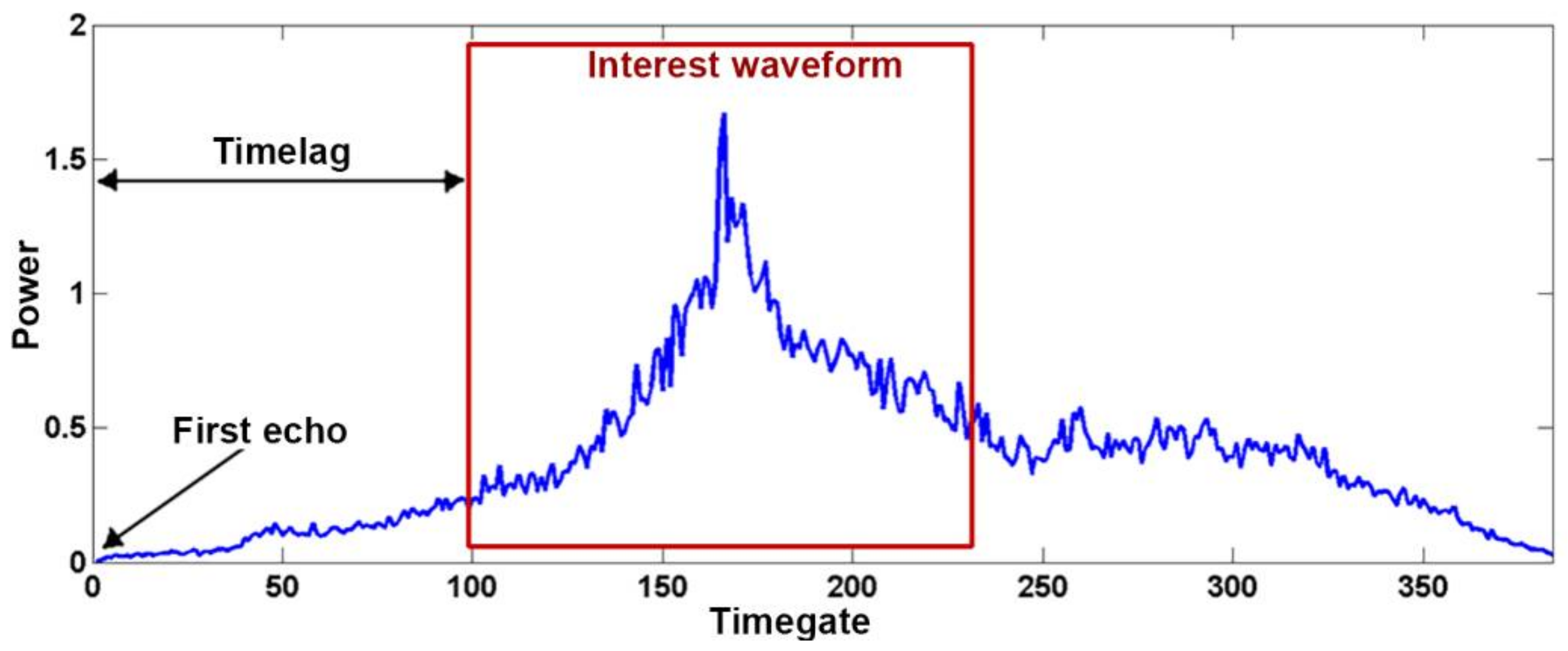
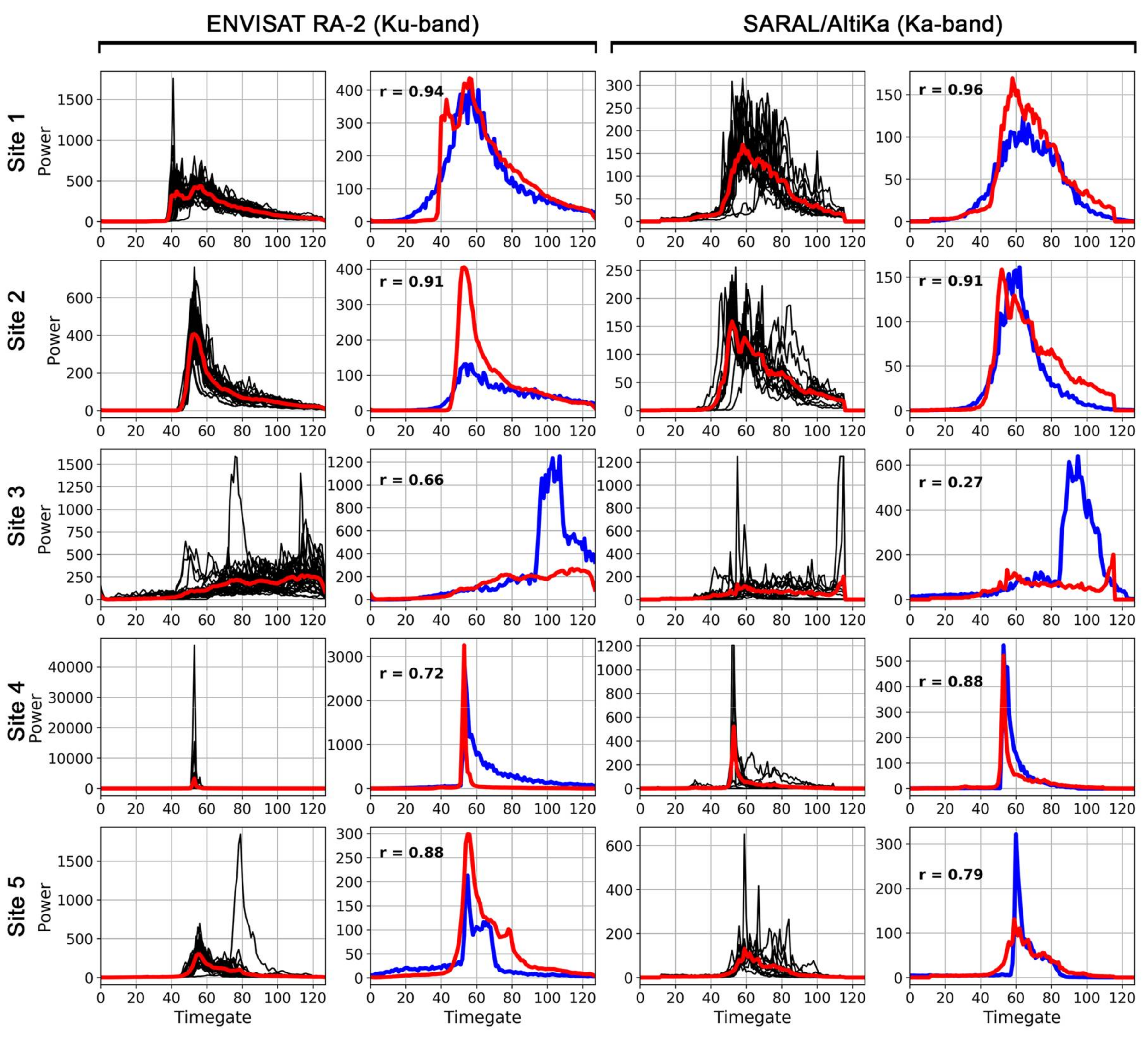
5.1. Comparison between Simulated and Real Waveforms
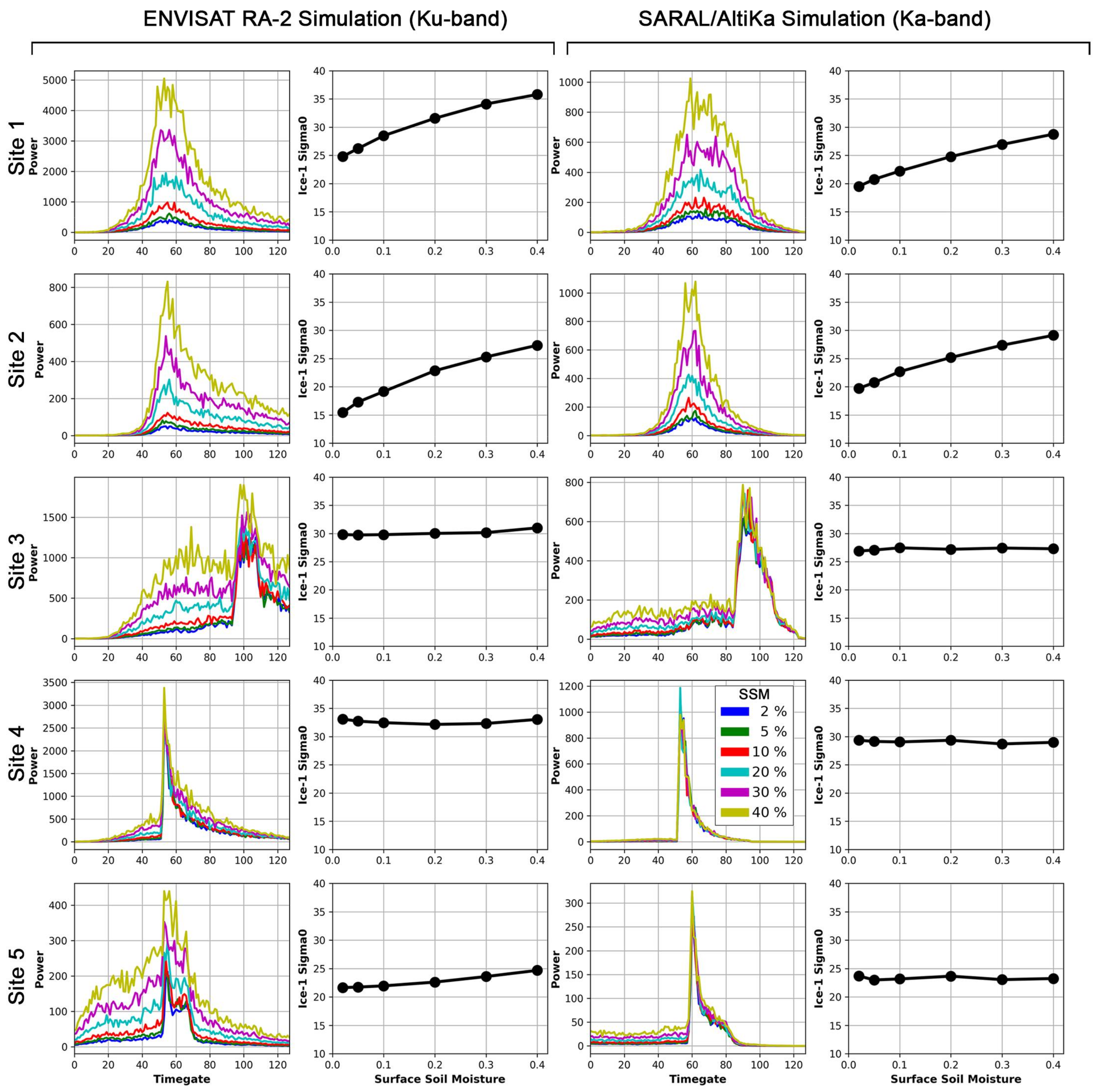
5.2. Impact of Surface Soil Moisture on Altimetry Signal
6. Conclusions
- (1)
- a more realistic description of the open water areas taking into account the small undulations of the surface as in [43],
- (2)
- accurate values of the roughness parameters at Ku and Ka-bands and their spatio-temporal variations over the study sites,
- (3)
- DEM at higher spatial resolution and with a better accuracy, to obtain more accurate simulation results.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
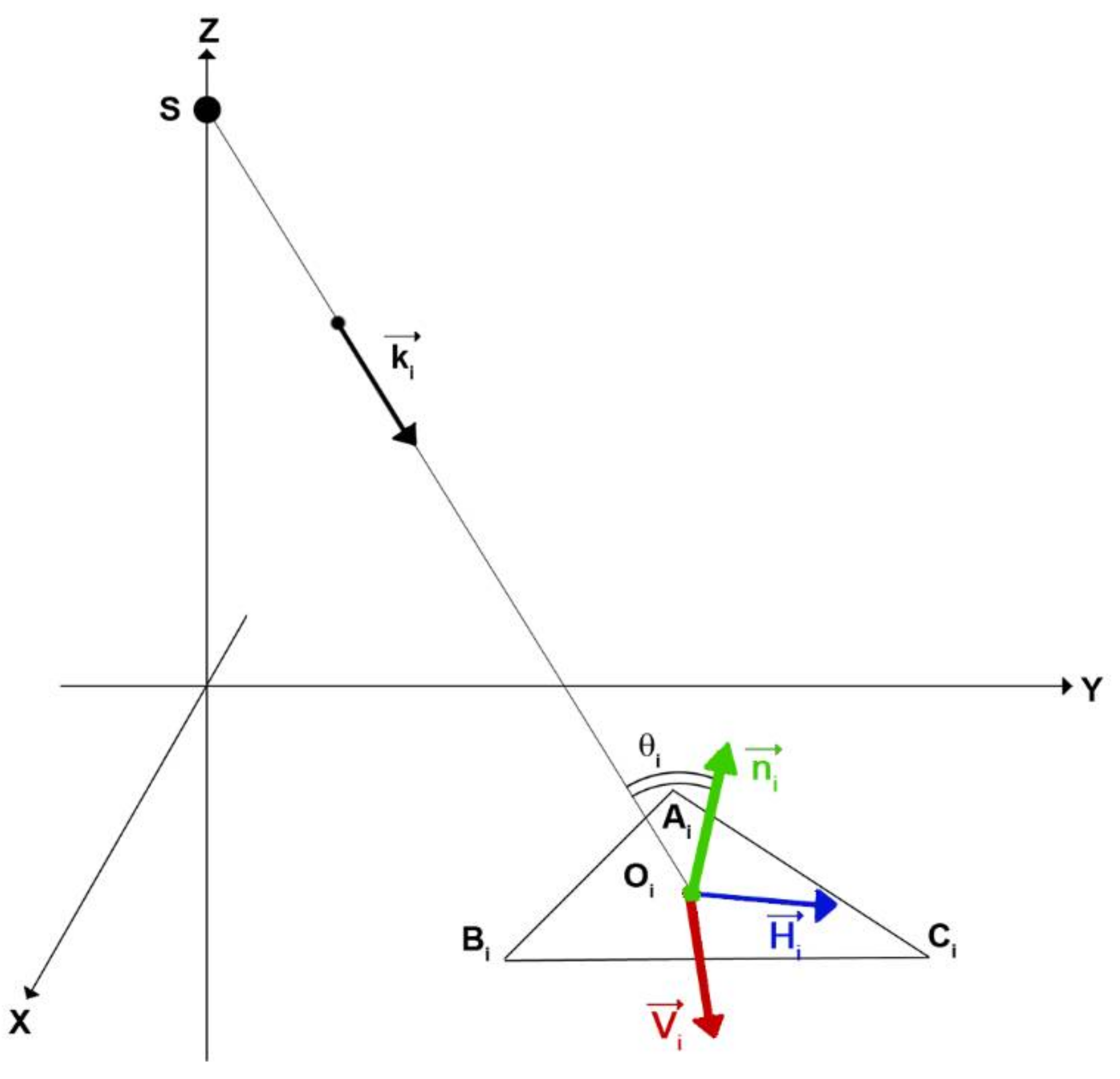
Appendix B
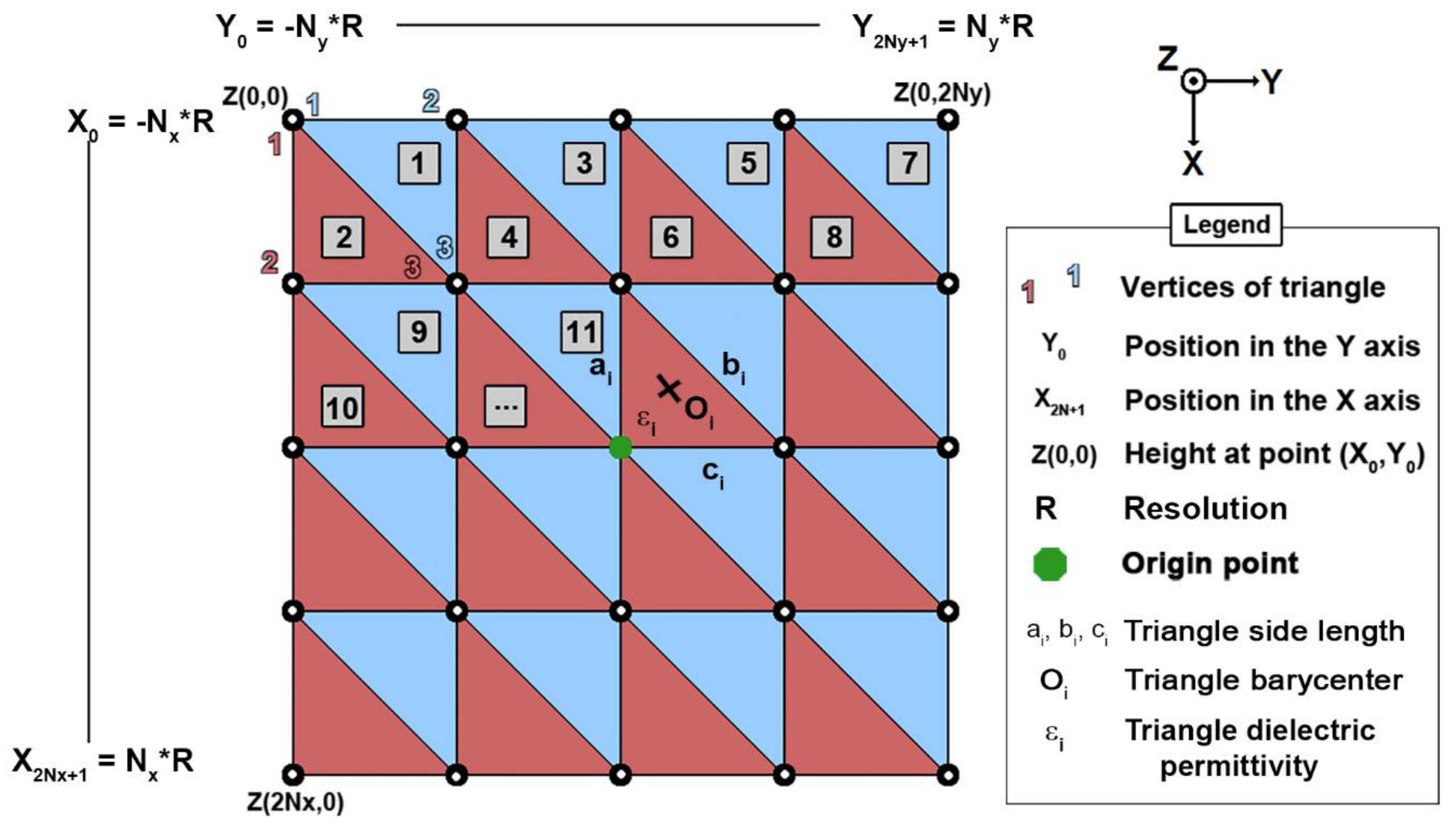
- -
- the mean X position (noted as Xi further on),
- -
- the mean Y position (noted as Yi further on),
- -
- the mean Z position (noted as Zi further on),
- -
- the X axis component of the perpendicular vector (noted as Nx),
- -
- the Y axis component of the perpendicular vector (noted as Ny),
- -
- the Z axis component of the perpendicular vector (noted as Nz),
- -
- the nature of the elementary surface (−1 for water, 0 for ground is the default value),
- -
- the root mean square height hrms (noted as hi),
- -
- the surface correlation length (noted as li),
- -
- the triangle area (noted as Ai),
- -
- the surface complex dielectric permittivity (noted as εri),
Appendix C
Appendix D
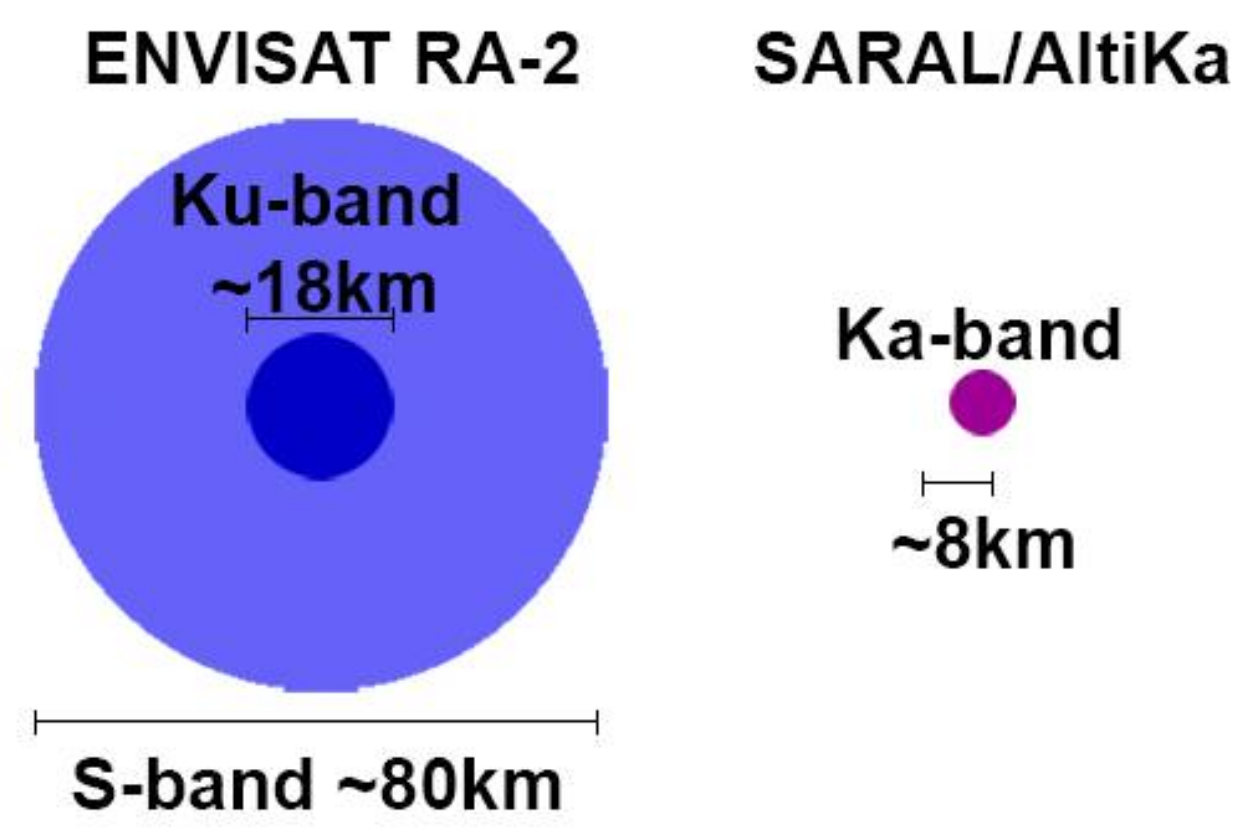
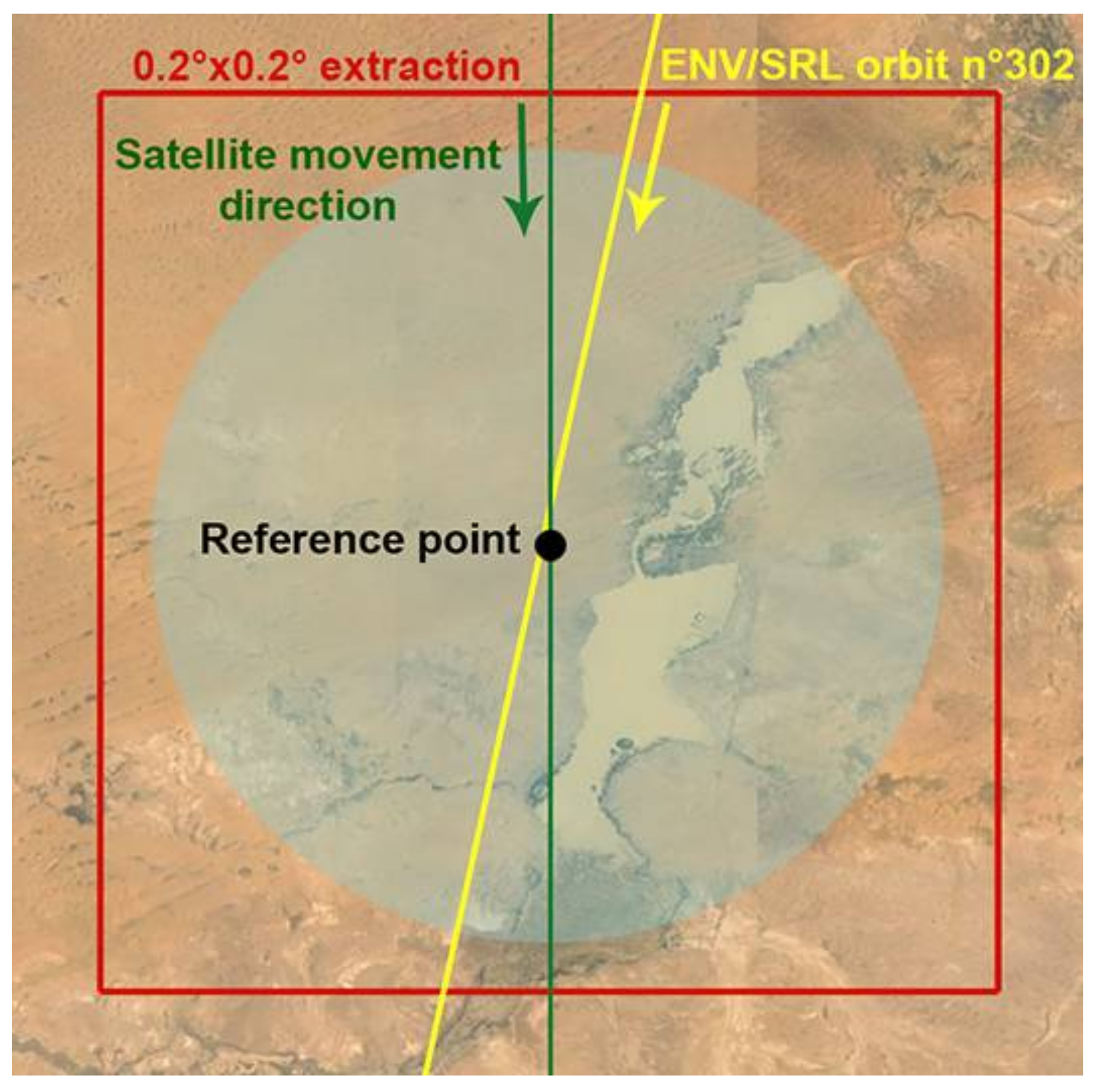
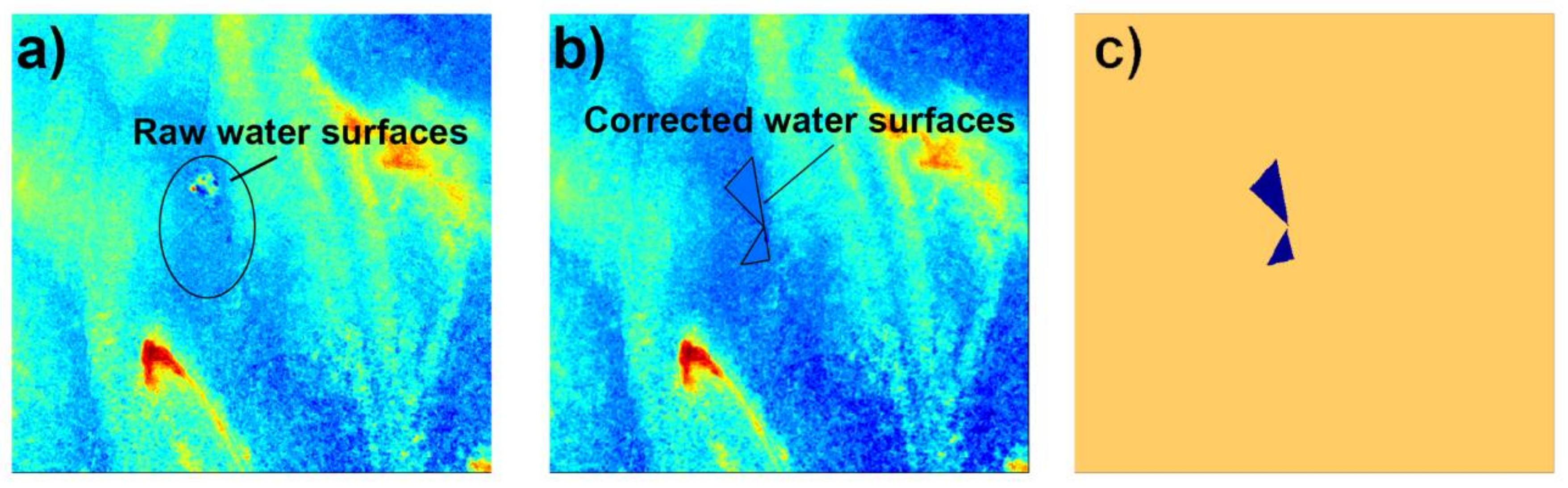
Appendix E
| ENVISAT RA-2 | SARAL AltiKa | |
|---|---|---|
| Mean satellite altitude (km) | 800 | 800 |
| Velocity on orbit (km s−1) | 7.45 | 7.47 |
| Apparent ground velocity (km s−1) | 6.62 | 6.64 |
| Frequency bands | Ku (13.5 GHz), S (3.2 GHz) | Ka (35.5 GHz) |
| Pulse duration (chirp sweep time) (µs) | 20 | 110 |
| Effective pulse duration (ns) | 3.125 | 1 |
| Bandwidth (MHz) | 320, 80, 20 (Ku) 160 (S) | 500 |
| Pulse repetition frequency (Hz) | 1795 (Ku) 449 (S) | ~3800 |
| Time between two pulses (T, µs) | 557 (Ku) 2230 (S) | ~263 |
| Antenna parabola diameter (m) | 1.2 | 1 |
| Footprint diameter (km) | ~18 | ~8 |
| Antenna gain | 37 dB | 44 dB |
| Emitted power (W) | 161 | 100 |
| Distance between two consecutive measurements | 3.69 m | 1.66 m |
| Void fraction (νa) | 0.36 | |
| Sand ground component S | 60 | |
| Clay ground component C | 20 | |
| Soil bulk density (rb) | 1.69 | |
| Alpha parameter | 0.65 | |
| Temperature (°C) | 30 | |
| Correlation length | 4.5 cm | |
| Height rms (roughness) | 0.35 cm | |
| Ku Band | Ka Band | |
|---|---|---|
| kl (rad) | 12.72 | 33.46 |
| l2 (10−3 m2) | 2.0 | 2.0 |
| 2.67sλ (10−3 m2) | 0.21 | 0.08 |
| ks (rad) | 0.99 | 2.60 |
Appendix F
| Simulation Site | ENVISAT RA-2 | SARAL/AltiKa | ||
|---|---|---|---|---|
| Empirical Gain (dB) | Timelag (ns) | Empirical Gain (dB) | Timelag (ns) | |
| Site 1 | 343.42 | 0 | 339.03 | 33 |
| Site 2 | 337.78 | −30 | 336.53 | 18 |
| Site 3 | 341.76 | 35 | 336.02 | 158 |
| Site 4 | 339.03 | 100 | 327.78 | 160 |
| Site 5 | 335.44 | 425 | 330 | 164 |
| Mean | 340.37 | n/a | 335.59 | n/a |
| STD | 2.28 | n/a | 2.62 | n/a |
References
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. GLACE Team Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Entekhabi, D.; Rodriguez-Iturbe, I. Analytical framework for the characterization of the space-time variability of soil moisture. Adv. Water Resour. 1994, 17, 35–45. [Google Scholar] [CrossRef]
- Small, E.E.; Kurc, S.A. Tight coupling between soil moisture and the surface radiation budget in semiarid environments: Implications for land-atmosphere interactions. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Mott, J.J. Factors Affecting Seed Germination in Three Annual Species from an Arid Region of Western Australia. J. Ecol. 1974, 62, 699. [Google Scholar] [CrossRef]
- Delon, C.; Mougin, E.; Serça, D.; Grippa, M.; Hiernaux, P.; Diawara, M.; Galy-Lacaux, C.; Kergoat, L. Modelling the effect of soil moisture and organic matter degradation on biogenic NO emissions from soils in Sahel rangeland (Mali). Biogeosciences 2015, 12, 3253–3272. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Jarlan, L.; Mougin, E.; Frison, P.L.; Mazzega, P.; Hiernaux, P. Analysis of ERS wind scatterometer time series over Sahel (Mali). Remote Sens. Environ. 2002, 81, 404–415. [Google Scholar] [CrossRef]
- Gruhier, C.; de Rosnay, P.; Kerr, Y.; Mougin, E.; Ceschia, E.; Calvet, J.C.; Richaume, P. Evaluation of AMSR-E soil moisture product based on ground measurements over temperate and semi-arid regions. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Gruhier, C.; De Rosnay, P.; Hasenauer, S.; Holmes, T.; De Jeu, R.; Kerr, Y.; Mougin, E.; Njoku, E.; Timouk, F.; Wagner, W.; et al. Soil moisture active and passive microwave products: Intercomparison and evaluation over a Sahelian site. Hydrol. Earth Syst. Sci. 2010, 14, 141–156. [Google Scholar] [CrossRef]
- Louvet, S.; Pellarin, T.; al Bitar, A.; Cappelaere, B.; Galle, S.; Grippa, M.; Gruhier, C.; Kerr, Y.; Lebel, T.; Mialon, A.; et al. SMOS soil moisture product evaluation over West-Africa from local to regional scale. Remote Sens. Environ. 2015, 156, 383–394. [Google Scholar] [CrossRef]
- Frison, P.L.; Mougin, E.; Hiernaux, P. Observations and Interpretation of Seasonal ERS-1 Wind Scatterometer Data over Northern Sahel (Mali). Remote Sens. Environ. 1998, 63, 233–242. [Google Scholar] [CrossRef]
- Frison, P.-L.; Jarlan, L.; Mougin, E. Using Satellite Scatterometers to Monitor Continental Surfaces. In Land Surface Remote Sensing in Continental Hydrology; Elsevier: New York, NY, USA, 2016; pp. 79–113. ISBN 9781785481048. [Google Scholar]
- De Jeu, R.A.M.; Wagner, W.; Holmes, T.R.H.; Dolman, A.J.; van de Giesen, N.C.; Friesen, J. Global Soil Moisture Patterns Observed by Space Borne Microwave Radiometers and Scatterometers. Surv. Geophys. 2008, 29, 399–420. [Google Scholar] [CrossRef]
- Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An Improved Soil Moisture Retrieval Algorithm for ERS and METOP Scatterometer Observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
- Holgate, C.M.; De Jeu, R.A.M.; van Dijk, A.I.J.M.; Liu, Y.Y.; Renzullo, L.J.; Vinodkumar; Dharssi, I.; Parinussa, R.M.; Van Der Schalie, R.; Gevaert, A.; et al. Comparison of remotely sensed and modelled soil moisture data sets across Australia. Remote Sens. Environ. 2016, 186, 479–500. [Google Scholar] [CrossRef]
- Tansey, K.J.; Millington, A.C.; Battikhi, A.M.; White, K.H. Monitoring soil moisture dynamics using satellite imaging radar in northeastern Jordan. Appl. Geogr. 1999, 19, 325–344. [Google Scholar] [CrossRef]
- Moran, M.S.; Hymer, D.C.; Qi, J.; Sano, E.E. Soil moisture evaluation using multi-temporal synthetic aperture radar (SAR) in semiarid rangeland. Agric. For. Meteorol. 2000, 105, 69–80. [Google Scholar] [CrossRef]
- Baup, F.; Mougin, E.; Hiernaux, P.; Lopes, A.; De Rosnay, P.; Chenerie, I. Radar Signatures of Sahelian Surfaces in Mali Using ENVISAT-ASAR Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2354–2363. [Google Scholar] [CrossRef]
- Baup, F.; Mougin, E.; De Rosnay, P.; Hiernaux, P.; Frappart, F.; Frison, P.L.; Zribi, M.; Viarre, J. Mapping surface soil moisture over the Gourma mesoscale site (Mali) by using ENVISAT ASAR data. Hydrol. Earth Syst. Sci. 2011, 15. [Google Scholar] [CrossRef]
- Ridley, J.; Strawbridge, F.; Card, R.; Phillips, H. Radar backscatter characteristics of a desert surface. Remote Sens. Environ. 1996, 57, 63–78. [Google Scholar] [CrossRef]
- Fatras, C.; Frappart, F.; Mougin, E.; Grippa, M.; Hiernaux, P. Estimating surface soil moisture over Sahel using ENVISAT radar altimetry. Remote Sens. Environ. 2012, 123. [Google Scholar] [CrossRef]
- Fatras, C.; Frappart, F.; Mougin, E.; Frison, P.-L.; Faye, G.; Borderies, P.; Jarlan, L. Spaceborne altimetry and scatterometry backscattering signatures at C- and Ku-bands over West Africa. Remote Sens. Environ. 2015, 159. [Google Scholar] [CrossRef]
- Frappart, F.; Fatras, C.; Mougin, E.; Marieu, V.; Diepkilé, A.T.; Blarel, F.; Borderies, P. Radar altimetry backscattering signatures at Ka, Ku, C, and S bands over West Africa. Phys. Chem. Earth 2015, 83–84. [Google Scholar] [CrossRef]
- Bonnefond, P.; Verron, J.; Aublanc, J.; Babu, K.; Bergé-Nguyen, M.; Cancet, M.; Chaudhary, A.; Crétaux, J.-F.; Frappart, F.; Haines, B.; et al. The Benefits of the Ka-Band as Evidenced from the SARAL/AltiKa Altimetric Mission: Quality Assessment and Unique Characteristics of AltiKa Data. Remote Sens. 2018, 10, 83. [Google Scholar] [CrossRef]
- Uebbing, B.; Forootan, E.; Braakmann-Folgmann, A.; Kusche, J. Inverting surface soil moisture information from satellite altimetry over arid and semi-arid regions. Remote Sens. Environ. 2017, 196, 205–223. [Google Scholar] [CrossRef]
- Fatras, C.; Borderies, P.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Frappart, F.; Mougin, E. Radar Backscattering Coefficient over Bare Soils at Ka-Band Close to Nadir Angle. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1290–1294. [Google Scholar] [CrossRef]
- Hallikainen, M.; Ulaby, F.; Dobson, M.; El-Rayes, M.; Wu, L. Microwave Dielectric Behavior of Wet Soil-Part 1: Empirical Models and Experimental Observations. IEEE Trans. Geosci. Remote Sens. 1985, 23, 25–34. [Google Scholar] [CrossRef]
- Dobson, M.; Ulaby, F.; Hallikainen, M.; El-rayes, M. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar] [CrossRef]
- Malmberg, C.G.; Maryott, A.A. Dielectric constant of water from 0 to 1000 °C. J. Res. Natl. Bur. Stand. 1956, 56, 1–8. [Google Scholar] [CrossRef]
- Nashashibi, A.; Ulaby, F.T.; Sarabandi, K. Measurement and modeling of the millimeter-wave backscatter response of soil surfaces. IEEE Trans. Geosci. Remote Sens. 1996, 34, 561–572. [Google Scholar] [CrossRef]
- Ulaby, F.T. Radar Polarimetry for Geoscience Applications; Fawwaz, T., Elachi, C., Eds.; Artech House: Norwood, MA, USA, 1990; ISBN 0890064067. [Google Scholar]
- Ruck, G.T.; Barrick, D.E.; Stuart, W.D.; Krichbaum, C.K. Radar Cross Section Handbook; Plenum Press: New York, NY, USA, 1970; Volume 1. [Google Scholar]
- Chelton, D.B.; Ries, J.C.; Haines, B.J.; Fu, L.-L.; Callahan, P.S. Chapter 1 Satellite Altimetry. In Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Elsevier: New York, NY, USA, 2001; Volume 69, 131p, ISBN 0074-6142. [Google Scholar]
- Biancamaria, S.; Frappart, F.; Leleu, A.-S.; Marieu, V.; Blumstein, D.; Desjonquères, J.-D.; Boy, F.; Sottolichio, A.; Valle-Levinson, A. Satellite radar altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2017, 59, 128–146. [Google Scholar] [CrossRef]
- CTOH (Center for Topographic studies of the Ocean and Hydrosphere). Available online: http://ctoh.legos.obs-mip.fr (accessed on 9 April 2018).
- Zelli, C. ENVISAT RA-2 advanced radar altimeter: Instrument design and pre-launch performance assessment review. Acta Astronaut. 1999, 44, 323–333. [Google Scholar] [CrossRef]
- Tachikawa, T.; Hato, M.; Kaku, M.; Iwasaki, A. The characteristics of ASTER GDEM version 2. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar] [CrossRef]
- Steunou, N.; Desjonquères, J.D.; Picot, N.; Sengenes, P.; Noubel, J.; Poisson, J.C. AltiKa Altimeter: Instrument Description and In Flight Performance. Mar. Geod. 2015, 38, 22–42. [Google Scholar] [CrossRef]
- Mougin, E.; Hiernaux, P.; Kergoat, L.; Grippa, M.; de Rosnay, P.; Timouk, F.; Le Dantec, V.; Demarez, V.; Lavenu, F.; Arjounin, M.; et al. The AMMA-CATCH Gourma observatory site in Mali: Relating climatic variations to changes in vegetation, surface hydrology, fluxes and natural resources. J. Hydrol. 2009, 375. [Google Scholar] [CrossRef]
- Frappart, F.; Hiernaux, P.; Guichard, F.; Mougin, E.; Kergoat, L.; Arjounin, M.; Lavenu, F.; Koité, M.; Paturel, J.-E.; Lebel, T. Rainfall regime across the Sahel band in the Gourma region, Mali. J. Hydrol. 2009, 375, 128–142. [Google Scholar] [CrossRef]
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New Techniques in Satellite Altimeter Tracking Systems. In Proceedings of the 1986 International Geoscience and Remote Sensing Symposium on Remote Sensing, Zurich, Switzerland, 8–11 September 1986; pp. 1339–1344. [Google Scholar]
- Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100. [Google Scholar] [CrossRef]
- Boisot, O.; Pioch, S.; Fatras, C.; Caulliez, G.; Bringer, A.; Borderies, P.; Lalaurie, J.-C.; Guérin, C.-A. Ka-band backscattering from water surface at small incidence: A wind-wave tank study. J. Geophys. Res. Oceans 2015, 120, 3261–3285. [Google Scholar] [CrossRef]
| ENVISAT RA-2 | SARAL AltiKa | |
|---|---|---|
| Mean satellite altitude (km) | 800 | 800 |
| Velocity on orbit (km s−1) | 7.45 | 7.47 |
| Apparent ground velocity (km s−1) | 6.62 | 6.64 |
| Frequency bands | Ku (13.575 GHz), S (3.2 GHz) | Ka (35.75 GHz) |
| Pulse duration (chirp sweep time) (µs) | 20 | 110 |
| Effective pulse duration (ns) | 3.125 | 1 |
| Bandwidth (MHz) | 320, 80, 20 (Ku) 160 (S) | 500 |
| Pulse repetition frequency (Hz) | 1795 (Ku) 449 (S) | ~3800 |
| Time between two pulses (T, en µs) | 557 (Ku) 2230 (S) | ~263 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatras, C.; Borderies, P.; Frappart, F.; Mougin, E.; Blumstein, D.; Niño, F. Impact of Surface Soil Moisture Variations on Radar Altimetry Echoes at Ku and Ka Bands in Semi-Arid Areas. Remote Sens. 2018, 10, 582. https://doi.org/10.3390/rs10040582
Fatras C, Borderies P, Frappart F, Mougin E, Blumstein D, Niño F. Impact of Surface Soil Moisture Variations on Radar Altimetry Echoes at Ku and Ka Bands in Semi-Arid Areas. Remote Sensing. 2018; 10(4):582. https://doi.org/10.3390/rs10040582
Chicago/Turabian StyleFatras, Christophe, Pierre Borderies, Frédéric Frappart, Eric Mougin, Denis Blumstein, and Fernando Niño. 2018. "Impact of Surface Soil Moisture Variations on Radar Altimetry Echoes at Ku and Ka Bands in Semi-Arid Areas" Remote Sensing 10, no. 4: 582. https://doi.org/10.3390/rs10040582
APA StyleFatras, C., Borderies, P., Frappart, F., Mougin, E., Blumstein, D., & Niño, F. (2018). Impact of Surface Soil Moisture Variations on Radar Altimetry Echoes at Ku and Ka Bands in Semi-Arid Areas. Remote Sensing, 10(4), 582. https://doi.org/10.3390/rs10040582





