Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer
Abstract
1. Introduction
2. Materials and Methods
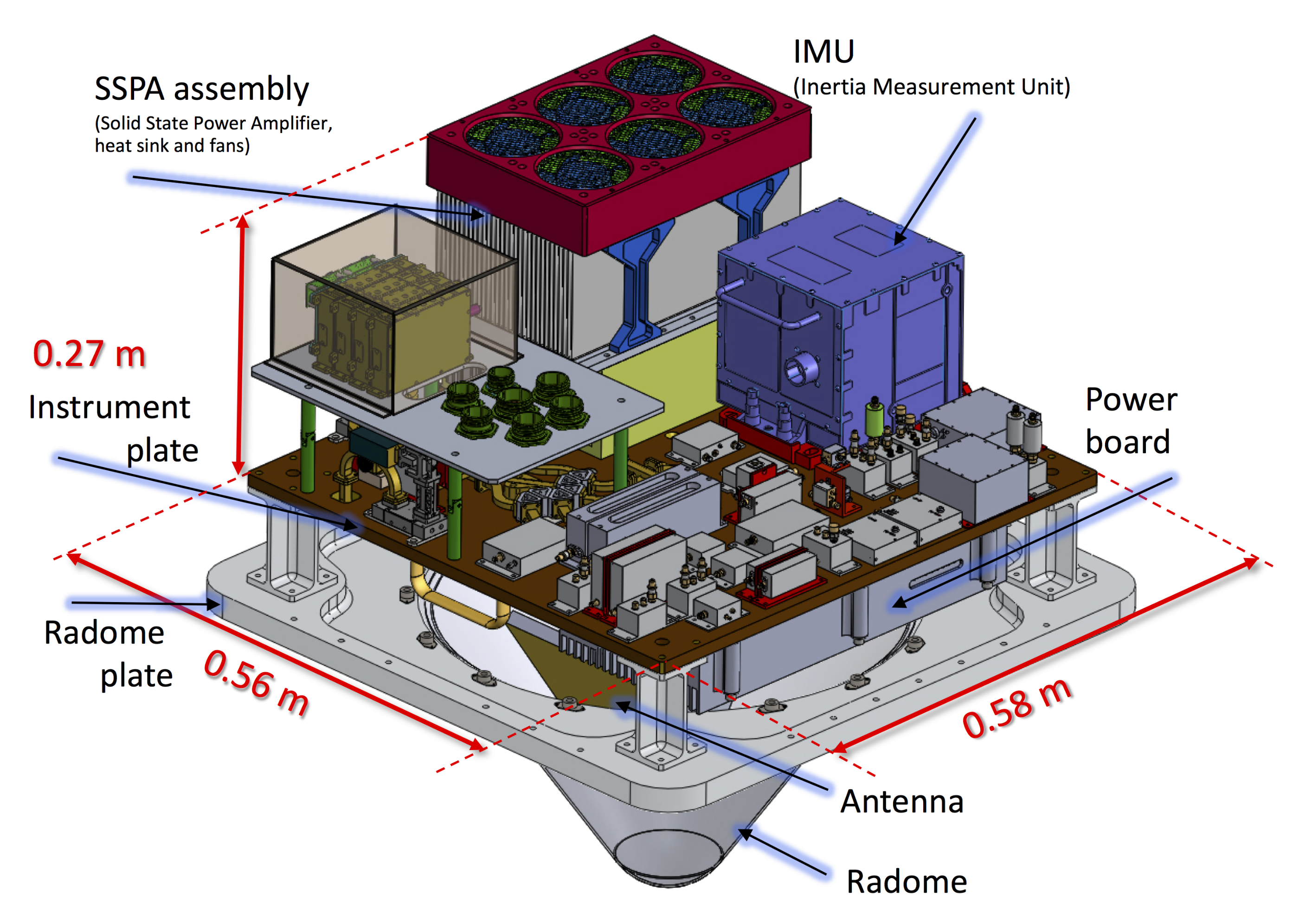
2.1. The DopplerScatt Instrument
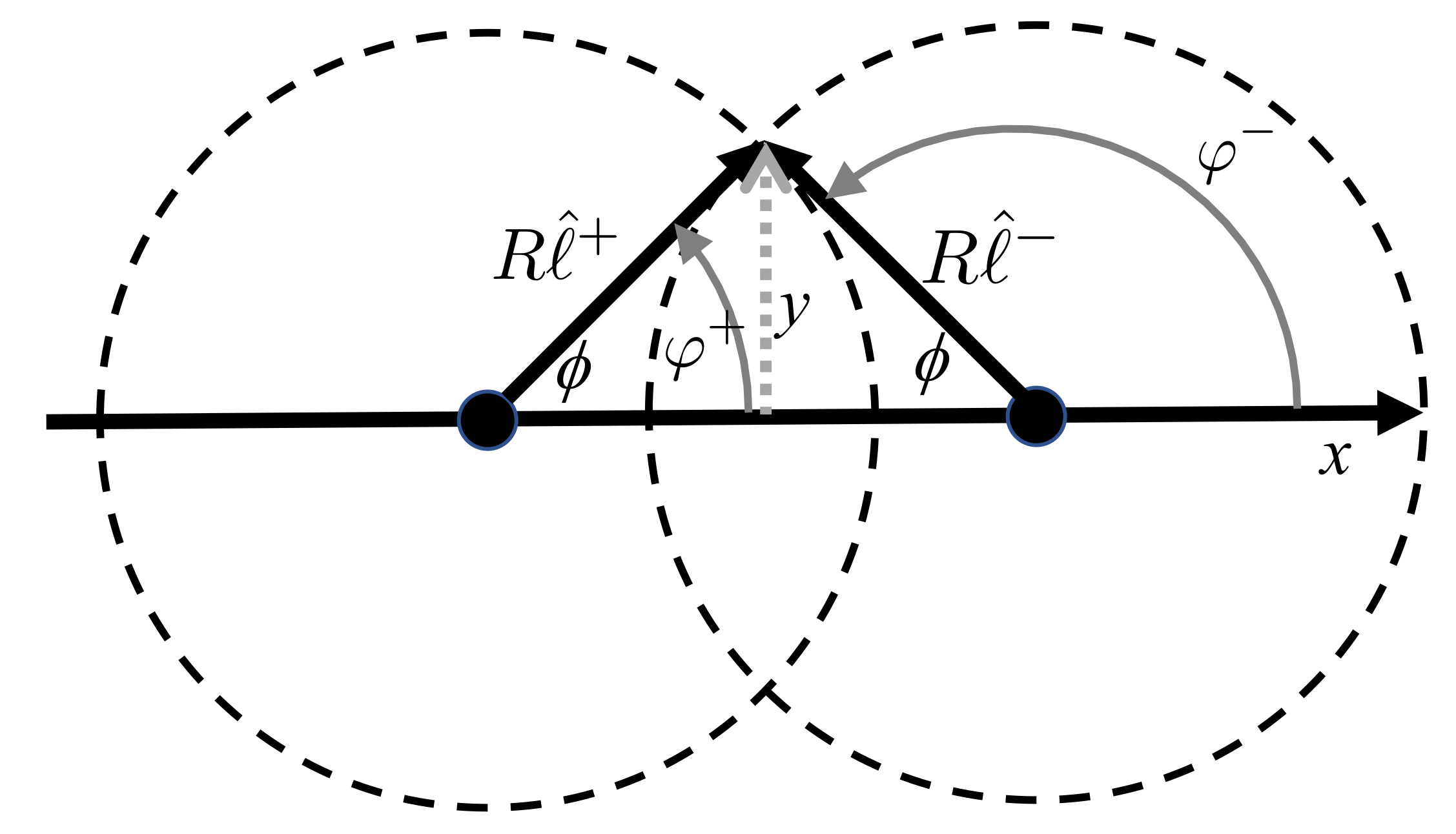
2.2. Current Measurement Principle
2.3. Estimation of Pulse-Pair Phase
2.4. Processing to and Radial Velocities
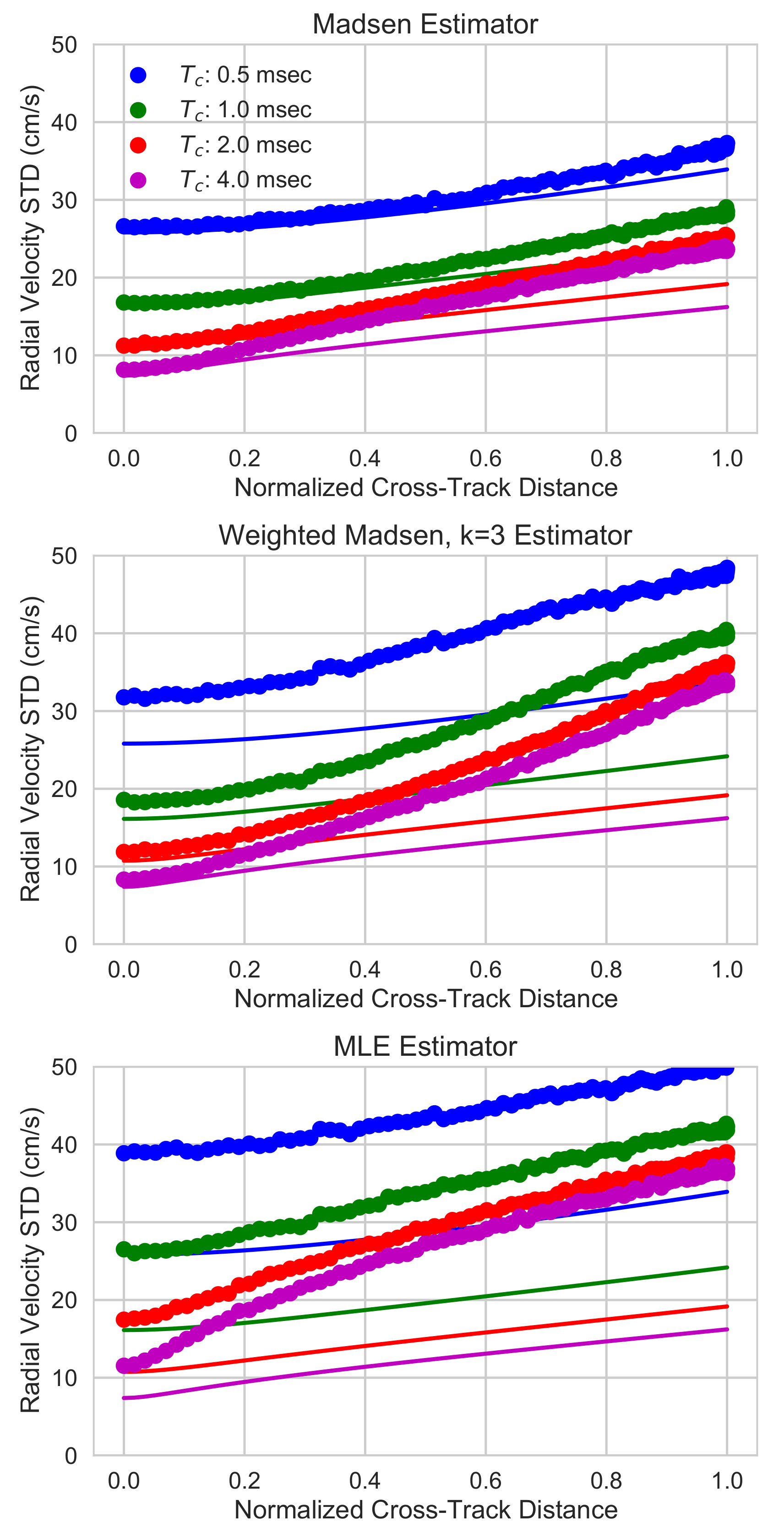
2.5. Estimating the Surface Velocities and Errors
2.6. Estimating the Wind Speed and Direction
2.7. Calibration
2.8. Radial Velocity Calibration
3. Results
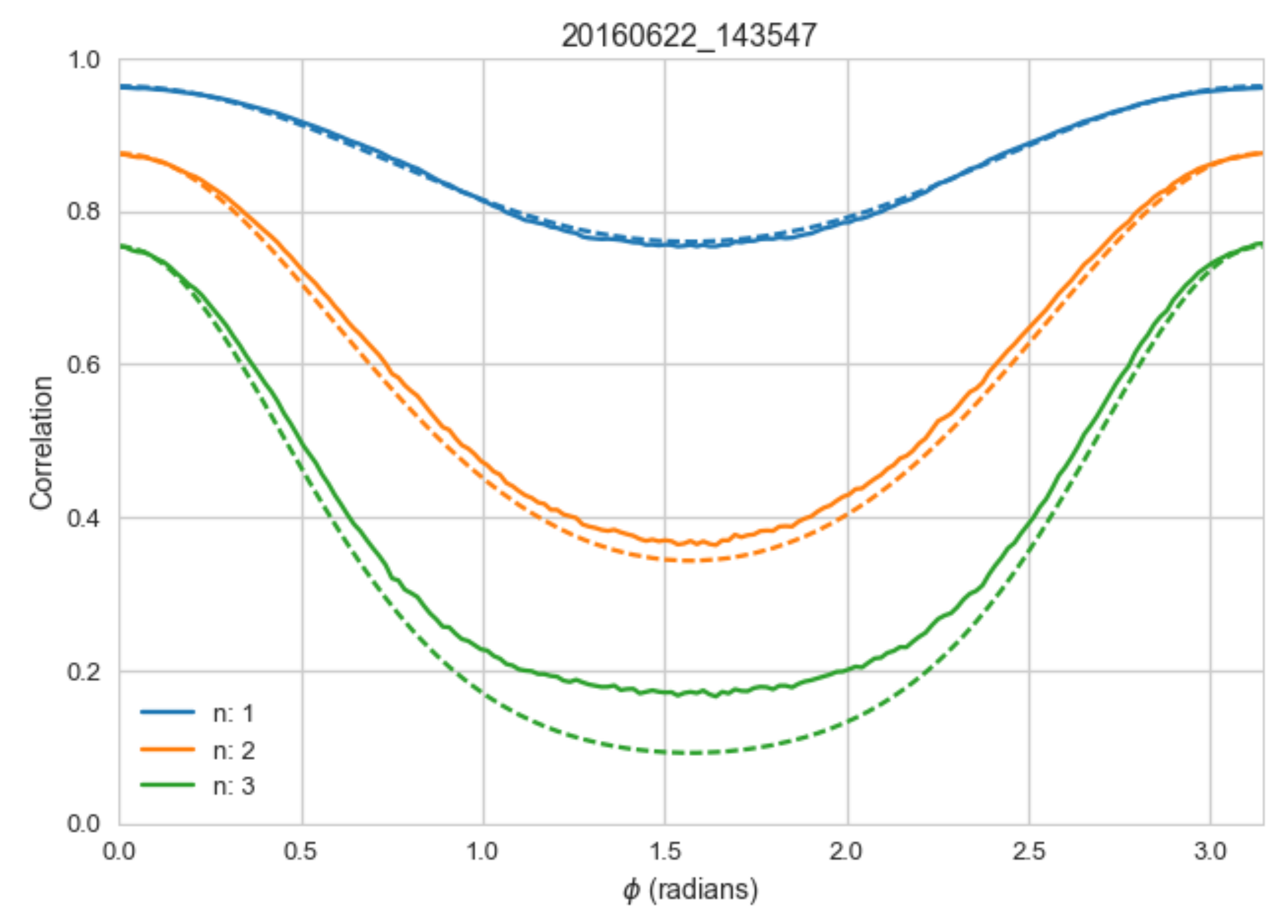
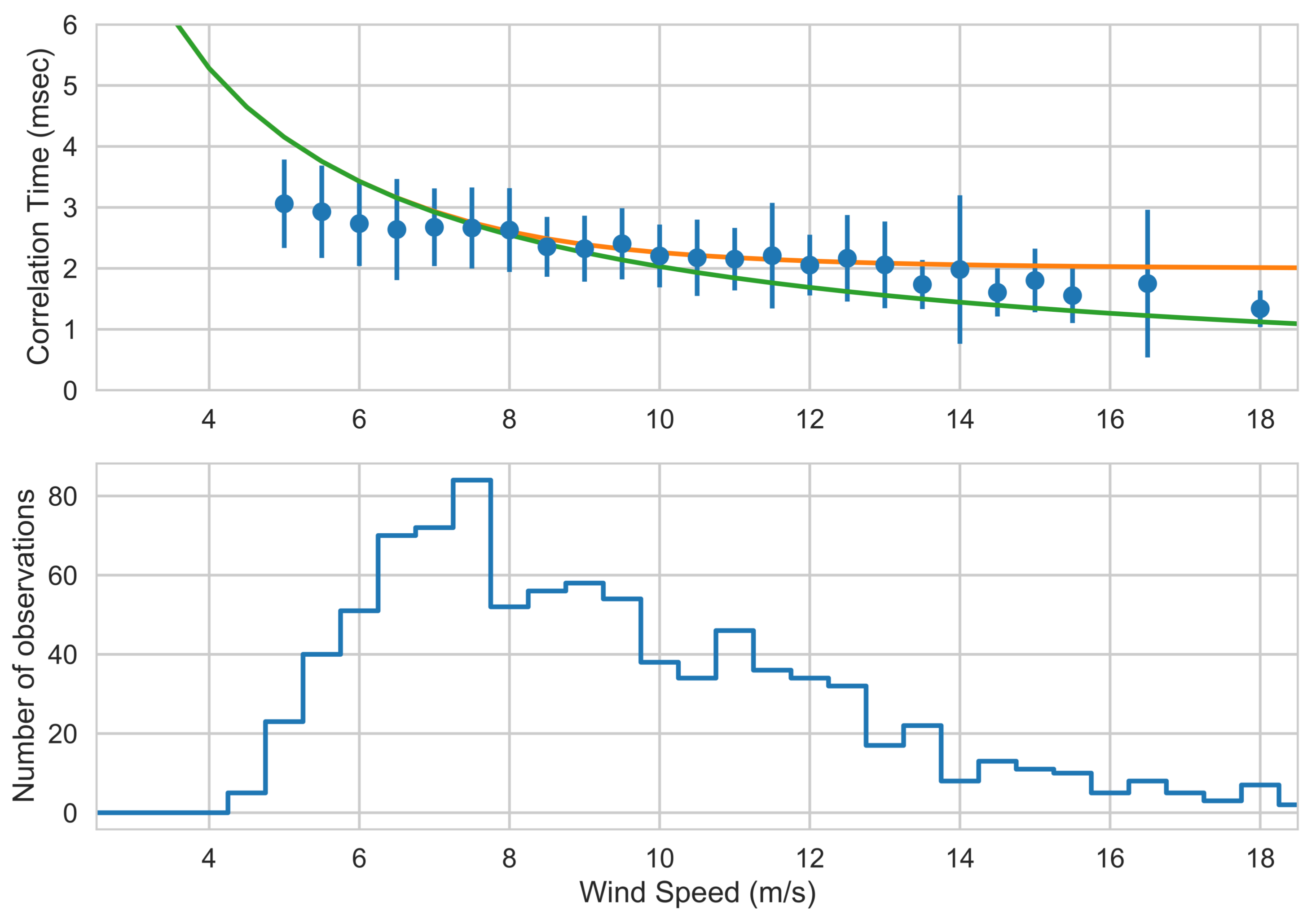
3.1. Ocean Temporal Correlation
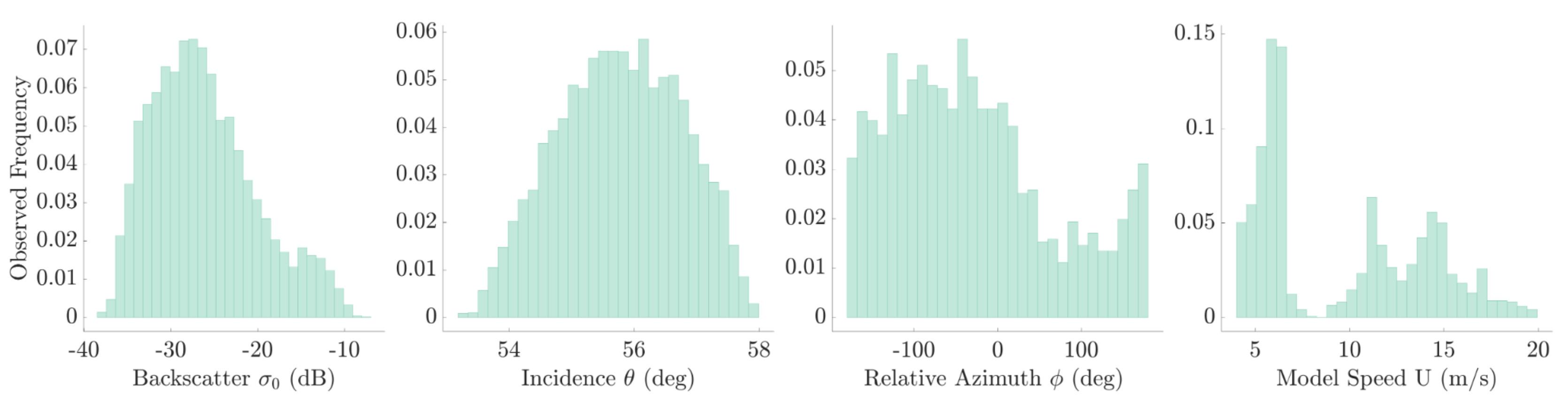
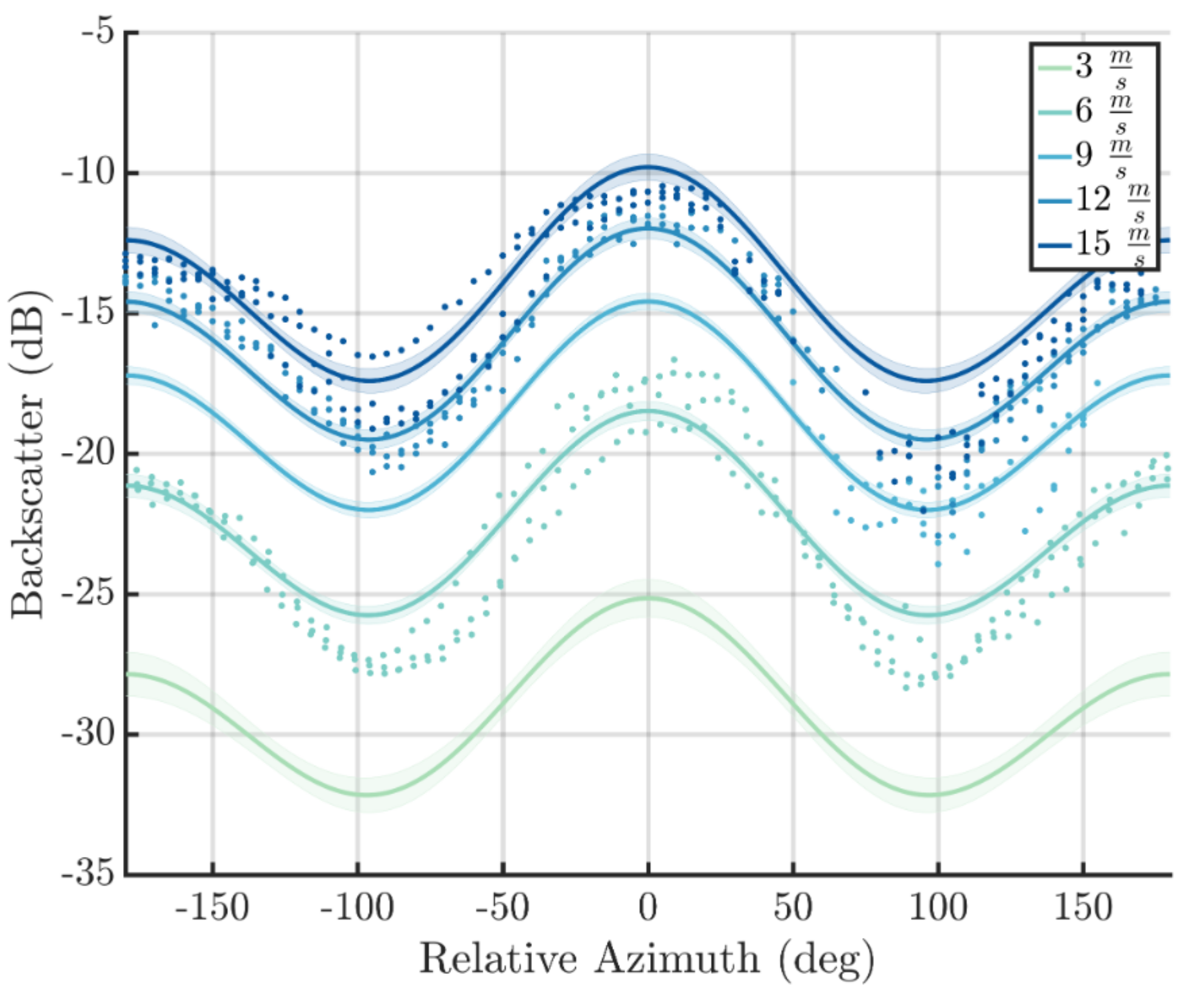
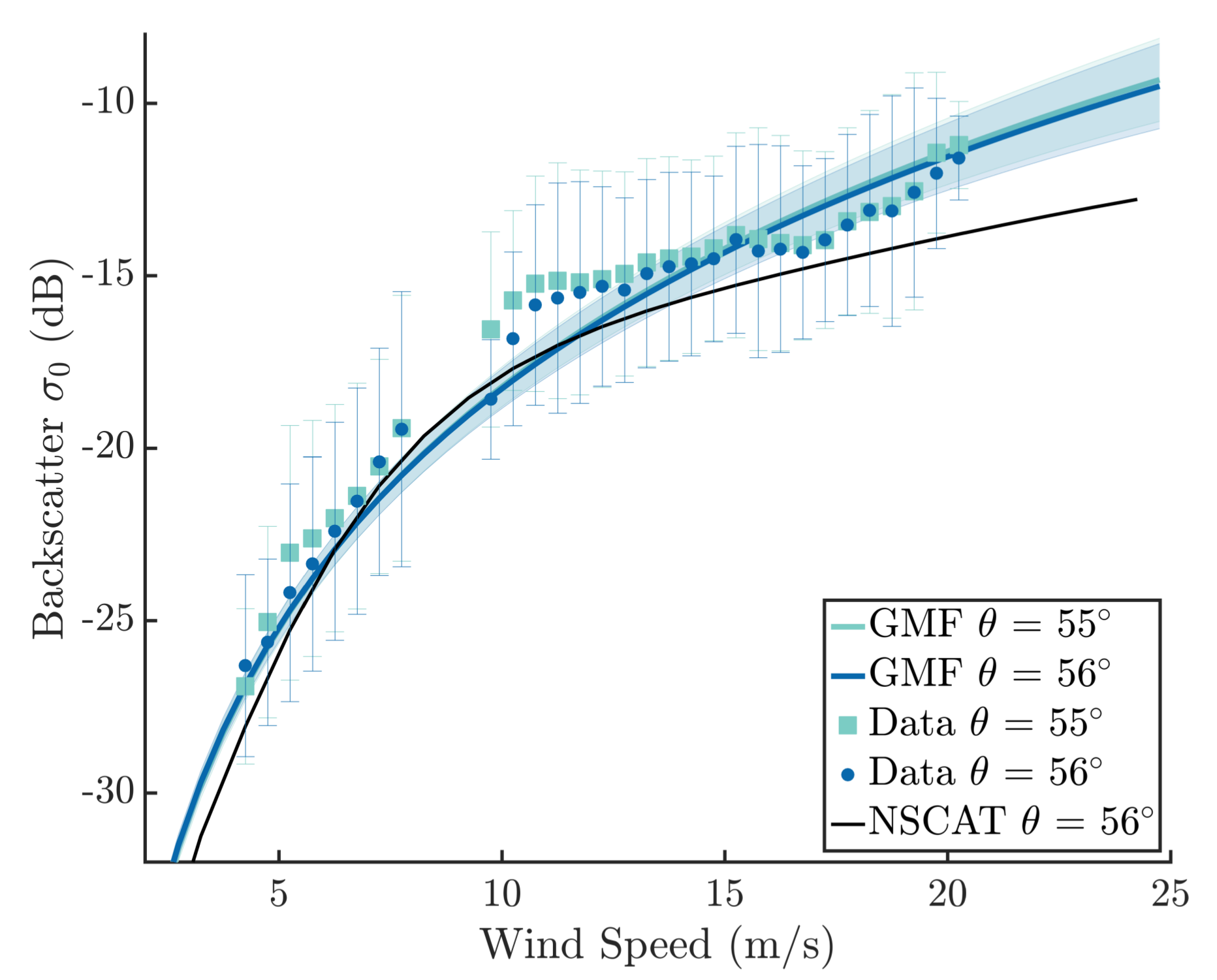
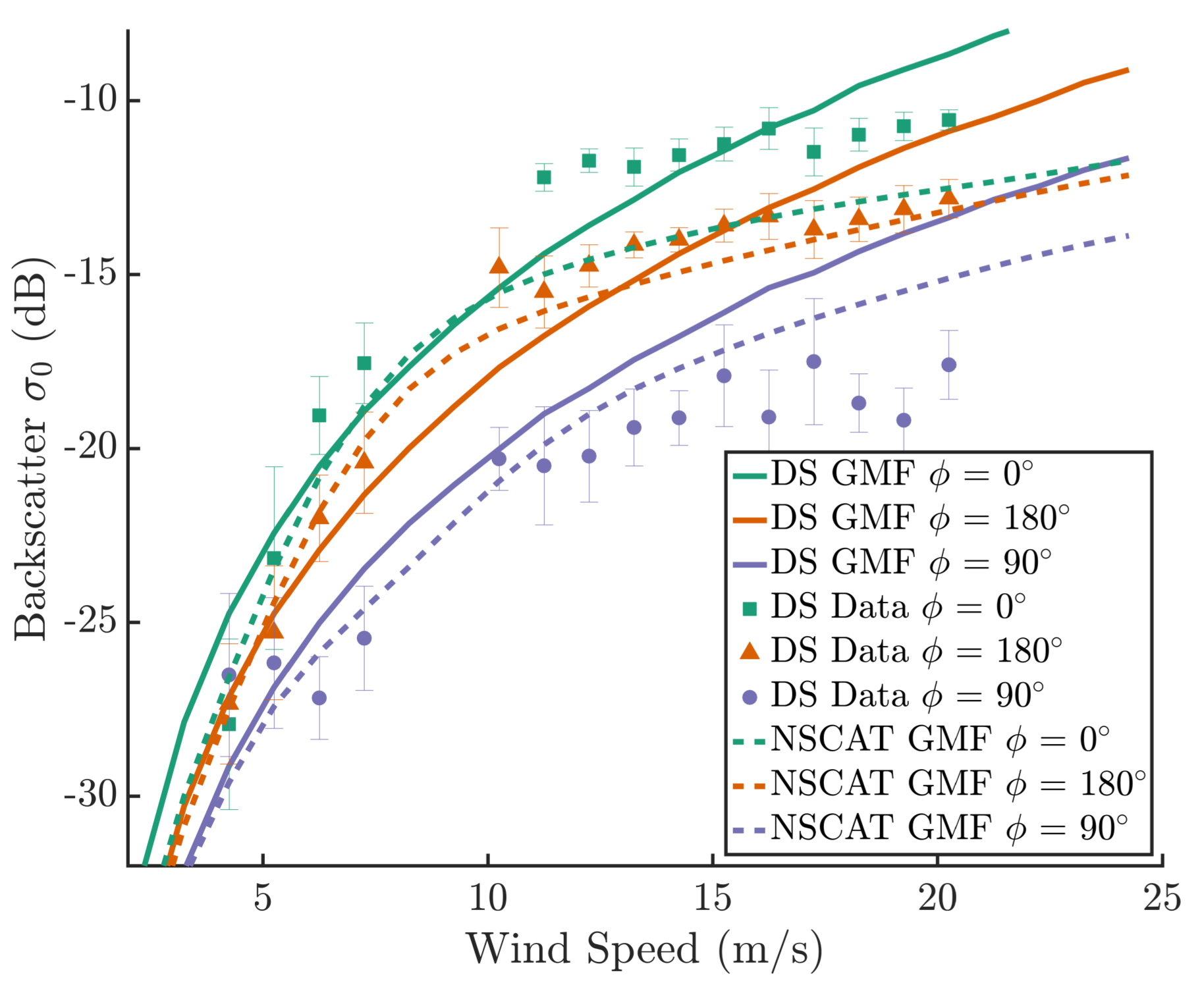
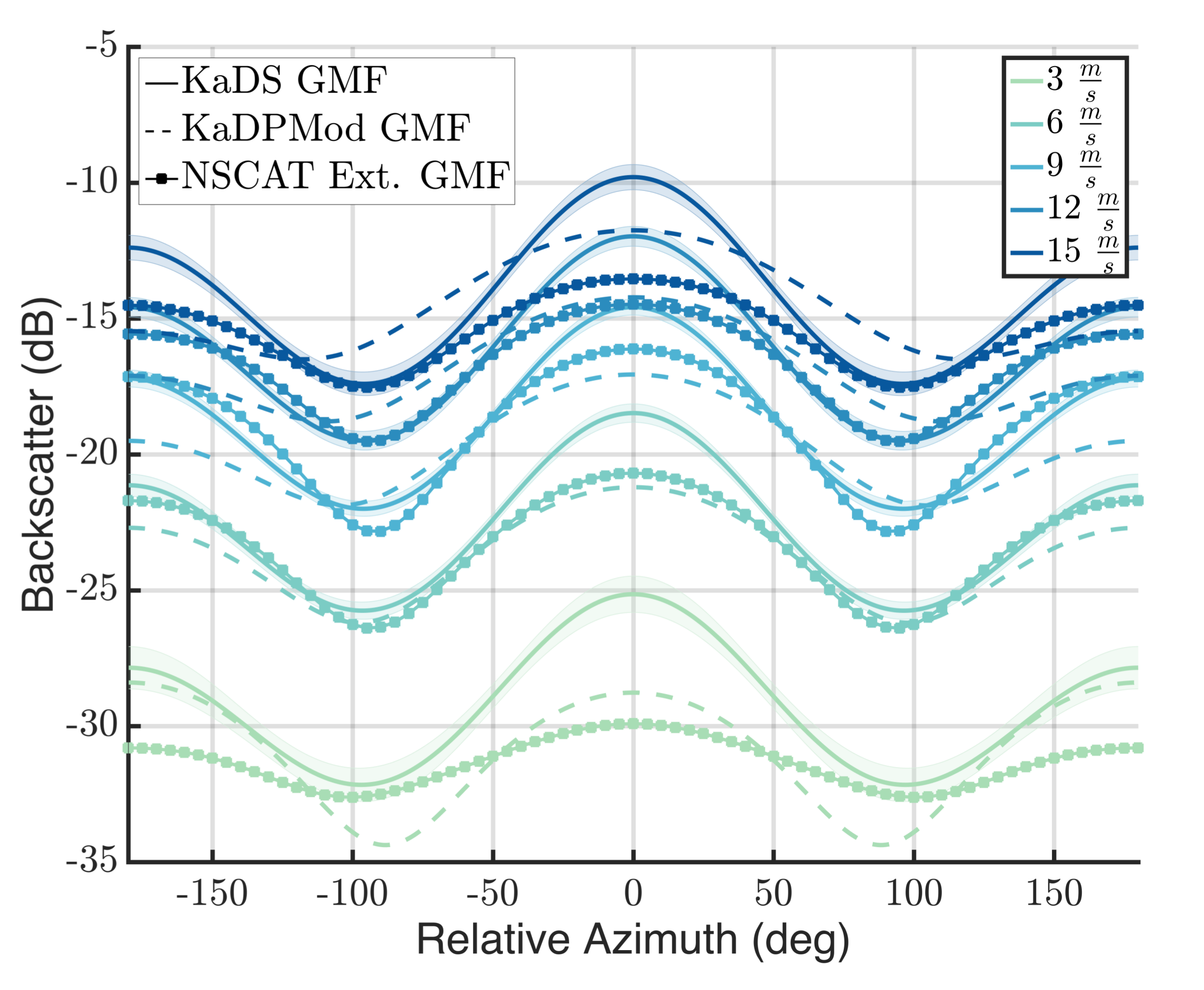
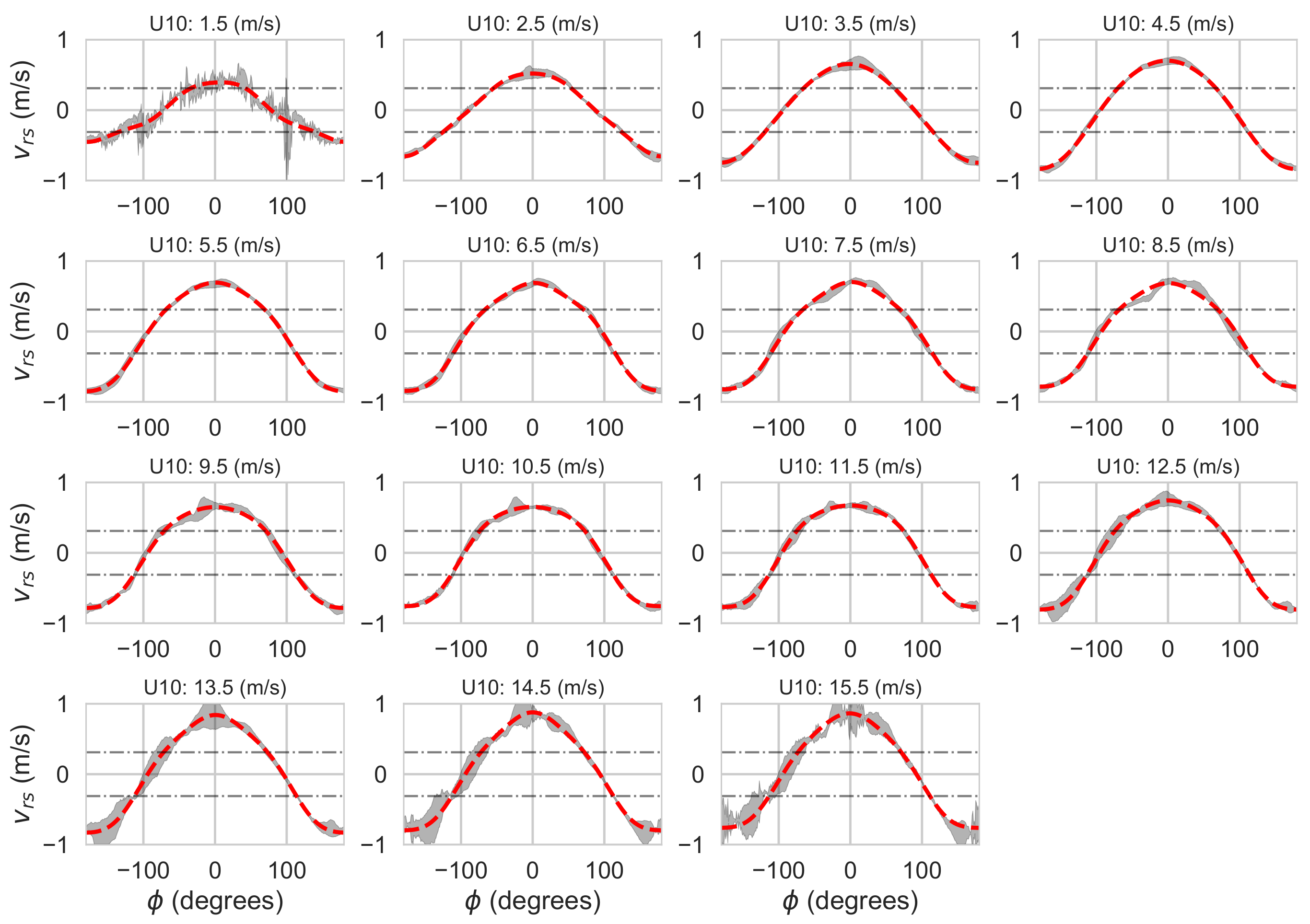
3.2. Wind Geophysical Model Function
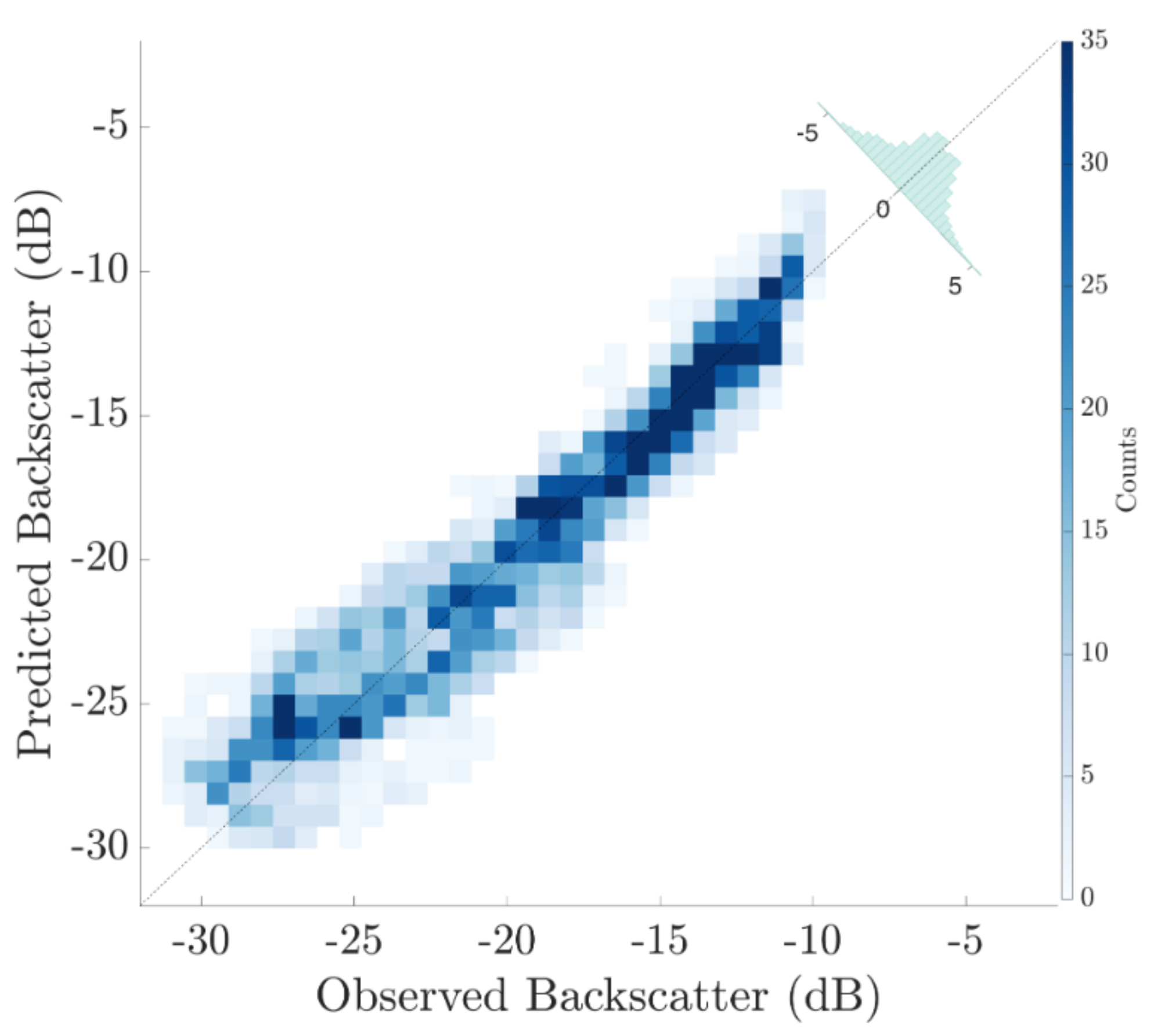
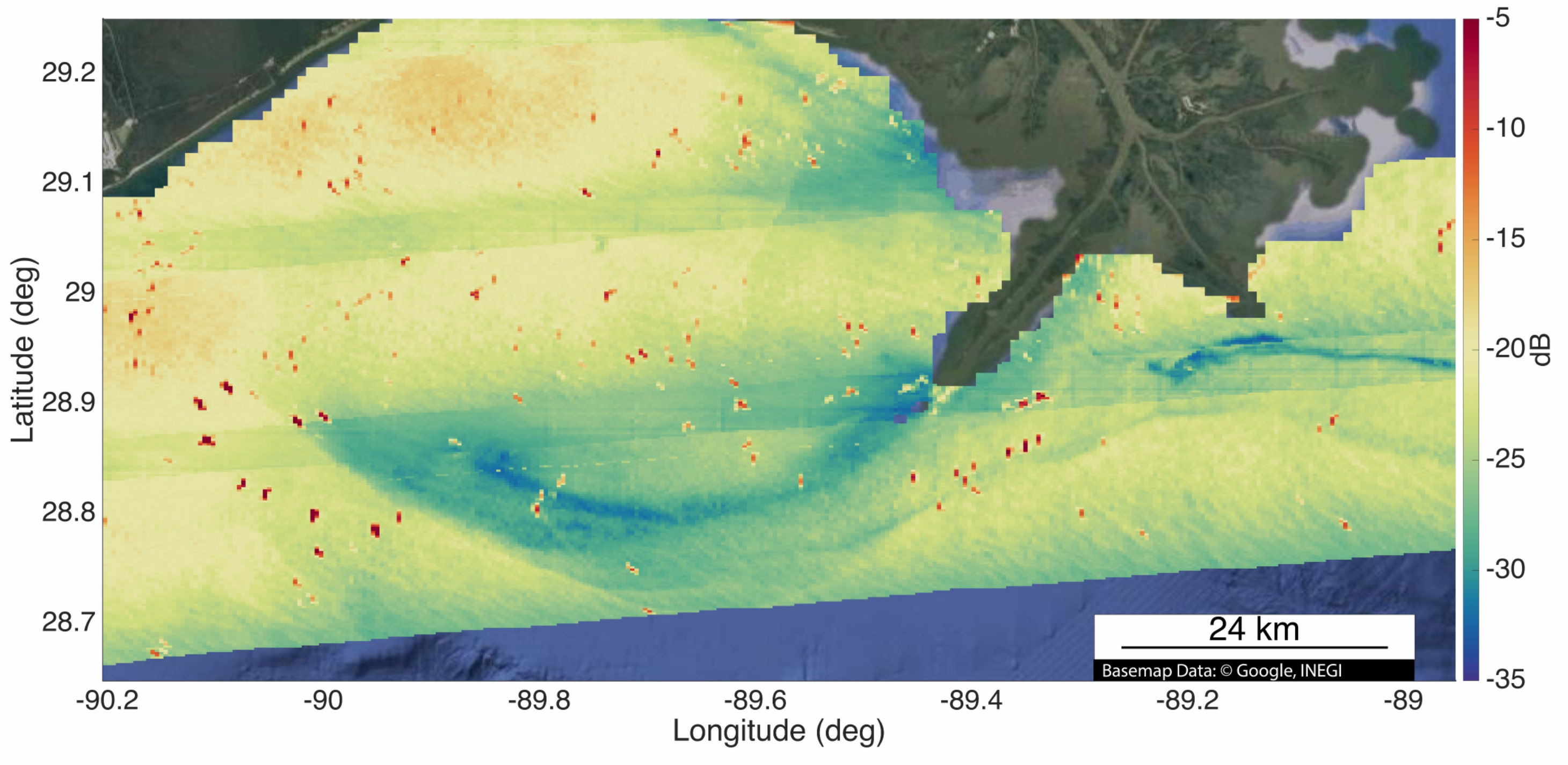
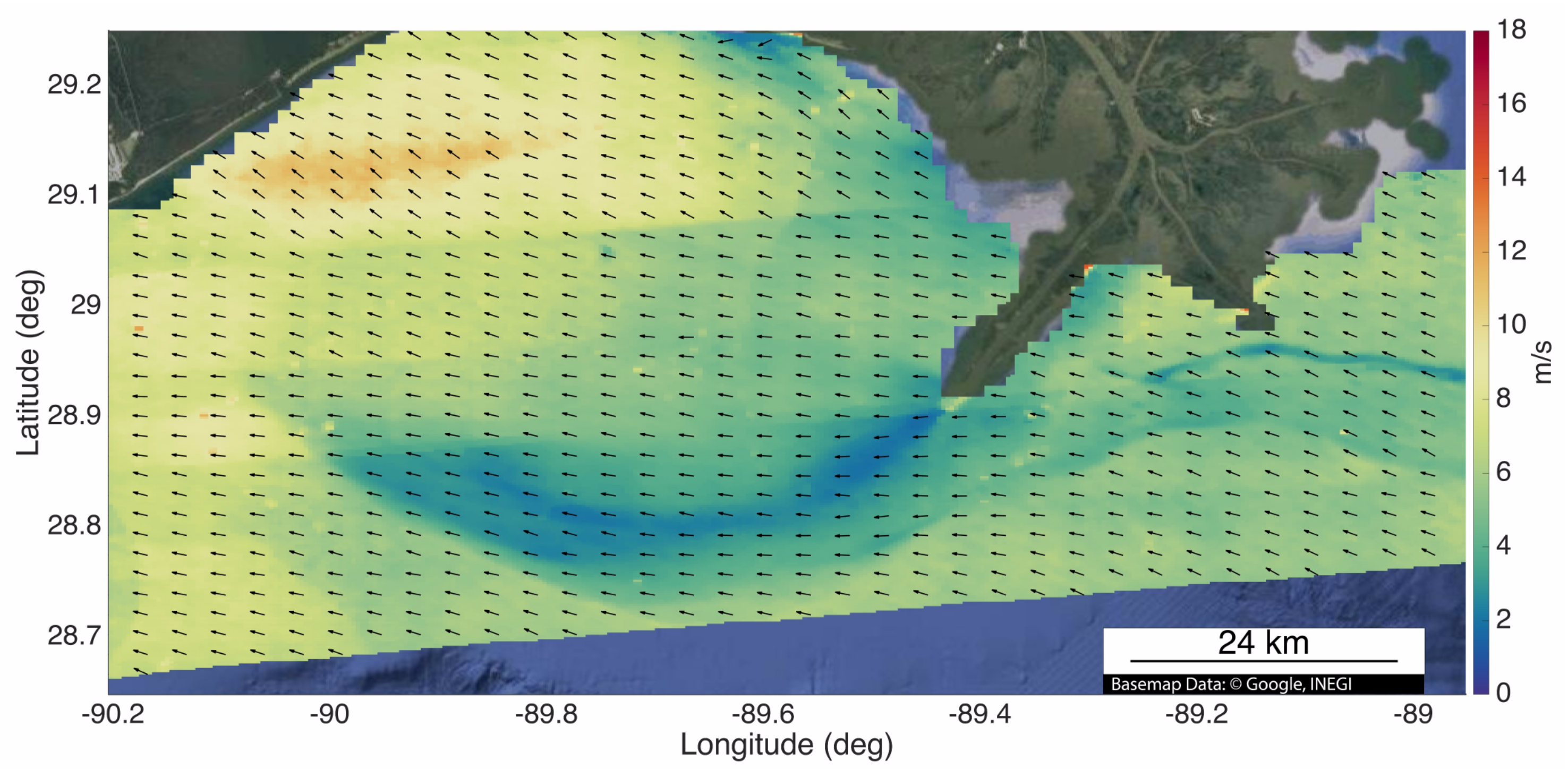
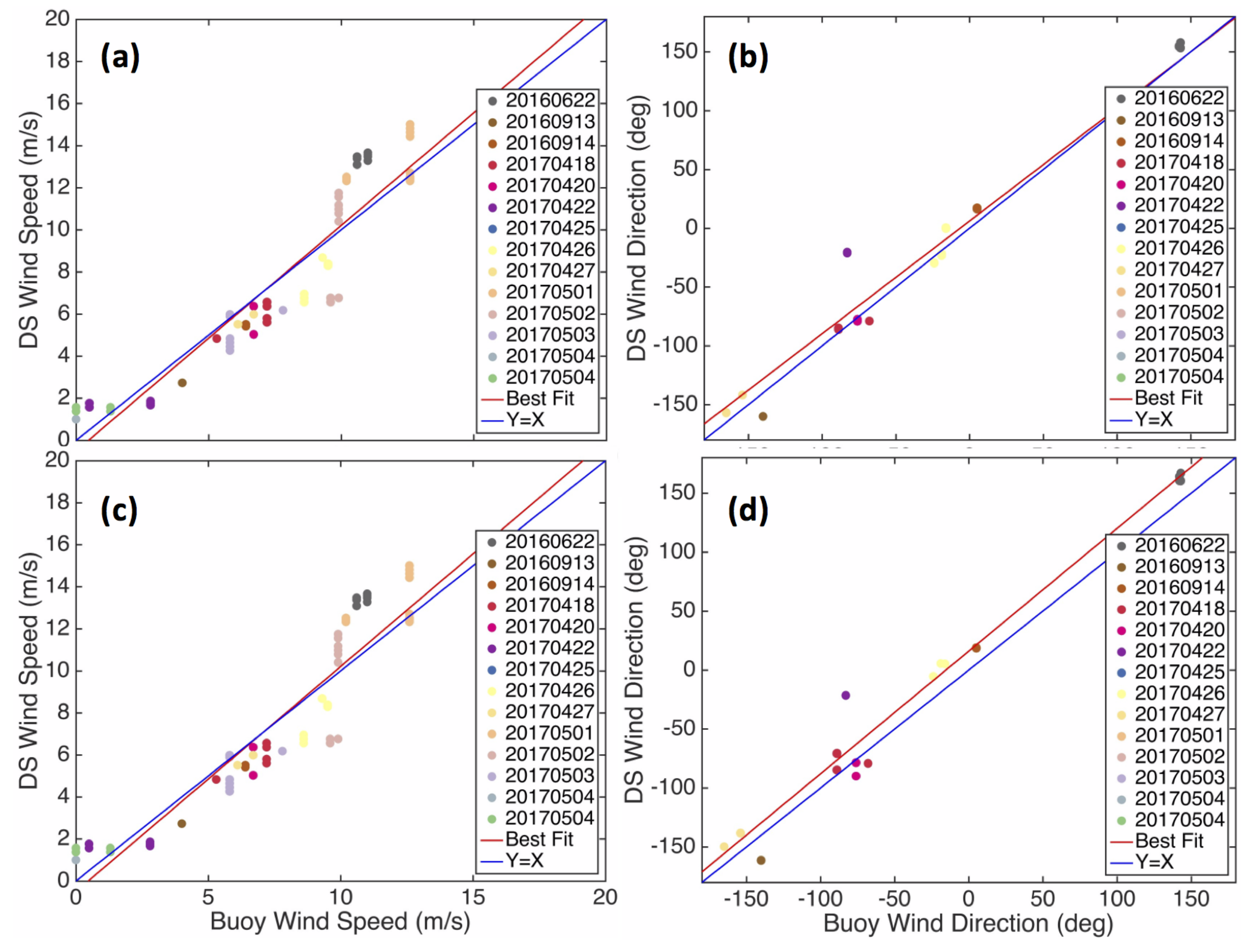
3.3. Wind Retrieval Results
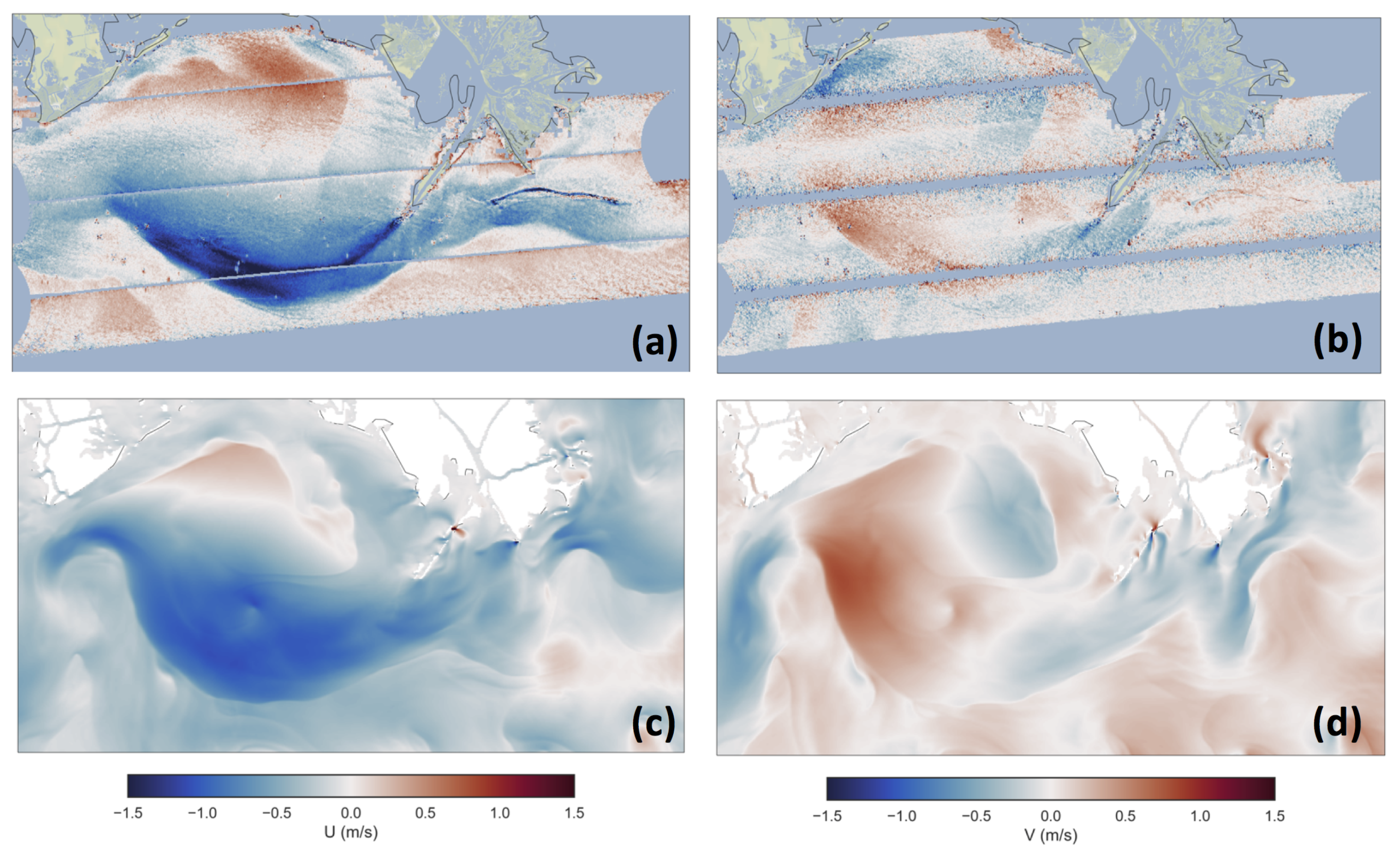
3.4. Surface Current Geophysical Model Function
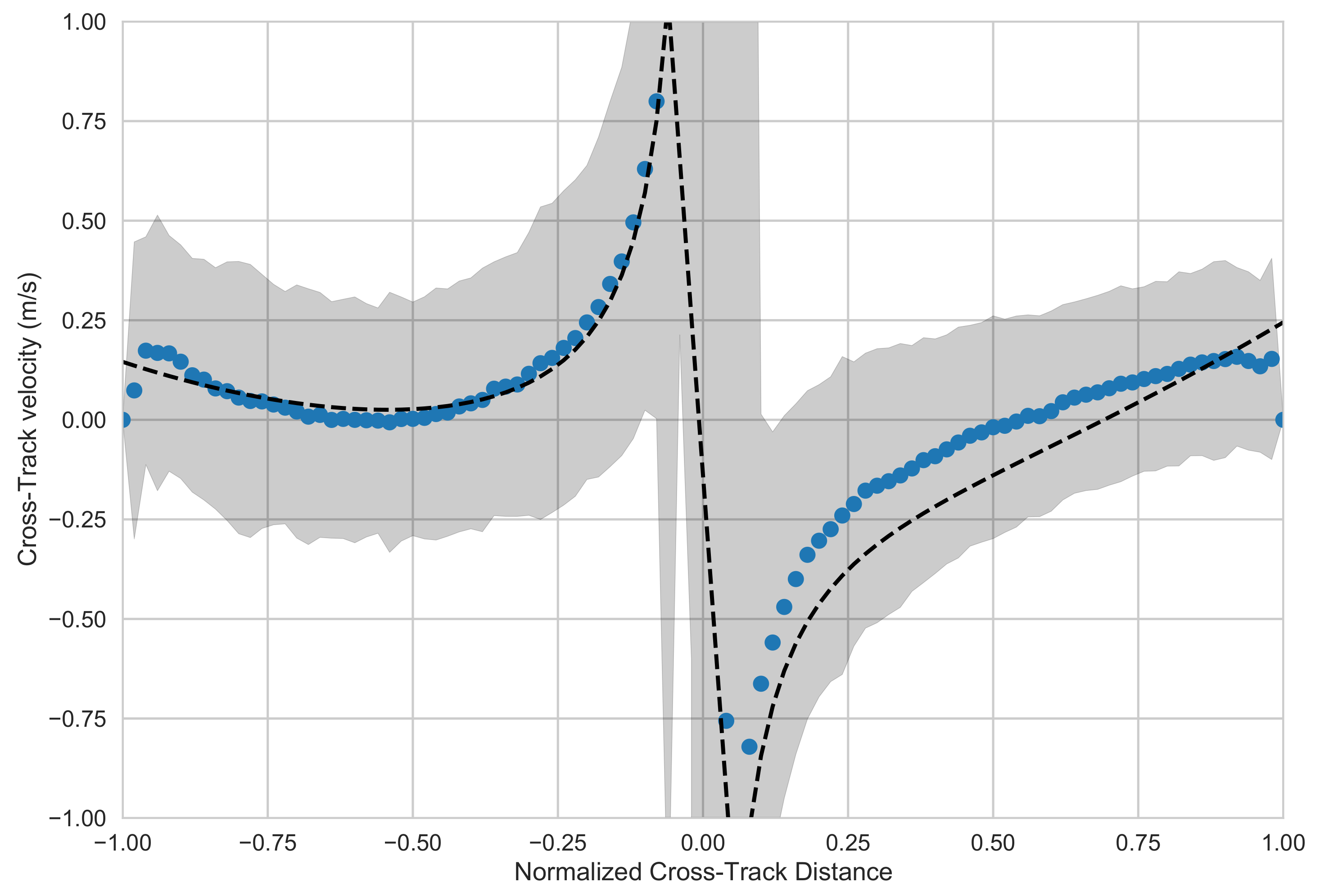
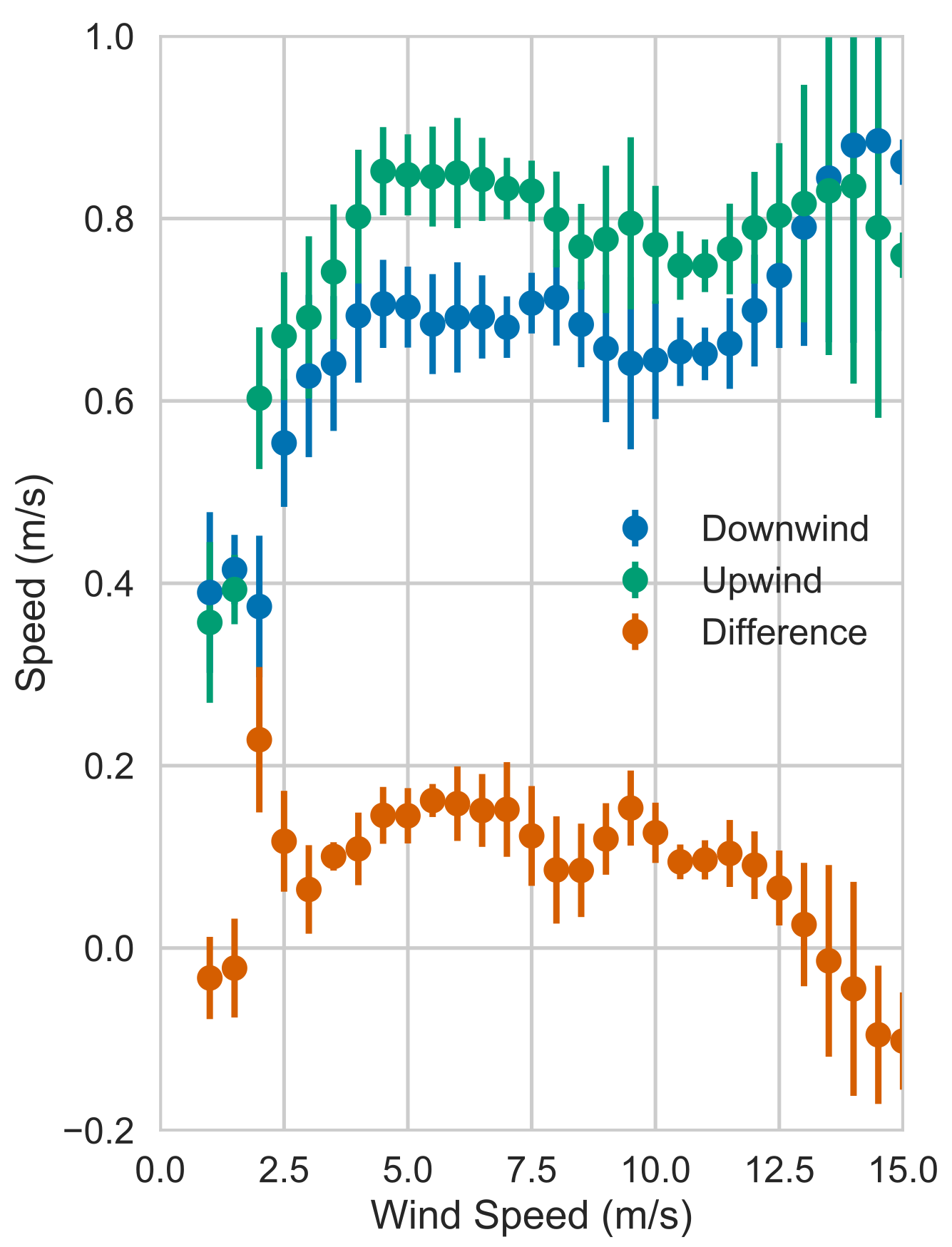
3.5. Ocean Current Retrieval Results
4. Discussion
5. Conclusions
- Development of an end-to-end measurement model including several effects, such as quantifying the impact of cross-section variations, not previously reported.
- Detailed examination of the pulse-pair estimation algorithm, including deriving an error estimator for the Doppler velocity and validating it with experimental data.
- Development of an end-to-end error budget including both random and systematic errors. The error model was validated against measurements and showed that the DopplerScatt instrument had good stability and noise performance for both and Doppler velocities.
- Development of new calibration techniques to remove errors caused by uncertainties in the antenna pointing and other systematic (e.g., model function) errors.
- Development of a wind estimation algorithm that uses backscatter and Doppler velocities in an innovative way so that winds vectors can be estimated using a single beam, rather than the traditional two-beam architecture.
- Determined the ocean correlation time at Ka-band as a function of wind speed. The correlation times observed (>2 ms) indicate that this measurement is scalable to spaceborne applications with reasonable performance.
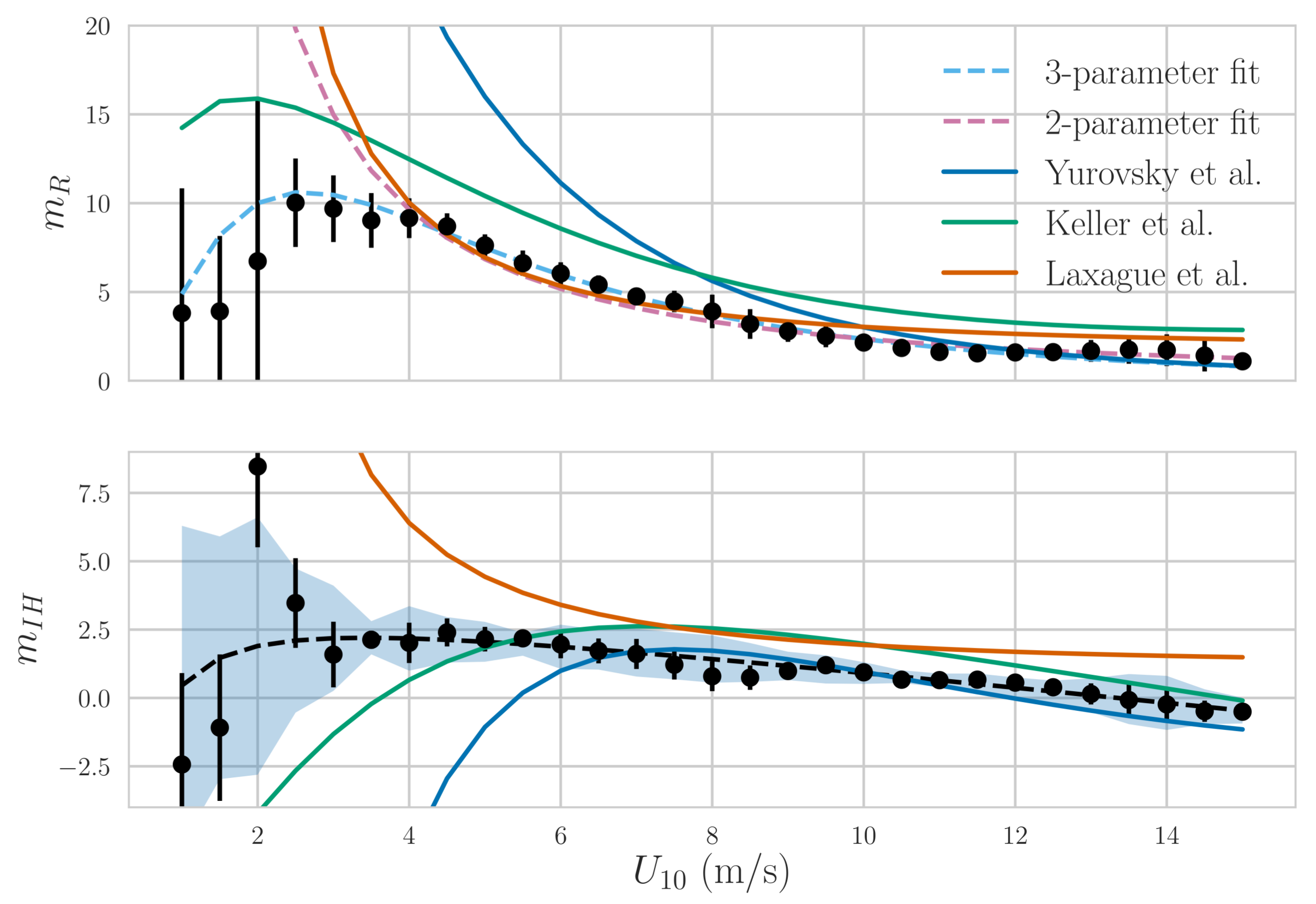
- Developed a Ka-band V-pol GMF which shows an overall sensitivity to wind speed similar to the one predicted by the Ku-band NSCAT GMF. The main difference between the two GMFs is in the much greater upwind cross-wind modulation seen at Ka-band, which will improve wind direction estimation. The observed modulation also exceeds the one observed at Ka-band from a platform in the Black Sea by Yurovsky et al. [23], but, due to platform geometry, the cross-wind sampling may not have been optimal for these incidence angles. Yurovsky et al. also have a global analytic form for their GMF that may constrain the modulation somewhat, and comparisons against actual data points (Yurovsky, personal communication) show better agreement with DopplerScatt observations than the analytic formula. Resolving these discrepancies will require additional data, but the current results, as well as those of Yurovsky et al., show that there is sufficient wind speed and direction sensitivity at Ka-band to obtain wind estimation performance similar to that of Ku-band scatterometers, such as QuikSCAT. Formal errors in the estimated wind speed and direction indicate performance better than spaceborne scatterometers, but the limited comparison against buoy data shows similar performance, possibly pointing to needed improvements in the GMF, possibly including current effects.
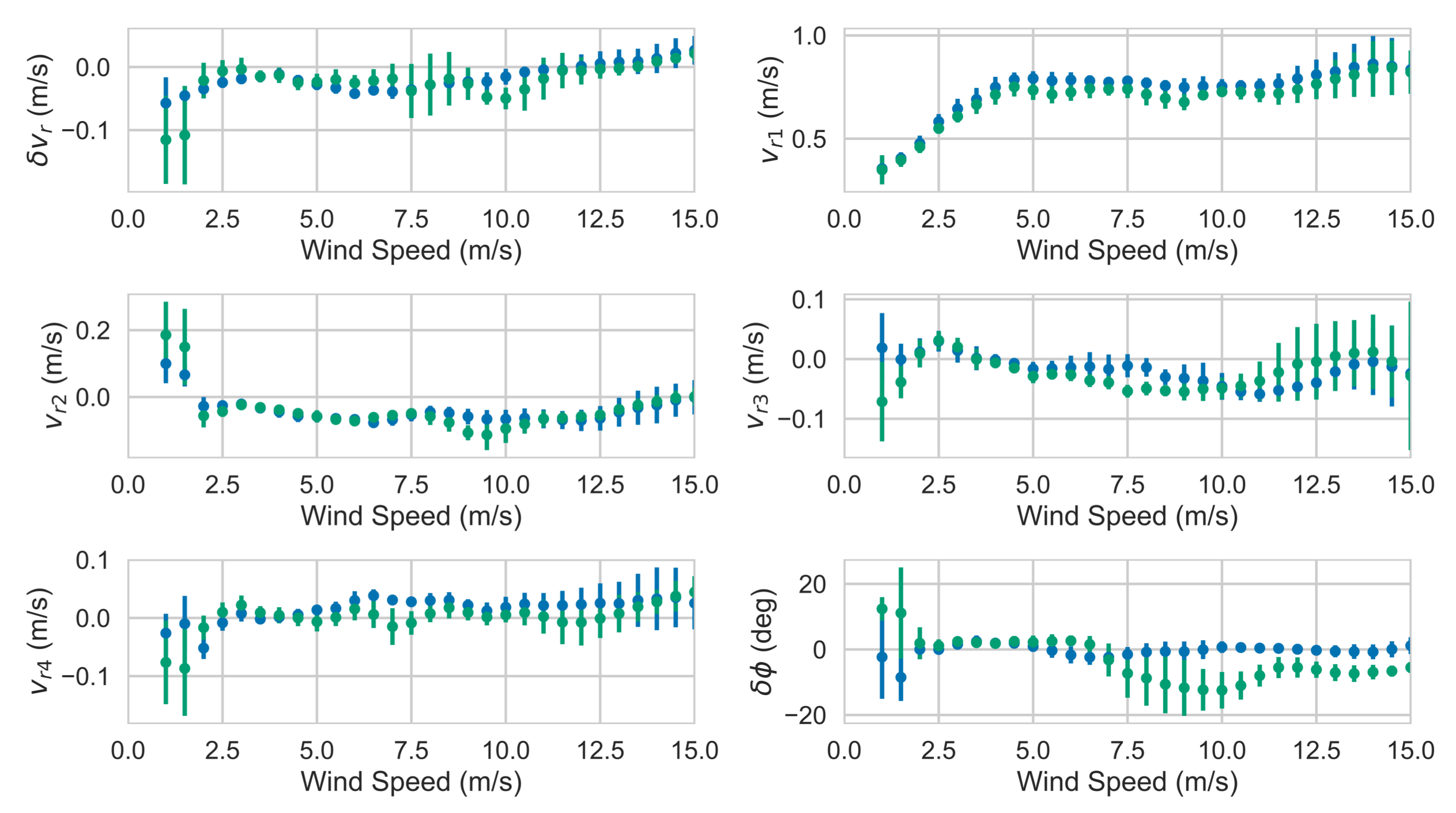
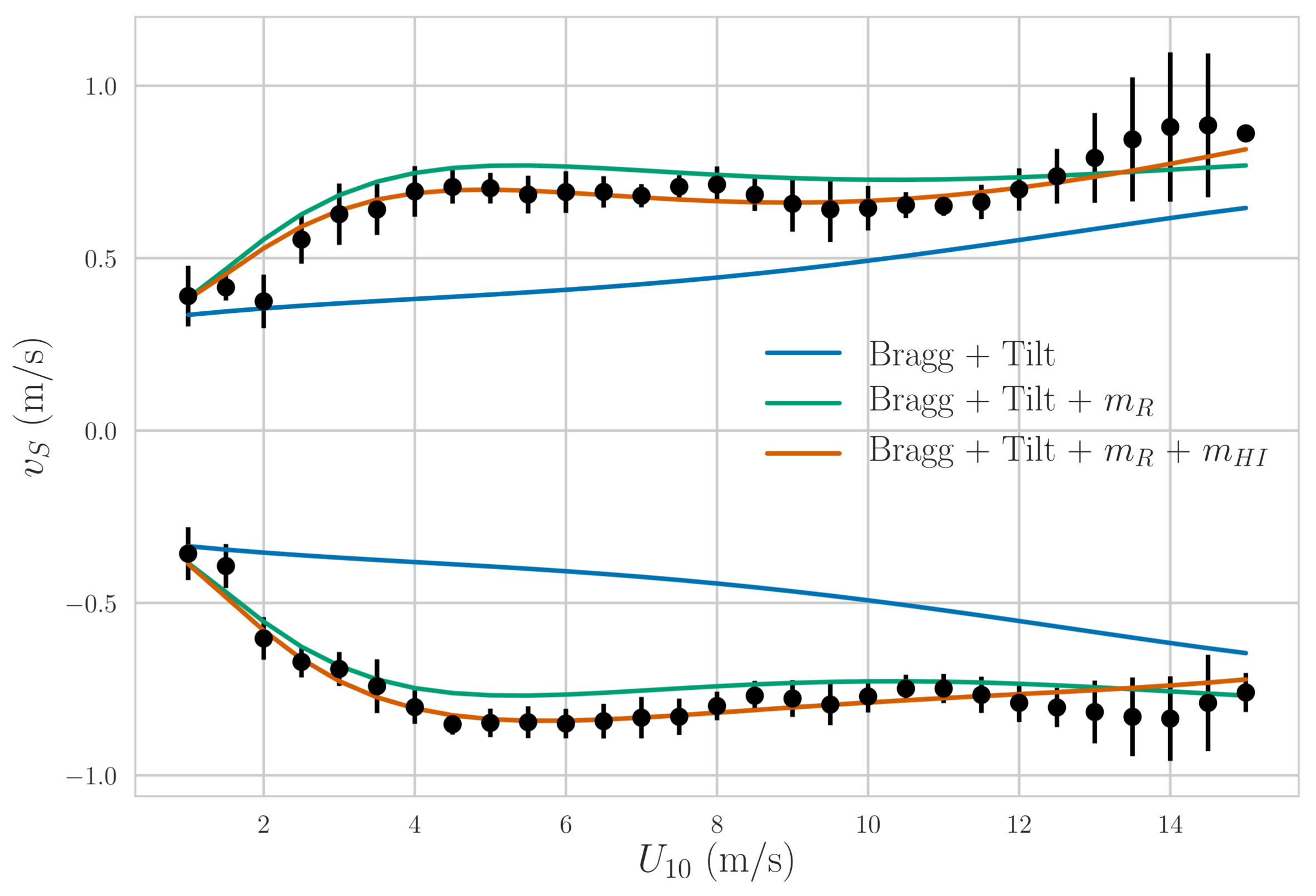
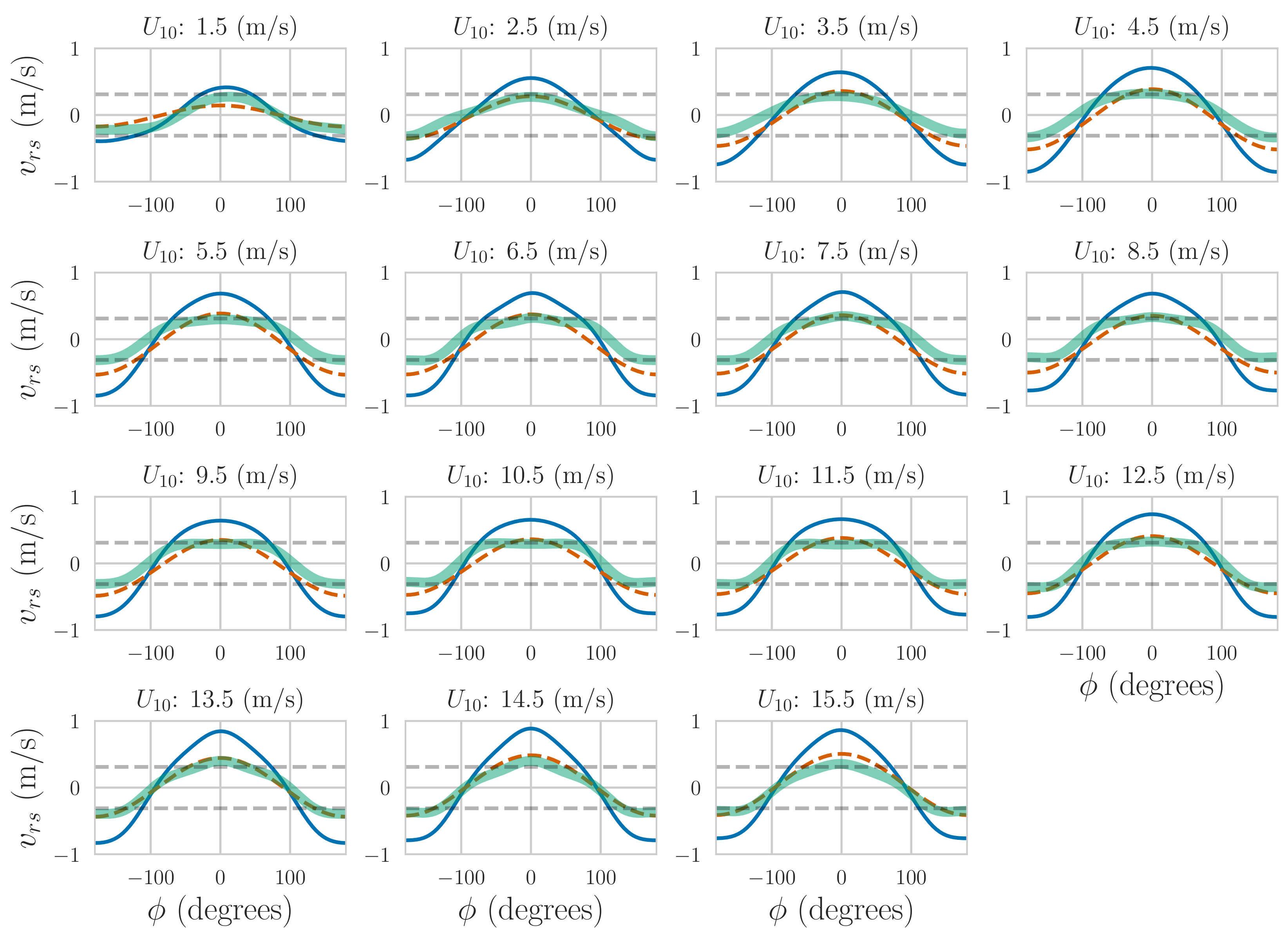
- Examined the local wind dependent part of the Doppler velocity signature. While the signature is roughly aligned with the wind direction, as for other frequencies, it deviates slightly from the true wind direction, in a fashion consistent with expected direction differences consistent with those expected for the sum of Lagrangian and Eulerian wind-driven currents [48]. However, the wind speed dependence of the Doppler currents is quite different from the one observed at C-band [8,13], where the Doppler velocity is nearly linearly dependent on wind speed. By contrast, at Ka-band, there is only a linear dependence for low winds, and the magnitude of the dependence stabilizes after a wind speed of about 4.5 m/s. In addition, the shape of the wind-dependent response is close to a sinusoid with azimuth angle; i.e., the expected response of a constant velocity vector, albeit, one that seems to propagate at a small angle to the wind direction, consistent with wind-drift measurements with HF radars [48]. This behavior was explained as due to the modulation of the backscatter cross section through a modulation transfer function (MTF) consistent with those previously observed at Ka-band. The lack of dependence of the wind correction with respect to wind speed makes the estimation of the non-wind driven part of the surface current much less sensitive to wind speed variations, although still sensitive to wind direction errors. Given that the wind-dependent correction can be made with the same instrument used for estimating the Doppler velocities, this combination is scalable to a spaceborne instrument.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
Appendix B.1. Estimator Derivation
Appendix B.2. Cramér–Rao Bound
Appendix C
| Coefficient | Value | Standard Error |
|---|---|---|
| −54.278 | 6.527 | |
| 0.259 | 0.117 | |
| 16.361 | 8.442 | |
| −0.267 | 0.152 | |
| 15.753 | 9.122 | |
| −0.236 | 0.164 | |
| 39.533 | 6.892 | |
| −0.318 | 0.125 | |
| −25.563 | 8.779 | |
| 0.456 | 0.159 | |
| −6.636 | 9.679 | |
| 0.127 | 0.175 |
Appendix D
| 1.5 | ||||||
| 2.0 | ||||||
| 2.5 | ||||||
| 3.0 | ||||||
| 3.5 | ||||||
| 4.0 | ||||||
| 4.5 | ||||||
| 5.0 | ||||||
| 5.5 | ||||||
| 6.0 | ||||||
| 6.5 | ||||||
| 7.0 | ||||||
| 7.5 | ||||||
| 8.0 | ||||||
| 8.5 | ||||||
| 9.0 | ||||||
| 9.5 | ||||||
| 10.0 | ||||||
| 10.5 | ||||||
| 11.0 | ||||||
| 11.5 | ||||||
| 12.0 | ||||||
| 12.5 | ||||||
| 13.0 | ||||||
| 13.5 | ||||||
| 14.0 | ||||||
| 14.5 | ||||||
| 15.0 | ||||||
| 15.5 |
Appendix E
References
- Kelly, K.; Dickinson, S.; McPhaden, M.; Johnson, G. Ocean Currents Evident in Satellite Wind. Geophys. Res. Lett. 2001, 28, 2469–2472. [Google Scholar] [CrossRef]
- Small, R.J.; deSzoeke, S.P.; Xie, S.P.; O’Neill, L.; Seo, H.; Song, Q.; Cornillon, P.; Spall, M.; Minobe, S. Air-sea interaction over ocean fronts and eddies. Dyn. Atmos. Oceans 2008, 45, 274–319. [Google Scholar] [CrossRef]
- Chelton, D.; Schlax, M.; Samelson, R. Summertime Coupling Between Sea Surface Temperature and Wind Stress in the California Current System. J. Phys. Oceanogr. 2006, 37, 495–517. [Google Scholar] [CrossRef]
- D’Asaro, E.; Lee, C.; Rainville, L.; Harcourt, R.; Thomas, L. Enhanced turbulence and energy dissipation at ocean fronts. Science 2011, 332, 318–322. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.; Zebker, H. Interferometric radar measurement of ocean surface currents. Nature 1987, 328, 707–709. [Google Scholar] [CrossRef]
- Goldstein, R.; Barnett, T.; Zebker, H. Remote sensing of ocean currents. Science 1989, 246, 1282–1285. [Google Scholar] [CrossRef] [PubMed]
- Frasier, S.; Camps, A. Dual-beam interferometry for ocean surface current vector mapping. IEEE Trans. Geosci. Remote Sens. 2001, 39, 401–414. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. 2005, 110, C07008. [Google Scholar] [CrossRef]
- Bao, Q.; Dong, X.; Zhu, D.; Lang, S.; Xu, X. The Feasibility of Ocean Surface Current Measurement Using Pencil-Beam Rotating Scatterometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3441–3451. [Google Scholar] [CrossRef]
- Fois, F.; Hoogeboom, P.; Le Chevalier, F.; Stoffelen, A.; Mouche, A. DopSCAT: A mission concept for simultaneous measurements of marine winds and surface currents. J. Geophys. Res. Oceans 2015, 120, 7857–7879. [Google Scholar] [CrossRef]
- Freeman, A. On ambiguities in SAR design. In Proceedings of the EUSAR 2006: 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006; Jet Propulsion Laboratory: Pasadena, CA, USA; National Aeronautics and Space Administration: Dresden, Germany, 2006. [Google Scholar]
- Madsen, S. Estimating the Doppler centroid of SAR data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 134–140. [Google Scholar] [CrossRef]
- Mouche, A.A.; Collard, F.; Chapron, B.; Dagestad, K.; Guitton, G.; Johannessen, J.A.; Kerbaol, V.; Hansen, M.W. On the use of Doppler shift for sea surface wind retrieval from SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2901–2909. [Google Scholar] [CrossRef]
- Spencer, M.; Wu, C.; Long, D. Improved Resolution Backscatter Measurements with the SeaWinds Pencil-Beam Scatterometer. IEEE Trans. Geosci. Remote Sens. 2000, 38, 89–104. [Google Scholar] [CrossRef]
- Spencer, M.; Tsai, W.; Long, D. High-Resolution Measurements With a Spaceborne Pencil-Beam Scatterometer Using Combined Range/Doppler Discrimination Techniques. IEEE Trans. Geosci. Remote Sens. 2003, 41, 567–581. [Google Scholar] [CrossRef]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: Active and Passive, Vol. III—Volume Scattering and Emission Theory, Advanced Systems and Applications; Addison-Wesley: Dedham, MA, USA, 1986; pp. 1797–1848. [Google Scholar]
- Winebrenner, D.P.; Hasselmann, K. Specular point scattering contribution to the mean synthetic aperture radar image of the ocean surface. J. Geophys. Res. 1988, 93, 9281–9294. [Google Scholar] [CrossRef]
- Romeiser, R.; Thompson, D.R. Numerical study on the along-track interferometric radar imaging mechanism of oceanic surface currents. IEEE Trans. Geosci. Remote Sens. 2000, 38, 446–458. [Google Scholar] [CrossRef]
- Johannessen, J.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations. Geophysi. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Reul, N.; Collard, F. Predicted Doppler shifts induced by ocean surface wave displacements using asymptotic electromagnetic wave scattering theories. Waves Random Complex Media 2008, 18, 185–196. [Google Scholar] [CrossRef]
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Johannessen, J.A.; Collard, F.; Dagestad, K.F.; Mouche, A.A. Simulation of radar backscatter and Doppler shifts of wave—Current interaction in the presence of strong tidal current. Remote Sens. Environ. 2012, 120, 113–122. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C.; Marquez, J.; Doody, S.; Navarro, V.; Buck, C. Wind-wave-induced velocity in ATI SAR ocean surface currents: First experimental evidence from an airborne campaign. J. Geophys. Res. Oceans 2016, 121, 1640–1653. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Dual Copolarized Empirical Model for the Sea Surface Radar Cross Section. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1629–1647. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Normalized Radar Backscattering Cross-Section and Doppler Shifts of the Sea Surface in Ka-band. In Proceedings of the Progress in Electromagnetics Research Symposium—Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017. [Google Scholar]
- Rodríguez, E.; Martin, J.M. Theory and design of interferometric synthetic aperture radars. IEE Proc. F 1992, 139, 147–159. [Google Scholar] [CrossRef]
- Kay, S. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice Hall Signal Processing Series; Prentice Hall: Upper Saddle River, NJ, USA, 1993; Volume 1. [Google Scholar]
- Schaeffer, P.; Faugere, Y.; Legeais, J.; Ollivier, A.; Guinle, T.; Picot, N. The CNES_CLS11 global mean sea surface computed from 16 years of satellite altimeter data. Mar. Geodesy 2012, 35, 3–19. [Google Scholar] [CrossRef]
- Ardhuin, F.; Aksenov, Y.; Benetazzo, A.; Bertino, L.; Brandt, P.; Caubet, E.; Chapron, B.; Collard, F.; Cravatte, S.; Dias, F.; et al. Measuring currents, ice drift, and waves from space: The Sea Surface KInematics Multiscale monitoring (SKIM) concept. Ocean Sci. Discuss. 2017, 2017, 1–26. [Google Scholar] [CrossRef]
- Plant, W.J. A two-scale model of short wind-generated waves and scatterometry. J. Geophys. Res. Oceans 1986, 91, 10735–10749. [Google Scholar] [CrossRef]
- Plant, W.J. A model for microwave Doppler sea return at high incidence angles: Bragg scattering from bound, tilted waves. J. Geophys. Res. 1997, 102, 21131–21146. [Google Scholar] [CrossRef]
- Plant, W.J.; Irisov, V. A joint active/passive physical model of sea surface microwave signatures. J. Geophys. Res. Oceans 2017, 122, 3219–3239. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross-section of the sea surface 1. Background model. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Draper, D.W.; Long, D.G. An assessment of SeaWinds on QuikSCAT wind retrieval. J. Geophys. Res. Oceans 2002, 107. [Google Scholar] [CrossRef]
- Stiles, B.W.; Pollard, B.D.; Dunbar, R.S. Direction interval retrieval with thresholded nudging: A method for improving the accuracy of QuikSCAT winds. IEEE Trans. Geosci. Remote Sens. 2002, 40, 79–89. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Freilich, M.H.; Legler, D.M.; Liu, W.T.; O’Brien, J.J. Wind observations from new satellite and research vessels agree. EOS Trans. Am. Geophys. Union 1997, 78, 597–602. [Google Scholar] [CrossRef]
- Verron, J.; Sengenes, P.; Lambin, J.; Noubel, J.; Steunou, N.; Guillot, A.; Picot, N.; Coutin-Faye, S.; Sharma, R.; Gairola, R.M.; et al. The SARAL/AltiKa Altimetry Satellite Mission. Mar. Geodesy 2015, 38, 2–21. [Google Scholar] [CrossRef]
- Wentz, F.J.; Mattox, L.A.; Peteherych, S. New algorithms for microwave measurements of ocean winds: Applications to Seasat and the special sensor microwave imager. J. Geophys. Res. Oceans 1986, 91, 2289–2307. [Google Scholar] [CrossRef]
- Wentz, F.J.; Smith, D.K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations. J. Geophys. Res. Oceans 1999, 104, 11499–11514. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; de Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Ricciardulli, L.; Wentz, F.J. A Scatterometer Geophysical Model Function for Climate-Quality Winds: QuikSCAT Ku-2011. J. Atmos. Ocean. Technol. 2015, 32, 1829–1846. [Google Scholar] [CrossRef]
- Masuko, H.; Okamoto, K.; Shimada, M.; Niwa, S. Measurement of microwave backscattering signatures of the ocean surface using X band and Ka band airborne scatterometers. J. Geophys. Res. Oceans 1986, 91, 13065–13083. [Google Scholar] [CrossRef]
- Walsh, E.J.; Vandemark, D.C.; Friehe, C.A.; Burns, S.P.; Khelif, D.; Swift, R.N.; Scott, J.F. Measuring sea surface mean square slope with a 36-GHz scanning radar altimeter. J. Geophys. Res. Oceans 1998, 103, 12587–12601. [Google Scholar] [CrossRef]
- Tanelli, S.; Durden, S.L.; Im, E. Simultaneous measurements of ku- and ka-band sea surface cross sections by an airborne Radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 359–363. [Google Scholar] [CrossRef]
- Vandemark, D.; Chapron, B.; Sun, J.; Crescenti, G.H.; Graber, H.C. Ocean Wave Slope Observations Using Radar Backscatter and Laser Altimeters. J. Phys. Oceanogr. 2004, 34, 2825–2842. [Google Scholar] [CrossRef]
- Donnelly, W.J.; Carswell, J.R.; McIntosh, R.E.; Chang, P.S.; Wilkerson, J.; Marks, F.; Black, P.G. Revised ocean backscatter models at C and Ku band under high-wind conditions. J. Geophys. Res. Oceans 1999, 104, 11485–11497. [Google Scholar] [CrossRef]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: Active and Passive. Volume I: Microwave Remote Sensing Fundamentals and Radiometry; Remote Sensing Series 2; Addison-Wesley: Boston, MA, USA, 1981. [Google Scholar]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. The Effects of SST-Induced Surface Wind Speed and Direction Gradients on Midlatitude Surface Vorticity and Divergence. J. Clim. 2010, 23, 255–281. [Google Scholar] [CrossRef]
- Ardhuin, F.; Marié, L.; Rascle, N.; Forget, P.; Roland, A. Observation and estimation of Lagrangian, Stokes, and Eulerian currents induced by wind and waves at the sea surface. J. Phys. Oceanogr. 2009, 39, 2820–2838. [Google Scholar] [CrossRef]
- Moller, D.; Frasier, S.J.; Porter, D.L.; McIntosh, R.E. Radar-derived interferometric surface currents and their relationship to subsurface current structure. J. Geophys. Res. Oceans 1998, 103, 12839–12852. [Google Scholar] [CrossRef]
- Laxague, N.J.; Haus, B.K.; Ortiz-Suslow, D.G.; Smith, C.J.; Novelli, G.; Dai, H.; Özgökmen, T.; Graber, H.C. Passive Optical Sensing of the Near-Surface Wind-Driven Current Profile. J. Atmos. Ocean. Technol. 2017, 34, 1097–1111. [Google Scholar] [CrossRef]
- Wu, J. Wind-induced drift currents. J. Fluid Mech. 1975, 68, 49–70. [Google Scholar] [CrossRef]
- Jenkins, A.D. Wind and wave induced currents in a rotating sea with depth-varying eddy viscosity. J. Phys. Oceanogr. 1987, 17, 938–951. [Google Scholar] [CrossRef]
- Broche, P.; Demaistre, J.; Forget, P. Mesure par radar décamétrique cohérent des courants superficiels engendrés par le vent. Oceanol. Acta 1983, 6, 43–53. [Google Scholar]
- Stewart, R.H.; Joy, J.W. HF Radio Measurements of Surface Currents; Deep Sea Research and Oceanographic Abstracts; Elsevier: New York, NY, USA, 1974; Volume 21, pp. 1039–1049. [Google Scholar]
- Efron, B.; Stein, C. The jackknife estimate of variance. Ann. Stat. 1981, 9, 586–596. [Google Scholar] [CrossRef]
- Rowley, C.; Mask, A. Regional and Coastal Prediction with the Relocatable Ocean Nowcast/Forecast System. Oceanography 2014, 27, 44–45. [Google Scholar] [CrossRef]
- Keller, W.C.; Wright, J.W. Microwave scattering and the straining of wind-generated waves. Radio Sci. 1975, 10, 139–147. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of Ka-band Doppler Radar Signals Backscattered from Sea Surface. IEEE Trans. Geosci. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Alpers, W.; Hasselmann, K. The two-frequency microwave technique for measuring ocean-wave spectra from an airplane or satellite. Bound. Layer Meteorol. 1978, 13, 215–230. [Google Scholar] [CrossRef]
- Hansen, M.; Collard, F.; Dagestad, K.F.; Johannessen, J.A.; Fabry, P.; Chapron, B. Retrieval of Sea Surface Range Velocities from Envisat ASAR Doppler Centroid Measurements. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3582–3592. [Google Scholar] [CrossRef]
- Santala, M.J.; Terray, E.A. A technique for making unbiased estimates of current shear from a wave-follower. Deep Sea Res. Part A Oceanogr. Res. Pap. 1992, 39, 607–622. [Google Scholar] [CrossRef]
- Keller, W.; Plant, W.; Petitt, R.; Terray, E. Microwave backscatter from the sea: Modulation of received power and Doppler bandwidth by long waves. J. Geophys. Res. Oceans 1994, 99, 9751–9766. [Google Scholar] [CrossRef]
- Laxague, N.J.; Curcic, M.; Björkqvist, J.V.; Haus, B.K. Gravity-capillary wave spectral modulation by gravity waves. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2477–2485. [Google Scholar] [CrossRef]
- Goodman, J. Statistical Optics; Wiley-Interscience: New York, NY, USA, 1985. [Google Scholar]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. Oceans 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Tayfun, M.A. On narrow-band representation of ocean waves: 1. Theory. J. Geophys. Res. Oceans 1986, 91, 7743–7752. [Google Scholar] [CrossRef]
- Chen, P.; Wang, X.; Liu, L.; Chong, J. A coupling modulation model of capillary waves from gravity waves: Theoretical analysis and experimental validation. J. Geophys. Res. Oceans 2016, 121, 4228–4244. [Google Scholar] [CrossRef]
- Feindt, F.; Schroeter, J.; Alpers, W. Measurement of the ocean wave-radar modulation transfer function at 35 GHz from a sea-based platform in the North Sea. J. Geophys. Res. Oceans 1986, 91, 9701–9708. [Google Scholar] [CrossRef]
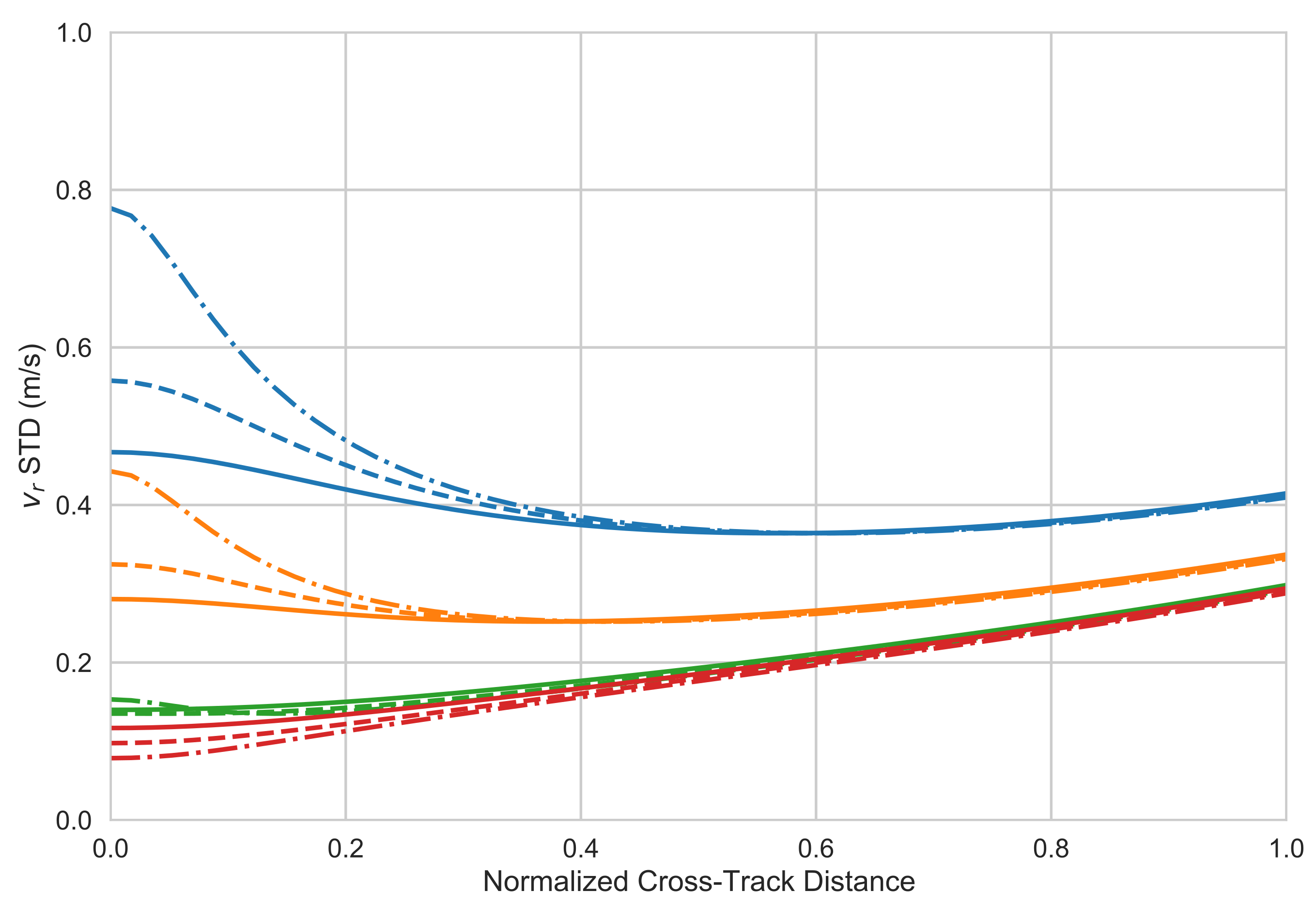
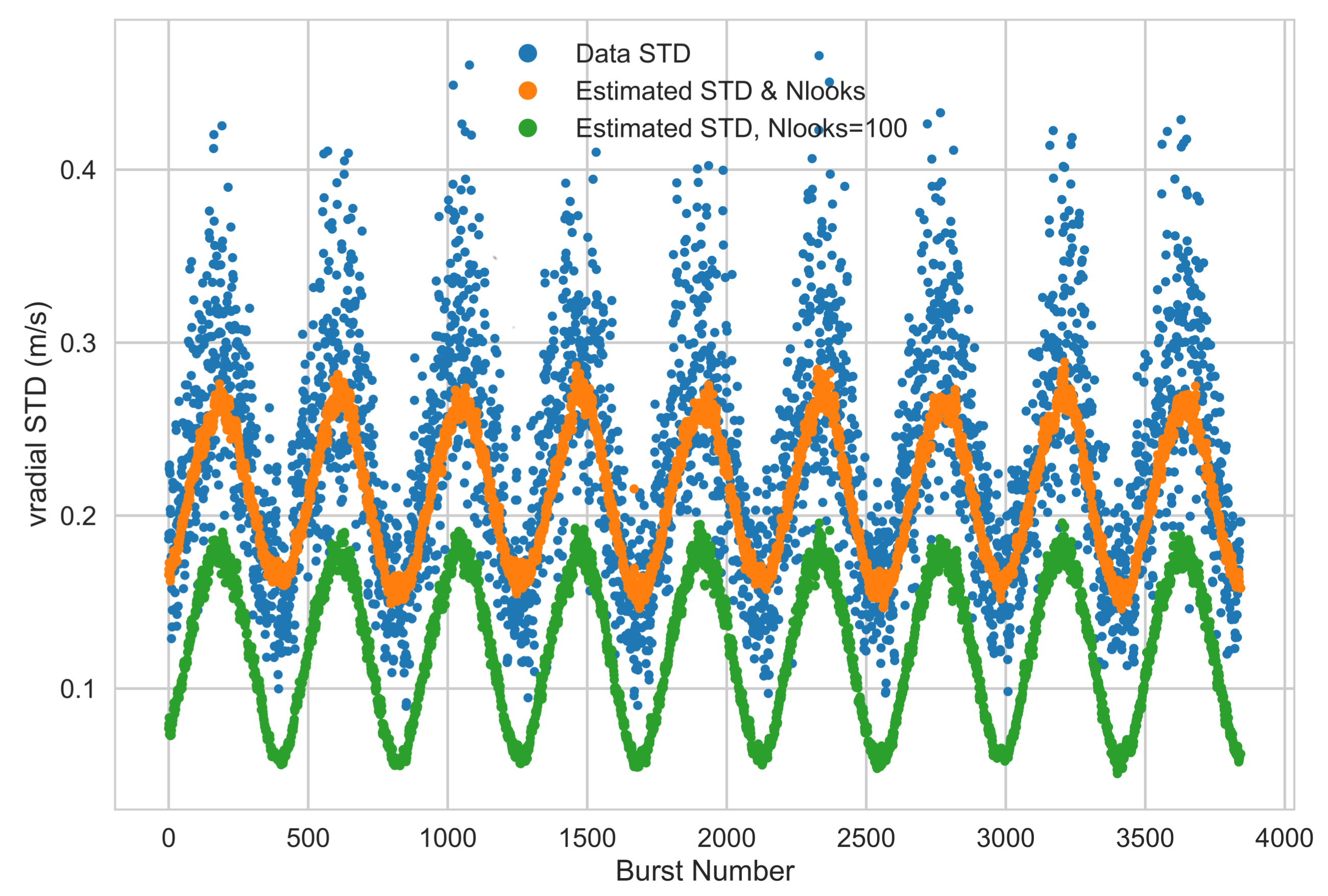
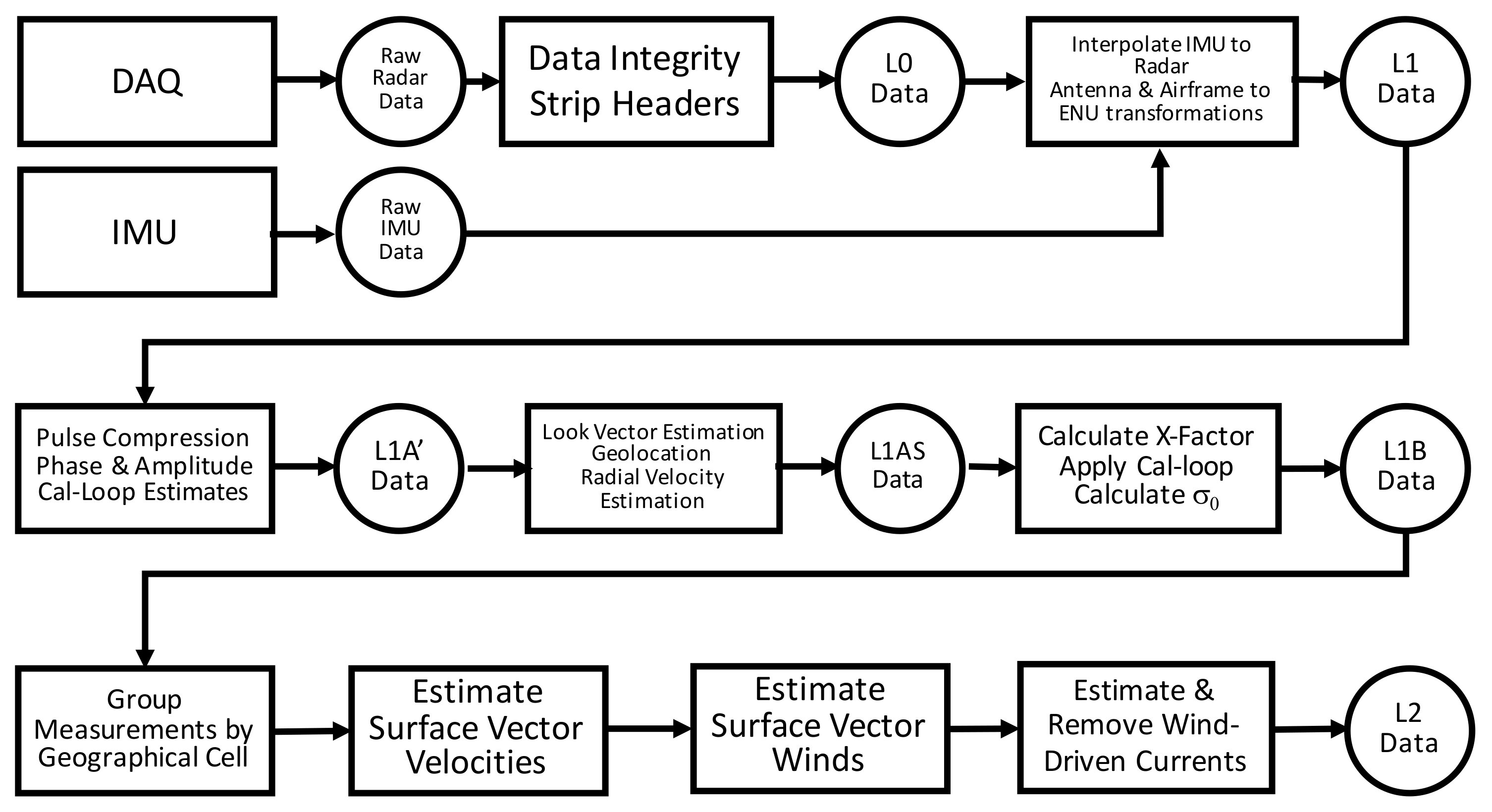
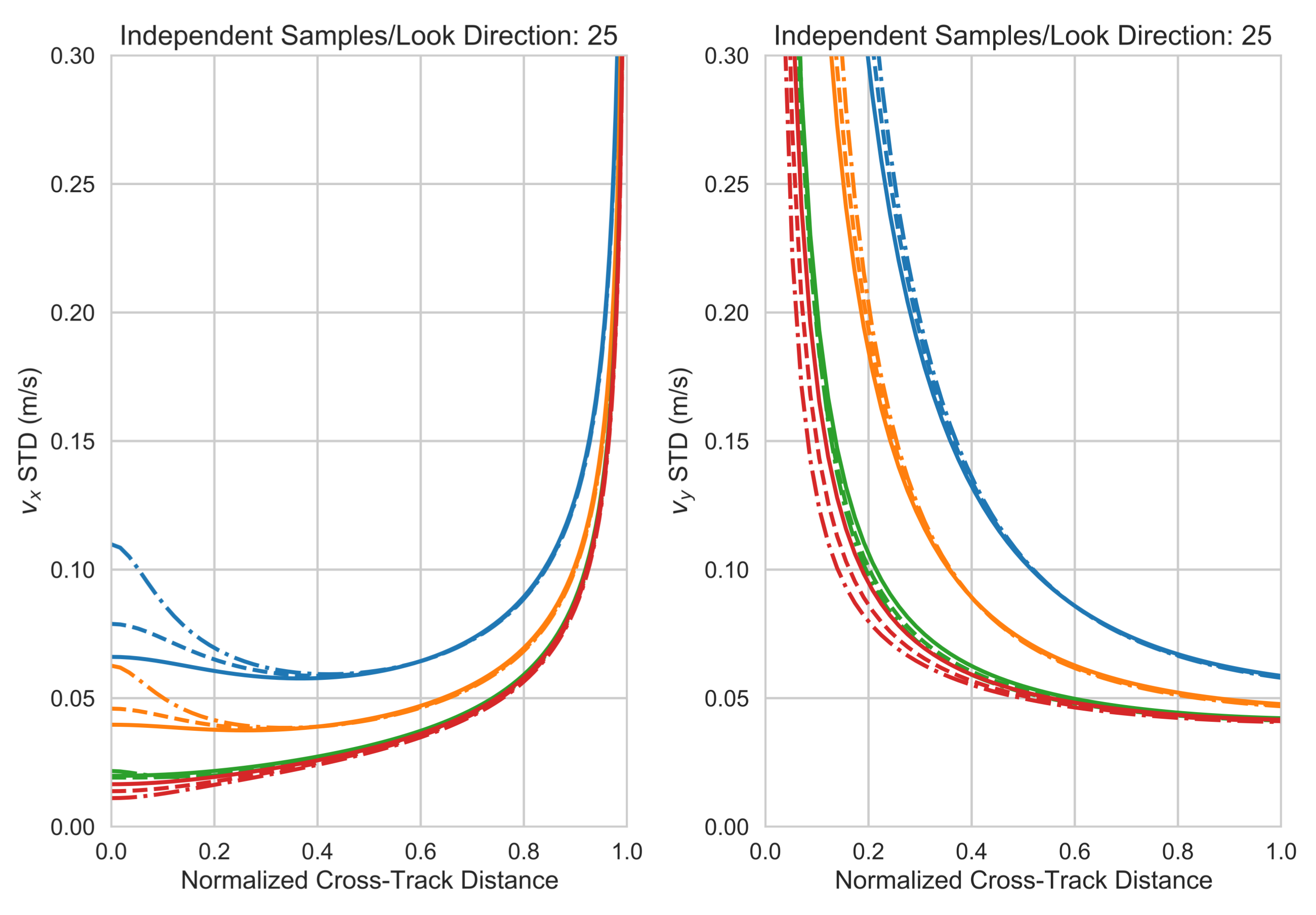
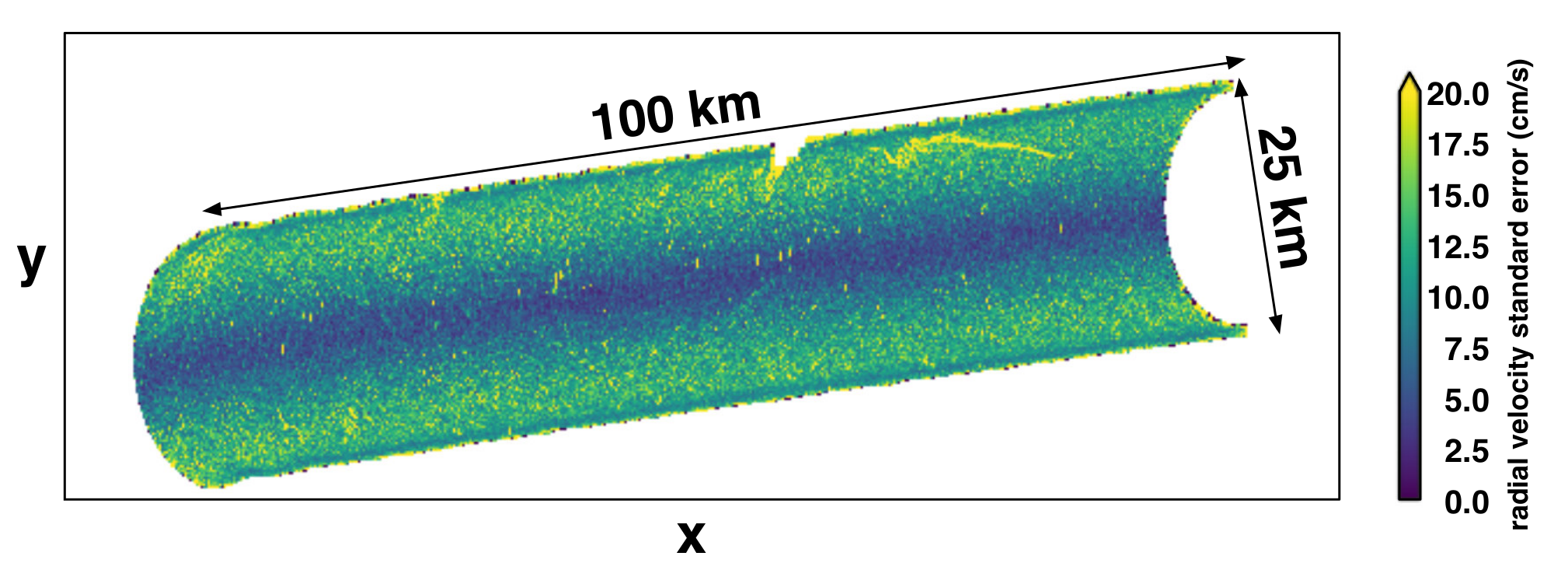

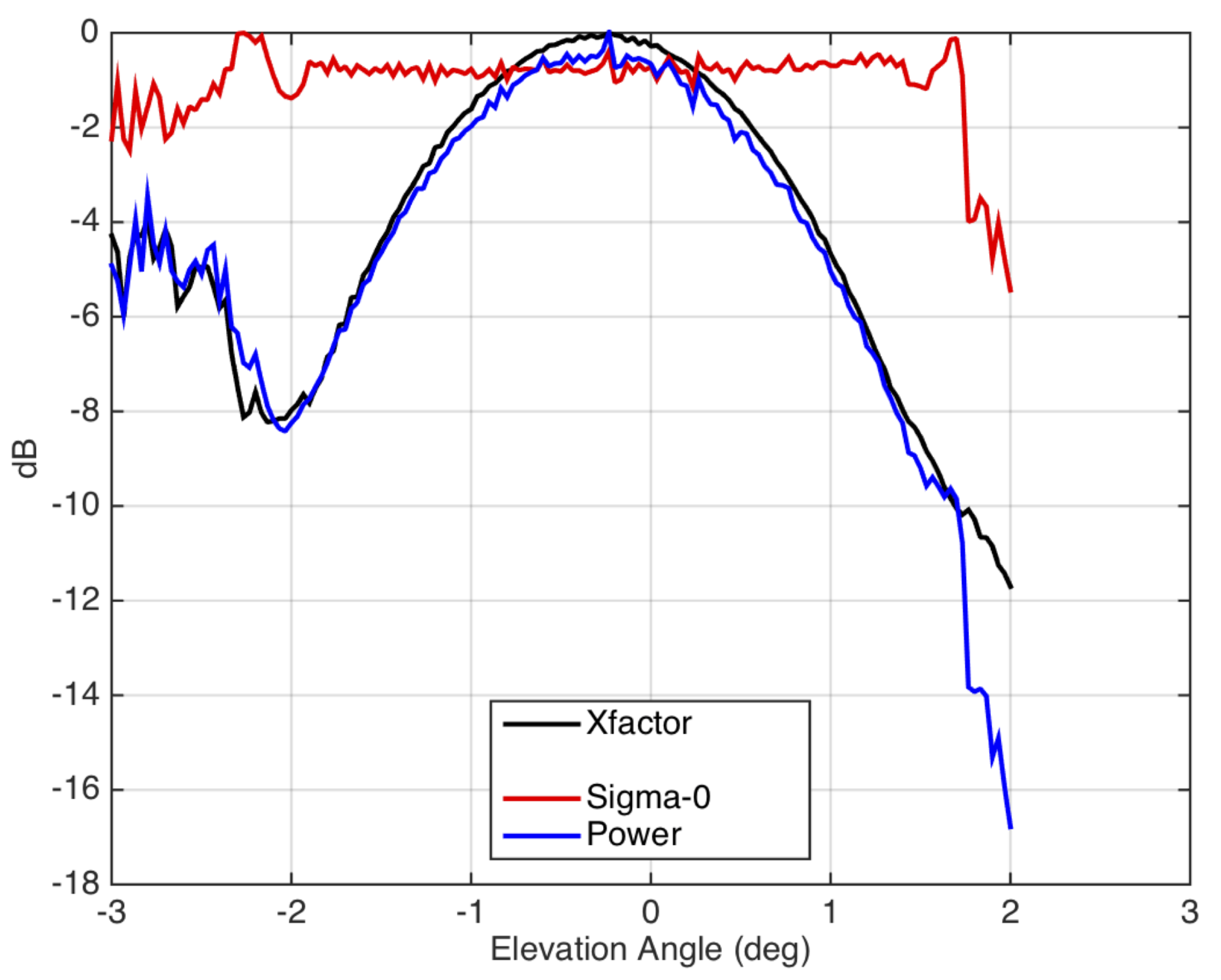

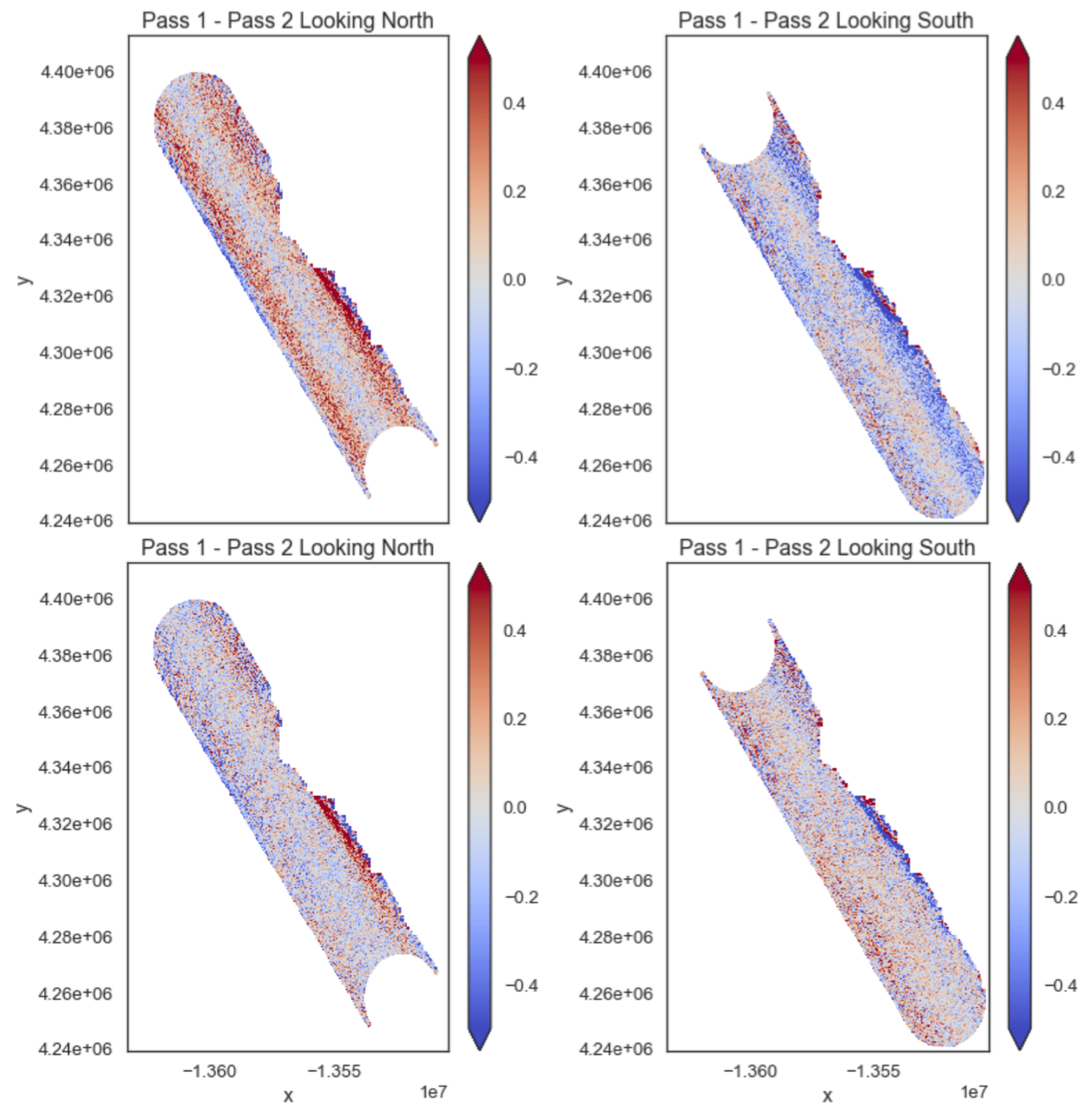
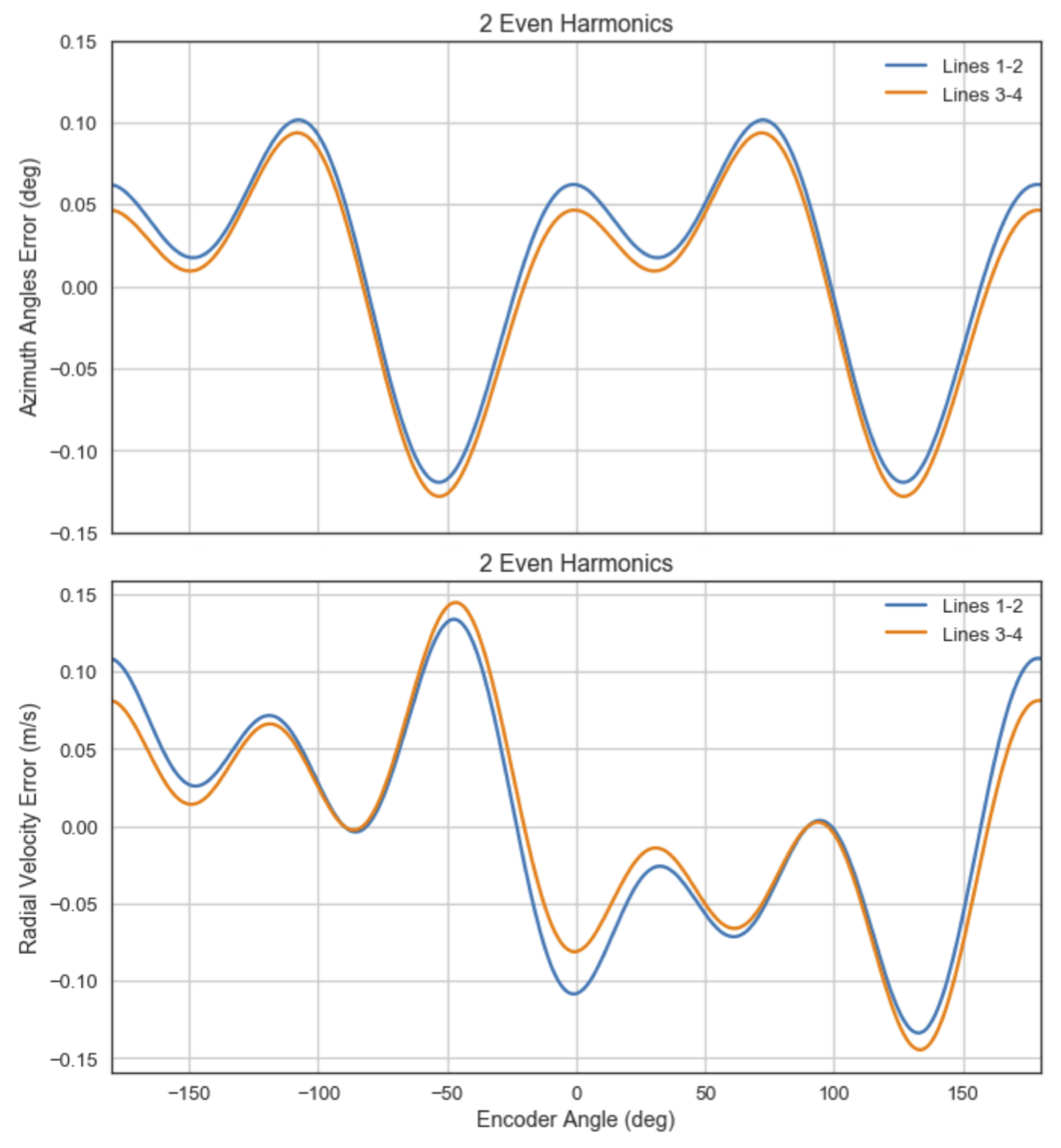

| Parameter | Value |
|---|---|
| Peak Power | 100 W |
| 3 dB Azimuth Beamwidth | |
| 3 dB Azimuth Footprint | 600 m |
| 3 dB Elevation Beamwidth | |
| 3 dB Elevation Footprint | 1.4 km |
| Nominal boresight angle | |
| Burst Repetition Frequency | 4.5 kHz |
| Inter-pulse Period | 18.4 s |
| Chirp length | 6.4 s |
| Pulses per burst | 4 |
| Pulse Bandwidth | 5 MHz |
| Azimuth Looks | 100 |
| Range Resolution | 30 m |
| Resolution in Elevation | 36.2 m |
| Resolution in Azimuth | 485 m |
| Nominal Platform Altitude | 8.53 km |
| Nominal Swath | 25 km |
| Scan Rate | 12 RPM |
| Noise Equivalent | −37 dB |
| Parameter | Accuracy |
|---|---|
| True Heading | 5 mdeg |
| Roll & Pitch | 2.5 mdeg |
| Attitude Drift | <0.01 deg/h |
| Velocity | 0.5 cm/s |
| Horizontal Position | <10 cm |
| Vertical Position | <20 cm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.W.; Niamsuwan, N.; Rodriguez Monje, R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. https://doi.org/10.3390/rs10040576
Rodríguez E, Wineteer A, Perkovic-Martin D, Gál T, Stiles BW, Niamsuwan N, Rodriguez Monje R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sensing. 2018; 10(4):576. https://doi.org/10.3390/rs10040576
Chicago/Turabian StyleRodríguez, Ernesto, Alexander Wineteer, Dragana Perkovic-Martin, Tamás Gál, Bryan W. Stiles, Noppasin Niamsuwan, and Raquel Rodriguez Monje. 2018. "Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer" Remote Sensing 10, no. 4: 576. https://doi.org/10.3390/rs10040576
APA StyleRodríguez, E., Wineteer, A., Perkovic-Martin, D., Gál, T., Stiles, B. W., Niamsuwan, N., & Rodriguez Monje, R. (2018). Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sensing, 10(4), 576. https://doi.org/10.3390/rs10040576






