A Consistent Combination of Brightness Temperatures from SMOS and SMAP over Polar Oceans for Sea Ice Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. SMOS
2.1.2. SMAP
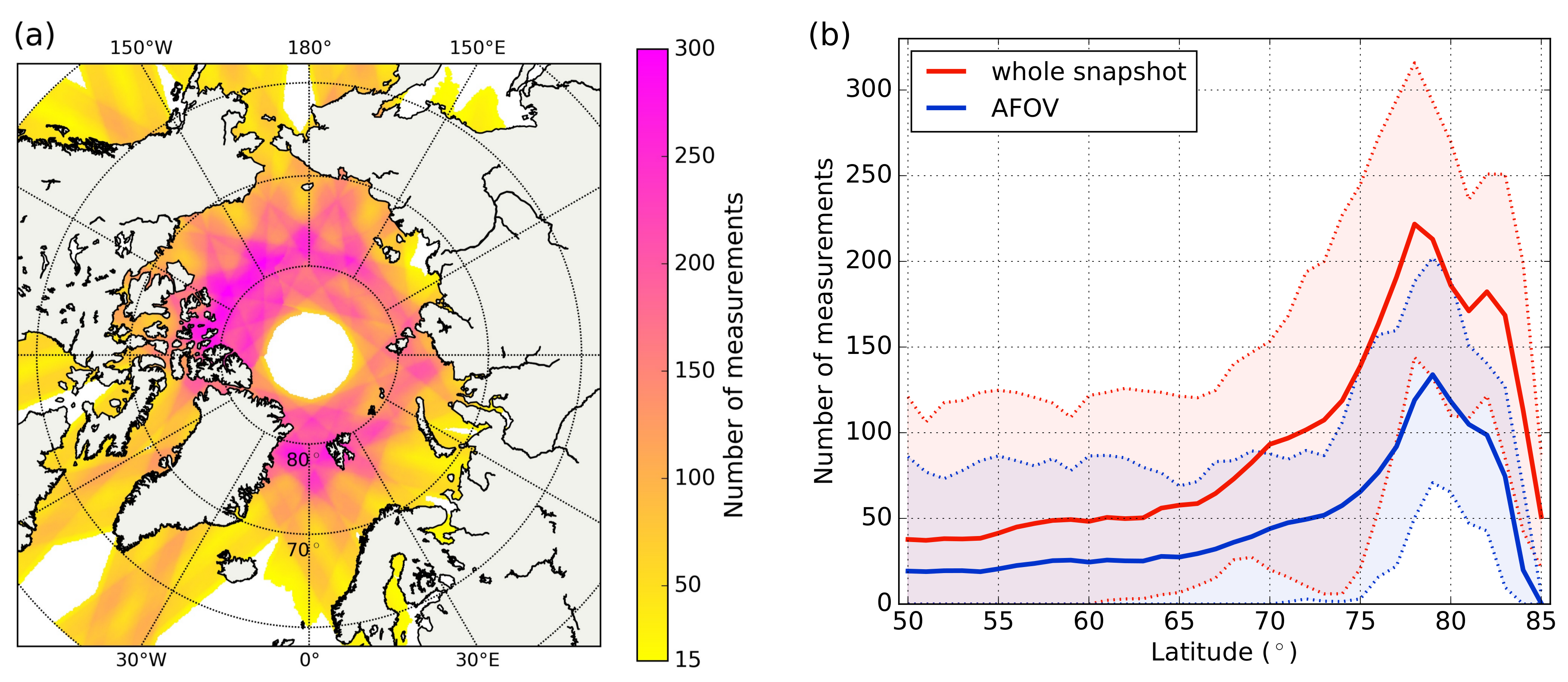
2.1.3. Gridding
2.2. Fitting SMOS Data to Different Incidence Angles
- Which fitting method is most suitable for the SMAP incidence angle of ?
- Are the same methods also applicable for other incidence angles—e.g., the Aquarius incidence angles (28.7, 37.8 and 45.6 [7]) or the Brewster angle (≈60)?
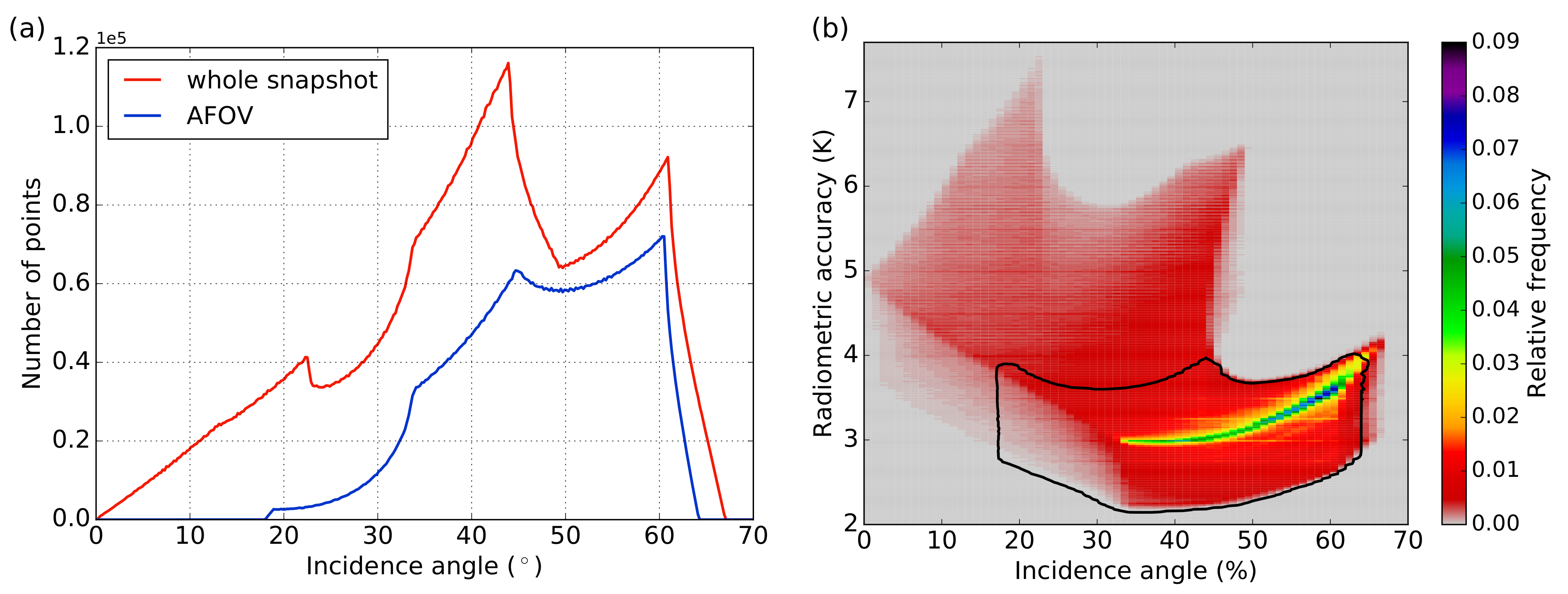
- Is it beneficial to consider only data from the alias-free field-of-view instead of from the whole snapshot?
2.2.1. Composing a Synthetic TB Dataset for Testing
2.2.2. Fitting Methods
- 1-bin mean (binmean):The simplest method is a binning of the brightness temperature values into incidence angle bins with a fixed width of . Here, we consider a bin width of .
- Bin mean with optimized interval (optmean):Instead of using a fixed bin width as in method 1, we consider a bin mean with an optimized bin width . The determination procedure of is described in Section 2.2.3.
- Weighted mean with optimized interval (wgmean):The different radiometric accuracy values (RA) of each measurement are used to calculate a weighted mean. As for method 2, an optimal interval width is determined for this procedure (Section 2.2.3).
- Linear fit with optimized interval (linear):and as functions of incidence angle are piecewise approximated by straight lines. We determine an optimal incidence angle interval within which data are considered for the linear fit (Section 2.2.3).
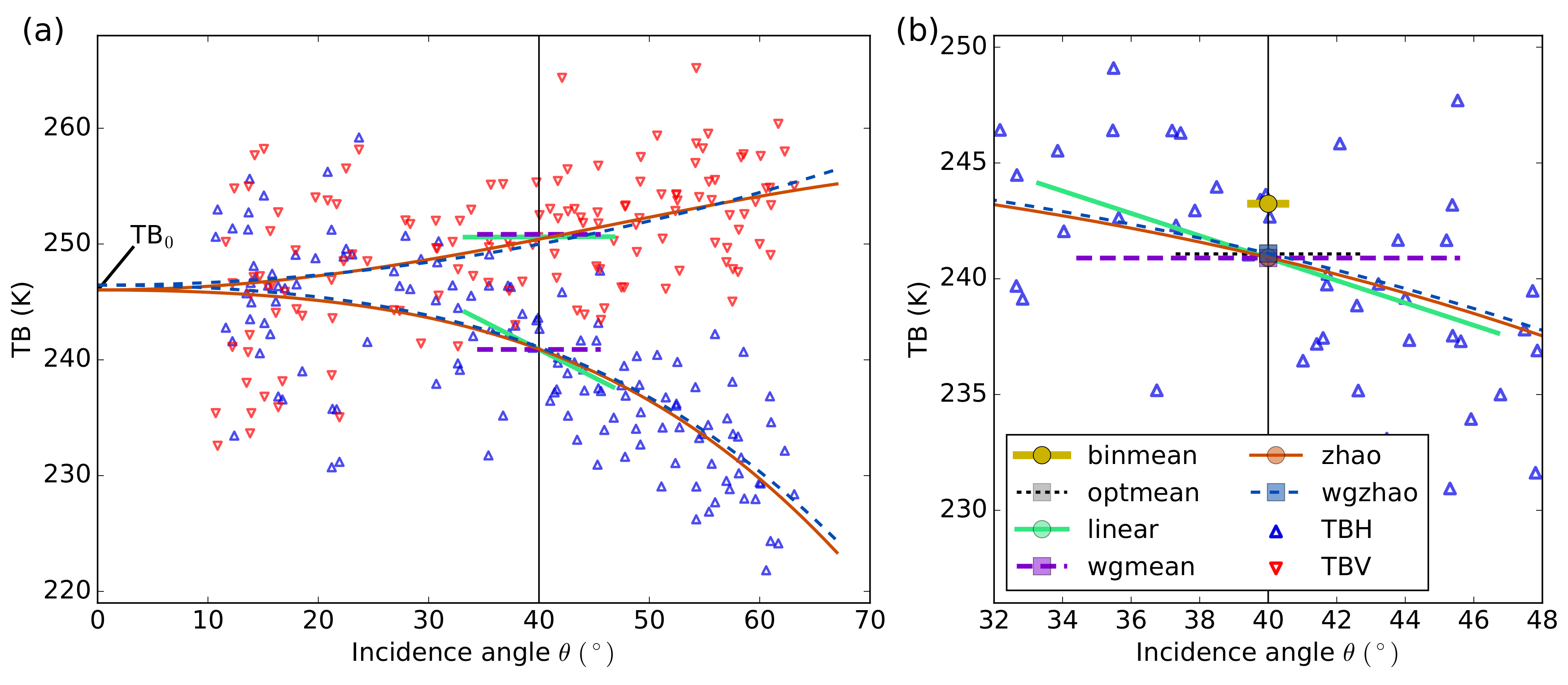
- Simple two-step fit based on Zhao et al. [12] (simplezhao):We also use a fitting function based on a formulation developed by Zhao et al. [12] to refine the characteristics of multi-angular SMOS observations. It consists of a two-step regression approach. As a first step, the brightness temperature at nadir ()—which is the same for H and V polarizations—is estimated from the brightness temperature intensity. In the original approach by Zhao et al. [12], was estimated from a quadratic fit to the brightness temperature intensities. We simplified this first step and calculate as the average of all brightness temperature intensity values with incidence angles below 40. Below 40, the change of the TB intensity with incidence angle is negligible [3]. is then used as a control point in the second step of the regression, where two separate functions are used for and :with . The fit is performed using a least-square method.
- Weighted Zhao fit (wgzhao):Zhao et al. [12] implemented the two-step regression approach described in method 5 by introducing additional weights based on the radiometric accuracy (RA) of the TB measurements. This means that, rather than minimizing as in method 5, the term is minimized.
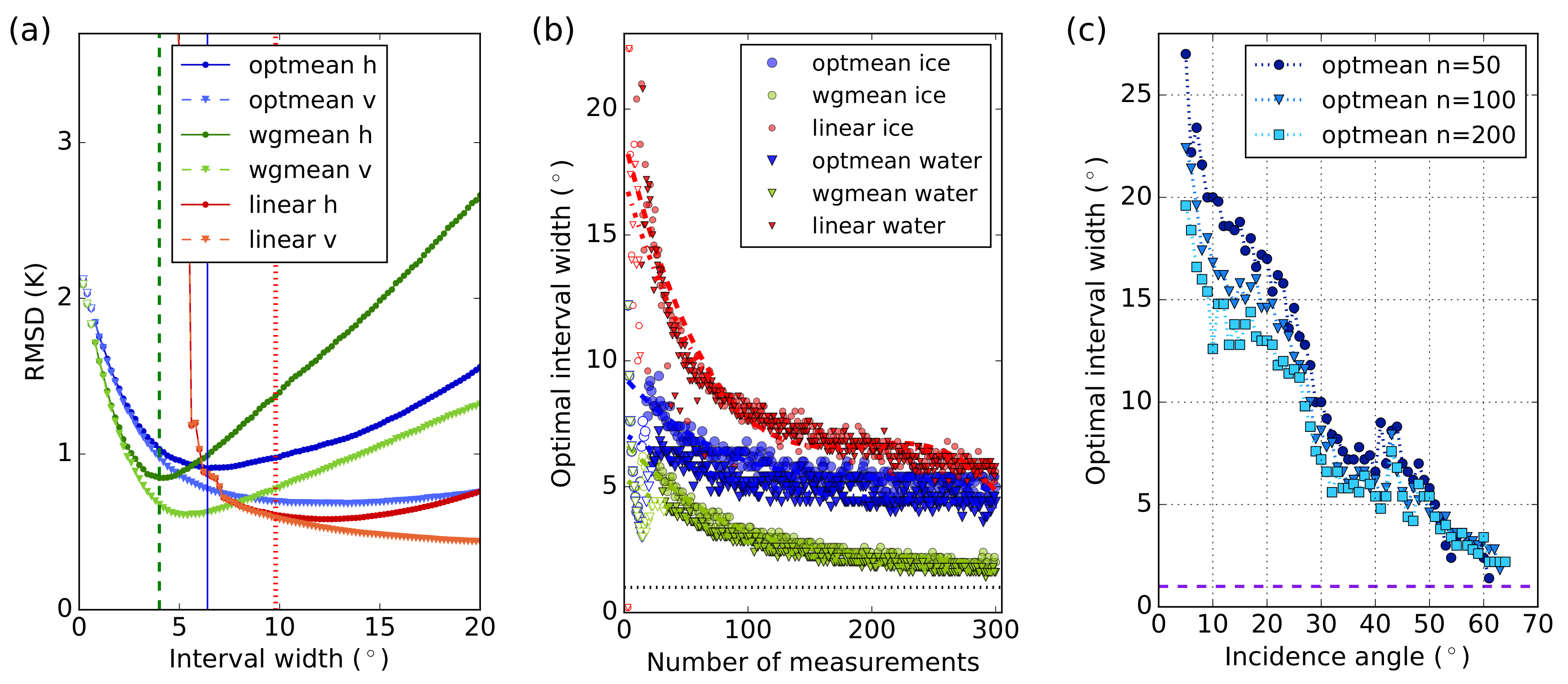
2.2.3. Optimal Interval
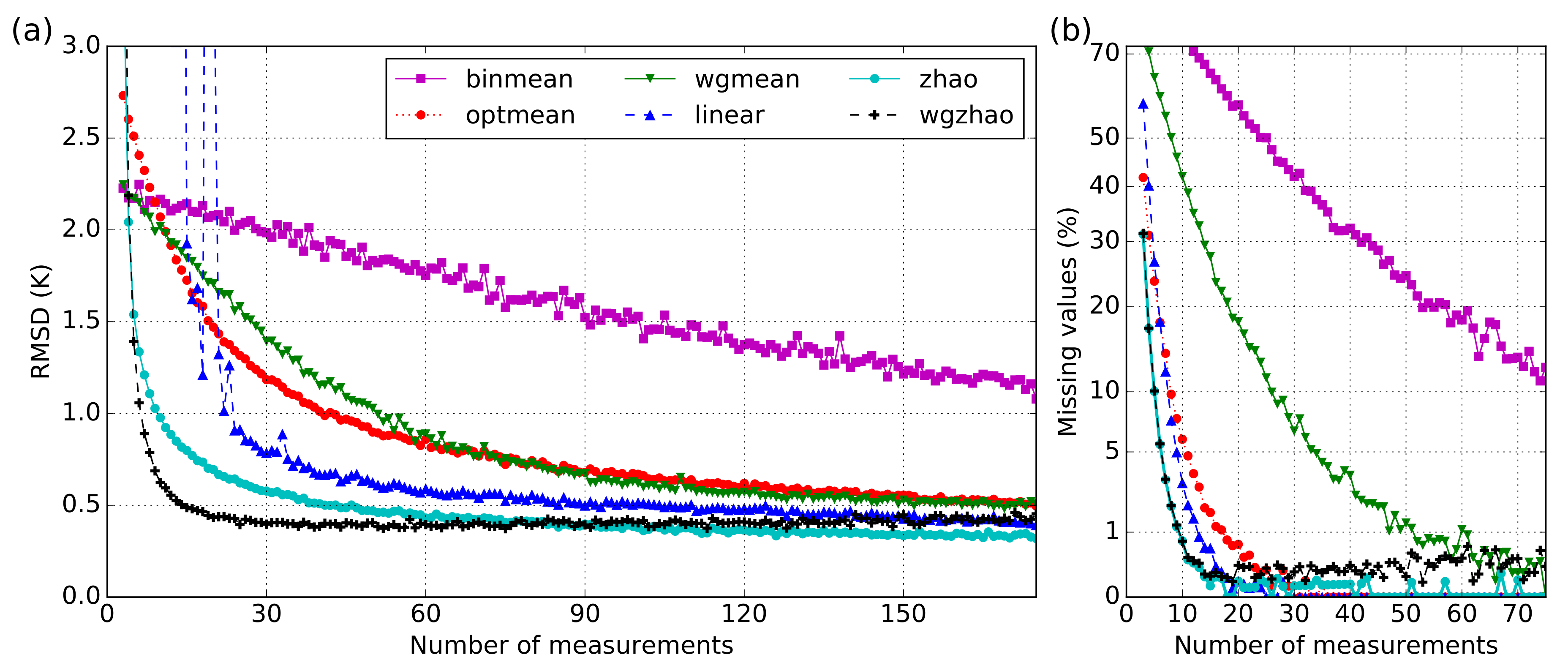
2.2.4. Results for Different Fitting Methods
2.2.5. Computing Performance
2.2.6. Final Choice of Optimal Fitting Method
2.3. Sea Ice Thickness Retrieval Algorithm
3. Results
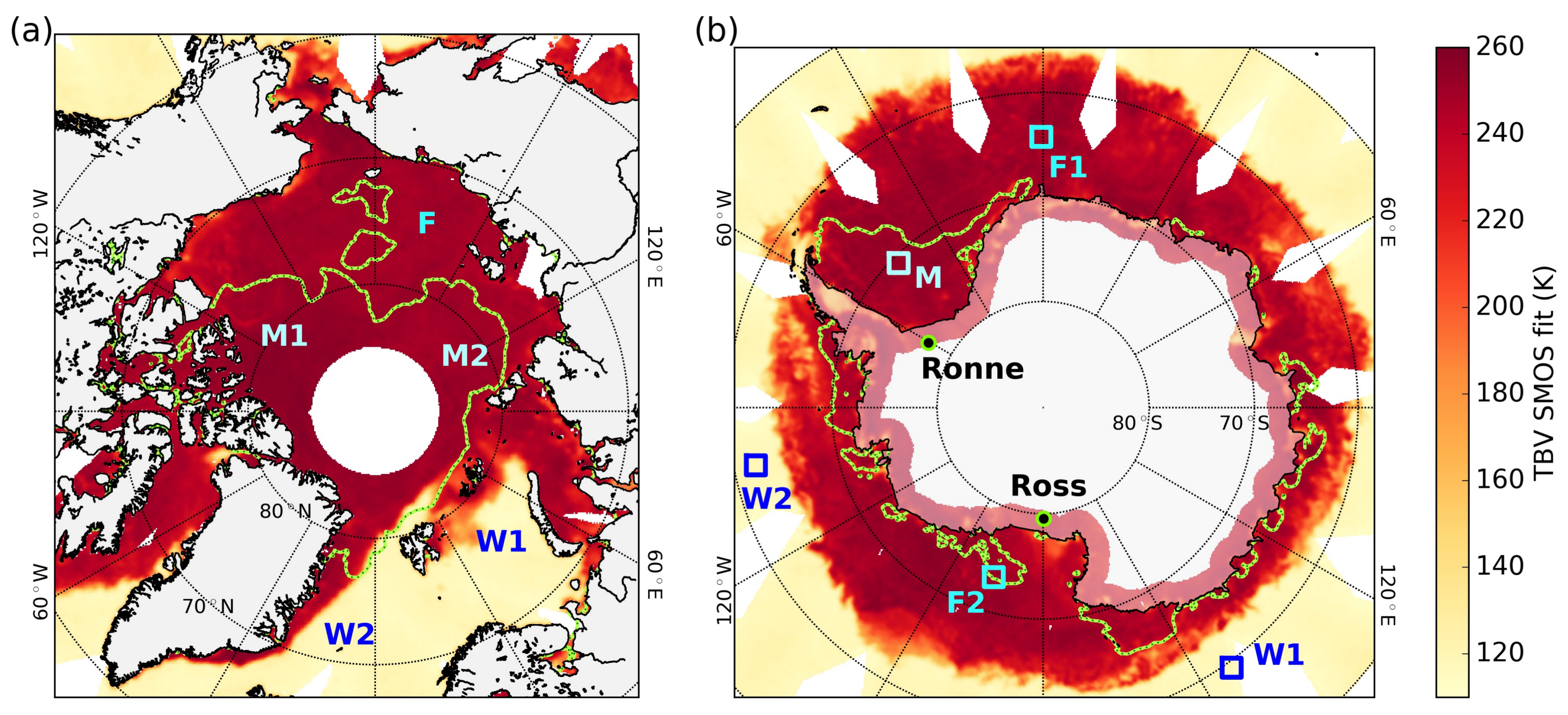
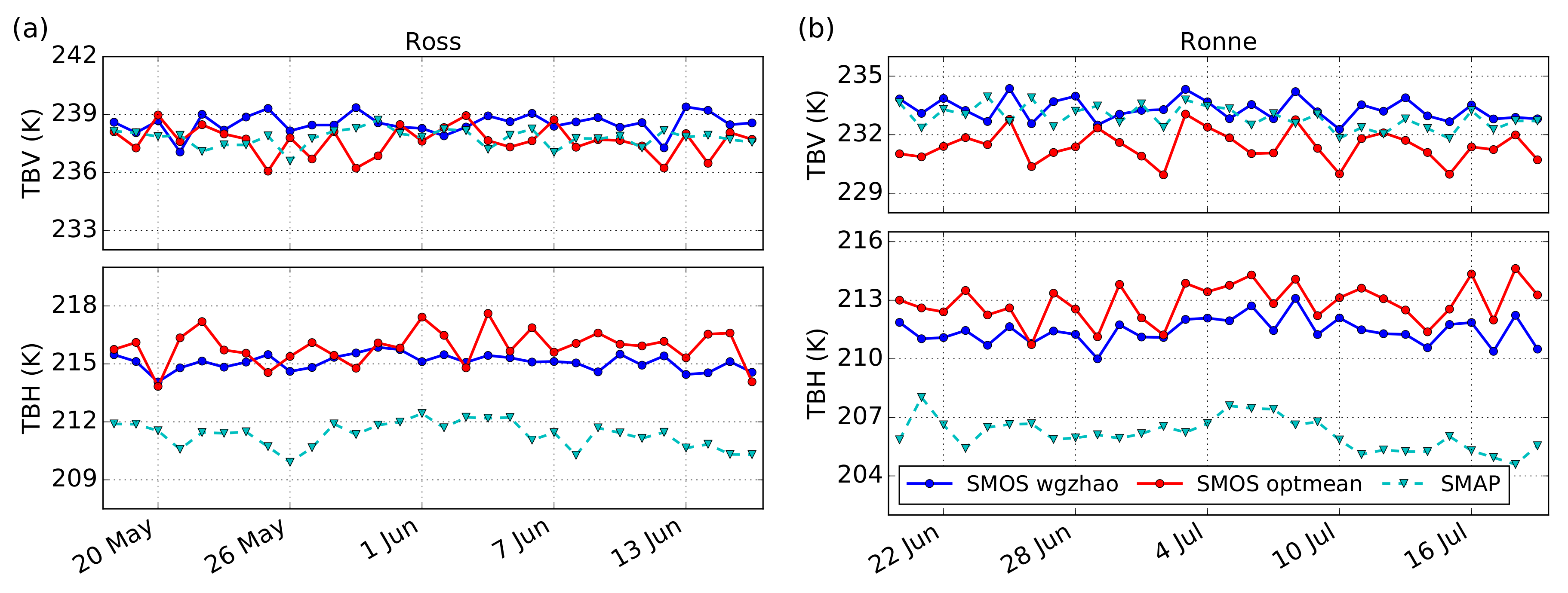
3.1. Brightness Temperature Comparison over a Stable Target Using Different Fitting Methods
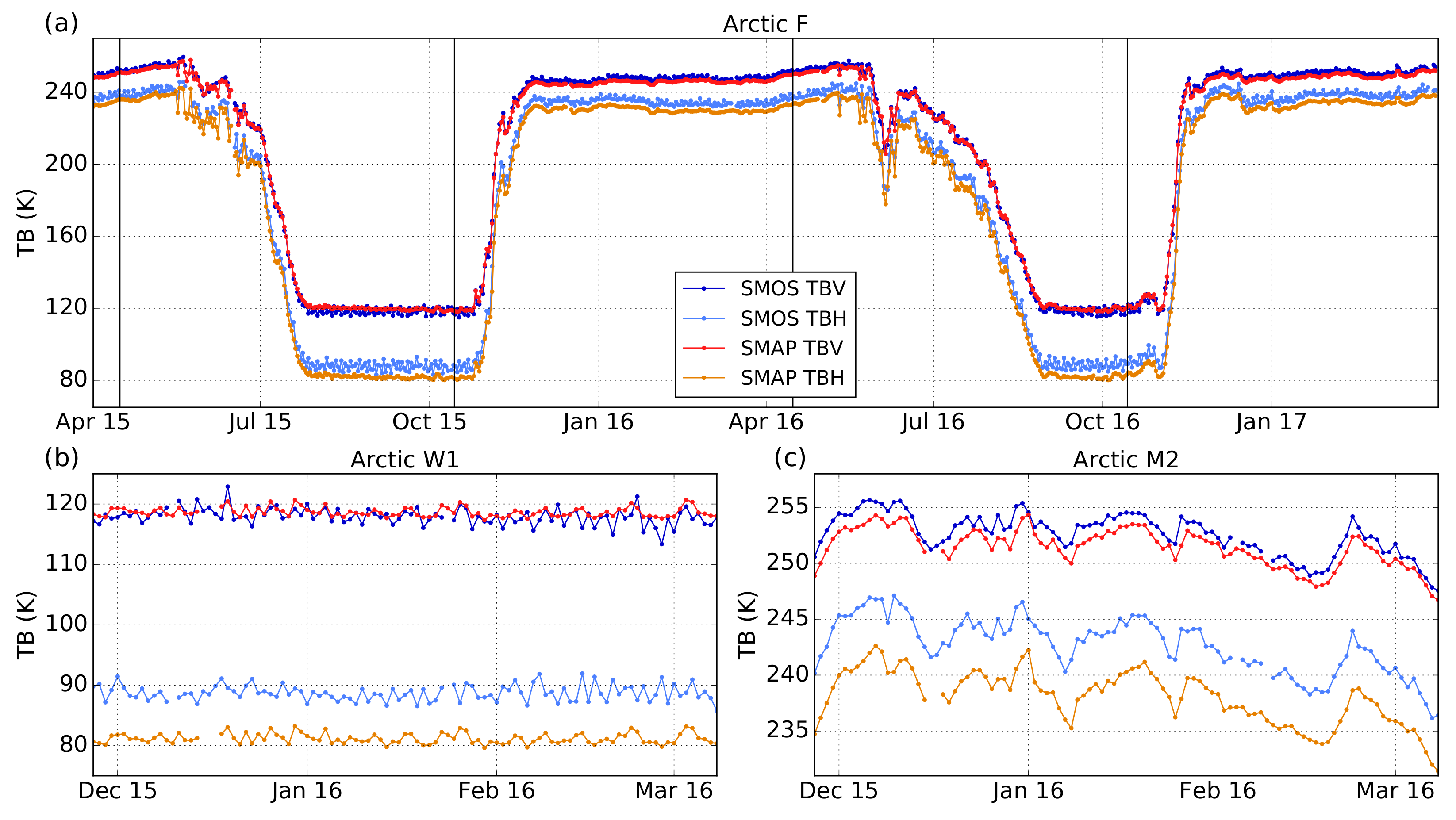
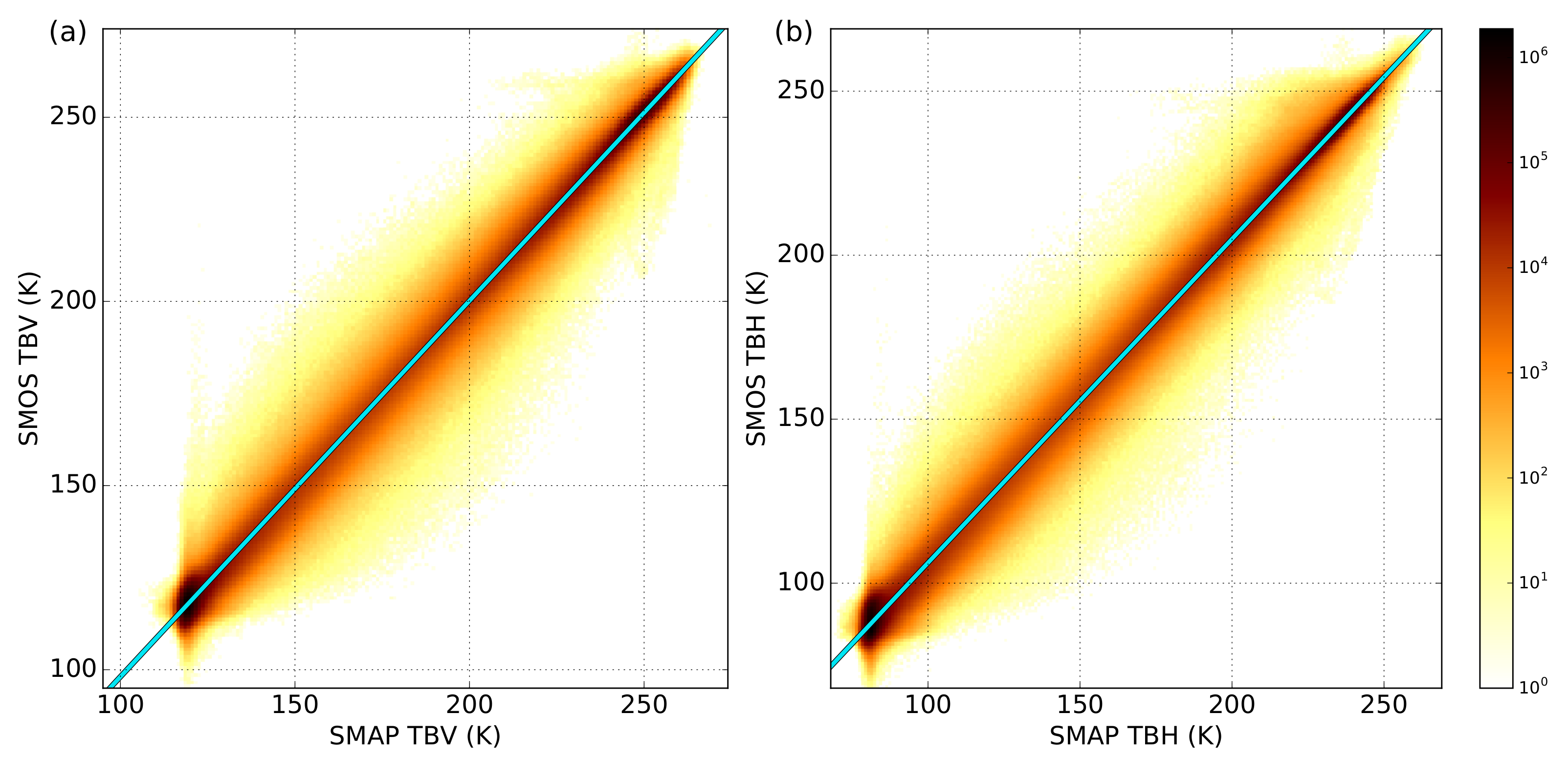
3.2. SMAP and SMOS Brightness Temperature Comparison
3.3. Sea Ice Thickness
3.3.1. SMOS and SMAP Sea Ice Thickness Comparison
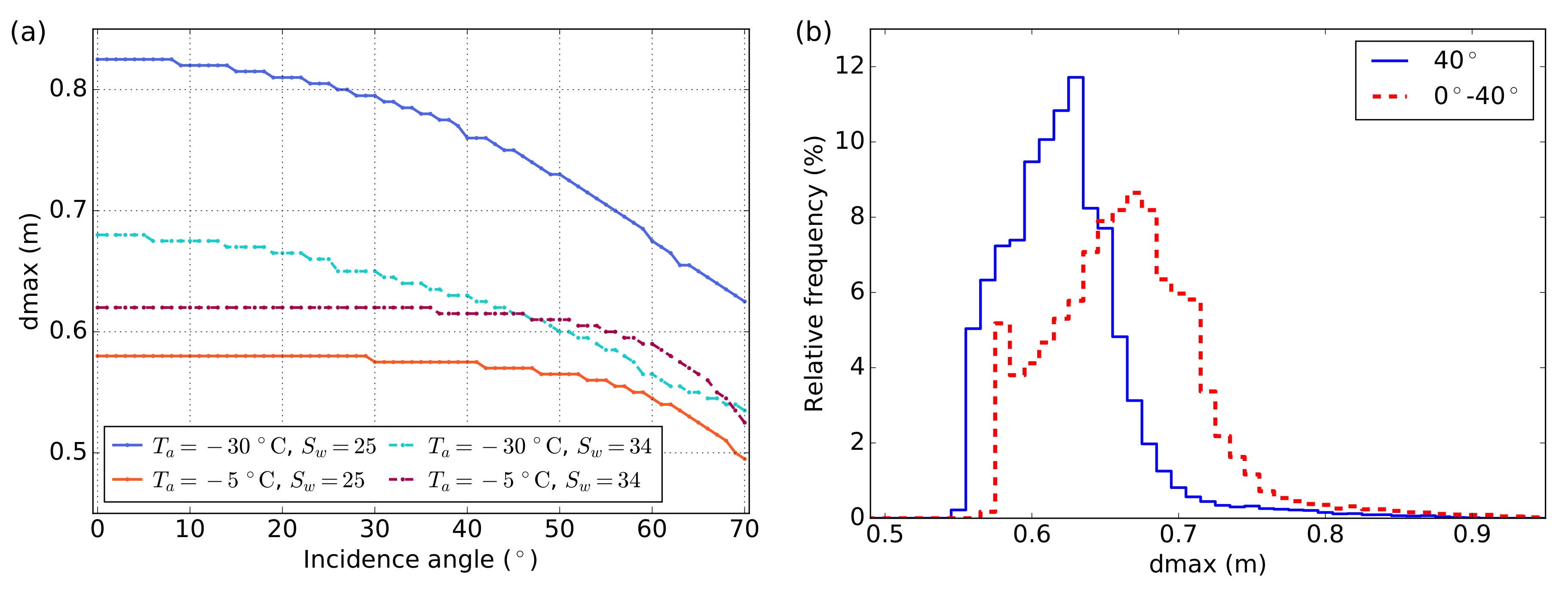
3.3.2. Incidence Angle Dependency
3.3.3. A Combined Sea Ice Thickness Product from SMOS and SMAP
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AFOV | Alias-free field-of-view |
| RFI | Radio frequency interference |
| RMSD | Root mean squared differences |
| SIT | Sea ice thickness |
| SMAP | Soil Moisture Active Passive |
| SMOS | Soil Moisture and Ocean Salinity |
| TB | Brightness temperature |
| TOA | Top of atmosphere |
References
- Richter, F.; Drusch, M.; Kaleschke, L.; Maaß, N.; Tian-Kunze, X.; Mecklenburg, S. Arctic sea ice signatures: L-band brightness temperature sensitivity comparison using two radiation transfer models. Cryosphere 2018, 12, 921–933. [Google Scholar] [CrossRef]
- Kaleschke, L.; Tian-Kunze, X.; Maaß, N.; Mäkynen, M.; Drusch, M. Sea ice thickness retrieval from SMOS brightness temperatures during the Arctic freeze-up period. Geophys. Res. Lett. 2012, 39, 5501. [Google Scholar] [CrossRef]
- Tian-Kunze, X.; Kaleschke, L.; Maaß, N.; Mäkynen, M.; Serra, N.; Drusch, M.; Krumpen, T. SMOS-derived thin sea ice thickness: algorithm baseline, product specifications and initial verification. Cryosphere 2014, 8, 997–1018. [Google Scholar] [CrossRef]
- Huntemann, M.; Heygster, G.; Kaleschke, L.; Krumpen, T.; Mäkynen, M.; Drusch, M. Empirical sea ice thickness retrieval during the freeze-up period from SMOS high incident angle observations. Cryosphere 2014, 8, 439–451. [Google Scholar] [CrossRef]
- Kaleschke, L.; Tian-Kunze, X.; Maaß, N.; Beitsch, A.; Wernecke, A.; Miernecki, M.; Müller, G.; Fock, B.H.; Gierisch, A.; Schlünzen, K.H.; et al. SMOS sea ice product: Operational application and validation in the Barents Sea marginal ice zone. Remote Sens. Environ. 2016, 180, 264–273. [Google Scholar] [CrossRef]
- Ricker, R.; Hendricks, S.; Kaleschke, L.; Tian-Kunze, X.; King, J.; Haas, C. A weekly Arctic sea-ice thickness data record from merged CryoSat-2 and SMOS satellite data. Cryosphere 2017, 11, 1607–1623. [Google Scholar] [CrossRef]
- Le Vine, D.M.; Lagerloef, G.S.E.; Colomb, F.R.; Yueh, S.H.; Pellerano, F.A. Aquarius: an instrument to monitor sea surface salinity from space. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2040–2050. [Google Scholar] [CrossRef]
- Al Bitar, A.; Mialon, A.; Kerr, Y.H.; Cabot, F.; Richaume, P.; Jacquette, E.; Quesney, A.; Mahmoodi, A.; Tarot, S.; Parrens, M.; et al. The global SMOS Level 3 daily soil moisture and brightness temperature maps. Earth Syst. Sci. Data 2017, 9, 293–315. [Google Scholar]
- De Lannoy, G.J.M.; Reichle, R.H.; Peng, J.; Kerr, Y.; Castro, R.; Kim, E.J.; Liu, Q. Converting Between SMOS and SMAP Level-1 Brightness Temperature Observations Over Nonfrozen Land. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1908–1912. [Google Scholar] [CrossRef]
- Maaß, N.; Kaleschke, L.; Tian-Kunze, X.; Drusch, M. Snow thickness retrieval over thick Arctic sea ice using SMOS satellite data. Cryosphere 2013, 7, 1971–1989. [Google Scholar] [CrossRef]
- Huntemann, M. Thickness Retrieval and Emissivity Modeling of Thin Sea Ice at L-band for SMOS Satellite Observations. Ph.D. Thesis, University of Bremen, Bremen, Germany, 2015. [Google Scholar]
- Zhao, T.; Shi, J.; Bindlish, R.; Jackson, T.J.; Kerr, Y.H.; Cosh, M.H.; Cui, Q.; Li, Y.; Xiong, C.; Che, T. Refinement of SMOS Multiangular Brightness Temperature Toward Soil Moisture Retrieval and Its Analysis Over Reference Targets. IEEE J. Appl. Earth Obs. Rem. Sens. 2015, 8, 589–603. [Google Scholar] [CrossRef]
- Bindlish, R.; Jackson, T.J.; Chan, S.; Colliander, A.; Kerr, Y. Integration of SMAP and SMOS L-band observations. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2546–2549. [Google Scholar]
- Al-Yaari, A.; Wigneron, J.P.; Kerr, Y.; Rodriguez-Fernandez, N.; O’Neill, P.; Jackson, T.; Lannoy, G.D.; Bitar, A.A.; Mialon, A.; Richaume, P.; et al. Evaluating soil moisture retrievals from ESA’s SMOS and NASA’s SMAP brightness temperature datasets. Remote Sens. Environ. 2017, 193, 257–273. [Google Scholar] [CrossRef]
- Huntemann, M.; Patilea, C.; Heygster, G. Thickness of thin sea ice retrieved from SMOS and SMAP. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5248–5251. [Google Scholar]
- Mecklenburg, S.; Drusch, M.; Kerr, Y.H.; Font, J.; Martin-Neira, M.; Delwart, S.; Buenadicha, G.; Reul, N.; Daganzo-Eusebio, E.; Oliva, R.; et al. ESA’s soil moisture and ocean salinity mission: Mission performance and operations. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1354–1366. [Google Scholar] [CrossRef]
- Zine, S.; Boutin, J.; Font, J.; Reul, N.; Waldteufel, P.; Gabarro, C.; Tenerelli, J.; Petitcolin, F.; Vergely, J.L.; Talone, M.; et al. Overview of the SMOS Sea Surface Salinity Prototype Processor. IEEE Trans. Geosci. Remote Sens. 2008, 46, 621–645. [Google Scholar] [CrossRef]
- SMOS L1C Processor. SMOS L1 Processor L1c Data Processing Model; Gutierrez, A., Castro, R., Vieira, P., Eds.; DEIMOS Engenharia: Lisboa, Portugal, 2014; Available online: https://earth.esa.int/documents/10174/1854456/SMOS_L1c-Data-Processing-Models (accessed on 5 March 2018).
- Camps, A.; Gourrion, J.; Tarongi, J.M.; Vall Llossera, M.; Gutierrez, A.; Barbosa, J.; Castro, R. Radio-Frequency Interference Detection and Mitigation Algorithms for Synthetic Aperture Radiometers. Algorithms 2011, 4, 155–182. [Google Scholar] [CrossRef]
- Piepmeier, J.R.; Focardi, P.; Horgan, K.A.; Knuble, J.; Ehsan, N.; Lucey, J.; Brambora, C.; Brown, P.R.; Hoffman, P.J.; French, R.T.; et al. SMAP L-Band Microwave Radiometer: Instrument Design and First Year on Orbit. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1954–1966. [Google Scholar] [CrossRef]
- Piepmeier, J.R.; Johnson, J.T.; Mohammed, P.N.; Bradley, D.; Ruf, C.; Aksoy, M.; Garcia, R.; Hudson, D.; Miles, L.; Wong, M. Radio-Frequency Interference Mitigation for the Soil Moisture Active Passive Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2014, 52, 761–775. [Google Scholar] [CrossRef]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-grid 2.0: Incremental but significant improvements for Earth-gridded data sets. ISPRS Int. J. Geo-Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef]
- SMAP L1C ATBD. Algorithm Theoretical Basis Document: Level 1C Radiometer Data Product; Chan, S., Njoku, E., Colliander, A., Eds.; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar]
- EUMETSAT Ocean and Sea Ice Satelitte Application Facility. Global sea ice concentration climate data records 1978–2015 (v1.2). Nor. Dan. Meteorol. Inst. 2015. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave remote sensing: Active and passive. volume 1-microwave remote sensing fundamentals and radiometry. Remote Sens. A 1981, 2, 1223–1227. [Google Scholar]
- Vant, M.R.; Ramseier, R.O.; Makios, V. The complex-dielectric constant of sea ice at frequencies in the range 0.1–40 GHz. J. Appl. Phys. 1978, 49, 1264–1280. [Google Scholar] [CrossRef]
- Klein, L.; Swift, C. An improved model for the dielectric constant of sea water at microwave frequencies. IEEE J. Ocean. Eng. 1977, 2, 104–111. [Google Scholar] [CrossRef]
- Kaleschke, L.; Lüpkes, C.; Vihma, T.; Haarpaintner, J.; Bochert, A.; Hartmann, J.; Heygster, G. SSM/I Sea Ice Remote Sensing for Mesoscale Ocean-Atmosphere Interaction Analysis. Can. J. Remote Sens. 2001, 27, 526–537. [Google Scholar] [CrossRef]
- Dinnat, E.; Le Vine, D. L-band radiometer calibration consistency assessment for the SMOS, SMAP and Aquarius instruments. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2047–2049. [Google Scholar]
- Bindlish, R.; Jackson, T.J.; Piepmeier, J.R.; Yueh, S.; Kerr, Y. Intercomparison of SMAP, SMOS and Aquarius L-band brightness temperature observations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2043–2046. [Google Scholar]
- Peng, J.; Misra, S.; Piepmeier, J.R.; Dinnat, E.P.; Meissner, T.; Vine, D.M.L.; Bindlish, R.; Amici, G.D.; Mohammed, P.N.; Yueh, S.H. ReCalibration and validation of the SMAP L-band radiometer. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2535–2538. [Google Scholar]
- Martín-Neira, M.; Oliva, R.; Corbella, I.; Torres, F.; Duffo, N.; Durán, I.; Kainulainen, J.; Closa, J.; Zurita, A.; Cabot, F.; et al. SMOS instrument performance and calibration after six years in orbit. Remote Sens. Environ. 2016, 180, 19–39. [Google Scholar] [CrossRef]
- Corbella, I.; Durán, I.; Wu, L.; Torres, F.; Duffo, N.; Khazâal, A.; Martín-Neira, M. Impact of Correlator Efficiency Errors on SMOS Land-Sea Contamination. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1813–1817. [Google Scholar] [CrossRef]

| Method Abbreviation | Method Description | |
|---|---|---|
| 1 | binmean | Fixed incidence angle bins with a width of 1 |
| 2 | optmean | Averaging over incidence angle bins with optimized width |
| 3 | wgmean | Same as optmean, but TBs are weighted by radiometric accuracy |
| 4 | linear | Linear fit of TBs within incidence angle interval with optimized width |
| 5 | simplezhao | Simplified two-step regression based on Zhao et al. [12] |
| 6 | wgzhao | Same as simplezhao, but TBs are weighted by radiometric accuracy |
| Method | Average Computing Time in ms |
|---|---|
| binmean | 0.06 (0.08) |
| optmean | 0.08 (0.11) |
| wgmean | 0.15 (0.19) |
| linear | 0.90 (0.96) |
| simplezhao | 36.6 (58.6) |
| wgzhao | 13.8 (37.0) |
| Location | SMOS wgzhao | SMOS optmean | SMAP | ||||
|---|---|---|---|---|---|---|---|
| TB | TB | TB | TB | TB | TB | ||
| Ross ice shelf, 18 May–16 June 2015 | mean (K) | 238.5 | 215.1 | 237.6 | 215.9 | 237.8 | 211.3 |
| 79.52 S, 179.69 E | std (K) | 0.5 | 0.4 | 0.8 | 0.9 | 0.4 | 0.7 |
| Ronne ice shelf, 20 June–19 July 2015 | mean (K) | 233.3 | 211.1 | 231.4 | 212.9 | 232.9 | 206.1 |
| 77.57 S, 29.46 W | std (K) | 0.6 | 0.7 | 0.8 | 1.0 | 0.6 | 0.8 |
| Surface Type/Box Name | Correl. Coeff. | Bias (K) | RMSD (K) | |||
|---|---|---|---|---|---|---|
| TB | TB | TB | TB | TB | TB | |
| Arctic | ||||||
| F | >0.99 | >0.99 | 0.7 | 5.0 | 2.0 (1.4) | 5.5 (2.1) |
| M1 | 0.99 | 0.99 | 1.3 | 4.2 | 2.0 (1.4) | 4.9 (2.5) |
| M2 | 0.99 | 0.99 | 0.4 | 4.9 | 2.2 (2.2) | 5.7 (2.8) |
| W1 | 0.31 | 0.32 | −1.2 | 7.0 | 2.0 (1.6) | 7.2 (1.8) |
| W2 | 0.05 | 0.09 | −0.1 | 5.9 | 6.3 (6.4) | 9.4 (7.3) |
| all open water surfaces | 0.16 | 0.14 | −0.8 | 6.5 | 4.1 (4.1) | 8.0 (4.6) |
| all thick ice surfaces in winter | 0.97 | 0.98 | 1.4 | 4.2 | 1.6 (0.9) | 4.3 (1.1) |
| Antarctic | ||||||
| F1 | >0.99 | >0.99 | 0.3 | 5.0 | 1.8 (1.7) | 5.5 (1.9) |
| F2 | >0.99 | >0.99 | 0.8 | 4.7 | 1.4 (0.9) | 4.9 (1.0) |
| M | >0.99 | 0.99 | 1.3 | 4.2 | 1.5 (0.7) | 4.3 (1.0) |
| W1 | 0.66 | 0.57 | −1.2 | 6.3 | 1.6 (1.1) | 6.4 (1.4) |
| W2 | 0.31 | 0.38 | −0.5 | 5.6 | 1.9 (2.1) | 6.0 (2.4) |
| all open water surfaces | 0.48 | 0.46 | −0.8 | 6.0 | 1.7 (1.7) | 6.3 (1.9) |
| all thick ice surfaces in winter | 0.94 | 0.96 | 1.4 | 3.8 | 1.5 (0.8) | 3.8 (1.0) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitt, A.U.; Kaleschke, L. A Consistent Combination of Brightness Temperatures from SMOS and SMAP over Polar Oceans for Sea Ice Applications. Remote Sens. 2018, 10, 553. https://doi.org/10.3390/rs10040553
Schmitt AU, Kaleschke L. A Consistent Combination of Brightness Temperatures from SMOS and SMAP over Polar Oceans for Sea Ice Applications. Remote Sensing. 2018; 10(4):553. https://doi.org/10.3390/rs10040553
Chicago/Turabian StyleSchmitt, Amelie U., and Lars Kaleschke. 2018. "A Consistent Combination of Brightness Temperatures from SMOS and SMAP over Polar Oceans for Sea Ice Applications" Remote Sensing 10, no. 4: 553. https://doi.org/10.3390/rs10040553
APA StyleSchmitt, A. U., & Kaleschke, L. (2018). A Consistent Combination of Brightness Temperatures from SMOS and SMAP over Polar Oceans for Sea Ice Applications. Remote Sensing, 10(4), 553. https://doi.org/10.3390/rs10040553






