Abstract
Remote sensing allows regional evapotranspiration (ET) values to be obtained. Surface conductance is a key variable in estimating ET and controls surface flux interactions between the underlying surface and atmosphere. Limited by the influence of clouds, ET can only be estimated on cloud-free days. In this study, a gap-filling method is proposed to acquire daily surface conductance, which was coupled into a Penman-Monteith (P-M) equation, to estimate the regional daily ET over the Hai River Basin. The gap-filling method is coupled with the canopy conductance, surface conductance and a simple time extension method, which provides more mechanisms and is more comprehensive. Field observations, including eddy covariance (EC) fluxes and meteorological elements from automatic weather station (AWS), were collected from two sites for calibration and validation. One site is located in Guantao County, which is cropped in a circular pattern with winter wheat and summer maize. The other site is located in Miyun County, which has orchard and summer maize crops. The P-M equation was inverted to the computed surface conductance at the field scale, and latent heat fluxes from EC were processed and converted to daily ET. The results show that the surface conductance model used in the gap-filling method performs well compared with the inverted surface conductance, which suggests that the model used here is reasonable. In addition, the relationship between the results estimated from the gap-filling method and EC measurements is more pronounced than that between the other method and the EC measurements. The values improve from 0.68 to 0.75 at the Guantao site and from 0.79 to 0.88 at the Miyun site. The improvement mainly occurs during the growing crop season, according to the temporal variations in the results.
1. Introduction
Energy and water flux exchange is an important physical process in the research field of hydrometeorology and global change. Quantitative research on surface heat flux contributes significantly to water cycle and climatic change interpretations. Evapotranspiration (ET) comprises vegetation transpiration and evaporation from water and soil, which serves as a key component in the interaction between the surface and atmosphere. Global total ET accounts for more than half of the total amount of precipitation. Accurate estimations of ET and its spatiotemporal distribution are meaningful for optimizing water resource management [1,2,3].
Ground observations and ET computations are highly precise in estimating individual sites or at local scales and include observations based on pan evaporation, lysimeter, Bowen ratio, eddy covariance (EC) and large aperture scintillometer (LAS) [4,5,6,7,8,9,10]. Comparably, EC can provide continuously precise measurements of water and heat flux over a homogeneous surface, revealing the character of mass and energy exchange between specific surface features and the atmosphere. EC measurements have been mostly used for parameter calibration and validation in land surface models in previous studies. However, field-scale measurements are limited by their spatial representation and are difficult to promote widely due to the cost. Regarding the underlying surface heterogeneity and turbulence complexity, regional interpolation of ET from sparse measurements is unreliable [11].
Remote sensing enables multi-temporal regional ET monitoring at low costs and multiple scales. Remote sensing-based ET models usually provide model input parameters from remote sensing measurements, such as land surface temperature, albedo and vegetation indexes, to separate sensible heat flux and latent heat flux to solve the surface energy balance equation. Satellites equipped with multi-scale, high-spectrum, multi-view angle sensors are currently designed to provide a more accurate description of surface topography and hydrothermal conditions.
The Penman-Monteith (P-M) [12,13] equation combines aerodynamics with energy balance and considers the surface conductance by mass transfer, which achieves the ET estimation for an unsaturated surface. Surface conductance is a crucial parameter in controlling energy and water exchanges between surface and atmosphere, which is influenced by vegetation-physiology, type of underlying surface and environmental factors and is more complex when mixed pixels exist. As remote sensing techniques develop, leaf area index ()-based surface conductance models have been put forward to estimate ET using the P-M equation [14,15,16,17]. However, accurate calibration for model parameters requires field observations that limit the application of models in wider areas.
Due to the difficulty in determining surface conductance, the Surface Energy Balance System (SEBS) [11,18,19] and Surface Energy Balance Algorithm for Land (SEBAL) [1,20,21] were developed to compute sensible heat flux and latent heat flux, and therefore, surface conductance can be acquired as a residual through the energy balance equation. SEBS complemented aerodynamic resistance with residual resistance, which is determined by KB-1, to solve the difference between the land surface temperature and aerodynamic temperature, as well as the difference between mass transfer and heat transfer. SEBS possesses a robust physical basis compared to SEBAL, but SEBS depends on highly accurate meteorological data. In addition, the precision of the model significantly depends on KB-1, which is difficult to determine. SEBAL assumes that the land surface temperature has a linear relationship with the difference between air temperature and aerodynamic temperature, and parameters in the linear relationship are computed by a hot point and cold point selected in the study area. The model has strict requirements for extreme points, which is always ensured empirically. The linear relationship proposed in the model depends on the uniformity of the surface and climatic conditions, which results in a geographic scale problem [22]. Limited by the availability of satellite data, both models only work on cloud-free days.
The Atmosphere-Land Exchange Inverse (ALEXI) model was developed as a robust regional framework for the two-source energy balance (TSEB) land surface model [23], which computes the local partitioning of the surface fluxes and radiometric temperature between the soil and vegetation components of a model grid cell [24]. The ALEXI model coupled the TSEB with an atmospheric boundary layer (ABL) model to simulate the land-atmosphere feedback of air temperature, which is used as a boundary condition for the sensible heat flux [25]. Given morning surface temperature rise measurements from geostationary satellites, ALEXI related the time-integrated sensible heat from the land surface during the morning hours to the rise in ABL temperature without requiring the near-surface air temperature measurement [25,26]. An associated flux disaggregation algorithm (DisALEXI), which is also built on the TSEB land surface representation, can be used to downscale the GEOS-based ALEXI flux estimates to a finer spatial scale using land surface temperature data from moderate- to high-resolution thermal infrared imaging systems [27,28,29,30,31]. Although regional daily ET can be obtained from ALEXI, the resolution depends on the geostationary satellite data, which are always in coarse resolution. Moreover, the models are limited by complexity during the computational process.
The ETWatch coupled residual method with the P-M equation is used to acquire regional daily ET. The residual method estimates sensible heat flux on cloud-free days and latent heat flux can be obtained as a residual from the energy balance equation. Subsequently, surface conductance for cloud-free days can be inverted using the P-M equation and extended to daily scale through several environmental variables. Daily ET can thus be estimated using the P-M equation with daily surface conductance [32,33,34,35]. In this study, an enhanced method for gap-filling of surface conductance is proposed and applied in Hai River Basin. Daily surface conductance can be estimated from those on clear-sky days with the method. The enhanced method couples a surface conductance model with a time extension method, which guarantees a strong, mechanistic physical process and is more comprehensive in considering impact factors. In addition, the gap-filling method can avoid calibration of empirical parameters and direct computation of surface conductance thus to ensuring precision and simplicity in estimating daily regional surface conductance. When coupled with ETWatch, daily regional ET can be obtained without complex computational procedures and are not limited by specific data. Multi-source remote sensing and meteorological data were collected for input. Field observations from two sites were used for calibration and validation.
2. Study Area and Data
2.1. Study Area
The Hai River Basin contains the largest water system in North China, which flows through eight provinces (112°–120°E, 35°–45°N) and covers approximately 320,600 km2. The basin has the semi-humid and monsoonal climate typical of mid-latitude regions. The climate is cold during the winter but recovers quickly in the spring, with a mean annual temperature range of 1.5–14 °C. The mean annual precipitation in the basin is 539 mm, and the mean annual ET is 512 mm, most of which occurs during the summer. Figure 1 shows the position and land cover map of the whole basin using multi-temporal MODIS data and an object-based classification method. The underlying surfaces of the basin are mainly mountains and plateaus in northern and western regions and plains in the southern and eastern regions. Winter wheat and summer maize are the two main crops grown on arable land and are rotated with the change of season. Figure 2 shows the phenology of the two crops.
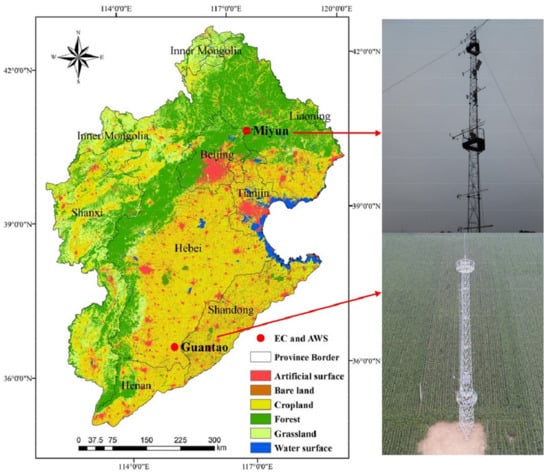
Figure 1.
Land cover of the Hai River Basin and locations of two stations (MY and GT).

Figure 2.
Phenology of crops at stations MY and GT.
Two ground observation sites within the basin, which have typical crop types, are selected for validation. These sites are Miyun station (MY) and Guantao station (GT). The positions of the two sites are displayed in Figure 1. Site MY is in a valley of Miyun County in Beijing, which is in the north of the basin (40°37′N, 117°19′E). MY has less rainfall and lower temperatures than the basin, and it is covered by 2.5 km2 of orchard and summer maize and is surrounded by mountains. Site GT is in the North China plain (36°30′N, 115°07′E), which has a homogeneous surface and is planted with two crops (winter wheat from October to June and summer maize from June to September). At both sites, an observation system consisting of EC and an automatic weather station (AWS) was installed to monitor the flux measurements and meteorological elements.
2.2. Site Measurements
The EC flux data are transferred automatically and simultaneously from the stations to the server. All data are sampled at a 10 Hz frequency and averaged every 30 min with the post-processing software EdiRe (University of Edinburgh) and EddyPro (Li-COR Biosciences) equipped instruments. Sensible and latent heat fluxes for 2016 were collected from both stations, and energy closure calibration was completed based on the Bowen ratio closure method, due to the data energy imbalance. To guarantee the flux data reliability, abnormal values were removed because of instrument malfunction and bad weather.
The 2016 meteorological data collected from the AWS contain six parameters: wind velocity, air temperature, relative humidity, pressure, net radiation and soil moisture. The data are recorded by loggers at an interval of 10 min, and then, they are averaged to acquire daily values. A small amount of data, which obviously deviated from physical meaning, were deleted and gap-filled with a linear interpolation method [36].
The flux data were collected for nearly the whole year from both stations and covered the main crop growing season. The meteorological data for station GT were adequate, whereas the last four months of data from station MY were lost due to an instrument malfunction. The detailed information from collected ground observations are listed in Table 1.

Table 1.
Information from collected ground observations.
2.3. Remote Sensing Data
In this study, several satellite datasets were collected and include MODIS, NCEP, FY-2D and AMSR-2. Four MODIS images were needed to cover the basin, and the preprocessing included radiometric, atmospheric and geometric corrections, which were already completed by the data supplier. MYD09GA and MYD11A1 are surface reflectance and land surface temperature products, respectively. The data were converted to image files from hierarchical data format (HDF) files, and then, they were mosaicked and clipped to the study area using interactive data language (IDL) programs. Normalized difference vegetation index () can be calculated using the MODIS 1,2-band, and land surface albedo was converted to broadband from narrowband [37]. Cloud pixels were detected using a method proposed by Ackerman [38]. Time series datasets for and albedo were computed by linear interpolation and smoothed by Savitzky-Golay filter [39]. MOD07 provided the atmospheric temperature and humidity profiles, and a planetary boundary layer (PBL) mixing height derived method was applied to extract information for a PBL [40]. All the MODIS products are 500 m and 1 km resolution and can be downloaded from the website of LAADS DAAC (https://ladsweb.modaps.eosdis.nasa.gov/). The wind velocity of a PBL can be extracted from NCEP reanalysis data, which has a spatial resolution of 2.5° and is provided by NOAA Earth System Research Laboratory (https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis2.html), according to the height of PBL. FY-2D is the second operational vehicle of the first-generation geostationary meteorological satellite system operated by the Chinese Meteorological Administration (CMA). The sensor aboard the satellite consists of one visible channel with a resolution of 1.25 km and four infrared channels with resolutions of 5 km. Products are distributed on data services website in HDF format (http://satellite.nsmc.org.cn/portalsite/default.aspx). Cloud data from the FY-2D satellite were used to compute the sunshine hours, instead of the interpolated meteorological sunshine hours [41,42]. AMSR-2 is a sensor aboard GCOM-W1, which can provide daily global soil moisture of the top soil with resolution of 10 km (https://gcom-w1.jaxa.jp/auth.html). All the above data were projected to Albers conical equal area projections and resampled to 1 km resolution using an earth resource development assessment system (ERDAS), which is a software package for processing remote sensing images.
In addition, daily meteorological elements, including wind velocity, air temperature, relative humidity and air pressure, which were recorded at 49 national weather stations over the basin, were collected from the China Meteorological Data Service Center. All parameters were corrected with a digital elevation model (DEM) and then interpolated into daily maps at 1 km resolution using the inverse distance weighting method [43]. The interpolated results were projected to Albers conical equal area projections as satellite data.
3. Methodology
3.1. Surface Conductance Model
3.1.1. Canopy Conductance
The canopy conductance () depends both on the atmospheric factors and upon available water content in the soil [44,45,46]. The model used in this study to calculate the canopy conductance () is as follows [47]:
was obtained using the following empirical equation:
The factor represents the effect of photosynthetically active radiation and can be defined as follows [48]:
and are minimum and maximum values of canopy conductance, respectively. is relatively insensitive in the calculation above and always set as a small constant () [46]. is the downward shortwave radiation, and is a limiting parameter associated with the actual underlying surface. is the leaf area index [49].
The second factor characterizes the soil water content influence on the root zone. Due to the difficulty obtaining the soil water content for the root zone in a region, the soil water content product of the top soil from ASMR-2 was used in combination with a transformed equation as follows [50]:
is the soil water content, and is the field capacity, which is approximately 0.75 times the soil’s porosity [51]. is the wilting point of the soil water content and is common for many herbaceous species [52]. Values recommended for and for different soil types were adopted [53].
The factor addresses the effects of the water vapour pressure deficit over the canopy and can be described as follows [48,49]. is a species-dependent empirical parameter. A larger leads to a smaller and , which increases the resistance of the canopy evaporation.
The factor takes into consideration the air temperature constraint and is proposed as follows [54]:
where is the air temperature above the canopy. is the optimal temperature for the growth of many crops and always set as 298 K. decreases when departs from the optimal temperature.
Several empirical parameters in the equations above are related to the actual surface and should be calibrated using ground observations. In this study, the calibrated results from other studies [53,55] were adopted, which are listed in Table 2.

Table 2.
Surface-dependent parameters settings.
3.1.2. Surface Conductance
Total ET is the sum of transpiration from the plant canopy and evaporation from the soil [15,16].
The P-M equation has been widely used in previous studies to calculate the ET of the land surface [14,16,17,33,44,45,50,56,57]. Therefore, the P-M equation is used for and in this study as described below:
where is the latent heat of evaporation, is the slope of the curve relating saturation water vapour pressure to temperature, is the psychrometric constant, and are the available energy absorbed by the land surface and canopy surface, respectively, is the air density, is the specific heat of air at a constant pressure, is the aerodynamic conductance, and and are surface conductance and canopy conductance, respectively. Five variables used here, i.e., , , , , , are assumed to be known or can be estimated using meteorological results. This study adopted without considering the stability corrections because the P-M equation is relatively insensitive to aerodynamic conductance, especially when >> [14]. Here was calculated as Equation (12) described, where is von Karman’s constant (0.41), is wind velocity, is the height of wind velocity, is zero displacement height, and are the roughness lengths to momentum water vapor transfer. The quantities , and were estimated using , and , where is canopy height [58]. The estimation of can be described as Equation (13), and the corresponding parameters including maximum height (), minimum height (), maximum () and minimum () of various underlying surface can refer to field measurements and exist achievements of other researchers [59]. equals the result of daily net radiation minus the daily soil heat flux . Daily can be neglected here due to its opposing character in the daytime versus nighttime. Daily can be estimated using sunshine hours from FY-2D, albedo from MODIS products and meteorological results [41].
Soil evaporation has an important role in the total ET, especially in sparse vegetation. The assumption that soil evaporation occurs at some fraction of the equilibrium rate at the soil surface is as follows [14,15]:
In the equations above, the total available energy is partitioned into that absorbed by the canopy surface and by the soil surface . The vegetation fraction , which is estimated from the , is applied in the ratio of total available energy absorbed by the canopy and soil:
The soil evaporation fraction used in this study is relevant to the top soil moisture status where evaporation occurs. According to the complementary relationship hypothesis, water vapour pressure deficit and humidity response to the variation in moisture in the top soil via land-atmosphere interactions [60,61], can be described as follows:
where is the air humidity, is the empirical parameter, which is set to 100, and is the added factor for adjustment. Combining Equations (9)–(16), the surface conductance can be obtained with the following:
3.2. Gap-Filling Method
ETWatch is an integration of the “residue approach” and P-M equation [25,32,33,34,35,43]. The residue approach is an energy balance model combined with the mass transfer method, which can compute ET on cloud-free days based on SEBS. ETWatch consists of several subsystems: net radiation model, soil heat flux model, sensible heat flux mode, aerodynamic roughness length model and PBL model. ETWatch computes ET on cloud-free days with multi-source remote sensing data. The basic files are used as auxiliary data in the computation of subsystems, which include a digital terrain model, latitude file, aspect file and slope file. The sensible heat flux is computed first, and then, the latent heat flux can be obtained as the residue. The latent heat flux can be converted to actual ET in diurnal scales through the latent heat of evaporation and evaporative fraction (EF) method [62,63]. Figure 3 shows the estimation flowchart for ET on cloud-free days.
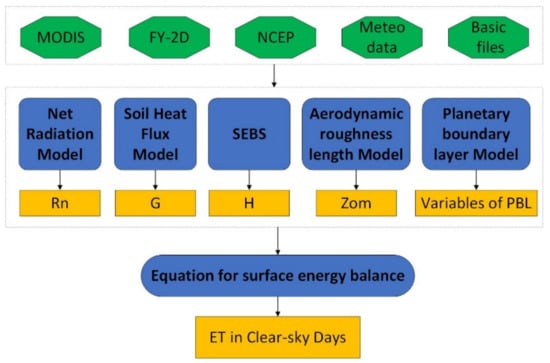
Figure 3.
Estimation flowchart for ET on cloud-free days. The green indicates input data, the blue indicates methods, the orange indicates results.
Daily ET data are difficult to acquire because of cloud cover over the basin. A gap-filling method of surface conductance extended from clear-sky surface conductance, which can be computed with clear-sky ET results from ETWatch and an inversion from the P-M equation, is proposed in this study to generate daily surface conductance and to compute the daily ET using the P-M equation.
where is the surface conductance on clear-sky days, is the diurnal latent heat flux on clear-sky days resulted from ETWatch, Equation (20) is the inversion of P-M equation. Equation (19) is an expression for surface conductance proposed in Section 3.1.2 and the right part of the equation can be marked as shown in Equation (21). The subscript and represent daily scale and clear-sky days respectively. Once the is acquired, daily surface conductance () can be estimated using the gap-filling method expressed as Equation (22). and have the same form according to Equation (21) and consist of a series of empirical parameters including , , , which remain unchanged for the same kind of land cover over time and several external variables such as vegetation fraction, temperature, radiation, wind velocity, etc., which change significantly. Therefore, the Equation (20) suggests that the daily surface conductance estimation is mainly based on the temporal variation in environmental factors between unclear-sky days and clear-sky days, which also indicates that surface-dependent parameters including minimum canopy conductance, empirical parameters related to the radiation and temperature factors have less important roles in the estimation because of their stabilities over time, although they have different values among land covers.
3.3. Evaluation Index
For the quantitative analysis of model performance, a set of evaluation indexes was selected. The coefficient of determination () is used to provide a measure of consistency between estimation and observation. The mean bias error () and the root-mean-square error () are usually used to measure the average difference between estimation and observation. The mean relative error () describes the relative extent of deviation of estimation from observation. The calculation methods of these evaluation indexes are listed as follows:
where is No.i time estimation and is No.i time measurement. and are mean of estimations and measurements respectively, and is the number of measurements.
4. Results
4.1. Estimation of Surface Conductance
Surface conductance can be estimated as the inversion of the P-M equation with EC and meteorological measurements. Therefore, the surface conductance model described in Section 3.1 was calibrated using inverted values calculated with part of site measurements and key parameters, such as and , which were determined at sites GT and MY. The surface conductance estimations using satellite and meteorological data at both sites were compared to the inverted results using site measurements. The validation results are shown in Figure 4. The sample numbers indicate that both satellite data and EC measurements are of good quality.
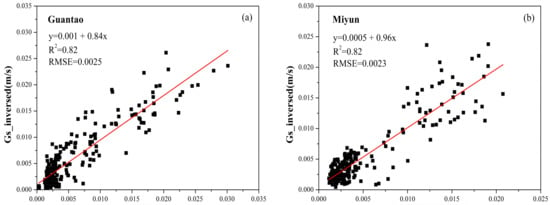
Figure 4.
Comparisons of surface conductance between inverted results of the P-M equation and estimated results of the surface conductance model at the Guantao (a) and Miyun (b) stations. The red line is fitting line. The black boxes indicate values of surface conductance.
As shown in the linear fitting results in Figure 4, GT shows a high coefficient of determination value ( = 0.82) and low root mean square error value ( = 0.0025 m/s). MY shows values similar to those of GT. Both sites have smaller fluctuations compared to the inverted results. In addition, the plots exhibit an obvious seasonal change with the crop calendar. The surface conductance estimations are relatively high values (scattered points greater than 0.015 m/s) from April to May and July to August at GT and from July to August at MY, which are consistent with the growth of the winter wheat and summer maize. A significant correlation between the estimation and inverted results indicated that the surface conductance model mentioned in this study can effectively estimate the surface conductance, when the empirical parameters are accurately calibrated.
4.2. Comparison between Different Methods with EC Measurements
The method proposed in this study (hereafter referred to as the enhanced method) and another method (hereafter referred to as original method) were coupled into the P-M equation to estimate the daily basin ET, and the comparison was executed to evaluate the performance of these two methods. The original method estimates the daily surface conductance by multiplication and temporal variation of limited variables including , net radiation (), soil moisture () and wind velocity () [33]. Equation (27) gives the expression of the original method. Figure 5 reports the estimation of daily ET plotted against the EC measurements at the GT and MY sites.
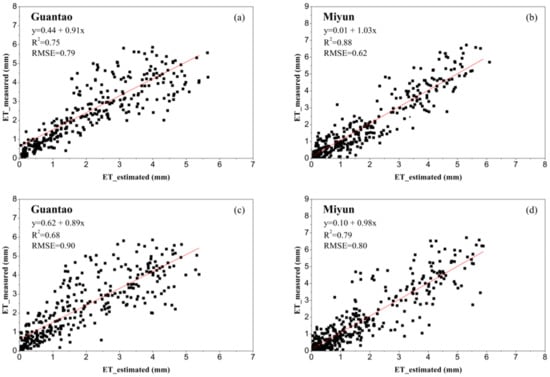
Figure 5.
Daily ET comparisons between estimations and EC measurements. (a) Estimation with enhanced method at GT site; (b) estimation with enhanced method at MY site; (c) estimation with original method in GT site; and (d) estimation with original method at MY site. The red line is fitting line. The black boxes indicate values of ET.
The figure above clearly demonstrates that two methods can estimate ET to a reasonable extent, while the enhanced method shows less dispersed results and a higher correlation with the measurements than the original method. For site GT, the values increase from 0.68 to 0.75, and the decreased from 0.90 to 0.79. The improvement mainly occurred during the crop growing season, which can be proven because the high ET values in the scatter plots displayed various distributions among the two methods. This finding indicates that the enhanced method can better describe the surface conductance variation in the crop growth. The same analysis was used to evaluate the differences between the two methods at site MY, and comparable results were obtained. The enhanced method also performed better than the original method, with values that improved from 0.79 to 0.88 and an that reduced from 0.80 to 0.62.
Due to the gaps in time series EC measurements and for convenient comparability, monthly averaged ET was calculated from the field observations and remote sensing estimations. Figure 6 shows a comparison of the results.
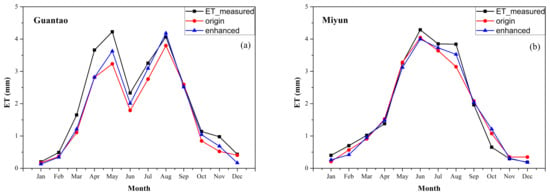
Figure 6.
Variation in the monthly averaged ET from both methods and EC measurements at stations Guantao (a) and Miyun (b).
As shown in Figure 2, winter wheat and summer maize reach their growth peaks in May and August, respectively. For site GT, the ET temporal variations correspond to the crop calendar, which fluctuates throughout the whole year and exhibits a relatively low value because of the winter wheat harvest. ET estimated from the enhanced method shows a characteristic advance compared to the original method, especially during the growing season. The former has less distinction with measurements in May and August than the latter, which suggests that the surface conductance model used in this paper can better reflect the physiological changes in the crops. For site MY, ET has high values from June to August, following the orchard and summer maize growth periods. The enhanced method also better estimates the peak growth of summer maize in August, compared to the original method.
Several statistical indices were selected to evaluate the estimation accuracy and consistency of measurements. The results are shown in Table 3. The and values of monthly averaged ET show the same trend as the daily results for both sites. The values range from −14.6% to −12.5% for the GT site and from −3.3% to −2.8% for the MY site, which indicates a smaller estimation deviation of the enhanced method from the measurements. The values also show notable differences among the results of both methods and show a preferable performance from the enhanced method. Both methods slightly underestimated the ET compared with field observations.

Table 3.
Comparison statistics of the daily and monthly averaged ET for both methods at the Guantao and Miyun sites.
4.3. Spatiotemporal Distribution of Results
The gap-filling method proposed in this study was applied combined with P-M equation to estimate regional daily ET for Hai River Basin. As shown in Figure 7, the ET spatial patterns showed a decrease from southeast to northwest and were consistent with the precipitation pattern. The precipitation in the east and southeast regions was significantly greater than in other regions, and accordingly, the ET values were high in this area. Further analysis of the land cover map (Figure 1) revealed that crops in the southeast region consumed more water than the forest in the northwest region and urban areas. In addition, the area around Bohai Bay showed the highest ET, where the surface was moist, and the rainfall was abundant. Crop land and forest were further classified into dry farmland and paddy field and into arbour forest and shrub forest, respectively, based on Figure 1. The annual ET values for different land covers were counted and are displayed in Figure 8. Water surface was the highest, with more than 700 mm. Paddy field was slightly higher than dry farmland, due to the different crops. For the forest, arbour evaporated more than shrub, while the ET of forest was less than the cropland. Grassland and artificial surface were the lowest among these classes. The difference between ET and precipitation in the artificial surface resulted from many urban areas being covered by impervious surfaces, such as roads and buildings. In addition, Figure 9 shows the temporal variation in the monthly ET over the whole basin. The values increased gradually from January to May and decreased in June, which was influenced by the variation in meteorological elements and phenology of winter wheat. A rapid recover in July and August was shown because of the growth of summer maize.
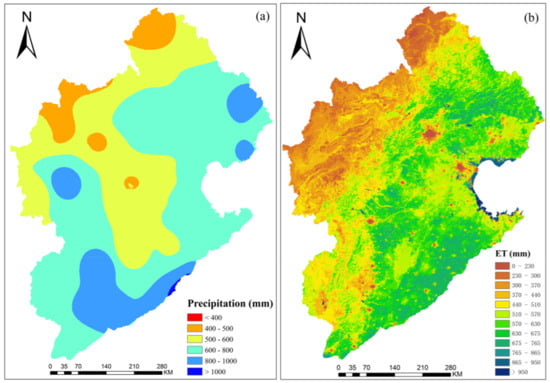
Figure 7.
Spatial distribution of (a) the annual precipitation and (b) annual ET over the Hai River Basin for 2016.
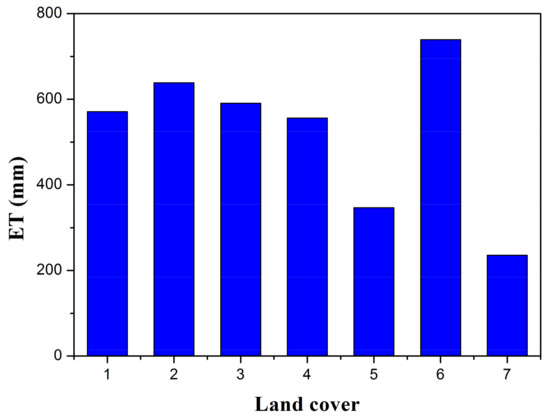
Figure 8.
Variation in the annual ET for different land covers over the whole basin from the enhanced method (1: Dry farmland, 2: Paddy field, 3: Arbour forest, 4: Shrub forest, 5: Grassland, 6: Water surface, 7: Artificial surface).
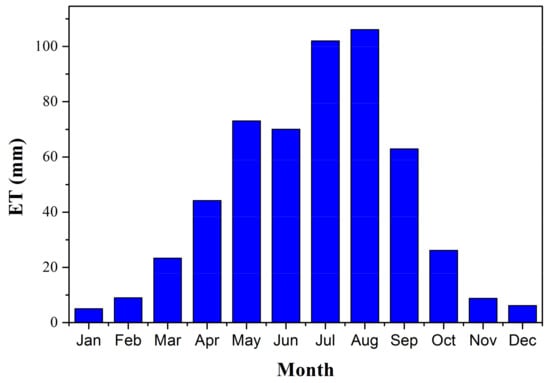
Figure 9.
Variation in the monthly ET over the whole basin from the enhanced method.
5. Discussion
Surface conductance is a key parameter in the P-M equation and is difficult to estimate, especially at the regional scale because of its complex underlying surface conditions. In this study, daily surface conductance is estimated from inverted surface conductance for a clear day to meet the requirements of the P-M equation to acquire the regional ET. The gap-filling method used here contains the estimation methods of the surface conductance and temporal change in surface variations, considering both the surface conductance mechanism and environmental factors.
Surface conductance has many impacting factors and cannot be displayed well by the model. To decrease the ET error when surface conductance is used in this study, a surface conductance simulation from the ET inversion is obtained through the P-M equation. Otherwise, ET is separated into two parts: vegetation transpiration calculated from the P-M equation and soil evaporation calculated from the equilibrium ET. Correspondingly, net radiation is also separated into two parts through the vegetation fraction, which simplifies the partition process of net radiation compared with others but matters little in the ET accuracy. In addition, the soil EF calculated through the land-atmosphere interactions replaces the soil moisture usage, can improve the applicability of the soil evaporation model and avoids soil conductance. For the canopy conductance, the Jarvis model is applied, because it performed well in many previous studies [44,46,47]. According to the results shown in Figure 4, the estimations from the surface conductance model have a near-linear relationship with the inversion results from the in situ measurements.
Accurate estimation of surface conductance requires calibration of several key parameters, including maximum canopy conductance, empirical parameters related to radiation, temperature, vapour pressure deficit and the adjustment factor in the soil evaporation calculation. All parameters should be calibrated with in situ measurements, meaning the field measurements for each type of land cover are needed for calibration, which is hard to accomplish. The surface conductance gap-filling method can avoid the calibration and adopt the reference values from other studies, as shown in Table 2. In this study, the surface conductance model is not used to calculate conductance values; it is only used for expression. Daily surface conductance is estimated from clear day surface conductance, which mainly depends on the environmental factor variations. The parameters mentioned above stay constant over time and therefore do not influence the results.
ET differs significantly in various land cover types. The method discussed here is applied only in two sites for two crops. The results are limited by the field datasets for specific underlying surfaces. Further research should be focus on the applicability of the method to other crops and land cover types, as well as in arid and semi-arid regions. In this study, two sites are surrounded by homogeneous and flat arable land. Therefore, field measurements are representative and matched for the MODIS pixels. As shown in Figure 5 and Figure 6, the method proposed in this study performed better than the original method. The latter contains only three environmental factors and adopted a multiplication form. Comparably, the former is more considerate and has a better mechanism. Surface conductance is strongly determined by the surface itself and the environmental factors, especially the meteorological elements. In the future, the contribution of variables for surface conductance should be studied to select the main variables, which will benefit the surface conductance simulation.
6. Conclusions
This study proposed a gap-filling method to acquire daily surface conductance from clear day surface conductance estimation. The method combines a time extension method with the canopy and a surface conductance model and is carried out with multi-source remote sensing data, coupled with the P-M equation to estimate the regional daily ET. The field observations over the winter wheat and summer maize for the two sites are obtained to validate the method’s performance. The results show that the method performs well at both sites, with the values reaching 0.75 and 0.88 at the Guantao and Miyun sites, respectively. Compared to other methods, the method proposed in this study increases the accuracy of the ET estimation to different degrees. The reason attributed to improvements might be the comprehensiveness of the impact factors and mechanism of the latter method. However, limited by the availability of in situ data in this study, this method is applied to only two crops. Further applications are necessary in different land cover types and climatic conditions.
Acknowledgments
This work was supported in part by National Key Research and Development Program (Grant No.: 2016YFA0600304), Advanced Science Foundation Research Project of Chinese Academy of Sciences (Grant No.: QYZDY-SSW-DQC014) and Science and Technology Service Network Initiative of Chinese Academy of Sciences (Grant.: KFJ-STS-ZDTP-009). We thank NASA, NOAA, CMA and JAXA for providing the remote sensing data. The authors also thank the Hai River Water Conservancy Commission and Beijing water conservancy and Hydropower Technology Center for providing the AWS and EC data.
Author Contributions
Jiaming Xu contributed to the research experiments, analyzed the data, and wrote the paper. Bingfang Wu conceived the experiments, and was responsible for the research analysis. Nana Yan, Weiwei Zhu, Qiang Xing and Shen Tan collected and preprocessed the original data. All the co-authors helped to revise the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bastiaanssen, W.G.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Choudhury, B. A biophysical process-based estimate of global land surface evaporation using satellite and ancillary data. In Observing Land from Space: Science, Customers and Technology; Springer: Berlin, Germany, 2000; pp. 119–126. [Google Scholar]
- Jiang, L.; Islam, S.; Guo, W.; Jutla, A.S.; Senarath, S.U.; Ramsay, B.H.; Eltahir, E. A satellite-based daily actual evapotranspiration estimation algorithm over south florida. Glob. Planet. Chang. 2009, 67, 62–77. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Brotzge, J.A.; Crawford, K.C. Examination of the surface energy budget: A comparison of eddy correlation and bowen ratio measurement systems. J. Hydrometeorol. 2003, 4, 160–178. [Google Scholar] [CrossRef]
- Brutsaert, W. Use of pan evaporation to estimate terrestrial evaporation trends: The case of the tibetan plateau. Water Resour. Res. 2013, 49, 3054–3058. [Google Scholar] [CrossRef]
- Kleissl, J.; Gomez, J.; Hong, S.-H.; Hendrickx, J.; Rahn, T.; Defoor, W. Large aperture scintillometer intercomparison study. Bound.-Layer Meteorol. 2008, 128, 133–150. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.; Jia, Z.; Zhu, M.; Bai, J.; Wang, J. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Schelle, H.; Durner, W.; Iden, S.C.; Fank, J. Simultaneous estimation of soil hydraulic and root distribution parameters from lysimeter data by inverse modeling. Procedia Environ. Sci. 2013, 19, 564–573. [Google Scholar] [CrossRef]
- Schrader, F.; Durner, W.; Fank, J.; Gebler, S.; Pütz, T.; Hannes, M.; Wollschläger, U. Estimating precipitation and actual evapotranspiration from precision lysimeter measurements. Procedia Environ. Sci. 2013, 19, 543–552. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (sebs) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and modis satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Leuning, R.; Zhang, Y.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using modis leaf area index and the penman-monteith equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on modis and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a modis global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar]
- Su, H.; McCabe, M.; Wood, E.; Su, Z.; Prueger, J. Modeling evapotranspiration during smacex: Comparing two approaches for local-and regional-scale prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar]
- Su, H.; Wood, E.; McCabe, M.; Su, Z. Evaluation of remotely sensed evapotranspiration over the ceop eop-1 reference sites. J. Meteorol. Soc. Jpn. Ser. II 2007, 85, 439–459. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.; Roerink, G.; Van der Wal, T. A remote sensing surface energy balance algorithm for land (sebal).: Part 2: Validation. J. Hydrol. 1998, 212, 213–229. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (sebal). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.L. How sensitive is sebal to changes in input variables, domain size and satellite sensor? J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Anderson, M.C.; Zaitchik, B.; Hain, C.R.; Crow, W.T.; Ozdogan, M.; Chun, J.A.; Evans, J. Comparison of prognostic and diagnostic surface flux modeling approaches over the nile river basin. Water Resour. Res. 2014, 50, 386–408. [Google Scholar] [CrossRef]
- Anderson, M.; Norman, J.; Diak, G.; Kustas, W.; Mecikalski, J. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental united states based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Alfieri, J.G.; Gao, F.; Hain, C.; Prueger, J.H.; Evett, S.; Colaizzi, P.; Howell, T.; Chávez, J.L. Mapping daily evapotranspiration at landsat spatial scales during the bearex’08 field campaign. Adv. Water Resour. 2012, 50, 162–177. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B. A multi-scale remote sensing model for disaggregating regional fluxes to micrometeorological scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
- Norman, J.; Anderson, M.; Kustas, W.; French, A.; Mecikalski, J.; Torn, R.; Diak, G.; Schmugge, T.; Tanner, B. Remote sensing of surface energy fluxes at 101-m pixel resolutions. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y. Monitoring daily evapotranspiration over two california vineyards using landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
- Wu, B.; Xiong, J.; Yan, N. Etwatch: Models and methods. J. Remote Sens. 2010, 15, 224–230. [Google Scholar]
- Wu, B.; Zhu, W.; Yan, N.; Feng, X.; Xing, Q.; Zhuang, Q. An improved method for deriving daily evapotranspiration estimates from satellite estimates on cloud-free days. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1323–1330. [Google Scholar] [CrossRef]
- Wu, B.-F.; Xiong, J.; Yan, N.-N.; Yang, L.-D.; Du, X. Etwatch for monitoring regional evapotranspiration with remote sensing. Adv. Water Sci. 2008, 19, 671–678. [Google Scholar]
- Xiong, J.; Wu, B.; Liu, S.; Yan, N.; Wu, F. Etwatch: Calibration methods. J. Remote Sens. 2011, 15, 240–254. [Google Scholar]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the hai river basin, China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo i: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Team, M.C.M.; Ackerman, S.; Strabala, K.; Menzel, P.; Frey, R.; Moeller, C.; Gumley, L.; Baum, B.; Schaaf, C.; Riggs, G. Discriminating clear-sky from cloud with modis algorithm theoretical basis document (mod35). ATBD Ref. ATBD-MOD-06 Ver. 1997, 4, 115. [Google Scholar]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality ndvi time-series data set based on the savitzky–golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Feng, X.; Wu, B.; Yan, N. A method for deriving the boundary layer mixing height from modis atmospheric profile data. Atmosphere 2015, 6, 1346–1361. [Google Scholar] [CrossRef]
- Wu, B.; Liu, S.; Zhu, W.; Yan, N.; Xing, Q.; Tan, S. An improved approach for estimating daily net radiation over the heihe river basin. Sensors 2017, 17, 86. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Liu, S.; Zhu, W.; Yu, M.; Yan, N.; Xing, Q. A method to estimate sunshine duration using cloud classification data from a geostationary meteorological satellite (fy-2d) over the heihe river basin. Sensors 2016, 16, 1859. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Yan, N.; Xiong, J.; Bastiaanssen, W.; Zhu, W.; Stein, A. Validation of etwatch using field measurements at diverse landscapes: A case study in hai basin of china. J. Hydrol. 2012, 436, 67–80. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Yang, K.; Ma, M.; Li, X.; Zhang, Z.; Wang, X. A revised surface resistance parameterisation for estimating latent heat flux from remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 76–84. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Xu, D.; Cai, J.; Li, F. Evapotranspiraton estimation based on scaling up from leaf stomatal conductance to canopy conductance. Agric. For. Meteorol. 2011, 151, 1086–1095. [Google Scholar] [CrossRef]
- Zhuang, Q.; Wu, B.; Yan, N.; Zhu, W.; Xing, Q. A method for sensible heat flux model parameterization based on radiometric surface temperature and environmental factors without involving the parameter kb−1. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 50–59. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Sellers, P.; Mintz, Y.; Sud, Y.E.A.; Dalcher, A. A simple biosphere model (sib) for use within general circulation models. J. Atmos. Sci. 1986, 43, 505–531. [Google Scholar] [CrossRef]
- Jarvis, P. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Phil. Trans. R. Soc. Lond. B 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Hu, G.; Jia, L. Monitoring of evapotranspiration in a semi-arid inland river basin by combining microwave and optical remote sensing observations. Remote Sens. 2015, 7, 3056–3087. [Google Scholar] [CrossRef]
- Thompson, N.; Barrie, I.; Ayles, M. The meteorological office rainfall and evaporation calculation system: Morecs, (July 1981). Hydrol. Memos 1981, 45, 27–306. [Google Scholar]
- Lambers, H.; Pons, T.; Chapin, F.S. Plant Physiological Ecology, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the penn state–ncar mm5 modeling system. Part i: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Dickinson, R.E. Modeling evapotranspiration for three-dimensional global climate models. Clim. Process. Clim. Sensit. 1984, 58–72. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Gellens-Meulenberghs, F. Evapotranspiration modelling at large scale using near-real time msg seviri derived data. Hydrol. Earth Syst. Sci. 2011, 15, 771. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C.; Wang, S. Predicting forest evapotranspiration by coupling carbon and water cycling based on a critical stomatal conductance model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4469–4477. [Google Scholar] [CrossRef]
- Yebra, M.; Van Dijk, A.; Leuning, R.; Huete, A.; Guerschman, J.P. Evaluation of optical remote sensing to estimate actual evapotranspiration and canopy conductance. Remote Sens. Environ. 2013, 129, 250–261. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Chen, X.L.; Su, Z.B.; Ma, Y.M.; Yang, K.; Wen, J.; Zhang, Y. An improvement of roughness height parameterization of the surface energy balance system (sebs) over the tibetan plateau. J. Appl. Meteorol. Climatol. 2013, 52, 607–622. [Google Scholar] [CrossRef]
- Bouchet, R. Evapotranspiration Reelle, Evapotranspiration Potentielle, et Production Agricole. Ann. Agron. 1963, 14, 743–824. [Google Scholar]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly avhrr and islscp-ii data, validated at 16 fluxnet sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Shuttleworth, W.; Gurney, R.; Hsu, A.; Ormsby, J. Fife: The Variation in Energy Partition at Surface Flux Sites; IAHS Publications: Wallingford, UK, 1989. [Google Scholar]
- Sugita, M.; Brutsaert, W. Daily evaporation over a region from lower boundary layer profiles measured with radiosondes. Water Resour. Res. 1991, 27, 747–752. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).