Thaw Subsidence of a Yedoma Landscape in Northern Siberia, Measured In Situ and Estimated from TerraSAR-X Interferometry
Abstract
1. Introduction
2. Study Area
3. Data and Methods
3.1. Field Measurements of Surface Displacement
3.1.1. Metal Pipes (2013–2017)
3.1.2. Fiberglass Poles (2014–2017)
3.1.3. Sources of Potential Errors in Field Measurements
3.2. SAR Data and Processing
3.3. Optical Satellite Imagery
4. Results
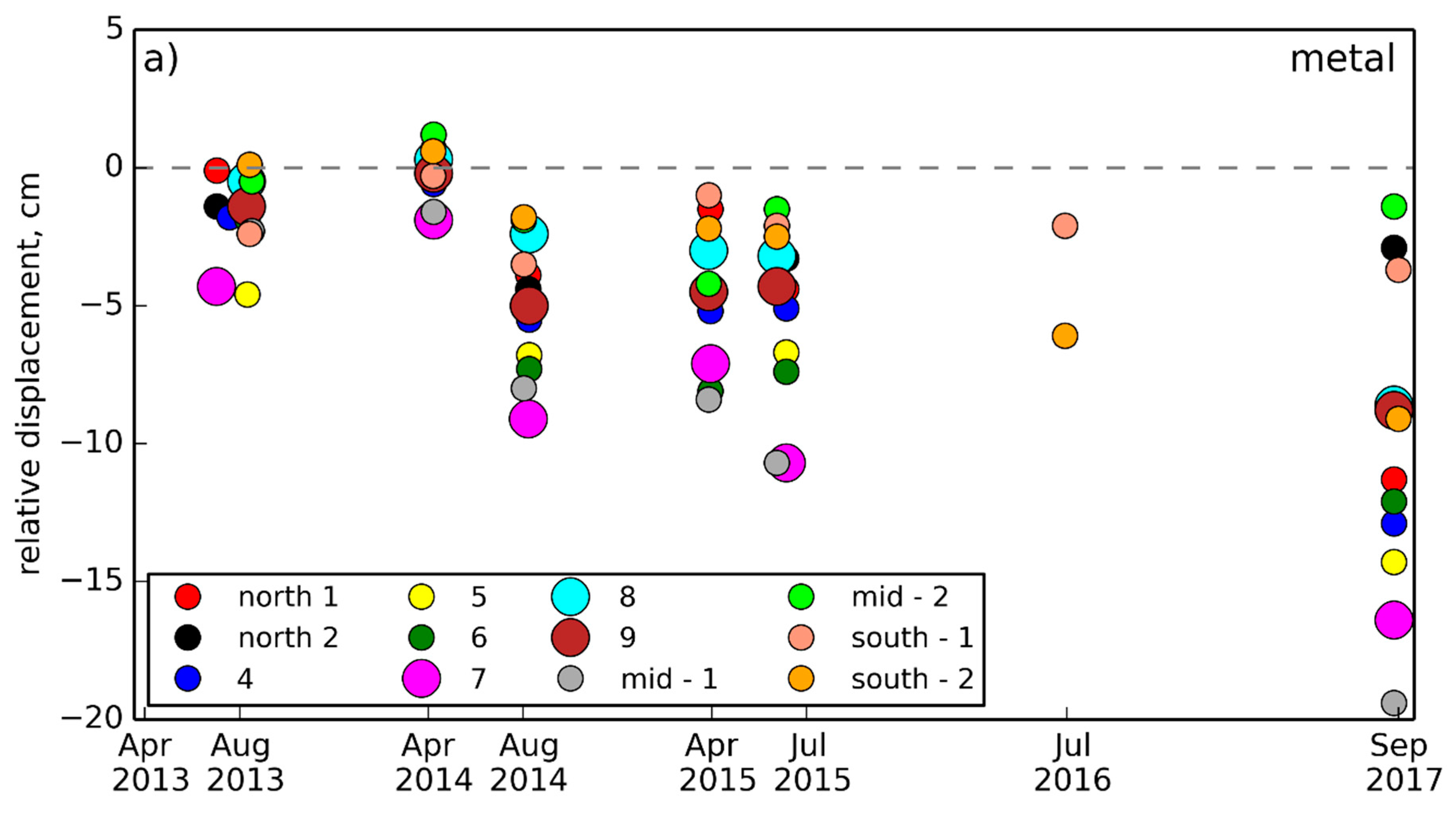
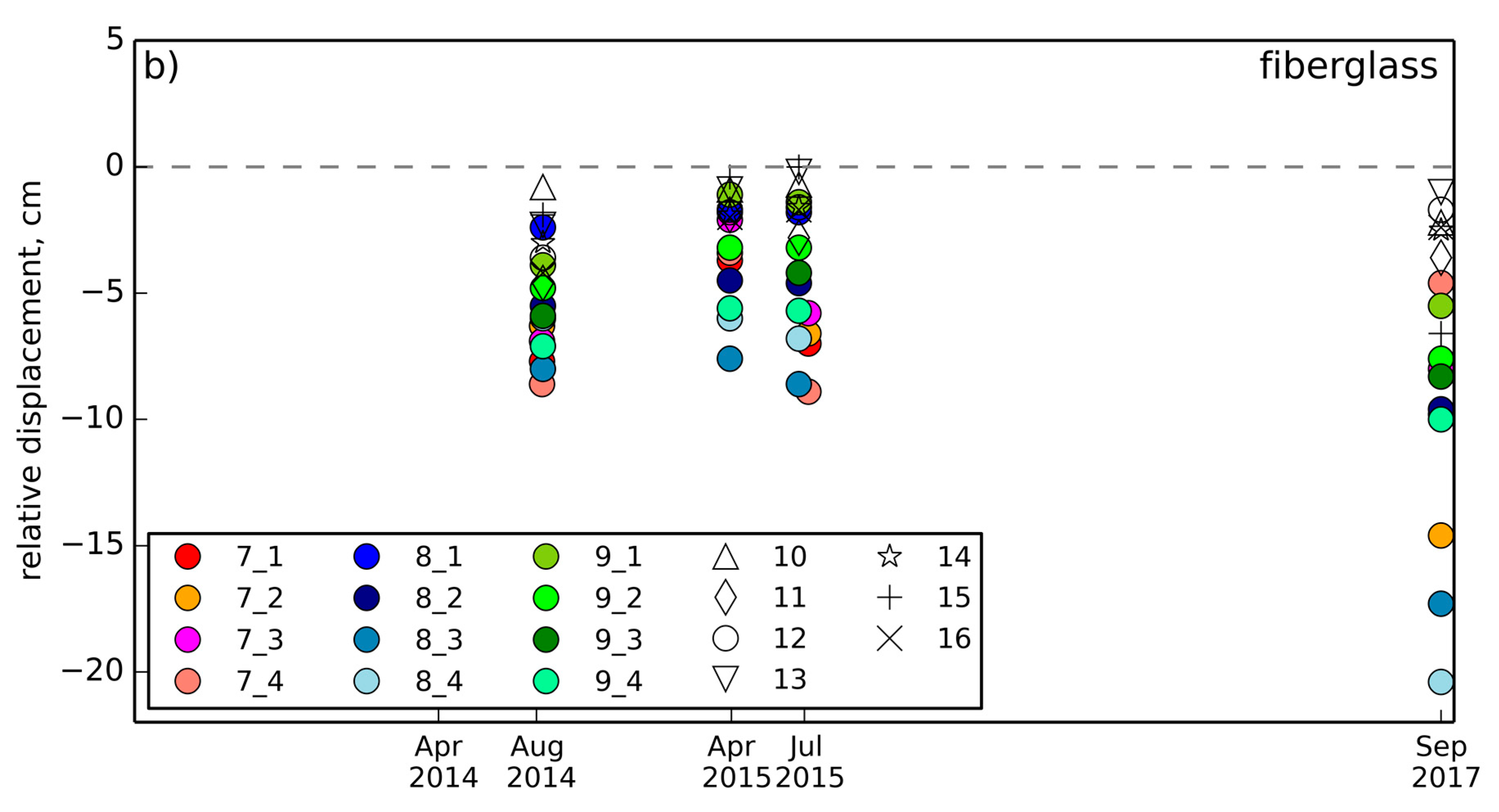
4.1. Field Measurements of Ground Displacement
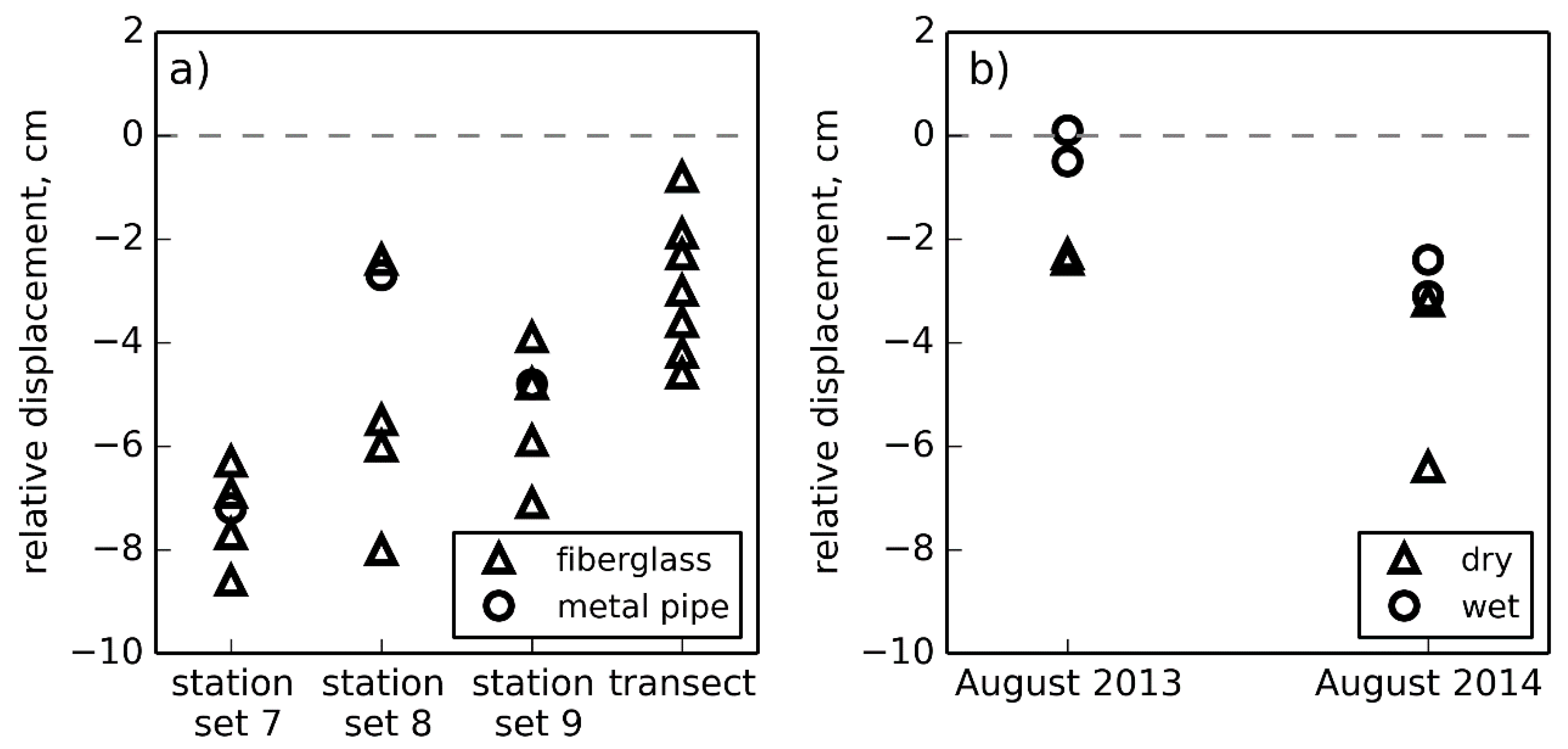
4.1.1. Seasonal Subsidence
4.1.2. Interannual Dynamics
4.1.3. Spatial Variability
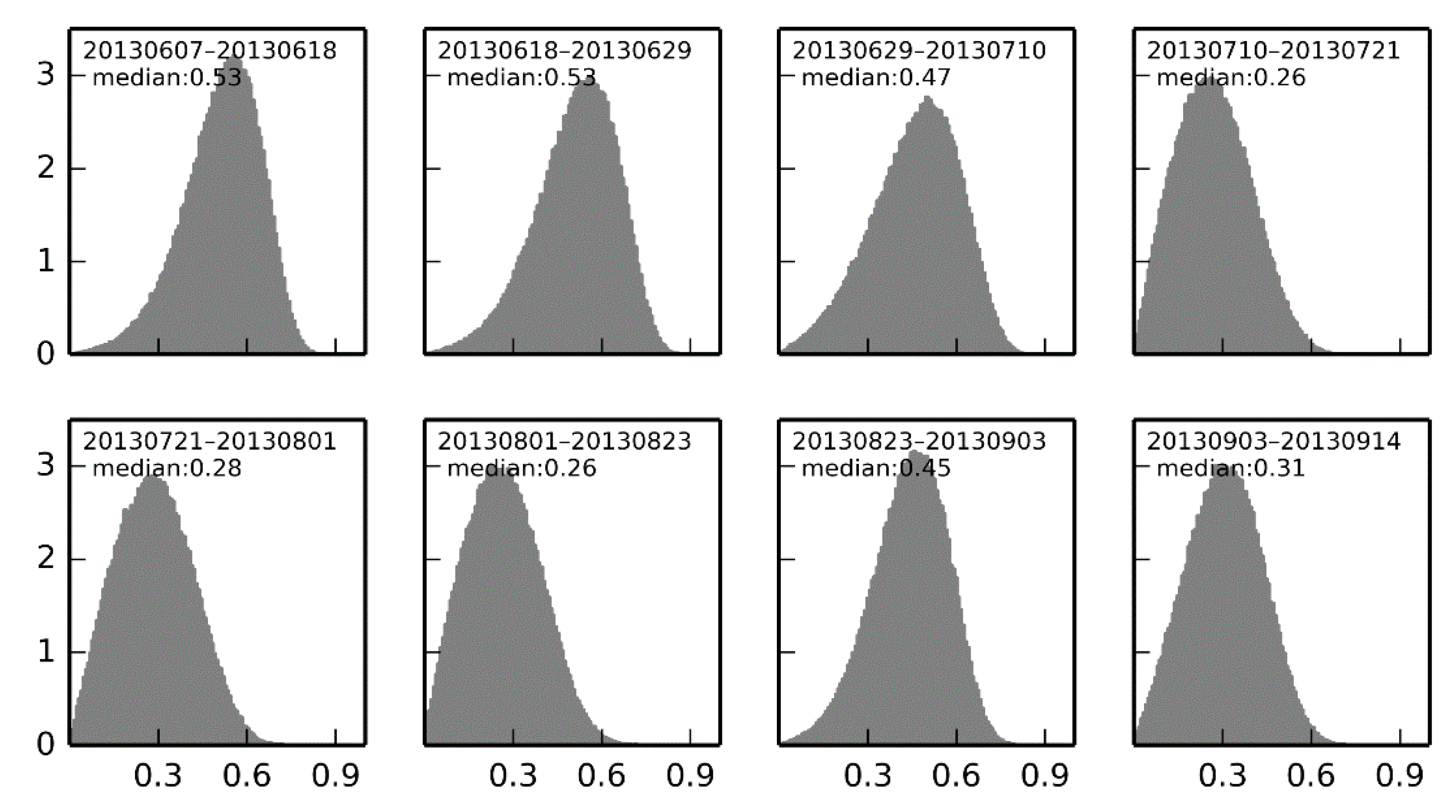
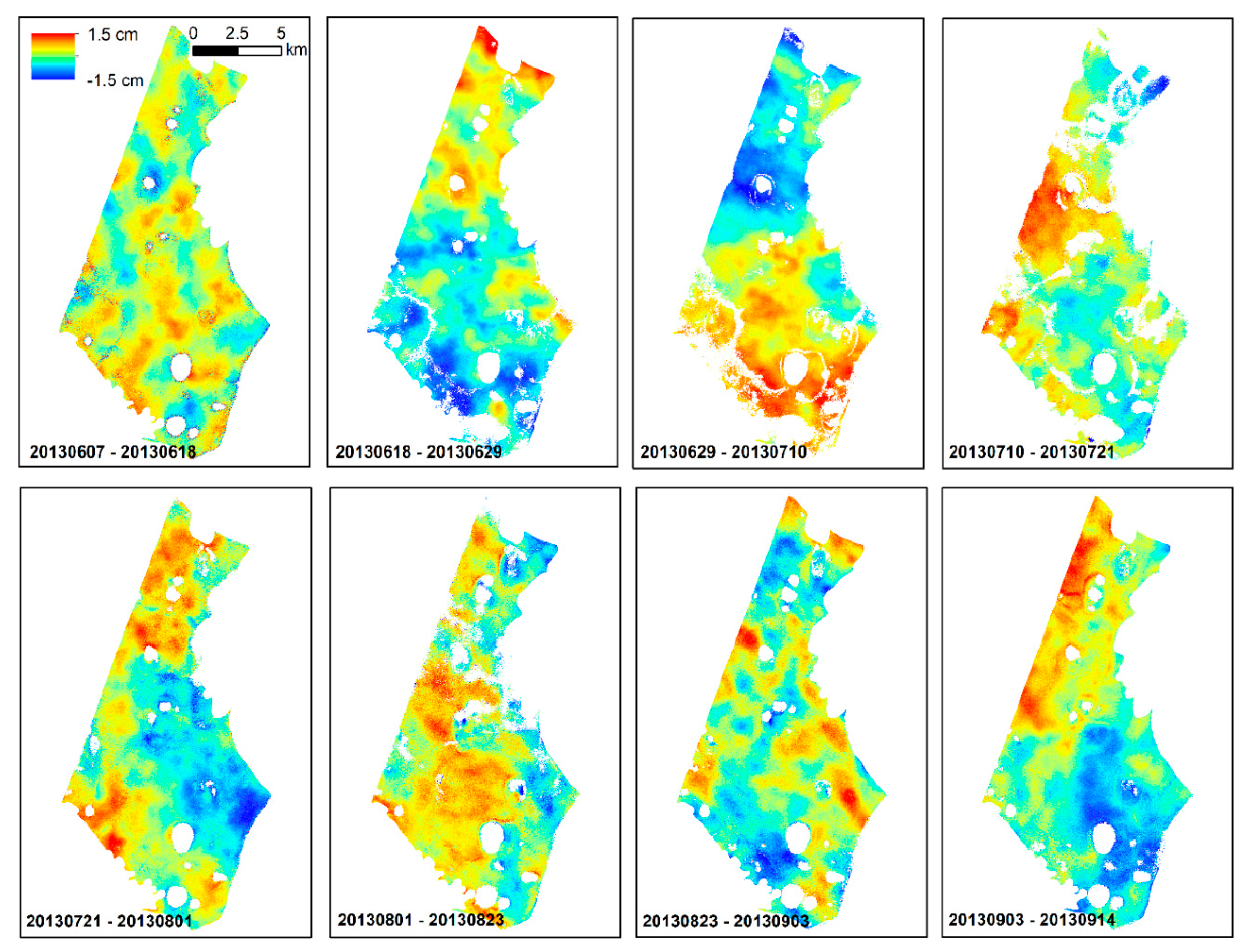
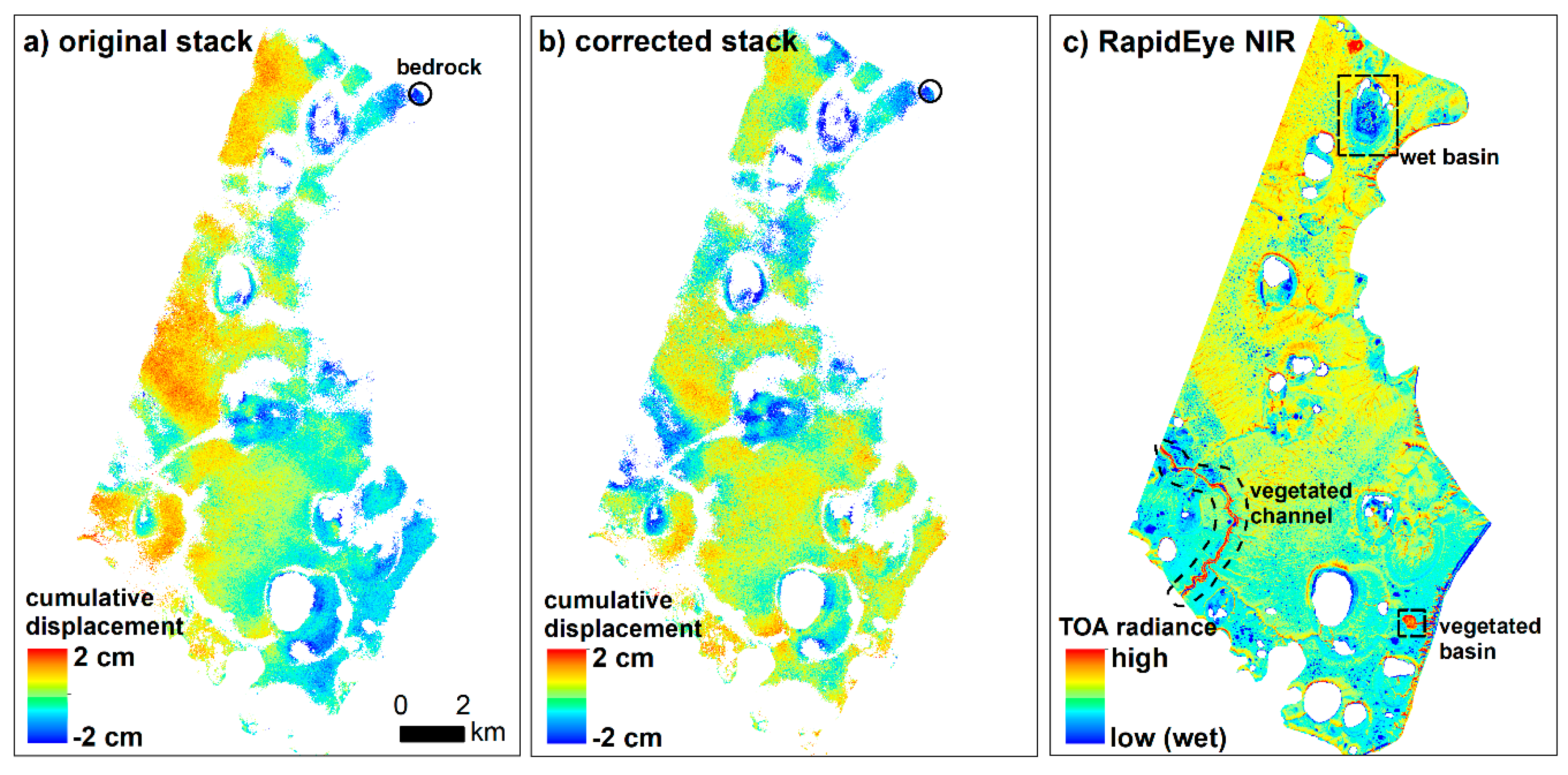
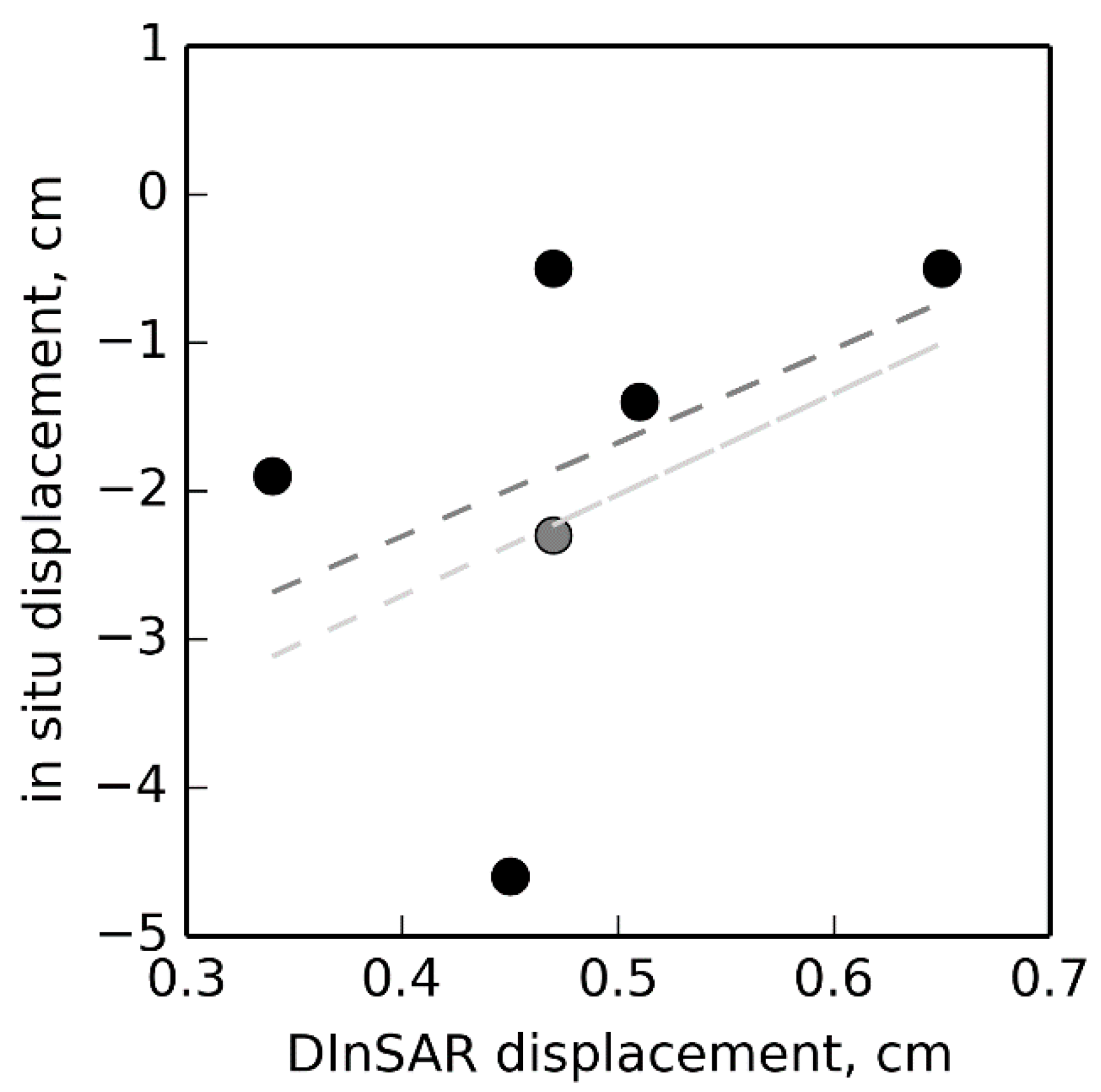
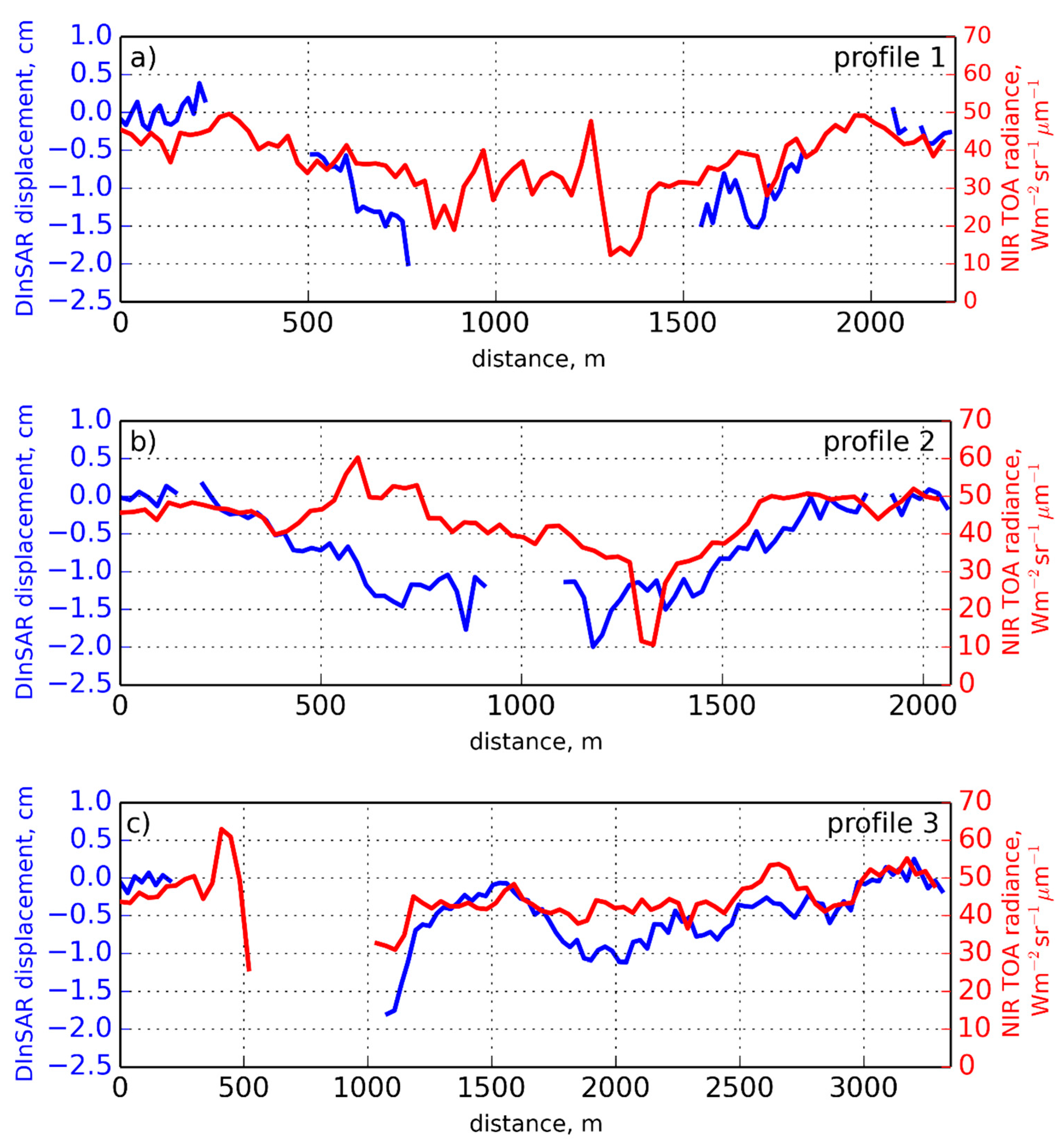
4.2. DInSAR
5. Discussion
5.1. Validity of In Situ Measurements
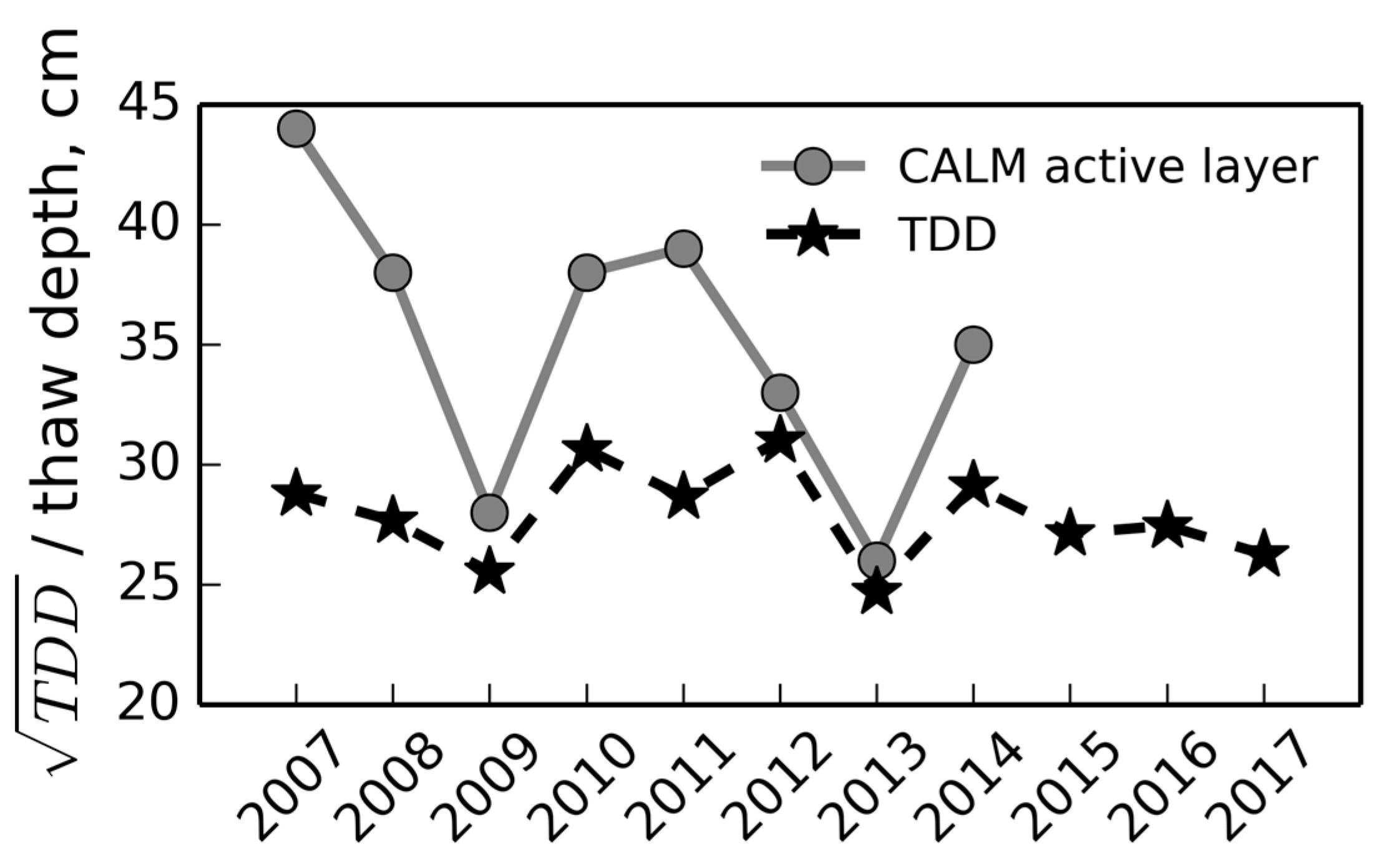
5.2. Temporal Variability of Ground Movements
5.3. Connection to Other Studies
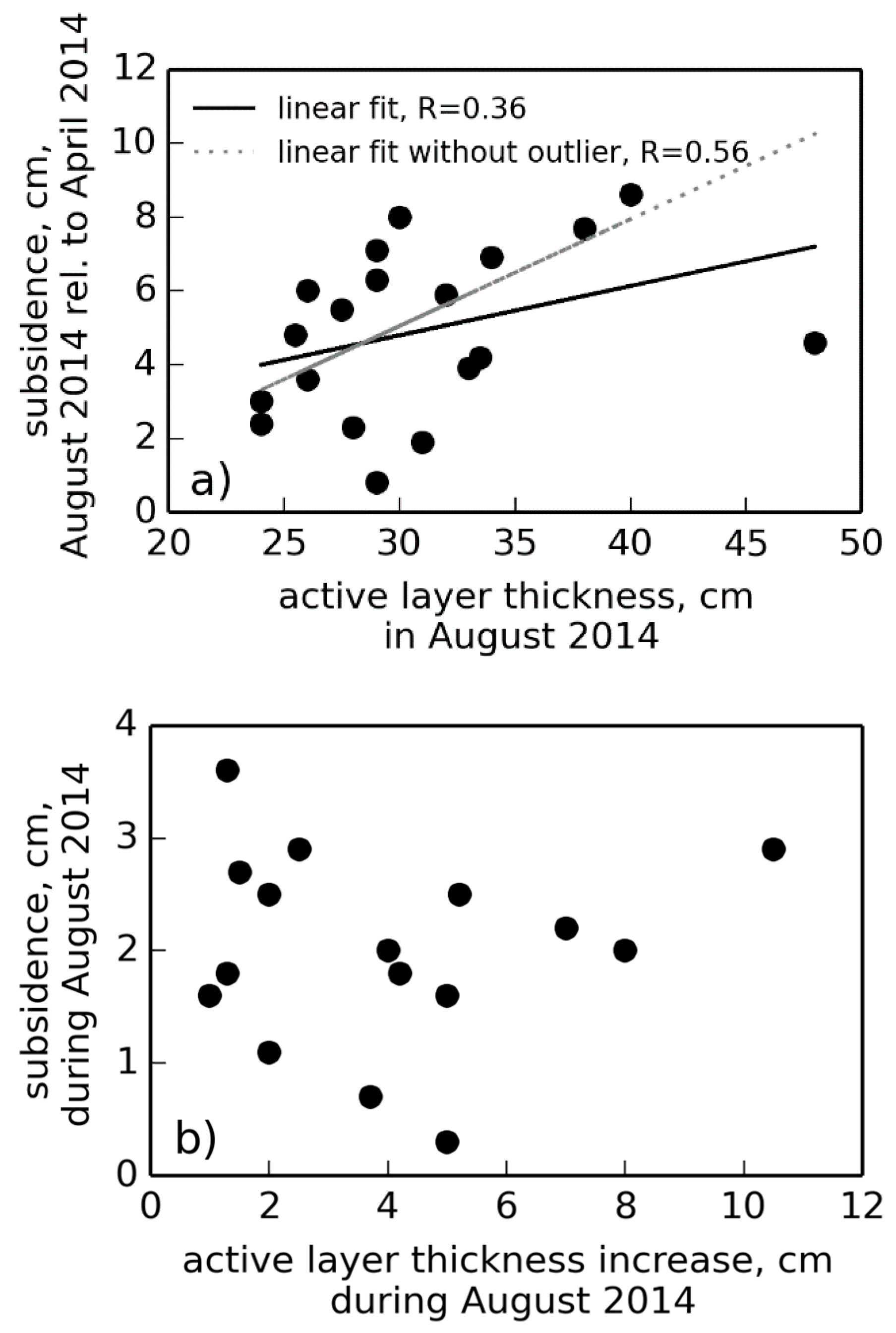
5.4. Relation between Subsidence and Active Layer Depth
5.5. Spatial Variability of Subsidence
5.6. DInSAR: Results, Errors, Validation, and Prospectives
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A

References
- Zhang, T.; Barry, R.G.; Knowldes, K.; Heginbottom, J.A.; Brown, J. Statistics and Characteristics of Permafrost and Ground-Ice Distribution in the Northern Hemisphere. Polar Geogr. 1999, 23, 132–154. [Google Scholar] [CrossRef]
- Melnikov, P.I. Vliyanie podzemnykh vod na glubokoe okhlazhdenie verkhnej zony zemnoj kory (Influence of ground waters on the deep cooling of upper Earth crust). In Merzlotno-Gidrogeologicheskie i Gidrogeotermicheskie Issledovaniya na Vostoke SSSR (Cryo-Hydrogeological and Hydrogeothermal Investigations in the East of USSR); Nauka: Moscow, USSR, 1967; pp. 24–29. (In Russian) [Google Scholar]
- French, H.M. The Periglacial Environment, 3rd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2007. [Google Scholar]
- Langer, M.; Westermann, S.; Heikenfeld, M.; Dorn, W.; Boike, J. Satellite-based modeling of permafrost temperatures in a tundra lowland landscape. Remote Sens. Environ. 2013, 135, 12–24. [Google Scholar] [CrossRef]
- Shiklomanov, N.I.; Streletskiy, D.A.; Little, J.D.; Nelson, F.E. Isotropic thaw subsidence in undisturbed permafrost landscapes. Geophys. Res. Lett. 2013, 40, 6356–6361. [Google Scholar] [CrossRef]
- Little, J.D.; Sandall, H.; Walegur, M.T.; Nelson, F.E. Application of differential global positioning systems to monitor frost heave and thaw settlement in tundra environments. Permafr. Periglac. Proc. 2003, 14, 349–357. [Google Scholar] [CrossRef]
- Beck, I.; Ludwig, R.; Bernier, M.; Strozzi, T.; Boike, J. Vertical movements of frost mounds in subarctic permafrost regions analyzed using geodetic survey and satellite interferometry. Earth Surf. Dyn. 2015, 3, 409–421. [Google Scholar] [CrossRef]
- Streletskiy, D.A.; Shiklomanov, N.I.; Little, J.D.; Nelson, F.E.; Brown, J.; Nyland, K.E.; Klene, A.E. Thaw subsidence in undisturbed tundra landscapes, Barrow, Alaska, 1962–2015. Permafr. Periglac. Proc. 2016, 28, 566–572. [Google Scholar] [CrossRef]
- Harris, C.; Luetschg, M.; Davies, M.C.; Smith, F.; Christiansen, H.H.; Isaksen, K. Field instrumentation for real-time monitoring of periglacial solifluction. Permafr. Periglac. Proc. 2007, 18, 105–114. [Google Scholar] [CrossRef]
- Akagawa, S.; Huang, S.L.; Kanie, S.; Fukuda, M. Movement due to heave and thaw settlement of a full-scale test chilled gas pipeline constructed in Fairbanks Alaska. In Proceedings of the OTC Arctic Technology Conference, Houston, TX, USA, 3–5 December 2012; Offshore Technology Conference: Houston, TX, USA, 2012. [Google Scholar]
- Nixon, M.; Tarnocai, C.; Kutny, L. Long-term active layer monitoring: Mackenzie Valley, northwest Canada. In Proceedings of the 8th International Conference on Permafrost, Zurich, Switzerland, 21–25 July 2003; pp. 821–826. [Google Scholar]
- Short, N.; LeBlanc, A.-M.; Sladen, W.; Oldenborger, G.; Mathon-Dufour, V.; Brisco, B. RADARSAT-2 D-InSAR for ground displacement in permafrost terrain, validation from Iqaluit Airport, Baffin Island, Canada. Remote Sens. Environ. 2014, 141, 40–51. [Google Scholar] [CrossRef]
- Wang, L.; Marzahn, P.; Bernier, M.; Jacome, A.; Poulin, J.; Ludwig, R. Comparison of TerraSAR-X and ALOS PALSAR Differential Interferometry With Multisource DEMs for Monitoring Ground Displacement in a Discontinuous Permafrost Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4074–4093. [Google Scholar] [CrossRef]
- Günther, F.; Overduin, P.P.; Yakshina, I.A.; Opel, T.; Baranskaya, A.V.; Grigoriev, M.N. Observing Muostakh disappear: Permafrost thaw subsidence and erosion of a ground-ice-rich island in response to arctic summer warming and sea ice reduction. Cryosphere 2015, 9, 151–178. [Google Scholar] [CrossRef]
- Rykhus, R.P.; Lu, Z. InSAR detects possible thaw settlement in the Alaskan Arctic Coastal Plain. Can. J. Remote Sens. 2008, 34, 100–112. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wahr, J. InSAR measurements of surface deformation over permafrost on the North Slope of Alaska. J. Geophys. Res. 2010, 115, F03023. [Google Scholar] [CrossRef]
- Strozzi, T.; Wegmuller, U.; Werner, C.; Kos, A. TerraSAR-X interferometry for surface deformation monitoring on periglacial area. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 5214–5217. [Google Scholar]
- Short, N.; Brisco, B.; Couture, N.; Pollard, W.; Murnaghan, K.; Budkewitsch, P. A comparison of TerraSAR-X, RADARSAT-2 and ALOS-PALSAR interferometry for monitoring permafrost environments, case study from Herschel Island, Canada. Remote Sens. Environ. 2011, 115, 3491–3506. [Google Scholar] [CrossRef]
- Zwieback, S.; Hensley, S.; Hajnsek, I. Soil Moisture Estimation Using Differential Radar Interferometry: Toward Separating Soil Moisture and Displacements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5069–5083. [Google Scholar] [CrossRef]
- Zwieback, S.; Liu, X.; Antonova, S.; Heim, B.; Bartsch, A.; Boike, J.; Hajnsek, I. A Statistical Test of Phase Closure to Detect Influences on DInSAR Deformation Estimates Besides Displacements and Decorrelation Noise: Two Case Studies in High-Latitude Regions. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5588–5601. [Google Scholar] [CrossRef]
- Antonova, S.; Kääb, A.; Heim, B.; Langer, M.; Boike, J. Spatio-temporal variability of X-band radar backscatter and coherence over the Lena River Delta, Siberia. Remote Sens. Environ. 2016, 182, 169–191. [Google Scholar] [CrossRef]
- Grigoriev, N.F. The temperature of permafrost in the Lena delta basin–deposit conditions and properties of the permafrost in Yakutia. Yakutsk 1960, 2, 97–101. (In Russian) [Google Scholar]
- Boike, J.; Kattenstroth, B.; Abramova, K.; Bornemann, N.; Chetverova, A.; Fedorova, I.; Fröb, K.; Grigoriev, M.; Grüber, M.; Kutzbach, L.; et al. Baseline characteristics of climate, permafrost and land cover from a new permafrost observatory in the Lena River Delta, Siberia (1998–2011). Biogeosciences 2013, 10, 2105–2128. [Google Scholar] [CrossRef]
- Boike, J.; Langer, M.; Lantuit, H.; Muster, S.; Roth, K.; Sachs, T.; Overduin, P.; Westermann, S.; McGuire, A.D. Permafrost—Physical Aspects, Carbon Cycling, Databases and Uncertainties. In Recarbonization of the Biosphere: Ecosystems and the Global Carbon Cycle; Lal, R., Lorenz, K., Hüttl, R.F.J., Schneider, B.U., von Braun, J., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 159–185. [Google Scholar]
- Grigoriev, M.N. Kriomorfogenez ust’evoy oblasti r. Leny (Cryomorphogenesis of the Lena River Mouth Area); Siberian Branch USSR Academy of Sciences: Yakutsk, Russian, 1993. [Google Scholar]
- Schirrmeister, L.; Grosse, G.; Schwamborn, G.; Andreev, A.; Meyer, H.; Kunitsky, V.V.; Kuznetsova, T.V.; Dorozhkina, M.; Pavlova, E.; Bobrov, A. Late Quaternary history of the accumulation plain north of the Chekanovsky Ridge (Lena Delta, Russia): A multidisciplinary approach. Polar Geogr. 2003, 27, 277–319. [Google Scholar] [CrossRef]
- Wetterich, S.; Kuzmina, S.; Andreev, A.; Kienast, F.; Meyer, H.; Schirrmeister, L.; Kuznetsova, T.; Sierralta, M. Palaeoenvironmental dynamics inferred from late Quaternary permafrost deposits on Kurungnakh Island, Lena Delta, Northeast Siberia, Russia. Quat. Sci. Rev. 2008, 27, 1523–1540. [Google Scholar] [CrossRef]
- Morgenstern, A.; Grosse, G.; Günther, F.; Fedorova, I.; Schirrmeister, L. Spatial analyses of thermokarst lakes and basins in Yedoma landscapes of the Lena Delta. Cryosphere 2011, 5, 849–867. [Google Scholar] [CrossRef]
- State Construction Committee of the USSR. Osnovaniya i Fundamenty na Vechnomezlykh Gruntakh (Bases and Foundations on Permafrost Soils); SNiP 2.02.04-88; State Construction Committee of the USSR: Moscow, Russian, 1991. [Google Scholar]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and interferometric processing software. In Proceedings of the ERS-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2000; p. 1620. [Google Scholar]
- Pitz, W.; Miller, D. The TerraSAR-X satellite. IEEE Trans. Geosci. Remote Sens. 2010, 48, 615–622. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Planet Labs Inc. Planet Imagery Product Specification: Planetscope & Rapideye. 2016. Available online: https://www.planet.com/products/satellite-imagery/files/1611.09_Spec_Sheet_Combined_Imagery_Product_Letter_DraftV3.pdf (accessed on 14 March 2018).
- Buchhorn, M.; Walker, D.A.; Heim, B.; Raynolds, M.K.; Epstein, H.E.; Schwieder, M. Ground-based hyperspectral characterization of Alaska tundra vegetation along environmental gradients. Remote Sens. 2013, 5, 3971–4005. [Google Scholar] [CrossRef]
- Liu, L.; Larson, K.M. Decadal changes of surface elevation over permafrost area estimated using reflected GPS signals. Cryosphere 2018, 12, 477–489. [Google Scholar] [CrossRef]
- Siewert, M.B.; Hugelius, G.; Heim, B.; Faucherre, S. Landscape controls and vertical variability of soil organic carbon storage in permafrost-affected soils of the Lena River Delta. Catena 2016, 147, 725–741. [Google Scholar] [CrossRef]
- Liu, L.; Schaefer, K.; Zhang, T.; Wahr, J. Estimating 1992–2000 average active layer thickness on the Alaskan North Slope from remotely sensed surface subsidence. J. Geophys. Res. 2012, 117, F01005. [Google Scholar] [CrossRef]
- Langer, M.; Westermann, S.; Muster, S.; Piel, K.; Boike, J. The surface energy balance of a polygonal tundra site in northern Siberia—Part 1: Spring to fall. Cryosphere 2011, 5, 151–171. [Google Scholar] [CrossRef]
- Overduin, P.P.; Kane, D.L. Frost Boils and Soil Ice Content: Field Observations. Permafr. Periglac. Proc. 2006, 17, 291–307. [Google Scholar] [CrossRef]
- Liu, L.; Schaefer, K.; Gusmeroli, A.; Grosse, G.; Jones, B.M.; Zhang, T.; Parsekian, A.D.; Zebker, H.A. Seasonal thaw settlement at drained thermokarst lake basins, Arctic Alaska. Atmos. Chem. Phys. 2014, 8, 815–826. [Google Scholar] [CrossRef]
- Rudy, A.C.; Lamoureux, S.F.; Treitz, P.; Short, N.; Brisco, B. Seasonal and multi-year surface displacements measured by DInSAR in a High Arctic permafrost environment. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 51–61. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M.; Motagh, M.; Heim, B.; Chabrillat, S.; Streletskiy, D.; Grosse, G.; Sachs, T.; Kohnert, K. Analysis of summer subsidence in Barrow, Alaska, using InSAR and hyperspectral remote sensing. In Proceedings of the 11th International Conference on Permafrost (ICOP), Potsdam, Germany, 20–24 June 2016; p. 870. [Google Scholar]
- Boike, J.; Wille, C.; Abnizova, A. Climatology and summer energy and water balance of polygonal tundra in the Lena River Delta, Siberia. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]


| Spring 2013 | Summer 2013 | Spring 2014 | Summer 2014 | Spring 2015 | Summer 2015 | Spring 2016 | Summer 2016 | Spring 2017 | Summer 2017 | |
|---|---|---|---|---|---|---|---|---|---|---|
| metal pipes | 25–30 April | irregularly during July and August | 22 April | 5–7 August and 22–23 August | 11 April | 8–20 July | - | - | - | 9–15 September |
| fiberglass poles | - | - | 22 April | 5–7 August and 22–23 August | 11 April | 8–20 July | - | - | - | 9–15 September |
| Station | Potential Subsidence, cm | Measured Subsidence, cm |
|---|---|---|
| south-1 | 0.88 | 1.4 |
| south-2 | 0.51 | −0.4 |
| mid-1 | 0.26 | −0.1 |
| mid-2 | 0.44 | 0.2 |
| north-1 | 0.6 | 0.1 |
| north-2 | 0.63 | 1.4 |
| 4 | 0.58 | 1.5 |
| 7 | 0.73 | 4.3 |
| 8 | 0.24 | −0.4 |
| 9 | 0.44 | 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonova, S.; Sudhaus, H.; Strozzi, T.; Zwieback, S.; Kääb, A.; Heim, B.; Langer, M.; Bornemann, N.; Boike, J. Thaw Subsidence of a Yedoma Landscape in Northern Siberia, Measured In Situ and Estimated from TerraSAR-X Interferometry. Remote Sens. 2018, 10, 494. https://doi.org/10.3390/rs10040494
Antonova S, Sudhaus H, Strozzi T, Zwieback S, Kääb A, Heim B, Langer M, Bornemann N, Boike J. Thaw Subsidence of a Yedoma Landscape in Northern Siberia, Measured In Situ and Estimated from TerraSAR-X Interferometry. Remote Sensing. 2018; 10(4):494. https://doi.org/10.3390/rs10040494
Chicago/Turabian StyleAntonova, Sofia, Henriette Sudhaus, Tazio Strozzi, Simon Zwieback, Andreas Kääb, Birgit Heim, Moritz Langer, Niko Bornemann, and Julia Boike. 2018. "Thaw Subsidence of a Yedoma Landscape in Northern Siberia, Measured In Situ and Estimated from TerraSAR-X Interferometry" Remote Sensing 10, no. 4: 494. https://doi.org/10.3390/rs10040494
APA StyleAntonova, S., Sudhaus, H., Strozzi, T., Zwieback, S., Kääb, A., Heim, B., Langer, M., Bornemann, N., & Boike, J. (2018). Thaw Subsidence of a Yedoma Landscape in Northern Siberia, Measured In Situ and Estimated from TerraSAR-X Interferometry. Remote Sensing, 10(4), 494. https://doi.org/10.3390/rs10040494





