Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea through Multivariate and Multifractal Analysis
Abstract
1. Introduction
2. Data Sets
2.1. Sea Surface Salinity SMOS Data
- Level 1 B product: the input data for the computation of the product in this work is the Level 1 Brightness Temperature product (L1B v620). This product is the output of the image reconstruction of the SMOS measurements and consists of the Fourier components of brightness temperatures in the antenna polarization reference frame. The latency of the products is 6–8 h. The L1B TB product is distributed by the ESA and it is freely available in [22].
- Objectively analyzed SMOS SSS maps provided by the Barcelona Expert Center: the global advanced debiased non-Bayesian L3 9-day SSS maps at available at [23] have been used for assessing the improvements of our proposed methodology at Level 3.
- Level 4 SMOS SSS maps provided by the Barcelona Expert Center: The global L4 advanced SSS maps at available at [23] have been used also for assessing the proposed methodology at Level 4, after applying the multifractal fusion with the OSTIA SST maps.
2.2. Sea Surface Salinity In Situ Data
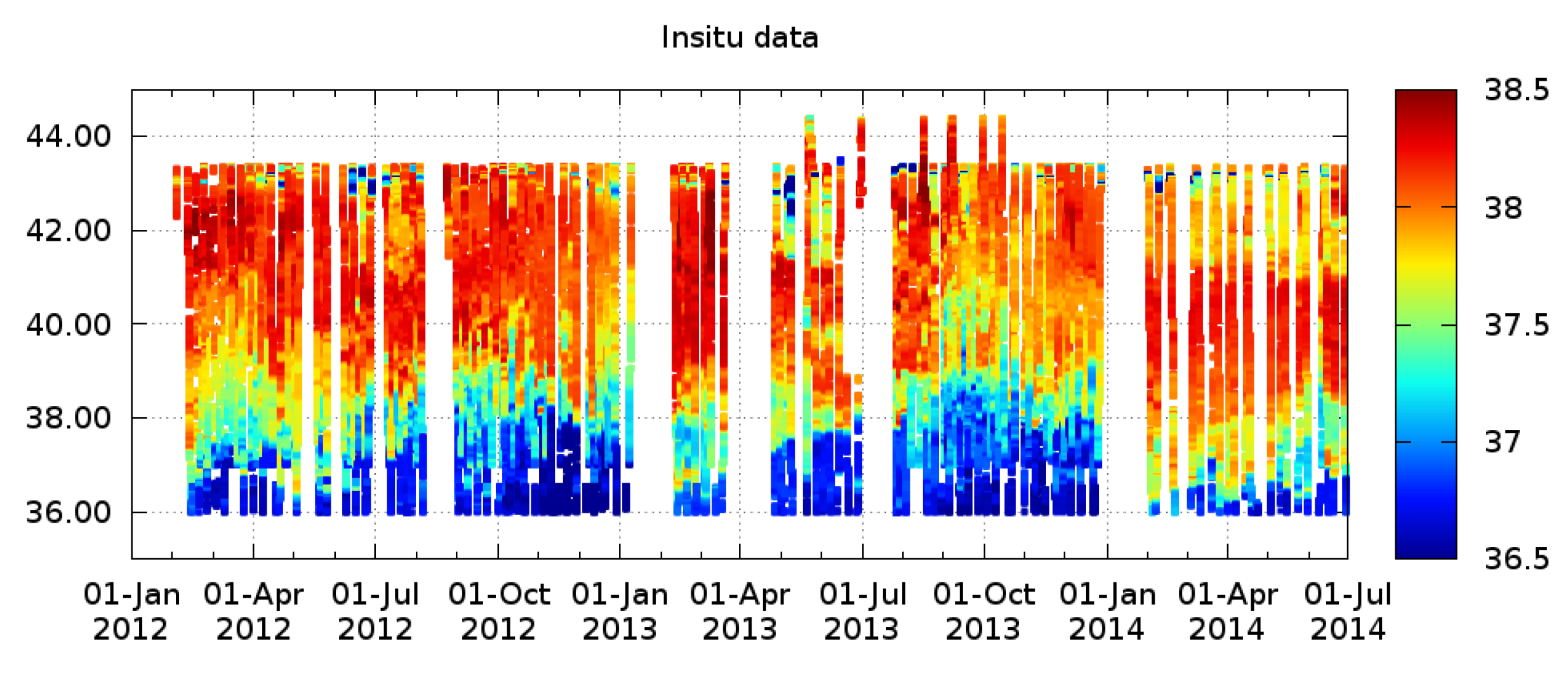
- Argo SSS: SSS data from Argo floats have been used in Section 3.2 for the characterization of the bias of the binned SMOS SSS products. After that, Argo data have been also compared with the resulting SMOS products in Section 4.1. The collocation of SMOS and Argo SSS has been performed as follows: we compare the uppermost SSS measurement provided by the Argo profile at the instant with the SMOS SSS field given by the 9-day map ( days). The Argo floats present errors on the conductivity records when measurements are done shallower than 0.5 m due to air bubbles. Therefore, those records are not considered for the analysis. Additionally, Argo SSS deeper than 10 m have not been considered in our study.
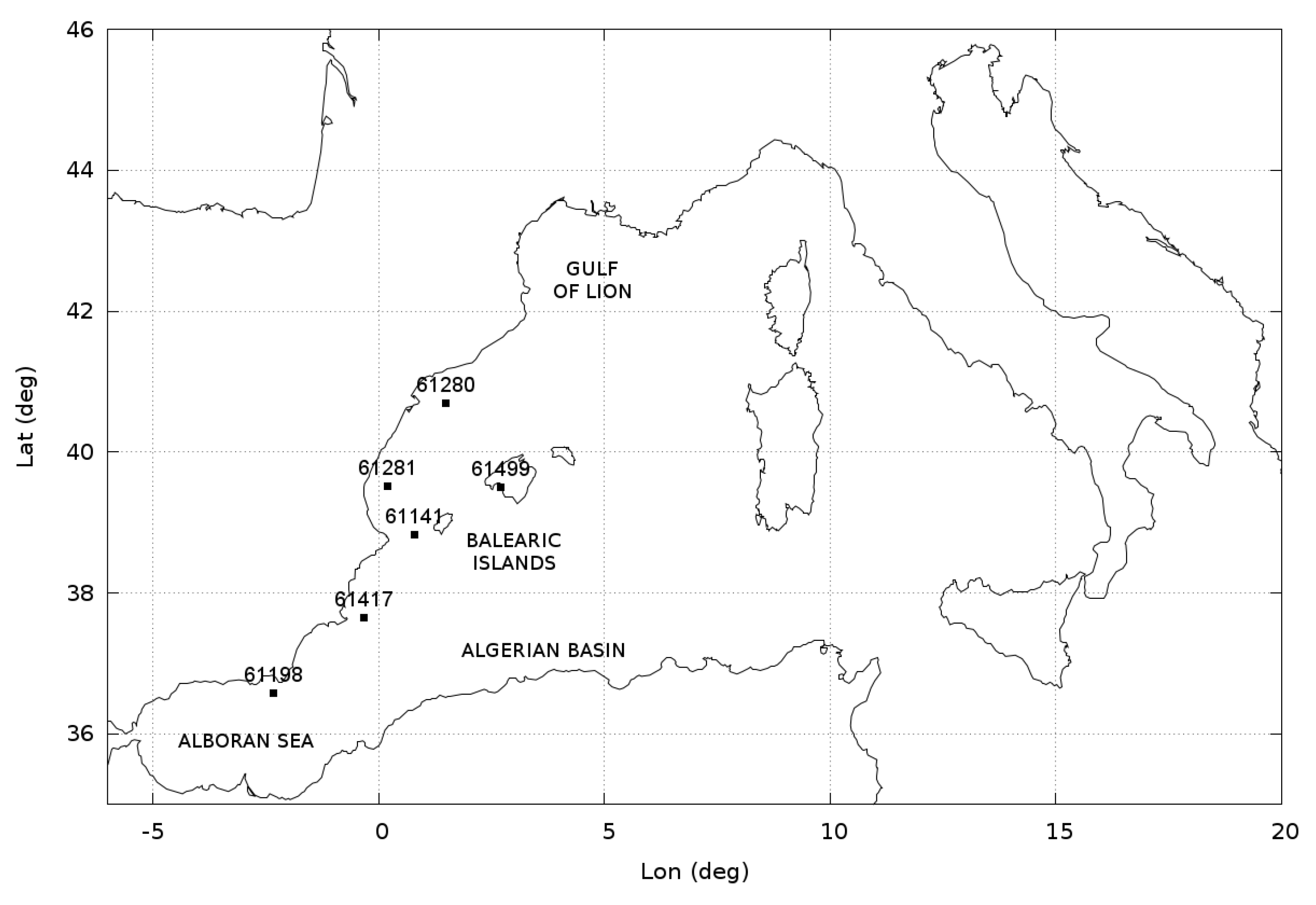
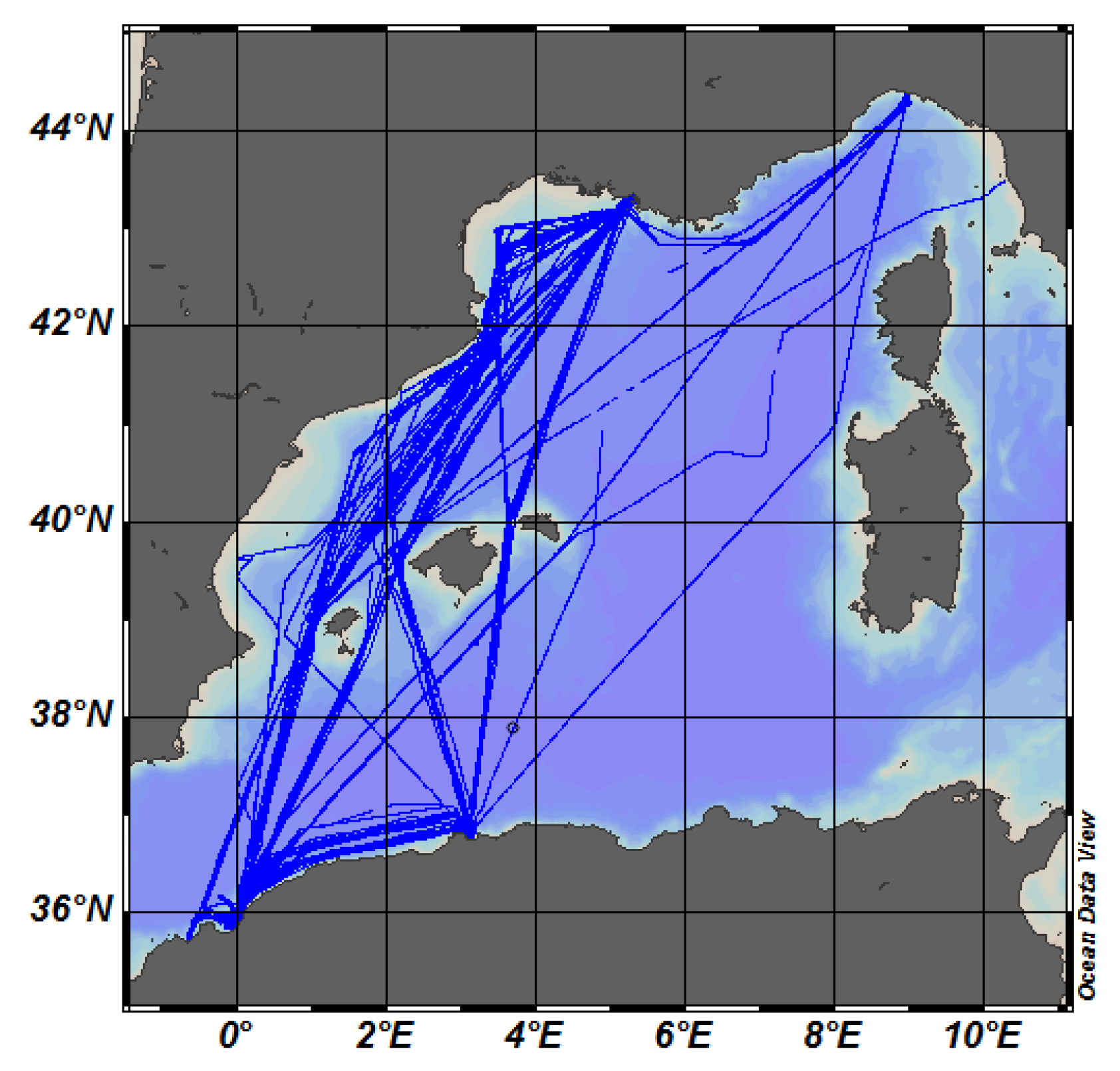
- SSS time series from six moorings located in the Western Mediterranean have been considered as part of the independent validation process described in Section 4.2 (see their location in Figure 1):
- -
- Four moorings are operated by Puertos del Estado ([24]): the moorings number 61,198, 61,417, 61,281 and 61,280.
- -
The collocation between mooring and SMOS SSS has been computed as follows: we have only considered data flagged as “good-quality”. In addition, salinity values out of the range [36:39] PSU (Practical Salinity Units) have been removed from the comparison. A sliding averaging window of nine days has been applied to the mooring data in order to compare both data (satellite and mooring) in a more similar temporal scale. Therefore, the mooring acquisition at time , which has been filtered with a centered 9-day window, has been compared with the SMOS SSS maps computed from the same 9-day period. - Data from the TRANSMED system thermosalinometer, ([29]) on board the MV Marfret Niolon [30] have been used in this study as independent source of data for validation in Section 4.3. Sea Surface Temperature (TRANSMED SST) and Sea Surface Salinity (TRANSMED SSS) are recorded underway at ∼3 m deep, during weekly trips between Marseilles, France, and Algeria. The data has been post-processed following water samples results and yearly recalibration of the thermosalinometers. In this case, the collocation strategy between satellite and in situ data is the same as the one used for the Argo comparison: the TRANSMED SSS acquired at time has been compared with the SMOS SSS 9-day map with the mid-day of the 9-day period. Each TRANSMED SSS measurement has been compared with the SMOS SSS corresponding to the cell (or in the case of L4) corresponding to the TRANSMED SSS location.
2.3. Sea Surface Temperature Data
- The daily Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) product (see [31]) has been used for the generation of the SMOS SSS L4 products (hereafter OSTIA SST). The OSTIA system is part of the Group for High Resolution Sea Surface Temperature (GHRSST). Access to OSTIA data is available at [25]. The OSTIA output is a daily global coverage combined SST and sea-ice concentration product on a 1/20deg. grid, based on measurements from several satellite and in situ SST data sets. OSTIA uses SST data in the common format developed by GHRSST and makes use of the uncertainty estimates and auxiliary fields as part of the quality control and analysis procedure. Satellite derived sea ice products from the EUMETSAT Ocean and Sea Ice Satellite application Facility (OSI-SAF) provide sea-ice concentration and edge data to the analysis system. After quality control of the SST observations, a bias correction is performed using ATSR-2/AATSR data as a key component. To provide the final SST analysis, a multi-scale optimal interpolation (OI) is performed using the previous analysis as the basis for a first guess field.
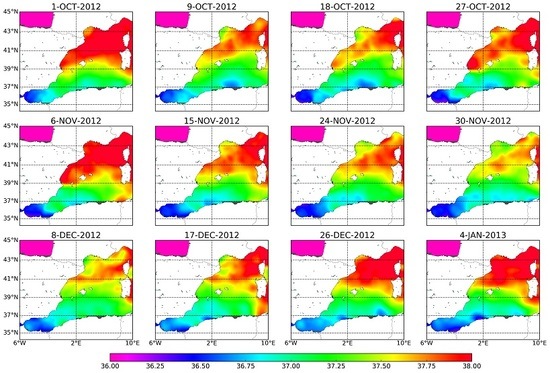
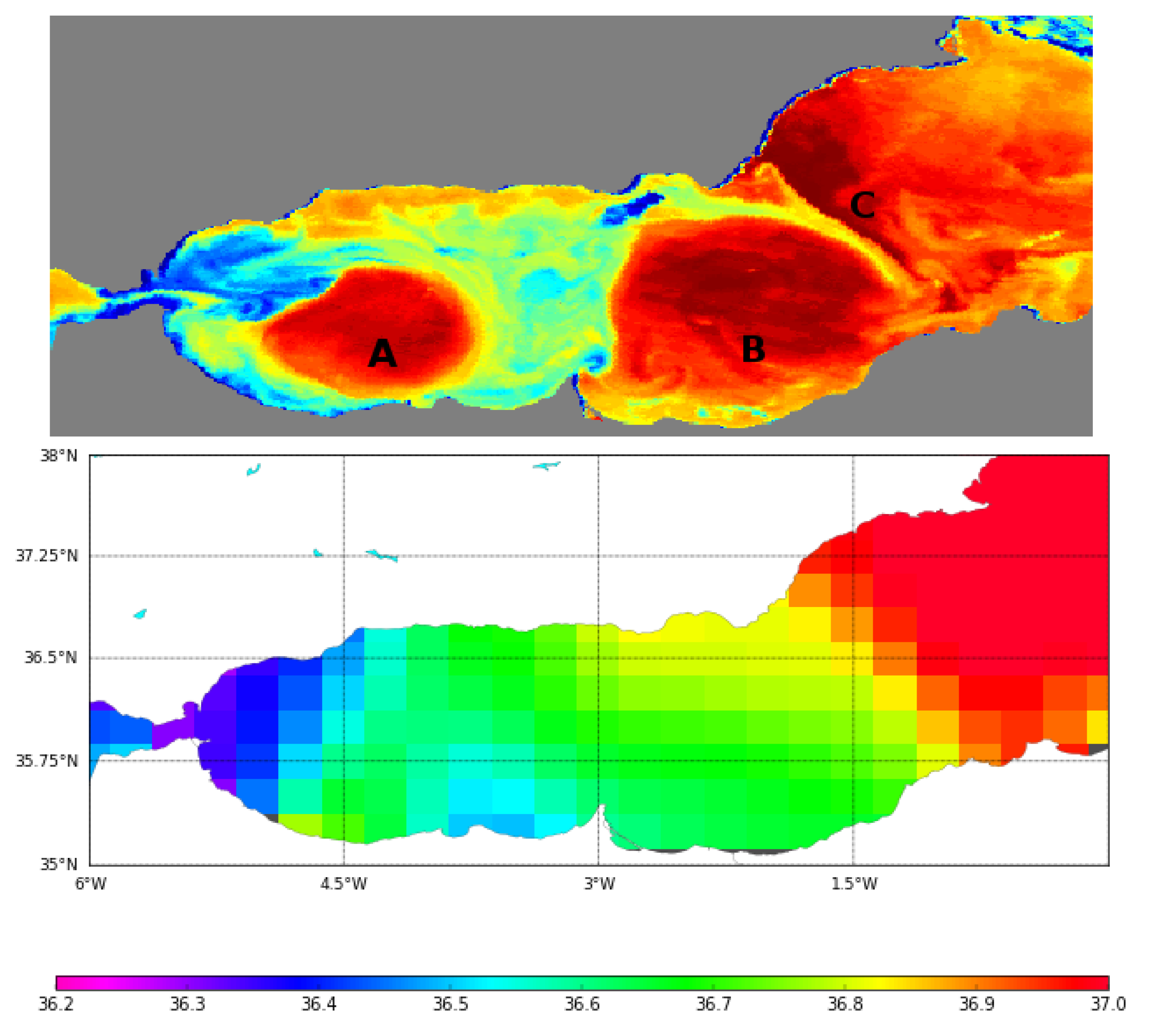
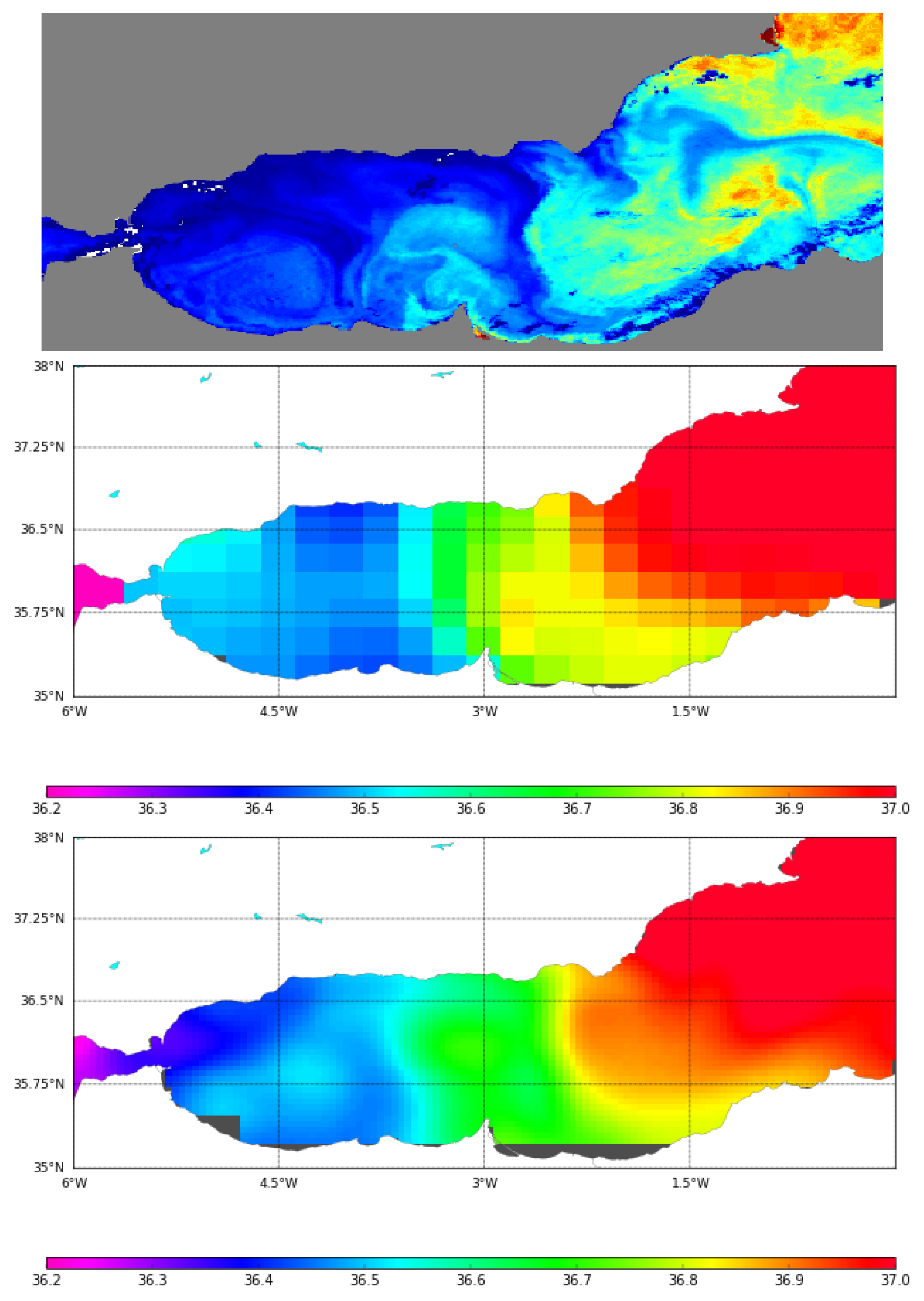
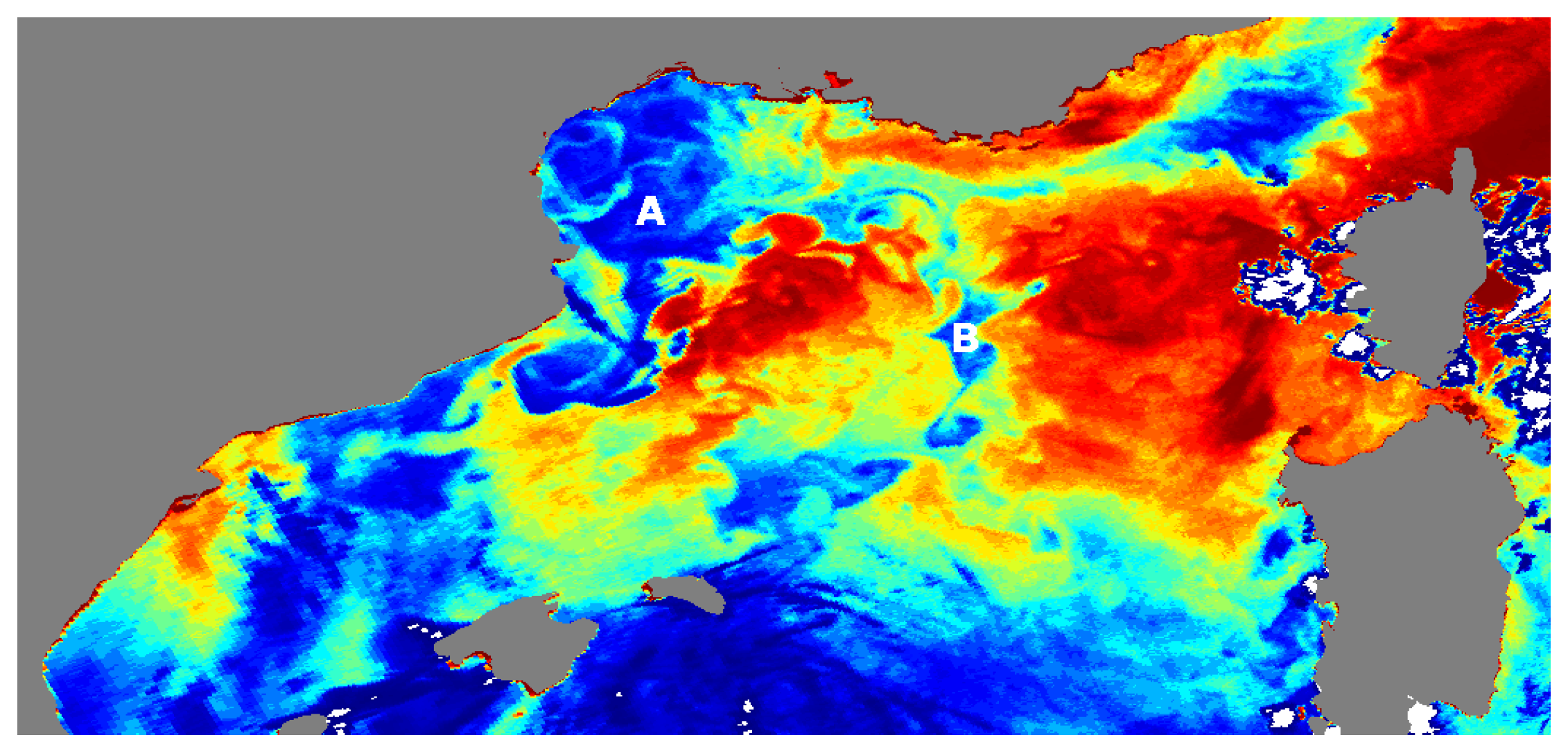
- Images of Brightness Temperature (Advances Very High Resolution Radiometer (AVHRR) channel 4) from satellites National Atmospheric and Oceanic Administration (NOAA) / AVHRR sensors at km have been used in Section 4.4 as reference data set in a qualitative assessment of the resulting spatial structures of the SMOS SSS products. Brightness temperature images (hereafter AVHRR images) are produced by the SATMOS (CNRS INSU/MeteoFrance) at the CMS Lannion from NOAA/AVHRR images, and processed at MIO (Available online: [32] (accessed on 19 March 2018)), (see [33]). Brightness Temperatures are relative temperatures, and the color scale is stretched to enhance the structures. These images do not include any compositing, and hence provide the best visualisation of the structures. As a result, the color scale is not relevant and it will not be included.
3. Methods
3.1. Debiased Non-Bayesian Retrieval of SSS
3.2. Mitigation of Time-Dependent Biases: Removal of EOFs from the DINEOF Basis
3.3. Reduction of White Noise by Means of Objective Analysis
3.4. Improving the Spatial and Temporal Resolution by Mean of Multifractal Fusion
4. Results
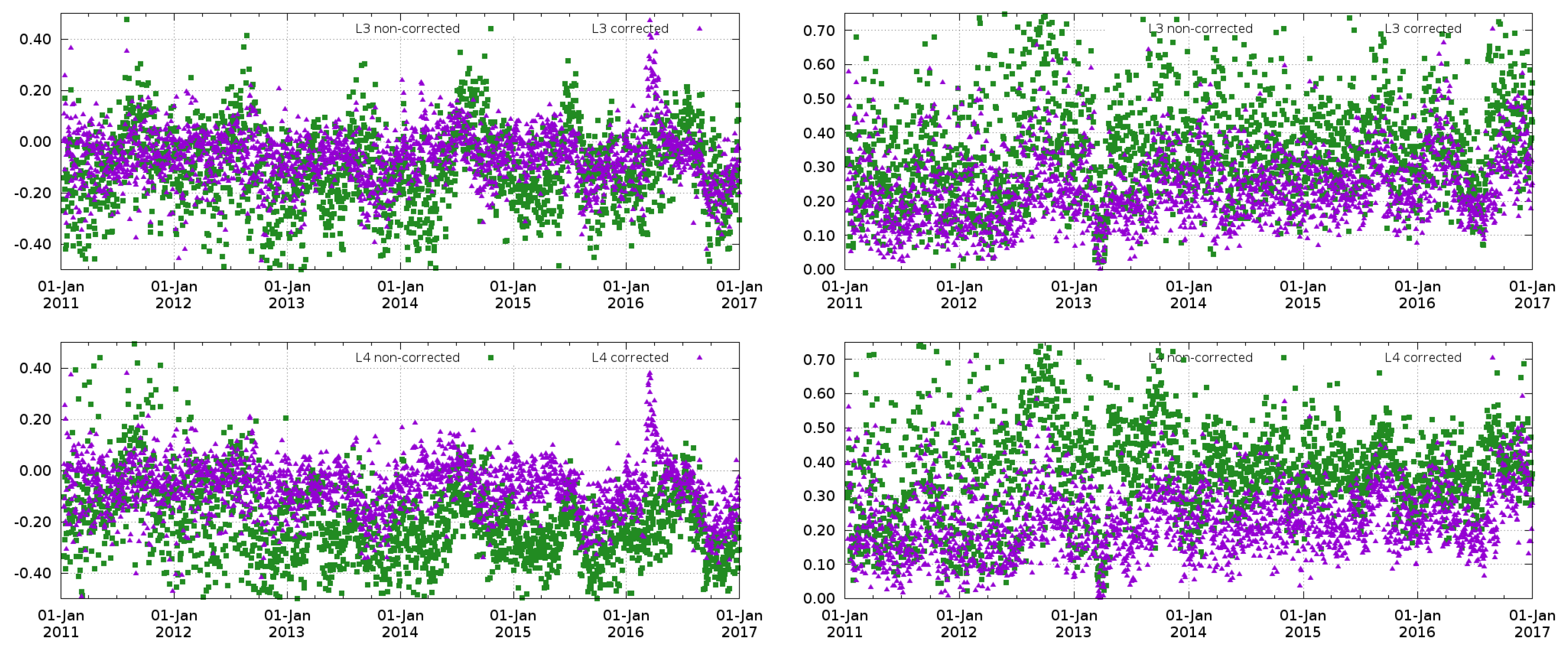
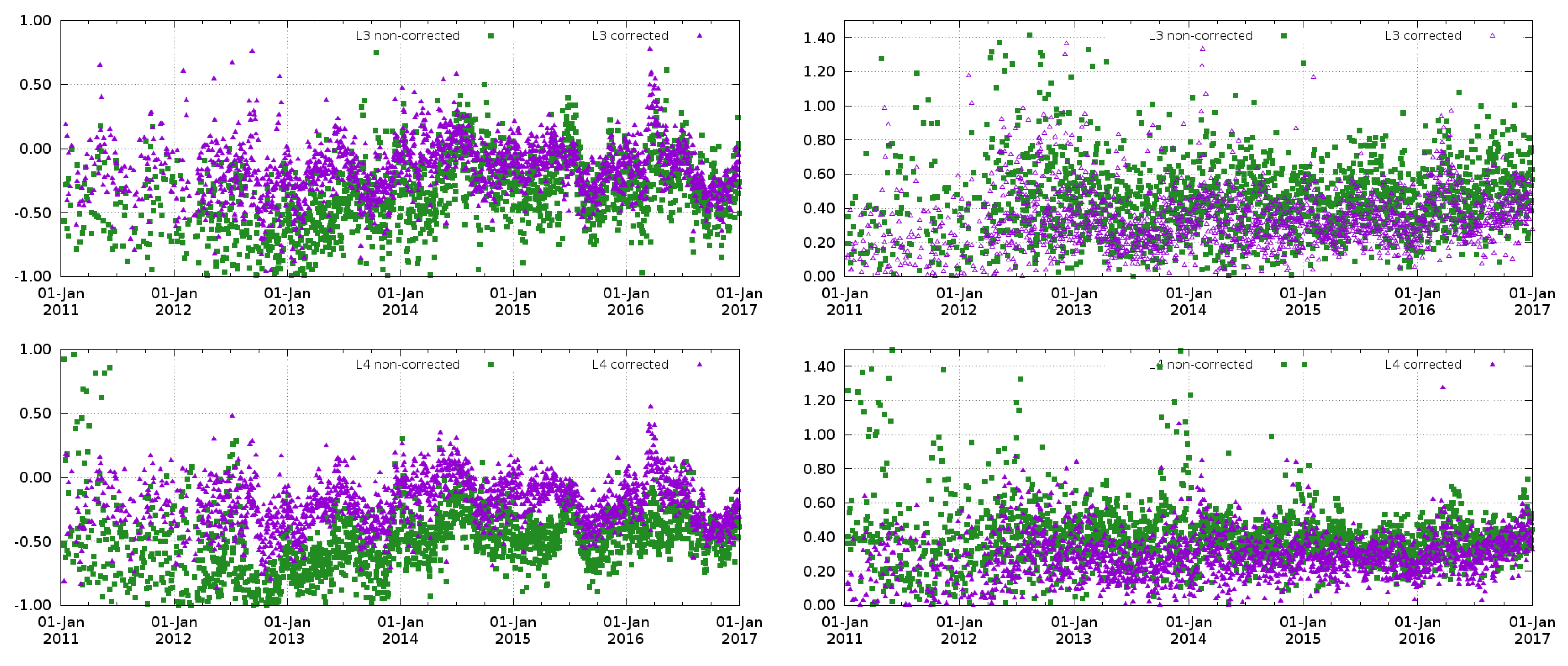
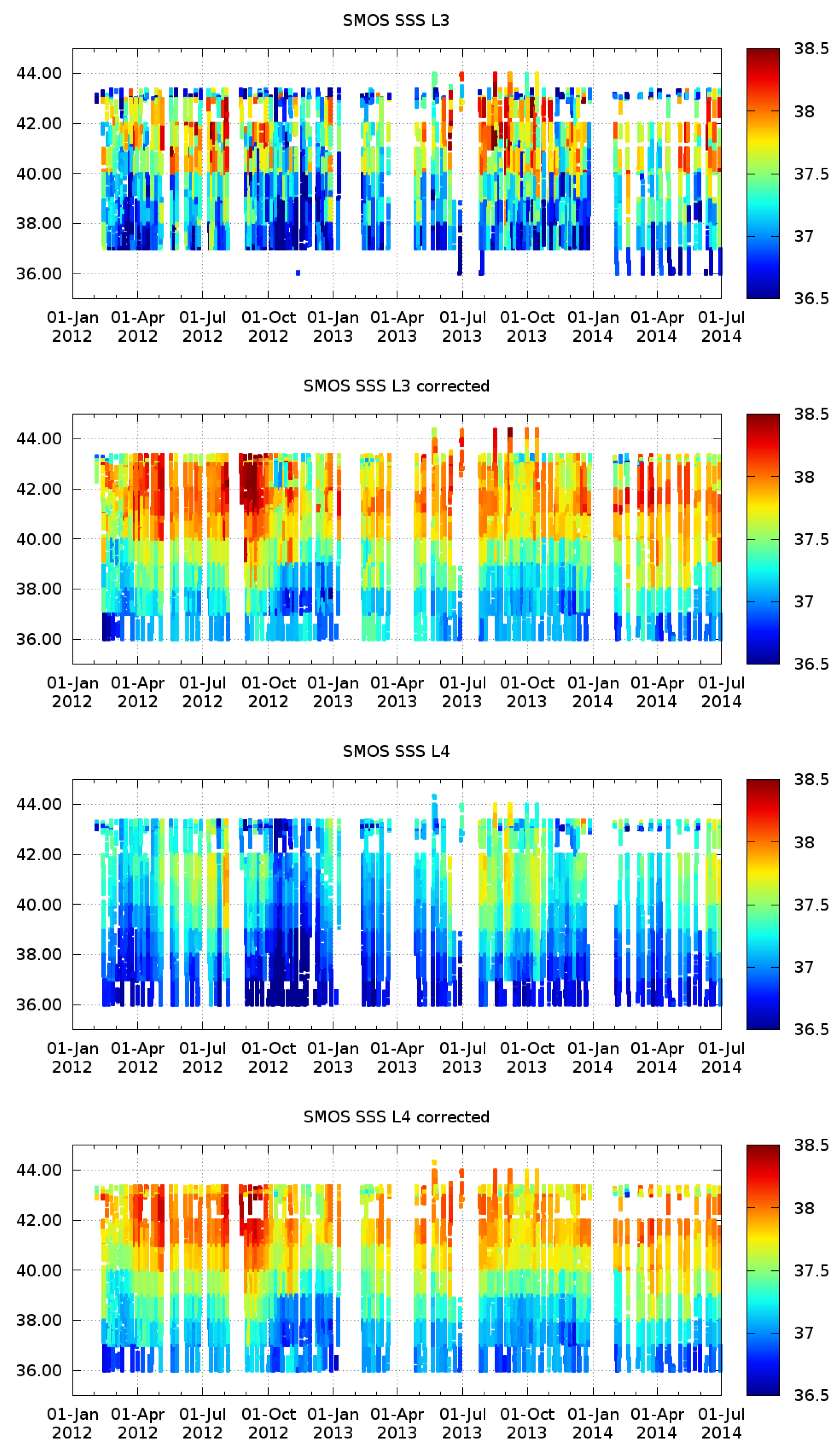
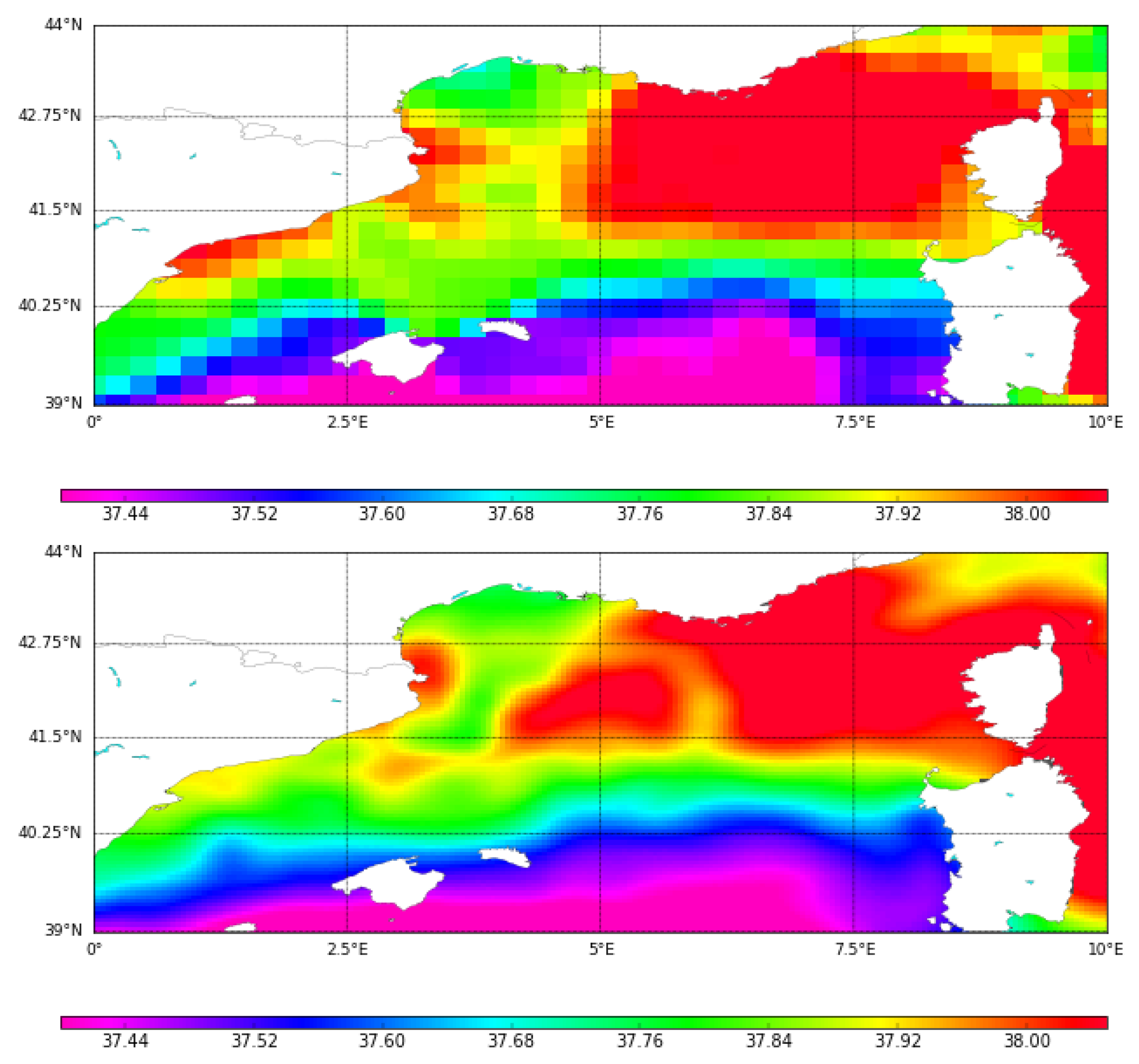
- SMOS SSS L3 corrected products (L3 corrected): objectively analyzed 9-day maps at resulting from the steps described in Section 3.1, Section 3.2 and Section 3.3.
- SMOS SSS L3 products (L3): They are the global debiased non-Bayesian advanced products (see Section 2.1). They result from the methodologies described in Section 3.1 and Section 3.3. The unique difference with respect to the corrected L3 product is the time-bias correction. Instead of applying DINEOF decomposition, these products are time-bias corrected by assuming that the mean value of the SMOS-based anomaly at each map is null (see [20] for more details).
- SMOS SSS L4 corrected products (L4 corrected): result from the multifractal fusion between the SMOS SSS L3 corrected maps and the OSTIA SST (step described in Section 3.4). They are provided at on a daily basis.
- SMOS SSS L4 products (L4): Multifractal fusion applied to the SMOS SSS L3 product (see Section 2.1).
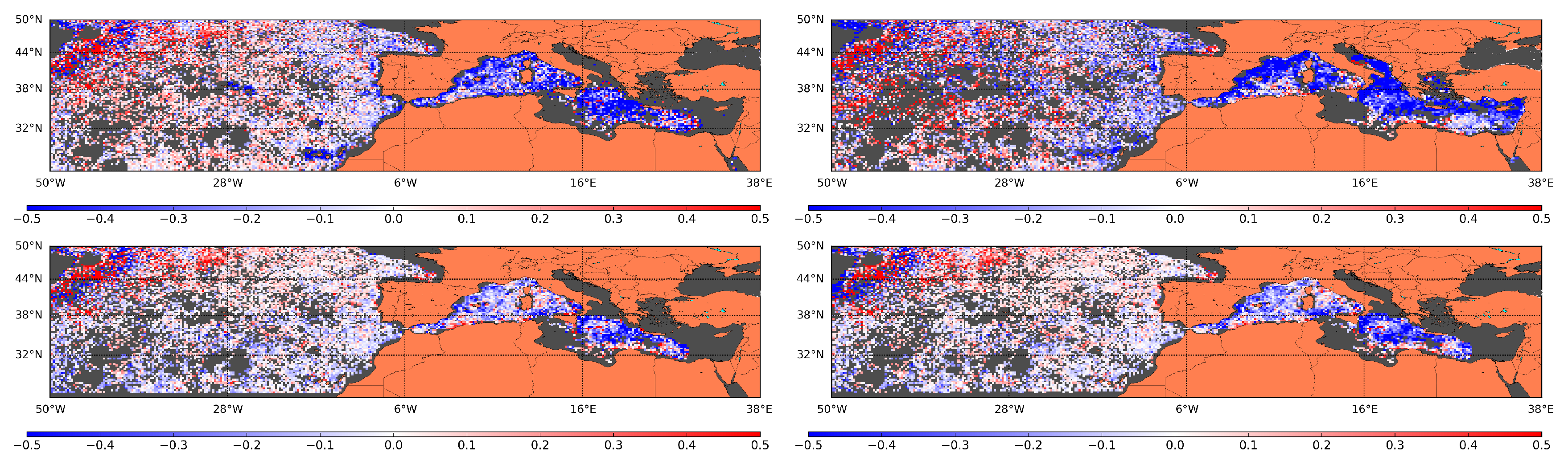
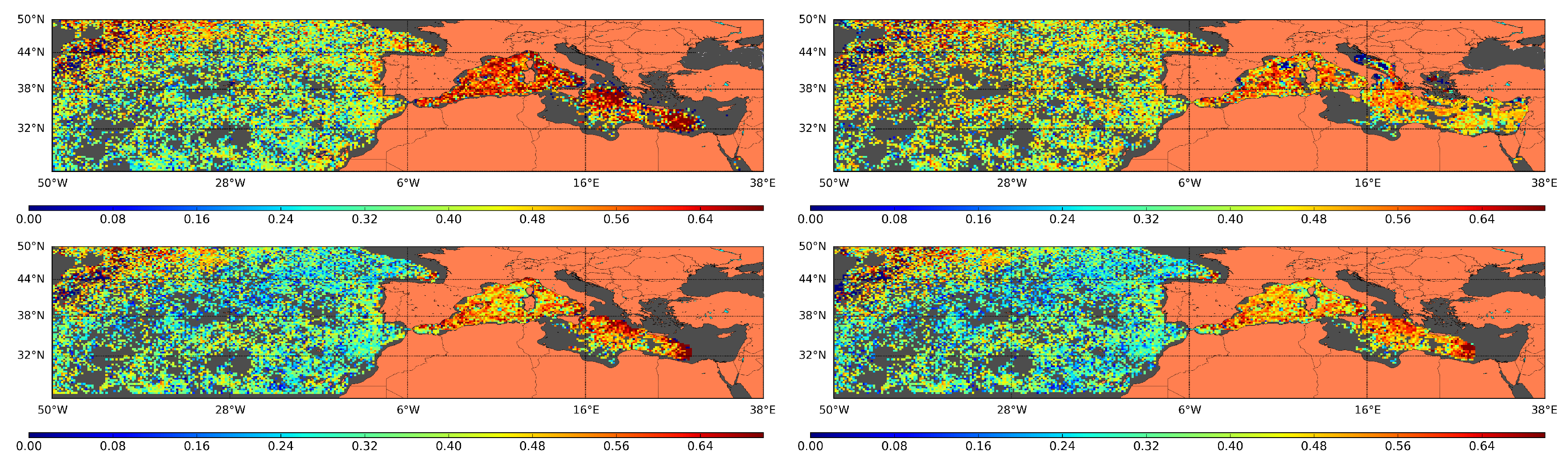
4.1. Comparison with Argo Floats
- Full domain (DOM), which includes part of the North Atlantic and the Mediterranean Sea and is defined in NE
- The Mediterranean Sea (MED) that is defined by the following rectangle NE.
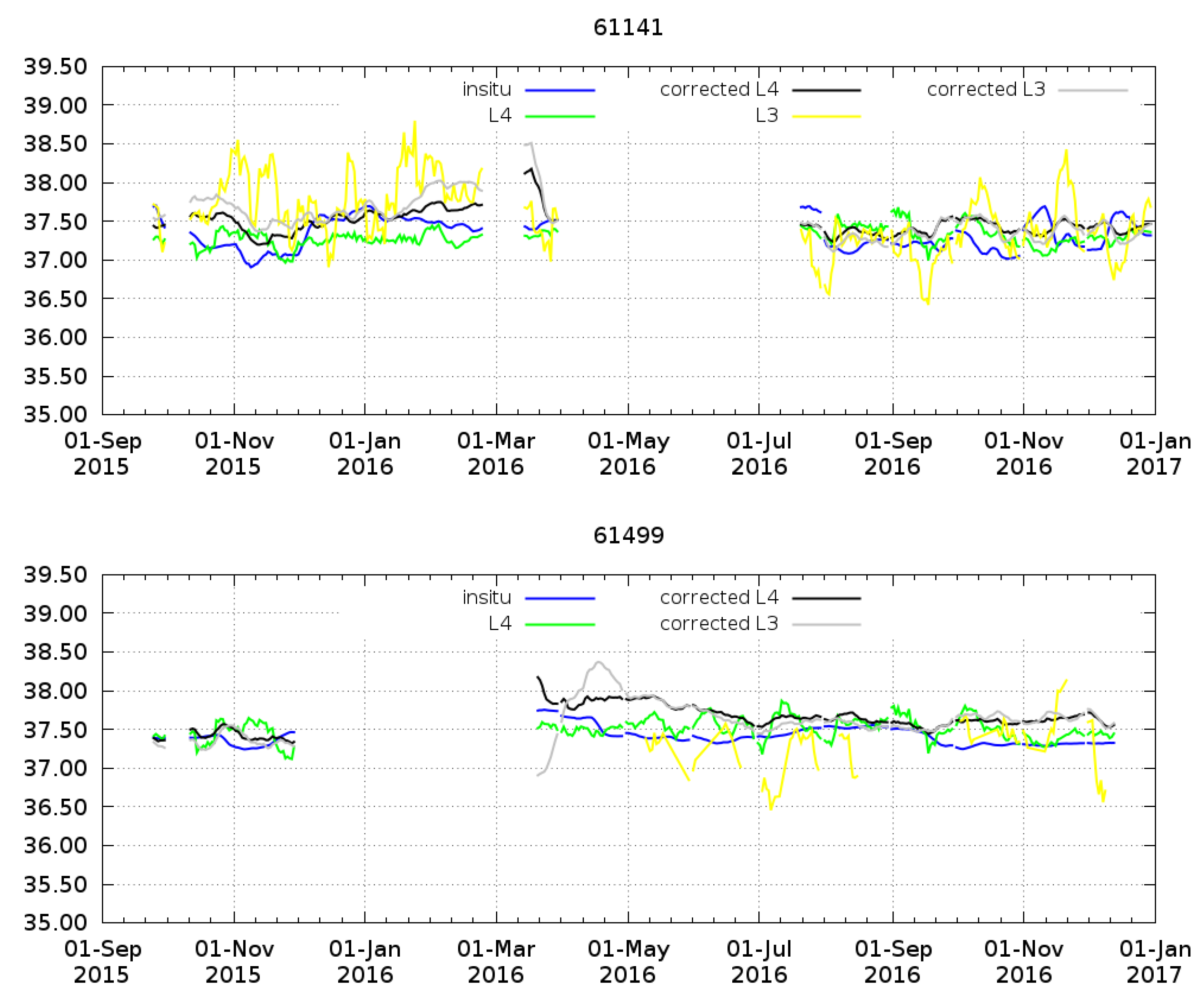
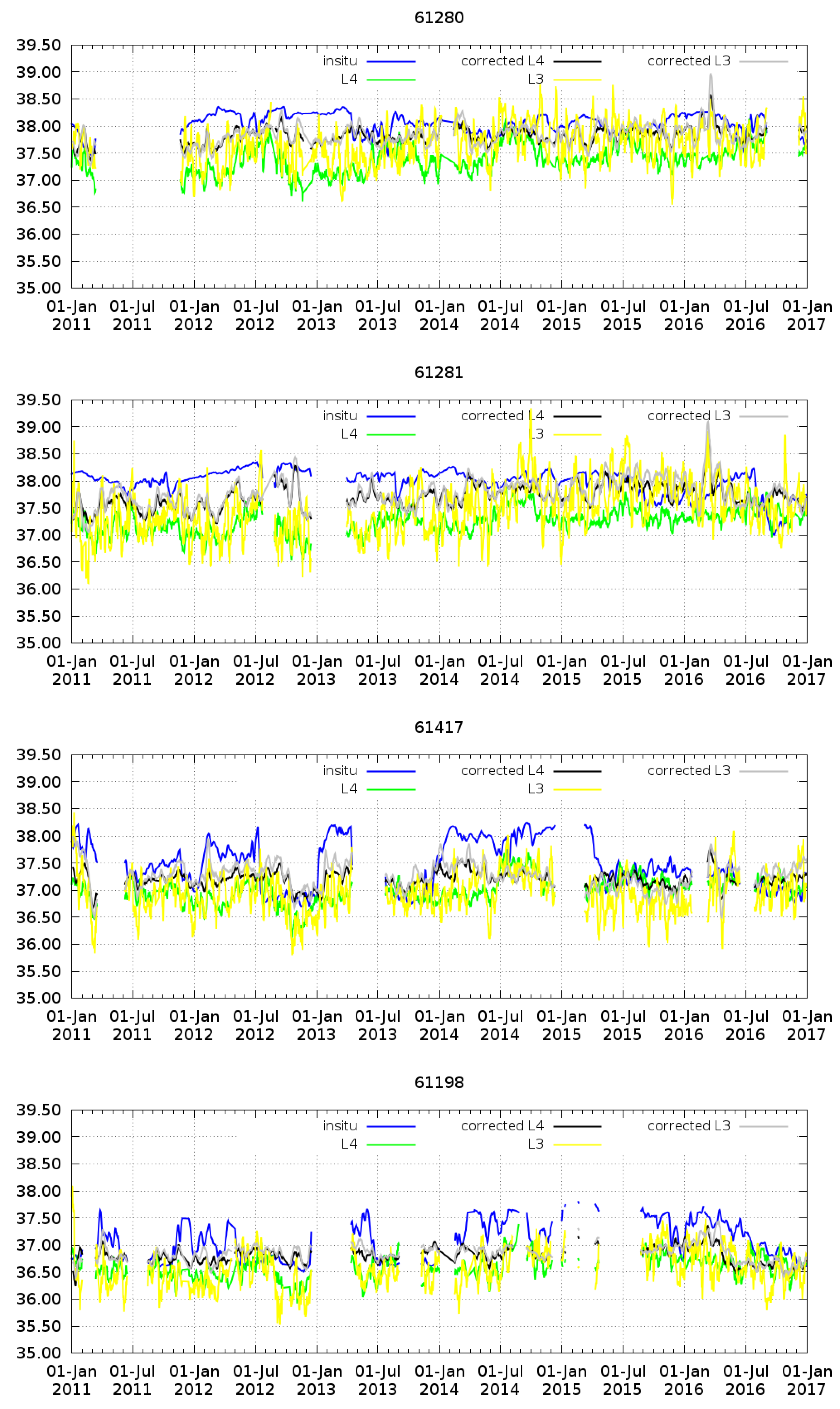
4.2. Comparison with Moorings Data
4.3. Comparison with TRANSMED SSS
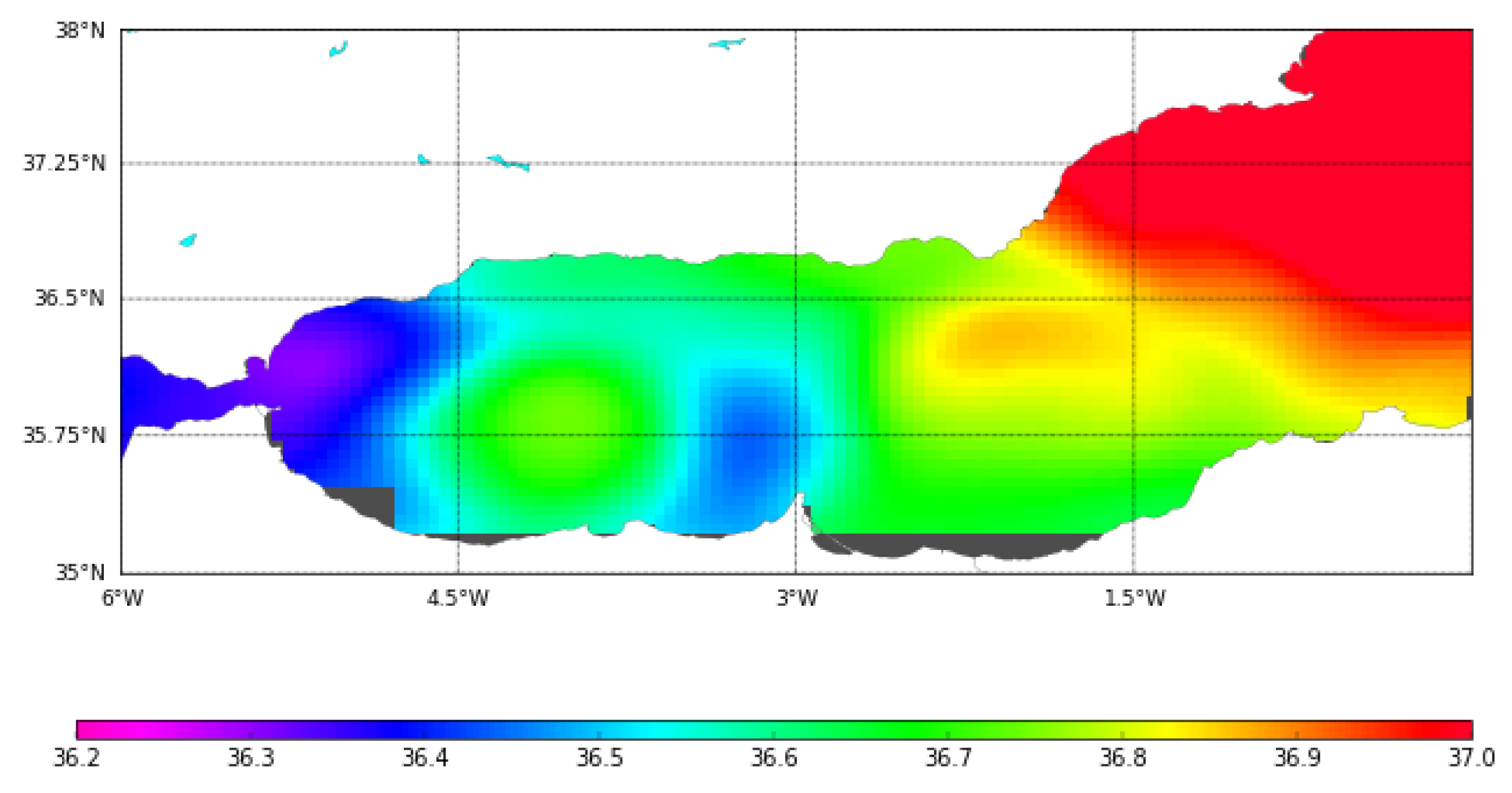
4.4. Spatial Structures: Qualitative Comparison with AVHRR Images
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Millot, C.; Taupier-Letage, I. Circulation in the Mediterranean Sea. In The Handbook of Environmental Chemistry, 5 Part K; Saliot, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 29–66. Available online: https://hal.archives-ouvertes.fr/hal-01191856 (accessed on 23 January 2018). [CrossRef]
- Taupier-Letage, I.; Puillat, I.; Millot, C.; Raimbault, P. Biological response to mesoscale eddies in the Algerian Basin. J. Geophys. Res. Oceans 2003, 108, 3245. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Font, J.; Garcia-Ladona, E.; Emelianov, M.; Millot, C.; Taupier-Letage, I. Spatial structure of anticyclonic eddies in the Algerian basin (Mediterranean Sea) analyzed using the Okubo-Weiss parameter. Deep Sea Res. II 2004, 51, 3009–3028. [Google Scholar] [CrossRef]
- Schroeder, K.; Garcìa-Lafuente, J.; Josey, S.; Artale, V.; Buongiorno-Nardelli, B.; Carrillo, A.; Gacic, M.; Gasparin, G.; Herrmann, M.; Lionello, P.; et al. Circulation of the Mediterranean Sea and its variability. In The Climate of the Mediterranean Region; Lionello, P., Ed.; Elsevier: Oxford, UK, 2012; pp. 187–256. [Google Scholar]
- Estournel, C.; Testor, P.; Damien, P.; D’ortenzio, F.; Marsaleix, P.; Conan, P.; Prieur, L. High resolution modelling of dense water formation in the north-western Mediterranean during winter 2012–2013: Processes and budget. J. Geophys. Res. Oceans 2016, 121, 5367–5392. [Google Scholar] [CrossRef]
- Waldman, R.; Somot, S.; Herrmann, M.; Testor, P.; Estournel, C.; Sevault, F.; Prieur, L.; Mortier, L.; Coppola, L.; Taillandier, V.; et al. Estimating dense water volume and its evolution for the year 2012–2013 in the Northwestern Mediterranean Sea: An observing system simulation experiment approach. J. Geophys. Res. Oceans 2016, 121, 6696–6716. [Google Scholar] [CrossRef]
- HYMEX (HYdrological Cycle in the Mediterranean EXperiment). Available online: https://www.hymex.org/ (accessed on 23 January 2018).
- Drobinski, P.; Ducrocq, V.; Allen, J.; Alpert, P.; Anagnostou, E.; Béranger, K.; Borga, M.; Braud, I.; Chanzy, A.; Davolio, S.; et al. HyMeX, a 10-year multidisciplinary project on the Mediterranean water 1 cycle. Bull. Am. Meteorol. Soc. 2014, 95, 1063–1082. [Google Scholar] [CrossRef]
- Somot, S.; Sevault, F.; Déqué, M.; Crépon, M. 21st century climate change scenario for the Mediterranean using a coupled atmosphere-ocean regional climate model. Glob. Planet. Change 2008, 63, 112–126. [Google Scholar] [CrossRef]
- Adloff, F.; Somot, S.; Sevault, F.; Jordà, G.; Aznar, R.; Déqué, M.; Herrmann, M.; Marcos, M.; Dubois, C.; Padorno, E.; et al. Mediterranean Sea response to climate change in an ensemble of twenty first century scenarios. Clim. Dyn. 2015, 45, 2775–2802. [Google Scholar] [CrossRef]
- Somot, S.; Houpert, L.; Sevault, F.; Testor, P.; Bosse, A.; Taupier-Letage, I.; Bouin, M.; Waldman, R.; Cassou, C.; Sanchez-Gomez, E.; et al. Characterizing, modelling and understanding the climate variability of the deep water formation in the North-Western Mediterranean Sea. Clim. Dyn. 2016, 1–32. [Google Scholar] [CrossRef]
- Herrmann, M.; Diaz, F.; Estournel, C.; Marsaleix, P.; Ulses, C. Impact of atmospheric and oceanic interannual variability on the Northwestern Mediterranean Sea pelagic planktonic ecosystem and associated carbon cycle. J. Geophys. Res. Oceans 2013, 118, 5792–5813. [Google Scholar] [CrossRef]
- Herrmann, M.; Estournel, C.; Diaz, F.; Adloff, F. Impact of climate change on the Northwestern Mediterranean Sea pelagic planktonic ecosystem and associated carbon cycle. J. Geophys. Res. Oceans 2014, 119, 5815–5836. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Drusch, M.; Kerr, Y.H.; Font, J.; Martin-Neira, M.; Delwart, S.; Buanadicha, G.; Reul, N.; Daganzo-Eurebio, E.; Oliva, R.; et al. ESA’s Soil Moisture and Ocean Salinity Mission: Mission Performance and Operations. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1354–1366. [Google Scholar] [CrossRef]
- Font, J.; Camps, A.; Borges, A.; Martín-Neira, M.; Boutin, J.; Reul, N.; Kerr, Y.; Hahne, A.; Mecklenburg, S. SMOS: The Challenging Sea Surface Salinity Measurement From Space. Proc. IEEE 2010, 98, 649–665. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Parard, G.; Beckers, J. Analysis of SMOS sea surface salinity data using DINEOF. Remote Sens. Environ. 2016, 180, 137–145. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Olmedo, E.; Turiel, A.; Ballabrera-Poy, J.; García--Ladona, E. Retrieval of eddy dynamics from SMOS sea surface salinity measurements in the Algerian Basin (Mediterranean Sea). Geophys. Res. Lett. 2016, 43, 6427–6434. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Umbert, M.; Hoareau, N.; Portabella, M.; Ballabrera-Poy, J.; Turiel, A. Improving time and space resolution of SMOS salinity maps using multifractal fusion. Remote Sens. Environ. 2016, 180, 246–263. [Google Scholar] [CrossRef]
- ESA. Available online: https://earth.esa.int/web/guest/-/level-1b-full-polarization-6889 (accessed on 23 January 2018).
- Global SMOS SSS Maps. Available online: http://bec.icm.csic.es/ocean-experimental-dataset-global/ (accessed on 23 January 2018).
- Puertos del Estado. Available online: http://www.puertos.es (accessed on 23 January 2018).
- Copernicus Marine Environment Monitoring Service. Available online: http://marine.copernicus.eu (accessed on 23 January 2018).
- OceanSITES. Available online: http://www.oceansites.org (accessed on 23 January 2018).
- SOCIB. Available online: http://www.socib.eu/?seccion=observingFacilities&facility=mooring&id=146 (accessed on 23 January 2018).
- SOCIB. Available online: http://www.socib.eu/?seccion=observingFacilities&facility=mooring&id=143 (accessed on 23 January 2018).
- TRANSMED. Available online: http://www.mio.univ-amu.fr/?TRANSMED (accessed on 23 January 2018).
- Taupier-Letage, I.; Bachelier, C.; Rougier, G. Thermosalinometer TRANSMED, Marfret Niolon, definitive data set. SEDOO OMP 2014. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- MIO. Available online: www.ifremer.fr/osis_2014 (accessed on 19 March 2018).
- Taupier-Letage, I. On the use of thermal infrared images for circulation studies: Applications to the eastern Mediterranean basin. In Remote Sensing of the European Seas; Barale, V., Gade, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Available online: https://hal.archives--ouvertes.fr/hal--01196705 (accessed on 23 January 2018).
- González-Gambau, V.; Olmedo, E.; Turiel, A.; Martínez, J.; Ballabrera-Poy, J.; Portabella, M.; Piles, M. Enhancing SMOS brightness temperatures over the ocean using the nodal sampling image reconstruction technique. Remote Sens. Environ. 2016, 180, 202–220. [Google Scholar] [CrossRef]
- Zweng, M.; Reagan, J.; Antonov, J.; Locarnini, R.; Mishonov, A.; Boyer, T.; Garcia, H.; Baranova, O.; Johnson, D.; Seidov, D.; et al. World Ocean Atlas 2013, Volume 2: Salinity; Levitus, A., Ed.; Mishonov Technical; NOAA: Silver Spring, MD, USA, 2013; pp. 39–74. [Google Scholar]
- Beckers, J.M.; Rixen, M. EOF calculations and data filling from incomplete oceanographic data sets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Rixen, M.; Beckers, J.M. Reconstruction of incomplete oceanographic data sets using Empirical Orthogonal Functions. Application to the Adriatic Sea surface temperature. Ocean Model. 2005, 9, 325–346. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Sirjacobs, D.; Beckers, J.M. Enhancing temporal correlations in EOF expansions for the reconstruction of missing data using DINEOF. Ocean Sci. 2009, 5, 475–485. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Beckers, J.M.; Weisberg, R.H. Multivariate Reconstruction of Missing Data in Sea Surface Temperature, Chlorophyll and Wind Satellite Fields. J. Geophys. Res. 2007, 112, C03008. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Vanhellemont, Q.; Ruddick, K.; Barth, A.; Beckers, J.M. Analysis of high frequency geostationary ocean colour data using DINEOF. Estuar. Coast. Shelf Sci. 2015, 159, 28–36. [Google Scholar] [CrossRef]
- Turiel, A.; Solé, J.; Nieves, V.; Ballabrera-Poy, B.; García-Ladona, E. Tracking oceanic currents by singularity analysis of Microwave Sea Surface Temperature images. Remote Sens. Environ. 2008, 112, 2246–2260. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; García-Ladona, E.; Font, J. Microcanonical multifractal formalism: Application to the estimation of ocean surface velocities. J. Geophys. Res. 2007, 112, 2156–2202. [Google Scholar] [CrossRef]
- Nieves, V.; Llebot, C.; Turiel, A.; Solé, J.; García-Ladona, E.; Estrada, M.; Blasco, D. Common turbulent signature in sea surface temperature and chlorophyll maps. Geophys. Res. Lett. 2007, L23602. [Google Scholar] [CrossRef]
- Umbert, M.; Hoareau, N.; Turiel, A.; Ballabrera-Poy, J. New blending algorithm to synergize ocean variables: The case of SMOS sea surface salinity maps. Remote Sens. Environ. 2014, 146, 188–200. [Google Scholar] [CrossRef]
- Hernández-Carrasco, I.; Sudre, J.; Garcon, V.; Yahia, H.; Garbe, C.; Paulmier, A.; Dewitte, B.; Illig, S.; Dadou, I.; González-Dávila, M.; et al. Reconstruction of super-resolution ocean pco2 and airsea fluxes of co2 from satellite imagery in the southeastern atlantic. Biogeosciences 2015, 12, 5229–5245. [Google Scholar] [CrossRef]
- González-Gambau, V.; Turiel, A.; Olmedo, E.; Martínez, J.; Corbella, I.; Camps, A. Nodal Sampling: A New Image Reconstruction Algorithm for SMOS. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2314–2328. [Google Scholar] [CrossRef]
- González-Gambau, V.; Olmedo, E.; Martínez, J.; Turiel, A.; Duran, I. Improvements on Calibration and Image Reconstruction of SMOS for Salinity Retrievals in Coastal Regions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3064–3078. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Oliva, R.; Corbella, I.; Torres, F.; Duffo, N.; Durán, I.; Kainulainen, J.; Closa, A.; Zurita, A.; Cabot, F.; et al. SMOS Instrument performance and calibration after 5 years in orbit. Remote Sens. Environ. 2016, 180, 19–39. [Google Scholar] [CrossRef]
- DINEOF Analysis of SMOS Sea Surface Salinity Data. Available online: http://www.gher.ulg.ac.be/WP/ (accessed on 23 January 2018).
- Argo. Argo float data and metadata from Global Data Assembly Centre (Argo GDAC). SEANOE 2000. [Google Scholar] [CrossRef]
- CIESM. Available online: www.ciesm.org/marine/programs/partnerships.htm (accessed on 23 January 2018).
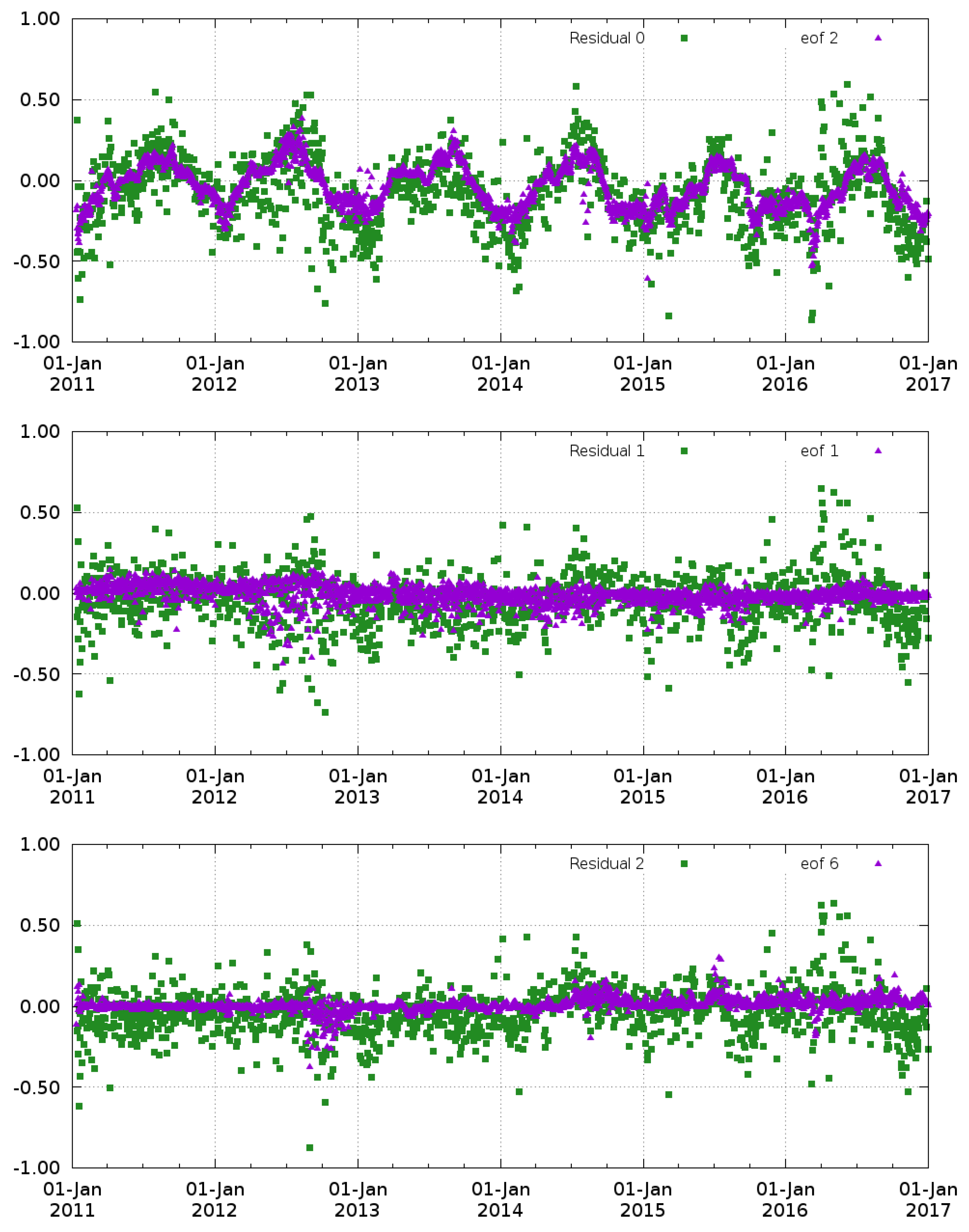

| Residual | EOF with Largest Correlation | Correlation | Mean | Std |
|---|---|---|---|---|
| 2 | 0.69 | −0.07 | 0.23 | |
| 1 | 0.46 | −0.04 | 0.17 | |
| 6 | 0.27 | −0.03 | 0.15 | |
| 3 | 0.28 | −0.05 | 0.15 | |
| 5 | 0.31 | −0.04 | 0.14 | |
| 7 | 0.21 | −0.05 | 0.14 | |
| 8 | 0.20 | −0.05 | 0.14 | |
| 4 | 0.19 | −0.05 | 0.13 | |
| 27 | 0.17 | −0.05 | 0.13 | |
| 9 | 0.16 | −0.05 | 0.13 |
| L3 | L3 Corrected | L4 | L4 Corrected | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | std | rms | mean | std | rms | mean | std | rms | mean | std | rms | |
| DOM | −0.12 | 0.35 | 0.41 | −0.06 | 0.24 | 0.26 | −0.20 | 0.38 | 0.46 | −0.07 | 0.23 | 0.26 |
| MED | −0.40 | 0.45 | 0.67 | −0.16 | 0.34 | 0.43 | −0.50 | 0.40 | 0.70 | −0.19 | 0.29 | 0.39 |
| Mooring ID | L3 | L3 Corrected | L4 | L4 Corrected | ||||
|---|---|---|---|---|---|---|---|---|
| mean | std | mean | std | mean | std | mean | std | |
| 61,198 | −0.50 | 0.40 | −0.20 | 0.31 | −0.46 | 0.35 | −0.25 | 0.32 |
| 61,417 | −0.52 | 0.49 | −0.19 | 0.44 | −0.46 | 0.46 | −0.26 | 0.42 |
| 61,141 | 0.20 | 0.48 | 0.20 | 0.28 | 0.03 | 0.24 | 0.14 | 0.20 |
| 61,499 | 0.22 | 0.32 | 0.20 | 0.27 | 0.09 | 0.17 | 0.23 | 0.15 |
| 61,281 | −0.51 | 0.56 | −0.22 | 0.38 | −0.73 | 0.36 | −0.27 | 0.34 |
| 61,280 | −0.38 | 0.43 | −0.21 | 0.25 | −0.66 | 0.34 | −0.22 | 0.22 |
| L3 | L3 Corrected | L4 | L4 Corrected | |
|---|---|---|---|---|
| Mean | −0.54 | −0.03 | −0.54 | −0.09 |
| Std | 0.39 | 0.27 | 0.28 | 0.25 |
| Nmeas | 75,129 | 97,530 | 88150 | 91,113 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olmedo, E.; Taupier-Letage, I.; Turiel, A.; Alvera-Azcárate, A. Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea through Multivariate and Multifractal Analysis. Remote Sens. 2018, 10, 485. https://doi.org/10.3390/rs10030485
Olmedo E, Taupier-Letage I, Turiel A, Alvera-Azcárate A. Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea through Multivariate and Multifractal Analysis. Remote Sensing. 2018; 10(3):485. https://doi.org/10.3390/rs10030485
Chicago/Turabian StyleOlmedo, Estrella, Isabelle Taupier-Letage, Antonio Turiel, and Aida Alvera-Azcárate. 2018. "Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea through Multivariate and Multifractal Analysis" Remote Sensing 10, no. 3: 485. https://doi.org/10.3390/rs10030485
APA StyleOlmedo, E., Taupier-Letage, I., Turiel, A., & Alvera-Azcárate, A. (2018). Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea through Multivariate and Multifractal Analysis. Remote Sensing, 10(3), 485. https://doi.org/10.3390/rs10030485