Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data
Abstract
1. Introduction
2. Data Descriptions and Processing
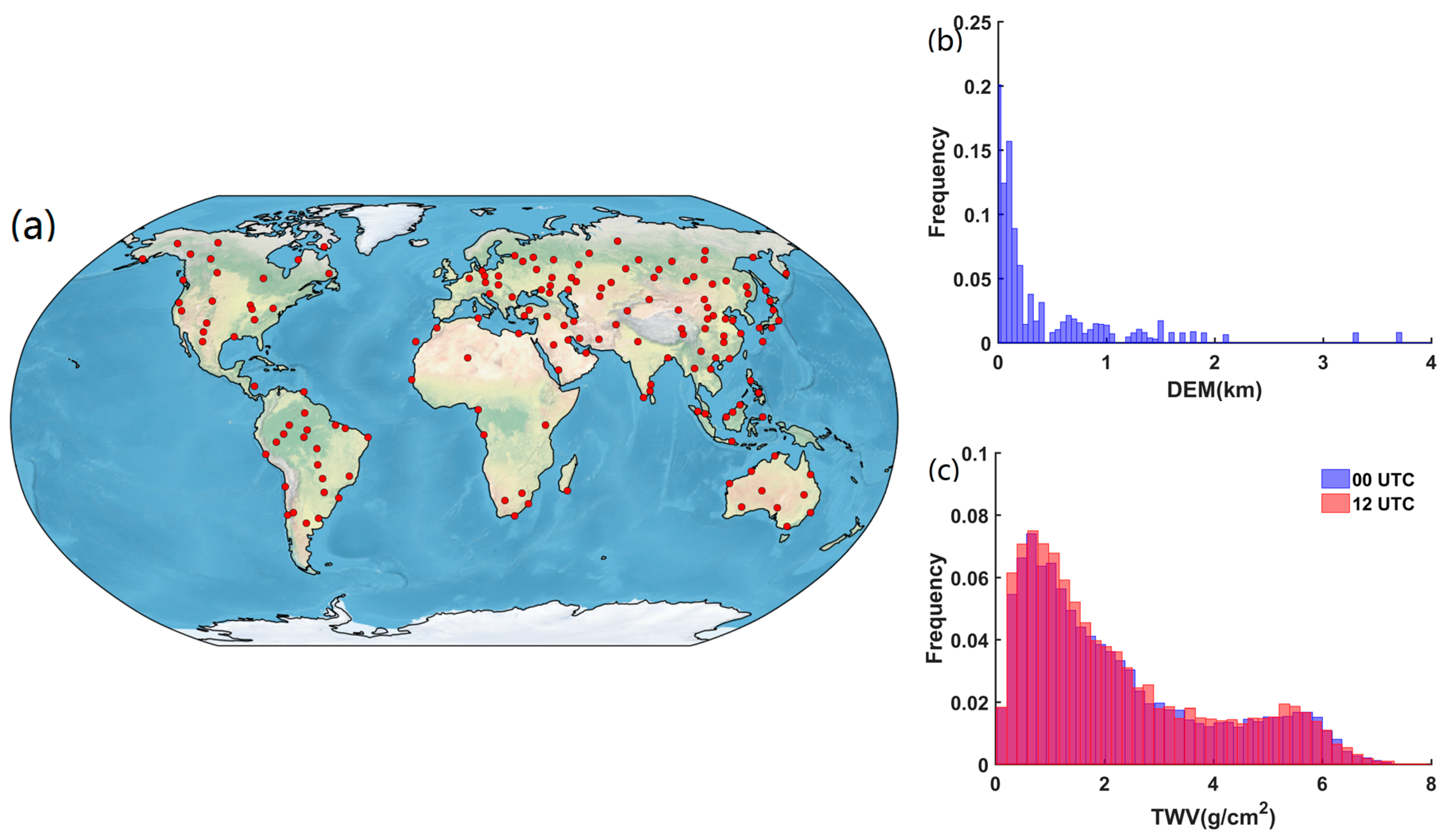
2.1. Global Radiosonde Observations
2.2. MERRA and MERRA2
2.3. ERA-Interim
2.4. NCEP/FNL and NCEP/R2
2.5. JRA-55
2.6. Atmospheric Parameter Simulation with MODTRAN
3. Results
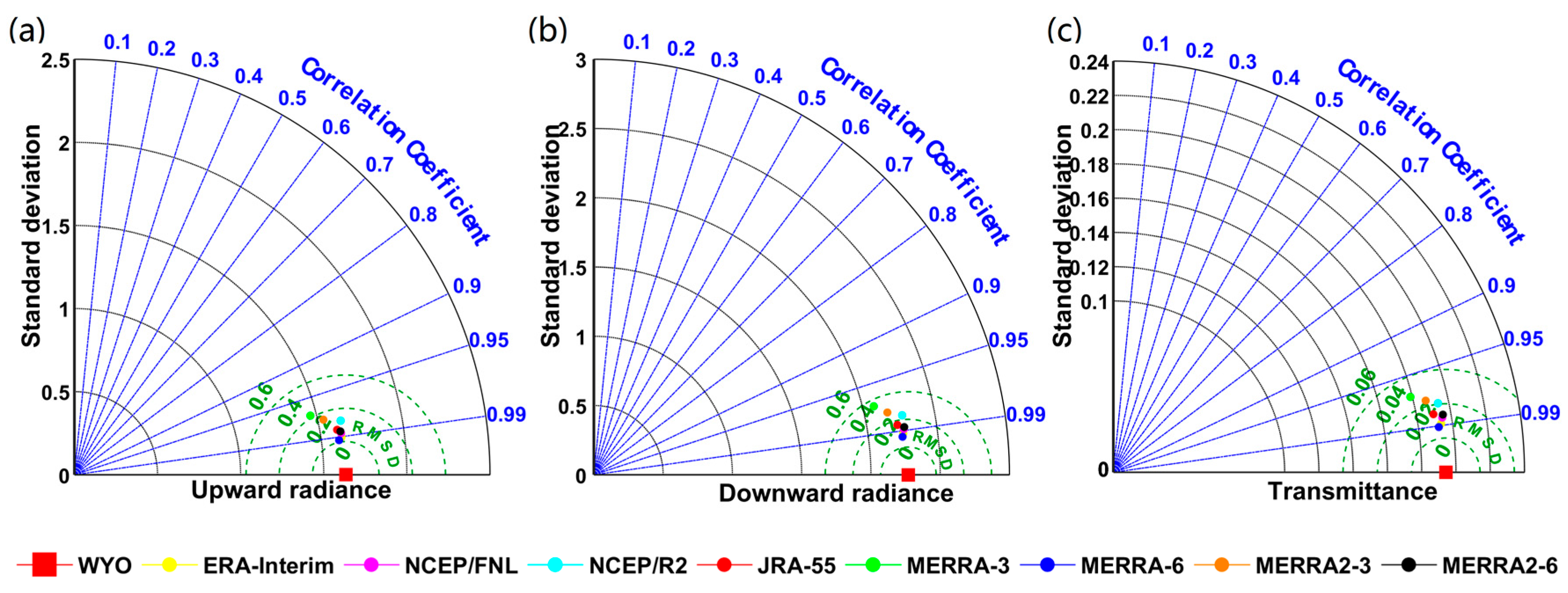
3.1. Atmospheric Parameters Evaluation
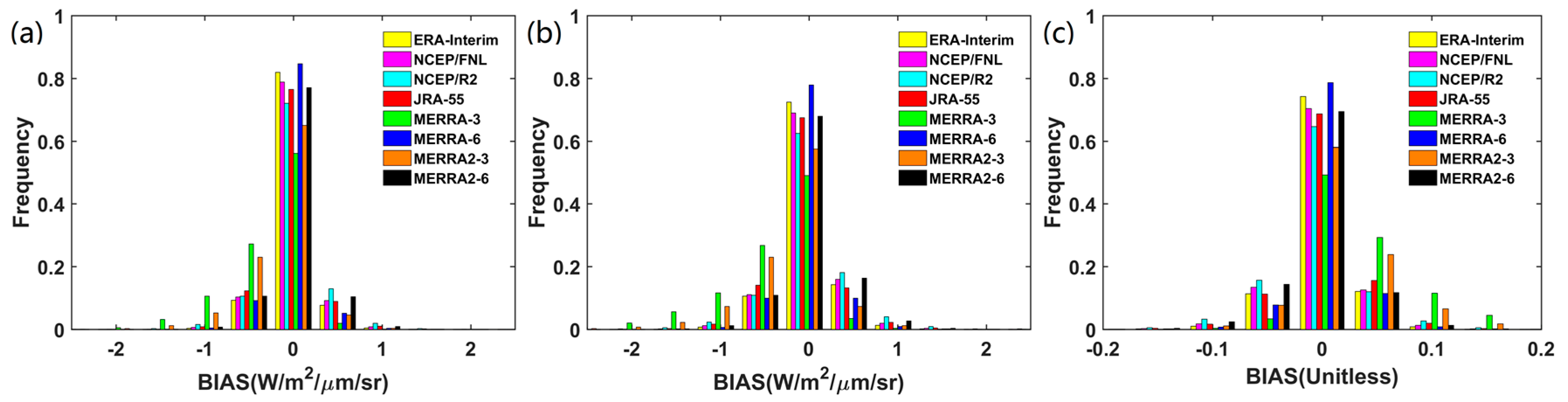
3.1.1. Overall Validation Results
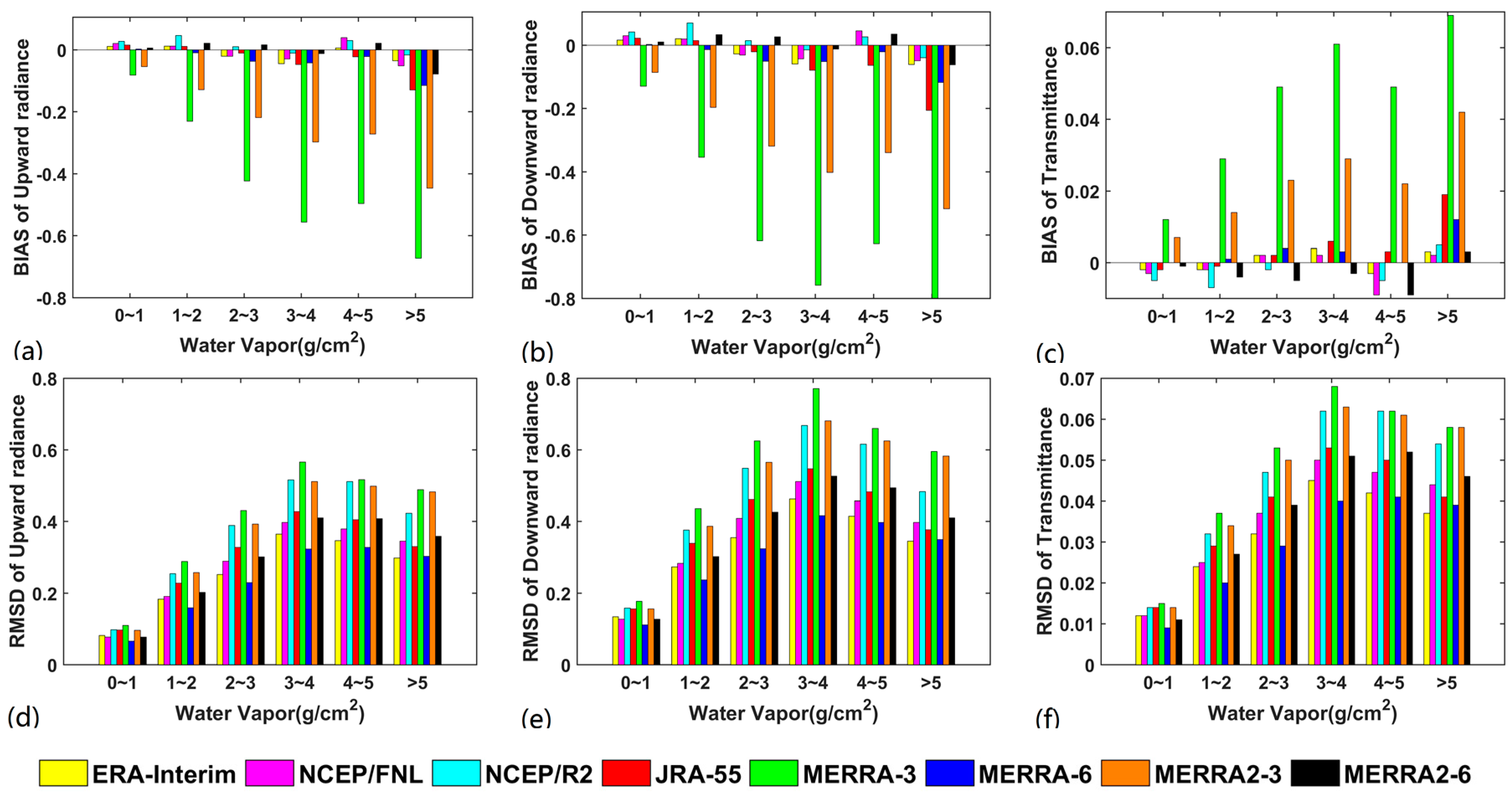
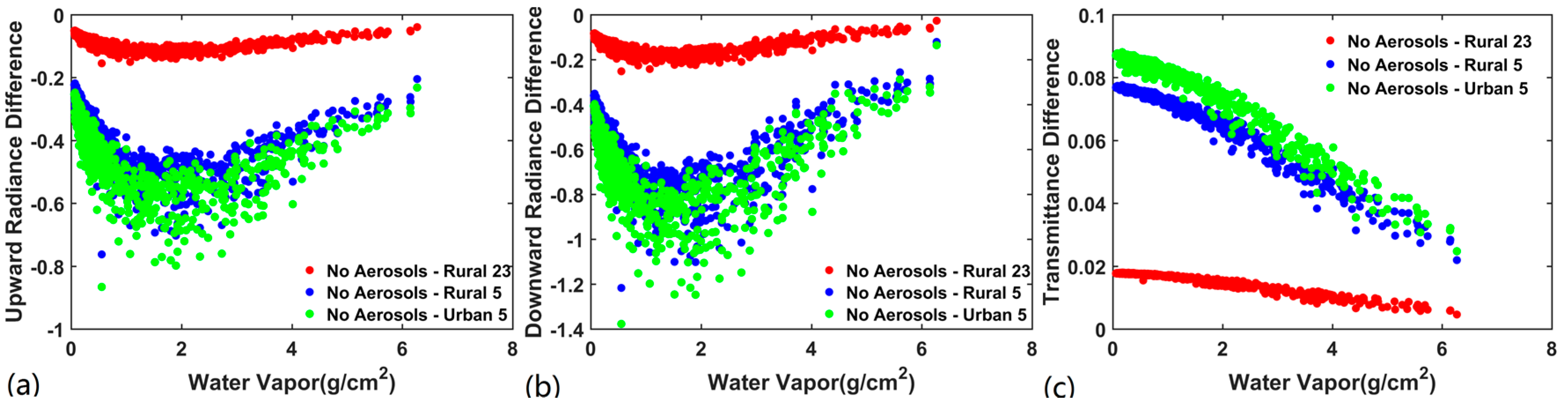
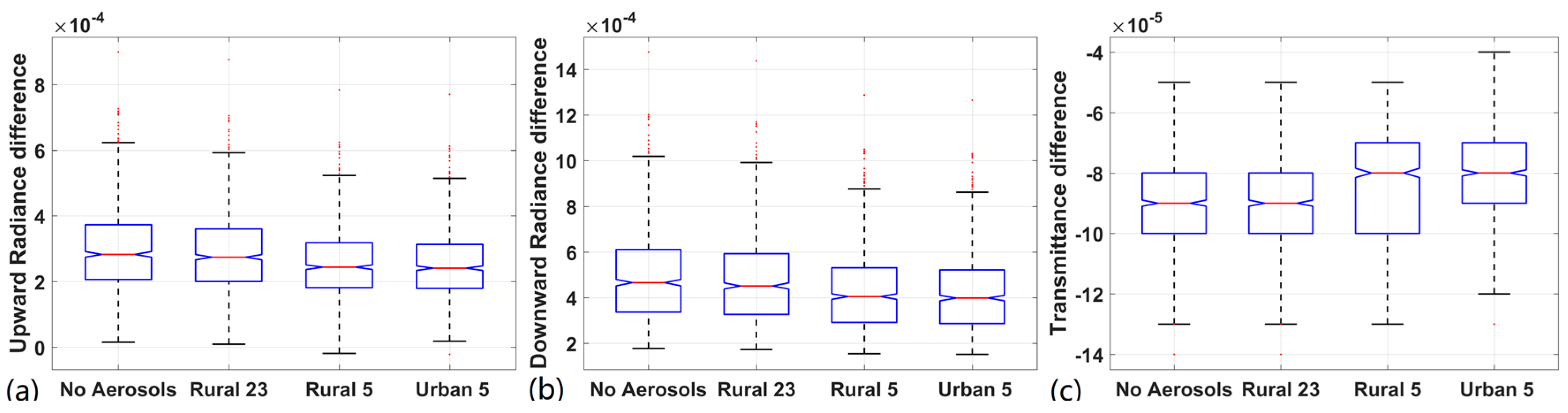
3.1.2. Validation Results for Various Water Vapor Contents
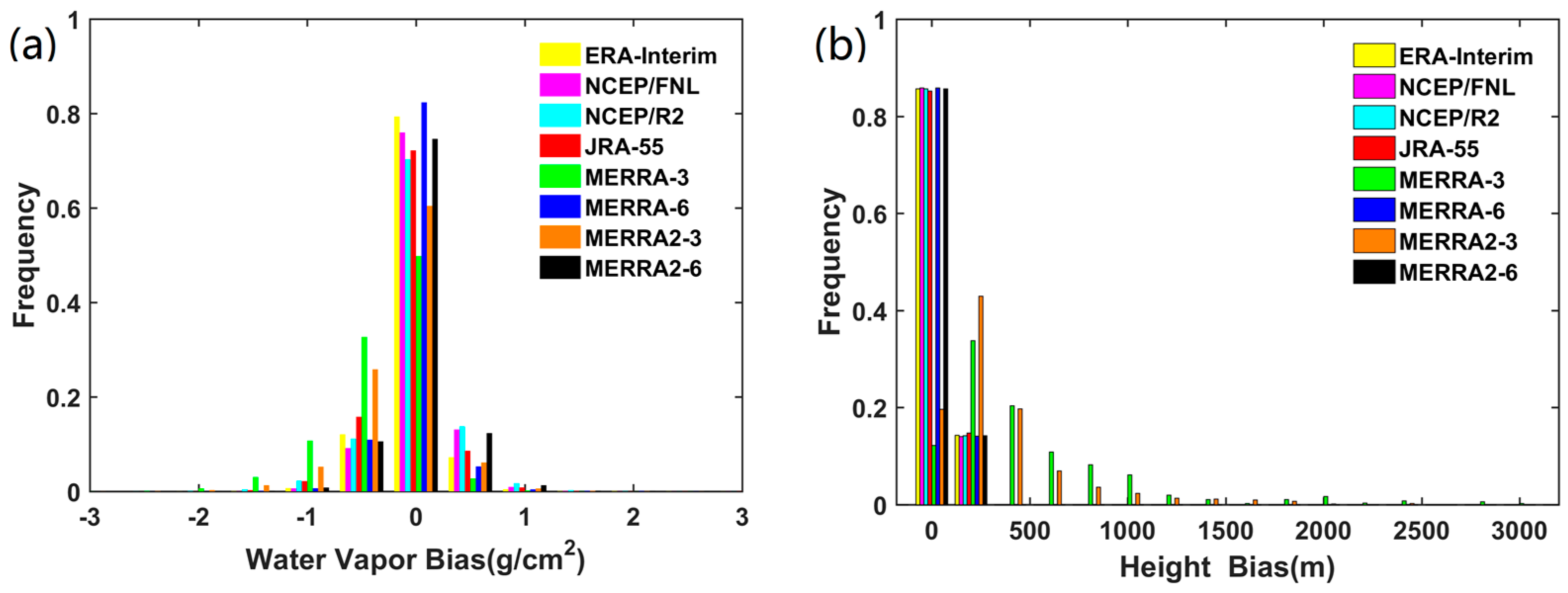
3.1.3. Validation Results for Different Elevations
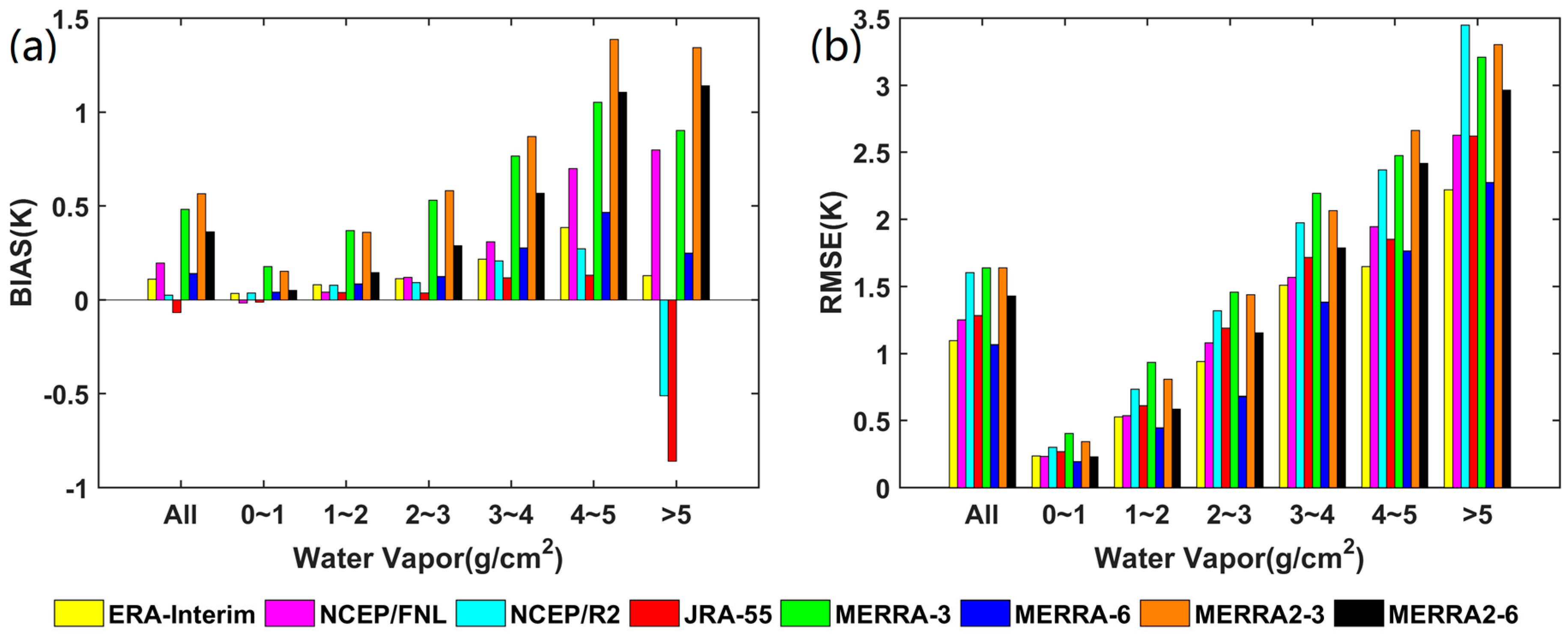
3.2. Application to Landsat 8 LST Retrieval
3.2.1. Simulation Data
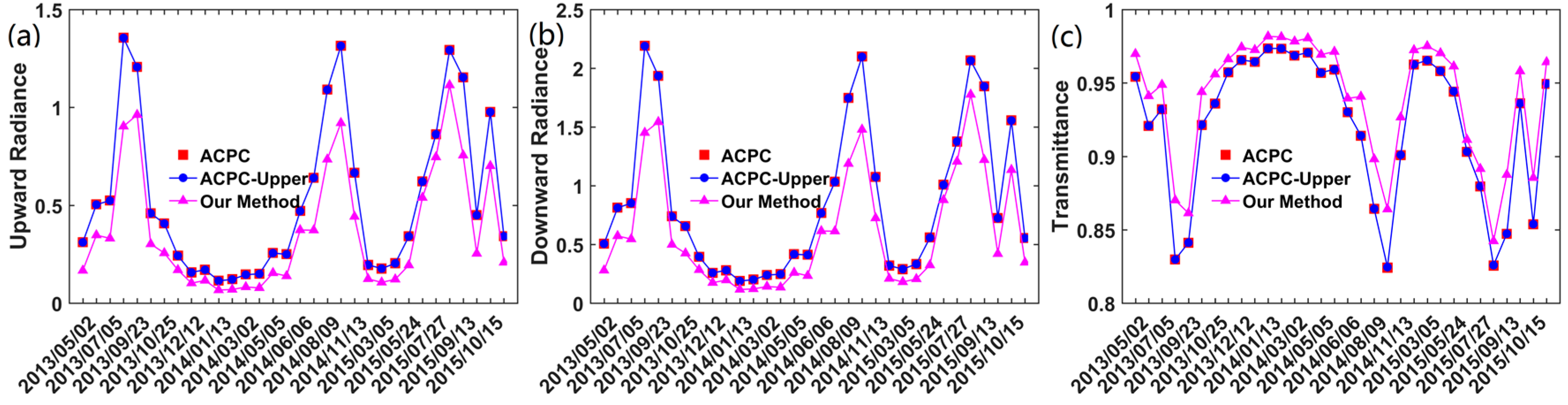
3.2.2. Real Data
4. Discussion
4.1. Intercomparison of Water Vapor Content
4.2. Comparison with Previous Studies
4.3. Effects of Parameter Settings in Radiative Transfer Model
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature form space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Li, Z.; Tang, B.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and prespectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Wang, J.; Li, X. A stepwise refining algorithm of temperature and emissivity separation for hyperspectral thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1588–1597. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Frate, F.D.; Drusch, M.; Jimenez-Munoz, J.C.; Manunta, P.; Regan, A. Review of thermal infrared applications and requirements for future high-resolution sensors. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2963–2972. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at landsat resolution by fusing landsat and modis data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.L. A physics-based algorithm for retrieving land-surface emissivity and temperature from eos/modis data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Meng, X.; Li, H.; Du, Y.; Liu, Q.; Zhu, J.; Sun, L. Retrieving land surface temperature from landsat 8 TIRS data using RTTOV and ASTER GED. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 4302–4305. [Google Scholar]
- Cheng, J.; Ren, H. Land-surface temperature and thermal-infrared emissivity. In Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Liang, S., Li, X., Wang, J., Eds.; Academic Press: Cambridge, MA, USA, 2012; pp. 235–271. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. 2003, 108, 4688. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.J.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (aster) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A. Mono-window algorithm for retrieving land surface temperature from landsat tm data and its application to the Israel-Egype border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Valor, E.; Niclòs, R. Comparison between different sources of atmospheric profiles for land surface temperature retrieval from single channel thermal infrared data. Remote Sens. Environ. 2012, 117, 199–210. [Google Scholar] [CrossRef]
- Li, H.; Liu, Q.; Du, Y.; Jiang, J.; Wang, H. Evaluation of the NCEP and MODIS atmospheric products for single channel land surface temperature retrieval with ground measurements: A case study of hj-1b IRS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1399–1408. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 3014–3016. [Google Scholar]
- Cook, M.; Schott, J.; Mandel, J.; Raqueno, N. Development of an operational calibration methodology for the landsat thermal data archive and initial testing of the atmospheric compensation component of a land surface temperature (lst) product from the archive. Remote Sens. 2014, 6, 11244–11266. [Google Scholar] [CrossRef]
- Tardy, B.; Rivalland, V.; Huc, M.; Hagolle, O.; Marcq, S.; Boulet, G. A software tool for atmospheric correction and surface temperature estimation of landsat infrared thermal data. Remote Sens. 2016, 8, 696. [Google Scholar] [CrossRef]
- Pérez-Planells, L.; García-Santos, V.; Caselles, V. Comparing different profiles to characterize the atmosphere for three modis tir bands. Atmos. Res. 2015, 161–162, 108–115. [Google Scholar] [CrossRef]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. In Validation of a web-based atmospheric correction tool for single thermal band instruments. Earth Obs. Syst. 2005, 5882, 136–142. [Google Scholar]
- Rosas, J.; Houborg, R.; McCabe, M. Sensitivity of landsat 8 surface temperature estimates to atmospheric profile data: A study using modtran in dryland irrigated systems. Remote Sens. 2017, 9, 988. [Google Scholar] [CrossRef]
- Skokovic, D.; Sobrino, J.A.; Jimenez-Munoz, J.C. Vicarious calibration of the landsat 7 thermal infrared band and lst algorithm validation of the etm+ instrument using three global atmospheric profiles. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1804–1811. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, T.; Li, Q.; Frauenfeld, O.W.; Qin, D. Evaluation of ERA-40, NCEP-1, and NCEP-2 reanalysis air temperatures with ground-based measurements in China. J. Geophys. Res. 2008, 113, D15115. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2012, 117, D05102. [Google Scholar] [CrossRef]
- Decker, M.; Brunke, M.A.; Wang, Z.; Sakaguchi, K.; Zeng, X.; Bosilovich, M.G. Evaluation of the reanalysis products from GSFC, NCEP, and ECMWF using flux tower observations. J. Clim. 2012, 25, 1916–1944. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, S.; Wang, G.; Yao, Y.; Jiang, B.; Cheng, J. Evaluation of the reanalysis surface incident shortwave radiation products from NCEP, ECMWF, GSFC, and JMA using satellite and surface observations. Remote Sens. 2016, 8, 225. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K. MERRA: NASA’S modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Global Modeling and Assimilation Office (GMAO). MAI3CPASM: Inst3_3D_Asm_Cp: MERRA 3D IAU State, Meteorology Instantaneous 3-Hourly V5.2.0, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2008. Available online: https://doi.org/10.5067/8D4LU4390C4S (accessed on 31 December 2016).
- Global Modeling and Assimilation Office (GMAO). MAI6NPANA: inst6_3d_ana_Np: MERRA 3D Analyzed State, Meteorology Instantaneous 6-Hourly V5.2.0, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2008. Available online: https://doi.org/10.5067/ADAWH64DCRU0 (accessed on 31 December 2016).
- Global Modeling and Assimilation Office (GMAO). MERRA-2 inst3_3d_asm_Np: 3d,3-Hourly, Instantaneous, Pressure-Level, Assimilation, Assimilated Meteorological Fields V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2015. Available online: https://doi.org/10.5067/QBZ6MG944HW0 (accessed on 31 December 2016).
- Global Modeling and Assimilation Office (GMAO). MERRA-2 inst6_3d_ana_Np: 3d,6-Hourly, Instantaneous, Pressure-Level, Analysis, Analyzed Meteorological Fields V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2015. Available online: https://doi.org/10.5067/A7S6XP56VZWS (accessed on 31 December 2016).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P. The era-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts. ERA-Interim Project. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Dataset. 2009. Available online: https://doi.org/10.5065/D6CR5RD9 (accessed on 31 December 2016).
- National Centers for Environmental Prediction; National Weather Service; NOAA; US Department of commerce. NCEP FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Dataset; 2000. Available online: https://doi.org/10.5065/D6M043C6 (accessed on 31 December 2016).
- National Centers for Environmental Prediction; National Weather Service; NOAA/US Department of Commerce. NCEP/DOE Reanalysis 2 (R2). Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Dataset; 2000. Available online: http://rda.ucar.edu/datasets/ds091.0/ (accessed on 31 December 2016).
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II reanalysis (r-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Japan Meteorological Agency/Japan. Jra-55: Japanese 55-Year Reanalysis, Daily 3-Hourly and 6-Hourly Data. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Dataset; 2013. Available online: https://doi.org/10.5065/D6HH6H41 (accessed on 31 December 2016).
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H. The jra-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Kondratiev, K.Y.A. Radiation in the Atmosphere. In International Geophysics Series; Academic Press: New York, NY, USA, 1969; p. 911. [Google Scholar]
- Ellicott, E.; Vermote, E.; Petitcolin, F.; Hook, S.J. Validation of a new parametric model for atmospheric correction of thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 295–311. [Google Scholar] [CrossRef]
- Garcia-Santos, V.; Valor, E.; Caselles, V.; Mira, M.; Galve, J.M.; Coll, C. Evaluation of different methods to retrieve the hemispherical downwelling irradiance in the thermal infrared region for field measurements. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2155–2165. [Google Scholar] [CrossRef]
- Zhai, P.; Eskridge, R.E. Atmospheric water vapor over china. J. Clim. 1997, 10, 2643–2652. [Google Scholar] [CrossRef]
- Gao, L.; Bernhardt, M.; Schulz, K. Elevation correction of era-interim temperature data in complex terrain. Hydrol. Earth Syst. Sci. 2012, 16, 4661–4673. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (hiwater): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J.; Liang, S. Estimating land surface temperature from feng yun-3c/mersi data using a new land surface emissivity scheme. Remote Sens. 2017, 9, 1247. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Cao, B.; Du, Y.; Xiao, Q.; Liu, Q. Hiwater: Dataset of Thermal Infrared Spectrum Observed by Bomem mr304 in the Middle Reaches of the Heihe River Basin. Available online: http://card.westgis.ac.cn/data/488378f9-543b-496b-8fb7-e209b1dc34f3 (accessed on 17 June 2017).
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term global land surface satellite (glass) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Estimating global land surface broadband thermal-infrared emissivity using advanced very high resolution radiometer optical data. Int. J. Digit. Earth 2013, 6, 34–49. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Estimating the broadband longwave emissivity of global bare soil from the MODIS shortwave albedo product. J. Geophys. Res. Atmos. 2014, 119, 614–634. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS lst products in an arid area of northwest china. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Mattar, C.; Sobrino, J.A.; Julien, Y.; Morales, L. Trends in column integrated water vapour over europe from 1973 to 2003. Int. J. Climatol. 2011, 31, 1749–1757. [Google Scholar] [CrossRef]
- Mattar, C.; Durán-Alarcón, C.; Jiménez-Muñoz, J.C.; Santamaría-Artigas, A.; Olivera-Guerra, L.; Sobrino, J.A. Global atmospheric profiles from reanalysis information (GAPRI): A new database for earth surface temperature retrieval. Int. J. Remote Sens. 2015, 36, 5045–5060. [Google Scholar] [CrossRef]
- Simmons, A.J.; Willett, K.M.; Jones, P.D.; Thorne, P.W.; Dee, D.P. Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Gomis-Cebolla, J.; Jimenez, J.C.; Sobrino, J.A. Lst retrieval algorithm adapted to the amazon evergreen forests using MODIS data. Remote Sens. Environ. 2018, 204, 401–411. [Google Scholar] [CrossRef]
- Windahl, E.; Beurs, K.D. An intercomparison of landsat land surface temperature retrieval methods under variable atmospheric conditions using in situ skin temperature. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 11–27. [Google Scholar] [CrossRef]
- Bento, V.; DaCamara, C.; Trigo, I.; Martins, J.; Duguay-Tetzlaff, A. Improving land surface temperature retrievals over mountainous regions. Remote Sens. 2017, 9, 38. [Google Scholar] [CrossRef]
- Galve, J.M.; Coll, C.; Caselles, V.; Valor, E. An atmospheric radiosounding database for generating land surface temperature algorithms. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1547–1557. [Google Scholar] [CrossRef]
- Chedin, A.; Scott, N.A.; Wahiche, C.; Moulinier, P. The improved initialization inversion method: A high resolution physical method for temperature retrievals from satellites of the tiros-n series. J. Appl. Meteorol. 1985, 24, 128–143. [Google Scholar] [CrossRef]
- Coll, C.; Galve, J.M.; Sanchez, J.M.; Caselles, V. Validation of landsat-7/etm+ thermal-band calibration and atmospheric correction with ground-based measurements. IEEE Trans. Geosci. Remote Sens. 2010, 48, 547–555. [Google Scholar] [CrossRef]
| Data Source | Data Periods | Temporal Resolution | Spatial Resolution | Vertical Resolution | Download Link | Data Availability |
|---|---|---|---|---|---|---|
| MERRA-3 | 1979 to 2016 | 3 hourly | 1.25° × 1.25° | 42 pressure levels | https://disc.sci.gsfc.nasa.gov/ | All data is available for free |
| MERRA-6 | 6 hourly | 1/2° × 2/3° | ||||
| MERRA2-3 | 1980 to Present | 3 hourly | 0.5° × 0.625° | 42 pressure levels | ||
| MERRA2-6 | 6 hourly | |||||
| ERA-Interim | 1979 to Present | 6 hourly | 0.75° × 0.75° | 37 pressure levels | http://apps.ecmwf.int/datasets/ | |
| NCEP/DOE Reanalysis 2 | 1979 to Present | 6 hourly | 2.5° × 2.5° | 17 pressure levels | https://rda.ucar.edu/datasets/ds091.0/ | |
| NCEP/FNL | 1999 to Present | 6 hourly | 1.0° × 1.0° | 21 pressure levels | https://rda.ucar.edu/datasets/ds083.2/ | |
| JRA-55 | 1958 to Present | 6 hourly | 1.25° × 1.25° | 27 pressure levels | http://jra.kishou.go.jp/JRA-55/index_en.html |
| Surface Elevation | 0~0.5 km | 0.5~1 km | 1~2 km | >2 km | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bias | RMSD | R | bias | RMSD | R | bias | RMSD | R | bias | RMSD | R | ||
| Upward Radiance | ERA-Interim | −0.92 | 11.06 | 99.0 | 2.59 | 15.52 | 98.6 | 3.54 | 21.23 | 96.8 | 5.87 | 32.29 | 93.1 |
| NCEP/FNL | −0.46 | 12.45 | 98.8 | 1.72 | 18.10 | 98.1 | 2.36 | 22.41 | 96.6 | 1.47 | 32.29 | 91.0 | |
| NCEP/R2 | 0.46 | 15.67 | 98.0 | 1.72 | 24.14 | 96.7 | 5.90 | 33.03 | 92.4 | 17.61 | 42.57 | 90.1 | |
| JRA-55 | −1.84 | 12.91 | 98.7 | 2.59 | 21.55 | 97.3 | 8.26 | 33.03 | 93.0 | −2.94 | 35.23 | 89.5 | |
| MERRA-3 | −15.67 | 19.82 | 97.1 | −20.69 | 31.03 | 94.5 | −30.67 | 38.92 | 89.4 | −35.23 | 55.78 | 69.1 | |
| MERRA-6 | −1.84 | 10.14 | 99.2 | 0.86 | 15.52 | 98.7 | 3.54 | 20.05 | 97.2 | 4.40 | 33.76 | 90.6 | |
| MERRA2-3 | −8.76 | 17.06 | 97.7 | −14.66 | 28.45 | 95.2 | −18.87 | 31.85 | 92.4 | −27.89 | 55.78 | 71.4 | |
| MERRA2-6 | −0.46 | 12.91 | 98.7 | 3.45 | 18.10 | 98.2 | 4.72 | 22.41 | 96.6 | 8.81 | 32.29 | 92.3 | |
| Downward Radiance | ERA-Interim | −0.79 | 9.78 | 99.1 | 2.43 | 14.81 | 98.6 | 3.55 | 20.15 | 96.9 | 4.93 | 28.39 | 94.2 |
| NCEP/FNL | −0.22 | 10.82 | 99.0 | 1.75 | 17.01 | 98.1 | 2.49 | 20.76 | 96.7 | 1.77 | 29.32 | 92.3 | |
| NCEP/R2 | 0.60 | 13.91 | 98.3 | 2.03 | 22.27 | 96.8 | 5.13 | 31.17 | 92.7 | 16.20 | 38.82 | 91.0 | |
| JRA-55 | −1.96 | 11.32 | 98.9 | 2.71 | 20.18 | 97.3 | 8.08 | 30.87 | 93.3 | −2.42 | 31.74 | 90.7 | |
| MERRA-3 | −14.32 | 17.95 | 97.3 | −20.46 | 28.49 | 94.7 | −30.04 | 37.36 | 89.3 | −34.82 | 52.69 | 71.0 | |
| MERRA-6 | −1.73 | 8.83 | 99.3 | 1.13 | 14.30 | 98.7 | 4.15 | 19.17 | 97.3 | 4.93 | 30.35 | 91.8 | |
| MERRA2-3 | −7.73 | 15.20 | 98.0 | −14.02 | 26.23 | 95.4 | −18.72 | 30.87 | 92.5 | −28.21 | 53.25 | 73.0 | |
| MERRA2-6 | −0.28 | 11.36 | 98.9 | 3.17 | 16.96 | 98.2 | 4.83 | 21.59 | 96.7 | 8.47 | 29.51 | 93.3 | |
| Transmittance | ERA-Interim | 0.14 | 4.19 | 98.9 | −0.48 | 2.87 | 98.5 | −0.57 | 2.61 | 96.8 | −0.56 | 3.13 | 93.8 |
| NCEP/FNL | −0.14 | 4.75 | 98.6 | −0.36 | 3.35 | 97.8 | −0.34 | 2.73 | 96.7 | 0.00 | 3.24 | 91.7 | |
| NCEP/R2 | −0.28 | 5.86 | 97.8 | −0.48 | 4.18 | 96.5 | −0.91 | 4.09 | 92.5 | −1.90 | 4.24 | 90.8 | |
| JRA-55 | 0.70 | 4.88 | 98.5 | −0.48 | 3.71 | 97.2 | −1.14 | 4.09 | 93.1 | 0.33 | 3.46 | 90.7 | |
| MERRA-3 | 5.30 | 6.98 | 97.0 | 3.59 | 5.14 | 94.6 | 3.52 | 4.66 | 90.4 | 3.80 | 5.69 | 70.0 | |
| MERRA-6 | 0.56 | 3.91 | 99.1 | −0.24 | 2.75 | 98.6 | −0.68 | 2.50 | 97.3 | −0.56 | 3.35 | 91.4 | |
| MERRA2-3 | 2.51 | 6.28 | 97.5 | 2.27 | 4.90 | 95.1 | 1.93 | 3.86 | 92.8 | 3.01 | 5.69 | 71.8 | |
| MERRA2-6 | −0.14 | 5.02 | 98.5 | −0.72 | 3.35 | 97.9 | −0.80 | 2.84 | 96.7 | −1.00 | 3.24 | 92.7 | |
| MERRA-3 | MERRA-6 | MERRA2-3 | MERRA2-6 | ERA-Interim | NCEP/FNL | NCEP/R2 | JRA-55 | |
|---|---|---|---|---|---|---|---|---|
| bias (K) | 0.16 | 0.20 | 0.21 | 0.24 | 0.07 | 0.24 | 0.23 | 0.32 |
| STD (K) | 1.96 | 1.97 | 1.96 | 1.96 | 1.93 | 1.98 | 1.97 | 2.02 |
| RMSE (K) | 1.96 | 1.97 | 1.96 | 1.97 | 1.93 | 1.99 | 1.98 | 2.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Cheng, J. Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data. Remote Sens. 2018, 10, 474. https://doi.org/10.3390/rs10030474
Meng X, Cheng J. Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data. Remote Sensing. 2018; 10(3):474. https://doi.org/10.3390/rs10030474
Chicago/Turabian StyleMeng, Xiangchen, and Jie Cheng. 2018. "Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data" Remote Sensing 10, no. 3: 474. https://doi.org/10.3390/rs10030474
APA StyleMeng, X., & Cheng, J. (2018). Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data. Remote Sensing, 10(3), 474. https://doi.org/10.3390/rs10030474